Simulations of Lattice Vibrations in a One-Dimensional Triatomic Network
Abstract
:1. Introduction
2. Formulation
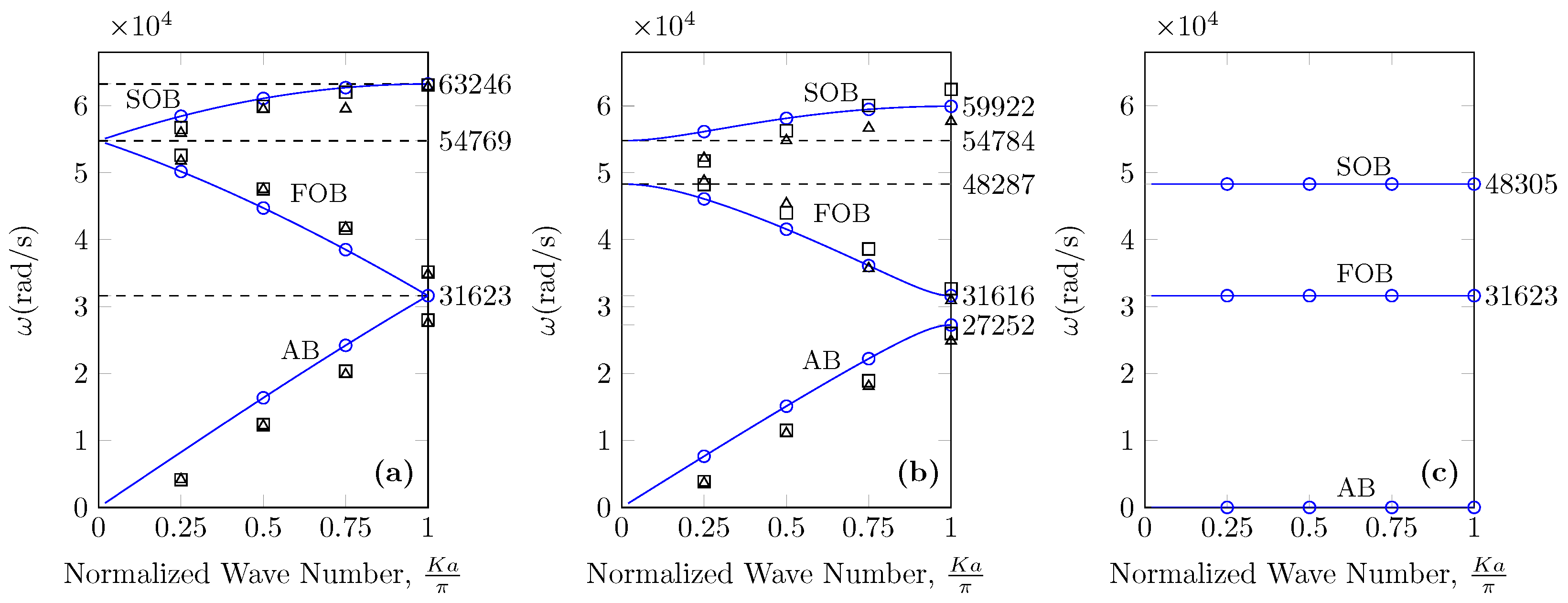
3. The Solution for the Mechanical Model
4. The Electrical Analogue Model
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- The Case of Phonons: Explanatory or Ontological Priority. Available online: http://philsci-archive.pitt.edu/15428/ (accessed on 26 September 2018).
- Rich, C.C.; Frontiera, R.R. Uncovering the Functional Role of Coherent Phonons during the Photoinduced Phase Transition in a Molecular Crystal. J. Phys. Chem. Lett. 2020, 11, 7502–7509. [Google Scholar] [CrossRef] [PubMed]
- Porter, I.J.; Zuerch, M.W.; Baranger, A.M.; Leone, S.R. Coherent Phonons in Antimony: An Undergraduate Physical Chemistry Solid-State Ultrafast Laser Spectroscopy Experiment. J. Chem. Educ. 2023, 100, 342–349. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Chapter 22—Classical Theory of the Harmonic Crystal. In Solid State Physics; Saunders College: Philadelphia, PA, USA, 1976; pp. 430–437. [Google Scholar]
- Kittel, C. Chapter 4—Phonons I. Crystal Vibrations. In Introduction to Solid State Physics, 8th ed.; Wiley: New York, NY, USA, 2005; pp. 89–104. [Google Scholar]
- Runk, R.B.; Stull, J.L.; Anderson, O.L. A Laboratory Linear Analog for Lattice Dynamics. Am. J. Phys. 1963, 31, 915–921. [Google Scholar] [CrossRef]
- Eggert, J.H. One-dimensional lattice dynamics with periodic boundary conditions: An analog demonstration. Am. J. Phys. 1997, 65, 108–116. [Google Scholar] [CrossRef]
- Scott, P.L. Vibrations of a Lattice Including Defects: Laboratory Demonstrations Using Electrical Analogs. Am. J. Phys. 1972, 40, 260–266. [Google Scholar] [CrossRef]
- Vega, D.; Vera, S.; Juan, A. A computer-aided modelling analogue for lattice dynamics. Eur. J. Phys. 1997, 18, 398–403. [Google Scholar] [CrossRef]
- Moy, B.T.; Koch, J.; Garg, A. Low-frequency dispersion of phonons in one-dimensional chains. Eur. J. Phys. 2020, 41, 035801. [Google Scholar] [CrossRef]
- Yannacone, S.; Sayala, K.D.; Freindorf, M.; Tsarevsky, N.V.; Kraka, E. Vibrational Analysis of Benziodoxoles and Benziodazolotetrazoles. Physchem 2021, 1, 45–68. [Google Scholar] [CrossRef]
- Parker, S.F. Assignment of the Vibrational Spectra of Diiron Nonacarbonyl, Fe2(CO)9. Physchem 2022, 2, 108–115. [Google Scholar] [CrossRef]
- El Boudouti, E.H.; Akjouj, A.; Dobrzynski, L.; Djafari-Rouhani, B.; Al-Wahsh, H.; Lévêque, G.; Pennec, Y. Chapter 2—Phonon Monomode Circuits. In Phononics, 1st ed.; Interface Transmission Tutorial Book Series; Elsevier Inc.: Amsterdam, The Netherlands, 2018; pp. 19–78. [Google Scholar]
- Van Haeverbeke, M.; Stock, M.; De Baets, B. Equivalent Electrical Circuits and Their Use Across Electrochemical Impedance Spectroscopy Application Domains. IEEE Access 2022, 10, 51363–51379. [Google Scholar] [CrossRef]
- Ding, G.; Sun, T.; Wang, X. Ideal nodal-net, nodal-chain, and nodal-cage phonons in some realistic materials. Phys. Chem. Chem. Phys. 2022, 24, 11175–11182. [Google Scholar] [CrossRef] [PubMed]
- Kesavasamy, K.; Krishnamurthy, N. Lattice vibrations in a linear triatomic chain. Am. J. Phys. 1978, 46, 815–819. [Google Scholar] [CrossRef]
- Bickham, S.R.; Kiselev, S.A.; Sievers, A.J. Stationary and moving intrinsic localized modes in one-dimensional monatomic lattices with cubic and quartic anharmonicity. Phys. Rev. B 1993, 47, 14206–14211. [Google Scholar] [CrossRef] [PubMed]
- Kiselev, S.A.; Bickham, S.R.; Sievers, A.J. Anharmonic gap mode in a one-dimensional diatomic lattice with nearest-neighbor Born-Mayer-Coulomb potentials and its interaction with a mass-defect impurity. Phys. Rev. B 1994, 50, 9135–9152. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Lim, K.-M.; Zhang, F.; Jiang, J. Dual-tuning mechanism for elastic wave transmission in a triatomic lattice with string stiffening. Wave Motion 2022, 112, 102951. [Google Scholar] [CrossRef]
- Simon, S.H. Part III—Toy Models of Solids in One Dimension. In The Oxford Solid State Basics; Oxford University Press: Oxford, UK, 2013; pp. 69–110. [Google Scholar]
- Wituła, R.; Słota, D. Cardano’s formula, square roots, Chebyshev polynomials and radicals. Math. Anal. Appl. 2010, 363, 639–647. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A Fresh Approach to Numerical Computing. SIAM Rev. 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Eaton, J.W. GNU Octave Manual. GNU. Available online: https://docs.octave.org/latest/ (accessed on 7 November 2023).
- Brinson, M.E.; Kuznetsov, V. A new approach to compact semiconductor device modelling with Qucs Verilog—A analogue module synthesis. Int. J. Numer. Model. Electron. Netw. 2016, 29, 1070–1088. [Google Scholar] [CrossRef]
- Feynman, R.P.; Leighton, R.; Sands, M. Chapter 25—Linear Systems and Review. In The Feynman Lectures of Physics I, 6th ed.; Addison-Wesley: Boston, MA, USA, 1977; pp. 25–34. [Google Scholar]
- Analogous Electrical and Mechanical Systems. Available online: https://lpsa.swarthmore.edu/Analogs/ElectricalMechanicalAnalogs.html (accessed on 10 October 2023).
- Pozar, D.M. Chapter 4—Microwave Network Analysis. In Microwave Engineering, 4th ed.; John Wiley Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 190–211. [Google Scholar]
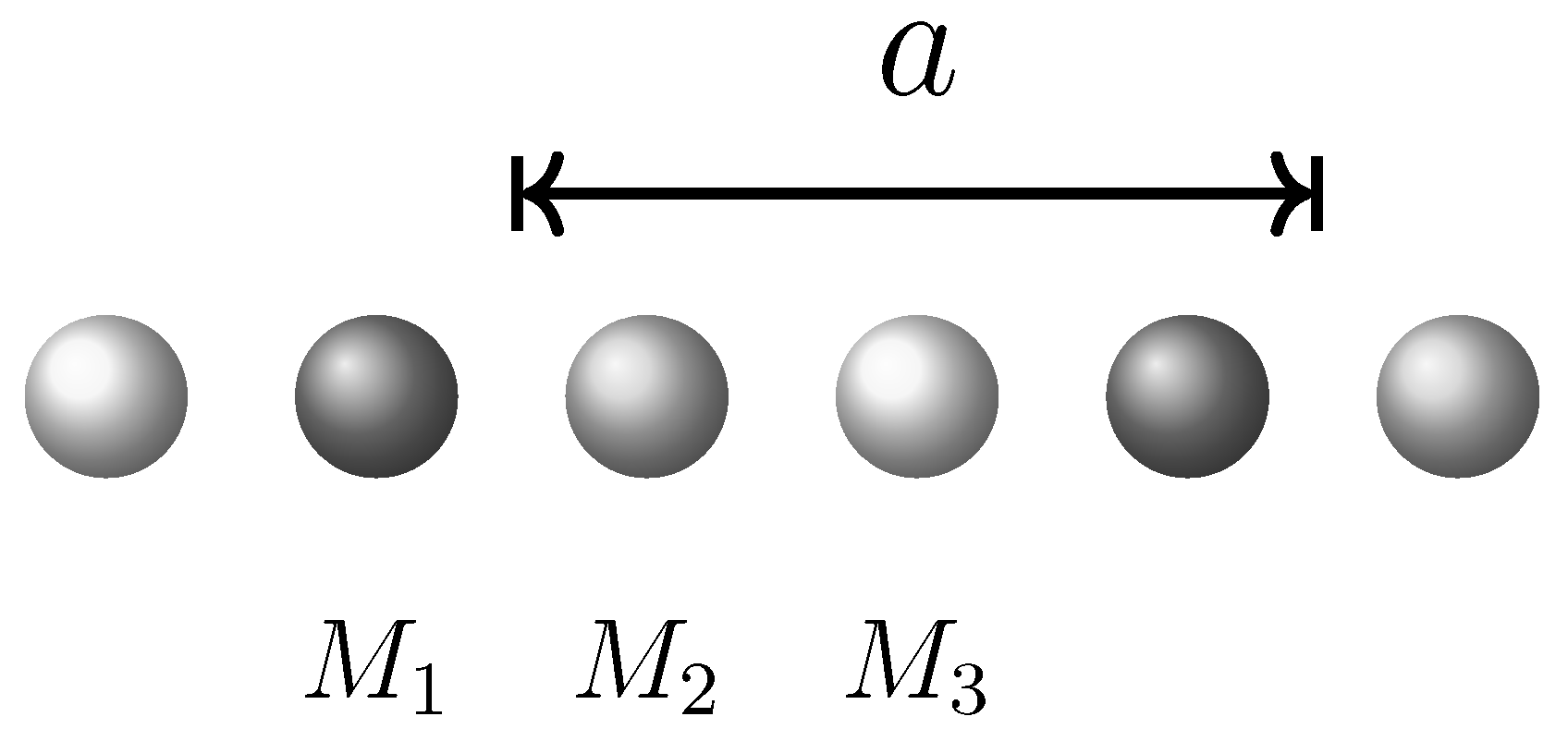
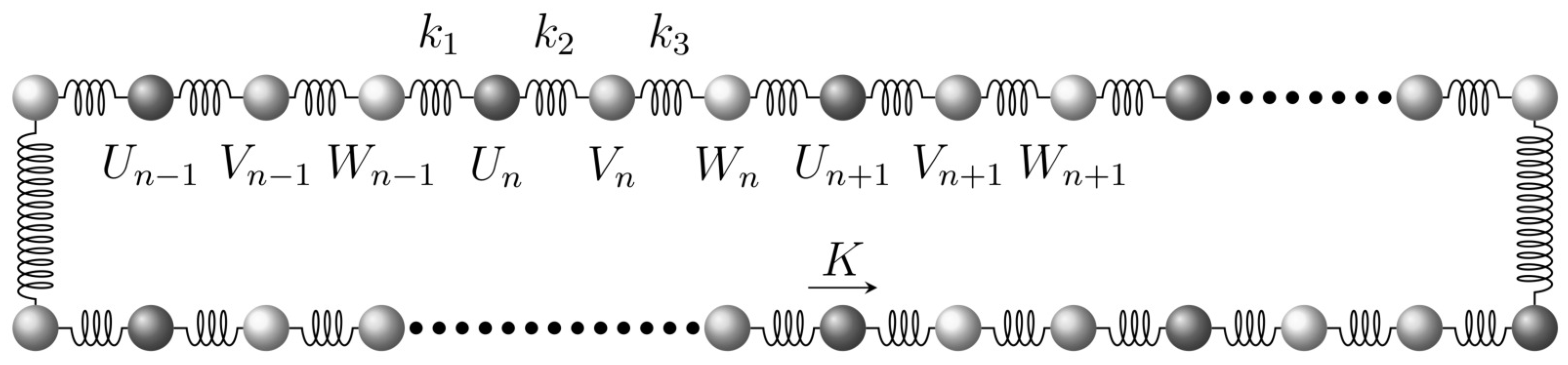

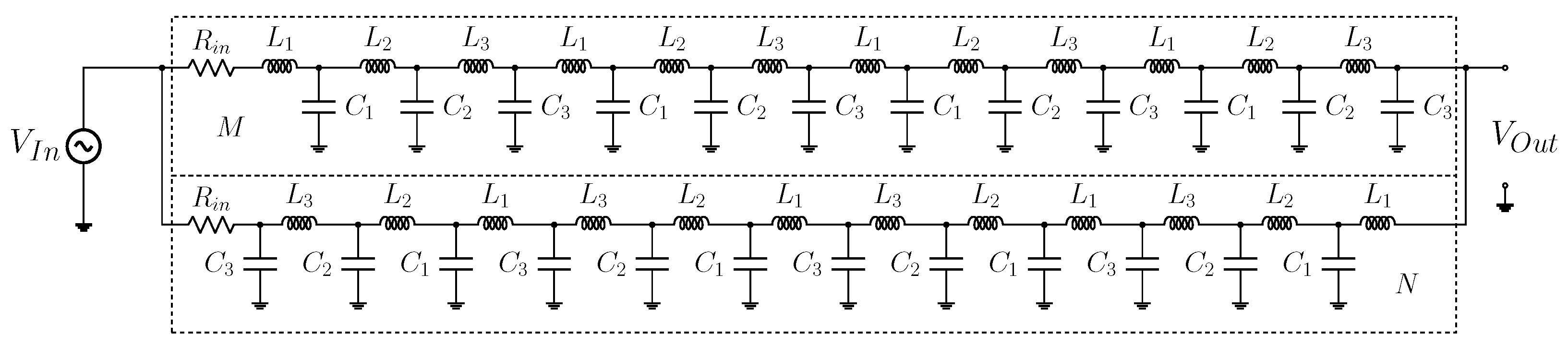

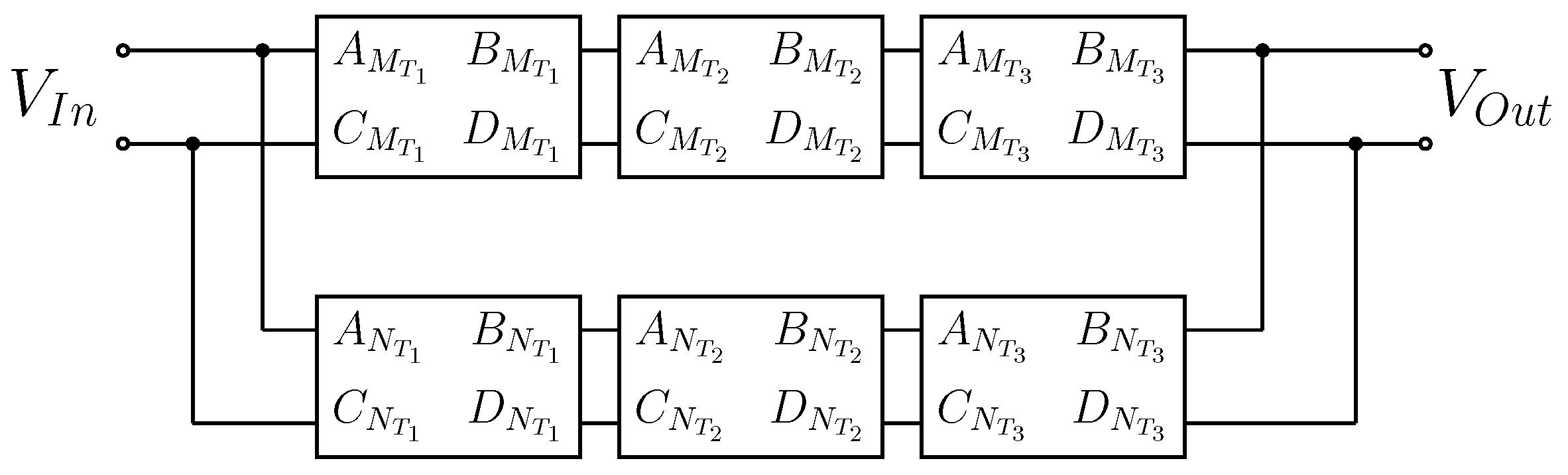
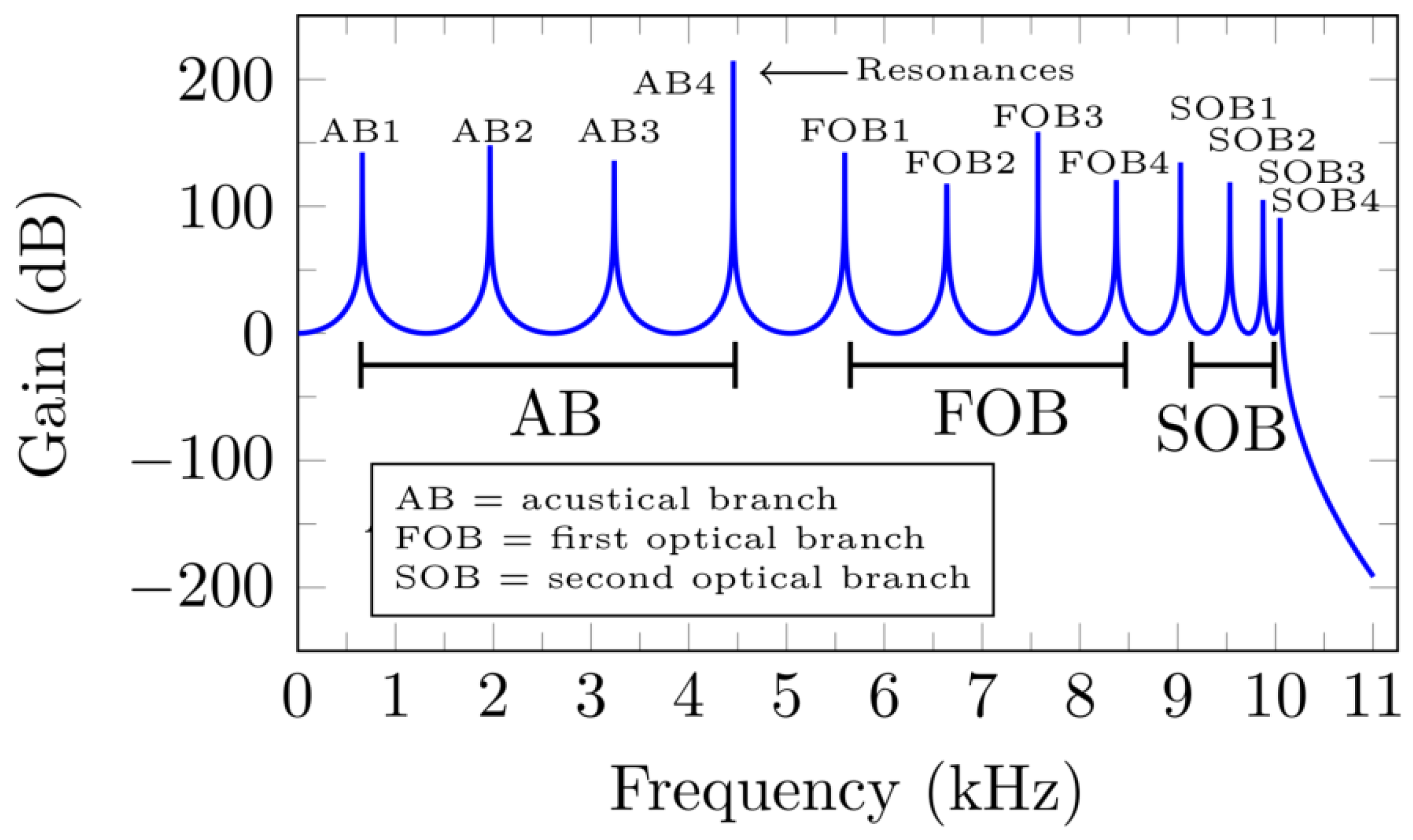
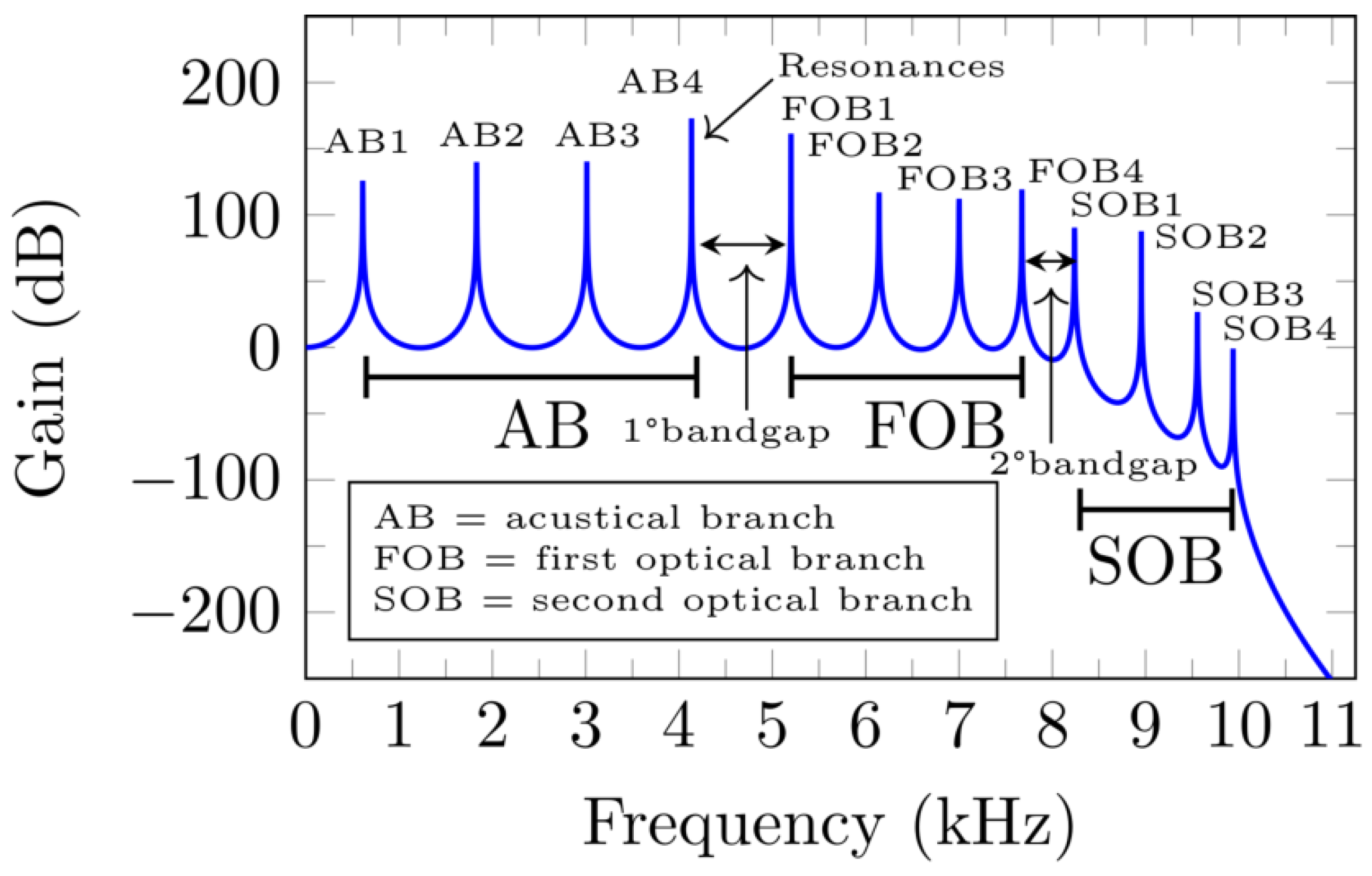
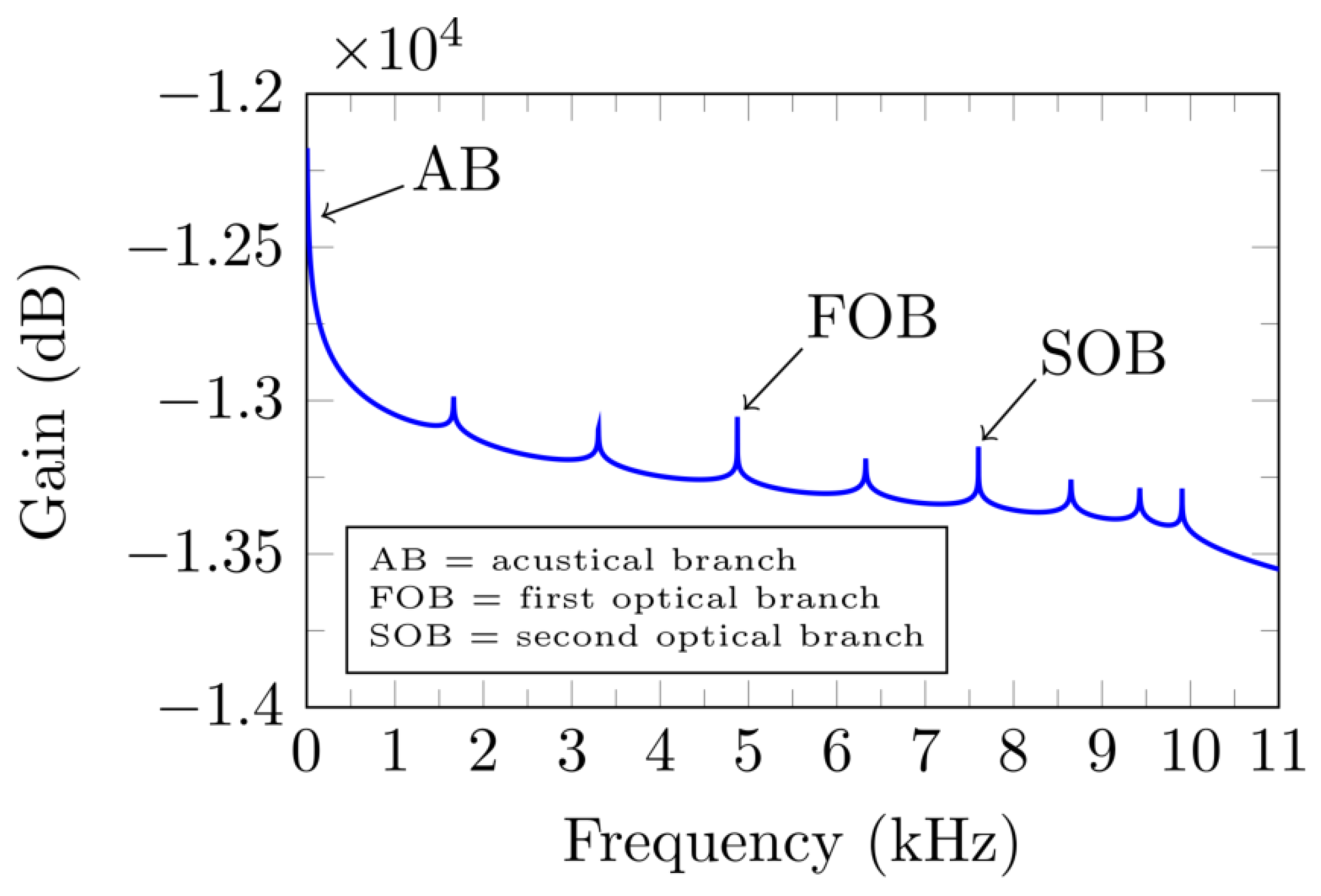
| Case I | Case II | Case III | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (N/m) | (Kg) | (F) | (H) | (N/m) | (Kg) | (F) | (H) | (N/m) | (Kg) | (F) | (H) | |
| i | ||||||||||||
| 1 | ||||||||||||
| 2 | 0 | 0 | ||||||||||
| 3 | ||||||||||||
| Mechanical Model | Electrical Analog | Direct Simulation | Ref. [16] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| I | II | III | I | II | III | I | II | III | I | II | III |
| 1.313 | 1.215 | 0 | 0.660 | 0.610 | – | 0.661 | 0.601 | 0.741 | – | – | – |
| 2.605 | 2.406 | 0 | 1.966 | 1.830 | 1.664 | 1.940 | 1.82 | 2.180 | – | – | – |
| 3.852 | 3.536 | 0 | 3.238 | 3.012 | 3.300 | 3.160 | 2.98 | 3.480 | – | – | – |
| 5.032 | 4.337 | 0 | 4.454 | 4.134 | 4.874 | 4.380 | 4.04 | 4.360 | – | 4.337 | 0 |
| 5.032 | 5.032 | 5.032 | 5.594 | 5.200 | – | 5.540 | 5.30 | – | 5.032 | 5.032 | – |
| 6.127 | 5.747 | 5.032 | 6.638 | 6.144 | – | 6.640 | 6.18 | – | – | – | – |
| 7.117 | 6.613 | 5.032 | 7.570 | 7.002 | – | 7.560 | 7.00 | – | – | – | – |
| 7.985 | 7.334 | 5.032 | 8.372 | 7.674 | 6.326 | 8.240 | 7.58 | 7.200 | 8.717 | 7.687 | 5.032 |
| 9.299 | 8.934 | 7.687 | 9.030 | 8.238 | 7.602 | 8.900 | 8.78 | 7.680 | – | 8.717 | 7.687 |
| 9.722 | 9.250 | 7.687 | 9.534 | 8.954 | 8.650 | 9.460 | 9.10 | 8.140 | – | – | – |
| 9.979 | 9.463 | 7.687 | 9.874 | 9.556 | 9.428 | 9.480 | 9.38 | 8.380 | – | – | – |
| 10.065 | 9.536 | 7.687 | 10.046 | 9.938 | 9.906 | 10.00 | 9.52 | 8.400 | 10.065 | 9.536 | – |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreyra, R.A.; Juan, A. Simulations of Lattice Vibrations in a One-Dimensional Triatomic Network. Physchem 2023, 3, 440-450. https://doi.org/10.3390/physchem3040028
Ferreyra RA, Juan A. Simulations of Lattice Vibrations in a One-Dimensional Triatomic Network. Physchem. 2023; 3(4):440-450. https://doi.org/10.3390/physchem3040028
Chicago/Turabian StyleFerreyra, Romualdo Alejandro, and Alfredo Juan. 2023. "Simulations of Lattice Vibrations in a One-Dimensional Triatomic Network" Physchem 3, no. 4: 440-450. https://doi.org/10.3390/physchem3040028
APA StyleFerreyra, R. A., & Juan, A. (2023). Simulations of Lattice Vibrations in a One-Dimensional Triatomic Network. Physchem, 3(4), 440-450. https://doi.org/10.3390/physchem3040028





