2. Electronic Terms of Dioxygen and Nitric Oxide
The molecular term symbol of the ground and some excited state of these diatomic radicals are determined in a short presentation by the total electronic spin angular momentum (S), by its projection S
z on the molecular
z-axis (Σ) [
2], by the orbital angular momentum z- projection (Λ), as well as their sum—total electronic momentum projection Ω = S
z + Λ
[2,3,4]. The quantum numbers for the observed values of projections of these momenta on the internuclear axis of a diatomic molecule are denoted as Σ, Ω, and Λ, and Ω = |Λ + Σ|. According to a common convention [
2,
3,
4,
5,
6], the states with Λ = 0, 1, 2, are denoted by Σ, Π, Δ symbols. (One should distinguish notations of spin projection and the case of Λ = 0, which are denoted by the same symbol Σ).
The quantum numbers, which determine the measured absolute value of the total spin and its projection on the
z-axis, are fixed in the quantum theory of angular momentum as eigenvalues of the corresponding square
S2 operator and the
Sz operator [
5]:
where
h-bar is
as usual and
h is the Planck constant.
For the singlet
1O
2 (
1Δ
g) and triplet
3O
2 (
3Σ
g−) state dioxygen, the spin quantum number is equal to S = 0 and S = 1, respectively. In the last case, the spin projection quantum number has values Σ = 0, ±1. For the zero S singlet state the projection is naturally absent (Σ = 0). In the case of the ground state
2NO radical S = 1/2, Σ = ±1/2 and two Ω values are possible (3/2 and ½). For analysis of ESR and optical spectra of diatomic molecules, one has to consider rotational nuclear angular momentum R [
2,
3,
4]. R is an operator related to the rotation of nuclei as a whole. Because of the axial symmetry of the field in diatomic molecules, only the orbital angular momentum projection of electrons on the
z-axis can be observed as a constant of motion [
2]. For the π
2 open shell of dioxygen, there are two possibilities for the electronic wave functions Ψ of states with Λ = 0; function Ψ can either change sign upon reflection in any plane, which contains internuclear axis z (Σ
− state), or not change sign (Σ
+ state). These symmetry restrictions are connected with a general property of all electrons in respect to their permutation [
4,
5]. For the triplet state (
3Σ
−), the spin part of the wave function is symmetric, but the spatial part is asymmetric in respect to permutation; this leads to a sign change upon reflection in a molecular plane since π
+ transforms to π
− [
4].
Terms may include one or two additional notions related to operations of symmetry of a molecule, namely g/u for homonuclear diatomic species, like O
2, with the inversion symmetry center or +/− in case Λ = 0. We will present the terms including these notations like it is presented in the literature [
2,
3,
4,
5,
6]. The total angular momentum is denoted as
J = Λ + R + S. The two additional notations are unimportant in the context of this mini-review. The contribution of nuclear momentum I and rotational momentum R into
J are mostly omitted here since main isotope
16O has no nuclear spin and for the
1O
2 (
1Δ
g) molecule, we will consider the ESR spectrum for the lowest rotational state R = 0. Detailed information on the terms of diatomic molecules can be found in ref. [
2,
3,
4,
5,
6].
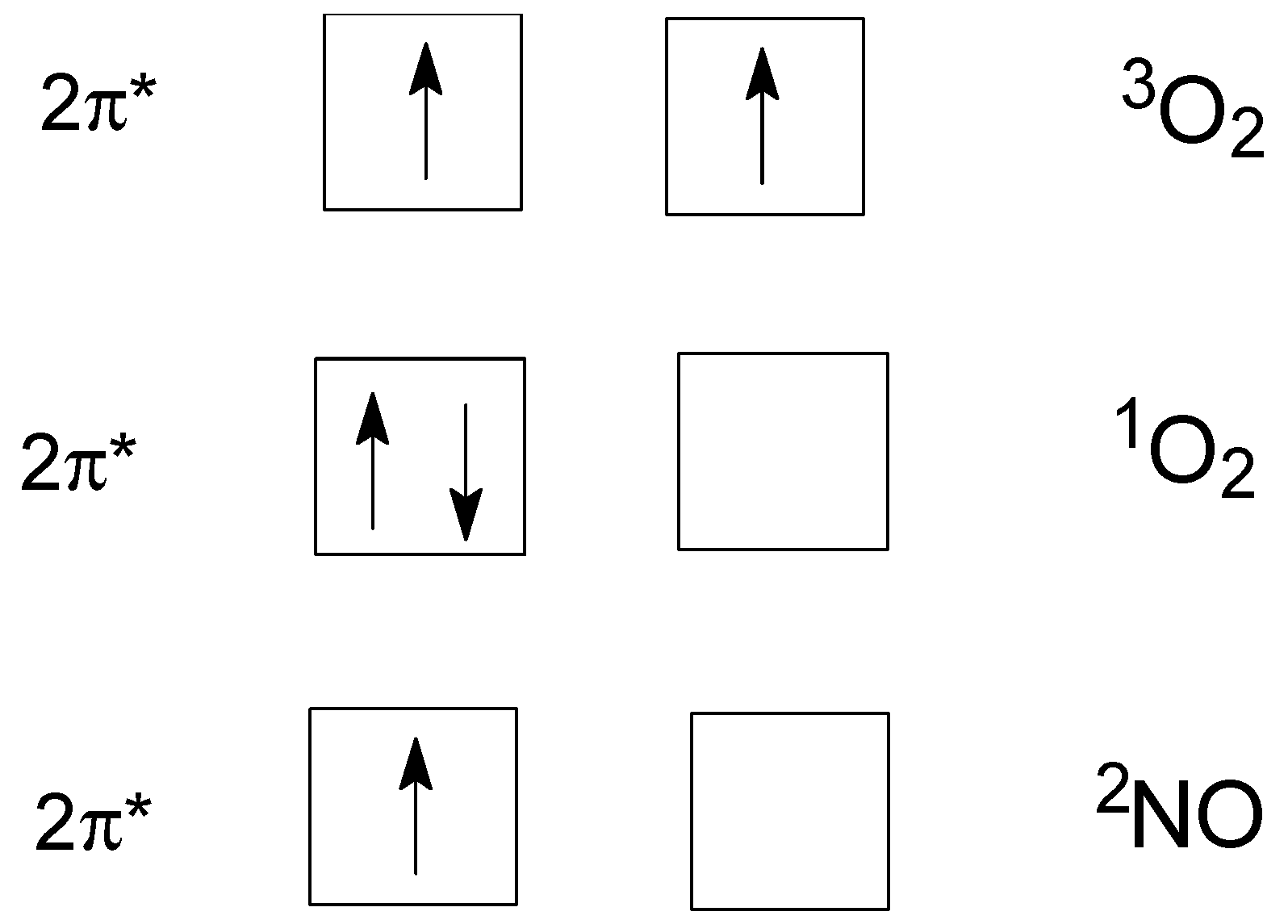
The terms are presented as 2S+1ΛΩ. Spin S of one electron is ½ and Ms = ± ½. Here, MS is a spin component along the field. The total spin quantum number S is used in the superscript of a term to denote the term multiplicity m = 2S + 1. Thus 1ΛΩ, 2ΛΩ, and 3ΛΩ correspond to a singlet state, doublet state (a radical), and a triplet state of a diatomic molecule, respectively. We deal with two molecules that have the highest occupied 2π* molecular orbital–antibonding π orbitals. The individual electron on two degenerate π*—orbitals has a projection of orbital momentum as quantum number λ = ±1. When we deal with two degenerateπ- orbitals, it is necessary to ascribe λ1 = +1 to an electron on one orbital and λ2 = −1 to another. Projection of a total orbital momentum for two electrons in the open 2π* shell Λ = λ1 + λ2 is denoted Σ, Π, and Δ for Λ = 0, 1, and 2, respectively.
ESR studies of dioxygen and nitrous oxide have been performed by numerous researchers [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18], but for their practical application in analytical purposes, we need to generalize common physical backgrounds and clarify some details that have not been considered yet.
The terms of heteronuclear diatomic radicals, 2ΠΩ (like the ground state of 2NO molecule) has the index Ω = Λ + Sz. Typical values of Ω are ½, 3/2. Transitions between different states in ESR spectra are allowed at ΔMJ = ±1. Here, MJ is a quantum number of the component of J, which is a total angular momentum, see above. MJ = ±1/2, ±3/2. We simplify the situation by ignoring molecular rotation in this case, which is acceptable for our goal.
Scheme 1 below presents an occupation of the highest molecular orbitals by electrons in these two species:
Table 1 below presents terms of diatomic molecules of interest and existence or a lack of corresponding EPR spectra in the gas and in the liquid phase. It is instructive to compare EPR data on the same species in the gas and in the liquid phase, see
Table 1.
We discuss the individual terms of
Table 1 below.
3. Dioxygen
Molecular oxygen (dioxygen) possesses a ground triplet state
3O
2 (
3Σ
g−). Triplet oxygen
3O
2 demonstrates a very broad (width of ca. 1 T [
7]) weak ESR spectrum in the liquid phase at low temperatures. Orbital angular momentum has a large contribution to the magnetism of molecules and in the case
3O
2 (
3Σ
g−) Λ = 0. Additionally, molecular rotations are quenched by the solvent. ESR of
3O
2 is not observed in liquid solutions at room temperature.
Molecules in the gas phase undergo free rotation. At the same time, they have quantized energy levels [
2]. Rotation of a molecule leads to the appearance of local magnetic fields, and these fields interact with an electronic spin magnetic moment in triplet state
3O
2 (
3Σ
g−) and with orbital magnetism in the excited singlet
1O
2 (
1Δg) oxygen. The rotation levels make an infinite ladder of spin-energy levels and rotational levels are inseparably interlaced with magnetic levels [
2]. This way, the ESR spectrum of
3O
2 consists of a huge number of components (lines). An intensive ESR spectrum is observed in the gas phase under low pressure, see
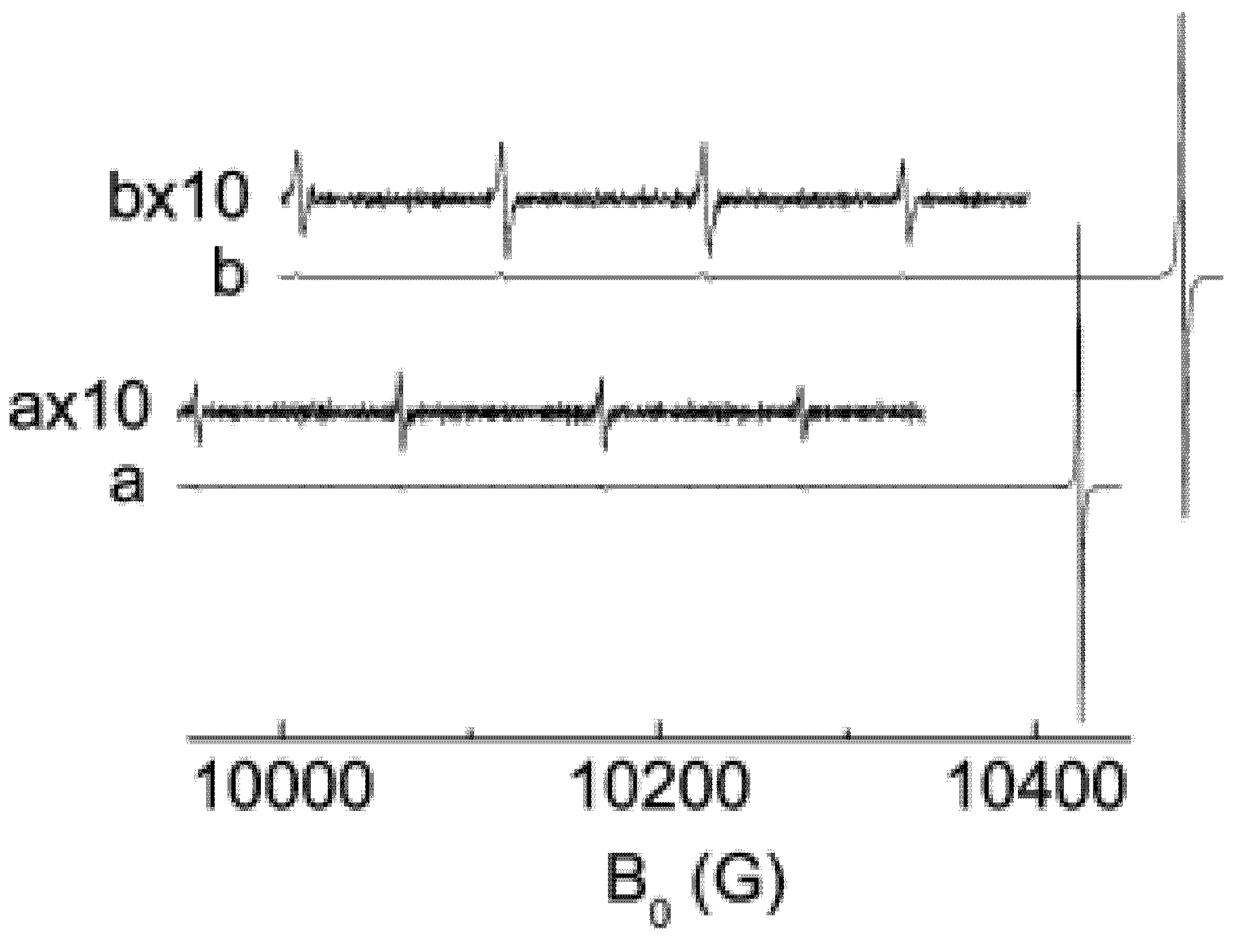
Figure 1:
The nearest in energy to the ground triple 3O
2 (
3Σ
g−) dioxygen is the electronically-excited state
1O
2 (a
1Δg); it provides another ESR spectrum (see
Scheme 1 and
Table 1). Singlet dioxygen (
1Δg) is 94 kJ/mol above the triplet ground state. There are many ways to generate labile singlet dioxygen [
9,
10,
12,
13,
14,
17,
19]. Singlet O
2 (
1Δg) molecule does not have spin (S = 0) but has an electronic orbital angular momentum Λ = 2 [
9,
10,
11,
12,
13,
14,
15,
16,
17]. Together with the rotational angular momentum (R), they form a total angular momentum,
J = Λ + R; it is quantized along the magnetic field axis with quantum number M
J. The O
2 (
1Δg) molecule belongs to the classical Hund’s case (a) when Λ is quantized along the molecular
z-axis [
2]. Values Λ and
J in this case are good quantum numbers [
3]. Thus, for the free rotating O
2 (
1Δg) molecule in the gas phase, the total momentum
J provides an ESR spectrum [
9,
13]. The Λ-doubling in the O
2 (
1Δg) molecule is expected to be very small [
4,
18], in fact, neither we nor other authors [
19] could resolve the Λ—doubling splitting in the singlet oxygen ESR spectrum. Zeeman energy of O
2 (
1Δg) in an external magnetic field
H can be described by the following equation for magnetic field interaction with molecular magnetic moment [
13,
20]:
The spin angular momentum projection is absent (Σ = 0) for the singlet oxygen and we have relation:
. For the lowest rotational level (
J = Λ = 2) we have
gJ = 2
gL/3 [
13]. The electronic magnetic moment along molecular axis
z is equal to 2
gLμB, where
μB =
is the Bohr magneton and
gL is the electronic orbital angular momentum g-factor, which is close to unity [
13]; small corrections to g-factor of the singlet O
2 (
1Δg) state are important for the EPR spectrum and are considered below.
Since
and
, all allowed transitions with
in the ESR spectrum of
1O
2 (
1Δg) dioxygen should have the same transition energy of about
. Only one transition 0 → 1 is close to the 0.667
resonance [
20], but all others are shifted [
9].
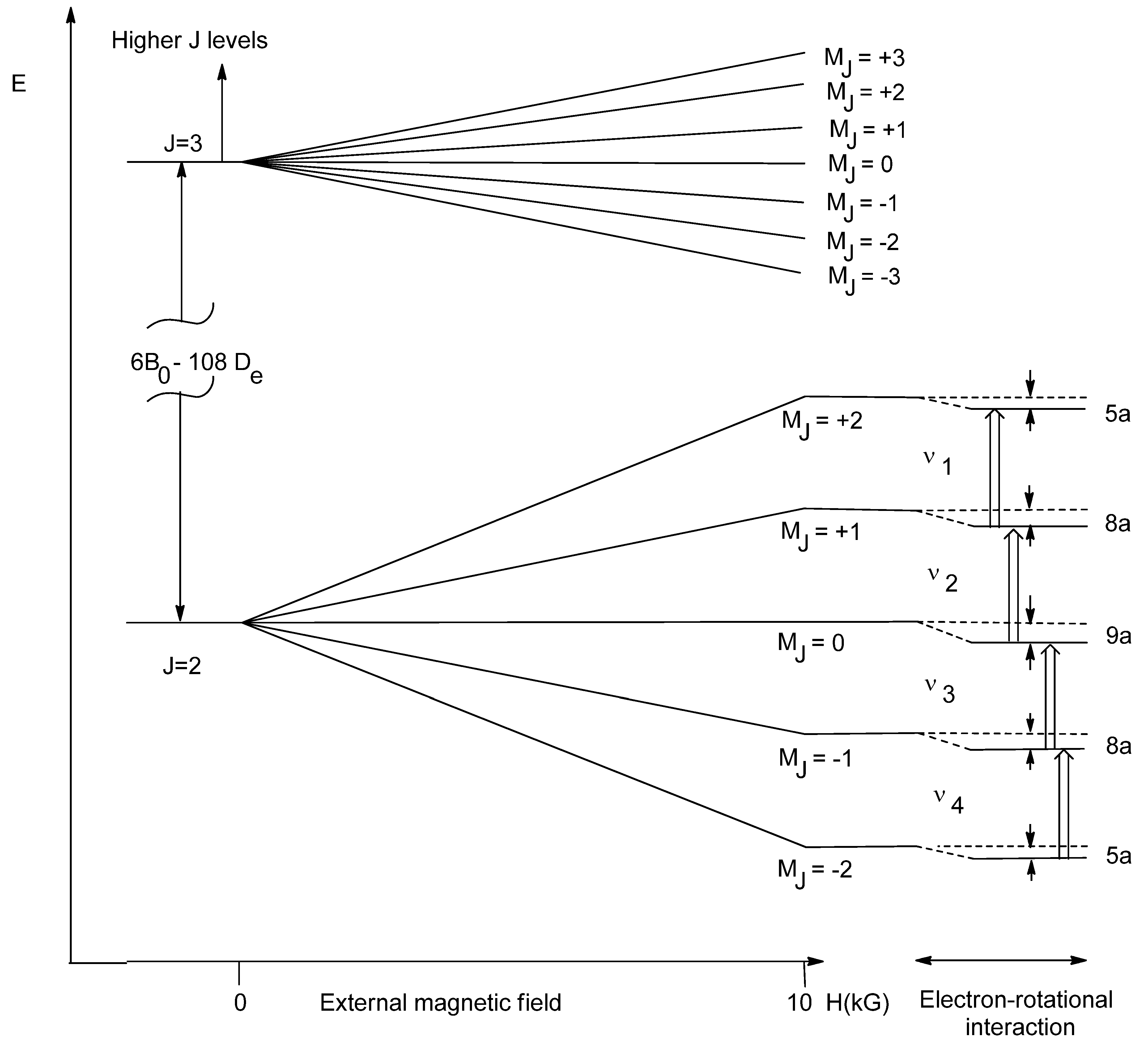
In the absence of electron-rotational interaction, all four EPR transitions in the ground state (
J = Λ = 2) of the singlet (
1Δg) dioxygen would be observed at the same field about
H ≈ 10 kG with the frequency (9624.92 MHz) of X-band ESR spectrum. Transition energies
hνi in the EPR spectrum (
Figure 1) are different (at a fixed field
H) because of perturbations from the upper rotational
J = 3 levels (see
Figure 2 below). They are equal to 0.65597 for (−2 → −1) transition, 0.66264 (−1 → 0), 0.66954 (0 → +1) and 0.67667 (+1 → +2) in the units
[
9,
13], see
Table 2 below. Thus, we have almost symmetrically split quartet EPR lines (
Figure 1). At the fixed microwave frequency
ν = 9.62492 GHz, the ESR X-band resonance signals are obtained at the magnetic field strength of about 10 kG, respectively [
9]. The account of interaction with the first excited rotational level R = 1(
J = 3) provides additional corrections to M
J sublevels of the ground rotational state
J = 2 in the second-order of perturbation theory; the results are presented in
Figure 2 below [
13].
One can see from
Table 2 and
Figure 2 that the splitting between nearest transition is equal to 2
a, which depends on the ratio of magnetic field
H2 and equilibrium rotational constant
Be of
1O
2 (
1Δ
g). Here
.
This prediction agrees well with the observed quartet splitting in ESR spectra of singlet dioxygen in the gas phase [
9,
13,
20].
There is no EPR spectrum of
1O
2 (
1Δ
g) in the liquid phase since the local electric fields of solvent molecules quench the orbital angular momentum [
2]. At any oxygen collision with a solvent molecule, the local electric fields remove the degeneracy of the (
1Δ
g) state; it splits into two close-lying sublevels which position depends on the particular geometry of any new collision and orbital angular momentum Λ is not anymore a good quantum number. (Non-zero orbital angular momentum can exist only in degenerate states) [
21]. Thus, the simple Zeeman energy picture, Equation (1), is completely distorted and rotational coherence is quenched.
High accuracy of ESR measurement in the gas phase provides a good agreement between perturbation theory and the observed quartet splitting in the ground rotational level
J = 2 of singlet oxygen [
13,
20]. However, this accuracy leads to additional problems with exact values of
-factor.
Rotational
-factor contains small contributions from relativistic mass-velocity dependence [
20] and non-diagonal orbital momenta terms responsible for mixing of different states induced by the shift operator L
+ and L
-. Similar contributions in combination with spin-orbit coupling (SOC) perturbation are responsible for the anisotropy of electronic spin g-factor; they are rather important for the ground triplet state of dioxygen
3O
2 (
3Σ
g−) and provide ESR signal deviation from the free-electron value (g
e = 2.0023). This deviation is big for the perpendicular component of g-tensor (as much as g
┴ = 2.0052 [
3,
22]), while g
|| is close to g
e value [
23,
24]. These parameters were first obtained from the ESR spectrum of solid oxygen [
3] and these parameters are supported by ab initio self-consistent field (SCF) calculations [
22,
24]. The electronic spin g-factor is connected with the spin-rotational coupling constant (γ) approximation is well developed for the ground and excited triplet states
3Σ
− of dioxygen [
24]. However, for the singlet O
2 (
1Δ
g) molecule, the rotational g-factor theory contains some discrepancies which will be shortly discussed [
13,
20].
4. A Short Introduction to the Theory of Rotational g-Factor for the Singlet O2 (1Δg) Molecule
The rotational
-factor includes the nuclear part
and the orbital part
[
25]. The nuclear rotational g-factor is simply determined by atomic mass (
MA) and charge (
ZA); it corresponds to the moment for bare nuclei of two atoms A and B [
4]. It does not contribute to the energy of the lowest rotational level K = 0 of the O
2 (
1Δ
g) molecule.
The orbital part in the first order of perturbation theory is equal [
25]:
where
are a mass of proton, electron and reduced mass of dioxygen,
R is the inter-nuclear distance,
is the perpendicular component of the orbital angular momentum operator for the i-th electron,
are eigenfunction and energy of the n-th singlet state of O
2 [
24,
25,
26]. The main contributions to the sum (4) provide
states [
24]. The lowest
state produces the largest contribution (−3.143
) at the equilibrium R
e distance [
25]. Complete active space (CAS) linear response calculations [
24] predict a value of −3.896
, which is in good agreement with the experimental estimation of (−3.957 ± 0.025) × 10
−4 obtained in ref. [
20].
The electronic rotational
gre-factor represents the magnetic moment produced by the rotation of “electrons following the nuclei” during molecular rotation [
13]. Miller [
20] has compared this electronic rotational
gre-factor for the
1O
2 (
1Δ
g) state with
gre-value for the ground 3O
2 (
3Σ
g−) states [(−3.98 ± 0.12) × 10
−4], also extracted from the experiment [
3], and noted that they coincide within the experimental error.
Arrington et al. [
13] have obtained S-band EPR spectra at 3 GHz for
J = 2 and
J = 3 levels (only two of six transitions for
J = 3 spectrum were detected because of high field resonances). The
values obtained from the S-band spectra are consistent within the
H field measurement error; for the
J = 2 spectrum, these g-factors are much more accurate [
19] than those obtained from the X-band EPR data [
8]. The averaged
values for
J = 2 are equal to 0.66663 and for
J = 3 it is 0.33340 in the S-bands ESR components [
13]. Then, the authors [
13] solved a system of two equations for two
J values
for
J = 2 and
for
J = 3 and found finally
(
). The late value for
of Arrington et al. [
13] is in good agreement with more accurate full EPR spectrum analysis of Miller [
20], but the rotational
gr-factor resolved by Miller is different,
, which is outside an experimental error [
13,
20]. Thus, the orbital magnetic moment of the O
2 (
1Δ
g) molecule is slightly different from a simple 2
μB value and this difference is crucial for the splitting between the quartet EPR lines, which appear through the second-order corrections [
20]. We will remind the reader that
gr =
gre +
grN =
gre + 2.723
; thus, the rotational
gr-factor represents a difference between two comparable values. Electronic contribution (
gre-factor) being almost equal to −3.96
for the O
2 (
1Δ
g) state and simultaneously close to
gre-value for the ground dioxygen O
2 (
3Σ
g−) state causes some doubts in researchers since Equation (4) provides different origins for both states [
13,
20]. Indeed, only
states of
1O
2 can contribute to the
gre-value for the ground triplet dioxygen [
22,
25].
The excited O
2 (
1Δ
g) is usually produced in the presence of great excess of the triplet ground state oxygen [
9,
27]. Thus, both ESR signals appear simultaneously in the same magnetic field ranges and the triplet ground state oxygen lines are used as an internal standard for the singlet excited O
2 (
1Δ
g) concentrations measurements [
9,
13]. However, the nature of the ESR signal for both states of dioxygen
3Σ
g−, Λ = 0 and
1Δ
g, Λ= 2 is rather different. The triplet state EPR transitions frequency is determined by spin g-factor (g
┴ = 2.0052) and by its anisotropy with g
|| = g
e parameter induced by SOC mixing, while the singlet delta dioxygen exhibits nearly symmetric quartet splitting due to electron-rotational interaction when O-O bond axes rotate around two perpendicular directions. In the late case, a value of rotational
Be constant determines the spitting of the quartet lines. Understanding this qualitative difference is essential for the choice of the field strength and microwave EPR frequency range for detection of both the ground
3O
2 (
3Σ
g−) and the excited
1O
2 (
1Δ
g) dioxygen.
Intensity analysis of the O
2 singlet–triplet transitions in the visible (λ 760 nm) and near IR (λ 1.27 μm) regions indicates that these bands have a magnetic-dipole origin and are induced by spin–orbit coupling (SOC) [
21,
22]. In optical spectroscopy, the ground is denoted by the letter X and excited states of other multiplicity are enumerated by small Latin letters
a,
b, etc. [
4]. The weak intensity of the O
2 (X
3Σ
g−)- O
2 (
a1Δ
g) band is determined by the same SOC-induced mixing with the
states which are responsible for rotational
gre-values in the ground triplet and the singlet excited O
2 states with similar contributions of the orbital angular momentum, Equation (4) [
28,
29,
30]. At the same time, the spin g-factor of the O
2 (X
3Σ
g−) state also depends on the similar orbital angular momentum contributions [
22]. A good agreement of all these calculations with experimental EPR and optical data support the reliability of the similar
gre-values for both O
2 (X
3Σ
g−) and O
2 (
a1Δ
g) states.
5. Nitric Oxide
Let us consider a free radical
2NO (
2Π
1/2), see
Scheme 1 and
Table 1. It has S = 1/2, S
z = ±1/2, Λ = 1. The total angular momentum about the molecular axis (neglecting rotation) is defined as
J = |Λ + S
z|. The lowest state of
2NO radical has
J = 1 − ½ = ½. Since the open–shell is occupied less than one-half (two double degenerate molecular orbitals (MO). These two MO has only one electron, and we get the regular spin–orbit coupling splitting. A formula for the spin g-factor of a diatomic radical has a factor (Λ − 2S) which is 0 for the current state [
13]. That means
2Π
1/2 state has g = 0 and is diamagnetic in both gas and liquid states due to a cancellation of orbital and spin angular momenta.
The next excited state of
2NO is
2Π
3/2, where S = ½, Λ = 1. This state has
J = 1 + 1/2 = 3/2.
J = 3/2 splits in an external magnetic field into four sublevels M
J with quantum numbers −3/2, −1/2, +1/2, +3/2. Thus, one expects three ESR transitions with the following changes in M
J: −3/2→−1/2; −1/2→+1/2; +1/2→+3/2. The first spectra of
2NO (
2Π
3/2) demonstrated namely three components [
2,
7,
10]. Non-magnetic
2Π
1/2 and paramagnetic
2Π
3/2 states of
2NO are very close in their energies. The excited state
2Π
3/2 is only 1.43 kJ/mole higher in energy than the ground
2Π
1/2 state [
14]. Let us consider the factors, which determine this energy splitting. The open-shell wave function of the doublet
2Π
J state can be presented in the following forms: for the case of less-than-half occupied open
π–shell we use Equation (5). We use Equation (6) for the case of more-than-half occupied
π–shell [
31]:
The Left and right parts of Equations (5) and (6) are the equivalent ways to present the electronic configuration of the same state. π and π with a bar on the top are used to distinguish the spin state of a spin orbital. One spin orbital may have s = ½ and the other will have s = −1/2 and vice versa.
The upper sign in these equations corresponds to
J = 3/2 and the lower sign corresponds to
J = 1/2. The imaginary form of wave function is necessary to satisfy the requirement
. We use here a common notation for the Slater determinant of many-electron wave function [
5]. Spin–orbit coupling (SOC) operator can be used in a simple effective single-electron form [
31,
32]:
where
is the SOC constant for the valence shell of atom
A,
and
are orbital and spin angular momentum operators, respectively for the
i-th electron. The SOC constants obtained from atomic spectra are equal
cm
−1 and
cm
−1 for nitrogen and oxygen, respectively [
31]. Since
J = |Λ + S
z|, there are two possible presentations for each J. Expectation energy of the SOC operator is equal
Let us take 2π*-molecular orbital of
2NO radical from the SCF calculation with the zero differential overlap approach within PM-3 method [
33]: 2
. This form of 2π-MO is in good agreement with the hyperfine coupling parameters fitting to ESR spectrum of gaseous
2NO molecule [
34]. Using these MO LCAO
coefficients we obtain the following splitting:
which is in reasonable agreement with the experiment [
23]. Even such a simple semi-empirical approach provides a quantitative explanation of the fine structure SOC splitting in
2NO radical.
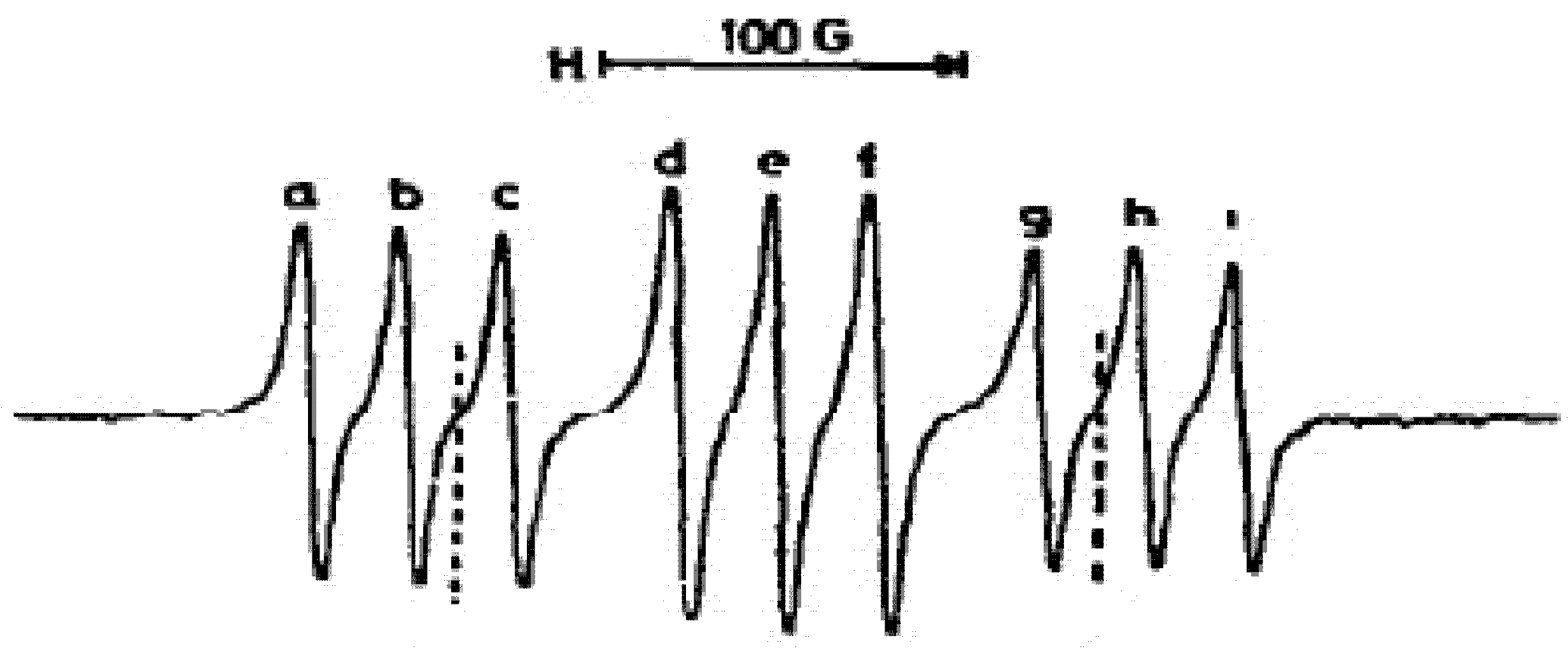
2Π
3/2 is easily accessible at room and lower temperatures; the thermal energy at room temperature is 2.5 kJ/mol. Thus, one can observe the X-band ESR spectrum of the excited
2Π
3/2 state, which is presented in
Figure 3:
One can see that each of the three major components splits into three components due to hyperfine coupling (HFC) with
14N nucleus. A highly resolved spectrum of
2NO (
2Π
3/2) has 27 components due to additional interactions [
10]. We calculated the HFC tensor for
14N isotope of
2NO radical by density functional theory with B3LYP/6–311++G(dp) approach [
33]; the isotropic HFC constant
a = 11.386 MHz, anisotropic HFC tensor component along the
z-axis is equal 74.673 MHz. The oxygen atom bears an electric charge of +0.091 e and spin density of 0.286, whereas the nitrogen has −0.091 e and 0.714, respectively. Other spectroscopic parameters are in a good agreement with experiment [
23]: r
e = 1.148 Ả, ν
e = 1980 cm
−1, B
e = 51.364 GHz, averaged polarizability α
av = 9.4
, dipole moment is equal −0.13 debye. The relatively small polarity and polarizability of
2NO radical explain its rather weak intermolecular interaction in the gas phase; thus its ESR spectrum at moderate pressure does not depend on the properties of foreign gases. The calculated HFC tensor of
2NO radical with natural isotope abundance does not contradict to experimental ESR spectrum (
Figure 3) [
10].
The first EPR spectrum of nitric oxide,
2NO (
2Π
3/2) was tentatively interpreted as being due to traditional magnetic–dipole transitions (MDT), since the MDT nature is typical for EPR signals [
10]. However, the latter the electric–dipole transitions (EDT) were shown to be more intense and prominent in this EPR spectrum. As many other
2Π states the
2NO (
2Π
3/2) state demonstrates a clear Λ–doubling effect [
14]. The EDT lines occur between opposite members of an Λ-doublet (-
+), while much weaker MDT transitions connect the same Λ-doublet members (-
-) or (+
+) [
4]. All these features are determined by relatively strong SOC (Equation (8)) in quasi degenerate 2π
x- and 2π
y- molecular orbitals of nitric oxide.
It is interesting to note that in homonuclear dioxygen molecules, all EDT’s are strongly forbidden by the central point (inversion) symmetry and only weak MDT are observed in the low-pressure gas phase in the triplet–singlet
b-X and
a-X transitions in the visible and near IR regions [
21]. However, the release of symmetry restriction in solvents permits the O
2 (
X3Σ
g−)- O
2 (
a1Δ
g) band at 1.2 μm to acquires EDT character and become much more intense because of strong spin–orbit coupling inside the dioxygen O
2 (π
g) open shell. Thus, many peculiarities of the optical and EPR spectra of two diatomic species,
2NO and O
2, being very important for atmospheric problems, strongly depend on spin–orbit coupling in 2π*- orbitals (
Scheme 1) which energy does not exceed 1–2 kJ/mol [
21,
32].
Spin and rotational energies depend upon each other. Collisions of 2NO (2Π3/2) with solvent molecules lead to a spin relaxation or an infinite boarding of components. Note, that gas-phase ESR spectra are observed at low pressure. An increase in pressure leads to the broadening of components.
6. ESR of Trapped 2NO
2NO is used as a probe of surfaces, different cages, nano-objects, and biological species. Adsorption of
2NO on surface vacancies, inside zeolites [
11,
15], or the C
60 cavity [
16], complexation with biological molecules [
18] leads to a quenching of the orbital momentumΛ; thus, the lowest
2Π
1/2 state of
2NO becomes paramagnetic and demonstrates ESR. In the adsorbed
2NO species, the 2π
x- and 2π
y- molecular orbitals (MO) are split by interaction with the surface and the energy splitting between the perturbed 2π
x and 2π
y MO is a measure of the spin g-factor anisotropy [
11].
2NO species is not any more an object of diatomic spectroscopy with proper quantization of orbital and rotational angular momenta. Instead, the polyatomic cluster is an object of the ground and excited states studies. The principal values of the g-tensor are used now to determine the MO splitting to characterize the electric field strength at the
2NO adsorption site. An example is presented in
Figure 4:
The sharp downward components (
Figure 4) arise due to hyperfine coupling on
14N nucleus of a bound
2NO and the g-factor just shows the position of the ESR signal.
To obtain an interpretation of the ESR spectrum in
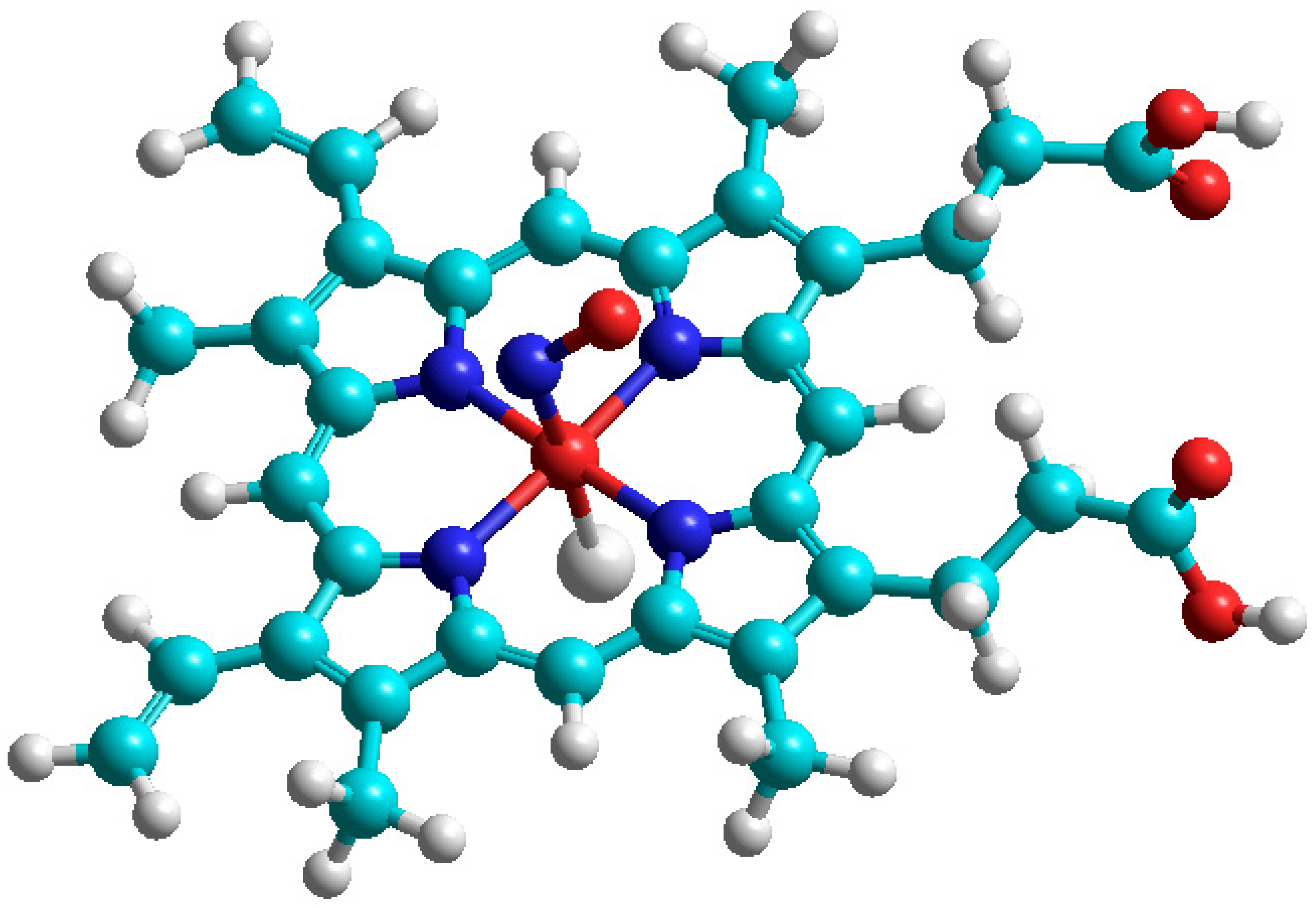
Figure 4, we simulated the
2NO complex with hemoglobin model by quantum chemical DFT calculation (
Figure 5) in the framework of B3LYP/6–31 G approach [
33]. The Fe-N coordination bond length is optimized to be 0.1866 nm with the angle Fe-N-O = 121.4°, the distance Fe-Cl = 0.2186 nm just simulates the Fe ion coordination with the protein residue. The calculated g-factor has components 2.0137, 20,082, and 1.9843, which are in qualitative agreement with the ESR spectrum in
Figure 4. A large portion of nonpaired spin is concentrated on Fe ions.
The calculated isotropic HFC constant on the 14N nucleus is equal to a = 15.78 MHz; anisotropic HFC tensor components are calculated at −30.2, −7.3, and 37.5 MHz. Thus, the Fermi-coupling a constant is slightly increased by 4.4 MHz in comparison with free NO radical, but the components of the HFC tensor are approximately half-diminished upon 2NO coordination to the iron center of hemoglobin. The Fe(II) ion provides a rather strong influence on the hyperfine structure of the EPR spectrum of nitric oxide.
These results are comparable with our previous theoretical DFT studies of
2NO and O
2 interactions with hemoglobin [
28,
29]. Hyperfine coupling on
14N nucleus is in agreement with the theory of the nitric oxide ESR spectrum made as early as 1950 [
30].
7. Conclusions and Perspectives
A newcomer may be very surprised that a singlet molecule 1O2 demonstrates an ESR spectrum in the gas phase. Due to the lack of spin in the molecule, it is better to use the term Electron Paramagnetic Resonance, which is achieved in this case where paramagnetism is due to the orbital momentum. The radical 2NO does not demonstrate the ESR spectrum in liquid solutions. ESR of these and other states can be understood considering the terms of these diatomic molecules.
2NO is an atmospheric pollutant. 2NO reacts with dioxygen and produces 2NO2, which is a pollutant as well. In the literature on environmental problems, both pollutants are often called NOx.
Air pollutant singlet dioxygen has a relatively short lifetime from milliseconds to less than 10 s [
14]. Specific lifetime depends upon pressure and the presence of quenchers of
1O
2. In the air atmosphere (P
tot = 1 atm),
1O
2 has a lifetime of 2.8 s measured with a quencher [
19]. During this time,
1O
2 diffuses approximately 1 cm [
19].
The gas pollutants exist in most cases in the presence of dioxygen. One or another strong line of ESR of
3O
2 (
3Σ
g−) (
Figure 1) can serve as a convenient internal standard for monitoring
1O
2 (
1Δ
g) or other gas pollutants.