Predicting 1,9-Decadiene−Water Partition Coefficients Using the 3D-RISM-KH Molecular Solvation Theory
Abstract
1. Introduction
2. Materials and Methods
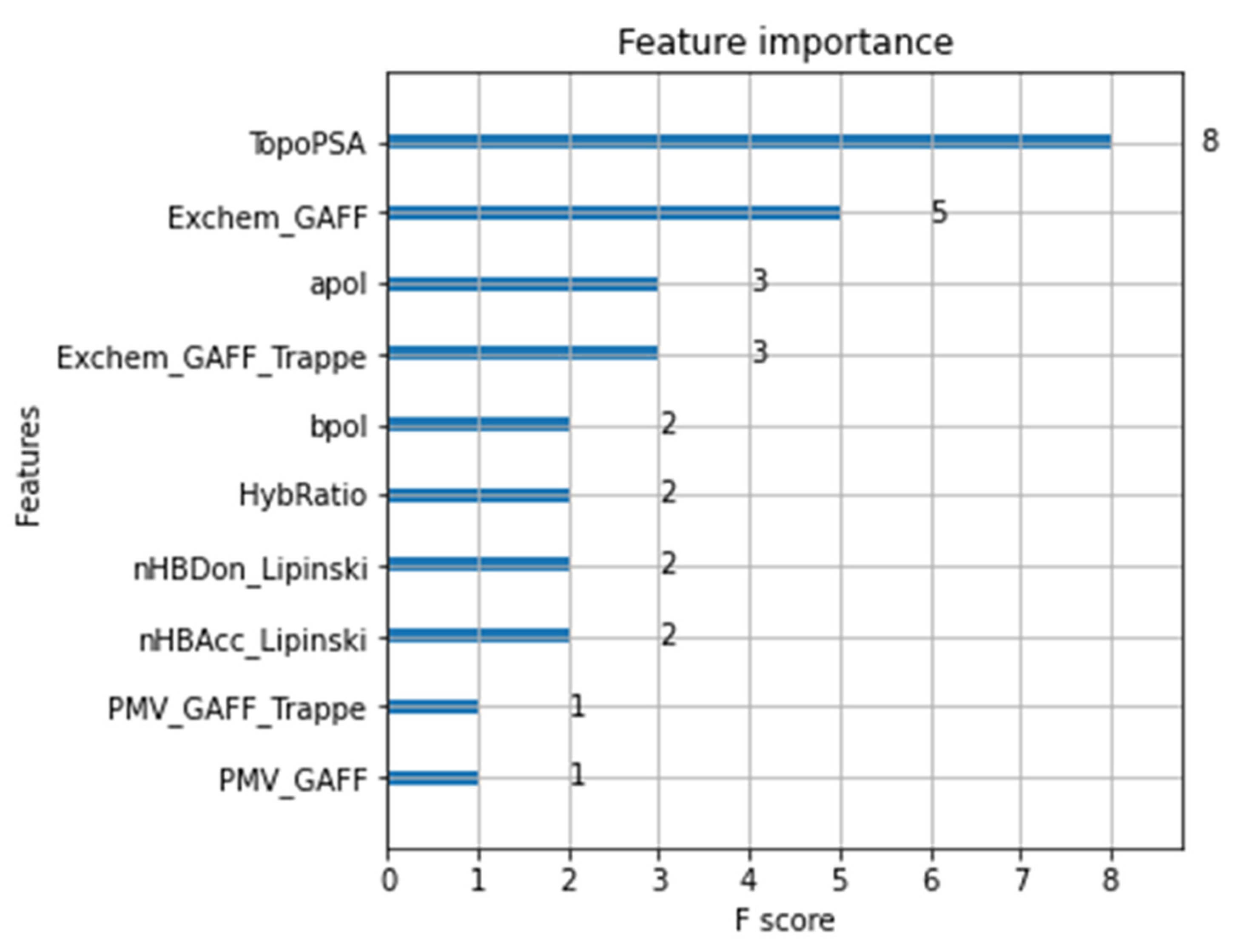
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bennion, B.J.; Be, N.A.; McNerney, M.W.; Lao, V.; Carlson, E.M.; Valdez, C.A.; Malfatti, M.A.; Enright, H.A.; Nguyen, T.H.; Lightstone, F.C.; et al. Predicting a Drug’s Membrane Permeability: A Computational Model Validated with in Vitro Permeability Assay Data. J. Phys. Chem B 2017, 121, 5228–5237. [Google Scholar] [CrossRef] [PubMed]
- Lanevskij, K.; Didziapetris, R. Physicochemical QSAR Analysis of Passive Permeability across Caco-2 Monolayers. J. Pharm. Sci. 2019, 108, 78–86. [Google Scholar] [CrossRef]
- Leung, S.S.F.; Sindhikara, D.J.; Jacobson, M.P. Simple Predictive Models of Passive Membrane Permeability Incorporating Size-Dependent Membrane-Water Partition. J. Chem. Inf. Model. 2016, 56, 924–929. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Dutta, D.; Wishart, D.S.; Kovalenko, A. Predicting PAMPA permeability using the 3D-RISM-KH theory: Are we there yet? J. Comput.-Aided Mol. Des. 2021, 35, 261–269. [Google Scholar] [CrossRef]
- Burton, P.S.; Conradi, R.A.; Hilgers, A.R.; Ho, N.F.H.; Maggiora, L.L. The relationship between peptide structure and transport across epithelial cell monolayers. J. Control. Rel. 1992, 19, 87–97. [Google Scholar] [CrossRef]
- Mueller, P.; Rudin, D.O.; Tien, H.T.; Wescott, W.C. Reconstruction of cell membranes structure in vitro and its transformation into an excitable system. Nature 1962, 94, 979–980. [Google Scholar] [CrossRef] [PubMed]
- Lomize, A.L.; Pogozheva, I.D. Physics-Based Method for Modeling Passive Membrane Permeability and Translocation Pathways of Bioactive Molecules. J. Chem. Inf. Model. 2019, 51, 3198–3213. [Google Scholar] [CrossRef] [PubMed]
- Lomize, A.L.; Hage, J.M.; Schnitzer, K.; Golobokov, K.; LaFaive, M.B.; Forsyth, A.C.; Pogozheva, I.D. PerMM: A Web Tool and Database for Analysis of Passive Membrane Permeability and Translocation Pathways of Bioactive Molecules. J. Chem. Inf. Model. 2019, 59, 3094–3099. [Google Scholar] [CrossRef]
- Mayer, P.T.; Anderson, B.D. Transport across 1,9-decadiene precisely mimics the chemical selectivity of the barrier domain in egg lecithin bilayers. J. Pharm. Sci. 2002, 91, 640–646. [Google Scholar] [CrossRef]
- Xiang, T.-X.; Anderson, B.D. The relationship between permeant size and permeability in lipid bilayer membranes. J. Memb. Biol. 1994, 140, 111–122. [Google Scholar] [CrossRef]
- Cao, Y.; Xiang, T.-X.; Anderson, B.D. Development of Structure−Lipid Bilayer Permeability Relationships for Peptide-like Small Organic Molecules. Mol. Pharm. 2008, 5, 371–388. [Google Scholar] [CrossRef]
- Abraham, M.H.; Acree, W.E., Jr. Linear free-energy relationships for water/hexadec-1-ene and water/deca-1,9-diene partitions, and for permeation through lipid bilayers; comparison of permeation systems. New J. Chem. 2012, 36, 1798–1806. [Google Scholar] [CrossRef]
- Nitsche, J.M.; Kasting, G.B. A critique of Abraham and Acree’s correlation for deca-1,9-diene/water partition coefficients. New J. Chem. 2013, 37, 283–285. [Google Scholar] [CrossRef]
- Nitsche, J.M.; Kasting, G.B. A correlation for 1,9-decadiene/water partition coefficients. J. Pharm. Sci. 2013, 102, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D.; McCoy, J.D.; Singer, S.J. Density functional theory of nonuniform polyatomic systems. I. General formulation. J. Chem. Phys. 1986, 85, 5971–5976. [Google Scholar] [CrossRef]
- Chandler, D.; McCoy, J.D.; Singer, S.J. Density functional theory of nonuniform polyatomic systems. II. Rational closures for integral equations. J. Chem. Phys. 1986, 85, 5977–5982. [Google Scholar] [CrossRef]
- Lowden, L.J.; Chandler, D. Solution of a new integral equation for pair correlation functions in molecular liquids. J. Chem. Phys. 1973, 59, 6587–6595. [Google Scholar] [CrossRef]
- Kovalenko, A. Molecular theory of solvation: Methodology summary and illustrations. Cond. Matt. Phys. 2015, 18, 32601. [Google Scholar] [CrossRef]
- Palmer, D.S.; Frolov, A.; Ratkova, E.; Fedorov, M.V. Towards a universal method for calculating hydration free energies: A 3D reference interaction site model with partial molar volume correction. J. Phys. Condens. Matt. 2010, 22, 492101. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. A molecular theory of liquid interfaces. Phys. Chem. Chem. Phys. 2005, 7, 1785–1793. [Google Scholar] [CrossRef] [PubMed]
- Kovalenko, A. Multiscale Modeling of Solvation. In Springer Handbook of Electrochemical Energy; Breitkopf, C., Swider-Lyons, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Kovalenko, A.; Gusarov, S. Multiscale methods framework: Self-consistent coupling of molecular theory of solvation with quantum chemistry, molecular simulations, and dissipative particle dynamics. Phys. Chem. Chem. Phys. 2017, 20, 2947–2969. [Google Scholar] [CrossRef] [PubMed]
- Ratkova, E.L.; Palmer, D.S.; Fedorov, M.V. Solvation Thermodynamics of Organic Molecules by the Molecular Integral Equation Theory: Approaching Chemical Accuracy. Chem. Rev. 2015, 13, 6312–6356. [Google Scholar] [CrossRef] [PubMed]
- Misin, M.; Palmer, D.S.; Fedorov, M.V. Predicting Solvation Free Energies Using Parameter-Free Solvent Models. J. Phys. Chem. B 2016, 120, 5724–5731. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Tirado-Rives, J. Potential energy functions for atomic-level simulations of water and organic and biomolecular systems. Proc. Natl. Acad. Sci. USA 2005, 102, 6665–6670. [Google Scholar] [CrossRef]
- Dodda, L.S.; Vilseck, J.Z.; Tirado-Rives, J.; Jorgensen, W.L. 1.14*CM1A-LBCC: Localized Bond-Charge Corrected CM1A Charges for Condensed-Phase Simulations. J. Phys. Chem. B 2017, 121, 3864–3870. [Google Scholar] [CrossRef]
- Dodda, L.S.; de Vaca, I.C.; Tirado-Rives, J.; Jorgensen, W.L. LigParGen web server: An automatic OPLS-AA parameter generator for organic ligands. Nucl. Acid. Res. 2017, 45, W331–W336. [Google Scholar] [CrossRef]
- Zoete, V.; Cuendet, M.A.; Grosdidier, A.; Michielin, O. SwissParam: A fast force field generation tool for small organic molecules. J. Comput. Chem. 2011, 32, 2359–2368. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L., III; MacKerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef]
- Malde, A.K.; Zuo, L.; Breeze, M.; Stroet, M.; Poger, D.; Nair, P.C.; Oostenbrink, C.; Mark, A.E. An Automated Force Field Topology Builder (ATB) and Repository: Version 1.0. J. Chem. Theory Comput. 2011, 7, 4026–4037. [Google Scholar] [CrossRef] [PubMed]
- Koziara, K.B.; Stroet, M.; Malde, A.K.; Mark, A.E. Testing and validation of the Automated Topology Builder (ATB) version 2.0: Prediction of hydration free enthalpies. J. Comput.-Aided Mol. Des. 2014, 28, 221–233. [Google Scholar] [CrossRef] [PubMed]
- Schmid, N.; Eichenberger, A.P.; Choutko, A.; Riniker, S.; Winger, M.; Mark, A.E.; van Gunsteren, W.F. Definition and testing of the GROMOS force-field versions 54A7 and 54B7. Eur. Biophys. J. 2011, 40, 843–856. [Google Scholar] [CrossRef] [PubMed]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminfo. 2011, 3, 33. [Google Scholar] [CrossRef]
- Case, D.A.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Ghoreishi, D.; Gilson, M.K.; et al. AMBER 2018; University of California: San Francisco, CA, USA, 2018. [Google Scholar]
- Wick, C.D.; Martin, M.G.; Siepmann, J.I. Transferable Potentials for Phase Equilibria. 4. United-Atom Description of Linear and Branched Alkenes and Alkylbenzenes. J. Phys. Chem. B 2000, 104, 8008–8016. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable Potentials for Phase Equilibria. 1. United-Atom Description of n-Alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Pettitt, B.; Rossky, P. Integral equation predictions of liquid state structure for waterlike intermolecular potentials. J. Chem. Phys. 1982, 77, 1451–1457. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247260. [Google Scholar] [CrossRef]
- Jakalian, A.; Jack, D.B.; Bayly, C.I. Fast, efficient generation of high-quality atomic charges. AM1-BCC model: II. Parameterization and validation. J. Comput. Chem. 2002, 23, 1623–1641. [Google Scholar] [CrossRef]
- Yap, C.W. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem. 2011, 32, 1466–1476. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Erić, S.; Kalinić, M.; Ilić, K.; Zloh, M. Computational classification models for predicting the interaction of drugs with P-glycoprotein and breast cancer resistance protein. SAR QSAR Environ. Res. 2014, 25, 939–966. [Google Scholar] [CrossRef]
- Xiang, T.-X.; Anderson, B.D. A computer simulation of functional group contributions to free energy in water and a DPPC lipid bilayer. Biophys. J. 2002, 82, 2052–2066. [Google Scholar] [CrossRef][Green Version]
- Lomize, A.L.; Pogozheva, I.D.; Mosberg, H.I. Anisotropic Solvent Model of the Lipid Bilayer. 1. Parameterization of Long-Range Electrostatics and First Solvation Shell Effects. J. Chem. Inf. Model. 2011, 51, 918–929. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kin, K.S.; Karthikeyan, S.; Singh, N.J. How Different Are Aromatic π Interactions from Aliphatic π Interactions and Non-π Stacking Interactions? J. Chem. Theory Comput. 2011, 7, 3471–3477. [Google Scholar]
- Ertl, P.; Rhode, B.; Selzer, P. Fast Calculation of Molecular Polar Surface Area as a Sum of Fragment-Based Contributions and Its Application to the Prediction of Drug Transport Properties. J. Med. Chem. 2000, 43, 3714–3717. [Google Scholar] [CrossRef]
- Kim, S.; Chen, J.; Cheng, T.; Gindulyte, A.; He, J.; He, S.; Li, Q.; Shoemaker, B.A.; Thiessen, P.A.; Yu, B.; et al. PubChem in 2021: New data content and improved web interfaces. Nucl. Acid. Res. 2011, 49, D1388–D1395. [Google Scholar] [CrossRef] [PubMed]
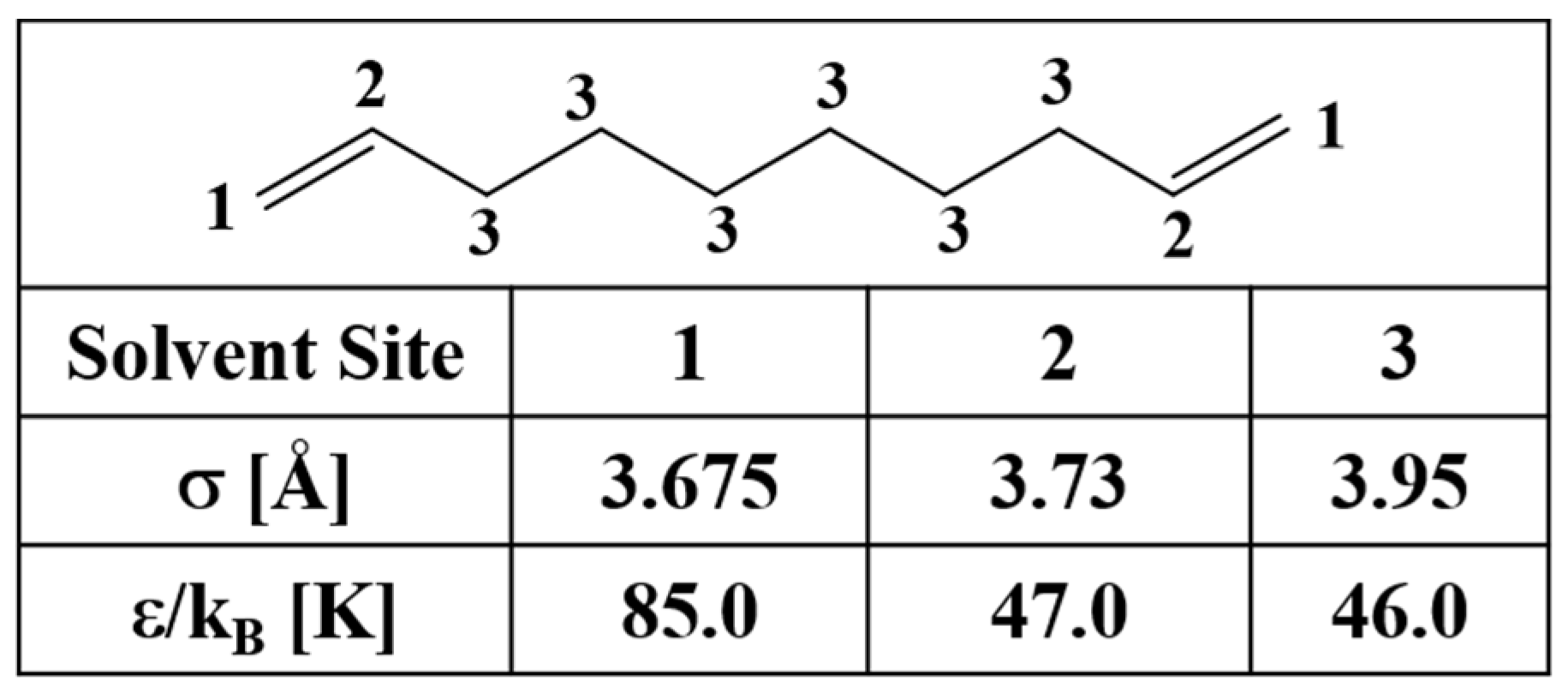

| Method | Density | Error Estimate |
|---|---|---|
| Experimental | 0.75 | - |
| CHARMM | 0.741 | 0.049 |
| GROMOS | 0.751 | 0.036 |
| OPLS | 0.728 | 0.068 |
| Force Field | g(C1-C1) a | g(C2-C2) a | g(CH2-CH2) a |
|---|---|---|---|
| CHARMM | 4.06/9.04 | 5.1/8.68 | 2.48/3.12 |
| OPLS | 3.94/9.02 | 5.06/8.86 | 2.56/3.22 |
| GROMOS-UA | 4.06/8.94 | 5.08/8.7 | 2.54/3.88 |
| RISM-KH (TraPPE) | 2.58 (3.88)/8.48 | 2.42 (4.2)/8.65 | 5.22/9.18 |
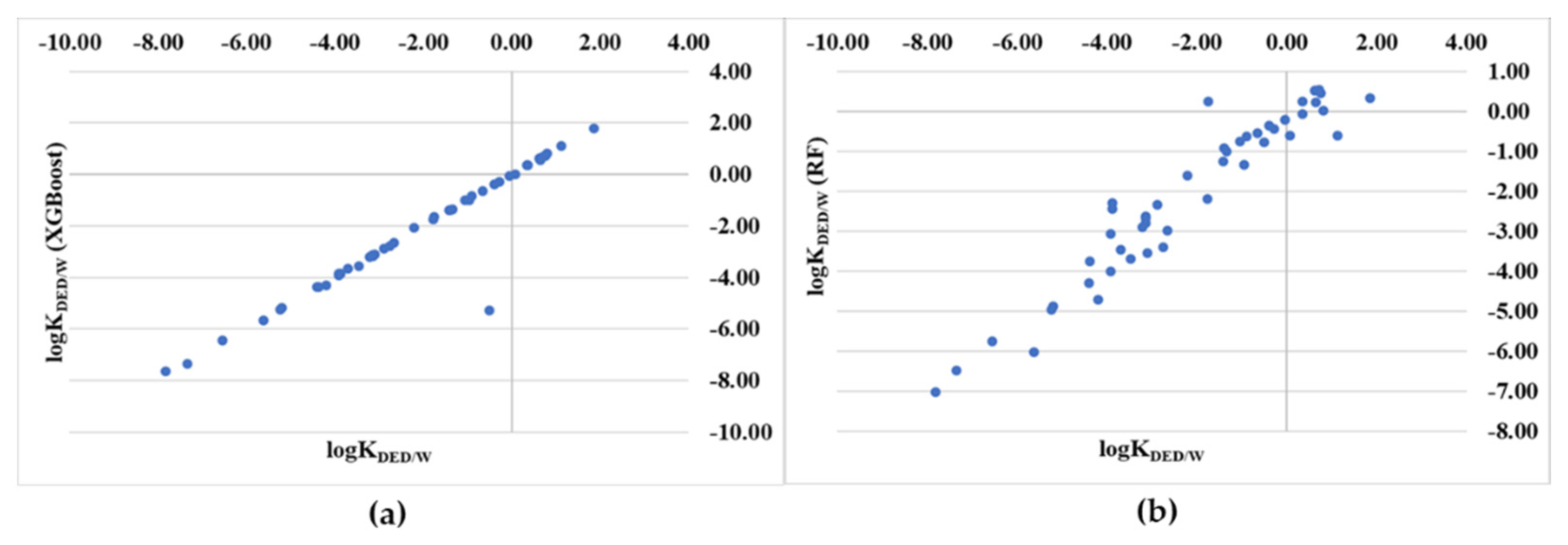
| CID a | LogK b | XGB c | RF d | LR e | CID a | LogK b | XGB c | RF d | LR e |
|---|---|---|---|---|---|---|---|---|---|
| 6324 | 1.85 | 1.79 | 0.33 | 1.73 | 284 | −3.21 | −3.21 | −2.90 | −3.13 |
| 264 * | −1.41 | −1.39 | −1.26 | −1.04 | 176 | −2.89 | −2.88 | −2.34 | −2.22 |
| 1292 | −3.15 | −3.13 | −2.64 | −3.29 | 178 * | −3.89 | −3.85 | −2.45 | −2.52 |
| 1001 | 0.62 | 0.61 | 0.50 | 0.54 | 190 * | −5.24 | −5.23 | −4.97 | −3.70 |
| 5610 | −1.35 | −1.36 | −1.00 | −1.06 | 243 | −0.51 | −5.28 | −0.79 | −0.97 |
| 9727 * | −1.75 | −1.66 | 0.25 | 0.09 | 6847 | 0.34 | 0.37 | 0.25 | 0.68 |
| 68,313 * | −0.90 | −0.85 | −0.64 | 0.90 | 7123 | 0.76 | 0.73 | 0.44 | 1.14 |
| 4657 | 0.65 | 0.56 | 0.22 | 0.11 | 2201 * | 0.81 | 0.82 | 0.02 | 2.96 |
| 104,735 * | 1.12 | 1.09 | −0.60 | 0.89 | 20,039 | −4.19 | −4.29 | −4.72 | −4.77 |
| 7470 | −0.05 | −0.07 | −0.22 | −0.64 | 13,730 | −5.62 | −5.66 | −6.01 | −6.24 |
| 74,234 * | −0.28 | −0.28 | −0.44 | −1.91 | 5755 | −3.10 | −3.10 | −3.55 | −3.01 |
| 308,473 * | −0.96 | −0.99 | −1.33 | −1.57 | 5754 * | −2.76 | −2.79 | −3.40 | −1.87 |
| 270,871 * | −1.77 | −1.76 | −2.20 | −2.25 | 999 | −1.05 | −1.00 | −0.76 | −1.61 |
| 76,360 * | −3.14 | −3.15 | −2.67 | −2.32 | 31,374 | −2.21 | −2.06 | −1.61 | −0.63 |
| 220,005 | −3.92 | −3.93 | −4.00 | −4.51 | 6584 | 0.07 | 0.00 | −0.61 | −1.46 |
| 23,273,690 | −4.40 | −4.37 | −4.29 | −4.61 | 15,684,457 * | −3.89 | −3.84 | −2.30 | −2.96 |
| 97,479 | −3.47 | −3.56 | −3.69 | −3.97 | 12,539,853 * | −3.13 | −3.16 | −2.79 | −3.41 |
| 129,821,671 | −3.70 | −3.65 | −3.46 | −4.46 | 2,728,789 | −2.66 | −2.66 | −2.98 | −3.60 |
| 129,821,666 * | −4.38 | −4.38 | −3.75 | −5.60 | 248,474 | −0.40 | −0.40 | −0.36 | −1.52 |
| 129,821,670 | −5.19 | −5.19 | −4.88 | −4.63 | 222,175 | −0.66 | −0.65 | −0.54 | 0.70 |
| 129,821,665 | −6.55 | −6.45 | −5.74 | −5.15 | 4,048,798 | 0.36 | 0.37 | −0.08 | −0.03 |
| 17,851,005 | −7.35 | −7.35 | −6.47 | −6.67 | 90,265 * | −1.40 | −1.39 | −0.93 | −0.49 |
| 54,472,514 | −7.82 | −7.63 | −7.03 | −6.83 | 1001 | 0.62 | 0.61 | 0.50 | 0.47 |
| 962 | −3.92 | −3.85 | −3.08 | −3.44 | 31,242 | 0.71 | 0.69 | 0.54 | 0.79 |
| Statistics | XGBoost | Random Forest (RF) | Linear Regression (LR) | XGB-2D-Descriptor Model |
|---|---|---|---|---|
| The Full Dataset | ||||
| RMSE | 0.05 | 0.68 | 0.92 | 0.12 |
| Spearman Correlation | 0.99 | 0.94 | 0.93 | 0.99 |
| Pearson Correlation | 0.99 | 0.96 | 0.92 | 0.99 |
| R2 | 0.99 | 0.90 | 0.84 | 0.99 |
| Test Set | ||||
| RMSE | 1.09 | 1.14 | 1.23 | 1.04 |
| Spearman Correlation | 0.72 | 0.73 | 0.88 | 0.75 |
| Pearson Correlation | 0.80 | 0.84 | 0.84 | 0.82 |
| R2 | 0.64 | 0.67 | 0.54 | 0.67 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, D.; Dutta, D.; Kovalenko, A. Predicting 1,9-Decadiene−Water Partition Coefficients Using the 3D-RISM-KH Molecular Solvation Theory. Physchem 2021, 1, 215-224. https://doi.org/10.3390/physchem1020015
Roy D, Dutta D, Kovalenko A. Predicting 1,9-Decadiene−Water Partition Coefficients Using the 3D-RISM-KH Molecular Solvation Theory. Physchem. 2021; 1(2):215-224. https://doi.org/10.3390/physchem1020015
Chicago/Turabian StyleRoy, Dipankar, Devjyoti Dutta, and Andriy Kovalenko. 2021. "Predicting 1,9-Decadiene−Water Partition Coefficients Using the 3D-RISM-KH Molecular Solvation Theory" Physchem 1, no. 2: 215-224. https://doi.org/10.3390/physchem1020015
APA StyleRoy, D., Dutta, D., & Kovalenko, A. (2021). Predicting 1,9-Decadiene−Water Partition Coefficients Using the 3D-RISM-KH Molecular Solvation Theory. Physchem, 1(2), 215-224. https://doi.org/10.3390/physchem1020015






