The Water Polymorphism and the Liquid–Liquid Transition from Transport Data
Abstract
:1. Introduction
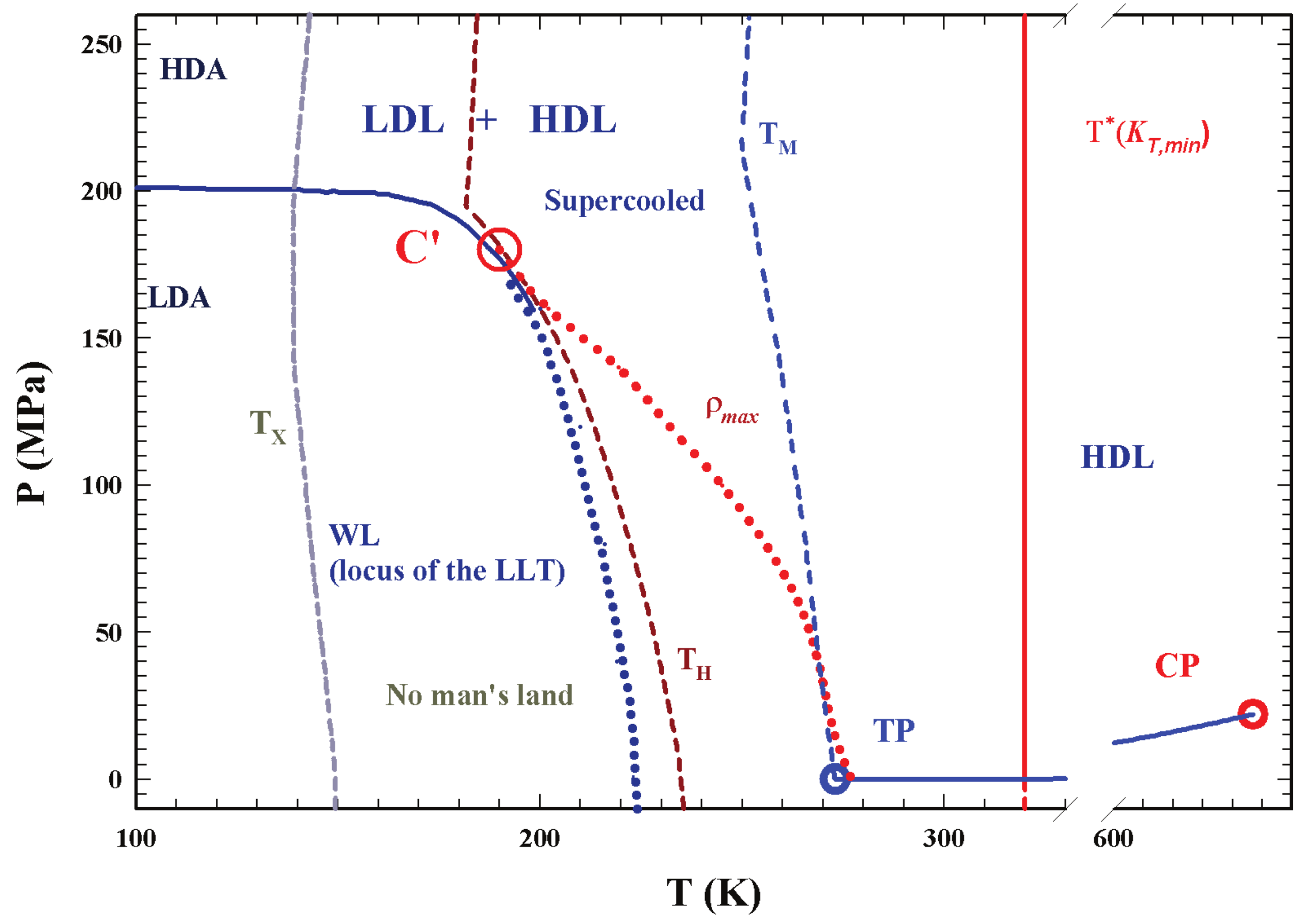
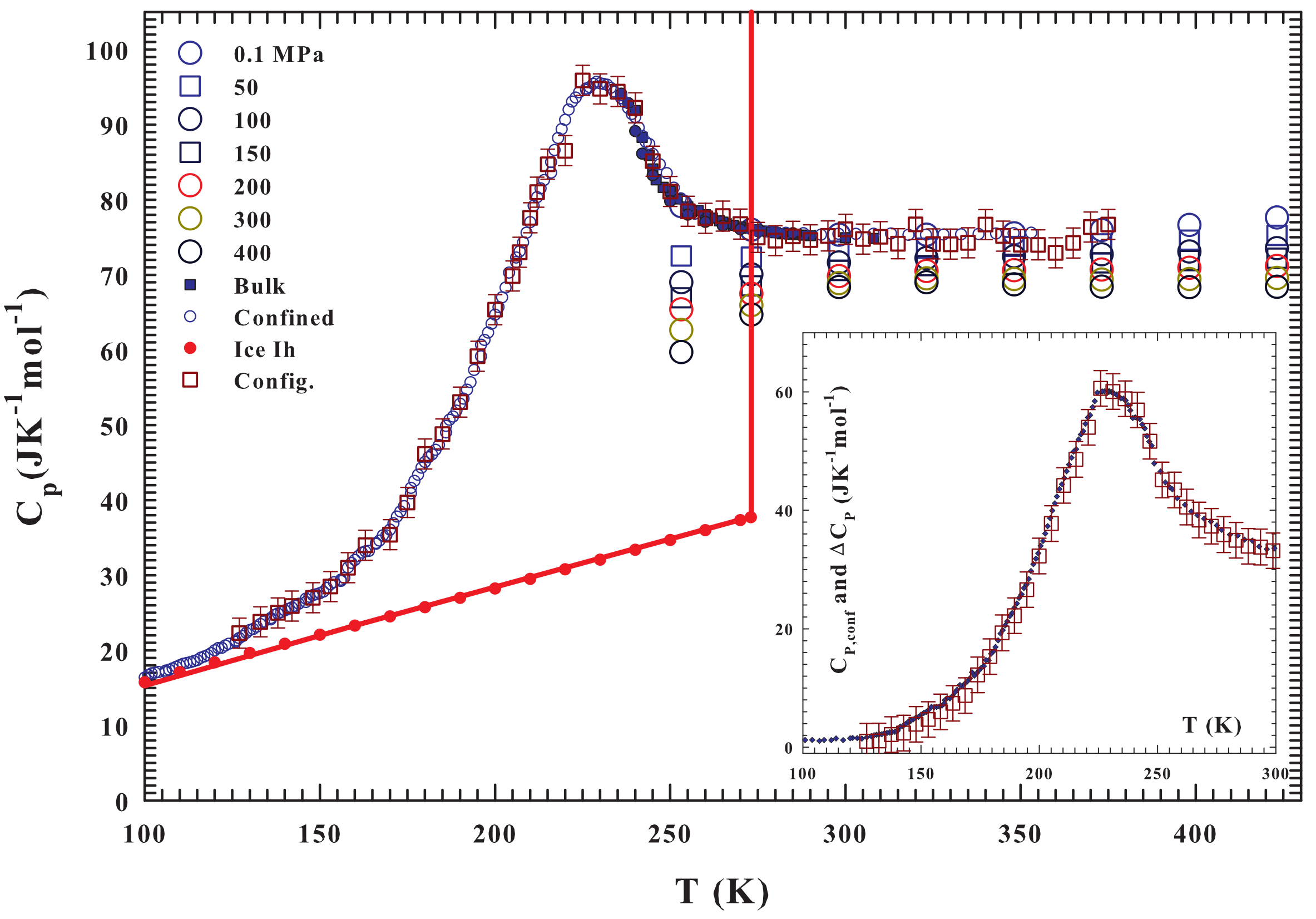
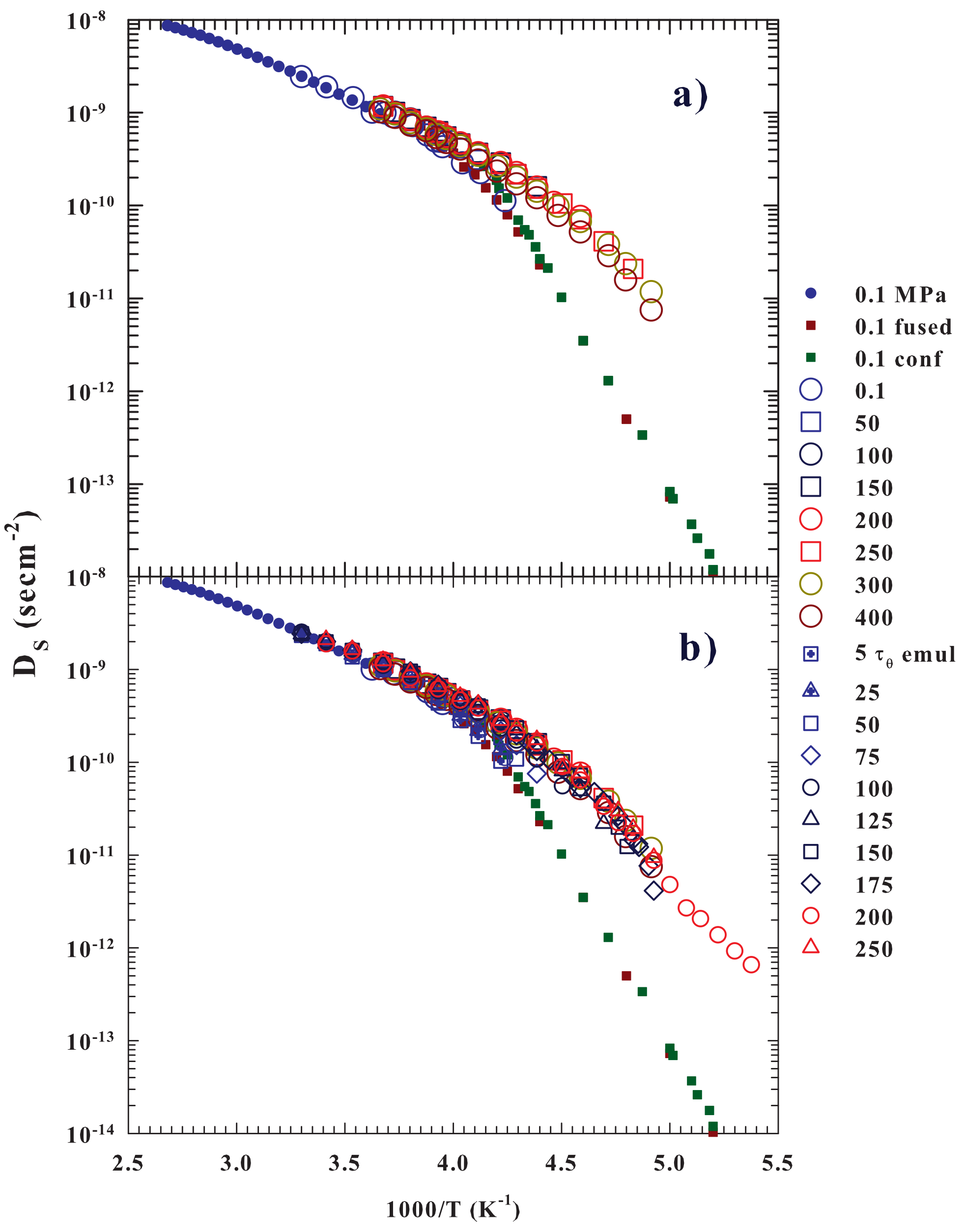
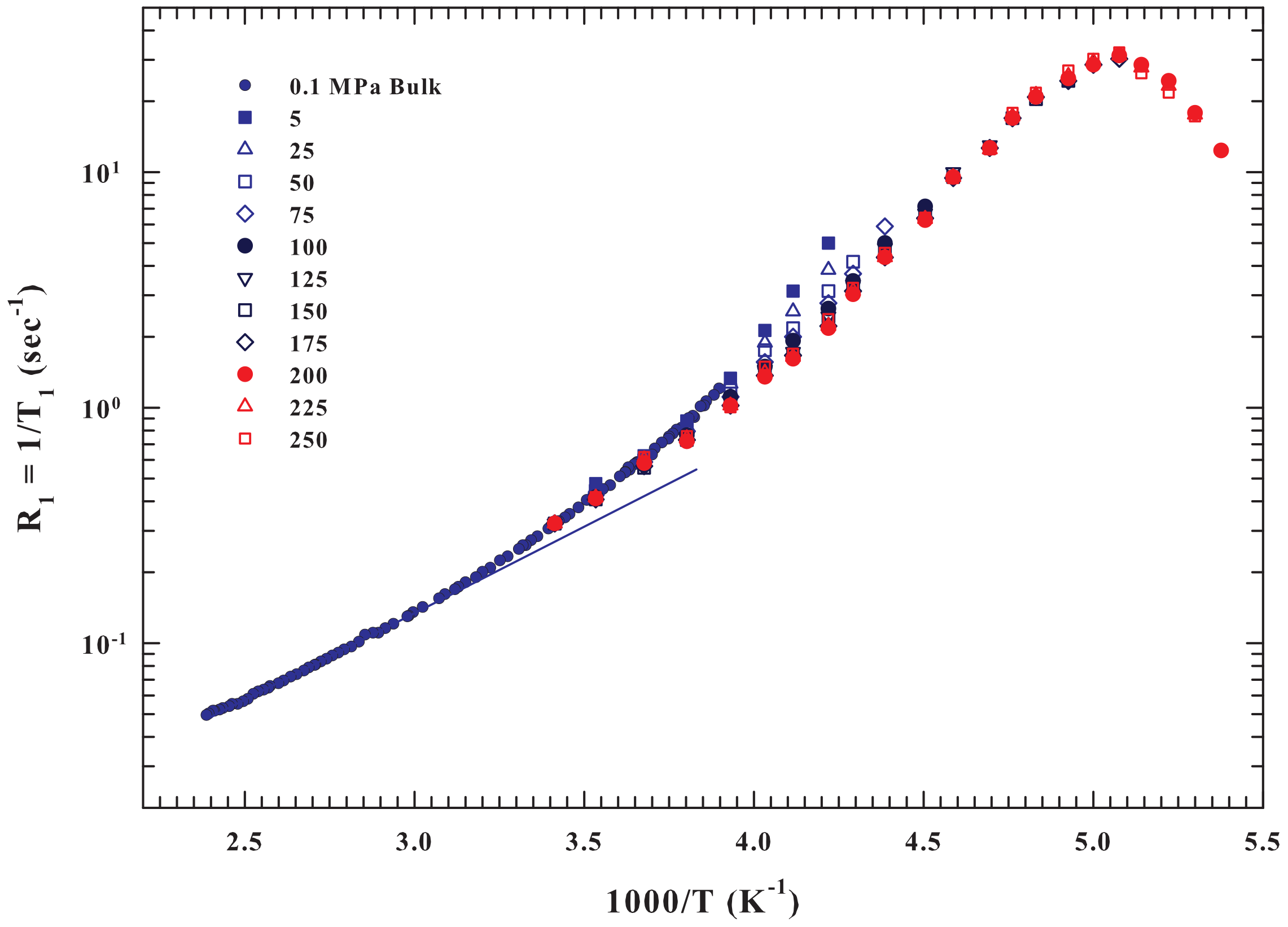
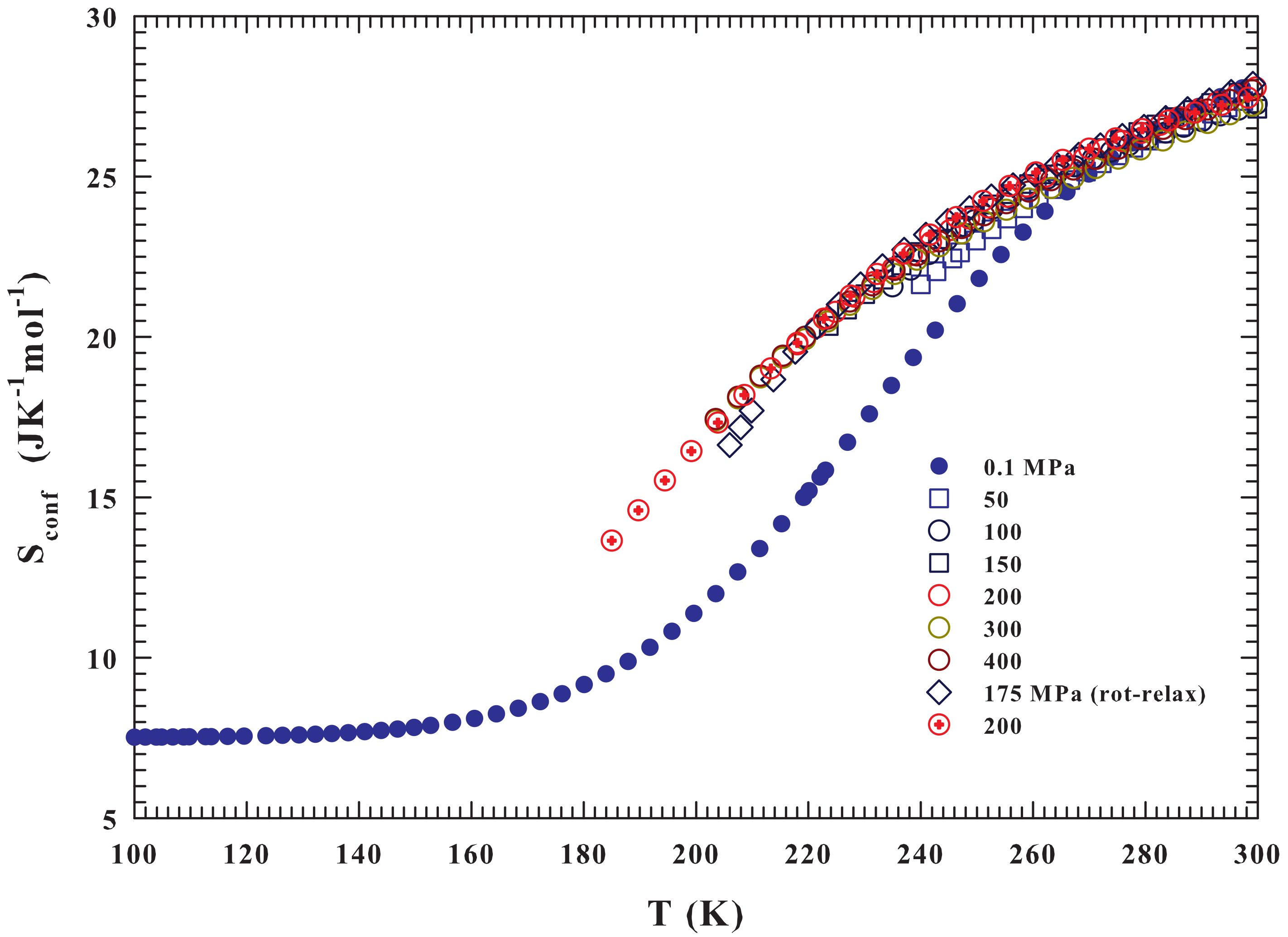
2. Results and Discussions
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ball, P. Water as an active constituent in cell biology. Chem. Rev. 2008, 108, 74–108. [Google Scholar] [CrossRef]
- Debenedetti, P.G.; Stanley, H.E. Supercooled and glassy water. Phys. Today 2003, 56, 40–46. [Google Scholar] [CrossRef]
- Speedy, R.J.; Angell, C.A. Isothermal compressibility of supercooled water and evidence for a thermodynamic singularity at −45 °C. J. Chem. Phys. 1976, 65, 851–858. [Google Scholar] [CrossRef]
- Poole, P.H.; Sciortino, F.; Essmann, U.; Stanley, H.E. Phase-behavior of metastable water. Nature 1992, 360, 324–328. [Google Scholar] [CrossRef]
- Mallamace, F. The liquid water polymorphism. Proc. Natl. Acad. Sci. USA 2009, 106, 15097–15098. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mallamace, F.; Broccio, M.; Corsaro, C.; Faraone, A.; Majolino, D.; Venuti, V.; Liu, L.; Mou, C.Y.; Chen, S.-H. Evidence of the existence of the low-density liquid phase in supercooled, confined water. Proc. Natl. Acad. Sci. USA 2008, 104, 424–428. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, L.M.; Mallamace, F.; Yan, Z.Y.; Starr, F.W.; Buldyrev, S.V.; Stanley, H.E. Appearance of a fractional Stokes-Einstein relation in water and a structural interpretation of its onset. Nat. Phys. 2009, 5, 565. [Google Scholar] [CrossRef]
- Lobban, C.; Finney, J.L.; Kuhs, W.F. The structure of a new phase of ice. Nature 1998, 391, 268–270. [Google Scholar] [CrossRef]
- Mishima, O.; Calvert, L.D.; Whalley, E. Melting Ice-I at 77 K and 10 K bar-a mew method of making amorphous solid. Nature 1984, 310, 393–397. [Google Scholar] [CrossRef]
- Mishima, O.; Calvert, L.D.; Whalley, E. An apparently first-order transition between two amorphous phases of ice induced by pressure. Nature 1985, 314, 76–78. [Google Scholar] [CrossRef]
- Mishima, O. Relationship between melting and amorphization of ice. Nature 1996, 384, 546–550. [Google Scholar] [CrossRef]
- Rapoport, E. Model for melting-curve at high pressure. J. Chem. Phys. 1967, 46, 2891. [Google Scholar] [CrossRef]
- Nemethy, G.; Scheraga, H. Structure of Water and Hydrophobic Bonding in Proteins. I. A Model for the Thermodynamic Properties of Liquid Water. J. Chem. Phys. 1962, 36, 3382. [Google Scholar] [CrossRef]
- Davis, C.M.; Litovitz, T.A. Two-State Theory of the Structure of Water. J. Chem. Phys. 1965, 42, 2563. [Google Scholar] [CrossRef]
- Jhon, M.S.; Grosh, J.; Ree, T.; Eyring, H. Significant-Structure Theory Applied to Water and Heavy Water. J. Chem. Phys. 1966, 44, 1465. [Google Scholar] [CrossRef]
- Kamb, B. Structure of high-pressure forms of ice. Science 1965, 150, 205. [Google Scholar] [CrossRef]
- Burton, E.F.; Oliver, W.F. X-ray diffraction patterns of ice. Nature 1935, 135, 505–506. [Google Scholar] [CrossRef]
- Loerting, T.; Salzmannm, C.; Kohl, I.; Mayer, E.; Hallbrucker, A. A second distinct structural “state” of high-density amorphous ice at 77 K and 1 bar. Phys. Chem. Chem. Phys. 2001, 3, 5355. [Google Scholar] [CrossRef]
- Mishima, O. Reversible first-order transition between two H2O amorphs at ∼0.2 GPa and ∼135 K. J. Chem. Phys. 1994, 100, 5910–5912. [Google Scholar] [CrossRef]
- Prielmeier, F.X.; Lang, E.W.; Speedy, R.J.; Lüdemann, H.-D. The pressure-dependence of self-diffusion in supercooled light and heavy-water. Ber. Bunsenges Phys. Chem. 1988, 92, 1111–1117. [Google Scholar] [CrossRef]
- Cerveny, S.; Mallamace, F.; Swenson, J.; Vogel, M.; Xu, L.M. Confined water as model of supercooled water. Chem. Rev. 2016, 116, 7608–7625. [Google Scholar] [CrossRef] [PubMed]
- Lang, E.; Lüdemann, H.D. Pressure and temperature-dependence of longitudinal proton relaxation-times in supercooled water to −87 °C and 2500 bar. J. Chem. Phys. 1977, 67, 718. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, Y.; Mishima, O. Experimentally proven liquid-liquid critical point of dilute glycerol-water solution at 150 K. J. Chem. Phys. 2014, 141, 094505. [Google Scholar] [CrossRef] [PubMed]
- Murata, K.-I.; Tanaka, H. Liquid-liquid transition without macroscopic phase separation in a water-glycerol mixture. Nat. Mater. 2012, 11, 436–443. [Google Scholar] [CrossRef] [PubMed]
- Mallamace, F.; Baglioni, P.; Corsaro, C.; Spooren, J.; Stanley, H.E.; Chen, S.-H. Transport properties of supercooled confined water. Riv. Nuovo Cimento 2011, 34, 253. [Google Scholar] [CrossRef]
- Xu, Y.; Petrik, N.G.; Scott Smith, R.; Kay, B.D.; Kimmel, G.A. Growth rate of crystalline ice and the diffusivity of supercooled water from 126 to 262 K. Proc. Natl. Acad. Sci. USA 2016, 113, 14921–14925. [Google Scholar] [CrossRef] [Green Version]
- Sjöström, J.; Swenson, J.; Bergman, R.; Kittaka, S. Investigating hydration dependence of dynamics of confined water: Monolayer, hydration water and Maxwell-Wagner processes. J. Chem. Phys. 2008, 128, 154503. [Google Scholar] [CrossRef] [Green Version]
- Mallamace, F.; Corsaro, C.; Stanley, H.E. A singular thermodynamically consistent temperature at the origin of the anomalous behavior of liquid water. Sci. Rep. 2012, 2, 993. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.M.; Kumar, P.; Buldyrev, S.V.; Chen, S.-H.; Poole, P.H.; Sciortino, F.; Stanley, H.E. Relation between the Widom line and the dynamic crossover in systems with a liquid–liquid phase transition. Proc. Natl. Acad. Sci. USA 2005, 102, 16558–16562. [Google Scholar] [CrossRef] [Green Version]
- Ito, K.; Moynihan, C.T.; Angell, C.A. Thermodynamic determination of fragility in liquids and a fragile-to-strong liquid transition in water. Nature 1999, 398, 492. [Google Scholar] [CrossRef]
- Chen, S.-H.; Mallamace, F.; Mou, C.Y.; Broccio, M.; Corsaro, C.; Faraone, A.; Liu, L. The violation of the Stokes-Einstein relation in supercooled water. Proc. Natl. Acad. Sci. USA 2006, 103, 12974–12978. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mallamace, F.; Corsaro, C.; Stanley, H.E. Possible relation of water structural relaxation to water anomalies. Proc. Natl. Acad. Sci. USA 2013, 110, 4899–4904. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.H.; Späh, A.; Pathak, H.; Perakis, F.; Mariedahl, D.; Amann-Winkel, K.; Sellberg, J.A.; Lee, J.H.; Kim, S.; Park, J.; et al. Maxima in the thermodynamic response and correlation functions of deeply supercooled water. Science 2017, 358, 1589–1593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, L.; Chen, S.-H.; Faraone, A.; Yen, C.W.; Mou, C.Y. Pressure dependence of fragile-to-strong transition and a possible second critical point in supercooled confined water. Phys. Rev. Lett. 2005, 95, 117802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Fazio, E.; Chen, S.-H. Some considerations on the water polymorphism and the liquid-liquid transition by the density behavior in the liquid phase. J. Chem. Phys. 2019, 151, 044504. [Google Scholar] [CrossRef]
- Abascal, J.L.; Vega, C. Widom line and the liquid-liquid critical point for the TIP4P/2005 water model. J. Chem. Phys. 2010, 133, 234502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abascal, J.L.; Vega, C. Note: Equation of state and compressibility of supercooled water: Simulations and experiment. J. Chem. Phys. 2011, 134, 186101. [Google Scholar] [CrossRef]
- Ni, Y.; Skinner, J.L. Evidence for a liquid-liquid critical point in supercooled water within the E3B3 model and a possible interpretation of the kink in the homogeneous nucleation line. J. Chem. Phys. 2016, 144, 214501. [Google Scholar] [CrossRef]
- Sellberg, J.A.; Huang, C.; McQueen, T.A.; Loh, N.D.; Laksmono, H.; Schlesinger, D.; Sierra, R.G.; Nordlund, D.; Hampton, C.Y.; Starodub, D.; et al. Ultrafast X-ray probing of water structure below the homogeneous ice nucleation temperature. Nature 2014, 510, 381–384. [Google Scholar] [CrossRef]
- Mallamace, F.; Branca, C.; Broccio, M.; Corsaro, C.; Mou, C.-Y.; Chen, S.-H. The anomalous behavior of the density of water in the range 30 K–373 K. Proc. Natl. Acad. Sci. USA 2007, 104, 18387–18391. [Google Scholar] [CrossRef] [Green Version]
- Erko, M.; Wallacher, D.; Hoell, A.; Hauß, T.; Zizak, I.; Paris, O. Density minimum of confined water at low temperatures: A combined study by small-angle scattering of X-rays and neutrons. Phys. Chem. Chem. Phys. 2012, 14, 3852–3858. [Google Scholar] [CrossRef]
- Bridgman, P.W. Water, in the liquid and five solid forms, under pressure. Proc. Am. Acad. Art. Sci. 1912, 47, 441–558. [Google Scholar] [CrossRef]
- Palmer, J.C.; Poole, P.H.; Sciortino, F.; Debenedetti, P.G. Advances in Computational Studies of the Liquid-Liquid Transition in Water and Water-Like Models. Chem. Rev. 2018, 118, 9129–9151. [Google Scholar] [CrossRef] [PubMed]
- Mallamace, D.; Corsaro, E.; Mallamace, F.; Stanley, H.E. Experimental tests for a liquid-liquid critical point in water. Sci. China-Phys. Mech. Astron. 2020, 63, 127001. [Google Scholar] [CrossRef]
- Adam, G.; Gibbs, J.H. On temperature dependence of cooperative relaxation properties uìin glass forming liquids. J. Chem. Phys. 1965, 43, 139. [Google Scholar] [CrossRef] [Green Version]
- Starr, F.; Angell, C.A.; Stanley, H.E. Prediction of entropy and dynamic properties of water below the homogeneous nucleation temperature. Phys. A 2003, 323, 51. [Google Scholar] [CrossRef] [Green Version]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Fazio, E.; Chen, S.-H.; Cupane, A. Specific Heat and Transport Functions of Water. Int. J. Mol. Sci. 2020, 21, 622. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P.; Buldyrev, S.V.; Becker, S.R.; Poole, P.H.; Starr, F.W.; Stanley, H.E. Relation between the Widom line and the breakdown of the Stokes-Einstein relation in supercooled water. Proc. Natl. Acad. Sci. USA 2007, 104, 9575–9579. [Google Scholar] [CrossRef] [Green Version]
- Lang, E.W.; Girlich, D.; Lüdemann, H.D.; Piculell, L.; Müller, D. Proton spin-lattice relaxation rate in supercooled H2O and H217O under high pressure. J. Chem. Phys. 1990, 93, 4796. [Google Scholar] [CrossRef] [Green Version]
- Handa, Y.P.; Mishima, O.; Whalley, E. High-density amorphous ice. III. Thermal properties. J. Chem. Phys. 1986, 84, 2766. [Google Scholar] [CrossRef]
- Archer, D.G.; Carter, R.W. Thermodynamic properties of the NaCl+H2O system. 4. Heat capacities of H2O and NaCl(aq) in cold-stable and supercooled states. J. Phys. Chem. B 2000, 104, 8563. [Google Scholar] [CrossRef]
- Tombari, E.; Ferrari, C.; Salvetti, G. Heat capacity anomaly in a large sample of supercooled water. Chem. Phys. Lett. 1999, 300, 749. [Google Scholar] [CrossRef]
- Lin, C.-W.; Trusler, J.P.M. The speed of sound and derived thermodynamic properties of pure water at temperatures between (253 and 473) K and at pressures up to 400 MPa. J. Chem. Phys. 2012, 136, 094511. [Google Scholar] [CrossRef] [PubMed]
- Oguni, M.; Maruyama, S.; Wakabayashi, K.; Nagoe, A. Glass transitions of ordinary and heavy water within silica-gel nanopores. Chem. Asian J. 2007, 2, 514. [Google Scholar] [CrossRef] [PubMed]
- Oguni, M.; Kanke, Y.; Namba, S. Thermal properties of the water confined within nanopores of silica MCM-41. AIP Conf. Proceed. 2008, 982, 34. [Google Scholar]
- Stejskal, E.O.; Tanner, J.E. Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. J. Chem. Phys. 1965, 42, 288. [Google Scholar] [CrossRef] [Green Version]
- Götze, W.; Sjögren, L. Relaxation processes in supercooled liquids. Rep. Prog. Phys. 1992, 55, 241. [Google Scholar] [CrossRef]
- Mallamace, F.; Corsaro, C.; Mallamace, D.; Vasi, C.; Stanley, H.E. The thermodynamical response functions and the origin of the anomalous behavior of liquid water. Farad. Disc. 2013, 167, 95. [Google Scholar] [CrossRef] [PubMed]
- Catalán, J.; del Valle, J.C. Molecule 1-Methyl-5-nitroindoline Probes the Structural Change of Liquid Water with Temperature. ACS Omega 2018, 3, 18930–18934. [Google Scholar] [CrossRef]
- Abragam, A. The Principles of Nuclear Magnetism; Oxford. U. P.: London, UK, 1961. [Google Scholar]
- Bloembergen, N.; Purcell, E.M.; Pound, R.V. Relaxation Effects in Nuclear Magnetic Resonance Absorption. Phys. Rev. 1948, 73, 679. [Google Scholar] [CrossRef]
- Kubo, R.; Tomita, K. A general theory of magnetic resonace absorption. J. Phys. Soc. Jpn. 1954, 9, 888. [Google Scholar] [CrossRef]
- Hindman, J.C.; Svirrnickas, A.; Wood, M. Relaxation processes in water-study of proton spin-lattice relaxation time. J. Chem. Phys. 1973, 59, 1517. [Google Scholar] [CrossRef]
- Hindman, J.C. Relaxation processes in water-viscosity, self-diffusion, and spin-lattice relaxation-kinetic model. J. Chem. Phys. 1974, 60, 4488. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Weber, T.A. Hidden structure in liquids. Phys. Rev. A 1982, 25, 978. [Google Scholar] [CrossRef]
- Mallamace, F.; Branca, C.; Corsaro, C.; Leone, N.; Spooren, J.; Chen, S.-H.; Stanley, H.E. Transport properties of glass-forming liquids suggest that dynamic crossover temperature is as important as the glass transition temperature. Proc. Natl. Acad. Sci. USA 2010, 107, 22457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yip, S.; Short, M.P. Multiscale materials modelling at the mesoscale. Nat. Mat. 2013, 12, 774. [Google Scholar] [CrossRef] [PubMed]
- Hestand, N.J.; Skinner, J.L. Perspective: Crossing the Widom line in no man’s land: Experiments, simulations, and the location of the liquid-liquid critical point in supercooled water. J. Chem. Phys. 2018, 149, 140901. [Google Scholar] [CrossRef] [Green Version]
- Mallamace, F.; Mensitieri, D.; Mallamace, D.; Salzano de Luna, M.S.; Chen, S.-H. Some aspects of the liquid water thermodynamic behavior: From the stable to the deep supercooled regime. Int. J. Mol. Sci. 2020, 21, 7269. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallamace, F.; Mallamace, D.; Mensitieri, G.; Chen, S.-H.; Lanzafame, P.; Papanikolaou, G. The Water Polymorphism and the Liquid–Liquid Transition from Transport Data. Physchem 2021, 1, 202-214. https://doi.org/10.3390/physchem1020014
Mallamace F, Mallamace D, Mensitieri G, Chen S-H, Lanzafame P, Papanikolaou G. The Water Polymorphism and the Liquid–Liquid Transition from Transport Data. Physchem. 2021; 1(2):202-214. https://doi.org/10.3390/physchem1020014
Chicago/Turabian StyleMallamace, Francesco, Domenico Mallamace, Giuseppe Mensitieri, Sow-Hsin Chen, Paola Lanzafame, and Georgia Papanikolaou. 2021. "The Water Polymorphism and the Liquid–Liquid Transition from Transport Data" Physchem 1, no. 2: 202-214. https://doi.org/10.3390/physchem1020014
APA StyleMallamace, F., Mallamace, D., Mensitieri, G., Chen, S.-H., Lanzafame, P., & Papanikolaou, G. (2021). The Water Polymorphism and the Liquid–Liquid Transition from Transport Data. Physchem, 1(2), 202-214. https://doi.org/10.3390/physchem1020014








