Simplified Gravity Load Collapse Dynamic Analysis of Old-Type Reinforced Concrete Frames
Abstract
1. Introduction
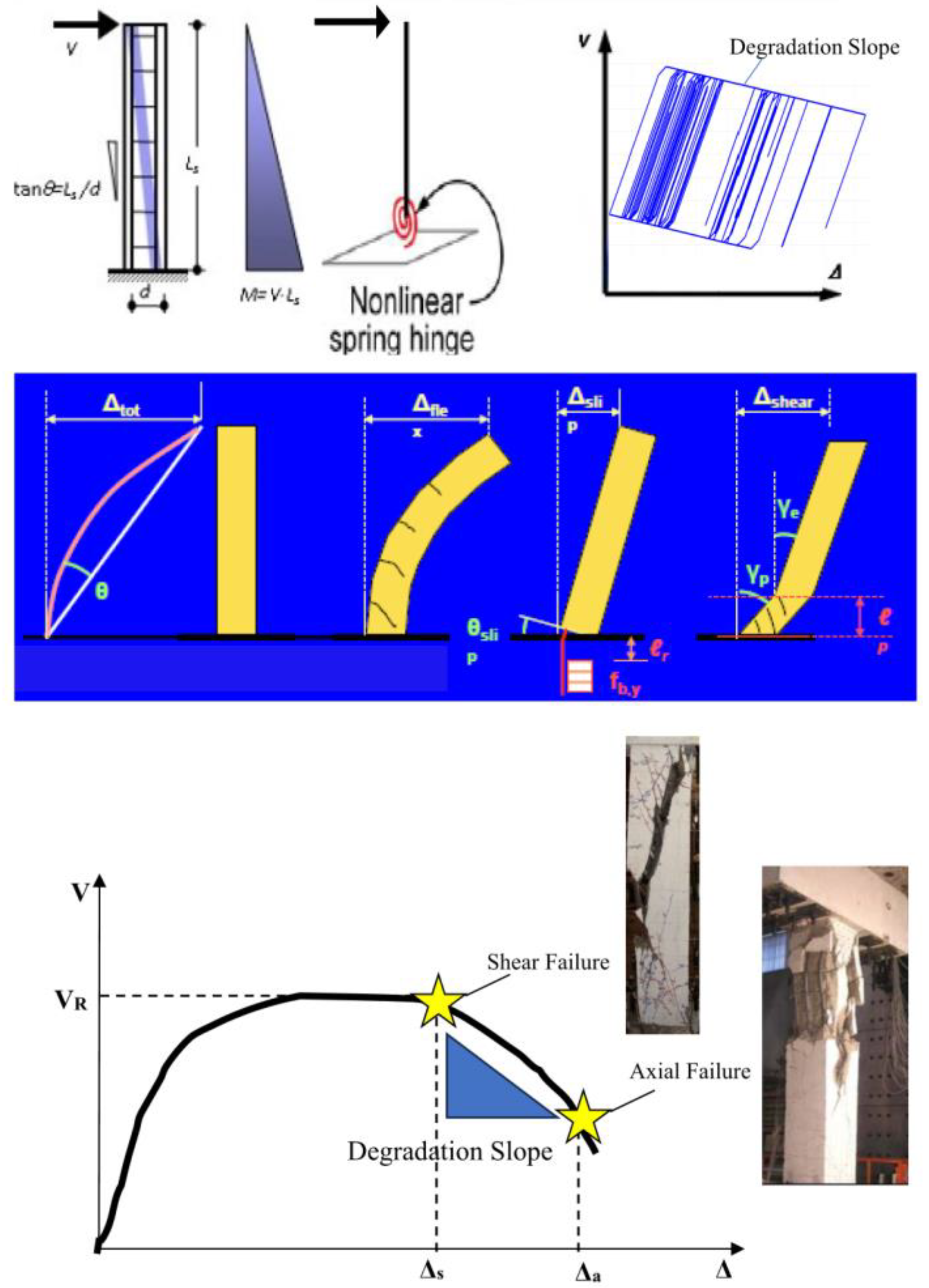
- The formulation of path-dependent one-component element response with strength degradation due to shear and axial failures is described in detail.
- Self-developed MATLAB [32] code is created in order to run a nonlinear dynamic analysis on one-story, two-bay reinforced concrete frames experiencing both shear and axial failures, which were simulated with the above formulated beam element.
- The proposed analytical model can also address the stress state of a column under full cyclic load reversals, accounting for both flexure- and shear-dominated response conditions in RC columns, while also considering the contribution of anchorage or lap-splice pull-out slip to the total drift.
- A reduced computational model for prediction of dynamic response of old reinforced concrete structures under seismic loads is developed based on the moment–rotation envelope results from cantilever shear-critical columns analyzed by Phaethon Windows software (Version 1.0).
- Inelastic frame structures experiencing shear, axial, or pull-out failures are modeled in this study by placing a rigid plastic spring at the location where shear failure is predicted considering the contribution of anchorage and pull-out slip in the total drift and applying a degradation slope. The negative slope connects the point on the moment–rotation envelope where shear failure occurs to the point of axial failure.
- The advantage of the proposed approach is that the inelastic deformation at the member ends depends solely on the moment applied at the end, allowing any moment–rotation hysteretic model to be assigned to the spring, hence simplifying the analytical and numerical modeling.
2. Materials and Methods
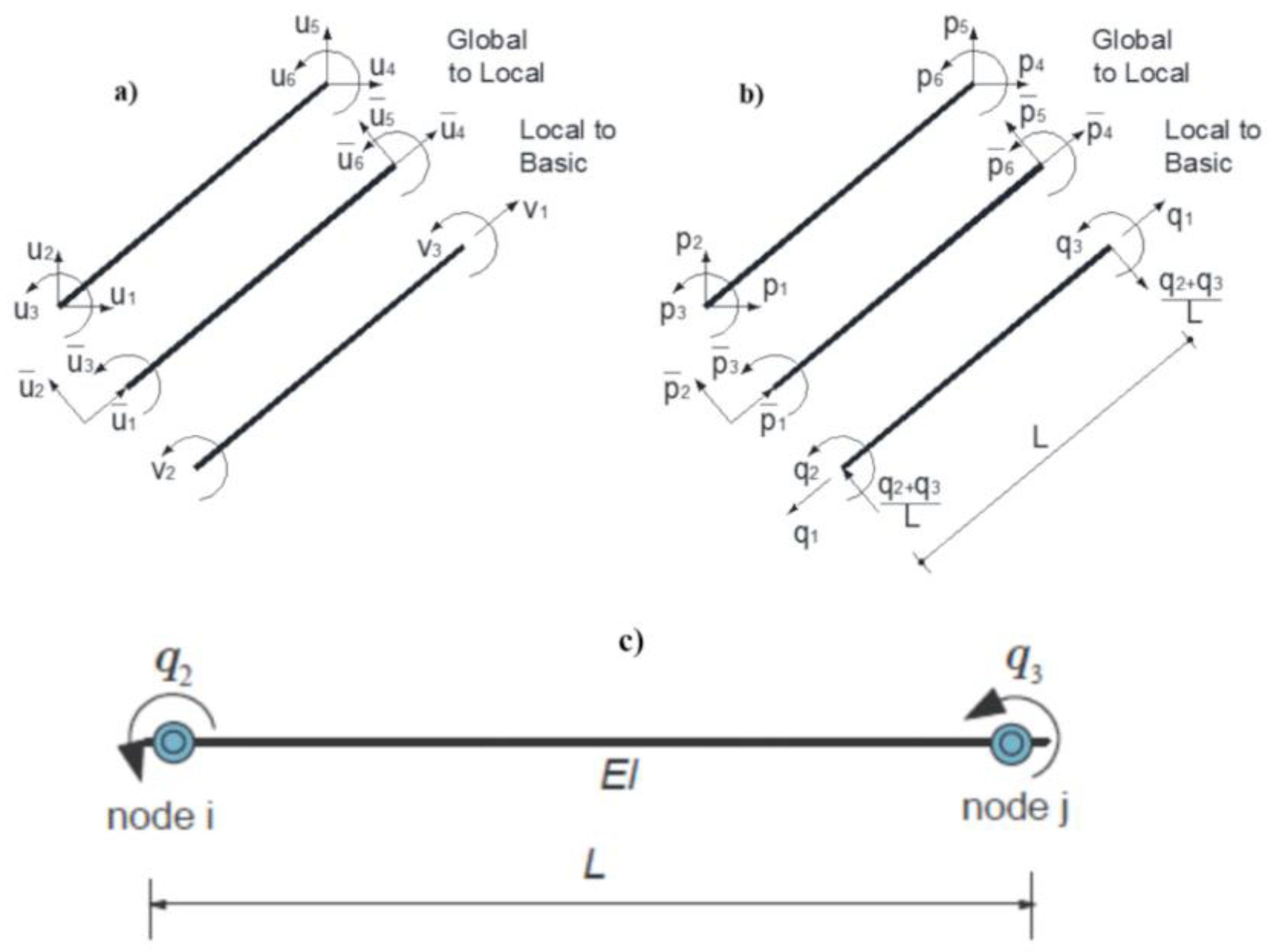
2.1. Path-Dependent Element Response with Strength Degradation
- Additive deformation decomposition
- Force–deformation relation
- Yield condition with
- Flow rule iff
- Kuhn–Tucker conditions and and for k = 2,3
- Consistency condition for k = 2,3
2.2. Experimental Test Setup
3. Results
3.1. Pushover Analysis of Center Shear-Critical RC Cantilever Column
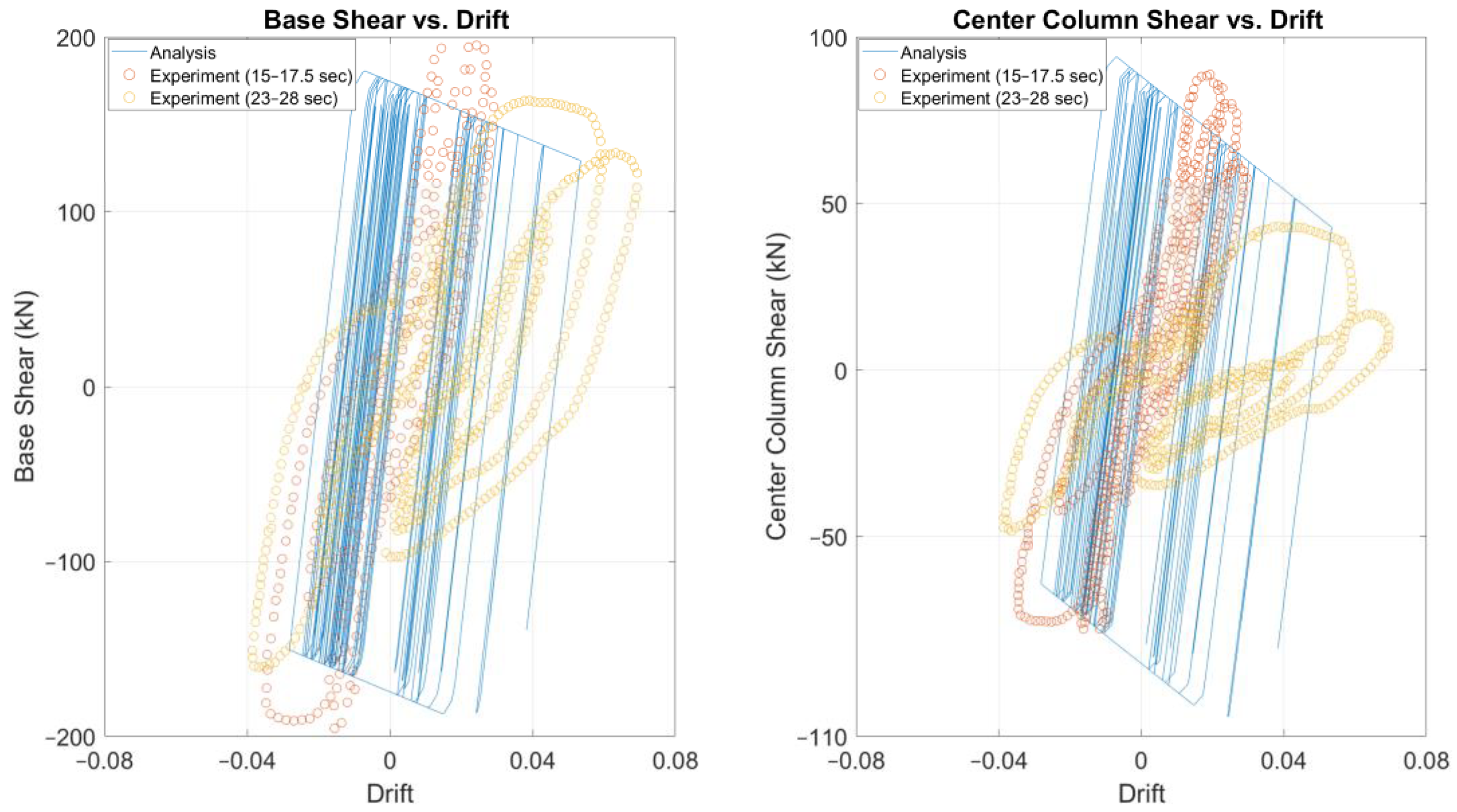
3.2. Nonlinear Time-History Analysis of Specimen 2
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Megalooikonomou, K.G. Modeling the Behavior of Shear-Critical Reinforced Concrete Columns Under Lateral Loads. Ph.D. Thesis, Department of Civil and Environmental Engineering, Faculty of Engineering, University of Cyprus, Nicosia, Cyprus, December 2019. [Google Scholar] [CrossRef]
- Megalooikonomou, K.G. Seismic Assessment and Retrofit of Reinforced Concrete Columns, 1st ed.; Cambridge Scholars Publishing: Newcastle upon Tyne, UK, 2019; p. 387. [Google Scholar]
- Elwood, K.J.; Moehle, J.P. Drift capacity of reinforced concrete columns with light transverse reinforcement. Earthq. Spectra 2005, 21, 71–89. [Google Scholar] [CrossRef]
- Elwood, K.J.; Moehle, J.P. Axial Capacity Model for Shear-Damaged Columns. ACI Struct. J. 2005, 102, 578–587. [Google Scholar]
- Asteris, P.G.; Antoniou, S.T.; Sophianopoulos, D.S.; Chrysostomou, C.Z. Mathematical Macromodeling of Infilled Frames: State of the Art. J. Struct. Eng. ASCE 2011, 137, 1508–1517. [Google Scholar] [CrossRef]
- Gicev, V.; Trifunac, M.D. Non-Linear Earthquake Waves in Seven-Storey Reinforced Concrete Hotel; Report CE 06-03; Deptartment of Civil Engineering, University of Southern California: Los Angeles, CA, USA, 2006. [Google Scholar]
- Palomo, I.R.I.; Frappa, G.; de Almeida, L.C.; Trautwein, L.M.; Pauletta, M. Analytical and numerical models to determine the strength of RC exterior beam–column joints retrofitted with UHPFRC. Eng. Struct. 2024, 312, 118244. [Google Scholar] [CrossRef]
- ACI Committee 318; Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary. American Concrete Institute: Farmington Hills, MI, USA, 2014.
- Fib Model Code Chapter 6: Interface Characteristics; Ernst & Sohn Publications: Berlin, Germany, 2010; p. 434.
- AASHTO LRFD Bridge Design Specifications and Commentary, 3rd ed.; American Association of State Highway Transportation Officials: Washington, DC, USA, 2013; p. 1264.
- Morsch, E. Der Eisenbetonbau-Seine Theorie und Anwendung, 5th ed.; Wittwer: Stuttgart, Germany, 1922; Volume 1, Part 1. [Google Scholar]
- Ritter, W. Die Bauweise Hennebique. Schweiz. Bauztg. 1899, 33, 59–61. [Google Scholar]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- Vecchio, F.J.; Collins, M.P. The modified compression field theory for reinforced concrete elements subjected to shear. ACI J. Proc. 1986, 83, 219–231. [Google Scholar]
- Filippou, F.C.; Fenves, G.L. Methods of analysis for earthquake-resistant structures. In Earthquake Engineering: From Engineering Seismology to Performance-Based Engineering; Bozorgnia, Y., Bertero, V.V., Eds.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Mergos, P.E.; Kappos, A.J. A distributed shear and flexural flexibility model with shear–flexure interaction for R/C members subjected to seismic loading. Earthquake Eng. Struct. Dyn. 2008, 37, 1349–1370. [Google Scholar] [CrossRef]
- Ceresa, P.; Petrini, L.; Pinho, R. Flexure-shear fiber beam-column elements for modeling frame structures under seismic loading-state of the art. J. Earthq. Eng. 2007, 11, 46–88. [Google Scholar] [CrossRef]
- Vecchio, F.J.; Collins, M.P. Predicting the Response of Reinforced Concrete Beams Subjected to Shear Using Modified Compression Field Theory. ACI Struct. J. 1988, 85, 258–268. [Google Scholar]
- Zeris, C.A. Three-Dimensional Nonlinear Response of Reinforced Concrete Buildings. Ph.D. Thesis, Department of Civil and Environmental Engineering, University of California, Berkeley, CA, USA, 1986. [Google Scholar]
- Bentz, E.C. Sectional Analysis of Reinforced Concrete Members. Ph.D. Thesis, Department of Civil Engineering, University of Toronto, Toronto, ON, Canada, 2000. [Google Scholar]
- Megalooikonomou, K.G. Monotonic and Cyclic Seismic Analyses of Old-Type RC Columns with Short Lap Splices. Constr. Mater. 2024, 4, 329–341. [Google Scholar] [CrossRef]
- Giberson, M.F. The Response of Nonlinear Multi-Story Structures Subjected to Earthquake Excitation; EERL Report; Earthquake Engineering Research Laboratory, California Institute of Technology: Pasadena, CA, USA, 1967. [Google Scholar]
- Giberson, M.F. Two Nonlinear Beams with Definition of Ductility. J. Struct. Div. ASCE 1969, 95, 137–157. [Google Scholar] [CrossRef]
- Zimos, D.K.; Mergos, P.E.; Kappos, A.J. Modelling of R/C members accounting for shear failure localisation: Finite element model and verification. Earthq. Eng. Struct. Dyn. 2018, 47, 1631–1650. [Google Scholar] [CrossRef]
- Zou, X.; Gong, M.; Zuo, Z.; Liu, Q. An efficient framework for structural seismic collapse capacity assessment based on an equivalent SDOF system. Eng. Struct. 2024, 300, 117213. [Google Scholar] [CrossRef]
- Zou, X.; Gong, M.; Zuo, Z. An efficient method based on shear models for structural seismic response prediction considering hysteretic characteristics. Bull. Earthq. Eng. 2024, 22, 6607–6642. [Google Scholar] [CrossRef]
- Hwang, H.; Oh, K.; Choi, I.; Kang, J.; Shin, J. Rapid Estimation Method of Allowable Axial Load for Existing RC Building Structures to Improve Sustainability Performance. Sustainability 2024, 16, 6578. [Google Scholar] [CrossRef]
- Lapiro, I.; Eid, R.; Kovler, K. Degradation of RC Columns under Combined Exposure to Axial Loading, Stray Currents, and Chloride Ingress. Materials 2024, 17, 1295. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, H.; Fan, Z.; Mu, Z. Crack Propagation Law of Reinforced Concrete Beams. Appl. Sci. 2024, 14, 409. [Google Scholar] [CrossRef]
- LeBorgne, M.R.; Ghannoum, W.M. Analytical element for simulating lateral-strength degradation in reinforced concrete columns and other frame members. J. Struct. Eng. 2014, 140, 04014038. [Google Scholar] [CrossRef]
- Baradaran Shoraka, M.; Elwood, K.J. Mechanical model for non-ductile reinforced concrete columns. J. Earthq. Eng. 2013, 17, 937–957. [Google Scholar] [CrossRef]
- MATLAB: User’s Guide, Version R2024b; Mathworks Inc.: Natick, MA, USA, 2024.
- Megalooikonomou, K.G. KADET-based One-component Beam Model for the Simulation of Cyclic Lateral Response of URM walls. In Proceedings of the 18th World Conference on Earthquake Engineering (18WCEE), Milan, Italy, 1–5 July 2024. [Google Scholar]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer: New York, NY, USA, 1998. [Google Scholar]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Dover Publications: Mineola, NY, USA, 2000. [Google Scholar]
- Tastani, S.P.; Pantazopoulou, S.J. Reinforcement and concrete bond: State determination along the development length. J. Struct. Eng. ASCE 2013, 139, 1567–1581. [Google Scholar] [CrossRef]
- Elwood, K. Shake Table Tests and Analytical Studies on the Gravity Load Collapse of Reinforced Concrete Frames. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2002. [Google Scholar]
- Elwood, K.J.; Moehle, J.P. Dynamic collapse analysis for a reinforced concrete frame sustaining shear and axial failures. Earthq. Eng. Struct. Dyn. 2008, 37, 991–1012. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures, Theory and Applications to Earthquake Engineering, 5th ed.; Pearson Education: London, UK, 2017; p. 960. [Google Scholar]







| Case | Axial Load (kN) | Width (mm)–Depth (mm) | Shear Span (mm)– Straight Anchorage Length (mm) | Clear Cover (mm) | Concrete Strength (MPa) | Number–Diameter (mm)–Reinforcing Ratio of Longitudinal Bars | Yielding Strength of Long. Bars (MPa) | Ultimate Strength (MPa)–Spacing (mm)–Diameter (mm)–Ratio of Transv. Reinf. |
|---|---|---|---|---|---|---|---|---|
| Elwood and Moehle [37,38]–(Spec. 2–Center Column) | 308.132 | 230 230 | 814 298 | 25.4 | 24.27 | 4 and 4 12.7 and 15.875 0.0245 | 479.18 | 717 152 4.9 0.00236 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Megalooikonomou, K.G. Simplified Gravity Load Collapse Dynamic Analysis of Old-Type Reinforced Concrete Frames. Constr. Mater. 2024, 4, 704-720. https://doi.org/10.3390/constrmater4040038
Megalooikonomou KG. Simplified Gravity Load Collapse Dynamic Analysis of Old-Type Reinforced Concrete Frames. Construction Materials. 2024; 4(4):704-720. https://doi.org/10.3390/constrmater4040038
Chicago/Turabian StyleMegalooikonomou, Konstantinos G. 2024. "Simplified Gravity Load Collapse Dynamic Analysis of Old-Type Reinforced Concrete Frames" Construction Materials 4, no. 4: 704-720. https://doi.org/10.3390/constrmater4040038
APA StyleMegalooikonomou, K. G. (2024). Simplified Gravity Load Collapse Dynamic Analysis of Old-Type Reinforced Concrete Frames. Construction Materials, 4(4), 704-720. https://doi.org/10.3390/constrmater4040038





