Fracture Undulation Modelling in Discontinuum Analysis: Implications for Rock-Mass Strength Assessment

Abstract

Synthetic rock mass (SRM) models commonly represent fractures as planar surfaces, potentially oversimplifying the complex geometries observed in natural rock masses. This study investigates whether incorporating large-scale fracture undulations significantly affects predicted rock-mass strength compared to conventional flat joint representations. Using the Finite-Discrete Element Method (FDEM), we analyzed multiple discrete fracture network (DFN) configurations under uniaxial and biaxial loading conditions, comparing models with geometrically simplified planar fractures against those incorporating conceptual undulated surfaces. Results reveal counterintuitive and inconsistent patterns across different DFN geometrical realizations, demonstrating that network topology and connectivity patterns govern overall behaviour more than individual fracture geometry. These findings challenge assumptions that geometric simplification can be systematically compensated through parameter adjustments. However, given that detailed fracture characterization data are typically unavailable until design completion, and even accessible rock outcrops provide only limited 2D surface exposures of inherently 3D fracture networks, pursuing sophisticated geometric representations may be impractical. Instead, engineering practice should focus on quantifying inherent variability bounds.

1. Introduction

In the past decades, the landscape of rock-mass characterization and modelling has undergone a dramatic transformation. Many may be familiar with the quote by Box [1] that “All models are wrong but some are useful.” The meaning of this quote extends beyond the models we use daily for rock engineering problems, and it raises questions about the robustness of scientific model-building. A key indicator of model simplicity is the number of parameters it includes and the number of features it attempts to capture. Quoting Box’s [1], “models with fewer parameters are considered parsimonious. Parsimony offers several advantages: (I) when the underlying reality has simple patterns, keeping models simple helps reveal these patterns while unnecessary complexity can hide them; (ii) simpler models typically provide more precise predictions; (iii) constantly adding complexity is not always practical since there is no natural stopping point.”

This last point is analogous to Jevons’ Paradox [2], which describes the counterintuitive economic phenomenon where improving the efficiency of a resource leads to increased consumption of that resource rather than conservation. Just as Jevons observed that more efficient steam engines led to greater coal consumption in 19th-century England, the field of computational modelling faces a similar dynamic.

As technological innovation continuously increases the availability of faster computers with greater processing power and memory, engineers and researchers find themselves with expanded computational capacity. This increased efficiency may tempt engineers to exploit the additional capability by creating increasingly complex models. What begins as a reasonable increase in model sophistication can quickly spiral into an endless pursuit of ever-greater detail and elaboration. This computational version of Jevons’ Paradox manifests in several ways: models incorporate more parameters, attempt to capture additional physical phenomena, increase spatial or temporal resolution, or expand the scope of systems being analyzed. While each incremental addition may seem justified individually, the cumulative effect can lead to models that are computationally intensive, difficult to validate, and potentially less reliable despite their apparent sophistication. The parallel is particularly striking because, in both cases, the underlying assumption that “more efficiency enables better outcomes” proves problematic. Just as improved coal efficiency did not reduce overall coal consumption, improved computational efficiency does not necessarily lead to better engineering solutions. While it may just enable more complex simulations, it does not guarantee that those simulations will capture the correct failure mechanism. This highlights the importance of maintaining disciplined approaches to model development that prioritize essential features over exhaustive detail.

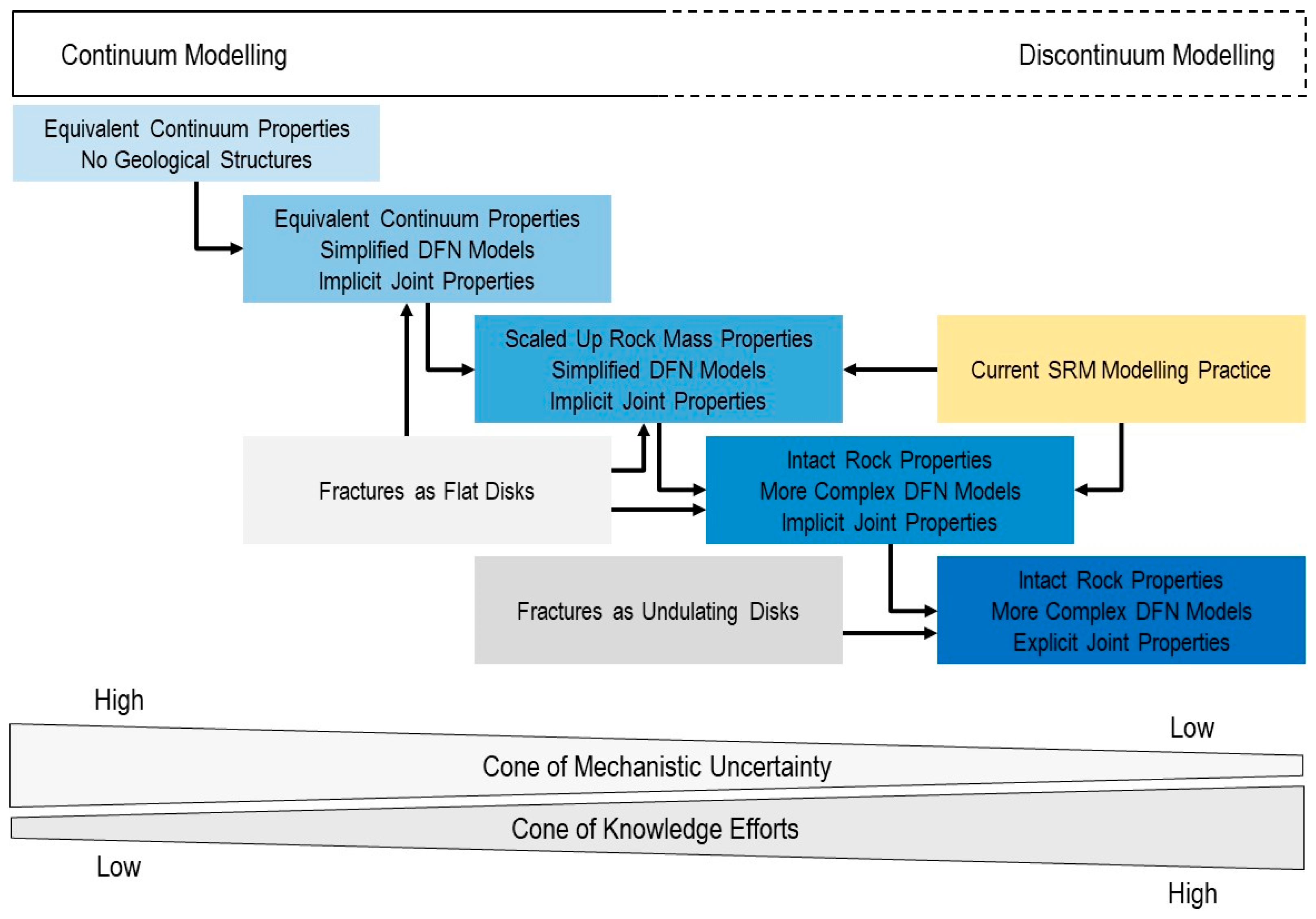
Figure 1 illustrates the spectrum of modelling practices currently employed in rock engineering projects, ranging from continuum to discontinuum models, and emphasizes the approaches that can be used to represent fracture networks within these models. The objective of this paper is to highlight a critical knowledge gap in current synthetic rock mass (SRM) modelling approaches, that is, the systematic representation of fractures as planar surfaces. The objective is to test the hypothesis of whether this geometrical simplification may introduce artificial failure mechanisms that do not reflect real rock-mass behaviour. The concern addressed here focuses specifically on large-scale fracture undulations at the metre scale, distinct from small-scale surface roughness, which is typically characterized by established metrics such as the Joint Roughness Coefficient (JRC) in the Barton-Bandis criterion [3].

While small-scale roughness affects local shear strength parameters, large-scale undulations influence stress distributions and failure propagation mechanisms across the modelled rock mass. A fundamental contradiction exists in current SRM modelling practices. Despite significant advances in computational capabilities that enable increasingly sophisticated small-scale rock mass simulations with enhanced resolution and complex constitutive models, these improvements have been achieved while systematically ignoring the potential impacts of large-scale fracture undulations. This represents a curious inverse relationship between technological capability and geometric fidelity. At the same time, it underutilizes valuable field data that can be collected during site investigations using modern mapping techniques, including terrestrial laser scanning and photogrammetry, which capture natural undulations and non-planar characteristics.

The assumption of planar fractures represents a fundamental geometric simplification that raises several important questions:

• Do flat fracture representations adequately capture stress concentration patterns around fracture tips and intersections?
• How do simplified geometries affect the prediction of progressive failure mechanisms in jointed rock masses?
• What is the cumulative effect of geometric simplification on the assessment of rock-mass strength?
• Do current modelling approaches properly represent the mechanical interaction between fracture networks and intact rock bridges?

These considerations suggest the need to evaluate whether the prevalent geometric simplification in SRM models fundamentally compromises their ability to accurately predict rock-mass behaviour. The research motivation lies not merely in technical implementation, but in determining whether the convenience of planar approximations comes at an unacceptable cost to engineering applications.

Before a detailed examination of the modelling approach and its outcomes, fundamental consideration must be given to the mapping of undulation data and the nature of rock mass strength itself. Adapting the words by Box [1], the authors of this paper, having made tentative inferences on the applicability of SRM models, “quickly switch their attitude from that of sponsor to that of critic.”

2. The Challenge of Mapping Undulation Data

While the focus of this paper is primarily the geometrical representation of fractures in SRM models, it is also important to recognize the trade-offs associated with the mapping and measurement of undulation data.

Joint undulation characteristics vary systematically with observation scale, presenting a fundamental challenge for model parameterization. Barton [4] addressed this issue by recommending the use of JRC (joint roughness coefficient) and conversion charts. The asperity amplitude or approximate JRC relationships, in conjunction with the updated conversion charts [5], accounted for scale effects. However, the limitations of these ubiquitous implementations require careful consideration. For example, Tannant et al. [6] found that scaled JRC estimates often produce values in excess of what would be considered reasonable when compared to field observations.

New techniques, such as semantic segmentation, offer promising options for directly extracting digital joint undulation profiles from images [5,7]. These methods can automatically identify and digitize fracture surface characteristics, potentially enabling rapid characterization of large fracture populations. However, implementation requires substantial training datasets to achieve reliable results; furthermore, its accuracy is contingent on quality datasets with impeccable visual and technical attributes, i.e., ample lighting and no shadows.

3D topography of joint surfaces can be reconstructed from overlapping image series to create detailed undulation profiles for thorough 3D analyses [8]. This approach offers the advantage of capturing complete surface morphology, rather than linear profiles, for comprehensive geometric characterization. Multiple images taken from different viewing angles and subsequent processing are required to generate accurate 3D surface models.

Direct surface measurements using laser scanning provide high-resolution 3D characterization of joint profiles, informing both roughness and large-scale undulation parameters [9]. Digitized models obtained through laser scanning typically achieve greater resolution and accuracy compared to computer vision, photogrammetry, and manual characterization methods. However, like photogrammetry, laser scanning requires specialized equipment and expertise. Indeed, the selection of appropriate joint undulation characterization methods is invariably constrained by project timelines, available budgets, and technical capabilities. Engineers must carefully evaluate trade-offs between data collection costs and the value of obtained geometric information. More sophisticated characterization methods provide greater detail but require intense resource commitments, the results of which may offer marginal improvements to engineering decisions.

Perhaps most critically, the transition from field characterization data to numerical model parameters necessitates additional interpretation and simplification steps, which introduce further uncertainty (Figure 2). Even high-quality geometric characterization must ultimately be translated into computationally tractable representations that balance geometric fidelity, numerical stability, and computational efficiency.

The systematic reduction in this rich geometric information to simplified planar representations may constitute a significant loss of critical input data that could influence model predictions.

3. The Illusion of Deterministic Rock-Mass Strength

As presented in [10], the fundamental question is not whether numerical models can help us determine rock mass strength, but instead whether they provide genuinely helpful information within the context of irreducible uncertainty. Rock-mass strength does not exist as a singular, deterministic value waiting to be discovered through increasingly sophisticated analysis. Instead, it manifests as a range of conditional responses that vary with scale, stress path, and time-dependent processes. This range reflects not only measurement uncertainty but also the inherent variability of natural rock mass systems. The same authors recognized the challenge of verifying whether our numerical results represent reality as a critical epistemological obstacle that underlies all rock mass modelling. Unlike laboratory specimens, which can be subjected to comprehensive strength testing at the scales relevant to engineering applications, rock masses cannot be tested directly for their strength. We cannot extract a 10 m cube of a jointed rock mass and test it to failure. This creates an uncomfortable reality: our most sophisticated SRM models produce results that, in many instances, cannot be validated against empirical truth.

Given these limitations, numerical models should serve primarily as tools for exploring and acknowledging the boundaries of our knowledge. Their highest value lies not in providing definitive answers, but in systematically confronting us with what we do not know and cannot know with certainty. The role of models should be to challenge our preconceptions and force explicit consideration of alternative scenarios, rather than reinforcing existing beliefs through seemingly sophisticated analysis.

However, models may fail to redirect our thinking if we unconsciously guide them toward conclusions we have already reached through other means. This represents a subtle but pervasive form of confirmation bias in engineering practice. When model inputs, boundary conditions, and constitutive relationships are selected based on implicit expectations about outcomes, the resulting analysis becomes a sophisticated form of circular reasoning rather than genuine investigation. For instance, the problem of adopting the same boundary and loading conditions in SRM modelling as those used in laboratory testing has been demonstrated to be a limitation of current SRM approaches [11]. The same authors have questioned the concept of Representative Elementary Volume (REV). They raised a provocative and somewhat controversial challenge that the idea of REV developed from SRM results has evolved into a methodological convenience for adopting conservative lower-bound material properties in continuum modelling approaches, or for deliberately reducing structural complexity in discontinuum models by omitting geometric details deemed below the scale of interest.

This leads to a profound methodological challenge. While engineering questions may appear well-defined and bounded (e.g., “What is the rock mass strength for a given project?”), the range of credible answers may be practically unbounded. The variability in potential responses depends entirely on modelling assumptions regarding:

• Fracture network geometry and connectivity
• Constitutive behaviour of intact rock and discontinuities
• In situ stress conditions and their spatial variation
• Groundwater conditions and temporal fluctuations
• Scale effects and representative volume considerations
• Time-dependent processes and their rates

Each assumption introduces its uncertainty distribution, and the cumulative effect can produce answer ranges that span multiple orders of magnitude. Acknowledging these limitations does not diminish the value of numerical modelling, but instead calls for more honest and sophisticated approaches to engineering practice. Modelling results should not be presented as definitive answers, but as structured methods for exploring uncertainty and testing the sensitivity of engineering decisions to various assumptions about unknowable parameters.

The goal shifts from seeking the “correct” answer to understanding which decisions remain robust across the range of plausible scenarios, and which require additional investigation or a conservative design approach. This represents a more mature and scientifically honest approach to rock engineering practice; one that embraces uncertainty as an inherent characteristic of the problem rather than a temporary limitation to be overcome through better modelling.

This discussion underscores a fundamental limitation in rock engineering. Questioning whether the models presented later in Section 4 are truly validated becomes meaningless when we recognize that no one has ever directly measured the strength of a 10 m cube rock mass under controlled conditions. At best, model results can be calibrated against empirical pillar strength formulae. However, empirical pillar strength formulae remain inherently semi-quantitative due to the subjective nature of distinguishing between “stable” and “failed” conditions when assessing pillar performance in mining environments.

4. Synthetic Rock Mass Modelling

Although the SRM acronym was formally introduced by Pierce et al. [12] and subsequently developed by Mas Ivars et al. [13], earlier numerical simulations of fractured rock masses that satisfy the essential criteria of modern SRM models can be traced to Carvalho et al. [14] and Elmo [15]. Notably, Elmo [15] provided the first comprehensive assessment that systematically addressed all three fundamental SRM components within a unified framework, establishing the methodological foundation for subsequent developments in the field. This early work demonstrated the critical importance of integrating field data collection, fracture network modelling, and mechanical simulation rather than treating these elements as independent modelling exercises.

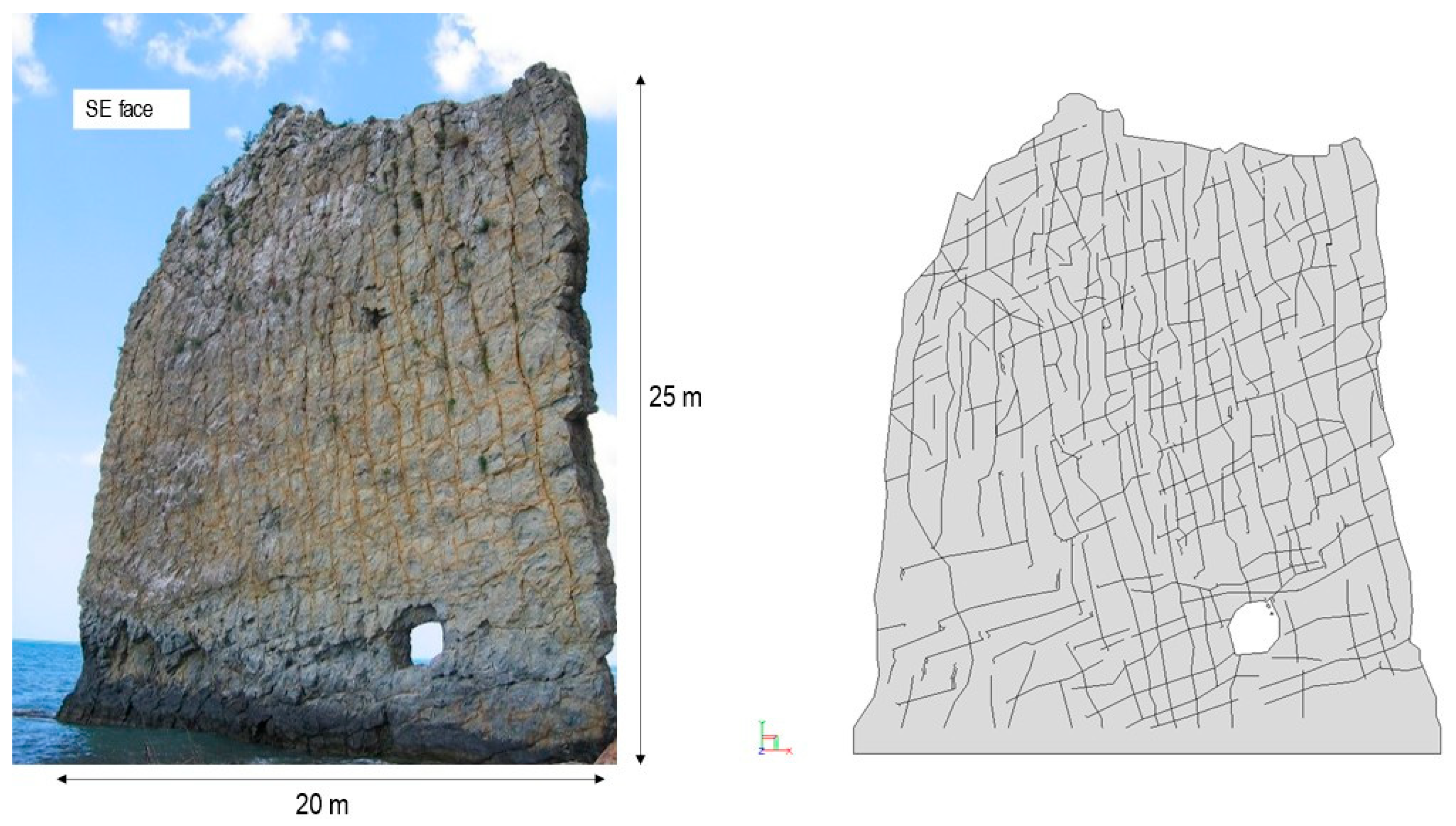
An equally significant aspect of SRM modelling has received surprisingly little attention in the literature. While continuum approaches explicitly require upscaled equivalent rock mass properties, discontinuum models face an analogous but less recognized scaling challenge. SRM models typically represent embedded Discrete Fracture Network (DFN) traces as geometrically simplified features, such as straight lines in two-dimensional analyses or planar surfaces in three-dimensional models. This geometric simplification necessitates a parallel upscaling of shear strength properties for discontinuities. The strength parameters must implicitly compensate for the mechanical effects of large-scale fracture undulations that natural fractures may exhibit in the field (see the example in Figure 3), but which are absent from the simplified geometric representation. In essence, discontinuum models face their version of the upscaling problem: they sacrifice geometric fidelity and attempt to recover mechanical accuracy through adjusted material properties.

Continuum methods simplify the discrete nature of fractured rock masses by compensating for it through equivalent properties, while discontinuum methods simplify fracture geometry by compensating for it through strength parameters. In both cases, critical aspects of real rock mass behaviour are replaced by parameter adjustments that may not adequately capture the complex mechanical interactions they are intended to represent.

The significance of fracture undulation representation varies considerably depending on the specific engineering context and loading conditions. Understanding these variations is crucial for making informed decisions about modelling complexity and resource allocation. The effects of geometric simplification become most pronounced under low normal stress conditions, where dilatancy mechanisms dominate fracture behaviour and the interlocking impacts of surface undulation exert primary control over shear resistance. Similarly, long-term stability assessments represent critical applications where progressive roughness degradation occurs over extended time periods, potentially altering the fundamental mechanical response of fracture networks.

While previous research has examined the effects of joint roughness on rock mass deformation and strength mobilization [16,17,18], remarkably little work has systematically investigated the potential effects of large-scale geometric undulation on SRM model behaviour. This research gap is particularly significant given that such undulations can be observed and mapped in field investigations but systematically excluded from numerical representations (see earlier Figure 2 and Figure 3, and later Figure 4). The model shown in Figure 4 represents a fractured rock mass subjected to gravitational loading; as such, it can reasonably be considered comparable to a uniaxially loaded SRM model.

The shear strength of discontinuities in SRM models is typically characterized using either Mohr-Coulomb failure criteria or the Barton-Choubey formulation [3]. Note that this paper does not question the fundamental validity of these well-established methods for characterizing discontinuity shear strength under controlled laboratory conditions. However, a critical concern arises regarding the application of characterization methods developed to replicate simple direct shear testing conditions to complex three-dimensional rock masses. The implicit assumption is that surface undulation has a negligible impact on rock mass interlocking mechanisms and, consequently, on overall modelled rock mass strength. However, this assumption requires careful reconsideration. Several researchers have demonstrated that smooth and rough joints exhibit markedly different mobilization patterns in physical rock mass replicas, with these differences being sufficiently pronounced to alter fundamental failure mechanisms [20,21,22]. These findings suggest that surface morphology has a more significant influence on rock mass behaviour than is typically recognized in numerical modelling practice.

Surface morphology influences both shear strength and dilation behaviour of natural fractures at low confinements; however, these critical factors may be inadequately captured when fractures are represented as straight lines in 2D analyses or flat surfaces in 3D models. The mechanical complexity introduced by geometric undulation may not necessarily be recovered through parameter adjustments alone.

Recognizing this limitation, Ambah and Elmo [23] presented an initial comparative study examining a series of 2D SRM models where embedded fracture traces are represented using two contrasting approaches: as straight lines with implicit frictional shear strength (expressed as ϕ = ϕ_b + i), versus as undulated lines with frictional resistance explicitly defined through the combination of basic friction angle (ϕ_b) and the geometric contribution of undulation. This paper expands on their work and presents some interesting results and conclusions.

5. SRM Modelling Results

The Finite-Discrete Element Method (FDEM) provides a hybrid modelling approach that effectively bridges the conceptual and computational gap between traditional continuum and discontinuum methods. This coupled approach allows for the simultaneous treatment of intact rock deformation through finite element formulations and discrete fracture behaviour through contact mechanics algorithms. The mathematical foundation and implementation details of the FDEM formulation employed in this study are comprehensively described by Munjiza et al. [24] and Owen et al. [25]. The study presented in this paper utilizes the proprietary FDEM code Elfen [26], which incorporates a coupled elastoplastic fracture mechanics constitutive framework. This implementation enables realistic simulation of progressive fracturing processes, including crack initiation, propagation, and coalescence within both intact rock material and along pre-existing discontinuities.

5.1. Model Set Up

Table 1. Material properties for DFN-A and DFN-B Models (base case intact rock conditions).

Rock	Unit	Value	Joints	Unit	Value
σt	MPa	2.4	cj	MPa	0
Gf	J m−2	5.9	ϕj	º	35
Ei	GPa	20.1	Kn	GPa m−1	50
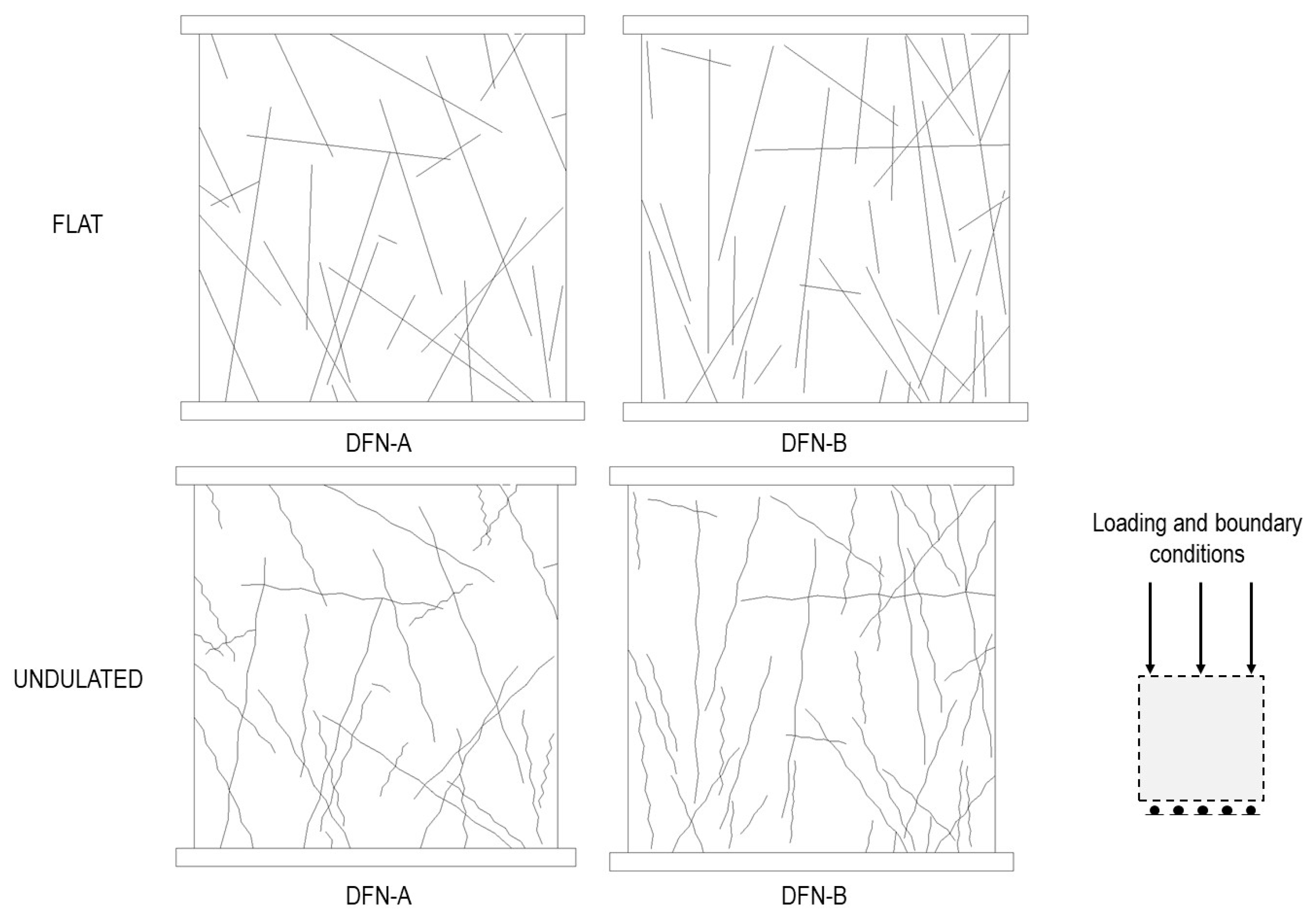
c	MPa	9.5	Ks	GPa m−1	5
ϕ	º	57

presents the mechanical properties assigned to intact rock and joint materials used throughout the modelling programme. The geometric configurations of the SRM models are illustrated in Figure 5 and Figure 6, with model dimensions of 10 m × 10 m under uniaxial and biaxial loading conditions. These configurations are based on the SRM model framework previously described by Elmo et al. [27], ensuring consistency with established modelling protocols while enabling direct comparison of results. The material properties are listed in Table 1 and

Table 2. Material properties for DFN-1, DFN-2 and DFN-3 Models.

Rock	Unit	Value	Joints	Unit	Value
σt	MPa	7.4	cj	MPa	0
Gf	J m−2	94.0	ϕj	º	35
Ei	GPa	49.0	Kn	GPa m−1	50
c	MPa	17.6	Ks	GPa m−1	5
ϕ	º	52.5

. These are also equivalent to those used by Elmo et al. (2020) in their SRM models. The symbols σ_t, G_f, E_i, c, ϕ, K_n, K_s refer to intact rock tensile strength, fracture energy, Young’s Modulus, intact rock cohesion, intact rock friction, normal and shear strengths, respectively.

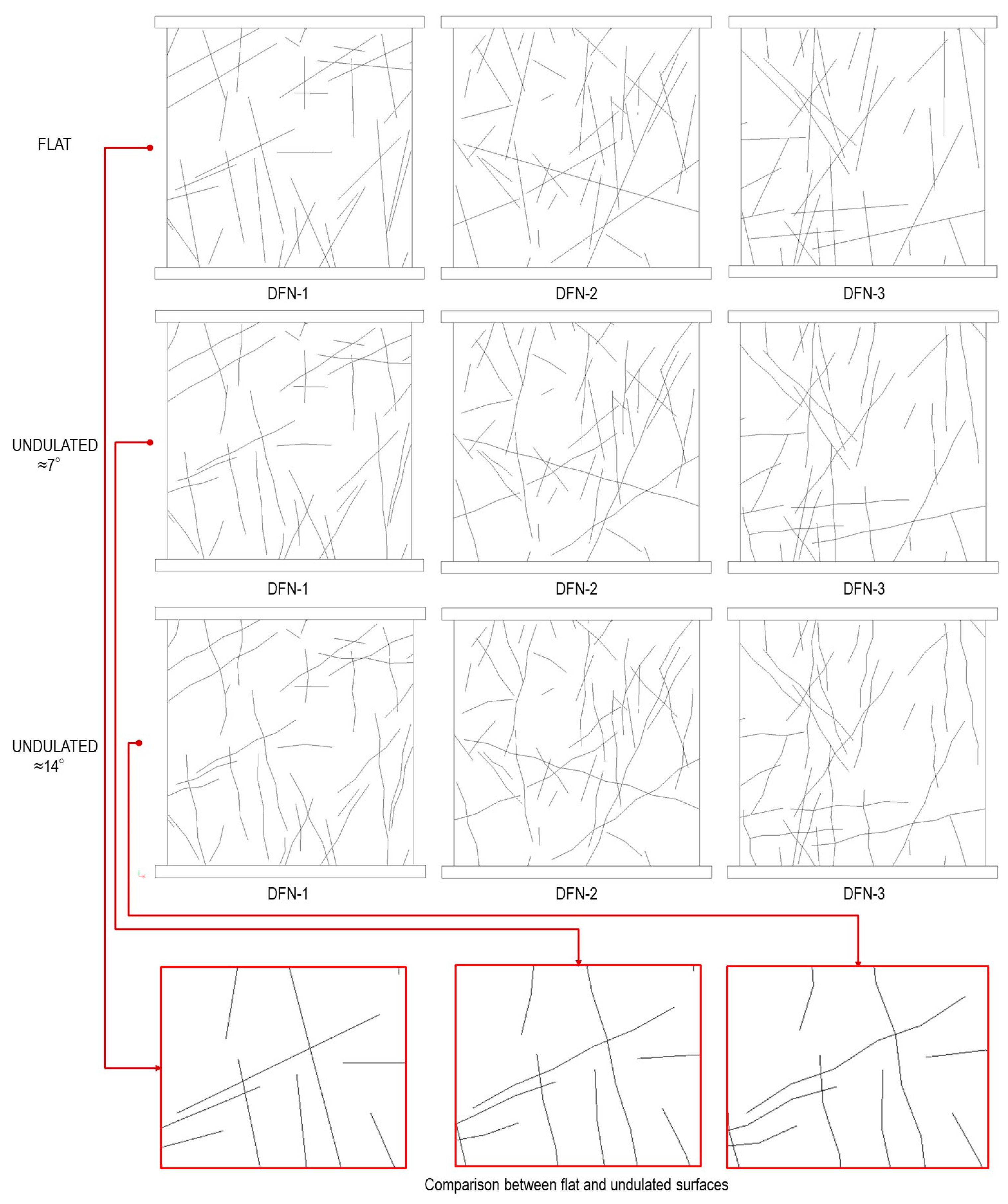
Characterizing the large-scale undulation, planarity, or stepped nature of natural fracture surfaces typically requires detailed analysis of accessible surface outcrops. However, for this initial investigation, the fracture undulation patterns implemented in the models are purely conceptual. The original planar DFN traces from [27] were manually modified to incorporate undulated geometries that represent idealized large-scale surface variations. It is important to note that no systematic attempt has been made to characterize these undulation patterns using established roughness quantification methods such as the Joint Roughness Coefficient (JRC) or standardized ISRM roughness profiles. Models DFN-A and DFN-B deployed relatively large and non-uniform undulations. However, Models DFN-1 to DFN-3 included many uniform undulations created to represent asperity angles of approximately 7 and 14 degrees (Figure 6).

These considerations reflect the conceptual nature of the current study, which focuses on demonstrating the potential mechanical significance of large-scale geometric undulation rather than precisely replicating specific field conditions.

5.2. SRM Results

The following analysis presents comparative results from five distinct DFN configurations to systematically evaluate the mechanical significance of fracture undulation representation in SRM models. Each configuration was analyzed under identical loading conditions using both planar and undulated fracture geometries, enabling direct assessment of geometric effects on predicted rock mass strength and failure mechanisms.

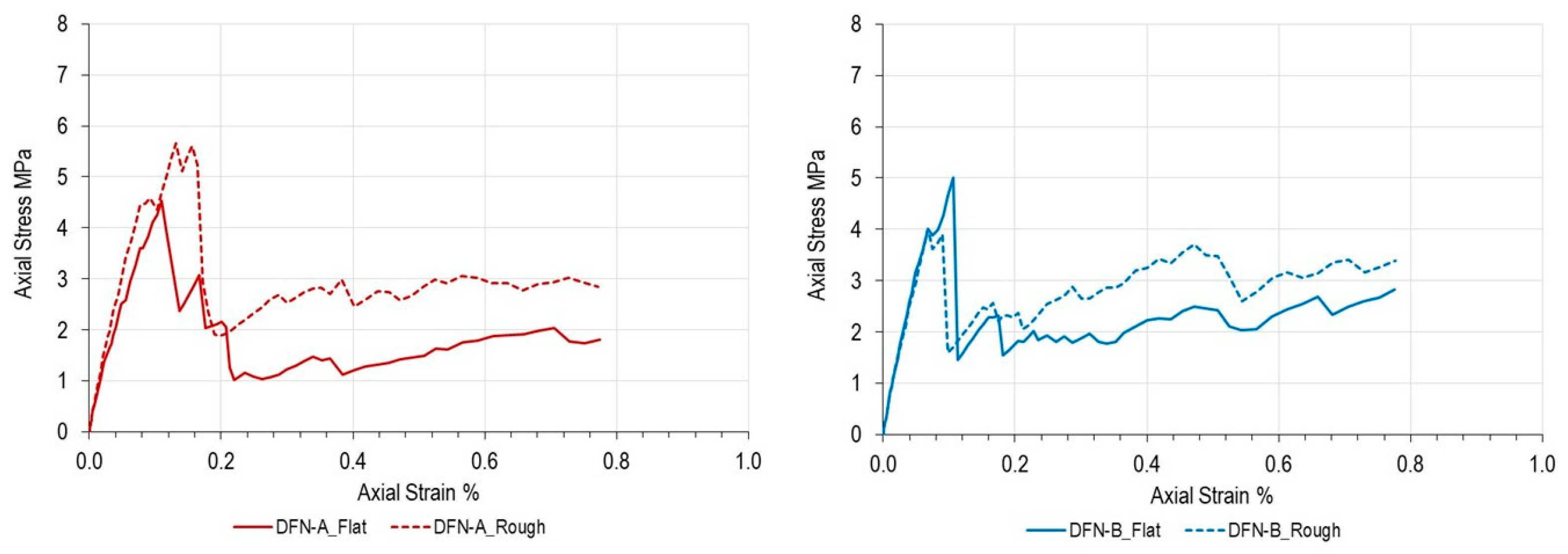
5.2.1. Models DFN-A and DFN-B

Figure 7 presents comparative results for models incorporating flat versus undulated fracture traces for DFN-A and DFN-B configurations, respectively. The results reveal a complex and counterintuitive pattern that challenges simplistic assumptions about geometric effects on rock mass strength. The DFN-A model with undulated fractures exhibits higher stress at failure compared to its flat counterpart. This increase reflects the additional shear resistance contributed by geometric undulation for equivalent friction angles assigned to the fracture traces in both models. For DFN-A, the difference in simulated strength between the two geometric representations is considered significant, with undulated traces yielding a uniaxial strength that is 25% higher than that of the flat traces. However, this seemingly logical relationship becomes inverted when examining the DFN-B results. The flat-fracture model yields strength values approximately 20% higher than the equivalent model with undulated traces. This reversal demonstrates that geometric effects on rock mass strength cannot be predicted solely from single-fracture considerations, highlighting the complex interaction between fracture geometry and network-scale behaviour. While shearing along individual fractures is indeed influenced by large-scale undulation, the behaviour of fractured rock masses containing multiple interacting discontinuities depends on fundamentally different mechanisms. The resulting strength and failure patterns become governed by the degree of connectivity and mechanical interlocking within the fracture network rather than the simple superposition of individual fracture responses. Importantly, interlocking should not be considered a directly measurable rock mass parameter in field investigations, as it emerges from the complex interaction between fracture geometry, network connectivity, and applied loading conditions. This emergent property cannot be predetermined from individual fracture characterization and varies dynamically with stress state and loading path.

To achieve equivalent strength predictions, the DFN-A model with flat surfaces requires increasing the joint friction angle to 40 degrees (+5 degrees compared to the baseline value (Figure 8). Due to the arbitrary process used to create the undulated fractures, the results demonstrate that geometric simplification cannot be compensated through simple parameter adjustments based on theoretical considerations alone, but requires empirical calibration against more realistic geometric representations.

The analysis was extended to investigate the influence of intact rock strength by incorporating stronger rock material properties (the same as those listed in Table 2), while maintaining all other modelling conditions. By doing so, in principle, the joint shear’s strength should mobilize earlier as there is more resistance to fracturing across the joints (for a given applied uniaxial load increment). The results, as shown in Figure 9, indicate a 38% and 11% increase in strength for DFN-A and DFN-B, respectively, when comparing undulated versus flat joints representations. These findings suggest that the impact of geometric simplification becomes more pronounced for stronger rock materials, where fracture behaviour exerts greater relative influence on overall rock mass response.

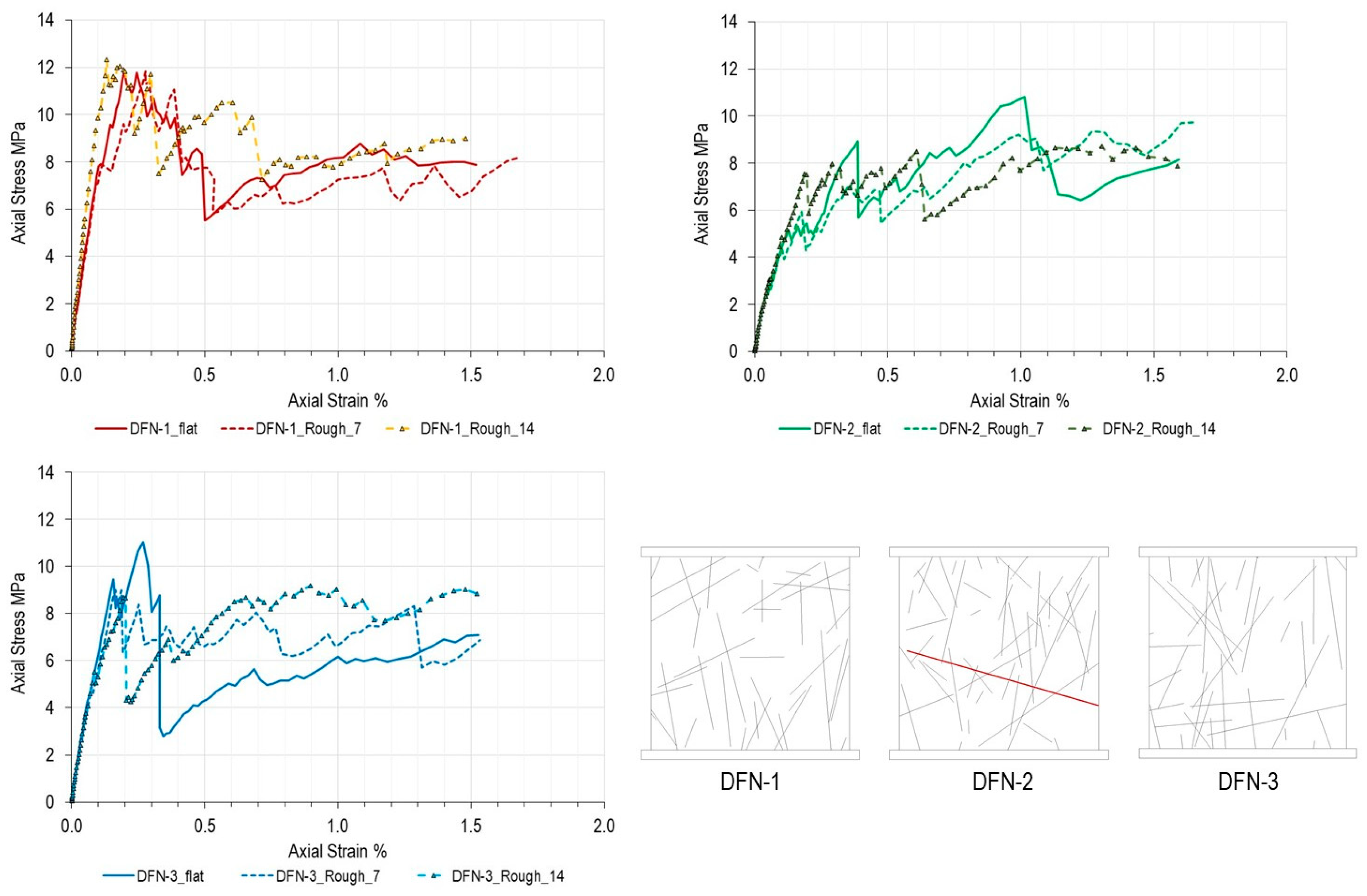
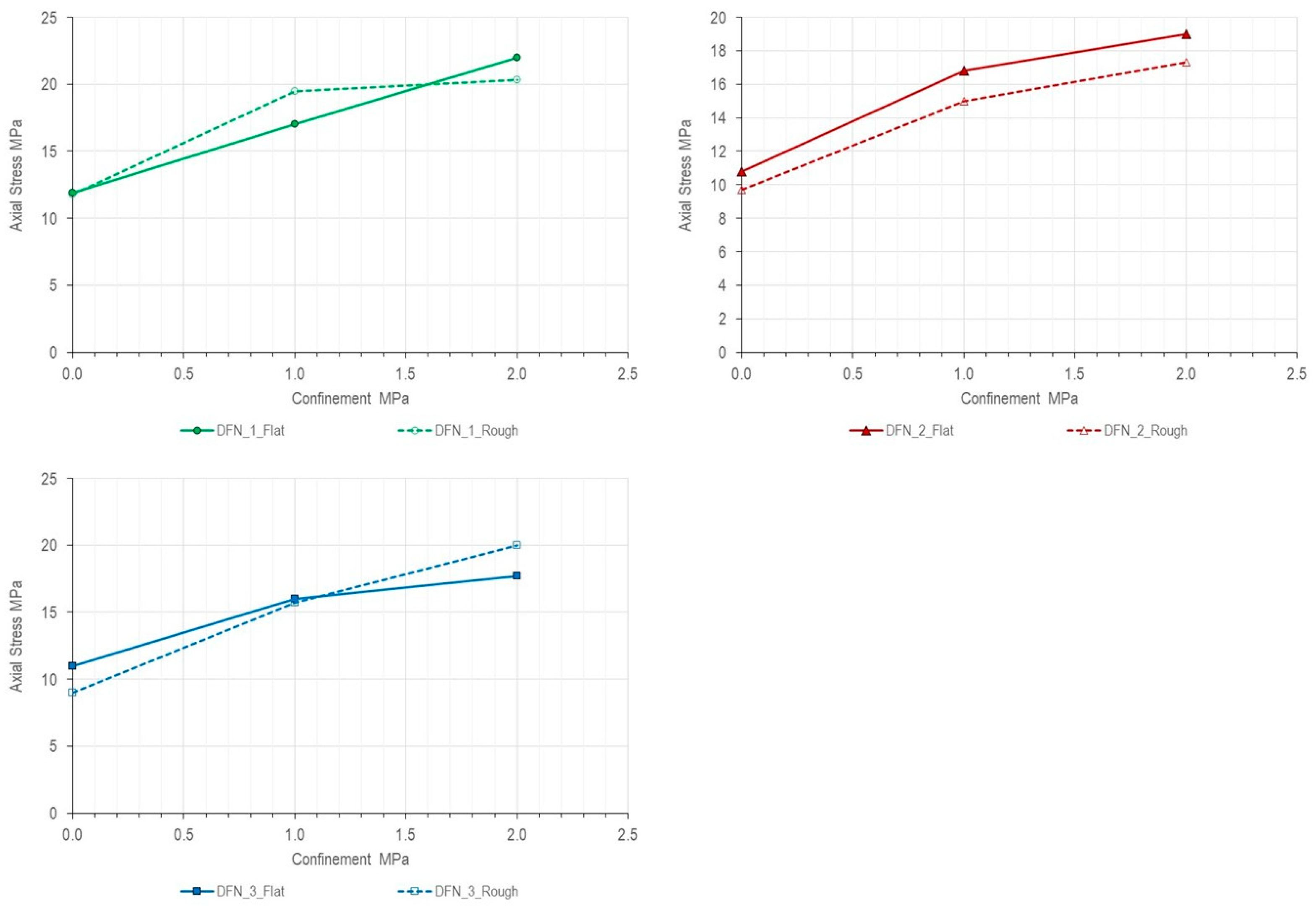
5.2.2. Models DFN-1 to DFN-3

Figure 10 presents comparative results for models incorporating flat versus undulated fracture traces for DFN-1, DFN-2 and DFN-3. The results are consistent with those presented in Figure 6 for Models DFN-A and DFN-B, which use intact rock material properties as listed in Table 2.

The DFN-1 model shows little strength difference between undulated and flat traces. DFN-2 exhibits slightly higher strength for the model with undulated traces, and DFN-3 exhibit slightly higher strength for the model with flat traces, which is counterintuitive in itself. This inconsistency across different joint geometries (flat vs. undulated) suggests that the overall fracture network configuration (relative to the assumed loading direction) primarily controls the modelled strengths. The results also support earlier observations that the effects of geometric simplification (flat vs. undulated traces) become less pronounced for stronger materials.

Interestingly, there appear to be marked differences in failure characteristics. DFN-1 shows a more brittle failure pattern with a sharp peak followed by significant strength reduction, particularly evident in the flat trace model. The undulated trace model exhibits higher residual strength, indicating that geometric undulation offers sustained resistance even after peak strength is mobilized. DFN-2 exhibits more ductile behaviour with gradual strength increase and sustained loading capacity. Albeit representing equivalent intensity conditions, each SRM model responds differently based on the underlying DFN configuration, reinforcing the conclusion that fracture network topology (i.e., connectivity) governs how geometric complexity influences overall fracturing behaviour. More specifically:

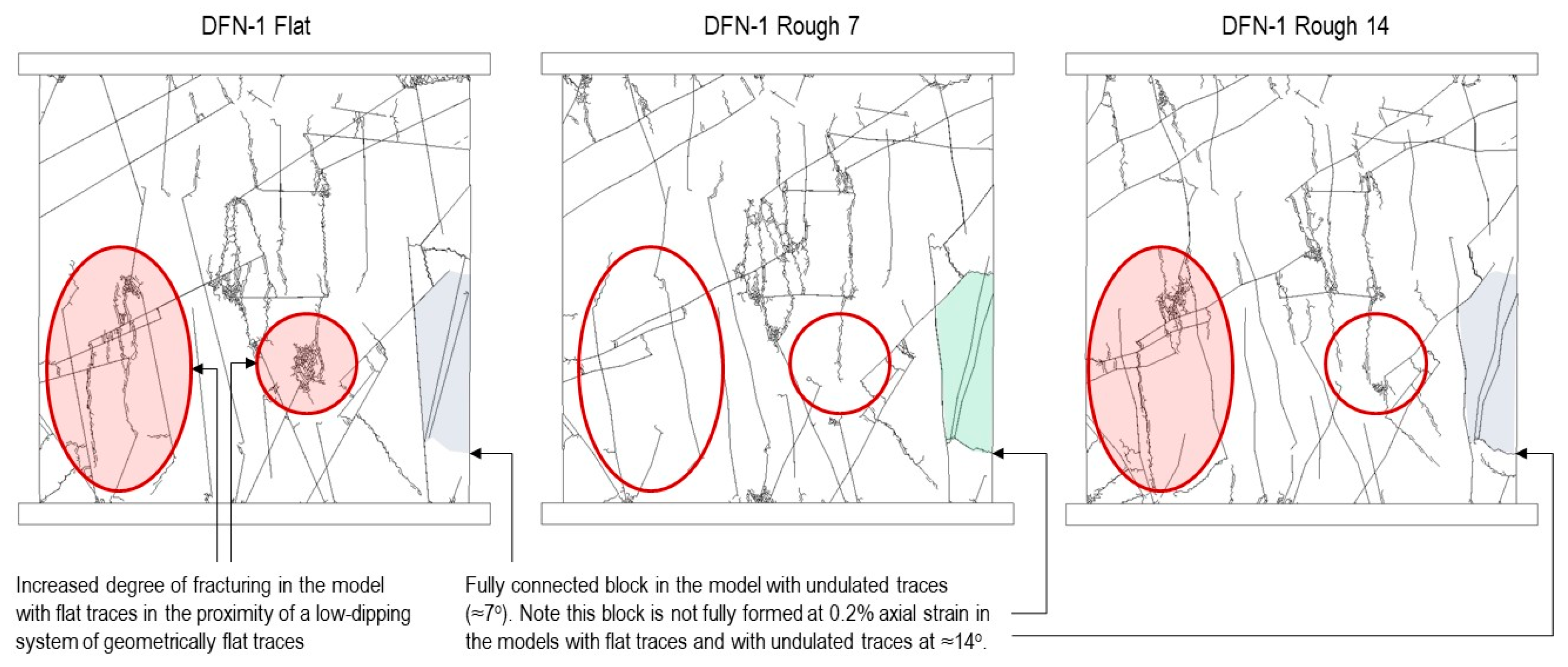
• Figure 11 shows how the model DFN-1 fracture surface geometry affects block formation and induced connectivity. The flat model develops distinct, fully connected blocks (red ovals with pink shading), particularly near low-dipping fracture systems. In contrast, the undulated models show reduced block formation and altered connectivity patterns. Fully formed blocks in flat models may not develop under identical conditions when fracture undulation is considered, highlighting the critical role of surface geometry in rock mass behaviour predictions.
• Figure 12 shows that model DFN-2 yields contrasting responses between flat and undulated fracture models. The flat model exhibits localized failure along a specific fracture zone (red circle), while undulated models show more distributed fracturing patterns (multiple red ovals). The annotations explain that undulation increases surface asperity, preventing slip along individual fractures and causing more complex, distributed failure patterns. Notably, the degree of fracturing appears relatively independent of the underlying geometry (flat vs. undulated), but the failure mechanisms and locations differ significantly.
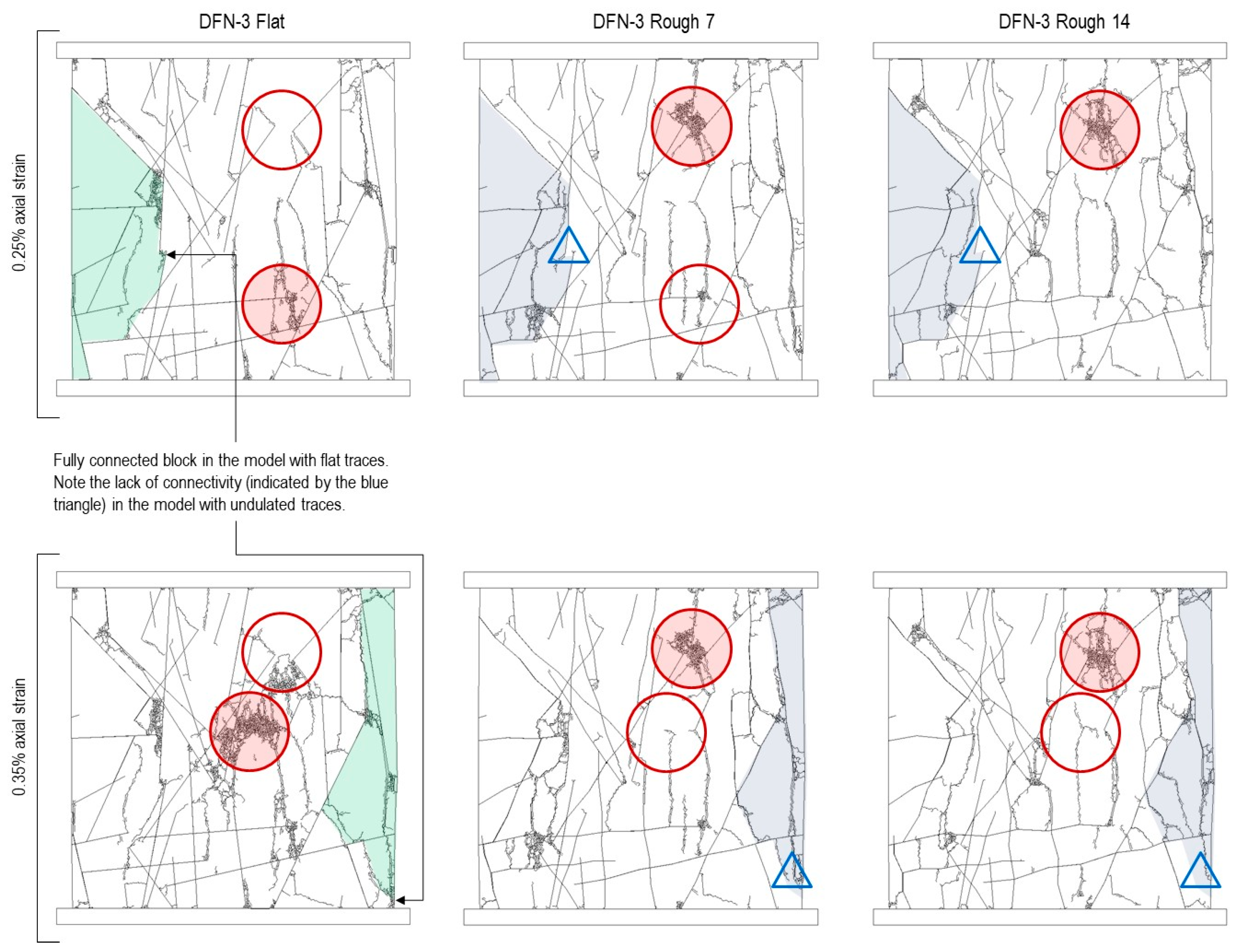
• Figure 13. The flat model shows extensive induced connectivity and block formation (green shaded regions), while undulated models show reduced induced connectivity (note the blue triangle indicating disconnected blocks). The red circles highlight areas where undulation prevents the formation of continuous failure planes that would otherwise develop in flat fracture models, demonstrating how surface roughness may significantly alter rock mass connectivity and failure mechanisms.

The results reinforce the conclusion that there is no such thing as a deterministic rock mass strength and further demonstrate the observation by Elmo et al. [28] that SRM strategies must consider multiple realizations of the same DFN model. The results also have implications for characterizing the strength of rock bridges. It becomes apparent that intact rock fracturing is a process that varies spatially (Figure 11) and temporally (Figure 12) as strain accumulates in the models. However, these conditions are not permitted by the conventional Jennings’ rock bridge percentage approach [29].

As shown in Figure 14 below, the significance of geometric representation varies with both confinement conditions and fracture network topology. For specific network configurations (models with 7 degrees of asperity, DFN-1 and DFN-3), the impact of fracture undulation is unnoticeable, even under relatively low normal stress conditions where we would expect dilatancy mechanisms to dominate. However, this relationship is not universal; indeed, DFN-2 exhibit a marked difference between undulated and flat trace configurations. The relatively higher strength of the model with undulated traces can be explained in terms of the geometric configuration, which includes a relatively persistent fracture dipping at approximately 18 degrees and almost entirely transecting the model. It is reasonable to assume that the undulated configuration would yield a higher resistance in shear.

Higher confinement conditions do not consistently suppress geometric effects across all network types, suggesting that simplified representations may be adopted based on specific network characteristics rather than loading conditions alone.

5.3. Discussion

Despite the preliminary nature of these models, the results suggest a fundamental issue that extends beyond the simple dichotomy of undulated versus flat fracture representations. The results demonstrate that the critical challenge lies not in the geometric problem per se, but rather in acknowledging the inherent variability of rock mass behaviour within complex discontinuity systems where loading conditions across individual fractures are more complex than those in controlled laboratory testing environments. We agree with Dr. Barton’s observation [30] that continuum modelling approaches fundamentally cannot capture the complex behaviour of fractured rock masses, where individual fractures and fracture sets exhibit distinct large-scale undulation and shear strength characteristics that extend beyond the capabilities of conventional Hoek-Brown and GSI methodologies, as evidenced by our SRM model results.

In laboratory direct shear tests, discontinuities experience uniform normal stress, controlled boundary conditions, and idealized loading paths. In contrast, rock masses represent complex systems where each discontinuity experiences unique stress states influenced by its position within the fracture network, local geometric constraints, stress redistribution effects, and interaction with neighbouring fractures. This fundamental disconnect between laboratory characterization methods and field conditions introduces variability that cannot be eliminated solely through improved geometric representation or by assuming shear strength properties to implicitly account for large-scale undulations.

The results underscore the uncomfortable truth that rock mass strength remains an inherently unbounded property. It defies precise and generalized quantification. Variability is not just an experimental error to be minimized, but a fundamental characteristic of fractured rock systems. The implication is that, in engineering practice, we may have to accept relatively large strength variations as an inherent characteristic of rock mass systems (see Figure 15). This acceptance represents a paradigm shift from seeking deterministic answers to developing robust design approaches that also remain viable across the temporal dimension of the project.

Note that the loading conditions in SRM models are much different from those experienced in, for example, a large slope model or along the boundary of a tunnel. Our results demonstrate that the debate over undulated versus flat fractures in SRM models, while technically interesting, may ultimately be secondary to the broader challenge of modelling complex systems where emergent behaviour arises from fracture network interactions that cannot be captured through the simple superposition of individual discontinuity responses under laboratory loading conditions. Each fracture’s contribution to overall rock mass behaviour depends on its role within the larger system, a role that changes dynamically with loading conditions and cannot be predetermined from laboratory characterization.

This observation can have profound implications for underground mining safety, particularly regarding the prediction and prevention of ground collapses. Falls of ground rarely result from the failure of a single discontinuity operating in isolation. Instead, they emerge from the complex interaction of multiple fractures, intact rock bridges, and changing stress conditions as mining progresses. As mining advances and stress fields redistribute around excavations, individual fractures that may have been stable under initial conditions can suddenly become critical failure pathways. The inability to predetermine from laboratory characterization the role of individual fractures within complex systems explains why traditional rock mass classification systems, while useful for general design guidance, often fail to predict specific failure events.

6. Conclusions

This paper has revealed a fundamental challenge in SRM modelling between computational efficiency and mechanistic behaviour. The comparison of planar versus undulated fracture representations in a series of SRM models demonstrated that geometric simplification, while computationally convenient, may inadequately capture critical aspects of rock mass behaviour under certain conditions. However, the significance of fracture undulation may vary substantially for each considered DFN realization and assumed intact rock material. The results also explain why the validation of SRM results against field behaviour remains challenging. Rock-mass strength is not deterministic, and the modelled response depends on unique combinations of network topology, loading conditions, and material properties specific to each engineering situation.

Simplified JRC-based methods may suffice for preliminary assessments, while critical stability analyses may require sophisticated photogrammetric or laser-scanning characterization. The selection criterion should ensure alignment between characterization methods, modelling approaches, and the engineering decisions dependent on the results. Emerging technologies (e.g., automated image analysis, drone-based photogrammetry, and portable laser scanning) continue to expand the practical feasibility of detailed fracture characterization. However, these technological advances must be integrated with an improved understanding of when such details meaningfully influence engineering outcomes.

The fundamental challenge remains translating complex natural geometry into numerical representations that capture essential mechanical behaviour while maintaining computational tractability. Rather than pursuing unattainable precision or defaulting to computational convenience, the choice between modelling approaches should be based on a systematic evaluation of loading conditions, design objectives, and the required balance between computational practicality and mechanical accuracy for specific applications. Success lies not in eliminating uncertainty, but in developing robust engineering decisions that remain valid across the inevitable range of rock mass behaviour.

This perspective suggests that future research efforts might be more productively directed toward understanding and quantifying the bounds of this inherent variability, specifically for the problem under consideration. As discussed in [10], a single, unified model to predict rock mass behaviour does not exist. The same authors state that models should not be considered as forecasting tools, but rather as a source of knowledge for decision-makers.