Finite Element Model-Based Behavior Evaluation of Pavement Stiffness Influence on Shallowly Buried Precast Arch Structures Subjected to Vehicle Load
Abstract
1. Introduction
2. Methods
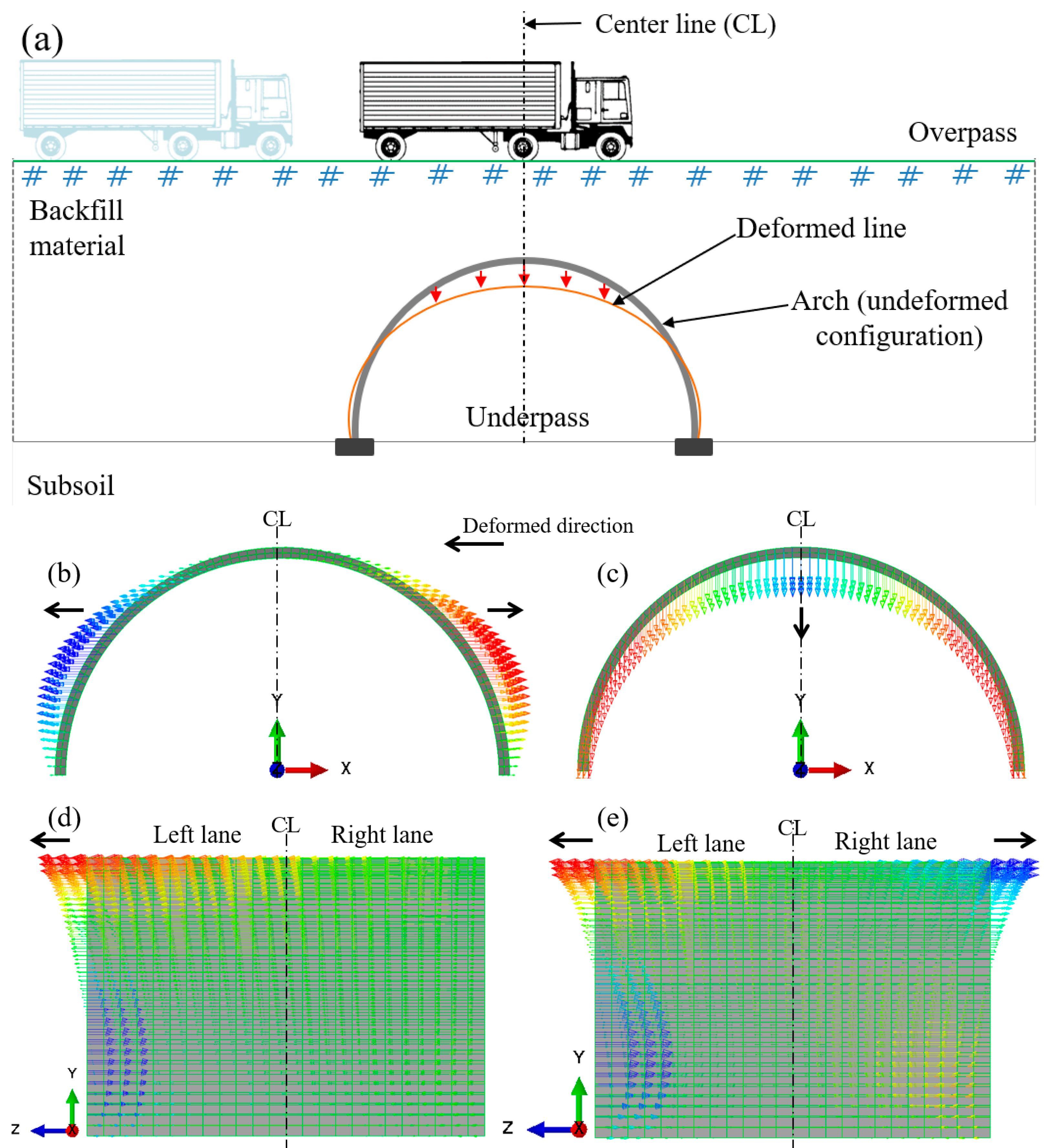
2.1. FEA Model of Studied BPAS
2.2. Material Model
2.3. Contact Surface and Joint Model
3. Pavement Structure and Vehicle Load
4. Results and Discussions
4.1. Response of Segmental Arch
4.2. Liveload Attenuation in Backfill Material
4.3. Influence of Backfill Material
5. Conclusions
- (1)
- The vehicle’s effect on the buried arch structure depends on the vehicle’s standing position on the structure. The arch area is relatively weaker than the other areas on the arch. The arch bending was reduced due to the soil-arching effect, and the dominant displacement direction was vertical. The displacement of the arch varied depending on the truck’s layout and the different pavement stiffness. The effect of vehicle loads on multiple lanes did not cause a significant displacement increase for segmental arch structures. The displacement of the arch was only significantly dependent on the degree of load concentration on the top of the arch and less dependent on multiple lanes of loads.
- (2)
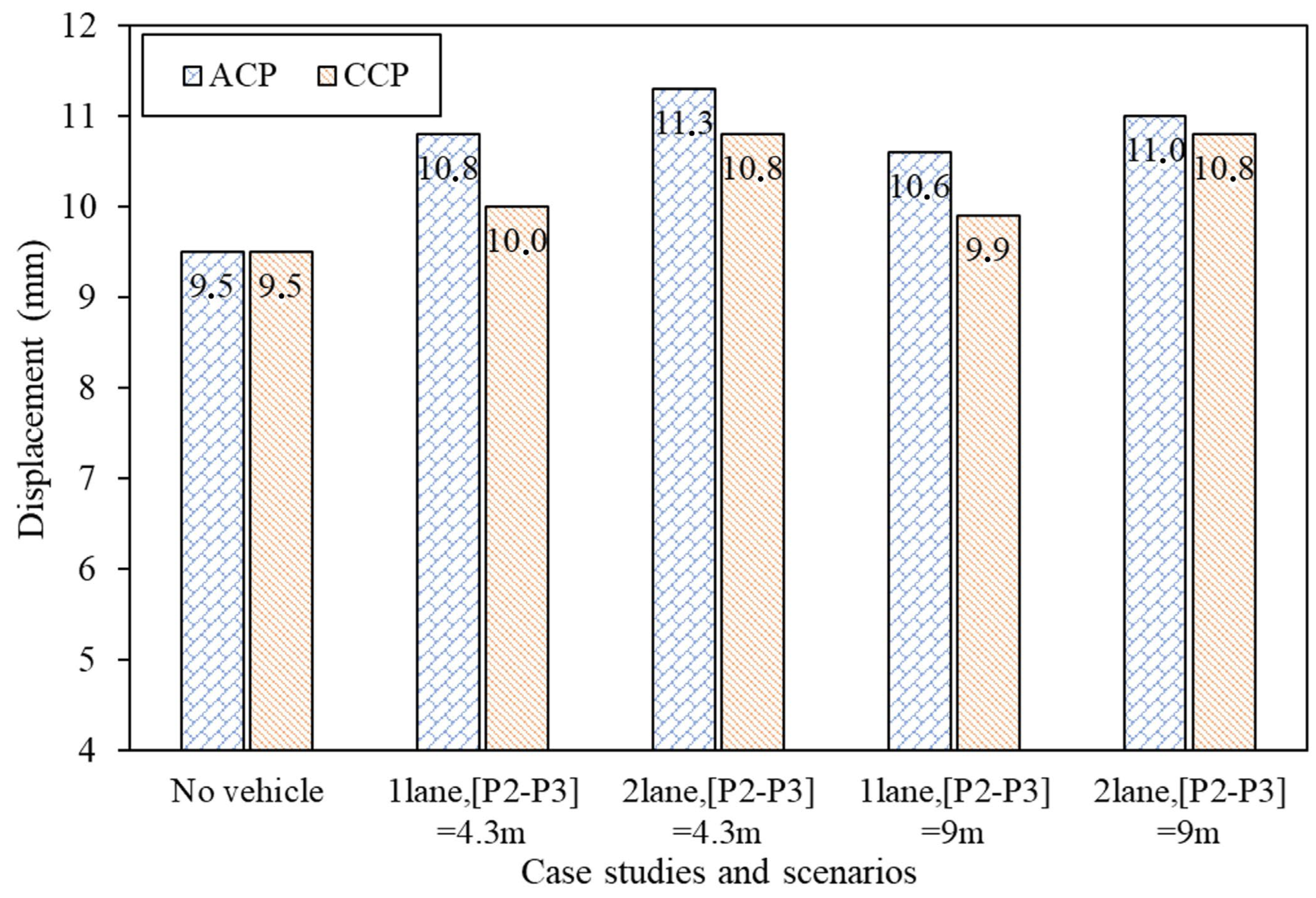
- The degree of increase in arch displacement with asphalt concrete pavement (ACP) was higher than that of cement concrete pavement (CCP) (15.0% versus 9.2%). Therefore, the influence of the vehicle load above on the buried arch structure tended to be higher for the softer pavement structure than the stiffer pavement structure (ACP compared with CCP). The additional displacement under vehicle load was significantly lower in the case of a loaded lane, and the truck rear axle spacing is 9 m.
- (3)
- The tensile stress zone distribution in the arch structure was not significantly dependent on the rear axle distance of the truck and the pavement structure. However, there was a difference in distribution coverage when the BPAS was loaded on single-lane loading and two-lane loading. The tensile stress in the arch structure of two load-carrying lanes was greater than that of a single load-carrying lane but not significantly (roundly 2%). The tensile stress in the arch structure increased insignificantly with additional vehicle load (around 3%).
- (4)
- The extent of wheel track pressure propagation depended not only on the magnitude of the axle load but also on the stiffness of the pavement structure. The CCP structure allowed the wheel load distribution on the backfill material to be better than the ACP structure. The extent of the influence zone of the backfill should be defined as 2.4 m wide from the bottom of the arch and on the prism plane created with a 45-degree transverse angle, which could enhance coverage of the vehicle’s affected area on the buried structure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BPAS | Buried precast arch structures |
| ACP | Asphalt concrete pavement |
| CCP | Cement concrete pavement |
| FEA | Finite Element Analysis |
| FEM | Finite Element Model |
References
- Abe, T.; Nakamura, M. The use of and the caution in the application of the culvert constructed by large pre-cast element in the expressway construction. Found Eng. Equip. 2014, 42, 8–11. [Google Scholar]
- Miyazaki, Y. Fundamental Study on Seismic Behavior of Hinge Types of Precast Arch Culverts in Culvert Longitudinal Direction. Ph.D. Dissertation, Kyoto University, Kyoto, Japan, 2019. [Google Scholar]
- Nguyen, V.-T.; Seo, J.; Ahn, J.-H.; Haldar, A.; Huh, J. Finite element analysis-aided seismic behavior examination of modular underground arch bridge. Tunn. Undergr. Space Technol. 2021, 118, 104166. [Google Scholar] [CrossRef]
- Abuhajar, O.; El Naggar, H.; Newson, T. Static soil culvert interaction the effect of box culvert geometric configurations and soil properties. Comput. Geotech. 2015, 69, 219–235. [Google Scholar] [CrossRef]
- Hashash, Y.M.; Hook, J.J.; Schmidt, B.; John, I.; Yao, C. Seismic design and analysis of underground structures. Tunn. Undergr. Space Technol. 2001, 16, 247–293. [Google Scholar] [CrossRef]
- Nguyen, V.-T.; Ahn, J.-H.; Haldar, A.; Huh, J. Fragility-based seismic performance assessment of modular underground arch bridges. Structures 2022, 39, 1218–1230. [Google Scholar] [CrossRef]
- Zhou, X.; Jin, D.; Ge, D.; Chen, S.; You, Z. Identify the Micro-Parameters for Optimized Discrete Element Models of Granular Materials in Two Dimensions Using Hexagonal Close-Packed Structures. Materials 2023, 16, 3073. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Yang, C.; Xu, F.; Li, J.; Jin, D. Reinforcement of Insufficient Transverse Connectivity in Prestressed Concrete Box Girder Bridges Using Concrete-Filled Steel Tube Trusses and Diaphragms: A Comparative Study. Buildings 2024, 14, 2466. [Google Scholar] [CrossRef]
- Orton Sarah, L.; Loehr, J.E.; Boeckmann, A.; Havens, G. Live-Load Effect in Reinforced Concrete Box Culverts under Soil Fill. J. Bridge Eng. 2015, 20, 04015003. [Google Scholar] [CrossRef]
- Seo, H.; Wood Timothy, A.; Javid Amir, H.; Lawson William, D. Simplified System-Level Pavement-Stiffness Model for Box Culvert Load-Rating Applications. J. Bridge Eng. 2017, 22, 04017066. [Google Scholar] [CrossRef]
- Acharya, R.; Han, J.; Parsons Robert, L. Numerical Analysis of Low-Fill Box Culvert under Rigid Pavement Subjected to Static Traffic Loading. Int. J. Geomech. 2016, 16, 04016016. [Google Scholar] [CrossRef]
- Park, J.-Y.; Sohn, D.-S.; Lee, J.-H.; Kim, S.-H.; Jeong, J.-H. Influence of Box Culverts on Behavior of Jointed Concrete Pavements. J. Perform. Constr. Facil. 2015, 29, 04014053. [Google Scholar] [CrossRef]
- American Association of State Highway and Transportation Officials. AASHTO LRFD Bridge Design Specifications, SI Units; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2017. [Google Scholar]
- TCVN11823; Road Bridge Design. National Standard: Hanoi, Vietnam, 2017.
- Alberta. Design Guidelines for Bridge Size Culverts; Government of Alberta: Edmonton, AB, Canada, 2004.
- Alshboul, O.; Almasabha, G.; Shehadeh, A.; Al Hattamleh, O.; Almuflih, A.S. Optimization of the Structural Performance of Buried Reinforced Concrete Pipelines in Cohesionless Soils. Materials 2022, 15, 4051. [Google Scholar] [CrossRef] [PubMed]
- Abaqus, V. 6.20 Documentation; Dassault Systemes Simulia Corporation: Vélizy-Villacoublay, France, 2020. [Google Scholar]
- Hognestad, E. Study of Combined Bending and Axial Load in Reinforced Concrete Members; University of Illinois at Urbana Champaign: Champaign, IL, USA, 1951. [Google Scholar]
- Lee, J.; Fenves, G.L. A plastic-damage concrete model for earthquake analysis of dams. Earthq. Eng. Struct. Dyn. 1998, 27, 937–956. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-damage model for cyclic loading of concrete structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- TCCS38:2022/TCĐBVN; Flexible Pavement Design—Specification and Guidelines. Ministry of Transport: Ha Noi, Vietnam, 2022.
- TCCS39:2022/TCĐBVN; Specifications for Design of Jointed Plain Cement Concrete Pavement for Highway. Ministry of Transport: Ha Noi, Vietnam, 2022.
- Jeon, S.H.; Yim, H.J.; Huh, J.; Cho, K.-I.; Ahn, J.-H. Full-scale field testing of a precast concrete buried arch bridge with steel outriggers: Field loading test. Eng. Struct. 2021, 242, 112563. [Google Scholar] [CrossRef]
- Sawamura, Y.; Ishihara, H.; Otani, Y.; Kishida, K.; Kimura, M. Deformation behavior and acting earth pressure of three-hinge precast arch culvert in construction process. Undergr. Space 2019, 4, 251–260. [Google Scholar] [CrossRef]
- Miyazaki, Y.; Sawamura, Y.; Kishida, K.; Kimura, M. Influence of longitudinal structural connectivity on seismic performance of three-hinged precast arch culverts. Soils Found. 2021, 61, 1681–1698. [Google Scholar] [CrossRef]
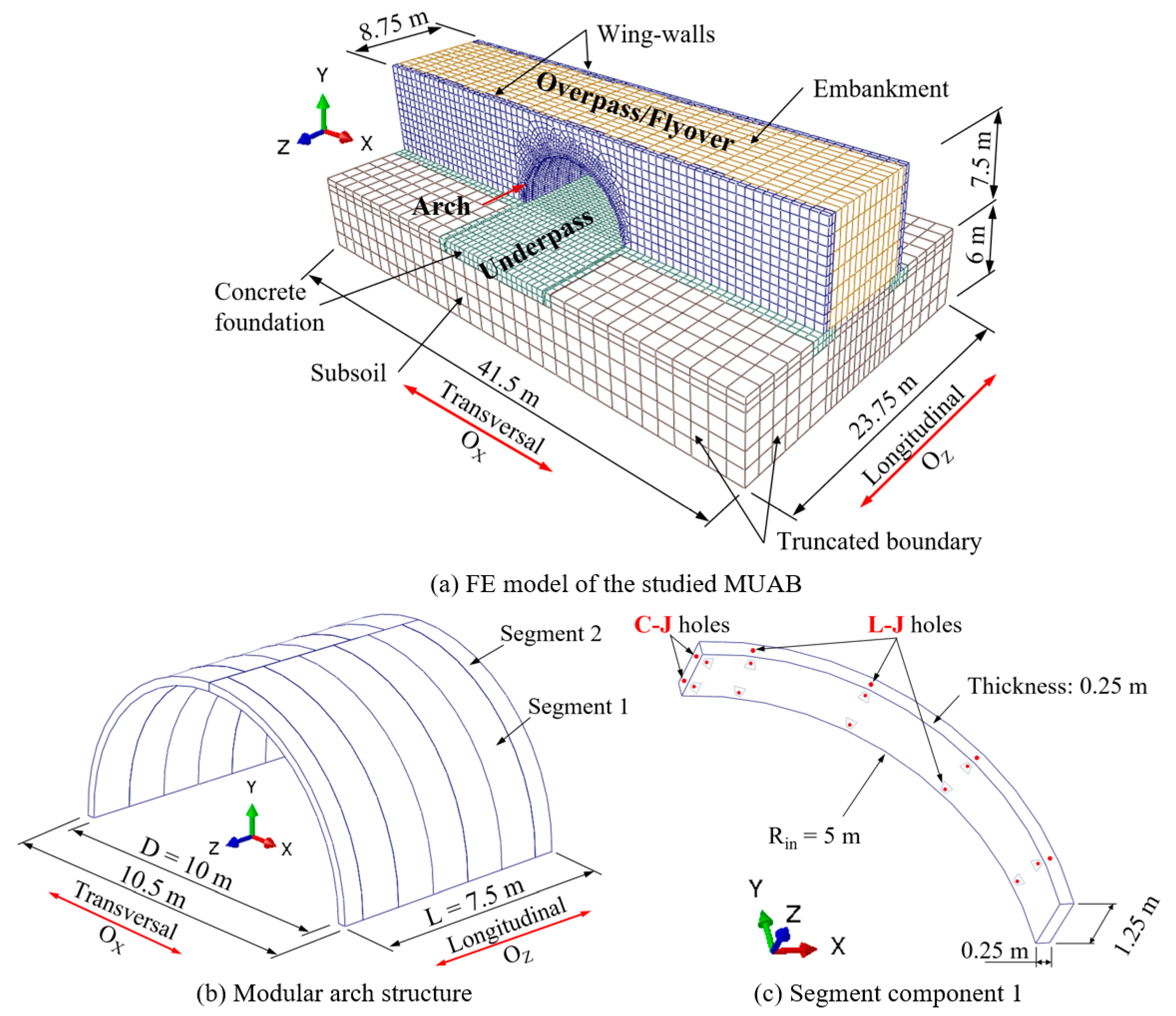
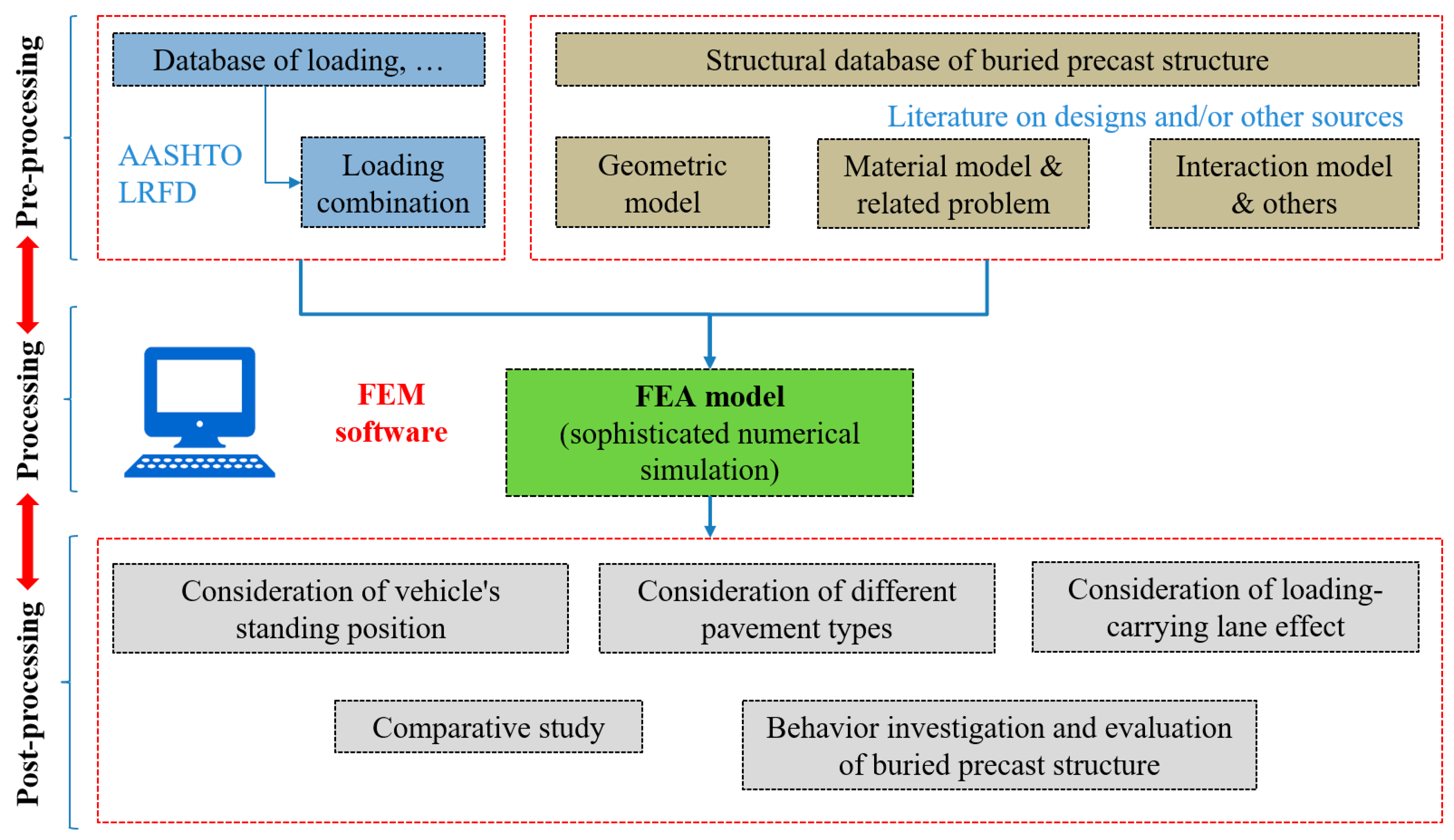


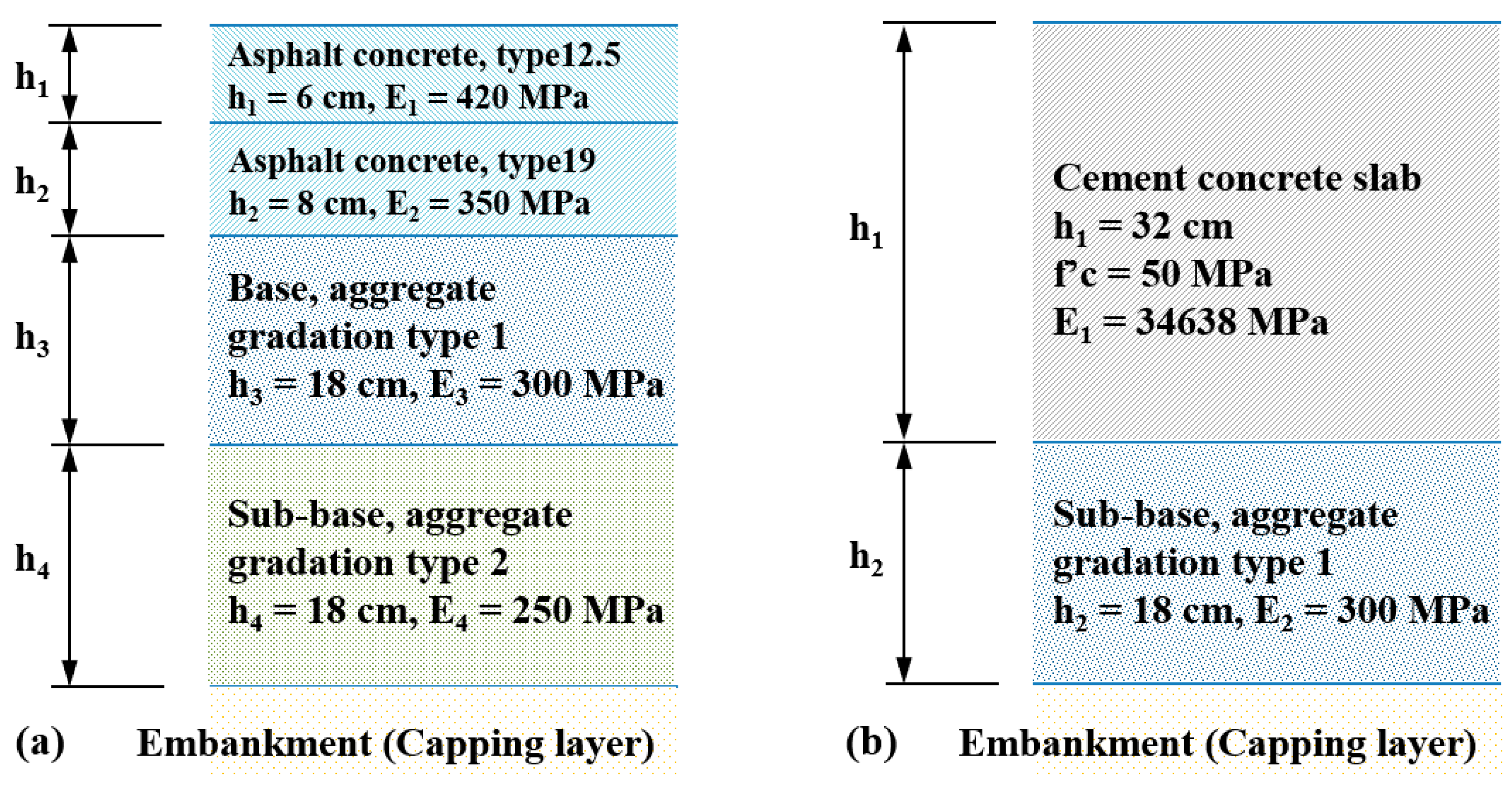
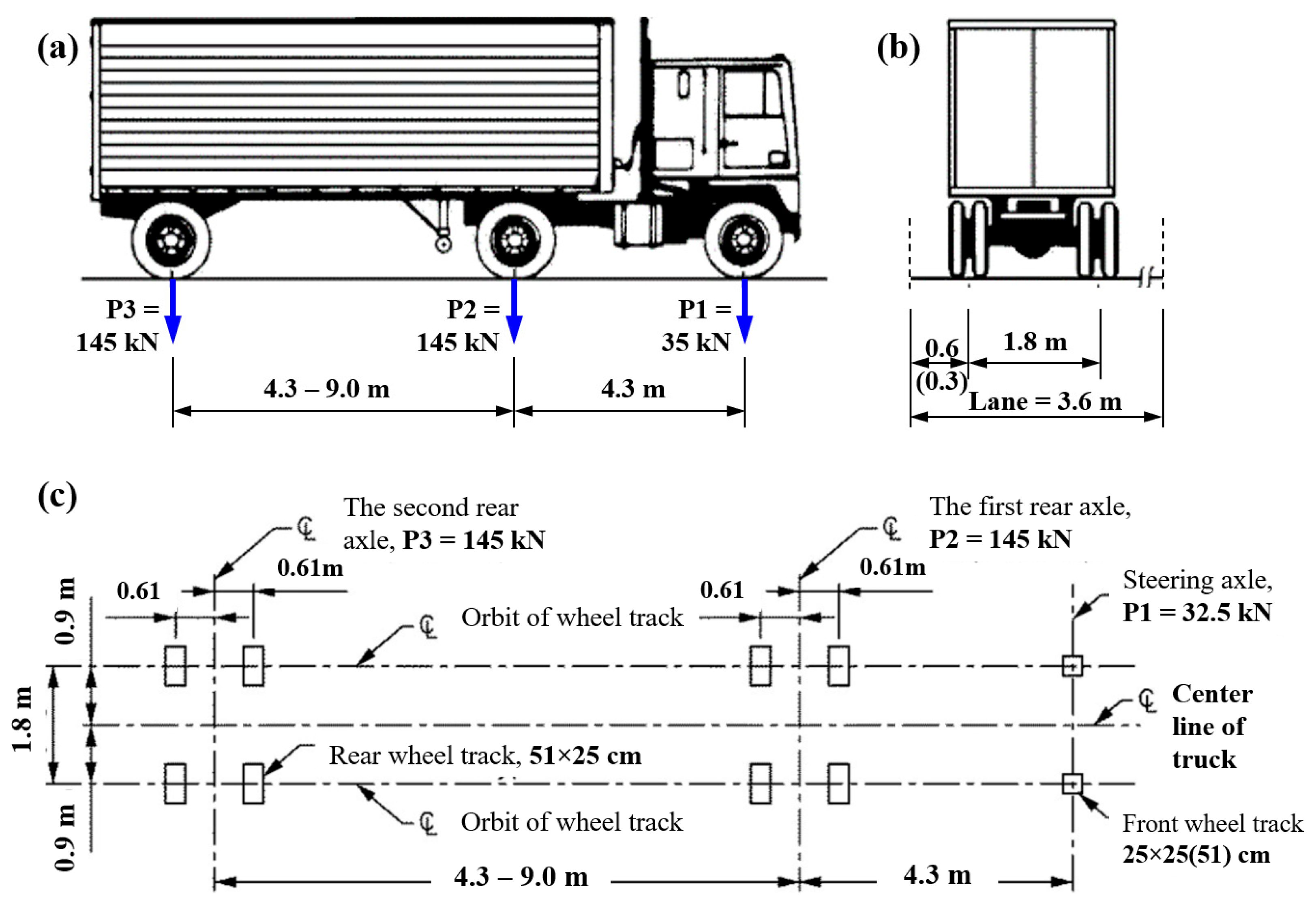






| Property | Unit | M40 | M30 |
|---|---|---|---|
| Mass density, γ | kg/m3 | 2450 | 2400 |
| Young’s modulus, Ec | MPa | 30,000 | 26,600 |
| Poisson’s ratio, υ | - | 0.2 | 0.2 |
| Compressive strength, f’c | MPa | 40 | 30 |
| Tensile strength, ft | MPa | 4 | 3 |
| Dilation angle | ° | 31 | 31 |
| Eccentricity | - | 0.1 | 0.1 |
| fb0/fc0 | - | 1.16 | 1.16 |
| K | - | 0.67 | 0.67 |
| Viscosity parameter | - | 0 | 0 |
| Property | Unit | Subsoil | Embankment |
|---|---|---|---|
| Mass density, γ | kg/m3 | 1800 | 1750 |
| Young’s modulus, E | MPa | 45 | 50 |
| Poisson’s ratio, υ | - | 0.33 | 0.28 |
| Internal friction angle, φ | ° | 25 | 35 |
| Dilatancy angle, Ψ | ° | 1 | 5 |
| Cohesion, c | KPa | 100 | 20 |
| Number of Truck Lane | Pavement Structure | |
|---|---|---|
| ACP | CCP | |
| Single lane | Case 1 (ACP-1lane) | Case 2 (CCP-1lane) |
| Two lanes | Case 3 (ACP-2lane) | Case 4 (CCP-2lane) |
| Scenarios | ACP (%) | CCP (%) |
|---|---|---|
| No vehicle | 0.0 | 0.0 |
| 1lane, [P2–P3] = 4.3 m | 13.7 | 5.3 |
| 2lane, [P2–P3] = 4.3 m | 18.9 | 13.7 |
| 1lane, [P2–P3] = 9 m | 11.6 | 4.2 |
| 2lane, [P2–P3] = 9 m | 15.8 | 13.7 |
| Average | 15.0 | 9.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, V.-T.; Huh, J. Finite Element Model-Based Behavior Evaluation of Pavement Stiffness Influence on Shallowly Buried Precast Arch Structures Subjected to Vehicle Load. Geotechnics 2025, 5, 50. https://doi.org/10.3390/geotechnics5030050
Nguyen V-T, Huh J. Finite Element Model-Based Behavior Evaluation of Pavement Stiffness Influence on Shallowly Buried Precast Arch Structures Subjected to Vehicle Load. Geotechnics. 2025; 5(3):50. https://doi.org/10.3390/geotechnics5030050
Chicago/Turabian StyleNguyen, Van-Toan, and Jungwon Huh. 2025. "Finite Element Model-Based Behavior Evaluation of Pavement Stiffness Influence on Shallowly Buried Precast Arch Structures Subjected to Vehicle Load" Geotechnics 5, no. 3: 50. https://doi.org/10.3390/geotechnics5030050
APA StyleNguyen, V.-T., & Huh, J. (2025). Finite Element Model-Based Behavior Evaluation of Pavement Stiffness Influence on Shallowly Buried Precast Arch Structures Subjected to Vehicle Load. Geotechnics, 5(3), 50. https://doi.org/10.3390/geotechnics5030050







