Machine Learning-Enhanced Analysis of Small-Strain Hardening Soil Model Parameters for Shallow Tunnels in Weak Soil
Abstract
1. Introduction
2. The Small-Strain Hardening-Soil-Model
- E50 (secant modulus for primary loading)—Governs soil stiffness under deviatoric loading.
- Eoed (oedometer modulus)—Defines soil stiffness under one-dimensional compression.
- Eur (unloading/reloading modulus)—Controls stiffness during unloading and reloading.
- Gref (reference shear modulus at small strains)—Represents soil stiffness at very small strains.
- γ0.7 (shear strain at 70% degradation of Gref)—Describes strain-dependent stiffness degradation.
- c (effective cohesion)—Governs shear strength.
- ϕ (effective friction angle)—A key parameter for soil shear strength.
- Ψ (dilatancy angle)—Defines volume expansion during shearing.
- m (power law parameter for stress-dependent stiffness)—Controls the nonlinear stiffness variation with confining pressure.
- K0 (lateral earth pressure coefficient for normally consolidated soil)—Governs the initial lateral stress state.
- OCR (overconsolidation ratio)—Represents pre-consolidation history.
- pref (reference pressure)—A scaling parameter for stiffness dependency.
3. Case Study Information
4. Finite-Element Modelling
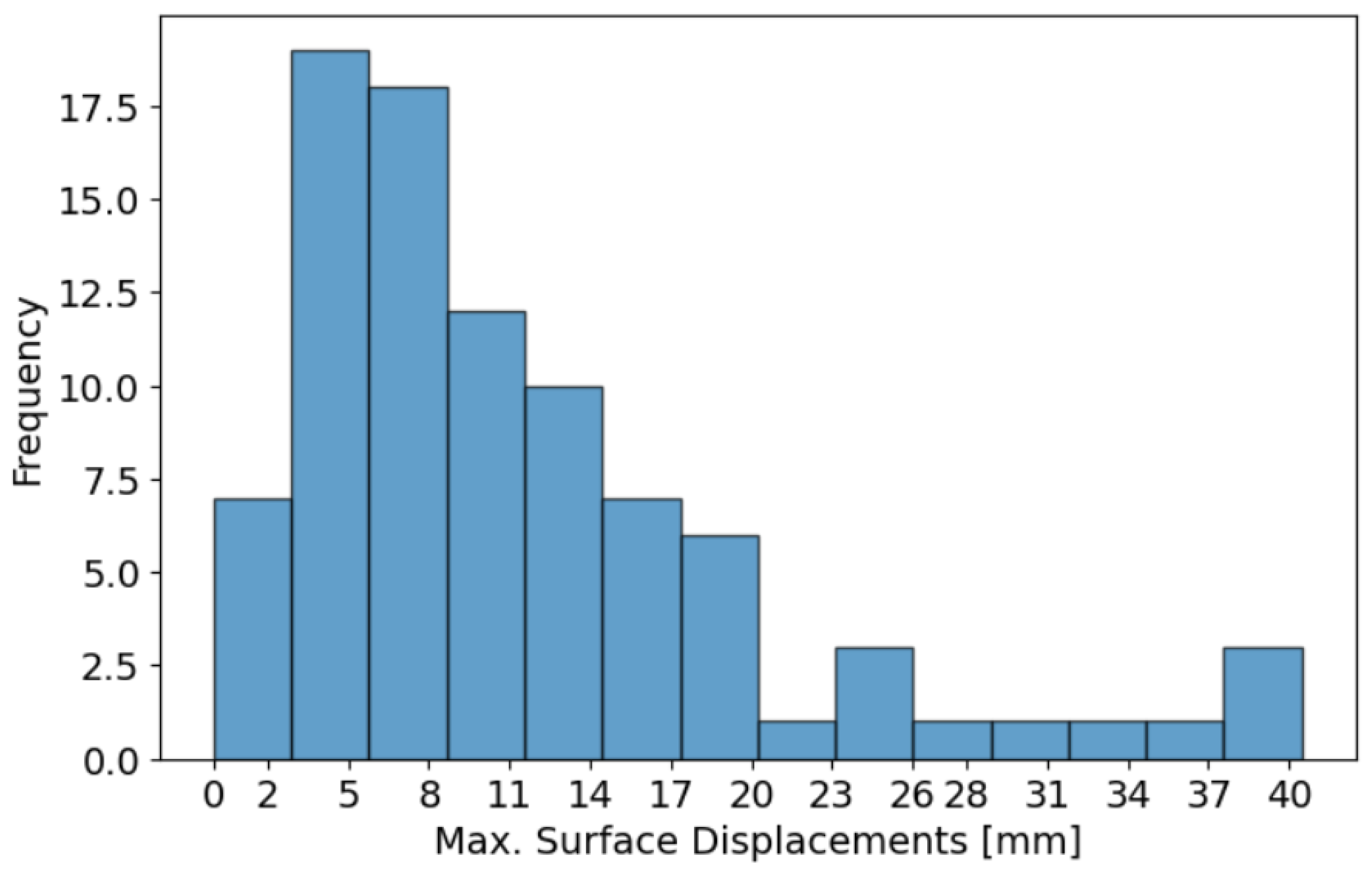
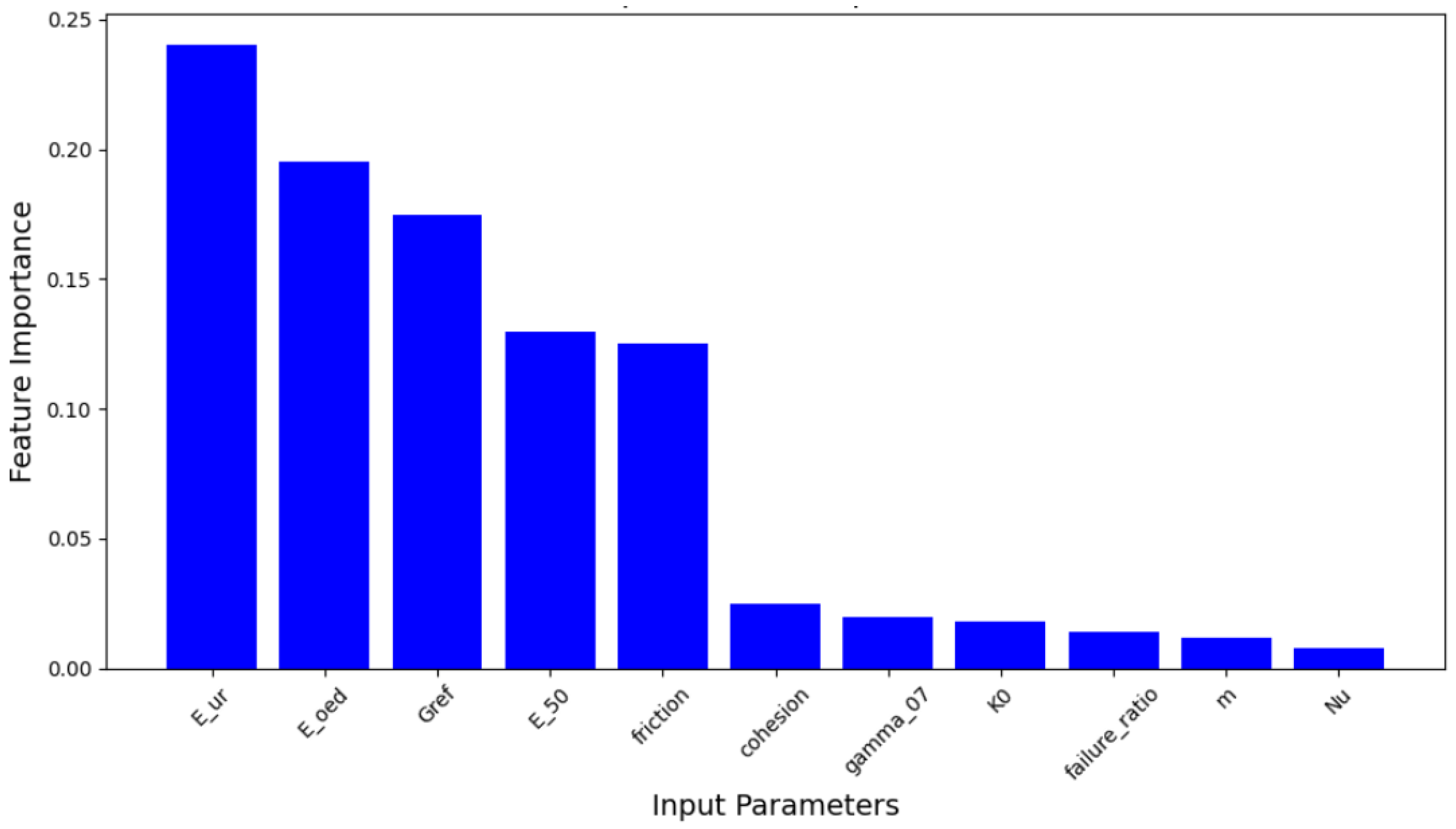
5. Machine-Learning Analysis
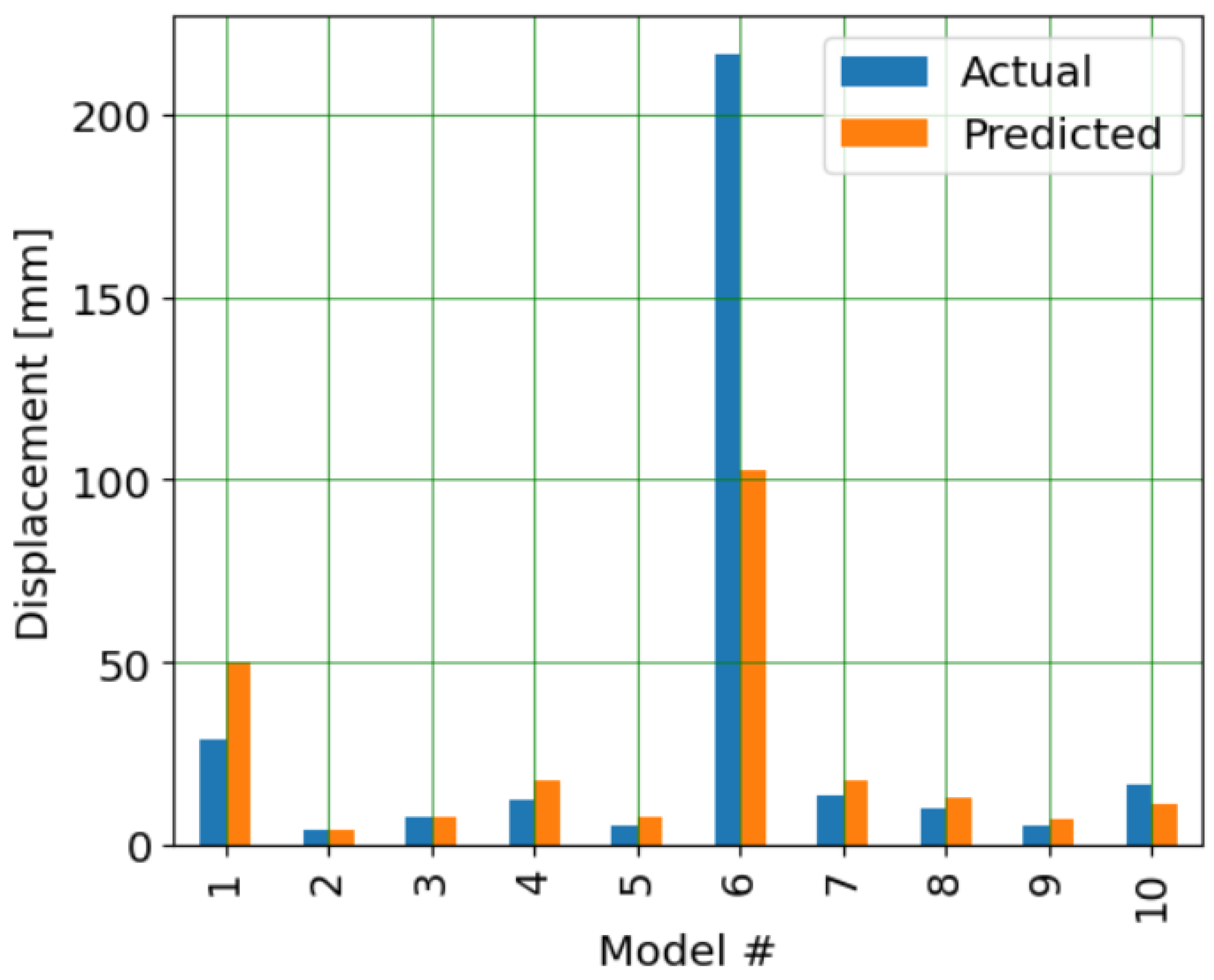
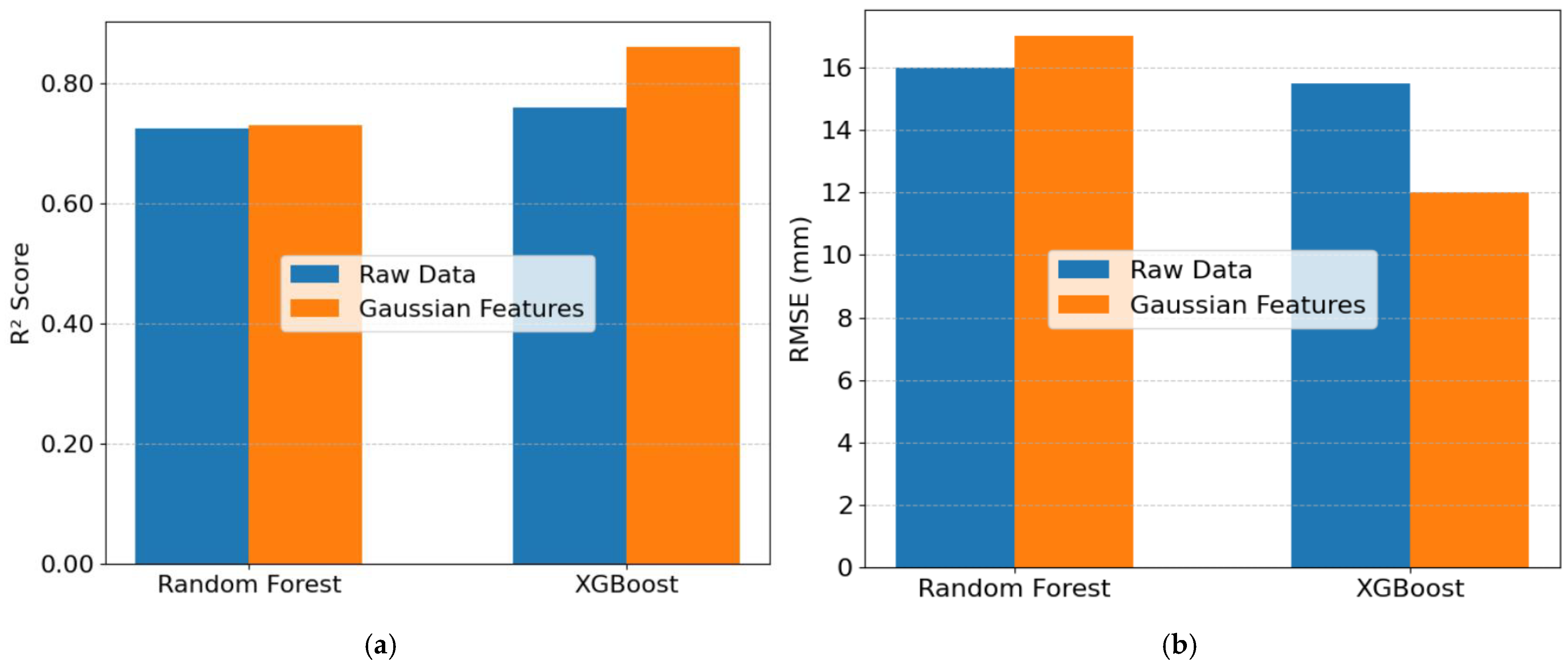
5.1. Regression Models
5.2. Classification Models
6. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lees, A. Geotechnical Finite Element Analysis; ICE Publishing: London, UK, 2013; ISBN 0727760874. [Google Scholar] [CrossRef]
- Schanz, T.; Vermeer, P.A.; Bonnier, P.G. The Hardening Soil Model: Formulation and Verification. In Beyond 2000 in Computational Geotechnics; Routledge: London, UK, 1999; Volume 1, pp. 281–296. [Google Scholar]
- Huynh, Q.T.; Lai, V.Q.; Boonyatee, T.; Keawsawasvong, S. Verification of Soil Parameters of Hardening Soil Model with Small-Strain Stiffness for Deep Excavations in Medium Dense Sand in Ho Chi Minh City, Vietnam. Innov. Infrastruct. Solut. 2022, 7, 15. [Google Scholar] [CrossRef]
- Hsiung, B. Numerical Investigation of the Three-Dimensional Performances of a Shield-Machine-Bored Tunnel in Loose Sands. Soil Mech. Found. Eng. 2020, 56, 427–435. [Google Scholar] [CrossRef]
- Wang, Y.; Kong, L.; Wang, Y.; Li, X. Analysis of Influence of Shield Tunneling on Overlying Underground Pipelines Based on HSS Model. IOP Conf. Ser. Mater. Sci. Eng. 2018, 423, 012017. [Google Scholar] [CrossRef]
- Eilat, T.; Mitelman, A.; McQuillan, A.; Elmo, D. A Comparative Study of Embedded Wall Displacements Using Small-Strain Hardening Soil Model. Geotechnics 2024, 4, 309–321. [Google Scholar] [CrossRef]
- Long, M. Database for Retaining Wall and Ground Movements Due to Deep Excavations. J. Geotech. Geoenviron. Eng. 2001, 127, 203–224. [Google Scholar] [CrossRef]
- Kelleher, J.D.; Tierney, B. Data Science; MIT Press: Cambridge, MA, USA, 2018; ISBN 0262347032. [Google Scholar]
- Castellon, J.; Ledesma, A. Small Strains in Soil Constitutive Modeling. Arch. Comput. Methods Eng. 2022, 29, 3223–3280. [Google Scholar] [CrossRef]
- Obrzud, R.F. On the Use of the Hardening Soil Small Strain Model in Geotechnical Practice. Numer. Geotech. Struct. 2010, 16, 1–17. [Google Scholar]
- Obrzud, R.; Truty, A. The Hardening Soil Model a Practical Guidebook; Zace Services Ltd.: Preverenges, Switzerland, 2018. [Google Scholar]
- Roskin, J.; Sivan, D.; Shtienberg, G.; Roskin, E.; Porat, N.; Bookman, R. Natural and Human Controls of the Holocene Evolution of the Beach, Aeolian Sand and Dunes of Caesarea (Israel). Aeolian Res. 2015, 19, 65–85. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Yang, H.; Wang, B. Failure Modes and Face Instability of Shallow Tunnels under Soft Grounds. Int. J. Damage Mech. 2019, 28, 566–589. [Google Scholar] [CrossRef]
- Hong, Q.; Lai, H.; Liu, Y. Failure Analysis and Treatments of Collapse Accidents in Loess Tunnels. Eng. Fail. Anal. 2023, 145, 107037. [Google Scholar]
- Mitelman, A.; Yang, B.; Elmo, D.; Giat, Y. Choosing between Prediction and Explanation in Geological Engineering: Lessons from Psychology. Interdiscip. Sci. Rev. 2023, 48, 651–668. [Google Scholar] [CrossRef]
- Rocscience Phase2 Version 6.020; Rocscience Inc.: Toronto, ON, Canada, 2007.
- Peck, R.B. Advantages and Limitations of the Observational Method in Applied Soil Mechanics. Geotechnique 1969, 19, 171–187. [Google Scholar]
- Mitelman, A.; Giat, Y. Key Factors in the Design of Urban Underground Metro Lines. Sustainability 2024, 16, 9293. [Google Scholar] [CrossRef]
- Likitlersuang, S.; Surarak, C.; Suwansawat, S.; Wanatowski, D.; Oh, E.; Balasubramaniam, A. Simplified Finite-Element Modelling for Tunnelling-Induced Settlements. Geotech. Res. 2014, 1, 133–152. [Google Scholar] [CrossRef]
- Cao, M.; Zhang, Z.; Du, Z.; Wang, L.; Lv, Y.; Zhang, J.; Wang, Y. Experimental Study of Hardening Small Strain Model Parameters for Strata Typical of Zhengzhou and Their Application in Foundation Pit Engineering. Buildings 2023, 13, 2784. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Mitelman, A.; Yang, B.; Urlainis, A.; Elmo, D. Coupling Geotechnical Numerical Analysis with Machine Learning for Observational Method Projects. Geosciences 2023, 13, 196. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2022; ISBN 1098122461. [Google Scholar]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A Comparative Analysis of Gradient Boosting Algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar]
- Furtney, J.K.; Thielsen, C.; Fu, W.; Le Goc, R. Surrogate Models in Rock and Soil Mechanics: Integrating Numerical Modeling and Machine Learning. Rock Mech. Rock Eng. 2022, 55, 2845–2859. [Google Scholar] [CrossRef]

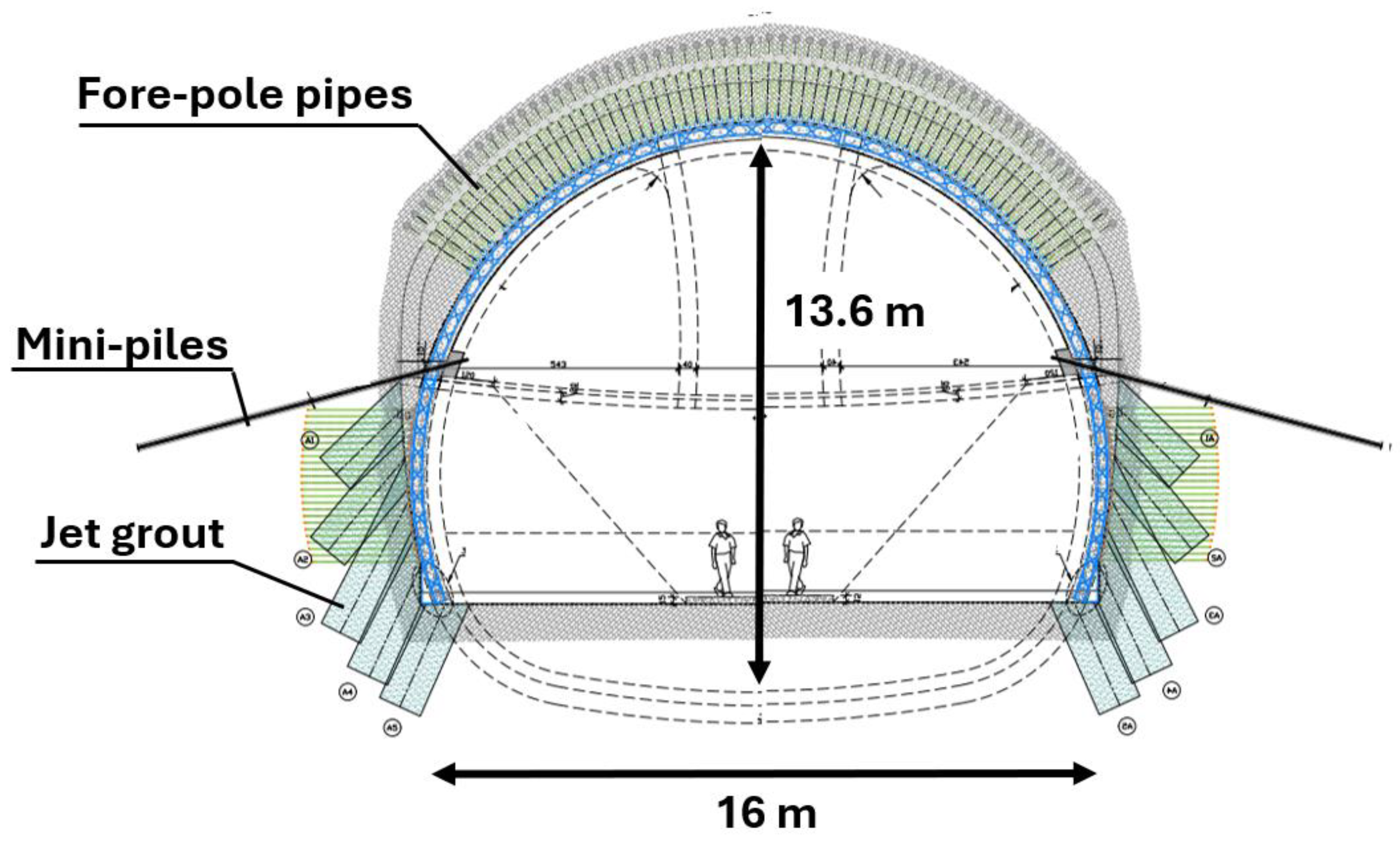



| Support Element | Input Parameter | Value |
|---|---|---|
| Tunnel liner | Thickness [cm] | 40 |
| Young’s modulus [MPa] | 30,000 | |
| Poisson ratio [-] | 0.2 | |
| Temporary tunnel invert | Thickness [cm] | 35 |
| Area (m2) | 30,000 | |
| Poisson ratio [-] | 0.2 | |
| Temporary side liner | Thickness [cm] | 10 |
| Young’s modulus [MPa] | 30,000 | |
| Poisson ratio [-] | 0.2 | |
| Inclined pile | Young’s modulus [MPa] | 200,000 |
| Area [m2] | 0.000484 | |
| Spacing [m] | 0.6 | |
| Poisson ratio [-] | 0.25 | |
| Jet Grout | Young’s modulus [MPa] | 1400 |
| Poisson ratio [-] | 0.3 | |
| Friction angle (degrees) | 34 | |
| Cohesion (MPa) | 0.93 |
| Parameter | Unit | Min | Max | Relationship |
|---|---|---|---|---|
| [MPa] | 1 | 150 | ||
| [MPa] | 0.5 | 225 | ||
| [MPa] | 1 | 1575 | ||
| [-] | 0.5 | 1 | ||
| υ | [-] | 0.2 | 0.3 | |
| [-] | 0.4 | 0.6 | ||
| ϕ | [Deg] | 20 | 40 | |
| Ψ | [Deg] | 0 | 10 | ϕ-30° |
| cohesion | [MPa] | 0 | 0.01 | |
| Rf | [-] | 0.6 | 0.9 | |
| ψ | [Deg] | 0 | 10 | |
| [MPa] | 1.1 | 2677.5 | ||
| [-] | 0.0001 | 0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eilat, T.; McQuillan, A.; Mitelman, A. Machine Learning-Enhanced Analysis of Small-Strain Hardening Soil Model Parameters for Shallow Tunnels in Weak Soil. Geotechnics 2025, 5, 26. https://doi.org/10.3390/geotechnics5020026
Eilat T, McQuillan A, Mitelman A. Machine Learning-Enhanced Analysis of Small-Strain Hardening Soil Model Parameters for Shallow Tunnels in Weak Soil. Geotechnics. 2025; 5(2):26. https://doi.org/10.3390/geotechnics5020026
Chicago/Turabian StyleEilat, Tzuri, Alison McQuillan, and Amichai Mitelman. 2025. "Machine Learning-Enhanced Analysis of Small-Strain Hardening Soil Model Parameters for Shallow Tunnels in Weak Soil" Geotechnics 5, no. 2: 26. https://doi.org/10.3390/geotechnics5020026
APA StyleEilat, T., McQuillan, A., & Mitelman, A. (2025). Machine Learning-Enhanced Analysis of Small-Strain Hardening Soil Model Parameters for Shallow Tunnels in Weak Soil. Geotechnics, 5(2), 26. https://doi.org/10.3390/geotechnics5020026







