A Critical Review of Cone Penetration Test-Based Correlations for Estimating Small-Strain Shear Modulus in North Sea Soils
Abstract
1. Introduction
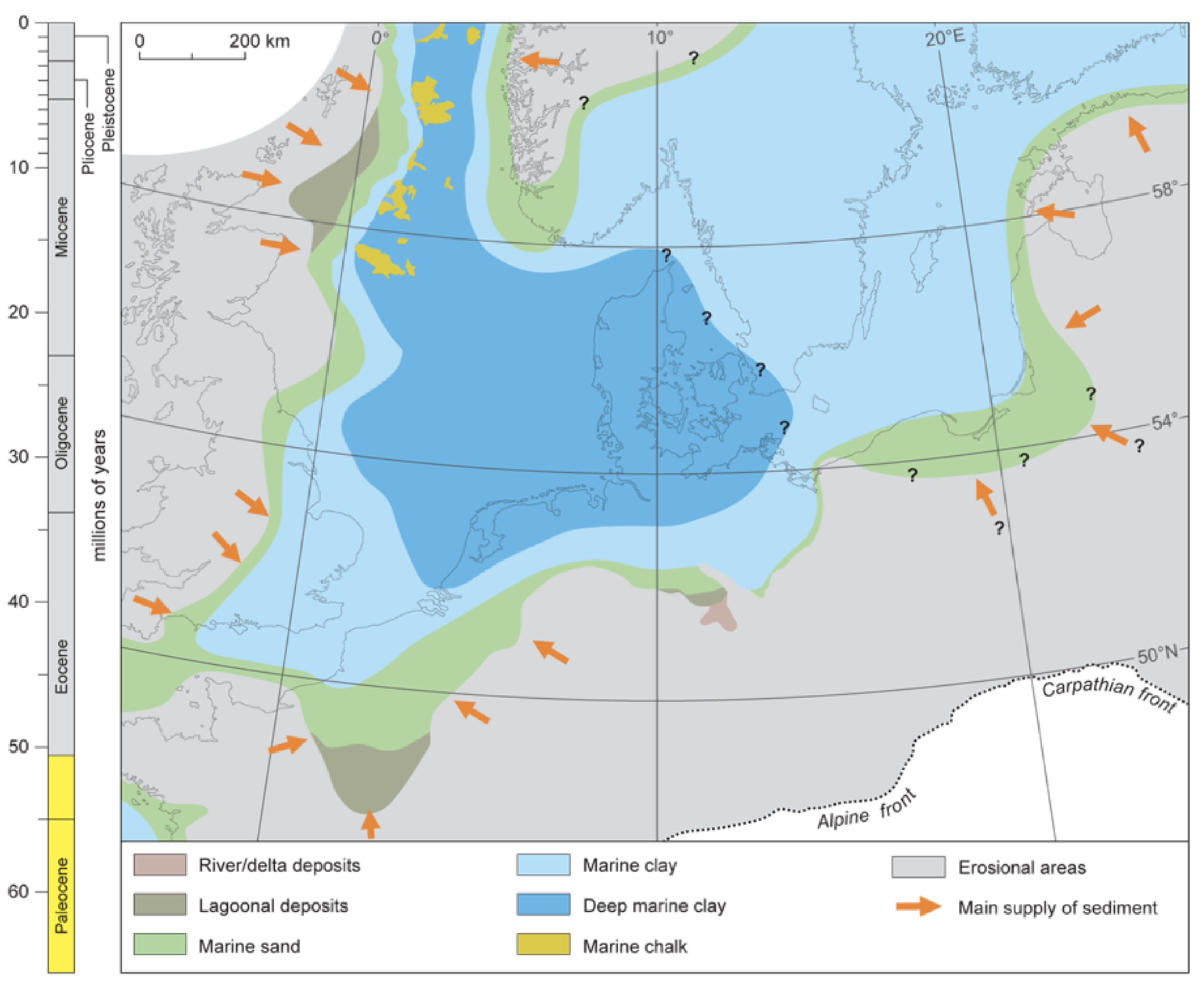
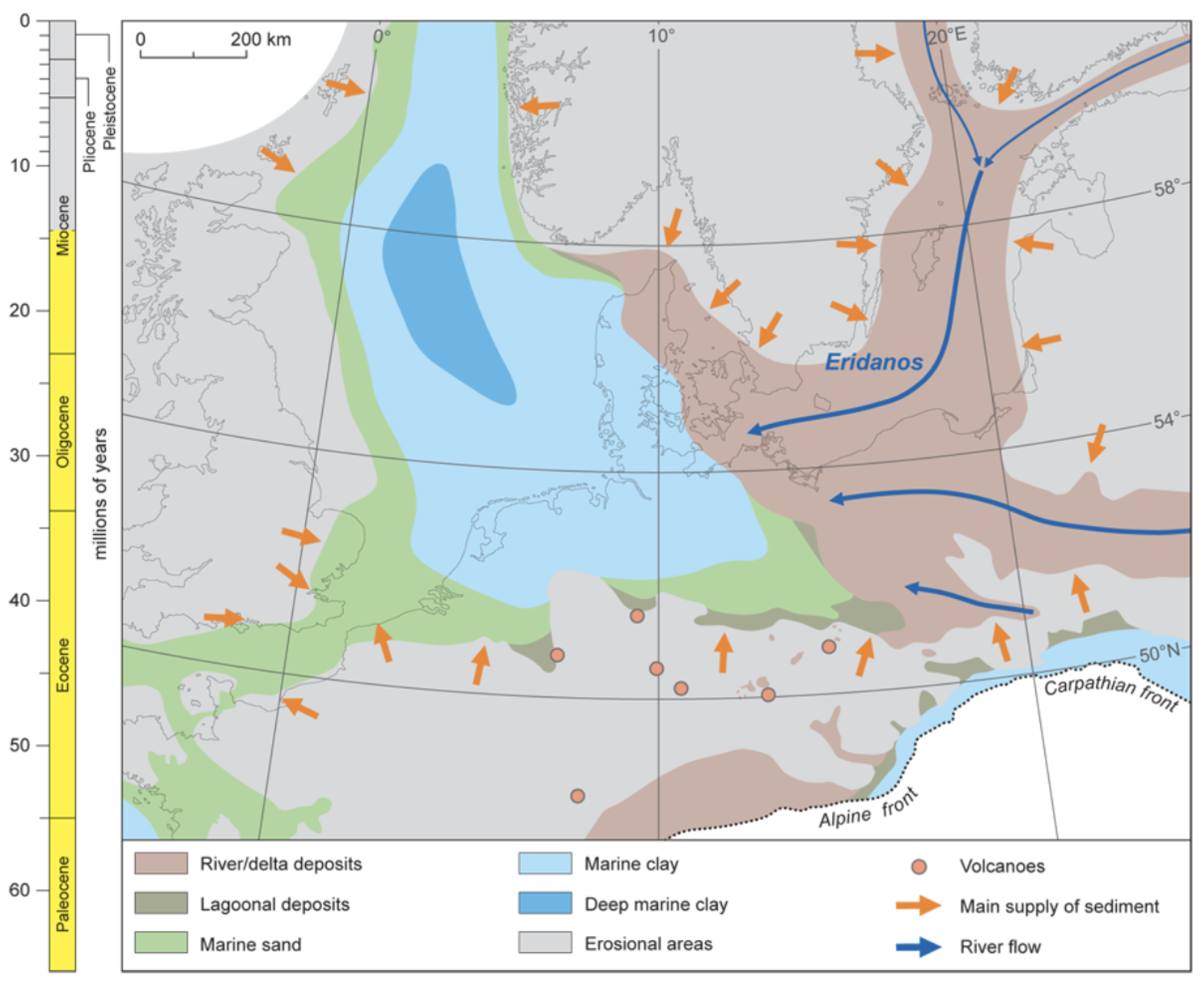
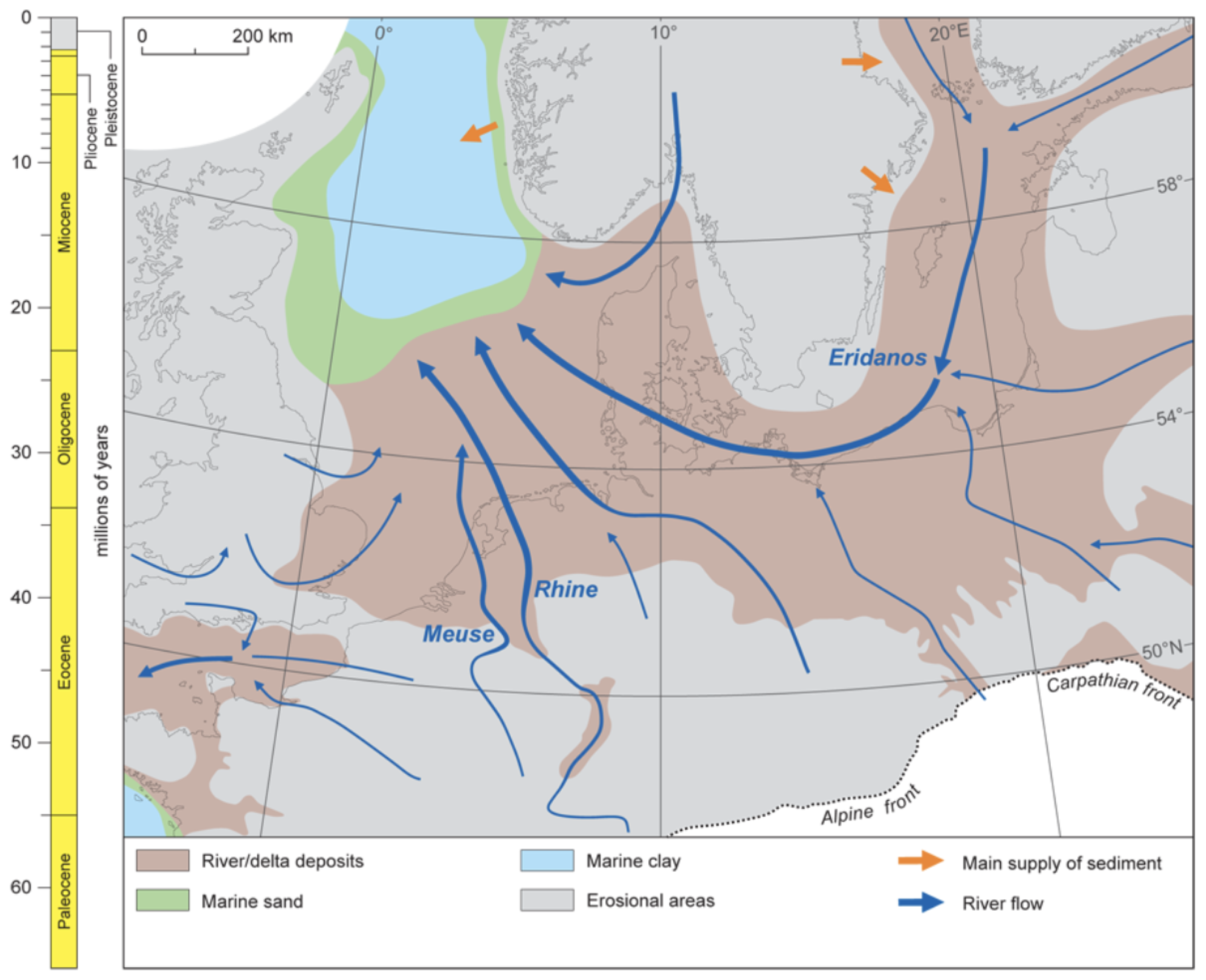
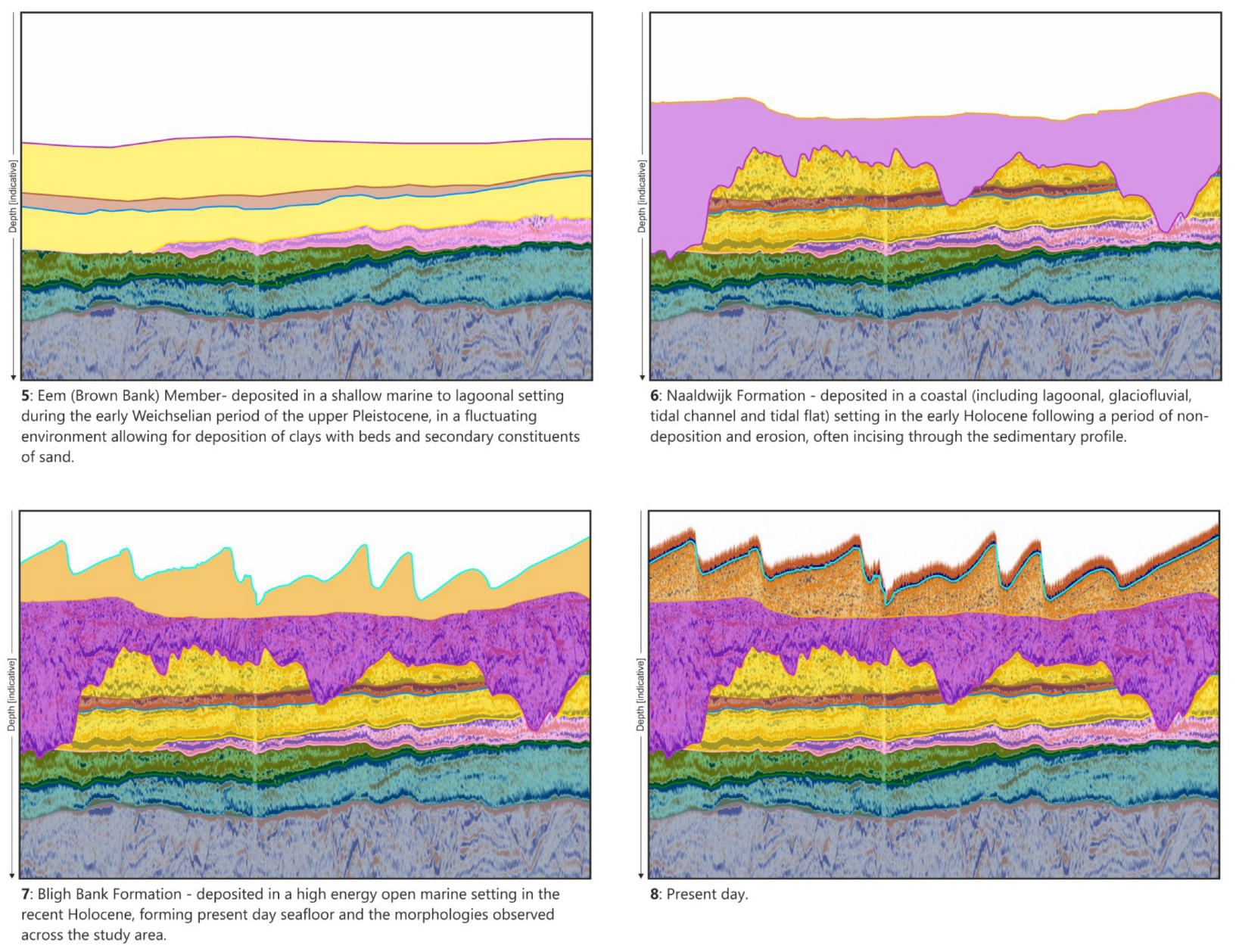
2. Geology of the Southern North Sea
3. Shear Wave Velocity Dataset
3.1. Geographic Locations
3.2. Measurement Setup
3.3. Data Processing
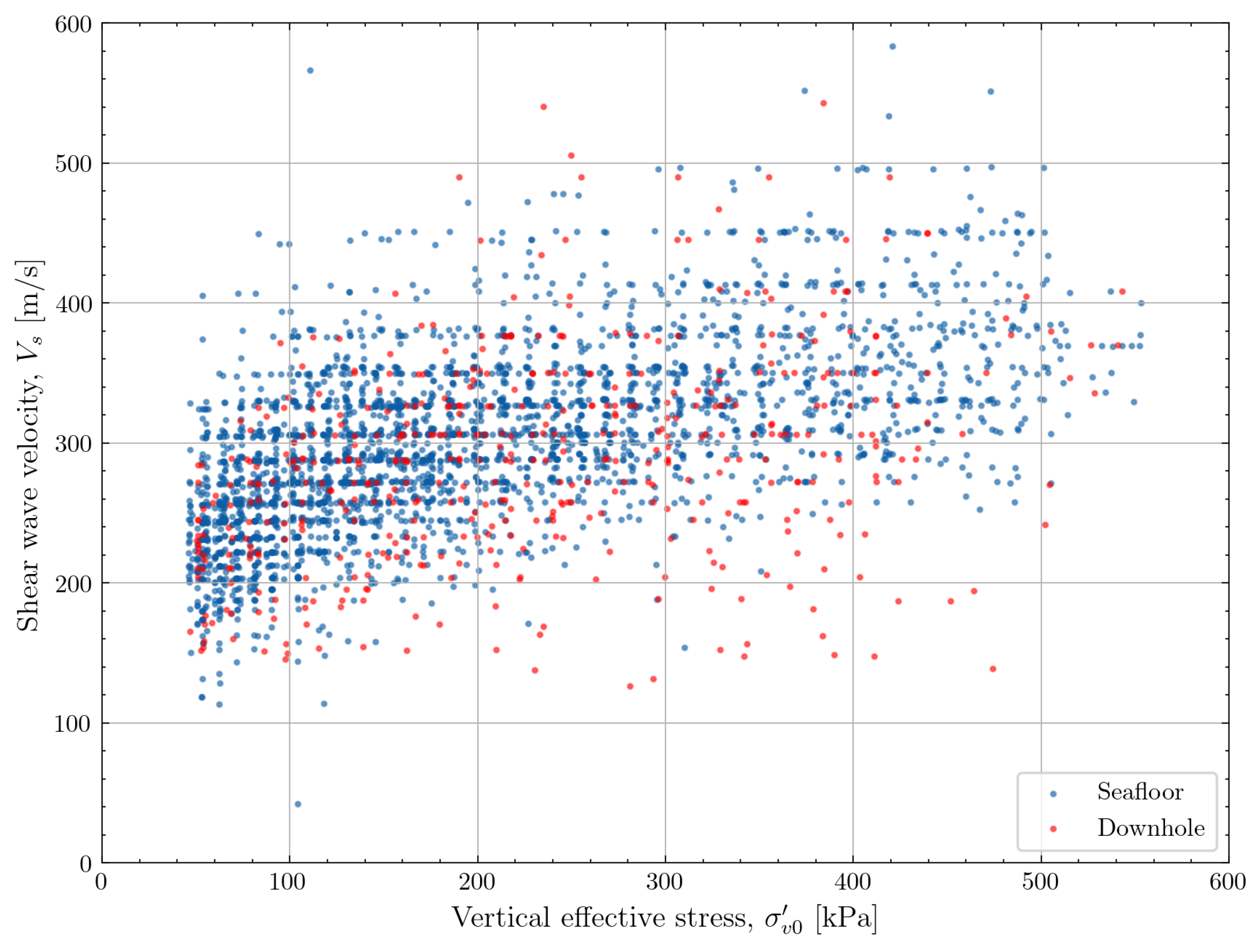
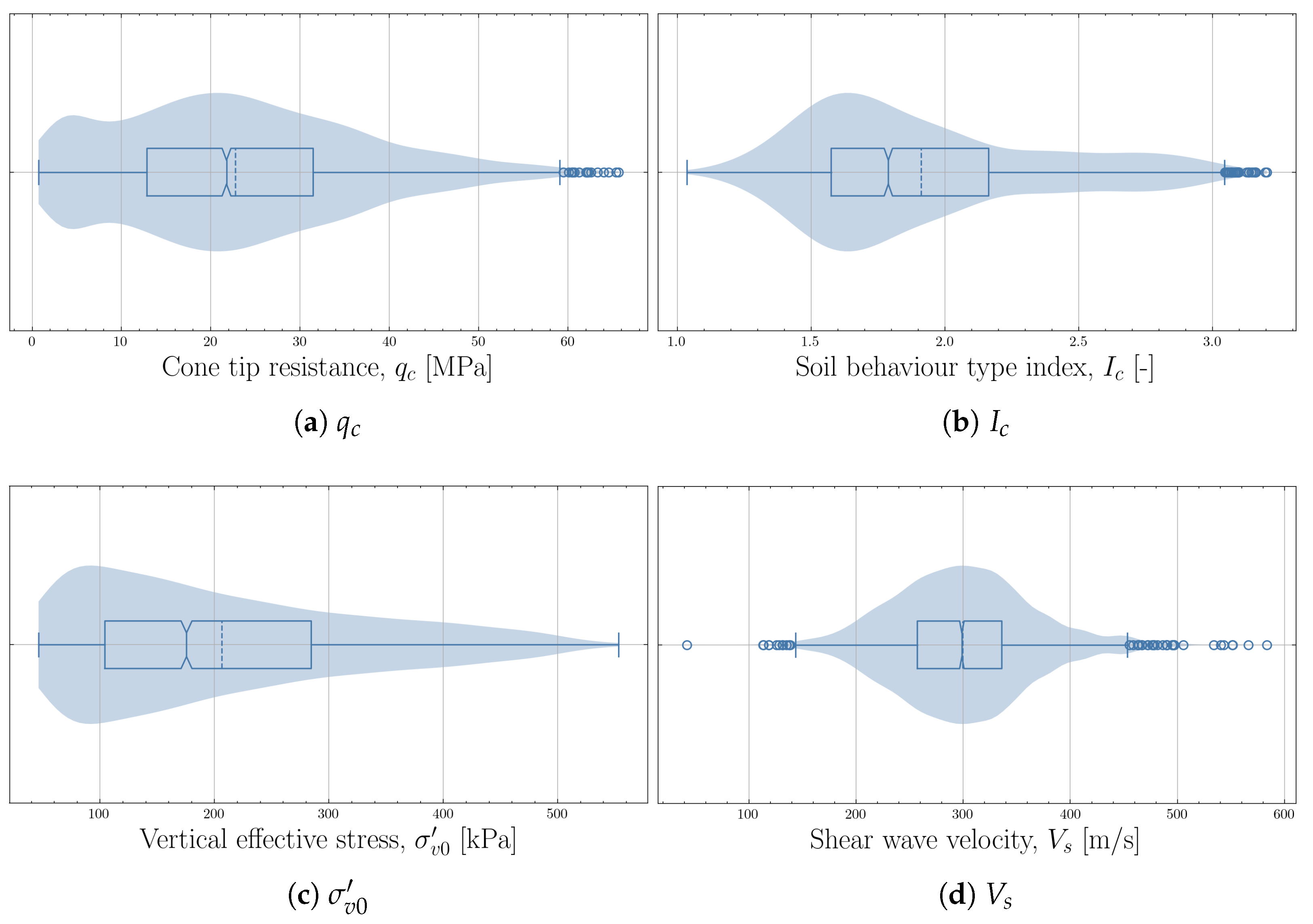
3.4. Dataset Overview
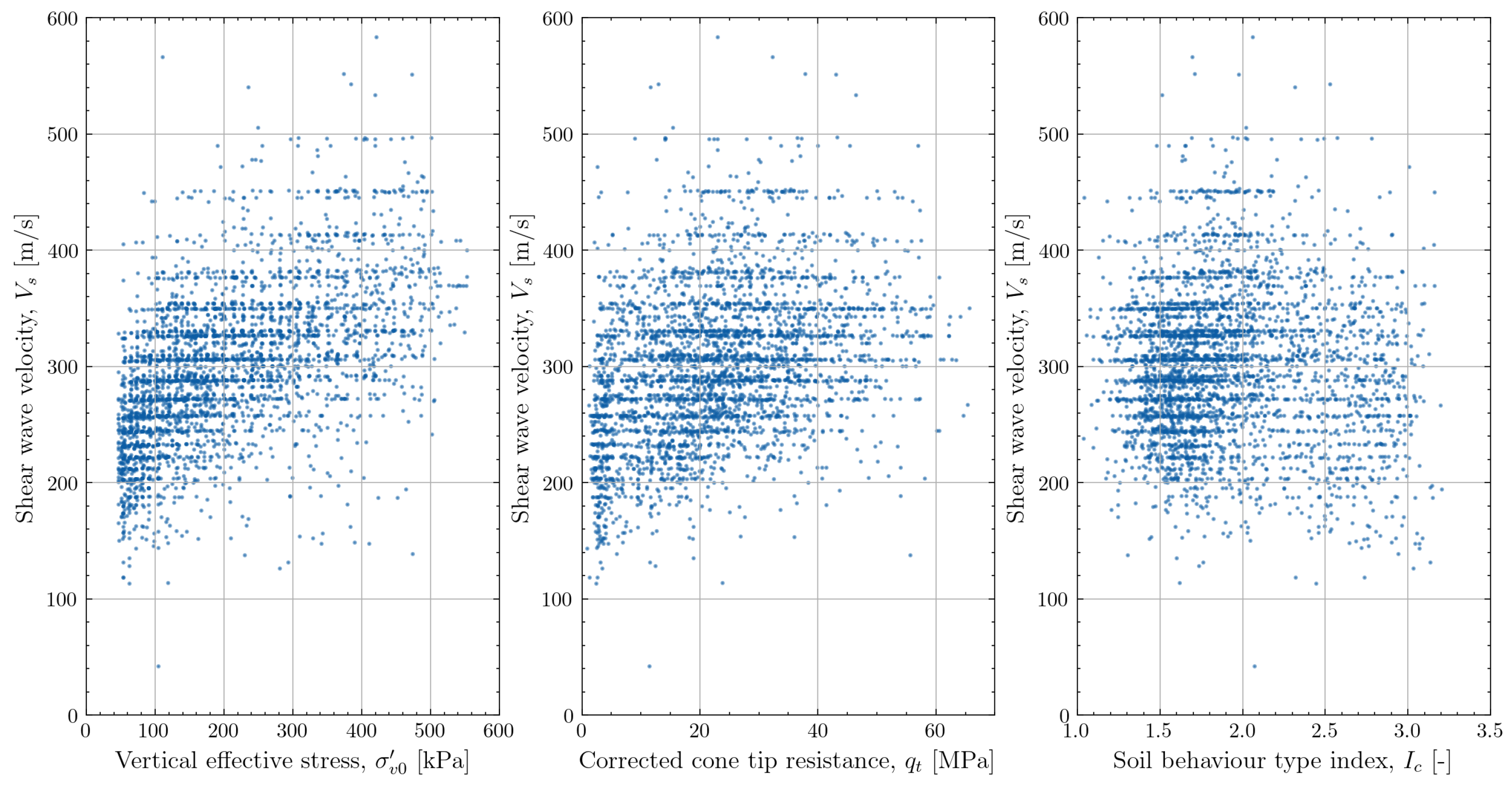
3.5. Observed Trends
4. Critical Review of Existing CPT-Based Correlations
4.1. Review of Correlations
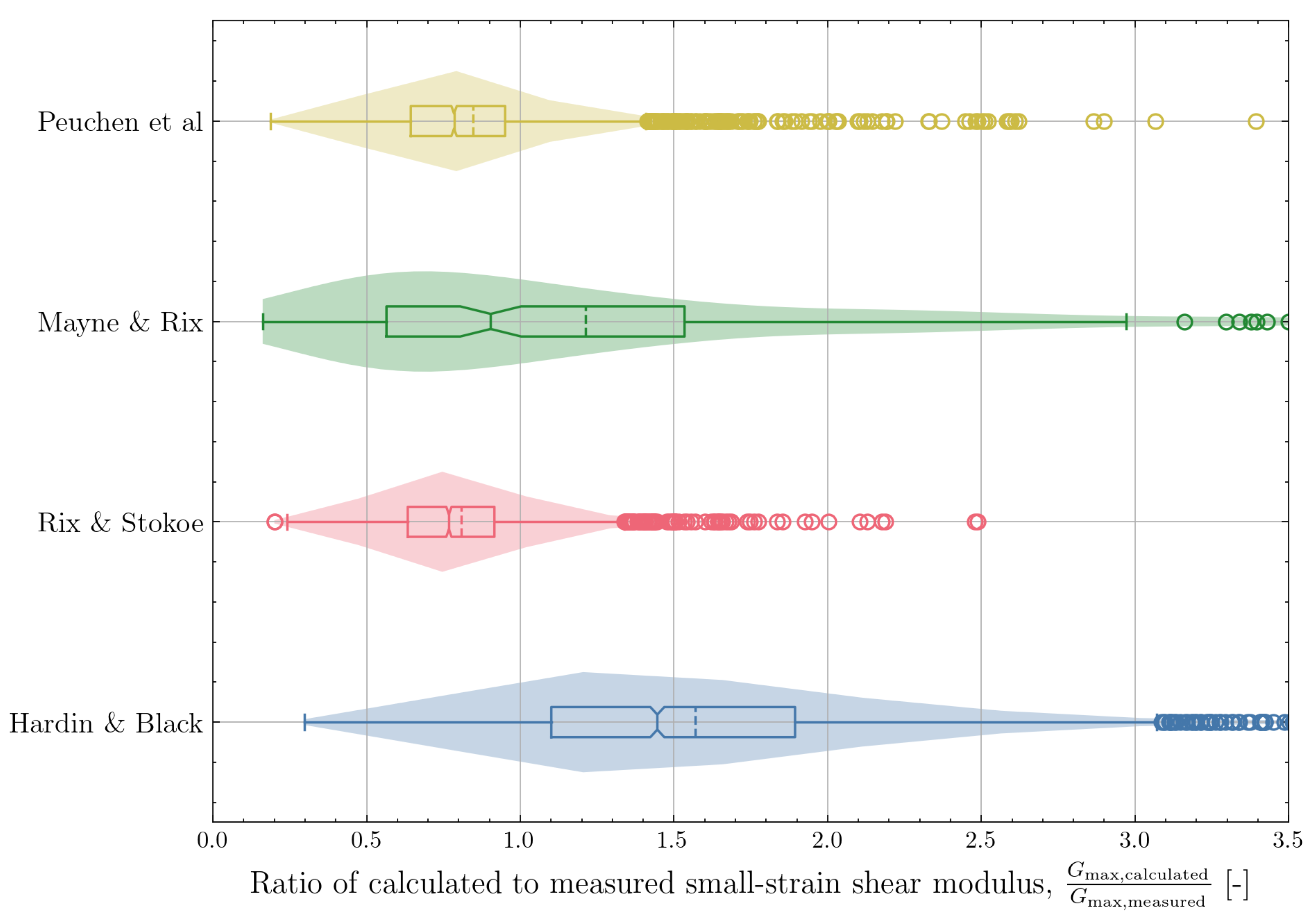
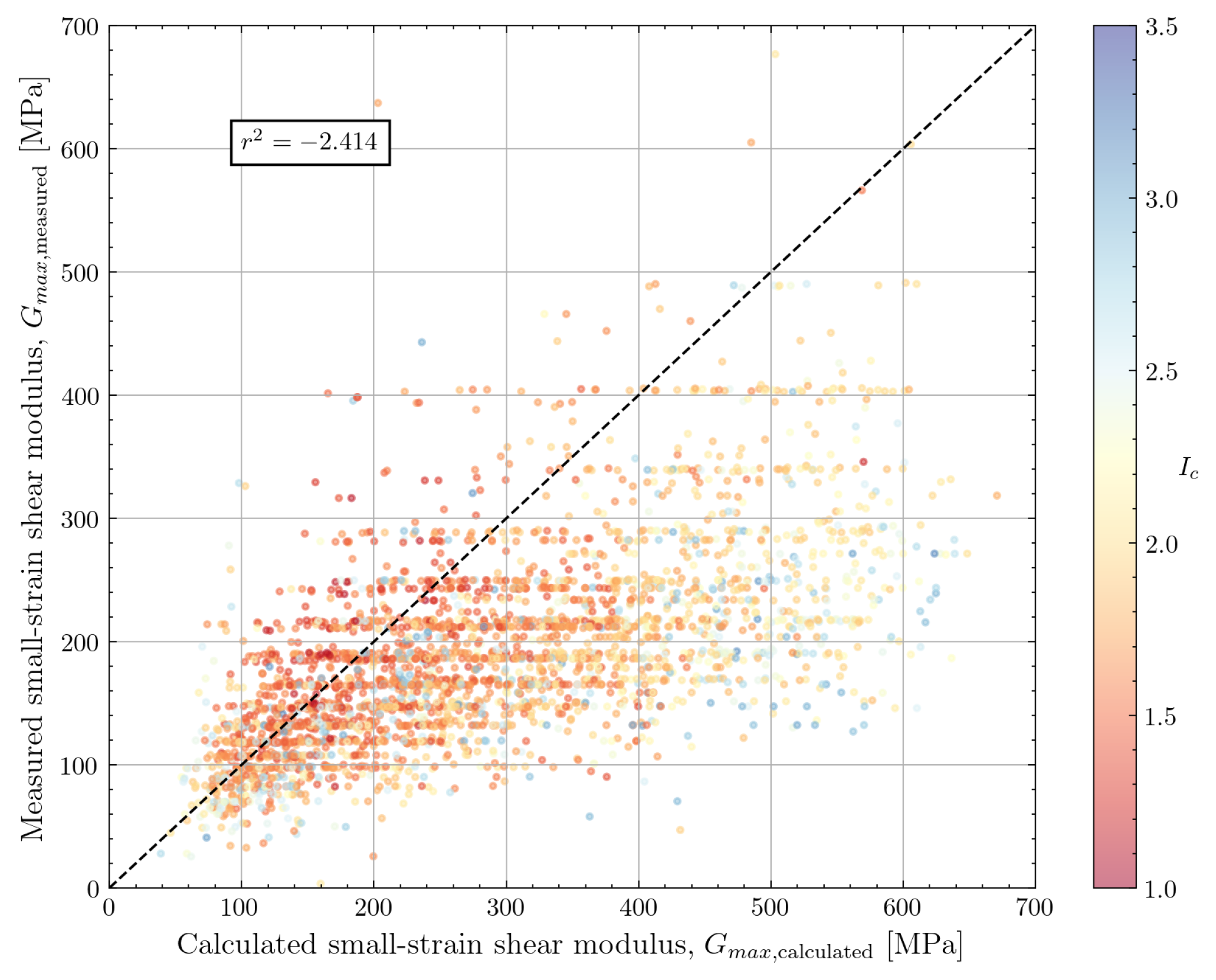
4.1.1. Hardin and Black (1968)
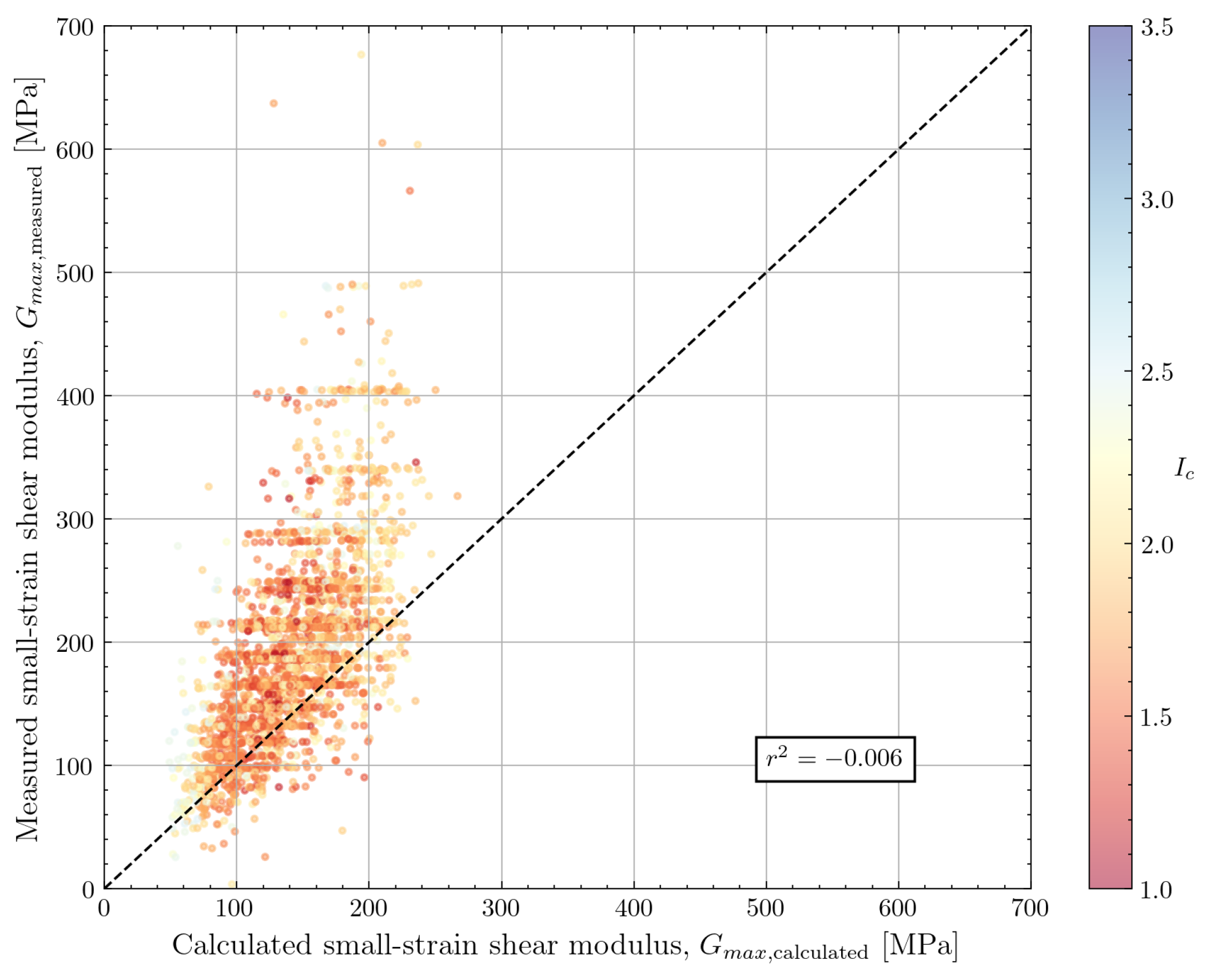
4.1.2. Rix and Stokoe (1991)
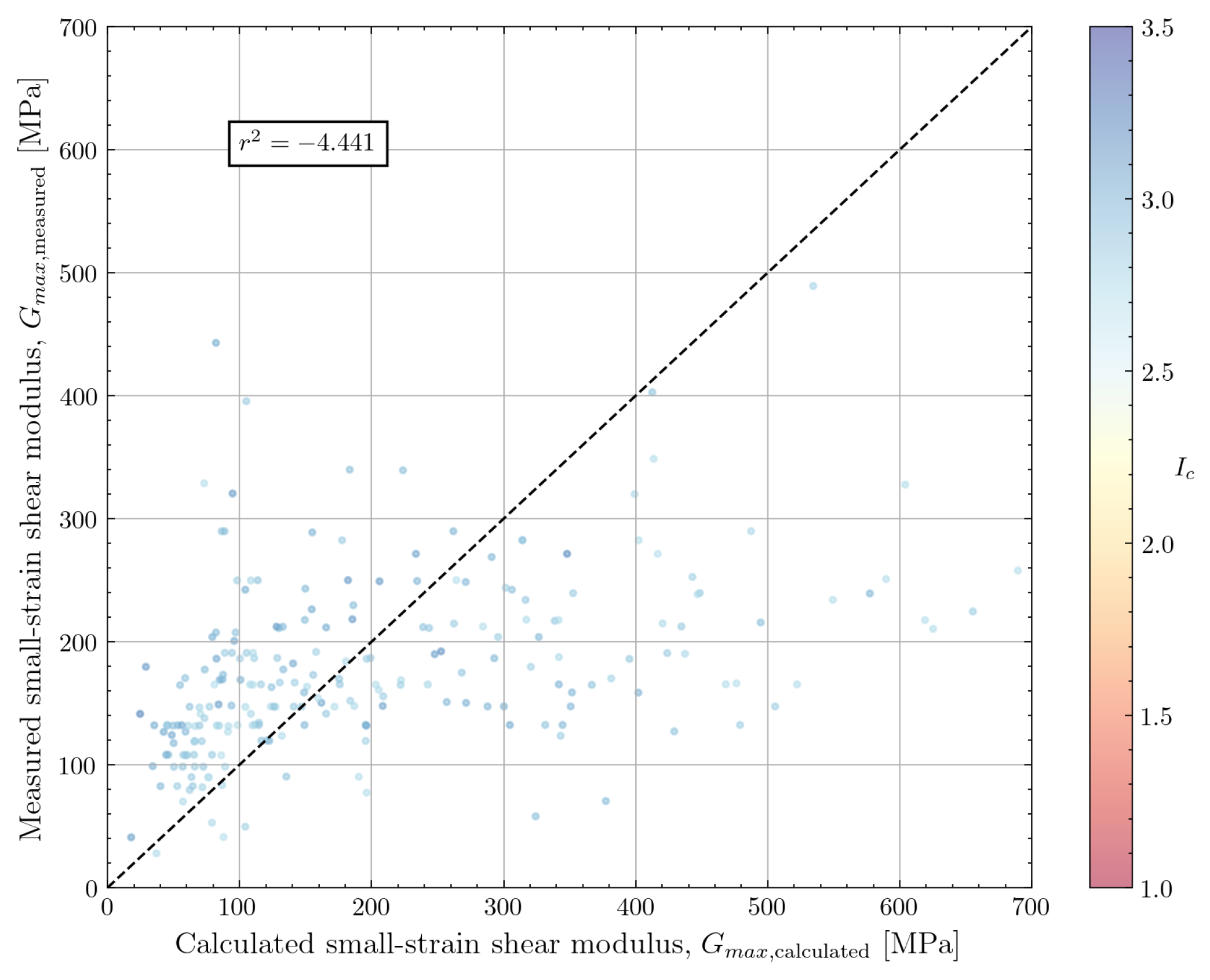
4.1.3. Mayne and Rix (1993)
4.1.4. Peuchen et al. (2020)
4.2. Review of Correlations
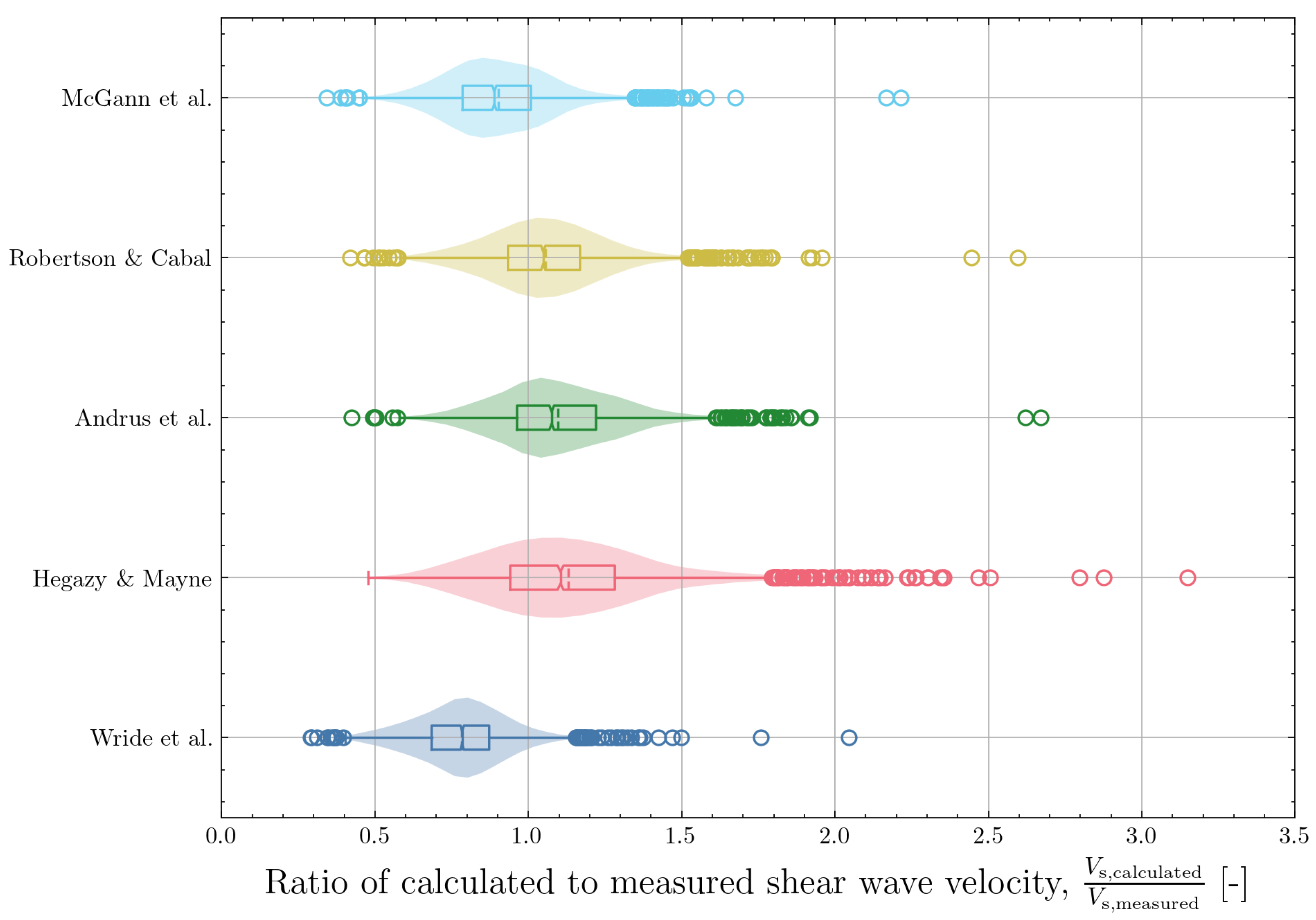
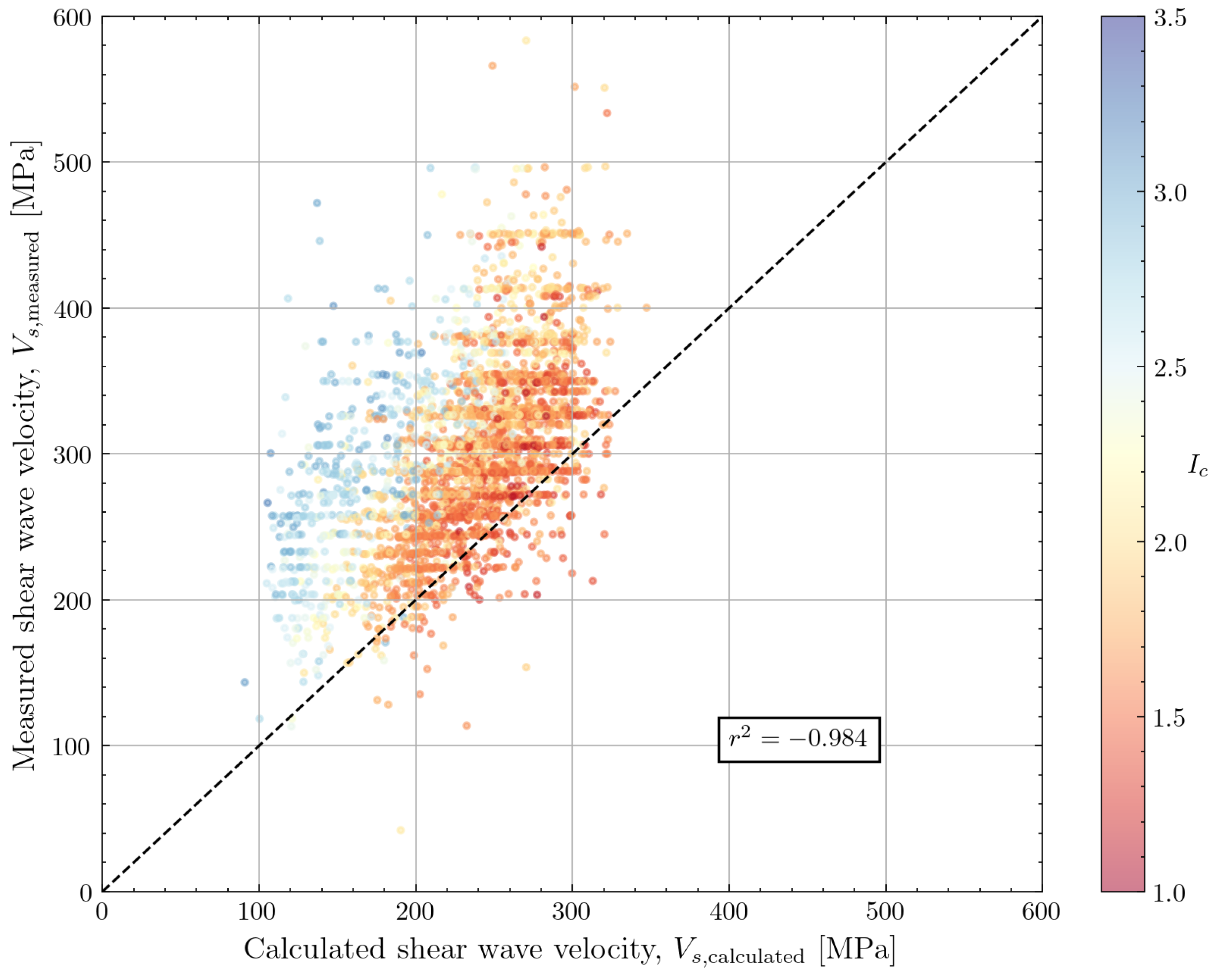
4.2.1. Wride et al. (2000)
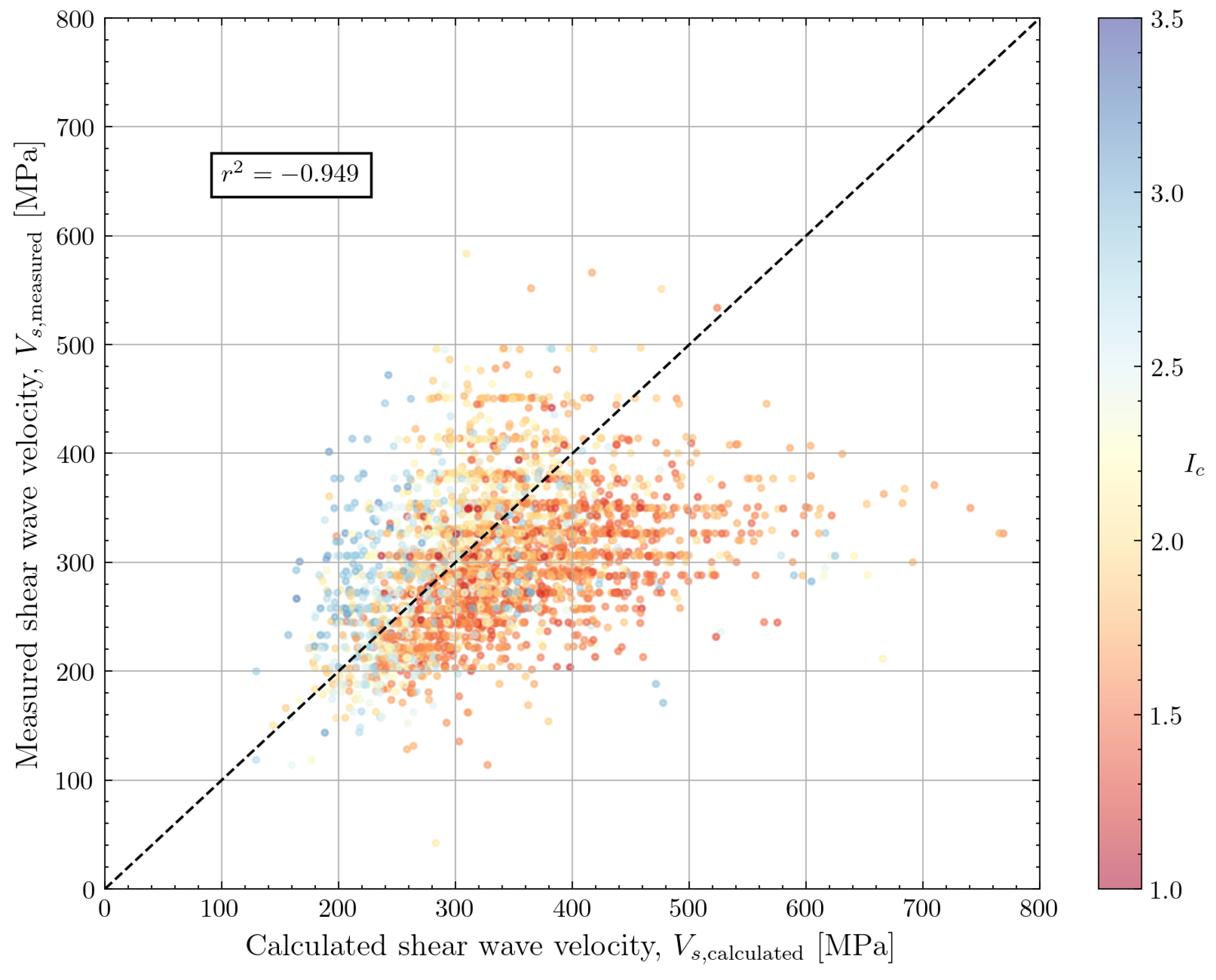
4.2.2. Hegazy and Mayne (2006)
4.2.3. Andrus et al. (2007)
4.2.4. Tonni and Simonini (2013)
4.2.5. Cha et al. (2014) and Lyu et al. (2021)
4.2.6. Robertson and Cabal (2015)
4.2.7. McGann et al. (2018)
4.3. Statistical Evaluation of CPT-Based Correlations for the North Sea Dataset
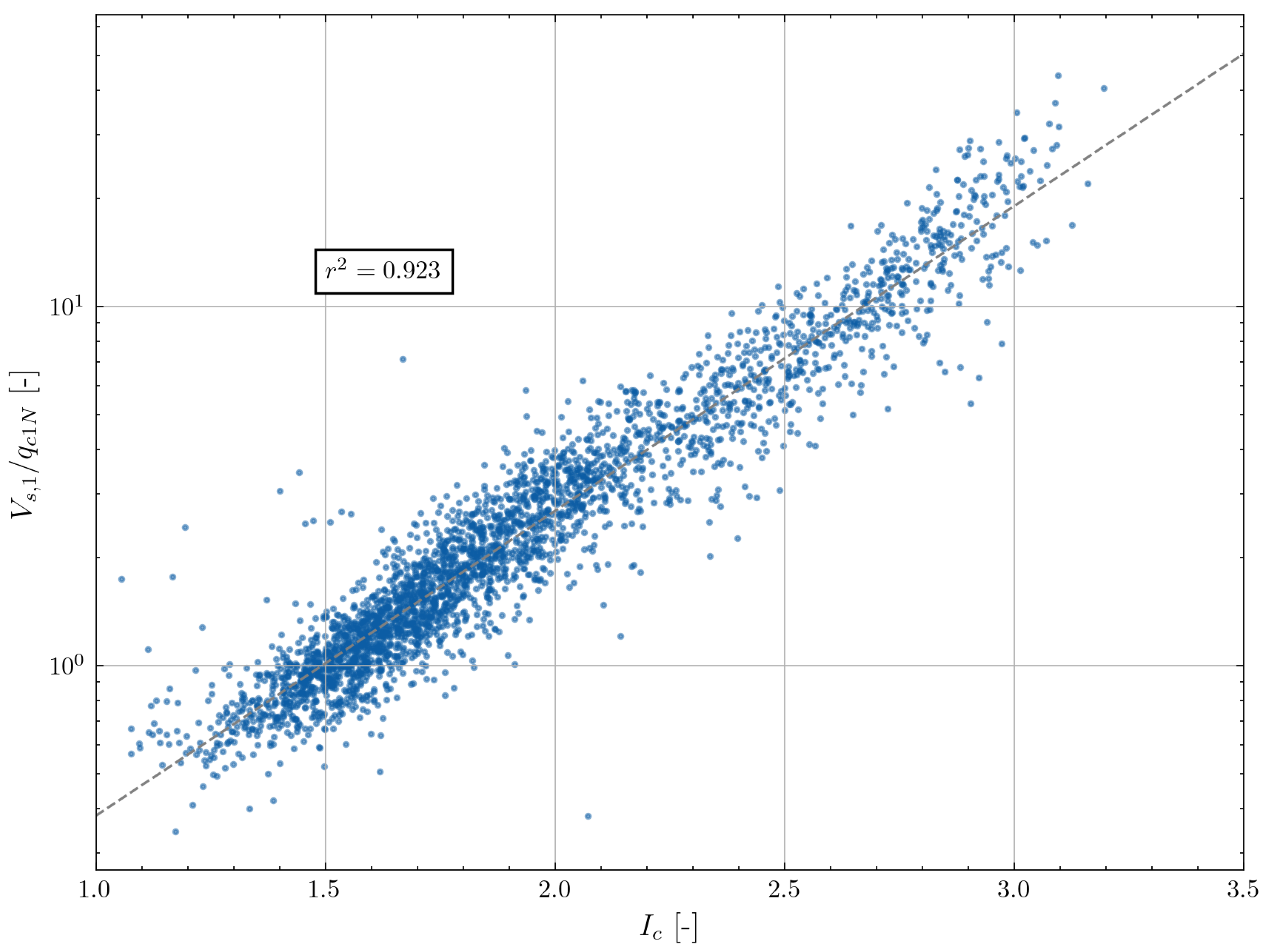
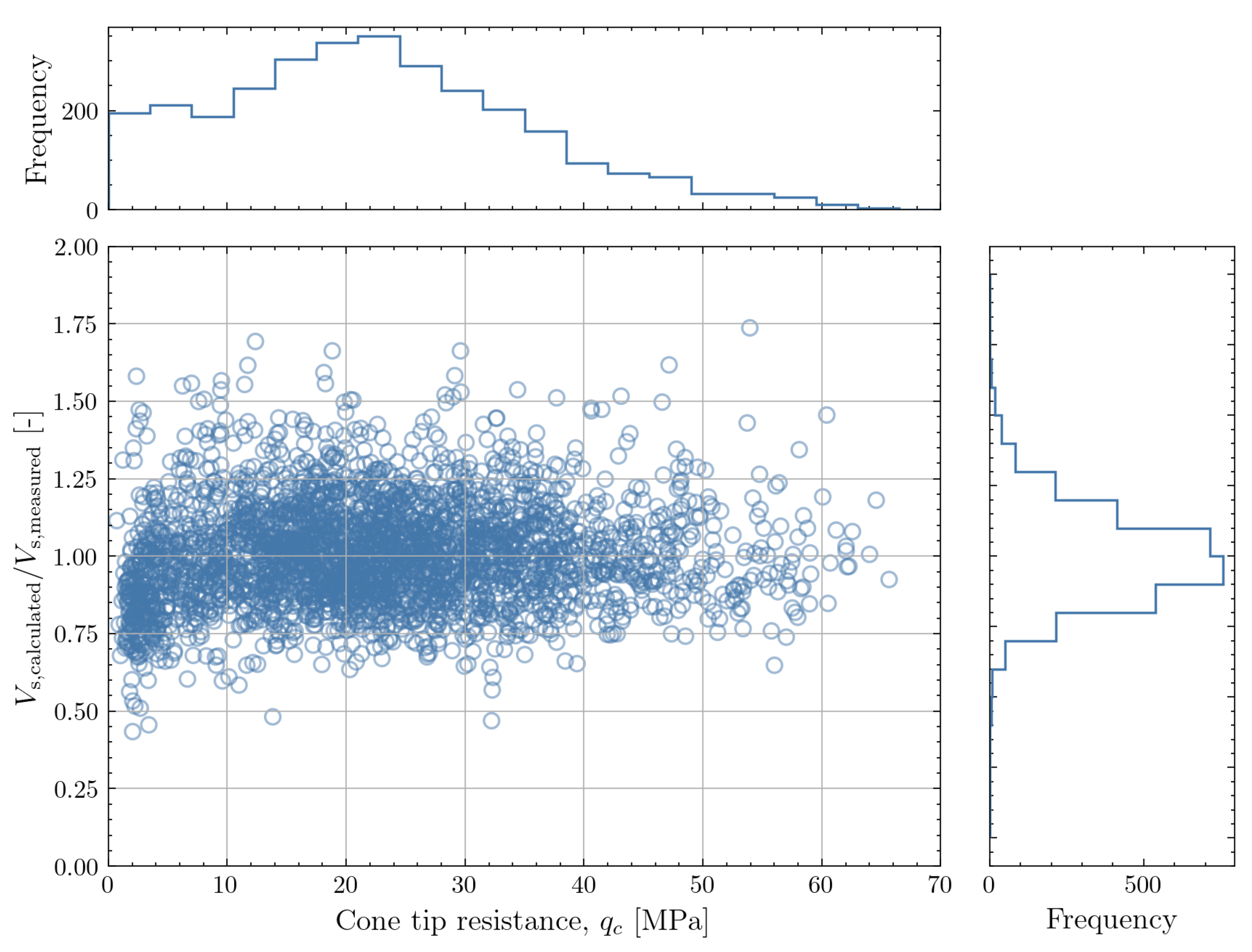
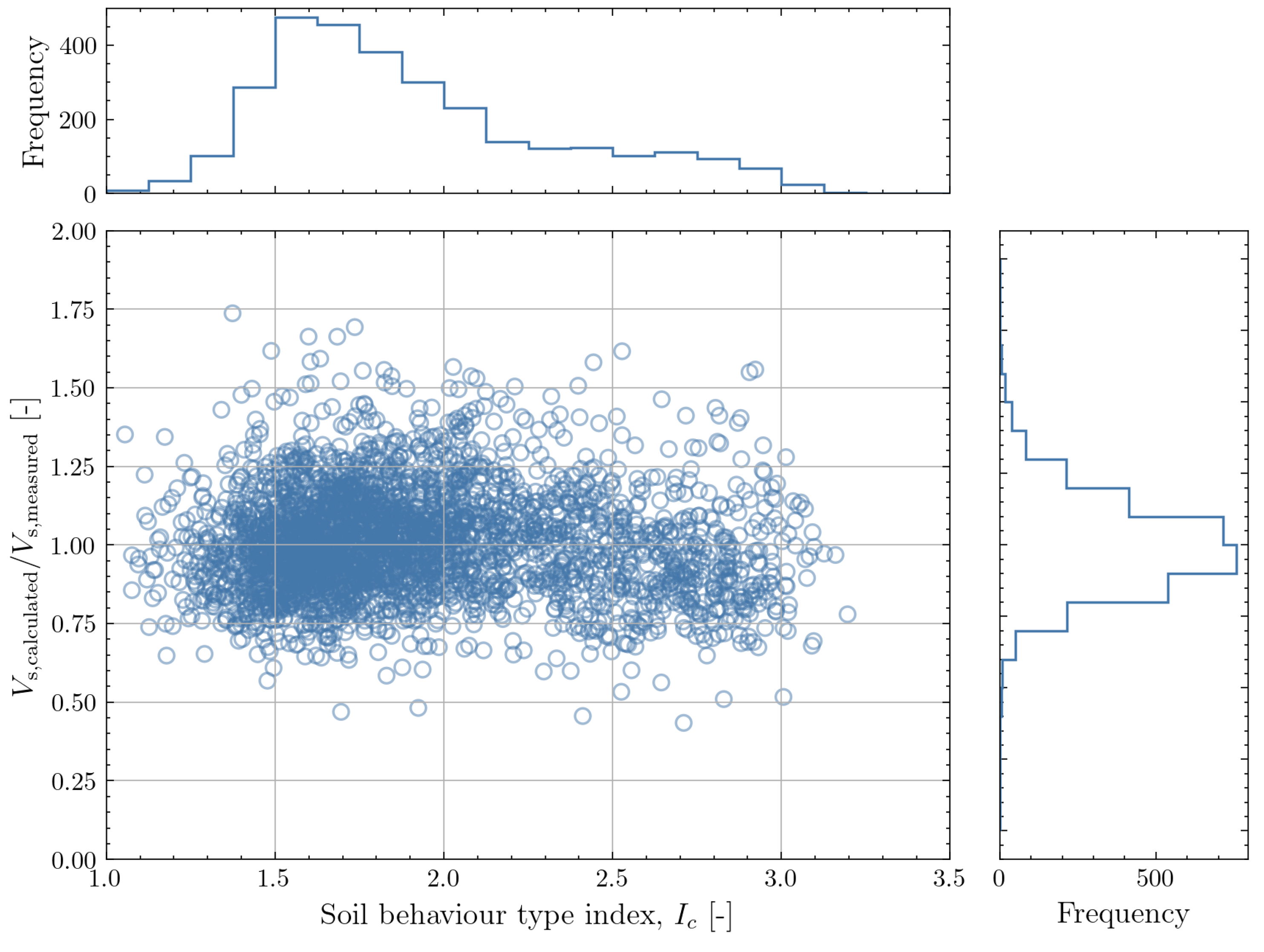
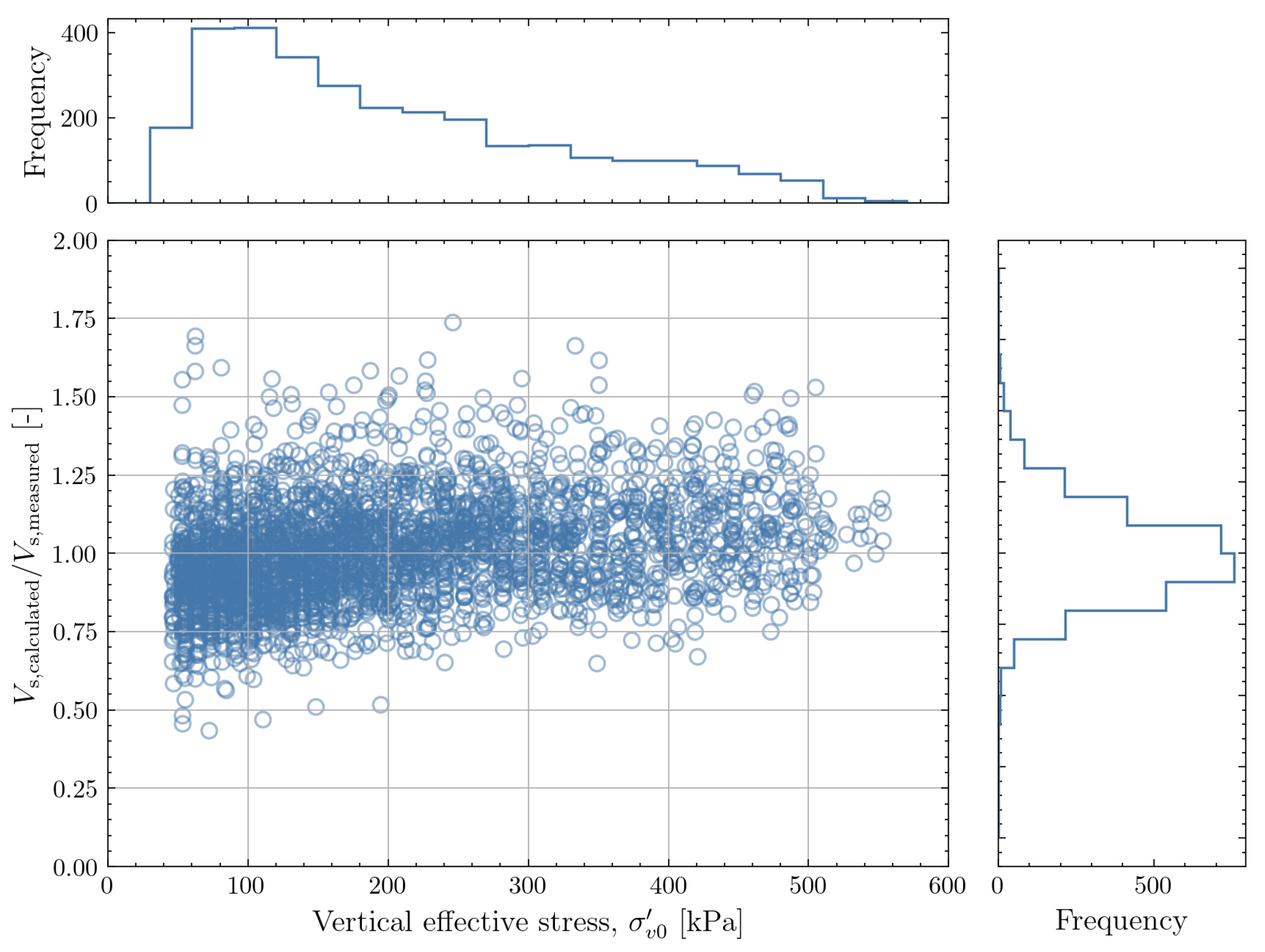
5. A New Stress-Dependent Model for SHEAR Wave Velocity
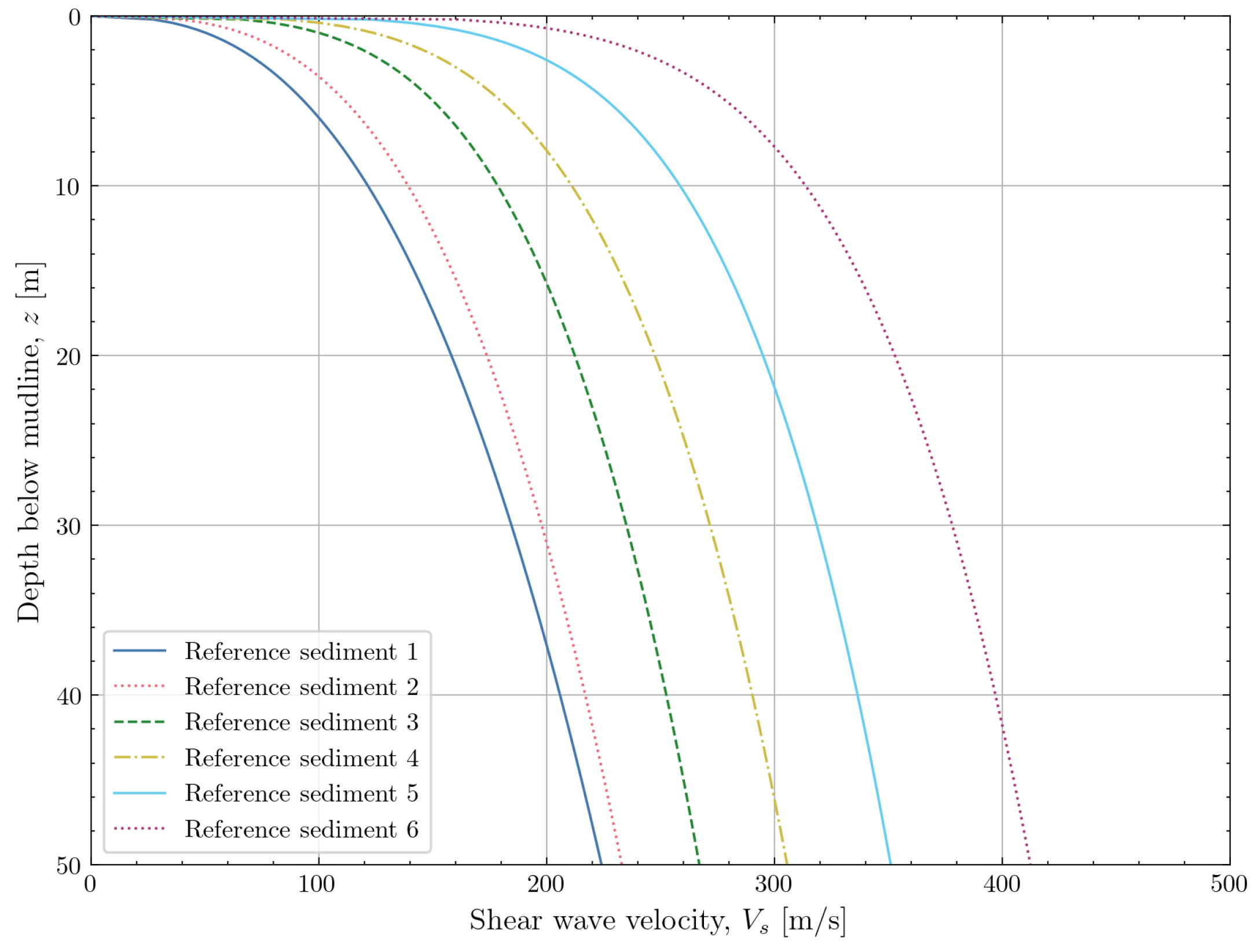
5.1. Soil Mechanical Background
5.2. Calibration of the Model Coefficients
5.3. Evaluation of the Newly Proposed Correlation
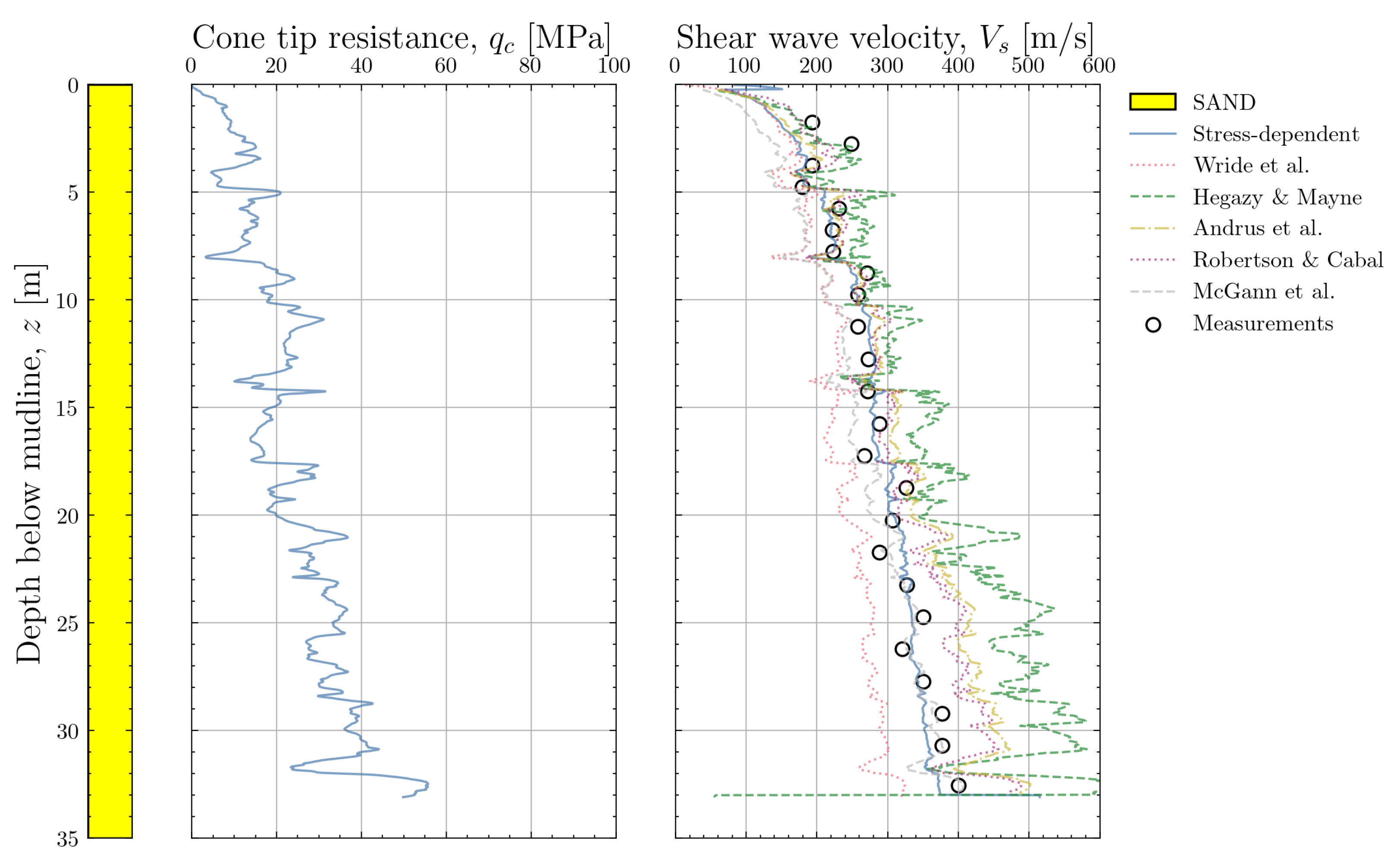
6. Application to Example Locations from the Southern North Sea
- IJV162-SCPT: A test location from the Ijmuiden Ver offshore wind farm zone characterised by uniform sandy conditions;
- IJV038-SCPT: A test location from the Ijmuiden Ver offshore wind farm zone characterised by a layered profile with an alternation of sand, clay and silt.
6.1. Sandy Location
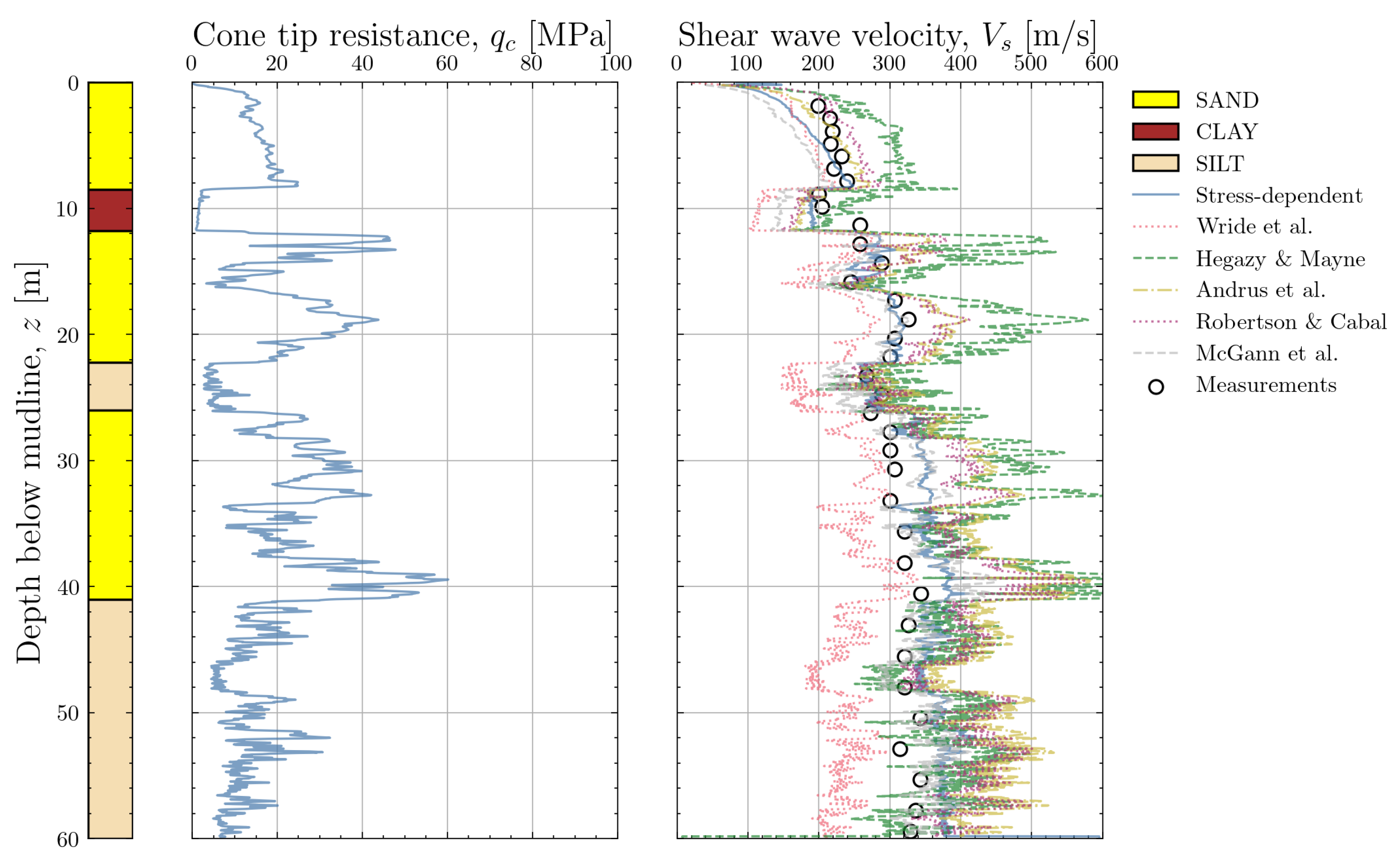
6.2. Layered Location
7. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
- Some or all data, models, or code that support the findings of this study are publically available:
- -
- Public-domain geotechnical data from the Dutch and German offshore wind farms as provided by RVO.nl and BSH
- -
- Processed S-PCPT data for the Dutch and German wind farms (DOI 10.5281/zenodo.10986518).
- Some or all data, models, or code generated or used during the study are proprietary or confidential in nature and may only be provided upon request with restrictions (e.g., anonymized data)
- -
- Geotechnical data from the Belgian and Danish offshore wind farms.
Conflicts of Interest
References
- WindEurope. Offshore Wind in Europe: Key Trends and Statistics 2019; Technical report; WindEurope asbl/vzw: Brussels, Belgium, 2020. [Google Scholar]
- Seidel, M.; Voormeeren, S.; van der Steen, J.B. State-of-the-art design processes for offshorewind turbine support structures. Stahlbau 2016, 85, 14. [Google Scholar] [CrossRef]
- Schafhirt, S.; Page, A.; Eiksund, G.R.; Muskulus, M. Influence of Soil Parameters on the Fatigue Lifetime of Offshore Wind Turbines with Monopile Support Structure. Energy Procedia 2016, 94, 10. [Google Scholar] [CrossRef]
- Simoncelli, M.; Zucca, M.; Ghilardi, M. Structural health monitoring of an onshore steel wind turbine. J. Civ. Struct. Health Monit. 2024, 1–15. [Google Scholar] [CrossRef]
- Devriendt, C.; Weijtjens, W.; El-Kafafy, M.; De Sitter, G. Monitoring resonant frequencies and damping values of an offshore wind turbine in parked conditions. IET Renew. Power Gener. 2014, 8, 433–441. [Google Scholar] [CrossRef]
- Kallehave, D.; LeBlanc, C.; Liingaard, M. Modification of the API P-Y formulation of initial stiffness of sand. In Proceedings of the 7th InternationalConference on Offshore Site Investigation and Geotechnics, London, UK, 12–14 September 2012; pp. 465–472. [Google Scholar]
- Byrne, B.; McAdam, R.A.; Burd, H.; Houlsby, G.; Martin, C.M.; Beuckelaers, W.; Zdravkovic, L.; Taborda, D.; Potts, D.; Jardine, R.; et al. PISA: New design methods for offshore wind turbine monopiles. In Proceedings of the 8th InternationalConference on Offshore Site Investigation and Geotechnics, London, UK, 12–14 September 2017; Volume 142, pp. 142–161. [Google Scholar]
- Hardin, B.O.; Black, W.L. Vibration modulus of normally consolidated clay. J. Soil Mech. Found. Div. 1968, 94, 353–369. [Google Scholar] [CrossRef]
- Rix, G.J.; Stokoe, K.H. Correlation of initial tangent modulus and cone penetration resistance. In Proceedings of the Calibration Chamber Testing; Elsevier: New York, NY, USA, 1991; pp. 351–362. [Google Scholar]
- Mayne, P.; Rix, G. Gmax-qc relationships for clays. Geotech. Test. J. GTJODJ 1993, 16, 54–60. [Google Scholar] [CrossRef]
- Wride, C.; Robertson, P.; Biggar, K.; Campanella, R.; Hofmann, B.; Hughes, J.M.; Küpper, A.; Woeller, D. Interpretation of in situ test results from the CANLEX sites. Can. Geotech. J. 2000, 37, 505–529. [Google Scholar] [CrossRef]
- Hegazy, Y.A.; Mayne, P.W. A global statistical correlation between shear wave velocity and cone penetration data. In Proceedings of the ASCE GeoShangai Conference Site and Geomaterial Characterization, Shanghai, China, 6–8 June 2006; American Society of Civil Engineers: Reston, VA, USA, 2006; pp. 243–248. [Google Scholar]
- Andrus, R.D.; Mohanan, N.P.; Piratheepan, P.; Ellis, B.S.; Holzer, T.L. Predicting shear-wave velocity from cone penetration resistance. In Proceedings of the 4th international conference on earthquake geotechnical engineering, Thessaloniki, Greece, 24–29 June 2007; Volume 2528. [Google Scholar]
- Tonni, L.; Simonini, P. Shear wave velocity as function of cone penetration test measurements in sand and silt mixtures. Eng. Geol. 2013, 163, 55–67. [Google Scholar] [CrossRef]
- Cha, M.; Santamarina, J.C.; Kim, H.S.; Cho, G.C. Small-strain stiffness, shear-wave velocity, and soil compressibility. J. Geotech. Geoenviron. Eng. 2014, 140, 06014011. [Google Scholar] [CrossRef]
- Robertson, P.; Cabal, K.L. Guide to Cone Penetration Testing; Technical Report; Gregg Drilling Inc.: Benicia, CA, USA, 2015. [Google Scholar]
- McGann, C.R.; Bradley, B.A.; Jeong, S. Empirical correlation for estimating shear-wave velocity from cone penetration test data for banks Peninsula loess soils in Canterbury, New Zealand. J. Geotech. Geoenviron. Eng. 2018, 144, 04018054. [Google Scholar] [CrossRef]
- Peuchen, J.; Kaltekis, K.; Klein, M.; Murali, M.; Erp, F.; Hicks, M. Characteristic Values for Geotechnical Design of Offshore Monopiles in Sandy Soils-Case Study. In Proceedings of the 4th International Symposium Frontiers in Offshore Geotechnics, Austin, TX, USA, 28–31 August 2022. [Google Scholar]
- Phoon, K.K.; Tang, C. Characterisation of geotechnical model uncertainty. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2019, 13, 101–130. [Google Scholar] [CrossRef]
- Cameron; Doorn, D.; Laban, C.; Streif, H. Geology of the Southern North Sea Basin. In Proceedings of the Coastlines of the Southern North Sea, The Eight Symposium on Coastal and Ocean Management, New Orleans, LA, USA, 19–23 July 1993; pp. 15–28. [Google Scholar]
- Ottesen, D.; Batchelor, C.; Dowdeswell, J.; Løseth, H. Morphology and pattern of Quaternary sedimentation in the North Sea Basin (52–62 N). Mar. Pet. Geol. 2018, 98, 836–859. [Google Scholar] [CrossRef]
- Fookes, P.G.; Parrish, D.G. Observations on small-scale structural discontinuities in the London Clay and their relationship to regional geology. Q. J. Eng. Geol. Hydrogeol. 1969, 1, 217–240. [Google Scholar] [CrossRef]
- Verschuren, M. An Integrated 3D Approach to Clay Tectonic deformation and the Development of a New 3D Surface Modeling Method. Ph.D. Thesis, Ghent University, Ghent, Belgium, 1992. [Google Scholar]
- Gibbard, P.L.; Lewin, J. Filling the North Sea Basin: Cenozoic sediment sources and river styles (André Dumont medallist lecture 2014). Geol. Belg. 2016, 19. [Google Scholar] [CrossRef]
- Fugro. IJmuiden Ver Wind Farm Zone – Sites I-IV - Integrated Ground Model. RVO Report IJV_20230127_RVO_IGM_FUG 04, 2023. Available online: https://offshorewind.rvo.nl/file/download/f6dc7eab-bd70-4eda-9354-2f48310c71ee/ijv_202231114_fugro_integrated-ground-model-f.pdf (accessed on 27 April 2024).
- Netherlands Enterprise Agency (RVO). Development of Offshore Wind Farms in the Netherlands; Netherlands Enterprise Agency (RVO): The Hague, The Netherlands, 2021. [Google Scholar]
- Bundesamt Für Seeschiffart und Hydrographie. Data Hub Preliminary Investigation of Sites; Bundesamt Für Seeschiffart und Hydrographie: Hamburg, Germany, 2023. [Google Scholar]
- SolidGround. Energinet Energy Island North Sea-Seismic Geotechnical Interpretation of Seismic Dual Setup; Technical Report. 2023. Available online: https://ens.dk/sites/ens.dk/files/Geotermi/1304_energyisland-seismic_geotechnical_interpretation_0.pdf (accessed on 27 April 2024).
- Masters, T.A.; Juszkiewicz, P.; Mandolini, A.; Christian, H. A Critical Appraisal of the Benefits of and Obstacles to Gaining Quality Data with Offshore Seismic CPT and PS Logging. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 2019. [Google Scholar]
- Masters, T.; Czech, T.; Sullivan, C.; Cambeilh, C.; Verbeek, G. A critical appraisal of methods for and obstacles to obtaining, processing and interpreting useful data from offshore seismic cone penetration testing. In Proceedings of the 9th International Conference on Offshore Site Investigation and Geotechnics, London, UK, 12–14 September 2023. [Google Scholar]
- Fitzpatrick, E.; Masters, T.; Soage Santos, R. Synthesis of a robust yet easy to implement method for site specific correlation between offshore Piezocone Penetration Test data and shear wave velocity. In Proceedings of the 9th International Conference on Offshore Site Investigation and Geotechnics, London, UK, 12–14 September 2023. [Google Scholar]
- Teng, Y.; Meyer, V.; Klinkvort, R.; Lunne, T.; Caferri, L.; Rose, M. Calibrating site-specific Vs correlations in clay and sand for two offshore wind farms. In Proceedings of the 9th International Conference on Offshore Site Investigation and Geotechnics, London, UK, 12–14 September 2023. [Google Scholar]
- Hintze, J.L.; Nelson, R.D. Violin plots: A box plot-density trace synergism. Am. Stat. 1998, 52, 181–184. [Google Scholar] [CrossRef]
- Stuyts, B. Shear Wave Velocities and Associated CPT Data for S-PCPT Testing in the North Sea. 2024. Available online: https://zenodo.org/records/10986519 (accessed on 27 April 2024).
- Mayne, P.; Peuchen, J.; Bouwmeester, D. Soil unit weight estimation from CPTs. In Proceedings of the 2nd International Symposium on Cone Penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010. [Google Scholar]
- Burd, H.J.; Taborda, D.M.; Zdravković, L.; Abadie, C.N.; Byrne, B.W.; Houlsby, G.T.; Gavin, K.G.; Igoe, D.J.; Jardine, R.J.; Martin, C.M.; et al. PISA design model for monopiles for offshore wind turbines: Application to a marine sand. Géotechnique 2020, 70, 1048–1066. [Google Scholar] [CrossRef]
- Stuyts, B.; Sastre Jurado, C.; Kheffache, A.; Gomez Bautista, D. Bayesian estimation of small-strain shear modulus from offshore CPT tests in the North Sea. In Proceedings of the Submitted to CPT22 Bologna, Bologna, Italy, 8–10 June 2022. [Google Scholar]
- Karray, M.; Lefebvre, G.; Ethier, Y.; Bigras, A. Influence of particle size on the correlation between shear wave velocity and cone tip resistance. Can. Geotech. J. 2011, 48, 599–615. [Google Scholar] [CrossRef]
- Hegazy, Y.; Mayne, P. Statistical correlations between VS and cone penetration data for different soil types. In Proceedings of the International Symposium on Cone Penetration Testing, CPT, Linkoping, Sweden, 4–5 October 1995; Volume 95, pp. 173–178. [Google Scholar]
- Simonini, P.; Ricceri, G.; Cola, S. Geotechnical characterization and properties of Venice lagoon heterogeneous silts. Characterisation Eng. Prop. Nat. Soils 2007, 4, 2289–2327. [Google Scholar]
- Lyu, C.; Park, J.; Carlos Santamarina, J. Depth-dependent seabed properties: Geoacoustic assessment. J. Geotech. Geoenviron. Eng. 2021, 147, 04020151. [Google Scholar] [CrossRef]
- ISO 19901-8; Petroleum and Natural Gas Industries—Specific Requirements for Offshore Structures Part 8: Marine Soil Investigations. International Organization for Standardization: Geneva, Switzerland, 2023.

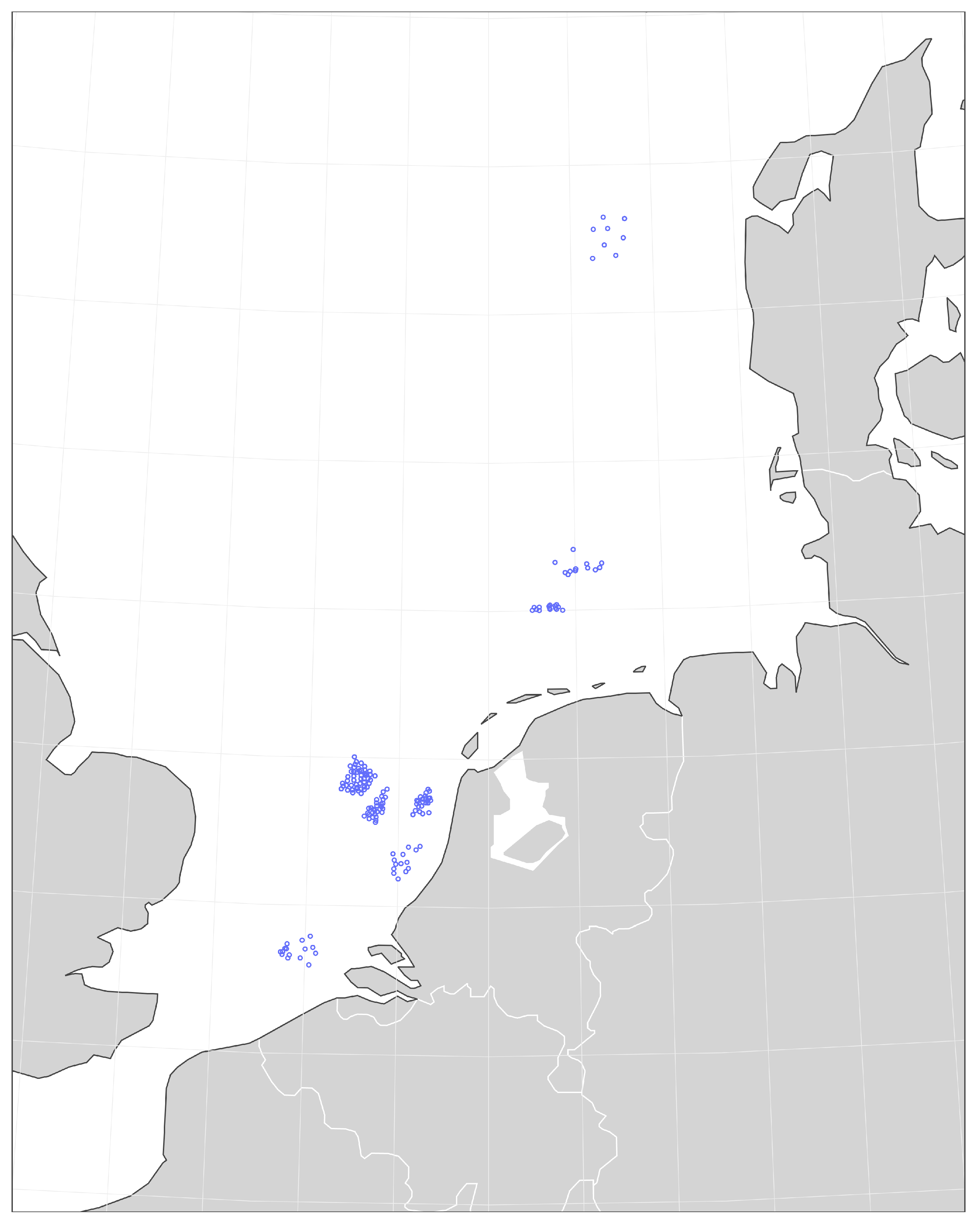



| Robertson Soil Type Class * | |||||||
|---|---|---|---|---|---|---|---|
| ProjectSite | # Locations | # Measurements | 3 | 4 | 5 | 6 | 7 |
| Belgian Zone | 7 | 85 | 22 | 36 | 13 | 6 | 8 |
| Borssele | 8 | 79 | 3 | 14 | 13 | 35 | 14 |
| Hollandse Kust Noord | 38 | 570 | 1 | 16 | 81 | 437 | 35 |
| Hollandse Kust West | 30 | 1229 | 15 | 60 | 260 | 887 | 7 |
| Hollandse Kust Zuid | 17 | 219 | 12 | 32 | 48 | 118 | 9 |
| Ten Noorden van Wadden-eilanden | 15 | 282 | 7 | 41 | 35 | 186 | 13 |
| Ijmuiden Ver | 66 | 1250 | 13 | 97 | 171 | 939 | 30 |
| German Zone | 14 | 238 | 2 | 18 | 36 | 142 | 40 |
| Danish Zone | 12 | 193 | 6 | 30 | 52 | 94 | 11 |
| Correlation | Predicted Property | Input Geotechnical Parameters |
|---|---|---|
| Hardin and Black (1968) [8] | , | |
| Rix and Stokoe (1991) [9] | , | |
| Mayne and Rix (1993) [10] | ||
| Wride et al. (2000) [11] | , | |
| Hegazy and Mayne (2006) [12] | , , | |
| Andrus et al (2007) [13] | , z, , geological age | |
| Tonni and Simonini (2013) [14] | , , , | |
| Cha et al. (2013) [15] | , , | |
| Robertson and Cabal (2015) [16] | , , | |
| McGann et al. (2018) [17] | , , z | |
| Peuchen et al. (2020) [18] | , , |
| Correlation | Predicted Property | N | COV | ||
|---|---|---|---|---|---|
| Hardin and Black (1968) [8] | 3058 | 1.570 | 0.652 | −2.414 | |
| Rix and Stokoe (1991) [9] | 2656 | 0.809 | 0.713 | −0.006 | |
| Mayne and Rix (1993) [10] | 237 | 1.213 | 0.742 | −4.441 | |
| Peuchen et al. (2020) [18] | 3058 | 0.846 | 0.733 | −0.017 | |
| Wride et al. (2000) [11] | 3058 | 0.782 | 0.214 | −0.984 | |
| Hegazy and Mayne (2006) [12] | 3058 | 1.131 | 0.260 | −0.949 | |
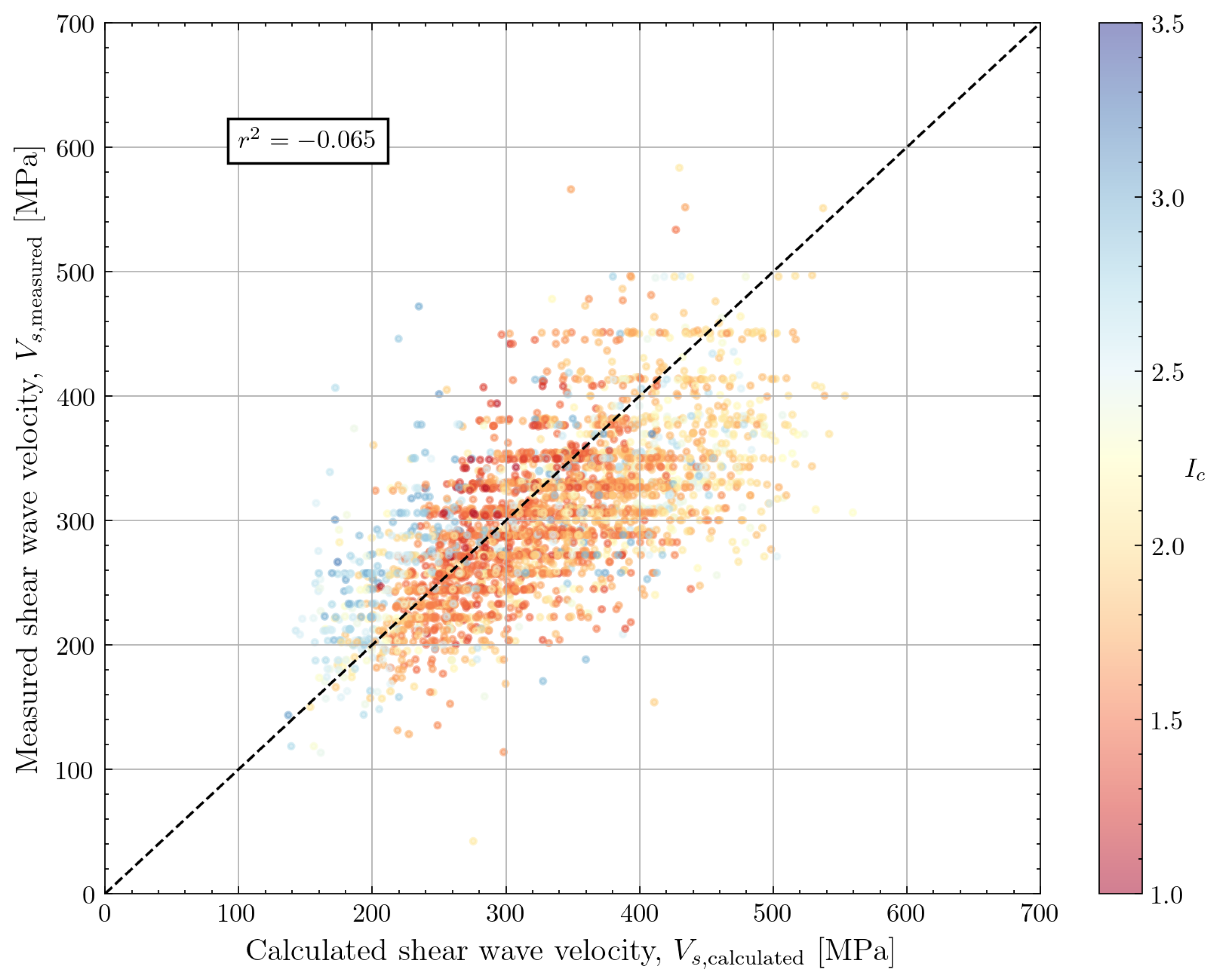
| Andrus et al. (2007) [13] | 3058 | 1.095 | 0.207 | −0.065 | |
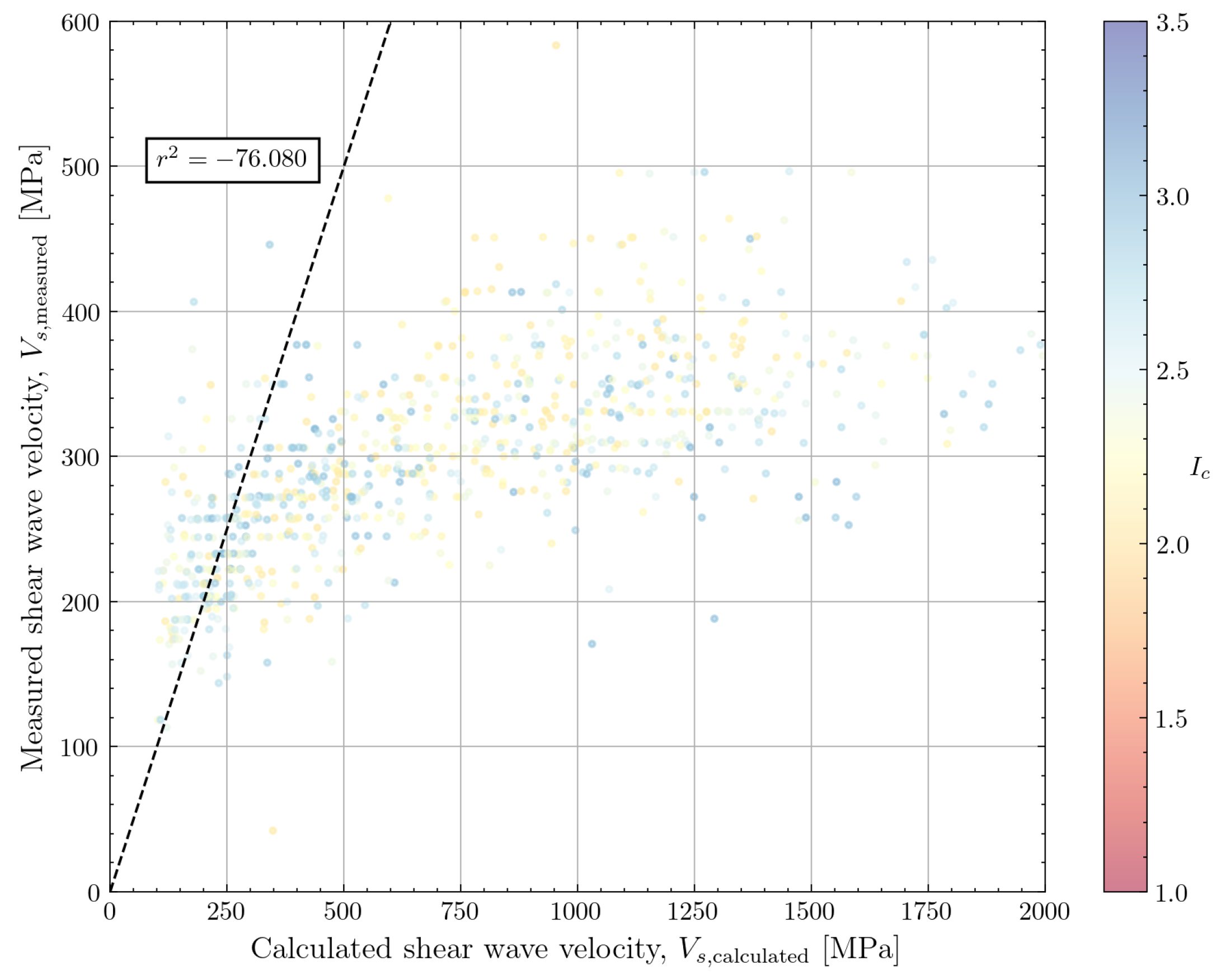
| Tonni and Simonini (2013) [14] | 863 | 2.320 | 0.550 | −76.080 | |
| Robertson and Cabal (2015) [16] | 3058 | 1.056 | 0.206 | 0.155 | |
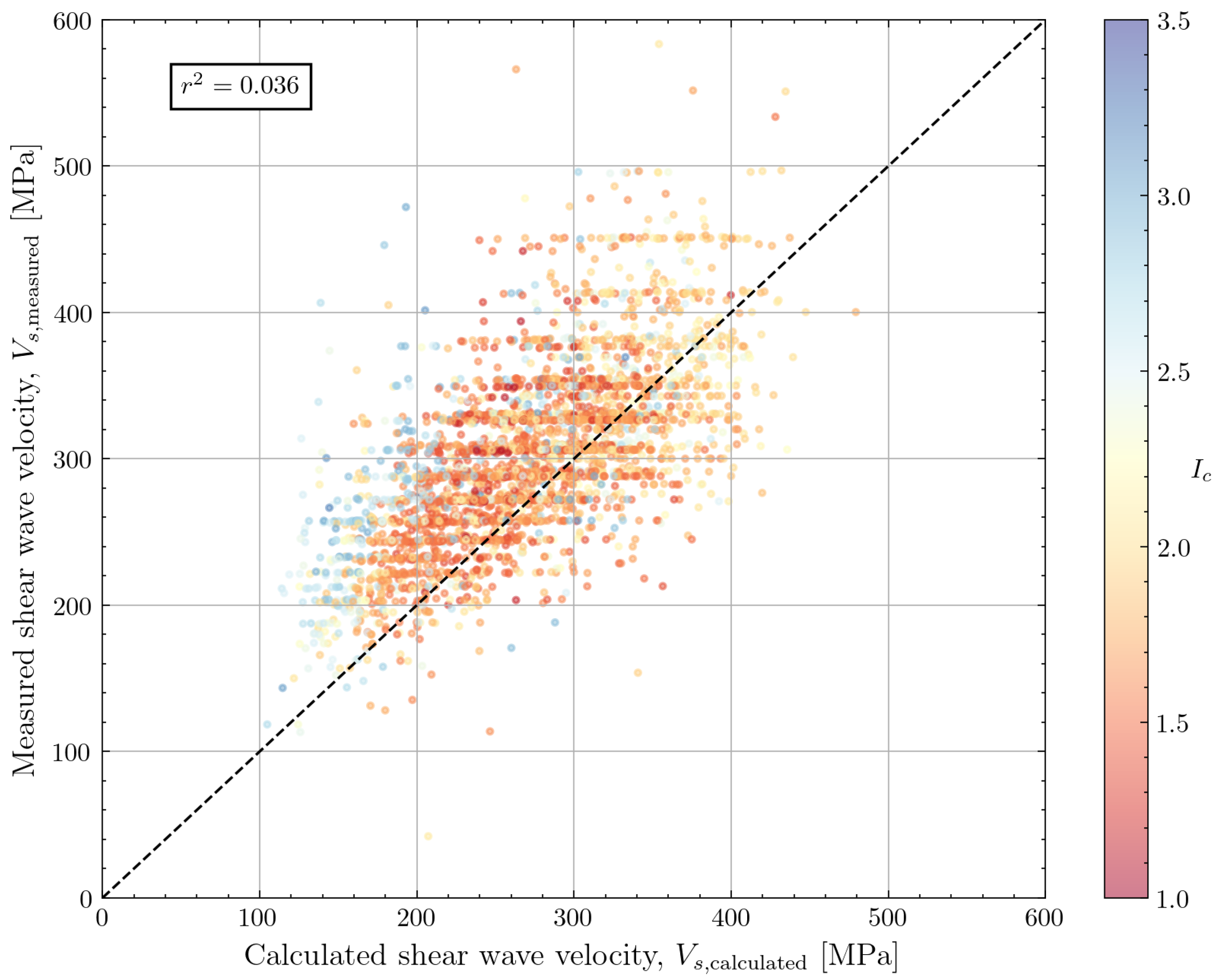
| McGann et al. (2018) [17] | 3058 | 0.901 | 0.207 | 0.036 |
| Correlation | ||||
|---|---|---|---|---|
| Wride et al. (2000) [11] | 0.782 | 0.811 | 0.214 | 0.073 |
| Hegazy and Mayne (2006) [12] | 1.131 | 1.232 | 0.260 | 0.154 |
| Andrus et al. (2007) [13] | 1.095 | 1.085 | 0.207 | 0.127 |
| Robertson and Cabal (2015) [16] | 1.056 | 1.075 | 0.206 | 0.093 |
| McGann et al. (2018) [17] | 0.901 | 0.878 | 0.207 | 0.149 |
| Stress-dependent correlation | 1.007 | 0.974 | 0.188 | 0.097 |
| Correlation | ||||
|---|---|---|---|---|
| Wride et al. (2000) [11] | 0.782 | 0.779 | 0.214 | 0.173 |
| Hegazy and Mayne (2006) [12] | 1.131 | 1.291 | 0.260 | 0.205 |
| Andrus et al. (2007) [13] | 1.095 | 1.187 | 0.207 | 0.175 |
| Robertson and Cabal (2015) [16] | 1.056 | 1.157 | 0.206 | 0.158 |
| McGann et al. (2018) [17] | 0.901 | 0.948 | 0.207 | 0.184 |
| Stress-dependent correlation | 1.007 | 1.033 | 0.188 | 0.184 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stuyts, B.; Weijtjens, W.; Jurado, C.S.; Devriendt, C.; Kheffache, A. A Critical Review of Cone Penetration Test-Based Correlations for Estimating Small-Strain Shear Modulus in North Sea Soils. Geotechnics 2024, 4, 604-635. https://doi.org/10.3390/geotechnics4020033
Stuyts B, Weijtjens W, Jurado CS, Devriendt C, Kheffache A. A Critical Review of Cone Penetration Test-Based Correlations for Estimating Small-Strain Shear Modulus in North Sea Soils. Geotechnics. 2024; 4(2):604-635. https://doi.org/10.3390/geotechnics4020033
Chicago/Turabian StyleStuyts, Bruno, Wout Weijtjens, Carlos Sastre Jurado, Christof Devriendt, and Anis Kheffache. 2024. "A Critical Review of Cone Penetration Test-Based Correlations for Estimating Small-Strain Shear Modulus in North Sea Soils" Geotechnics 4, no. 2: 604-635. https://doi.org/10.3390/geotechnics4020033
APA StyleStuyts, B., Weijtjens, W., Jurado, C. S., Devriendt, C., & Kheffache, A. (2024). A Critical Review of Cone Penetration Test-Based Correlations for Estimating Small-Strain Shear Modulus in North Sea Soils. Geotechnics, 4(2), 604-635. https://doi.org/10.3390/geotechnics4020033