Measurements of Shear Wave Velocity for Collapsible Soil
Abstract
1. Introduction
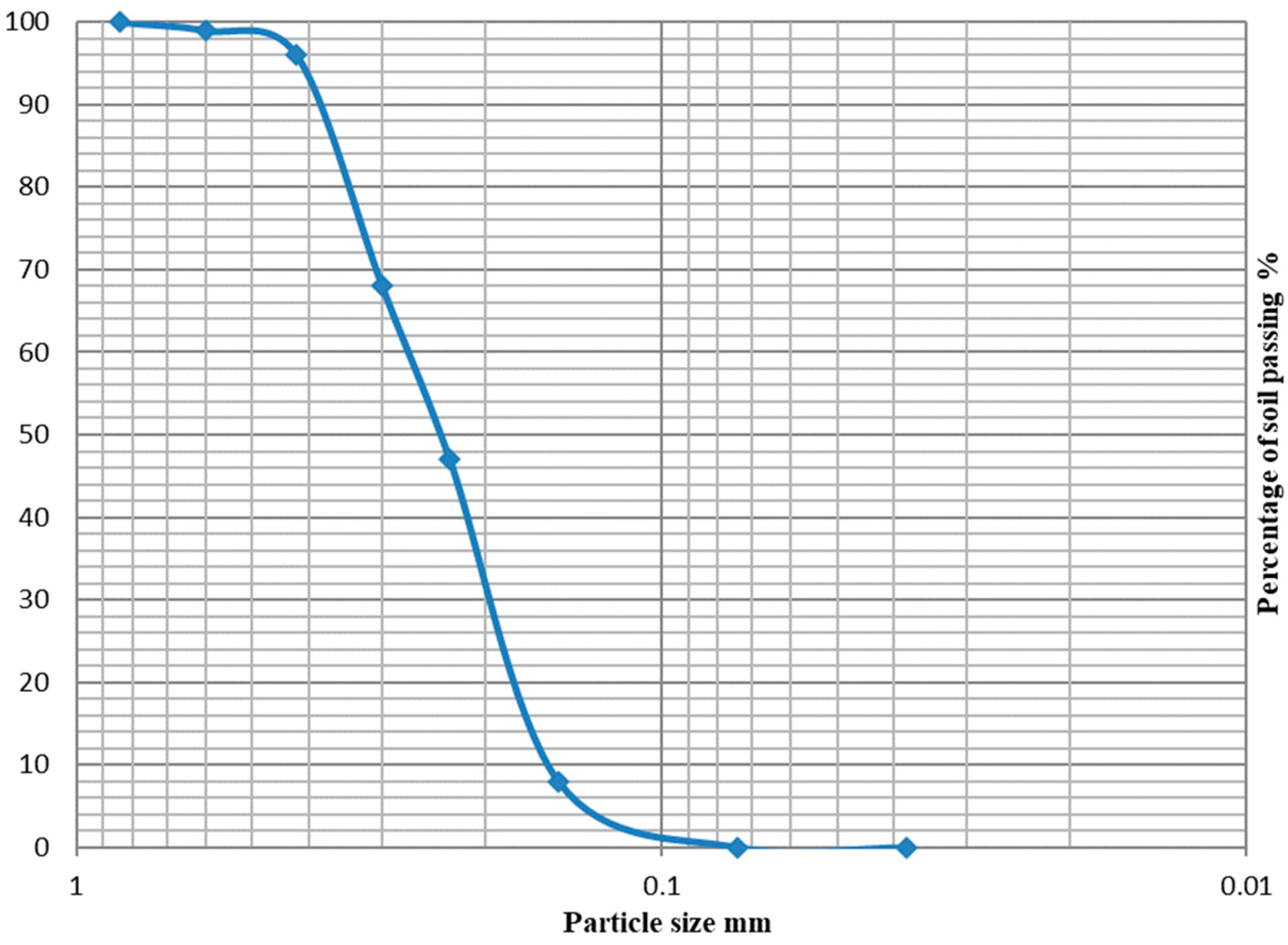
2. Material Properties and Sample Preparation
2.1. Dry Pluviation Specimen Preparation
2.2. Simulated Hydraulic Fill Specimen Preparation
3. Testing Procedure
4. Results and Discussion
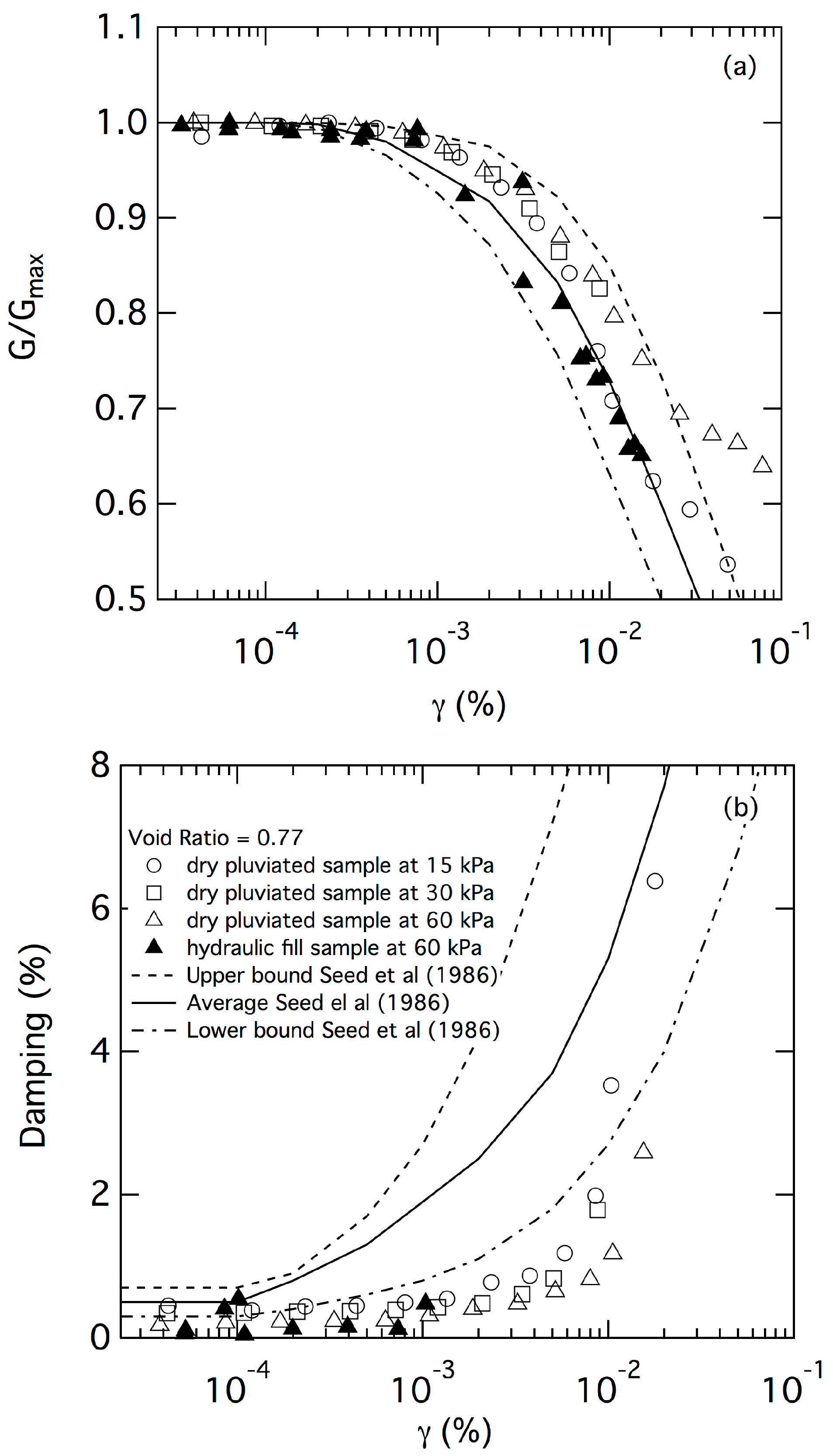
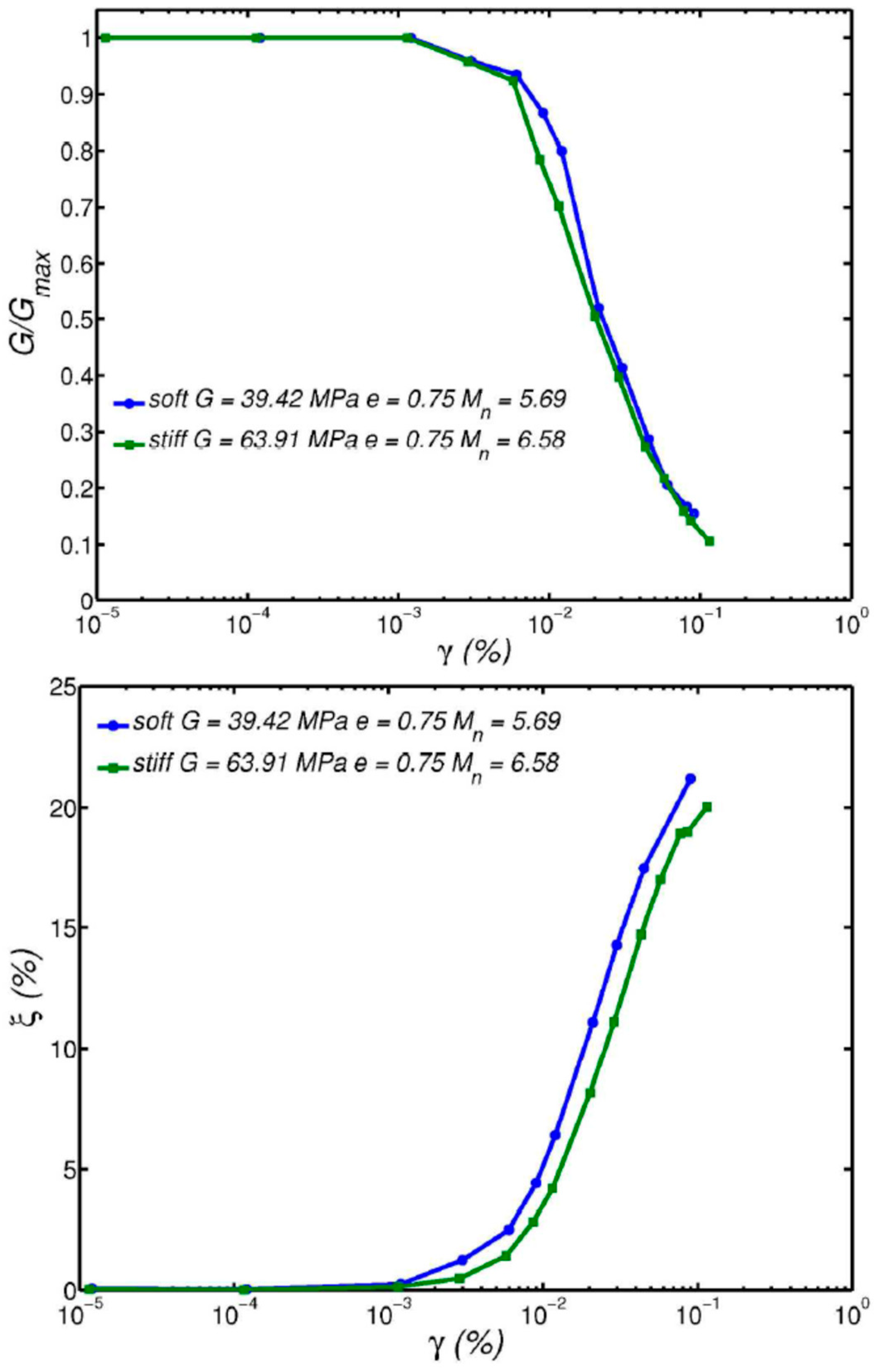
4.1. Modulus Reduction and Damping Curves
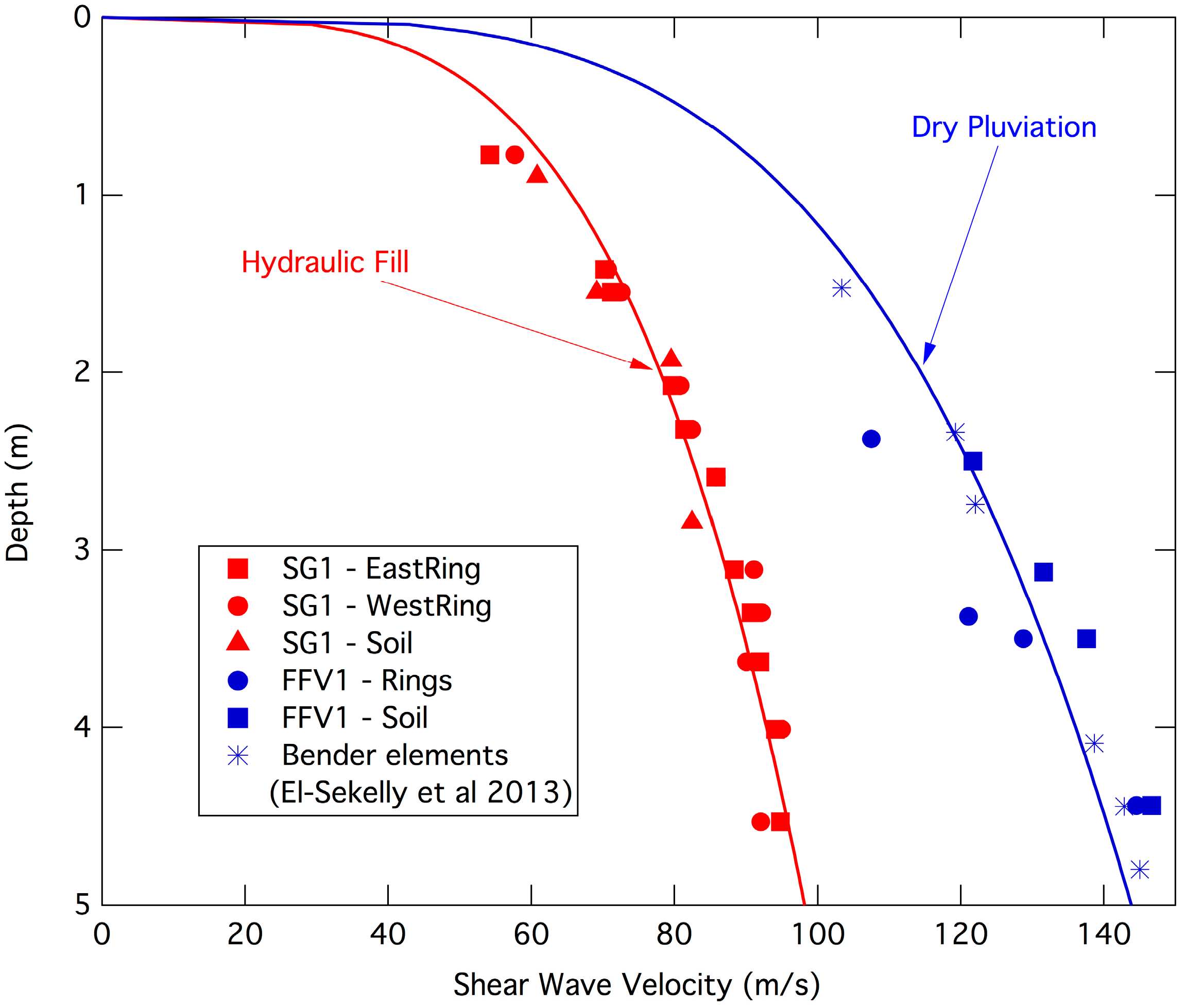
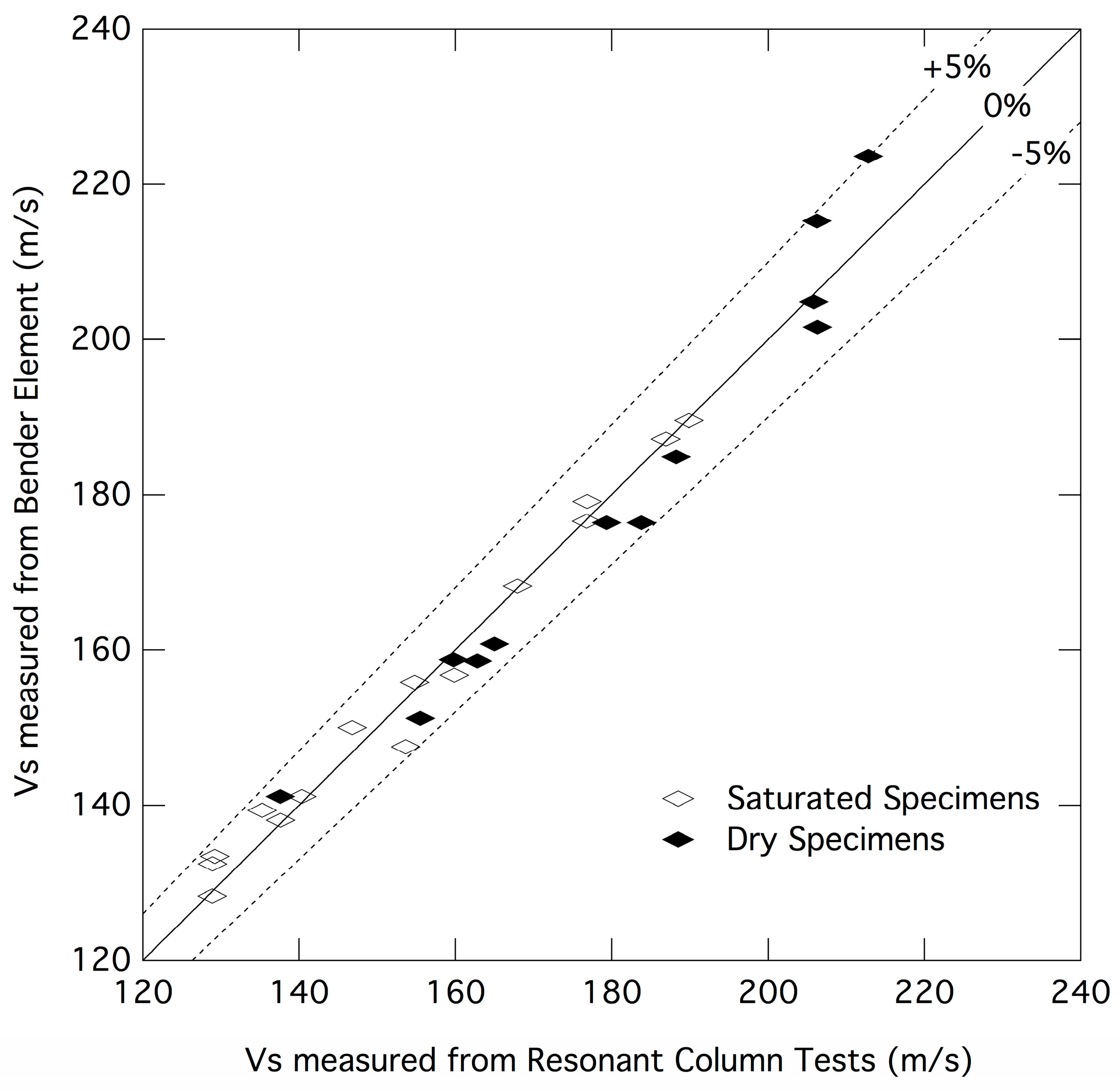
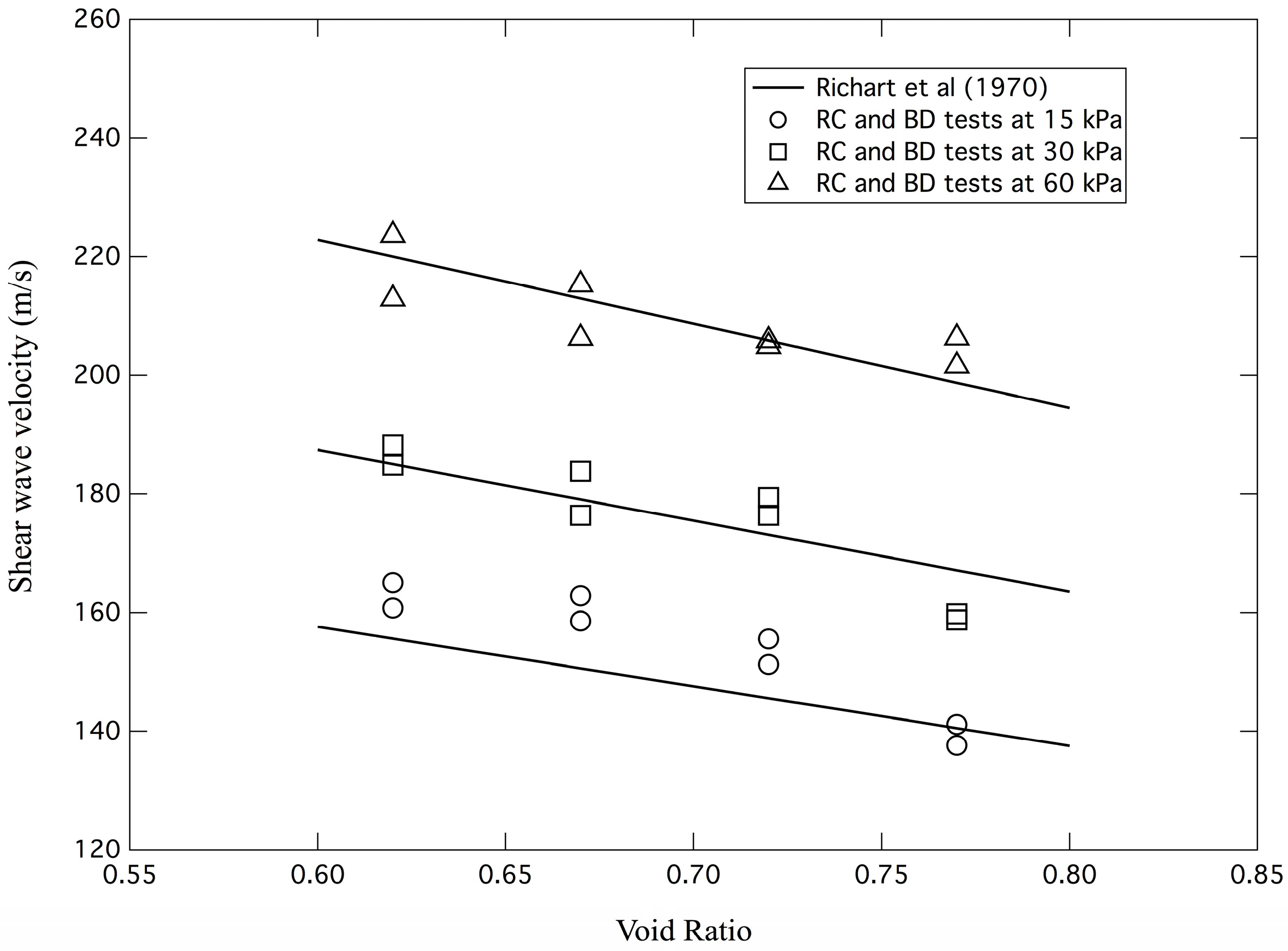
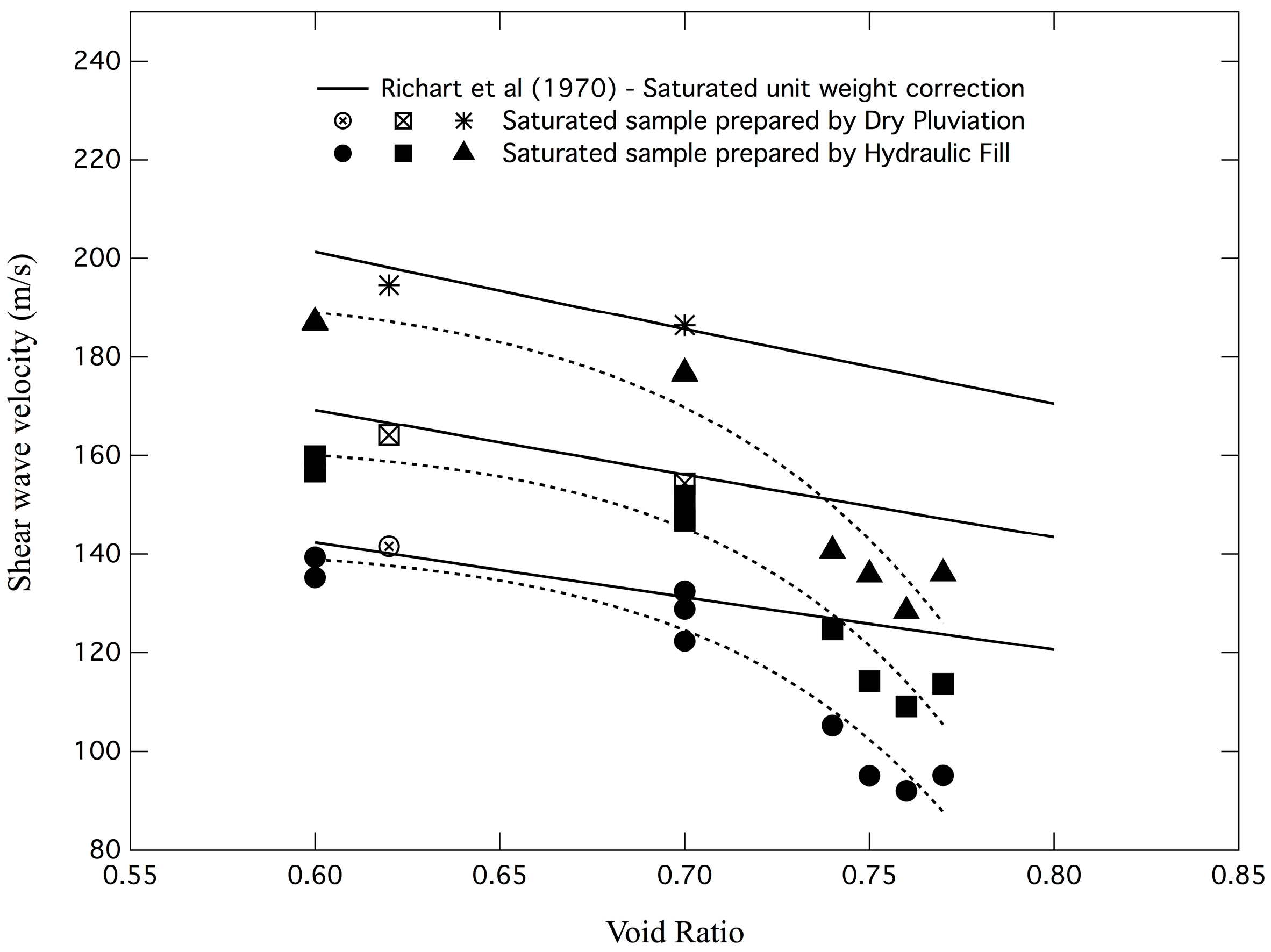
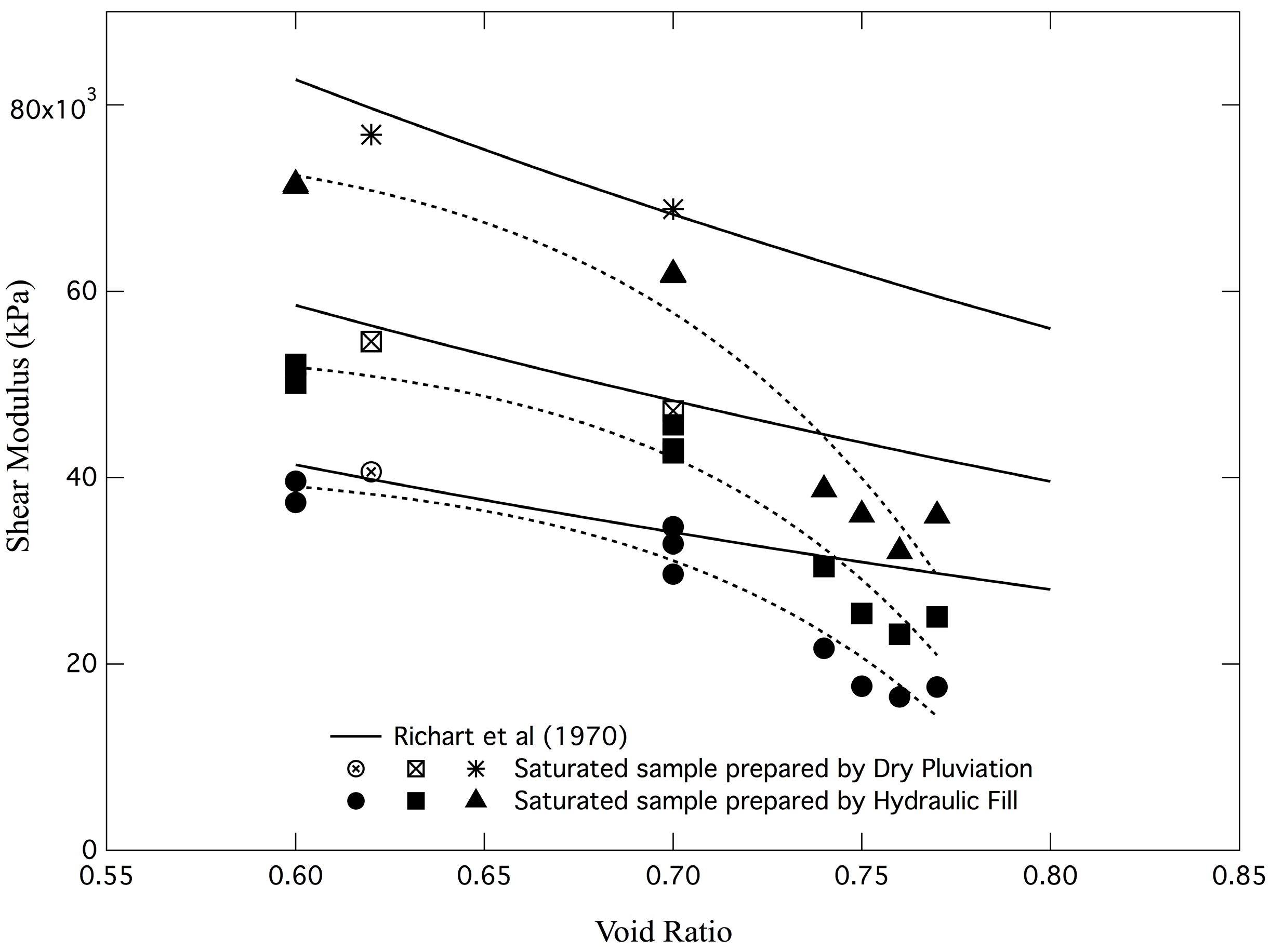
4.2. Low-Strain Shear Wave Velocities
4.3. Effect of Preshaking
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tatsuoka, F.; Iwasaki, T.; Yoshida, S.; Fukushima, S.; Sudo, H. Shear Modulus and Damping by Drained Tests on Clean Sand Specimens Reconstituted by Various Methods. Soils Found. 1979, 19, 39–54. [Google Scholar] [CrossRef]
- Rogers, C.D.F.; Dijkstra, T.A.; Smalley, I.J. Hydroconsolidation and subsidence of loess: Studies from China, Russia, North America and Europe. Eng. Geol. 1994, 37, 83–113. [Google Scholar] [CrossRef]
- Whitman, R.V. On liquefaction. In Proceedings of the 11th International Conference on Soil Mechanics and Foundation Engineering, San Francisco, CA, USA, 12–16 August 1985; A.A. Balkema: Rotterdam, The Netherlands, 1985; pp. 1923–1926. [Google Scholar]
- Opukumo, A.W.; Davie, C.T.; Glendinning, S.; Oborie, E. A review of the identification methods and types of collapsible soils. J. Eng. Appl. Sci. 2022, 69, 17. [Google Scholar] [CrossRef]
- Al-Rawas, A.A. State-of-the-art-review of collapsible soils. Sultan Qaboos Univ. J. Sci. [SQUJS] 2000, 5, 115–135. [Google Scholar] [CrossRef]
- Eslami, A.; Alimirzaei, M.; Aflaki, E.; Molaabasi, H. Deltaic soil behavior classification using CPTu records—Proposed approach and applied to fifty-four case histories. Mar. Georesources Geotechnol. 2017, 35, 62–79. [Google Scholar] [CrossRef]
- Loukidis, D.; Bardanis, M.; Lazarou, G. Classification, soil-water characteristic curve and swelling/collapse behaviour of the Nicosia marl, Cyprus. E3S Web Conf. 2016, 9, 11009. [Google Scholar] [CrossRef]
- Youd, T.L.; Perkins, J.B. Map showing liquefaction susceptibility of San Mateo County, California, 1987 (No. 1257-G). Available online: https://pubs.usgs.gov/publication/i1257G (accessed on 25 April 2024).
- Youd, T.L.; Hansen, C.M.; Barlett, S.F. Revised Multilinear Equations for Prediction of Lateral Spread Displacement. J. Geotech. Geoenvironmental Eng. 2002, 128, 1007–1017. [Google Scholar] [CrossRef]
- Gu, X.; Yang, J.; Huang, M.; Gao, G. Bender element tests in dry and saturated sand: Signal interpretation and result comparison. Soils Found. 2015, 55, 951–962. [Google Scholar] [CrossRef]
- Moon, S.W.; Ng, Y.C.; Ku, T. Global semi-empirical relationships for correlating soil unit weight with shear wave velocity by void-ratio function. Can. Geotech. J. 2018, 55, 1193–1199. [Google Scholar] [CrossRef]
- González, M.A. Centrifuge Modeling of Pile Foundation Response to Liquefaction and Lateral Spreading: Study of Sand Permeability and Compressibility Effects Using Scaled Sand Technique. Ph.D. Thesis, Rensselaer Polytechnic Institute, Troy, NY, USA, 2008. [Google Scholar]
- Abdoun, T.; Gonzalez, M.A.; Thevanayagam, S.; Dobry, R.; Elgamal, A.; Zeghal, M.; Mercado, V.; El Shamy, U. Centrifuge and Large Scale Modeling of Seismic Pore Pressures in Sands: A Cyclic Strain Interpretation. ASCE J. Geotech. Geoenvironmental Eng. 2013, 139, 1215–1234. [Google Scholar] [CrossRef]
- Dobry, R. Comparison Between Clean Sand Liquefaction Charts Based on Penetration Resistance and Shear Wave Velocity. In Proceedings of the 5th International Conference on Geotechnical Earthquake Engineering and Soil Dynamics and Symposium in Honor of Professor, I.M. Idriss, San Diego, CA, USA, 24–29 May 2010. [Google Scholar]
- Dobry, R.; Abdoun, T. An Investigation into Why Liquefaction Charts Work: A Necessary Step Toward Integrating the States of Art and Practice. Ishihara Lecture. In Proceedings of the 5th International Conference on Earthquake Geotechnical Engineering, Santiago, Chile, 10–13 January 2011. [Google Scholar]
- Richart, F.E.; Hall, J.R.; Woods, R.D. Vibrations of Soils and Foundation; Prentice Hall: Englewood Cliffs, NJ, USA, 1970. [Google Scholar]
- Anderson, D.G.; Stokoe II, K.H. Shear Modulus: A Time-Dependent Soil Property. Dynamic Geotechnical Testing, American Society of Testing and Materials; ASTM STP 654: Baltimore, MD, USA, 1978; pp. 66–90. [Google Scholar]
- Sharp, M.K.; Dobry, R.; Abdoun, T. Centrifuge Modeling of Liquefaction and Lateral Spreading of Virgin, Over-consolidated and Pre-Shaken Sand Deposits. Int. J. Phys. Model. Geotech. 2003, 3, 11–23. [Google Scholar]
- Choo, H.; Lee, C. Inverse effect of packing density on shear wave velocity of binary mixed soils with varying size ratios. J. Appl. Geophys. 2021, 194, 104457. [Google Scholar] [CrossRef]
- Mishra, P.; Chakrabortty, P. Prediction of void ratio and shear wave velocity for soil in quaternary alluvium using cone penetration tests. Bull. Eng. Geol. Environ. 2024, 83, 88. [Google Scholar] [CrossRef]
- Zuo, K.; Gu, X.; Gao, G. Evaluating liquefaction resistance of partially saturated sandy soil using the P-wave velocity. Soil Dyn. Earthq. Eng. 2024, 178, 108521. [Google Scholar] [CrossRef]
- El-Sekelly, W.; Mercado, V.; Abdoun, T.; Zeghal, M.; El-Ganainy, H. Bender elements and system identification for estimation of Vs. Int. J. Phys. Model. Geotech. 2013, 13, 111–121. [Google Scholar] [CrossRef]
- El-Shafee, O.O. Measurement of Shear Wave Velocity of Soil Specimen Prepared by Different Methods Using Resonant Column Device and Bender Elements. Master’s Thesis, Rensselaer Polytechnic Institute, Troy, NY, USA, 2011. [Google Scholar]
- Wu, S.; Gray, D.H.; Richart, F.E., Jr. Capillary effects on dynamic modulus of sands and silts. J. Geotech. Eng. 1984, 110, 1188–1203. [Google Scholar] [CrossRef]
- Bosscher, P.J.; Nelson, D.L. Resonant column testing of frozen Ottawa sand. Geotech. Test. J. 1987, 10, 123–134. [Google Scholar] [CrossRef]
- Al-Hunaidi, M.O.; Chen, P.A.; Rainer, J.H.; Tremblay, M. Shear moduli and damping in frozen and unfrozen clay by resonant column tests. Can. Geotech. J. 1996, 33, 510–514. [Google Scholar] [CrossRef]
- Chen, Y.C.; You, P.S. Evaluation of liquefaction potential by the test results of in-situ frozen samples. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Toulon, France, 23–28 May 2004; ISOPE: Mountain View, CA, USA; p. ISOPE-I. [Google Scholar]
- Seed, H.B.; Wong, R.T.; Idriss, I.M.; Tokimatsu, K. Moduli and Damping Factors for Dynamic Analysis of Cohesionless Soils. J. Geotech. Eng. ASCE 1986, 112, 1016–1032. [Google Scholar] [CrossRef]
- Hardin, B.O.; Richart, F.E. Elastic Wave Velocities in Granular Soils. J. Soil Mech. Found. Div. Proc. Am. Soc. Civ. Eng. 1963, 89, 33–65. [Google Scholar] [CrossRef]
- Tsinginos, C. A Micromechanical Investigation of the Effect of Fabric and Particle Shape on the Response of Granular Soils. Ph.D. Thesis, Rensselaer Polytechnic Institute, Troy, NY, USA, 2012. [Google Scholar]
- Zeghal, M.; Tsinginos, C. A Micromechanical Analysis of the Effect of Fabric on Low-strain Stiffness of Granular Soils. Soil Dyn. Earthq. Eng. 2015, 70, 153–165. [Google Scholar] [CrossRef]
- Sharp, M.K. Development of Centrifuge Based Prediction Charts for Liquefaction and Lateral Spreading from Cone Penetration Testing. Ph.D. Thesis, Rensselaer Polytechnic Institute, Troy, NY, USA, 1999. [Google Scholar]








| D50 (mm) | D10 (mm) | FC % | Minimum Void Ratio 1 | Maximum Void Ratio 2 | Gs | Maximum Dry Density (kg/cm3) | Minimum Dry Density (kg/cm3) |
|---|---|---|---|---|---|---|---|
| 0.258 | 0.155 | 0.1 | 0.61 | 0.8 | 2.665 | 1650 | 1476 |
| Void Ratio | σo’ (kPa) | Sample Preparation Method 1 | Test Method 2 | Remarks |
|---|---|---|---|---|
| 0.60 | 15 | HF | RC, BE | |
| 30 | HF | RC, BE | ||
| 60 | HF | RC, BE | ||
| 0.62 | 15 | DP, DPs | RC, BE | |
| 30 | DP, DPs | RC, BE | ||
| 60 | DP, DPs | RC, BE | ||
| 0.67 | 15 | DP | RC, BE | |
| 30 | DP | RC, BE | ||
| 60 | DP | RC, BE | ||
| 0.70 | 15 | HF, DPs | RC, BE | |
| 30 | HF, DPs | RC, BE | ||
| 60 | HF, DPs | RC, BE | ||
| 0.72 | 15 | DP | RC, BE | |
| 30 | DP | RC, BE | ||
| 60 | DP | RC, BE | ||
| 0.74 | 15 | HF | RC | |
| 30 | HF | RC | ||
| 60 | HF | RC | ||
| 0.75 | 15 | HF | RC | |
| 30 | HF | RC | ||
| 60 | HF | RC | Preshaking at σo’ of 60 kPa | |
| 0.76 | 15 | HF | RC | |
| 30 | HF | RC | ||
| 60 | HF | RC | Preshaking at σo’ of 60 kPa | |
| 0.77 | 15 | HF, DP | RC, BE | Bender element was only performed on a dry pluviated sample. |
| 30 | HF, DP | RC, BE | ||
| 60 | HF, DP | RC, BE | Preshaking at σo’ of 60 kPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
EI-Shafee, O.; Sasanakul, I.; Abdoun, T.; Zeghal, M. Measurements of Shear Wave Velocity for Collapsible Soil. Geotechnics 2024, 4, 430-446. https://doi.org/10.3390/geotechnics4020024
EI-Shafee O, Sasanakul I, Abdoun T, Zeghal M. Measurements of Shear Wave Velocity for Collapsible Soil. Geotechnics. 2024; 4(2):430-446. https://doi.org/10.3390/geotechnics4020024
Chicago/Turabian StyleEI-Shafee, Omar, Inthuorn Sasanakul, Tarek Abdoun, and Mourad Zeghal. 2024. "Measurements of Shear Wave Velocity for Collapsible Soil" Geotechnics 4, no. 2: 430-446. https://doi.org/10.3390/geotechnics4020024
APA StyleEI-Shafee, O., Sasanakul, I., Abdoun, T., & Zeghal, M. (2024). Measurements of Shear Wave Velocity for Collapsible Soil. Geotechnics, 4(2), 430-446. https://doi.org/10.3390/geotechnics4020024






