Modelling of Truck Tire–Rim Slip on Sandy Loam Using Advanced Computational Techniques
Abstract
1. Introduction
2. Materials and Methods
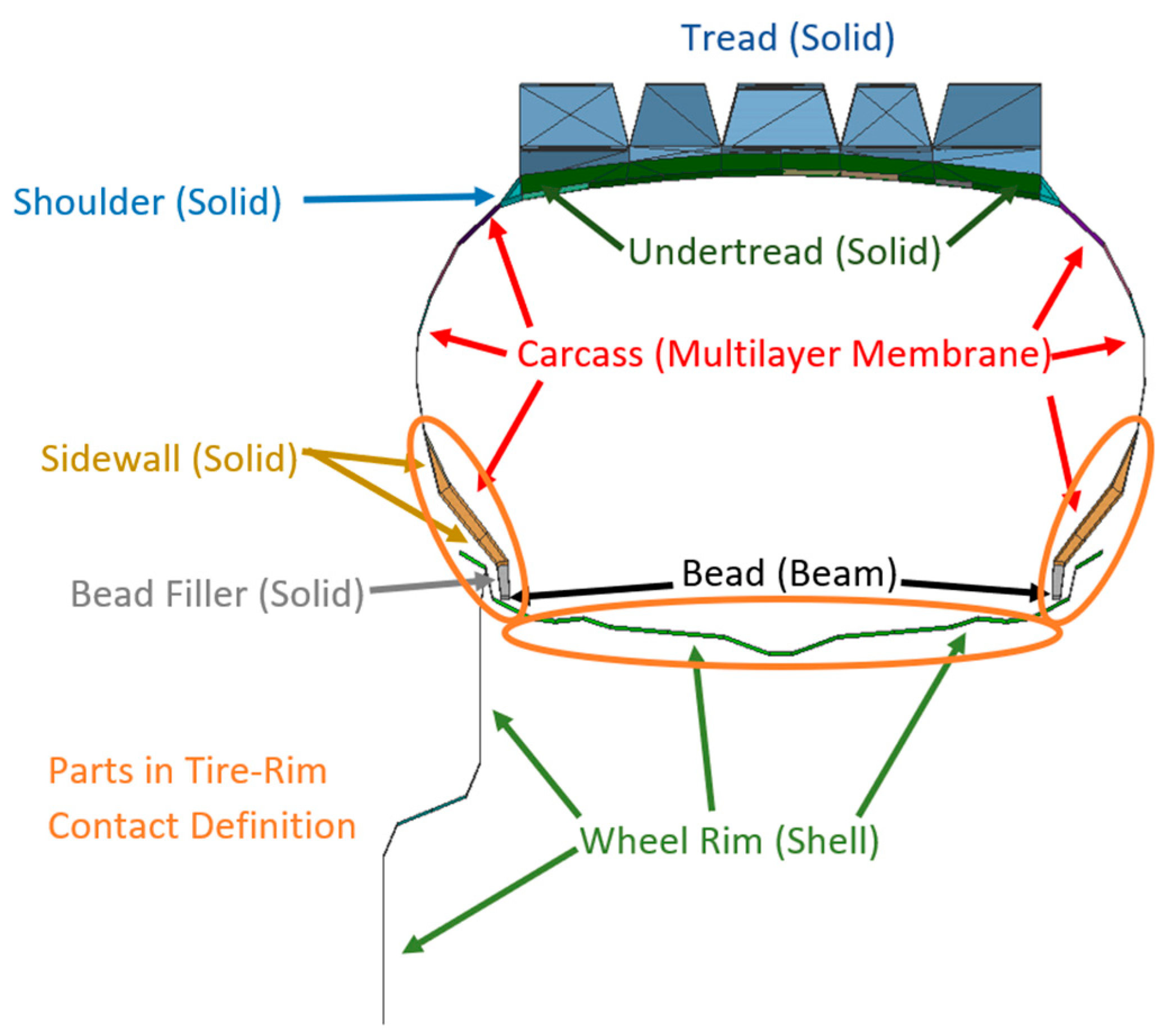
2.1. Tire Model
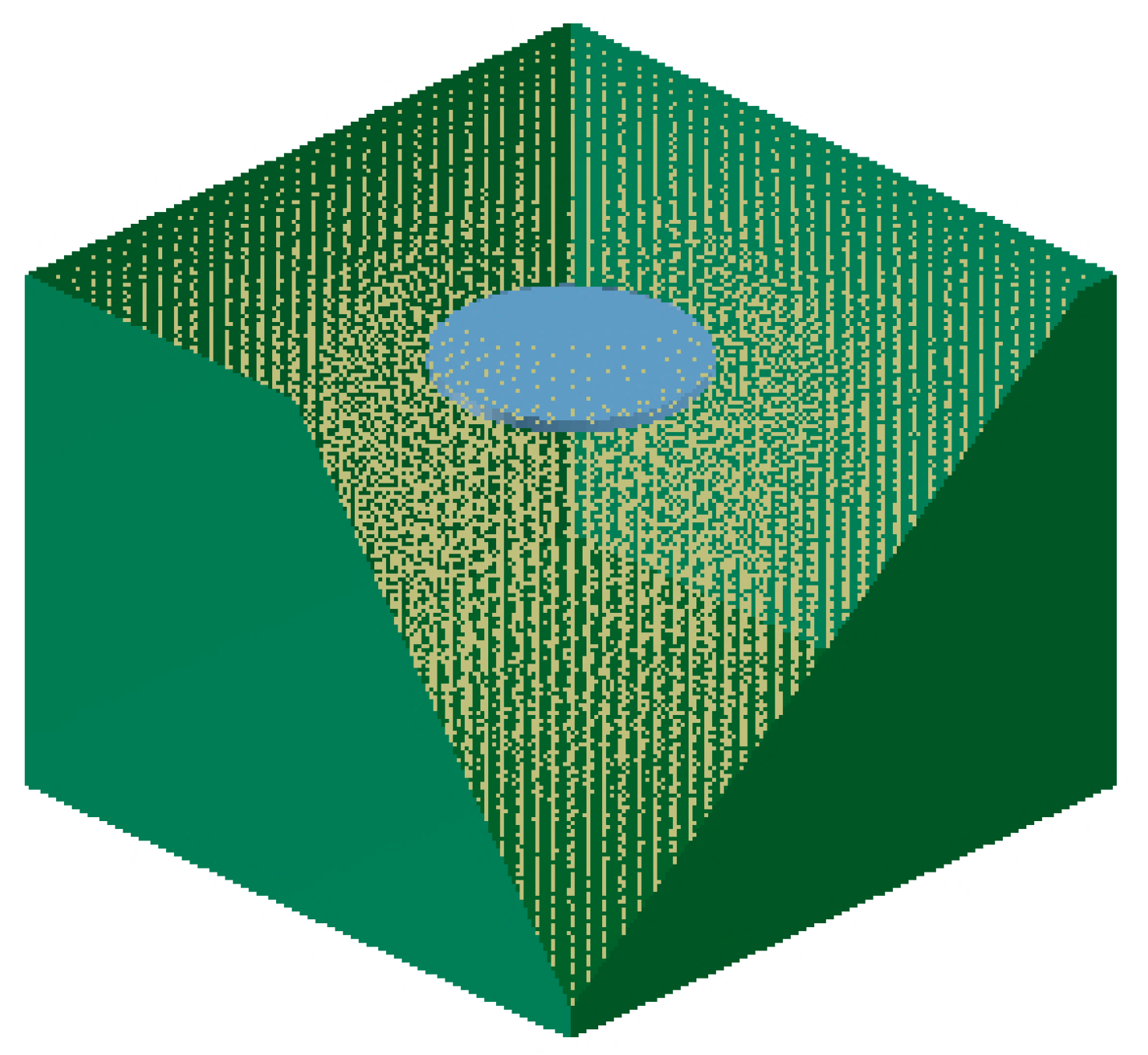
2.2. Contact Model
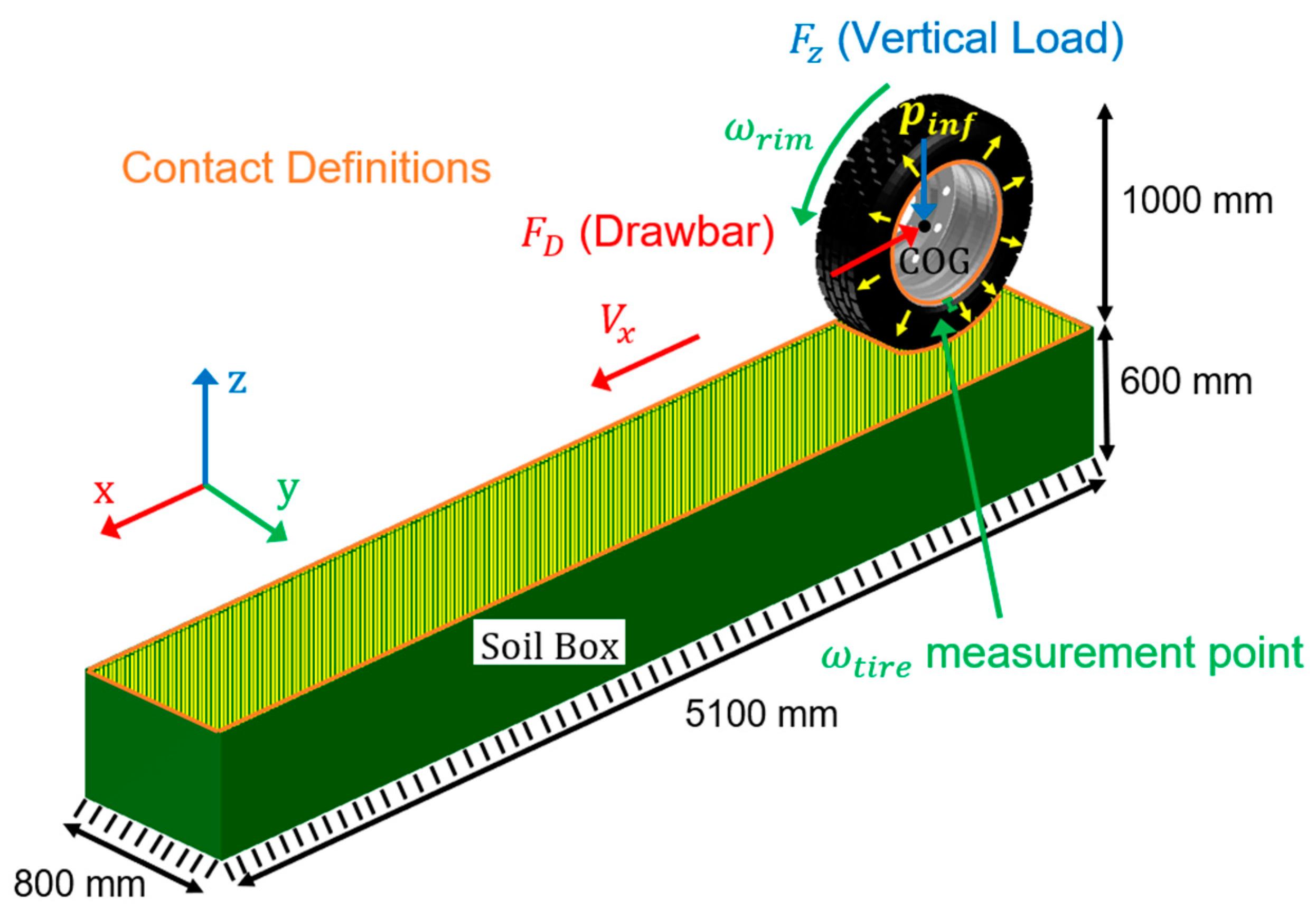
2.3. Boundary Conditions
2.4. Tire–Rim Slip Measurement
2.5. Soil Model and Calibration
3. Results
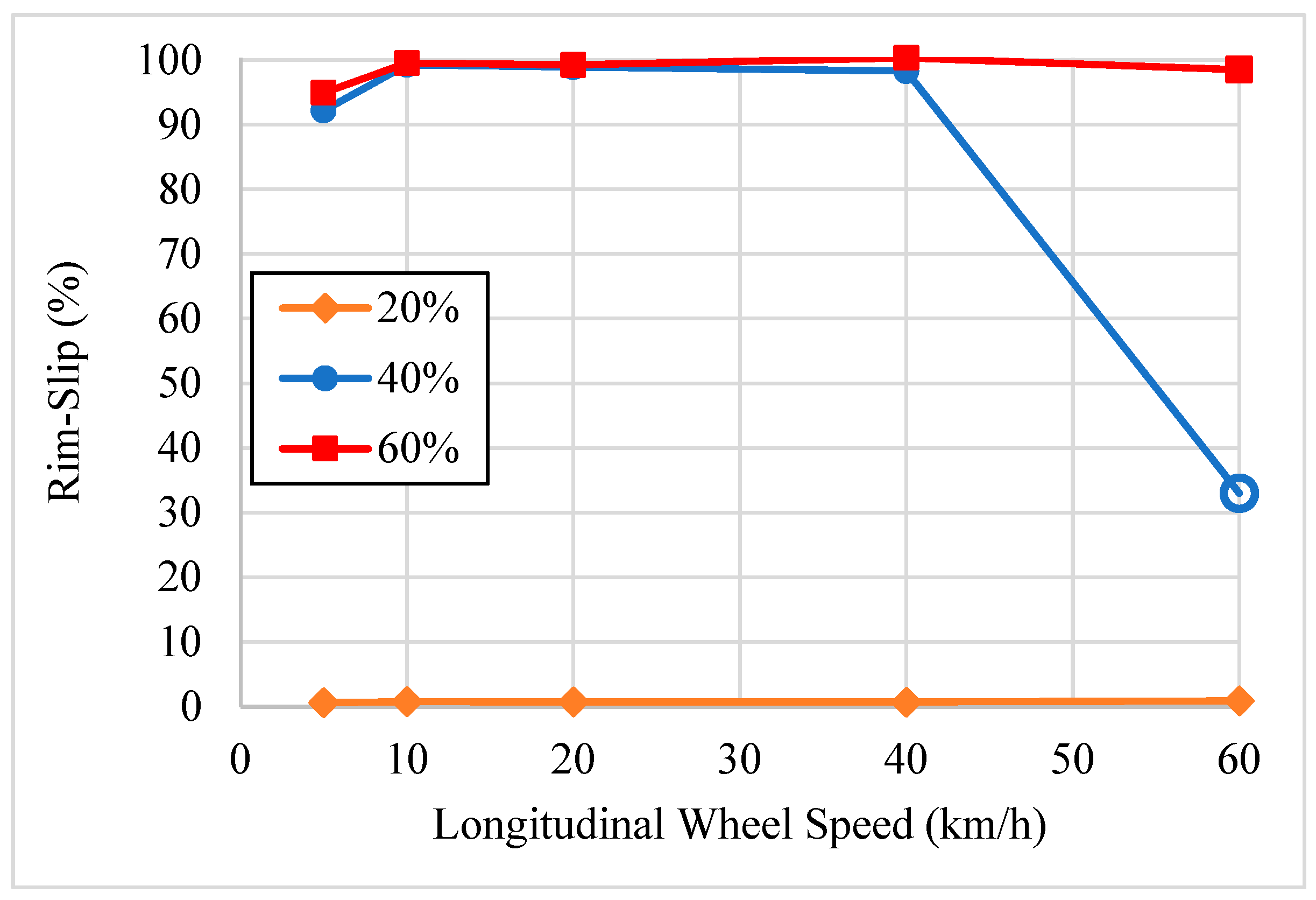
3.1. Effect of Longitudinal Wheel Speed
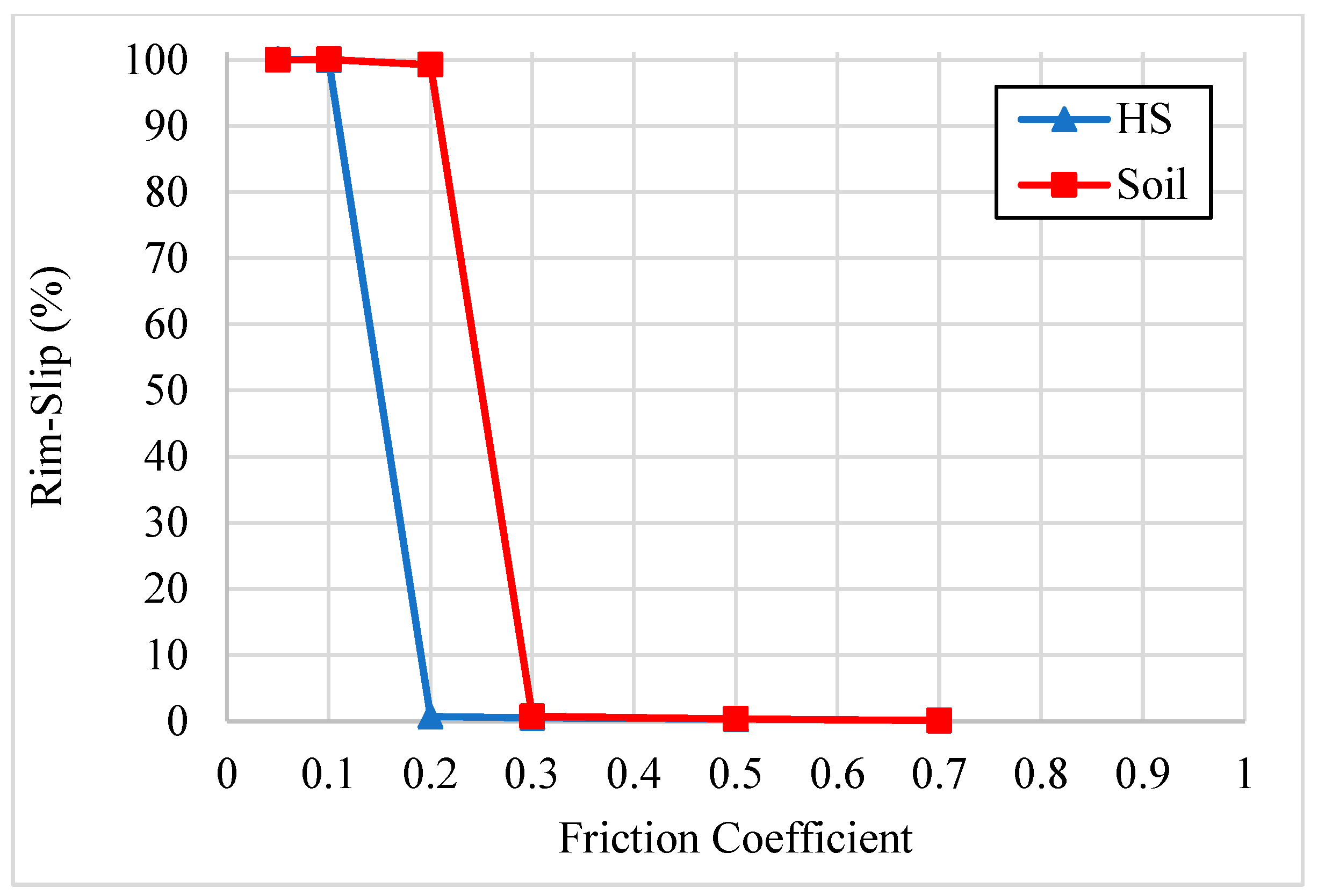
3.2. Effect of Friction Coefficient and Drawbar Load
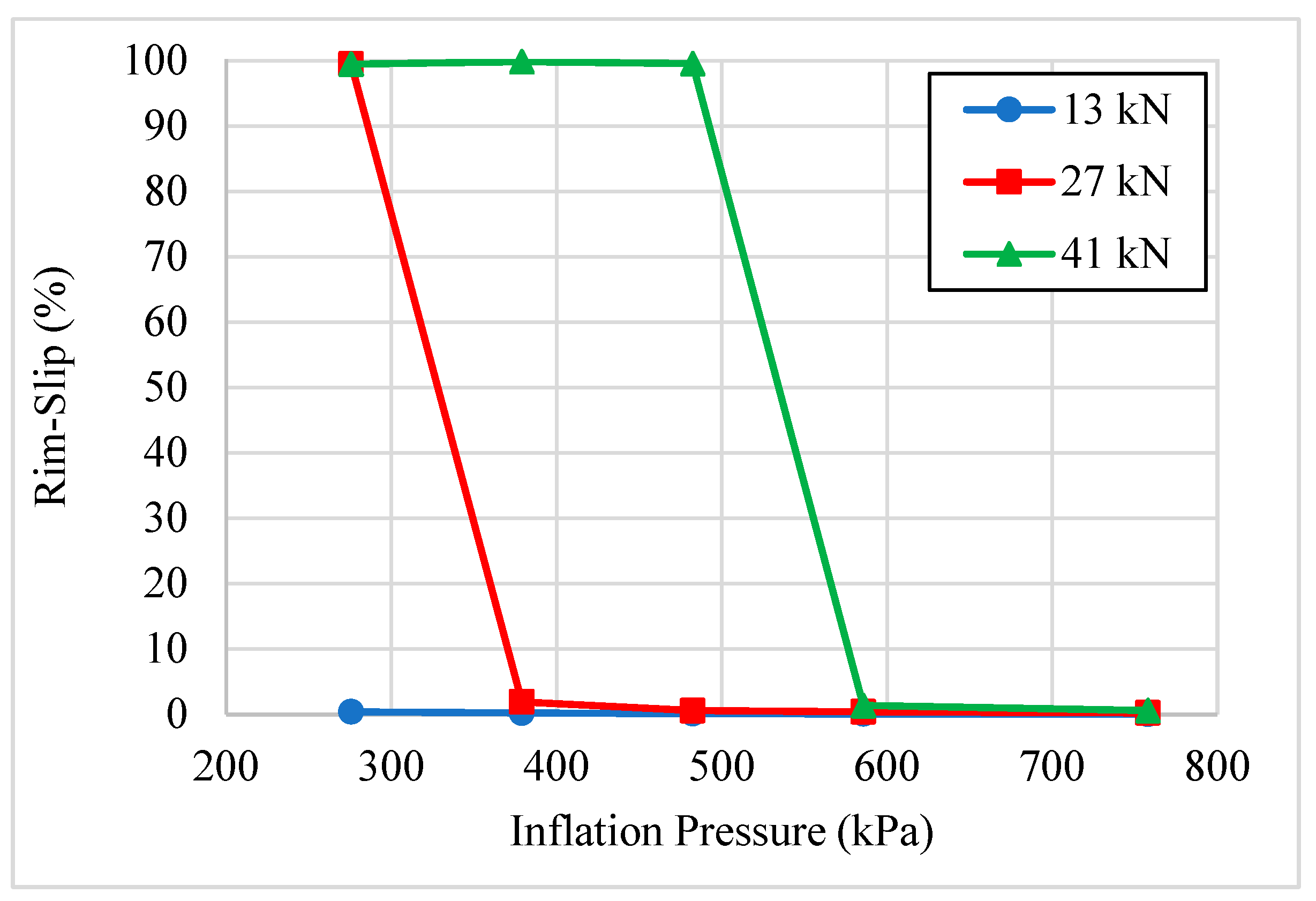
3.3. Effect of Vertical Load and Inflation Pressure
3.4. Comparison with Hard Surface
4. Conclusions
- A threshold effect was visible for rim-slip.
- Increased drawbar and vertical loads caused increased rim-slip, increased friction coefficient, and inflation pressure decreased rim-slip, and longitudinal wheel speed had a negligible effect on rim-slip.
- A particular longitudinal wheel speed and drawbar load combination resulted in an outlier simulation with unsteady results.
- Compared to the hard surface, rim-slip occurred on the soil at lower vertical loads, higher friction coefficients, and higher inflation pressures.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ASTM F2803-21; Standard Test Method for Evaluating Rim Slip Performance of Tires and Wheels. ASTM International: West Conshohocken, PA, USA, 2021. [CrossRef]
- Bishel, S. Land Vehicle Tire Qualification, AD1086645, U.S.; Army DEVCOM Ground Vehicle Systems Center: Warren, MI, USA, 2019; Available online: https://apps.dtic.mil/sti/pdfs/AD1086645.pdf (accessed on 10 February 2024).
- General Motors. Vibration Shortly After Tires are Mounted/Preventing Vibration from Wheel Slip (Tire Sliding on Wheel), 12-03-10-001B. 2014. Available online: https://static.nhtsa.gov/odi/tsbs/2014/MC-10137841-9999.pdf (accessed on 23 April 2021).
- Nitto Tire. Consumer Complaints for Vibration—Tire/Rim Slip, NTSD-12-015. 2014. Available online: https://www.nittotire.com/media/55ibthri/techbulletin_ntsd_12-015-rev-3.pdf (accessed on 29 April 2021).
- Collings, W.; El-Sayegh, Z.; Ren, J.; El-Gindy, M. Modelling of Off-Road Truck Tire-Rim Slip Using Finite Element Analysis. SAE Int. J. Adv. Curr. Pract. Mobil. 2022, 4, 2335–2341. [Google Scholar] [CrossRef]
- Pacejka, H. Tyre and Vehicle Dynamics, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2002. [Google Scholar]
- Pacejka, H. Analysis of the Dynamic Response of a Rolling String-Type Tire Model to Lateral Wheel-Plane Vibrations. Veh. Syst. Dyn. 1972, 1, 37–66. [Google Scholar] [CrossRef]
- Wong, J. Theory of Ground Vehicles, 3rd ed.; John Wiley and Sons: New York, NY, USA, 2001. [Google Scholar]
- Johnson, A.R.; Tanner, J.A.; Mason, A.J. A kinematically driven anisotropic viscoelastic constitutive model applied to tires. In Proceedings of the Workshop on Computational Modelling of Tires, Hampton, VA, USA, 26–27 October 1994; pp. 41–51. [Google Scholar]
- Reida, J.D.; Boesch, D.A.; Bielenberg, R.W. Detailed tire modeling for crash applications. Int. J. Crashworthiness 2007, 12, 521–529. [Google Scholar] [CrossRef]
- Barbani, D.; Pierini, M.; Baldanzini, N. FE modelling of a motorcycle tyre for full-scale crash simulations. Int. J. Crashworthiness 2012, 17, 309–318. [Google Scholar] [CrossRef]
- Orengo, F.; Ray, M.H.; Plaxico, C.A. Modeling tire blow-out in roadside hardware simulations using LS-DYNA. In Proceedings of the ASME 2003 International Mechanical Engineering Congress and Exposition, Transportation: Making Tracks for Tomorrow’s Transportation, Washington, DC, USA, 15–21 November 2003; pp. 71–80. [Google Scholar]
- Ballo, F.; Previati, G.; Gobbi, M.; Mastinu, G. Tire-rim interaction, a semi-analytical tire model. ASME. J. Mech. Des. 2018, 140, 041401. [Google Scholar] [CrossRef]
- Hu, X.; Liu, X.; Shan, Y.; He, T. Simulation and Experimental Validation of Sound Field in a Rotating Tire Cavity Arising from Acoustic Cavity Resonance. Appl. Sci. 2021, 11, 1121. [Google Scholar] [CrossRef]
- Hyttinen, J.; Österlöf, R.; Drugge, L.; Jerrelind, J. Constitutive rubber model suitable for rolling resistance simulations of truck tyres. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 174–192. [Google Scholar] [CrossRef]
- Anghelache, G.; Moisescu, R. Analysis of Rubber Elastic Behaviour and Its Influence on Modal Properties. Mater. Plast. 2008, 45, 143–148. [Google Scholar]
- Pomoni, M. Exploring Smart Tires as a Tool to Assist Safe Driving and Monitor Tire–Road Friction. Vehicles 2022, 4, 744–765. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, J.; Wang, F.; Dong, H.; Yan, Y.; Ren, Y.; Zhou, C.; Yin, G. Tire Road Friction Coefficient Estimation: Review and Research Perspectives. Chin. J. Mech. Eng. 2022, 35, 6. [Google Scholar] [CrossRef]
- Venturini, S.; Bonisoli, E.; Rosso, C.; Velardocchia, M. A tyre-rim interaction digital twin for biaxial loading conditions. Mech. Mach. Theory 2024, 191, 105491. [Google Scholar] [CrossRef]
- Gheshlaghi, F. Modeling and Analysis of Off-Road Tire Cornering Characteristics. Master’s Thesis, Ontario Tech University, Oshawa, ON, Canada, 2022. [Google Scholar]
- Lee, C. Rim Slip and Bead Fitment of Tires: Analysis and Design. Tire Sci. Technol. 2006, 34, 38–63. [Google Scholar] [CrossRef]
- Pelle, R. FEM Simulation of the Tire/Rim Seating Process. Tire Sci. Technol. 1994, 22, 76–98. [Google Scholar] [CrossRef]
- Reina, S. A Study of Layered Contact Problems with Particular Application to Tyre-Wheel Interfaces. Ph.D. Dissertation, Imperial College, London, UK, 2010. [Google Scholar]
- Cosseron, K.; Mellé, D.; Hild, F.; Roux, S. Optimal parameterization of tire-rim interaction for aircraft wheeSls. J. Aircr. 2019, 56, 2032–2046. [Google Scholar] [CrossRef]
- Cai, Y.; Zang, M.; Duan, E. Modeling and Simulation of Vehicle Responses to Tire Blowout. Tire Sci. Technol. 2015, 43, 242–258. [Google Scholar] [CrossRef]
- ESI Group. Virtual Performance Solution 2014: Solver Reference Manual; ESI Group: Rungis, France, 2014. [Google Scholar]
- Wriggers, P. Computational Contact Mechanics, 2nd ed.; Springer: Berlin, Germany, 2006; ISBN 978-3-540-32609-0. [Google Scholar]
- Herron, J.R. Application of ALE Contact to Composite Shell Finite Element Model for Pneumatic Tires. Master’s Thesis, University of Toledo, Toledo, OH, USA, 2005. [Google Scholar]
- Previati, G.; Ballo, F.; Gobbi, M.; Mastinu, G. Radial impact test of aluminium wheels—Numerical simulation and experimental validation. Int. J. Impact Eng. 2019, 126, 117–134. [Google Scholar] [CrossRef]
- Ge, H.; Quezada, J.C.; Le Houerou, V.; Chazallon, C. Multiscale analysis of tire and asphalt pavement interaction via coupling FEM–DEM simulation. Eng. Struct. 2022, 256, 113925. [Google Scholar] [CrossRef]
- Bekker, M.G. Land Locomotion Research Report No. 5; Detroit Arsenal: Warren, MI, USA, 1958. [Google Scholar]
- Reece, A.R. Problems of Soil Vehicle Mechanics; Rep. no. 8470, U.S.; Army Tank-Automotive Center: Warren, MI, USA, 1964; Available online: https://apps.dtic.mil/sti/citations/AD0450151 (accessed on 16 January 2021).
- Smith, W.; Melanz, D.; Senatore, C.; Iagnemma, K.; Peng, H. Comparison of discrete element method and traditional modeling methods for steady-state wheel-terrain interaction of small vehicles. J. Terramech. 2014, 56, 61–75. [Google Scholar] [CrossRef]
- Slade, J.L. Development of a New Off-Road Rigid Ring Model for Truck Tires Using Finite Element Analysis Techniques. Master’s Thesis, Pennsylvania State University, State College, PA, USA, 2009. [Google Scholar]
- Ranvir, D.S. Development of Truck Tire Terrain Finite Element Analysis Models. Master’s Thesis, Ontario Tech University, Oshawa, ON, Canada, 2013. [Google Scholar]
- Shokouhfar, S. A Virtual Test Platform for Analyses of Rolling Tyres on Rigid and Deformable Terrains. Ph.D. Dissertation, Concordia University, Montreal, QC, Canada, 2017. [Google Scholar]
- Swamy, V.S.; Pandit, R.; Yerro, A.; Sandu, C.; Rizzo, D.M.; Sebeck, K.; Gorsich, D. Review of modeling and validation techniques for tire-deformable soil interactions. J. Terramechanics 2023, 109, 73–92. [Google Scholar] [CrossRef]
- Cundall, P.; Strack, O. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Gorsich, D.; Letherwood, M.; Dasch, J. Predicting mobility in military operational scenarios. Truck. Off-Highw. Eng. 2022, 30, 14–18. [Google Scholar]
- Gingold, R.A.; Monaghan, J.J. Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Mon. Not. R. Astr. Soc. 1977, 181, 275–389. [Google Scholar] [CrossRef]
- Bagheri, M.; Mohammadi, M.; Riazi, M. A review of smoothed particle hydrodynamics. Comp. Part. Mech. 2023. [Google Scholar] [CrossRef]
- Tasora, A.; Mangoni, D.; Negrut, D.; Serban, R.; Jayakumar, P. Deformable soil with adaptive level of detail for tracked and wheeled vehicles. Int. J. Veh. Perform. 2019, 5, 60–76. [Google Scholar] [CrossRef]
- El-Sayegh, Z. Modelling and Analysis of Truck Tire-Terrain Interaction. Ph.D. Dissertation, Ontario Tech University, Oshawa, ON, Canada, 2020. [Google Scholar]
- Huang, W.; Wong, J.Y.; Preston-Thomas, J.; Jayakumar, P. Predicting terrain parameters for physics-based vehicle mobility models from cone index data. J. Terramechanics 2020, 88, 29–40. [Google Scholar] [CrossRef]
- DYNAmore GmbH. LS-DYNA Support: Contact Types. Available online: https://www.dynasupport.com/tutorial/contact-modeling-in-ls-dyna/contact-types (accessed on 9 February 2024).
- Heinrich, G.; Klüppel, M. Rubber friction, tread deformation and tire traction. Wear 2008, 265, 1052–1060. [Google Scholar] [CrossRef]
- Persson, B.N.J. Rubber friction: Role of the flash temperature. J. Phys. Condens. Matter 2006, 18, 7789. [Google Scholar] [CrossRef]
- Chae, S. Nonlinear Finite Element Modeling and Analysis of a Truck Tire. Ph.D. Dissertation, Pennsylvania State University, State College, PA, USA, 2006. [Google Scholar]
- El-Sayegh, Z.; El-Gindy, M.; Johansson, I.; Öijer, F. Off-road soft terrain modelling using smoothed particle hydrodynamics technique. In Proceedings of the ASME 2018 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, Quebec City, QC, Canada, 26–29 August 2018. [Google Scholar]



| Parameter | Range | Default Value |
|---|---|---|
| 5–60 km/h | 10 km/h | |
| 0.1–0.9 | 0.2 | |
| 20–90% | 60% | |
| 13–41 kN | 41 kN | |
| 276–758 kPa | 379 kPa |
| Coefficient | Units | Value |
|---|---|---|
| none | 1.10 | |
| kN/mn+1 | 74.6 | |
| kN/mn+2 | 2080 | |
| kPa | 3.3 | |
| deg | 33.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Collings, W.; El-Sayegh, Z.; Ren, J.; El-Gindy, M. Modelling of Truck Tire–Rim Slip on Sandy Loam Using Advanced Computational Techniques. Geotechnics 2024, 4, 229-241. https://doi.org/10.3390/geotechnics4010012
Collings W, El-Sayegh Z, Ren J, El-Gindy M. Modelling of Truck Tire–Rim Slip on Sandy Loam Using Advanced Computational Techniques. Geotechnics. 2024; 4(1):229-241. https://doi.org/10.3390/geotechnics4010012
Chicago/Turabian StyleCollings, William, Zeinab El-Sayegh, Jing Ren, and Moustafa El-Gindy. 2024. "Modelling of Truck Tire–Rim Slip on Sandy Loam Using Advanced Computational Techniques" Geotechnics 4, no. 1: 229-241. https://doi.org/10.3390/geotechnics4010012
APA StyleCollings, W., El-Sayegh, Z., Ren, J., & El-Gindy, M. (2024). Modelling of Truck Tire–Rim Slip on Sandy Loam Using Advanced Computational Techniques. Geotechnics, 4(1), 229-241. https://doi.org/10.3390/geotechnics4010012









