Abstract
Constructing embankments over soft soils is a challenge for geotechnical engineers due to large settlements. Among diverse ground-improvement methods, combining piles and geosynthetics (e.g., geosynthetic-reinforced piles, deep cement mixing columns, geotextile-encased columns) emerges as a reliable solution for time-bound projects and challenging ground conditions. While stress distribution within pile-supported embankments has been extensively studied, the load transfer efficiency of piled solutions with geosynthetic reinforcement remains less explored. The novelty in this study lies in the investigation of three different inclusion solutions from a common control case in the numerical model considering the role of geosynthetic reinforcement. This study investigates the load transfer mechanisms in embankments supported by various techniques including geosynthetic-reinforced piles, deep cement mixing columns, and geosynthetic-encased granular columns. Two-dimensional axisymmetric finite element models were developed for three cases of embankments supported by vertical inclusions. Numerical findings allow clarification of the soft ground and embankment characteristics which influence the arching and membrane efficiencies. Rigid piles outperform deep cement mixing (DCM) columns and geotextile-encased columns (GEC) in reducing settlements of soft ground. Geosynthetic reinforcements are particularly helpful for rigid pile solutions in high embankments due to their load transfer capability. Additionally, physical properties of fill soil can impact the inclusion solutions, with high shear resistance enhancing the arching effect and lower modulus subsoils showing better arching performance.
1. Introduction
Inclusion supports represent a dependable solution for the construction of embankments over soft foundation soils; single-stage construction is allowed without prolonged waiting periods and yields a substantial reduction in overall and differential settlements. Furthermore, pile supports are effective in difficult soil situations like landfills, brownfield sites, and uncertain deposits. In these cases, the behavior of the soil is not well understood, and testing its properties in a lab is difficult. Since piles bear a significant part of the embankment’s weight, detailed knowledge about the soil mechanics is not necessary. Additionally, when dealing with contaminated soil, using pile supports instead of consolidation methods helps prevent contact with potentially polluted water that can come from the ground during consolidation.
The technique of utilizing inclusion supports is termed geosynthetic-reinforced pile-supported (GRPS) embankments or geosynthetic-reinforced and column-supported (GRCS) embankments. Nevertheless, the materials used for the pile elements can have different properties. They can be either rigid, like steel or concrete piles, or somewhat flexible configurations. In contrast, the term “column” is employed to delineate semi-rigid vertical components, including cement mixing columns and geosynthetic-encased granular columns.
Numerical modeling has become an important tool for investigating the behavior and the load transfer mechanism on embankments supported by piles or columns with and without using geosynthetic reinforcement [1,2,3,4,5]. Despite numerous investigations and the presentation of numerous successful instances in the literature throughout time, the precise mechanism through which the embankment load is transferred to both the piles and the foundation soil remains inadequately comprehended.
In order to better understand the load transfer mechanisms developed within the embankment reinforced by inclusion on soft soils, numerical analyses have been developed for three types of vertical inclusions including rigid piles, DCM (deep cement mixing) columns, and GEC (geosynthetic-encased columns). The influences of the embankment height, geosynthetic stiffness, subsoil stiffness, friction angle, and cohesion of embankment fills are investigated to emphasize the influences on the soil arching and the membrane effect of geosynthetics. The numerical models are conducted for cases of embankments supported by geosynthetic-reinforced piles, deep cement mixing columns, and geosynthetic-encased columns. The study aims to provide a better understanding of the load transfer mechanisms and the roles of geosynthetic reinforcement in the technique of inclusion-reinforced embankments over soft ground.
2. Load Transfer Mechanisms in Pile Supports
2.1. Geosynthetic-Reinforced Piles
Geosynthetic-reinforced pile-supported embankments are now commonly used in building construction on soft soil, including highways and railways. The system of the geosynthetic-reinforced and pile-supported embankments includes different components, including embankment fills, geosynthetic materials, mattresses, piles, and subsoil layers. This solution helps to minimize the ground settlement and develop the load transfer mechanisms within the embankment. One or more layers of geosynthetic reinforcement can be installed over piles to increase the performance of the reinforced embankment system. The membrane effect of geosynthetics, resulting from their low bending rigidity, requires the generation of tensile forces. When subjected to strain, these forces play a role in enhancing load transfer to the piles and reducing the necessary area replacement ratio.
Numerous techniques have been studied to understand how loads are distributed and settlements occur in piled embankment systems. These approaches include analytical solutions, numerical simulations, and field investigations [6,7,8,9,10,11]. Various methods exist in the literature for determining load distribution in pile-supported embankments, according to the soil arching concept, which was first developed by Terzaghi [12]. Guido et al. [13] proposed a design approach using geogrid reinforcement, while Hewlett and Randolph [14] introduced a semi-spherical arching model. Based on plane-strain conditions, Carlsson [15] developed a method to design a GRPS solution. Kempfert et al. [16] presented a design approach derived from laboratory model experiments involving piled embankments. This method initially determines the load on a soft foundation soil without geosynthetic reinforcement. Then, it calculates the required tension in the geosynthetic reinforcement to handle that load. Van Eekelen et al. [17] suggested changes to the existing British standard [18] to address the challenges posed by the arrangement of piles in three dimensions. A German design guideline, EBGEO [19], incorporates an analysis method developed by Kempfert et al. [16]. This design method is derived from a 1:3 laboratory model of piled embankment systems. The process begins by estimating the load on the soft soil with no reinforcement, followed by determining the reinforcement tension needed to carry that load. This method has proven valuable for designing geosynthetic-reinforced embankments. However, the current design methods have not yet fully matched all the experimental results due to the fact that the behavior of GRPS is very complicated.
Recently, Pham and Dias [11] conducted numerical simulations based on a well-reported field experiment performed by Liu et al. [6] to investigate the performance of geosynthetic-reinforced and pile-supported embankments. By using a unit cell model, the study identified the role of fill soil cohesion in enhancing soil arching and load efficiency. In a study by Pham and Dias [20], a comparison was made between a set of experiments and results obtained from various design methods. The analysis showed significantly different results in predicting the load transfer mechanism. The study indicated that analytical methods that take into account the support of the subsoil layer, such as the EBGEO [19], provide better results than other methods that neglect the support capacity of the soil layer when compared to experimental data.
2.2. Deep Cement Mixing Columns
The DCM columns are typically applied through soft ground to transfer loads from the embankment and traffic to the strong stratum [21,22,23,24]. In order to limit the soft ground settlement, DCM columns are installed with the improvement ratios (defined as the percentage coverage of pile caps over the total foundation area) in the selection of 0.1–0.5. The length of DCM columns is in the range of 7.0–16.5 m which is decided due to the thickness of soft soils and the improvement types (floating and fixed columns). A square or triangular pattern can be chosen for the column grid. The elastic modulus of DCM columns varies from 30–170 MPa; in some cases, it can reach 880 MPa [25,26,27].
There is a limitation in studies of the load transfer of DCM columns, particularly the soil arching. Jamsawang et al. [27] conducted an FEM analysis based on field measurements to investigate the performance of DCM columns including load distribution. Then, Cui et al. [28] further developed that study to show the influence of the elastic modulus of DCM columns on the stress distribution. However, the arching effect has not yet been evaluated in these studies, as well as the effects of using geosynthetic reinforcement.
2.3. Geosynthetic-Encased Columns
Through the years, geosynthetic-encased columns (also known as granular piles or stone columns) have been commonly used in ground to improve the load-bearing capacity. Geosynthetics are used to encase the granular columns in order to mobilize hoop stress, to protect the reinforced material, and to develop the drainage and friction of the columns. Bergado et al. [29] conducted field studies indicating that the implementation of granular piles led to a remarkable increase in bearing capacity. Katti et al. [30] introduced a theory based on the particulate concept for improving soft ground using geosynthetically encased stone columns. Numerical and analytical models were conducted by Raithel and Kempfert [31] and Raithel et al. [32] to study the efficacy of geosynthetic-encased sand columns. Malarvizhi and Ilamparuthi [33] showcased the improved performance of such columns through laboratory tests, revealing that the ultimate bearing capacity of treated beds was three times that of untreated ones. Ayadat and Hanna [34] conducted experimental investigations, finding that the ultimate carrying capacity of stone columns encapsulated in geogrid textile material increases with the stiffness of the geosynthetic material used for encapsulation. Murugesan and Rajagopal [35] conducted an FEM analysis to identify a boost in the load-bearing capacity of granular piles resulting from their encasement. They observed that the influence of encasement declined with an increase in the diameter of the granular pile. Yoo [36] conducted numerical work based on FEM in order to confirm that geosynthetic encasement may enhance the stiffness of the granular column and support the load transfer mechanisms. Keykhosropour et al. [37] carried out numerical simulations to indicate that encasement stiffness and column diameter may encourage GEC performance. According to previous studies, GEC may improve the load-bearing capacity of stone columns by providing added confinement, particularly valuable in soft soils where it prevents stone displacement and hastens installation. However, limited literature exists on the performance of GEC including the load transfer efficiency, particularly when compared to other inclusion solutions.
2.4. Determination of Load Transfer Efficiency
Due to the difference in stiffness between the pile and the soft subsoil, variations in settlement normally develop and this causes arching within the embankment layer. In this study, the arching phenomenon in pile-supported embankments is characterized as a stress redistribution mechanism that enables the transfer of greater loads to the pile component while improving loads on both the geosynthetic material and the subsoil. The arching efficacy (Ea) is defined to evaluate the arching degree [1,11,12,14,16]; Equation (1) presents the function to determine Ea. In the cases of geosynthetics being used on top of the inclusions to increase the performance of the solution, the distributed load is influenced by the geosynthetic membrane. The stretching of the geosynthetic activates a portion of the geosynthetic’s inherent strength [11]. As a result, the geosynthetic functions as a “tensioned membrane”, bearing a load applied perpendicular to the piles. Hence, the effectiveness of the geosynthetic membrane effect (referred to as membrane efficacy), which is determined by Equation (2), is characterized by the proportion of the embankment load that is transferred onto the pile cap due to the stretching of the geosynthetic material.
where Ea is the arching efficacy (%), Pi is the load distributed on the inclusion cap by the arching phenomenon (kN), H is the embankment height (m), AE is zone area influenced by inclusions (m2), q is a surcharge (kN/m2), is the unit weight of embankment soils (kN/m3), Em is the geosynthetic membrane efficacy (%), and PGSY is the load transferred onto the pile cap by the geosynthetic membrane (kN).
2.5. German Design Method [19]
The vertical stress distributed on pile cap, σc and the vertical stress acting on the geosynthetic reinforcement, σs can be calculated as follows:
where,
where, q is the surcharge at the embankment surface (kN/m2), hg is the arch height, s is the distance between the pile centers, is pile cap area (m2), d is the pile diameter (m), H is the embankment height (m), and is the unit weight of fill soil (kN/m3).
3. Numerical Model
3.1. Description of FEM Simulation
In this study, the numerical modeling of the embankment stress distribution reinforced by inclusions is performed by using PLAXIS, version 2020 [38], a two-dimensional program developed based on FEM. A typical case is developed where cylindrical inclusions are used to support a granular embankment over soft ground. A triangular grid arrangement of inclusions is adopted in simulations. Due to the symmetry, only a quarter of the reinforced system is simulated in axisymmetric conditions in the numerical models. Figure 1 presents the finite element mesh of a unit cell in a two-dimensional view. The model mesh is made considering 15-node triangular elements. Considering the typical configurations of reinforced systems used in ground improvement for a base case, the diameter of the pile is selected as 0.7 m, pile spacing is 3.0 m, embankment height is 3.0 m, and the thickness of soft ground is 6.0 m. A layer of geosynthetic is placed above the inclusion in the cases where the geosynthetic membrane effect is considered. The unit cell bottom is fixed in both horizontal and vertical directions, which means that deformation is not allowed below the soft ground. In order to simplify the problem, a drained condition is adopted for this study. The tensile stiffness of geosynthetics is defined as the tensile force per unit width divided by the average strain in the materials.
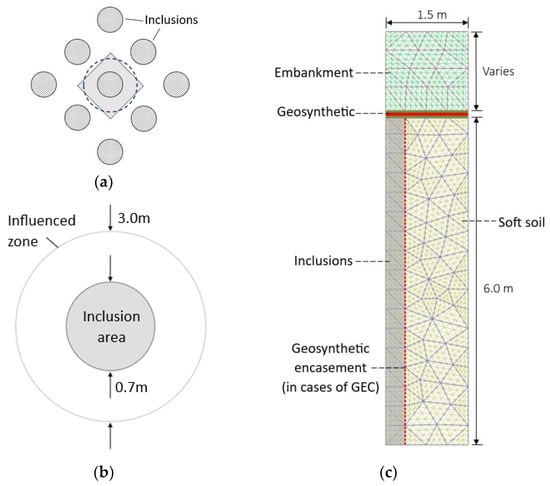
Figure 1.
FEM simulation of embankments reinforced with vertical inclusions on soft soil: Layout (a); Unit cell (b); FEM mesh (c).
In general, there are four different materials that are involved in the numerical models, including embankment fill, reinforced geosynthetics, inclusions (rigid piles, DCM columns, and GEC), and soft ground. Especially in the case of GEC being simulated, a geosynthetic layer is used as encasement. In this analysis, the geosynthetic materials and the rigid pile are modeled as linear elastic materials. Meanwhile, a linear elastic-perfectly plastic model with Mohr–Coulomb’s failure criterion was used to model the embankment fill, soft ground, materials of DCM columns, and GEC. The input parameters used for inclusions are based on significant studies in the field; specifically, rigid piles, DCM columns, and GEC are referenced from studies by Pham and Dias [11], Jamsawang et al. [27], and Yoo [36], respectively. All parameters used in the numerical analysis are presented in Table 1.

Table 1.
Parameters used in FEM simulations.
In this study, the interaction between geosynthetics and surrounding materials is considered by using interface elements, such as Geosynthetic/Inclusion, Geosynthetic/Embankment, Geosynthetic/Foundation, Encased-Geosynthetic/Columns, and Encased-Geosynthetic/Foundation interfaces. The interface characteristics are mainly defined based on the physical parameters of the surrounding soil with the friction angle fixed at 0.8 × φsoil [39]. The interaction between the rigid pile, DCM columns, and the soil was not considered during the analysis in order to avoid convergence problems and simplify the problem.
3.2. Numerical Procedure
In order to facilitate the comparison of the load transfer efficiency of three reinforced inclusions, several simplified assumptions are adopted for the numerical procedure:
- -
- The dimensions of inclusions are constant for different solutions. The installation process of inclusions is neglected.
- -
- The soft soil is considered homogenous. The creep effect of soft ground is not considered.
In order to evaluate the influences on load transfer mechanisms through inclusion solutions, some of the parameters are varied, such as embankment height (H = 0.5; 1.5; 2; 3; 4; 5; 6; and 10 m), fill characteristics (c = 0 kPa, 10 kPa, and 20 kPa; φ = 20°, 30°, 40°), subsoil modulus (Es = 1.5; 3.5; and 7.5 MPa), and geosynthetic stiffness (J = 1000, 2000, kN/m). In most cases, a single parameter is varied while keeping the remaining parameters constant.
4. Results and Discussions
4.1. Verification of Numerical Modeling
Verification was carried out to enhance the reliability of the numerical modeling through comparison with the German design method, EBGEO [19], due to the fact that it produced good agreement with experimental data, as noted by Pham and Dias [20]. The load transfer efficiencies on the rigid pile solution computed by FEM and estimated by EBGEO [19] for different heights are summarized in Table 2. The FEM and analytical method results are in good agreement for fill heights of 1.5 m and 2.0, with variations of 2.6% and 6.6%, respectively. Regarding the smaller embankment, EBGEO [19] overpredicts the arching efficiency, whereas the predicted results are greater when the embankment height increases to 3 m and 5 m. The comparison results on the arching efficiency between FEM simulations and several relevant studies are presented in Figure 2. The experiments were chosen with similar configurations, while the ratio of the embankment height to the pile spacing minus pile area, H/(s-a), ranged from 2.1 to 2.8, with a maximum value of 4.59. It is observed that the soil arching within the soil is fully established with the considered embankment height values. It is evident that the arching efficiency results calculated from the FEM model fall within the range of values reported in the mentioned studies. Indeed, arching efficiency values range from 49% to 69%; meanwhile, the numerical result calculated by the FEM model is 56% for the embankment height of 5 m. Given the acceptable differences and reasonably good agreement, the numerical model used in this study has been adopted for the parametric analysis of stress redistribution within an embankment reinforced by vertical inclusions on soft soils.

Table 2.
Comparison between numerical results and EBGEO on arching efficiency.
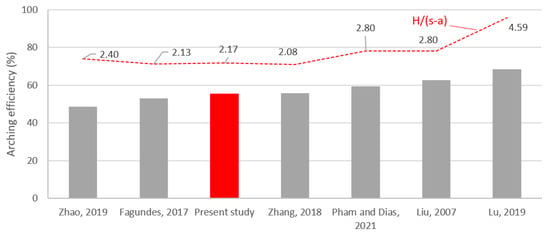
Figure 2.
Comparison of arching efficiency between present study and relevant studies including Zhao, 2019 [10], Fagundes, 2017 [7], Zhang, 2018 [8], Pham and Dias, 2021 [11], Liu, 2007 [6], and Lu, 2019 [9].
4.2. Inclusion Behaviors
Figure 3 presents the principal stresses within the reinforced embankment for three cases of inclusions. The load transfer can be seen as a change in the orientation of the principal stresses. Indeed, the stress from the embankment is directed towards the position of the pile and, therefore, the residual stress on soft soil is reduced. It can be noted that the numerical models well reproduced the inclusion behaviors.

Figure 3.
Principal stress within reinforced systems for three types of inclusions.
Figure 4 illustrates the computed geosynthetic strains for three types of inclusions at varying embankment heights. As the embankment height increases across the three inclusion types, a greater load is distributed to the subsoils, resulting in larger geosynthetic deflection. Consequently, the geosynthetic bears an increased load transfer to the inclusions, mobilizing a higher tensile force. The geosynthetic strain reaches its peak in the case of rigid piles, followed by DCM columns and GEC, respectively. This observation underscores that, given the same characteristics of geosynthetic reinforcement, the significance of geosynthetics becomes more pronounced in the context of rigid piles.
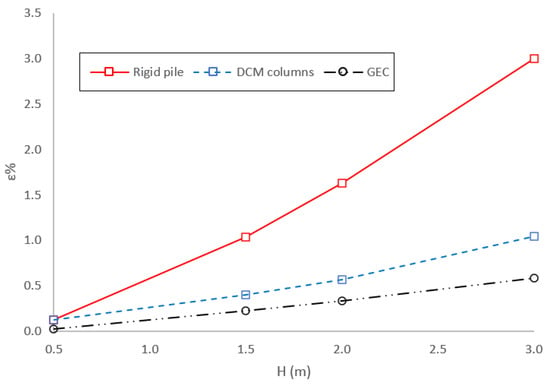
Figure 4.
Influence of embankment height on geosynthetic strain.
4.3. Total Settlements of Soft Ground
Figure 5 depicts the total settlement of soft soils under various embankment heights reinforced by inclusion solutions. A clear comparison with the case of not using inclusion solutions highlights that, when the natural ground undergoes deformation due to the embankment load, inclusion solutions significantly reduce the settlement of the soft ground. It is noteworthy that the considered rigid pile provides the most effective solution for settlement limitation, while the largest settlement occurs in cases involving GEC. The numerical analysis also incorporates the role of geosynthetics, assuming their placement over the inclusion head to provide support for the three inclusions. Obviously, geosynthetic acts differently for the three inclusions. Indeed, the use of geosynthetics had little effect on settlement reduction for the DCM and GEC column cases. Meanwhile, for rigid piles, using geosynthetics with a stiffness of 2000 kN/m can reduce settlement by a maximum of 15% when the embankment height reaches 10 m.
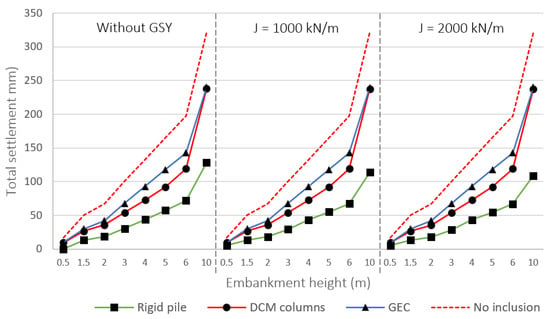
Figure 5.
Influence of embankment height and use of geosynthetics on total settlements.
The dependence of total settlement of soft ground on the shear strength of fill soils including cohesion and friction angle under inclusion supports is shown in Figure 6. It is evident to note that the friction angle and cohesion of fill soils can limit the settlement of soft ground. However, the effect of soil shear resistance is different for the three types of inclusions. In fact, the total settlement can be reduced by 35% in the case of rigid pile (friction angle equals 40°) considering the effect of soil cohesion. Meanwhile, using fill soil with an internal friction angle of 20 degrees, DCM columns, and GEC could limit by 11% and 4%, respectively, the amount of total settlement. A similar tendency can be noted for the influence of soil friction; as it increased from 20° to 40°, the decreases of total settlement under supports of the rigid pile, DCM columns, and GEC were 27%, 8%, and 3%, respectively. Thus, the effect of the shear strength of fill soil on rigid piles is greatest in the considered cases of reinforced inclusions.
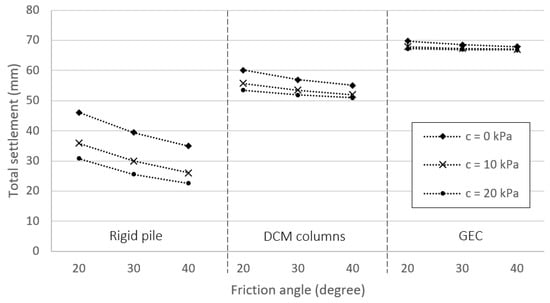
Figure 6.
Influences of friction angle and cohesion of embankment fill on maximum settlements.
Figure 7 demonstrates the influence of subsoil modulus on the total settlement of soft ground reinforced by inclusions. The total settlements increase with the decrease in the subsoil modulus. However, the increase in settlement of rigid piles is smaller than in the other two cases and it is more significant in the cases of high embankment (H = 5 m). The benefits of geosynthetics in reducing the total settlement are also considered under different heights (3 and 5 m) of embankment. The use of geosynthetic reinforcement on the pile’s head seems not to provide enough benefit for solutions of DCM columns in both considered embankment heights. Nevertheless, geosynthetic reinforcement allows reducing the settlement in the cases of rigid piles and GEC supporting a 5 m height embankment. Indeed, the settlement can be reduced by 7% and 8% if geosynthetic reinforcement is used to support rigid piles and GEC, respectively, over the weakest soft ground.
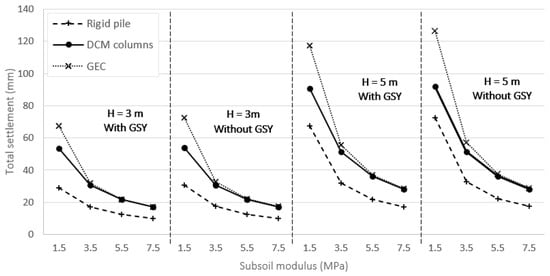
Figure 7.
Influences of subsoil modulus and embankment height on maximum settlements.
4.4. Stress Distribution
The stress distribution acting over the surface of soft ground reinforced by inclusions is presented in Figure 8. The stresses are computed for four embankment heights (0.5, 1.0, 2.0, and 3.0 m) in three cases of inclusion types. Note that the increase in stresses is obtained at the inclusion areas to confirm the load distribution occurred due to the act of inclusion. Nevertheless, the load transfer mechanism seems to be different due to the embankment height between inclusion solutions. In the case of the low embankment (0.5 m), the distributed load at the inclusion area is not very different between solutions, and it seems to be concentrated at the edge of the inclusions. Meanwhile, the significant differences can be seen for high embankments (from 1.0 m to 3.0 m). The stress distribution on the rigid pile head is significantly larger than the other solutions. Furthermore, the load has a uniform distribution on the inclusion surface. Comparing DCM columns and GEC, although the inclusion modulus is assumed to be the same, DCM columns show more effectiveness than the GEC solution in concentrating stress.
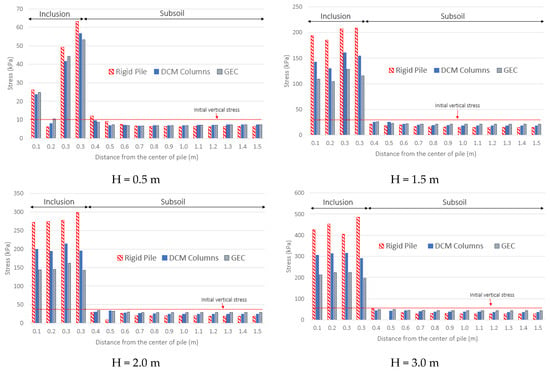
Figure 8.
Stress distribution over systems of soft ground supported by inclusions.
4.5. Arching Effect
Equation (1) indicates that the efficiency of the arching effect varies between 0 and 100%, representing the absence of soil arching to its complete realization. Figure 9 demonstrates the influences of embankment fill strengthening (cohesion and internal friction) on the arching efficiency for cases where the embankment block is 3 m high. Obviously, using a high shear resistance of embankment fill enhances the arching effect occurring in the three inclusion solutions. In fact, an increase in both friction angle and cohesion of filling soil allows an increase in arching efficiency. However, the arching effect between inclusion solutions is different and this explains the results of settlement reduction, which are presented in Figure 6. First, the calculated arching efficiency of the rigid pile ranges from 25 to 50%, while it is from 21 to 35% and from 15 to 22% for DCM columns and GEC, respectively. Second, the maximum increase can be noted in the case of a rigid pile under the effect of soil cohesion. In fact, the arching efficiency increases by 70% if the cohesion of the filling material increases from 0 to 20 kPa with its friction angle equal to 20°. For the similarly considered embankment fill, the increments obtained for DCM columns and GEC are 60% and 39%, respectively.
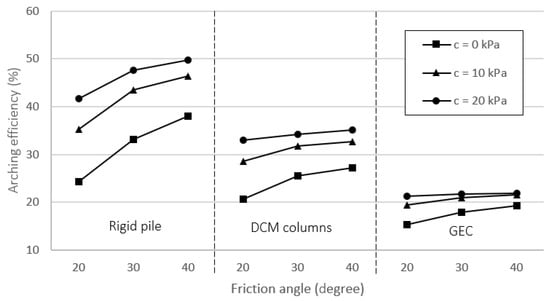
Figure 9.
Influences of friction angle and cohesion of embankment fill on arching efficiency.
As presented in Figure 10, arching efficiency reduces with increasing the subsoil modulus. The stiffness differences between inclusion and soft ground cause the stress distribution. As the soft ground modulus increases, the difference in stiffness between inclusion and soft soil reduces. This explains the decreasing tendency obtained for three inclusion solutions in Figure 10. Note the responses are different between inclusions. When the subsoil modulus increases from 1.5 MPa to 7.5 MPa, the estimated reductions in arching efficiencies are 62% for the case of DCM columns and approximately 45% for both cases of rigid pile and GEC. Based on these results, it can be noted that the influence of subsoil modulus is significant on the arching phenomenon occurring above inclusions.
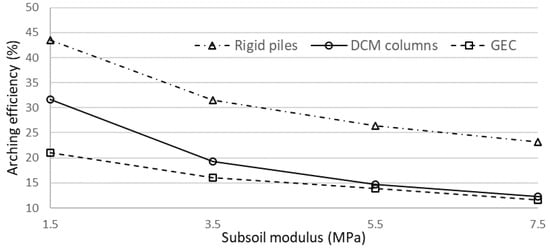
Figure 10.
Influences of subsoil modulus on arching efficiency.
4.6. Membrane Effect
In cases of geosynthetics used to reinforce inclusion-supported embankments over soft ground, the membrane effect is another phenomenon that allows the load distribution to act over soft ground. Figure 11 illustrates the influence of friction angle and cohesion of embankment fill on membrane efficiency acting above soft ground supported by inclusion supported by geosynthetic reinforcement. Regarding cases of rigid piles and DCM columns, it should be noted that the membrane efficiency, which is determined by Equation (2), becomes lower when the cohesion and friction angle of filling soil increases. Conversely, the slight increase in membrane effect when the shear resistance of the filling soil increases can be noted for the case of GEC. According to the numerical results, the influence of the membrane effect on DCM columns and GEC solutions is minimal as the membrane efficiency is less than 5%. Geosynthetics play a more significant role in rigid pile solutions, especially in cases of low shear resistance of the filling material.
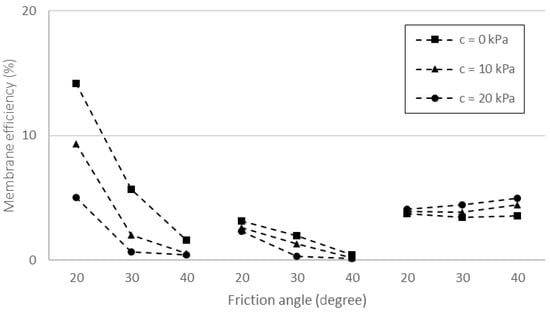
Figure 11.
Influences of friction angle and cohesion of embankment fill on membrane efficiency.
By comparing the numerical results presented in Figure 9 and Figure 11, the influence of the shear resistance of the fill material with the arching effect and the membrane effect is generally opposite. As the shear resistance of the material increases, the arching effect increases, while the membrane effect decreases. A material with good shear resistance enhances the load transfer to the head of inclusions through the arching effect, thereby reducing the portion of the load that continues to transfer through the membrane effect. This is particularly observed in the cases of rigid piles and DCM columns.
The dependency of the membrane effect on subsoil modulus is presented in Figure 12 as the decreased tendencies can be noted. As the subsoil modulus increases, the variation between the stiffness of inclusions and soft soil is reduced. Consequently, more stresses remain on the soft ground. This can explain why the geosynthetic acts less to transfer loads onto the inclusions due to the membrane effect. Moreover, the numerical results show that the effect of geosynthetic reinforcement is insignificant in the considered cases, as the calculated membrane efficiencies are less than 4%. In the cases of GEC, the effectiveness of geosynthetics is evident in the considered soft soils. However, for the other two solutions, the impact of geosynthetics becomes almost negligible as the modulus of the soft soil increases.
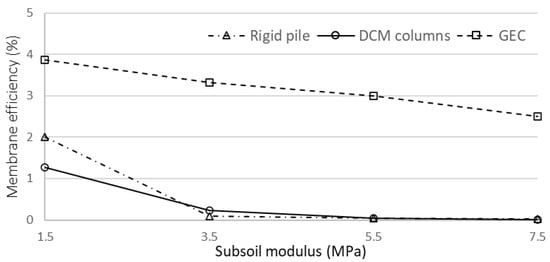
Figure 12.
Influences of subsoil modulus on membrane efficiency.
5. Conclusions
In this study, 2D axisymmetric FEM calculations were used to investigate the behavior of embankments reinforced by inclusions over soft soils, considering the support of geosynthetic reinforcements. The results of the numerical study demonstrated that inclusions could reduce the soft ground total settlements and promote soil arching within the embankments. The numerical results’ analysis indicates that the inclusion system’s performance is very different between rigid piles, DCM columns, and GEC with the use of geosynthetic reinforcements. The main conclusions can be drawn as follows:
- -
- The total settlements on soft ground are more effectively reduced when using rigid piles compared to DCM columns and GEC. However, the difference reduces in the case of low-height embankments,
- -
- Geosynthetic reinforcement proves to be more effective when combined with rigid pile solutions, especially for high embankments and low shear resistance of filling material, as it enhances the reinforced system performance to reduce subsoil settlements. On the other hand, geosynthetic reinforcement offers limited support in the case of GEC solutions, and it appears to have no impact on the performance of DCM columns,
- -
- The properties of the fill soil have a significant influence on the performance of inclusion solutions. The use of fill material with high shear resistance enhances the arching effect. Furthermore, the arching phenomenon is more effective in subsoils with a lower modulus.
Author Contributions
Methodology, M.-T.P.; Software, D.-D.P. and D.-L.V.; Validation, M.-T.P.; Formal analysis, D.-D.P. and D.-L.V.; Investigation, D.-D.P. and D.-L.V.; Writing—original draft, M.-T.P.; Writing—review & editing, D.D.; Supervision, D.D.; Project administration, M.-T.P.; Funding acquisition, M.-T.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Murata Science Foundation grant number 23VH07 and Ho Chi Minh City University of Technology (HCMUT), VNU-HCM, Vietnam.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to ethical.
Acknowledgments
We would like to thank Ho Chi Minh City University of Technology (HCMUT), VNU-HCM, Vietnam for the support of time and facilities for this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Low, B.K.; Tang, S.K.; Choa, V. Arching in piled embankments. J. Geotech. Eng. 1994, 120, 1917–1938. [Google Scholar] [CrossRef]
- Hu, S.; Zhuang, Y.; Wu, Y.; Zhang, X.; Dong, X. Numerical Study of Bearing Capacity of the Pile-Supported Embankments for the Flexible Floating, Rigid Floating and End-Bearing Piles. Symmetry 2022, 14, 1981. [Google Scholar] [CrossRef]
- Han, J.; Collin, J.G.; Huang, J. Recent development of geosynthetic- reinforced column-supported embankment. In Proceedings of the 55th Highway Geology Symposium, Kansas City, MO, USA, 7–10 September 2004; pp. 299–321. [Google Scholar]
- Chen, R.P.; Xu, Z.Z.; Chen, Y.M.; Ling, D.S.; Zhu, B. Field tests on pile-supported embankments over soft ground. J. Geotech. Geoenviron. Eng. 2010, 136, 777–785. [Google Scholar] [CrossRef]
- Vo, D.N.; Pham, M.T.; Le, V.A.; To, V.N. Load Transfer Acting in Basal Reinforced Piled Embankments: A Numerical Approach. Transp. Infrastruct. Geotech. 2022. [Google Scholar] [CrossRef]
- Liu, H.L.; Ng, C.W.; Fei, K. Performance of a geogrid-reinforced and pile-supported highway embankment over soft clay: Case study. J. Geotech. Geoenviron. Eng. 2007, 133, 1483–1493. [Google Scholar] [CrossRef]
- Fagundes, D.F.; Almeida, M.S.; Thorel, L.; Blanc, M. Load transfer mechanism and deformation of reinforced piled embankments. Geotext. Geomembr. 2017, 45, 1–10. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, S.; Zhao, H.; Deng, Y. Performance of geosynthetic-reinforced and pile-supported embankment with consideration of soil arching. J. Eng. Mech. 2018, 144, 06018005. [Google Scholar] [CrossRef]
- Lu, W.; Miao, L.; Wang, F.; Zhang, J.; Zhang, Y.; Wang, H. A case study on geogrid-reinforced and pile-supported widened highway embankment. Geosynth. Int. 2019, 27, 261–274. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, C.; El-Korchi, T.; Song, H.; Tao, M. Performance of geogrid-reinforced and PTC pile-supported embankment in a highway widening project over soft soils. J. Geotech. Geoenviron. Eng. 2019, 145, 06019014. [Google Scholar] [CrossRef]
- Pham, A.T.; Dias, D. 3D Numerical study of the performance of geosynthetic-reinforced and pile-supported embankments. Soils Found. 2021, 61, 1319–1342. [Google Scholar] [CrossRef]
- Terzaghi, K. Theoretical Soil Mechanics; John Wiley & Sons: New York, NY, USA, 1943; pp. 11–15. [Google Scholar]
- Guido, V.A.; Kneuppel, J.D.; Sweeney, M.A. Plate loading tests on geogrid reinforced earth slabs (New Orleans). Proc. Geosynthetics. 1987, 87, 216–225. [Google Scholar]
- Hewlett, W.J.; Randolph, M.F. Analysis of piled embankments. Ground Eng. 1988, 21, 12–18. [Google Scholar]
- Carlsson, B. Reinforced Soil, Principles for Calculation; Terratema, A.B., Ed.; Linköping, Sweden, 1987. [Google Scholar]
- Kempfert, H.G.; Gobel, C.; Alexiew, D.; Heitz, C. German recommendations for the reinforced embankments on pile-similar elements. In Proceedings of the 3rd European Geosynthetics Conference, Munich, Germany, 1–4 March 2004; pp. 279–284. [Google Scholar]
- Van Eekelen, S.J.M.; Bezuijen, A.; Van Tol, A.F. Analysis and modification of the British Standard BS8006 for the design of piled embankments. Geotext. Geomembr. 2011, 29, 345–359. [Google Scholar] [CrossRef]
- BS 8006; Code of Practice for Strengthened/Reinforced Soils and Other Fills. British Standard Institution: London, UK, 2010.
- EBGEO Recommendations for Design and Analysis of Earth Structures Using Geosynthetic Reinforcements; Digital in English; German Geotechnical Society; John Wiley & Sons: London, UK, 2011; ISBN 978-3-433-60093-1.
- Pham, A.T.; Dias, D. Comparison and evaluation of analytical models for the design of geosynthetic-reinforced and pile-supported embankments. Geotext. Geomembr. 2021, 49, 528–549. [Google Scholar] [CrossRef]
- Han, J.; Oztoprak, S.; Parsons, R.L.; Huang, J. Numerical analysis of foundation columns to support widening of embankments. Comput. Geotech. 2007, 34, 435–448. [Google Scholar] [CrossRef]
- Okyay, U.S.; Dias, D. Use of lime and cement treated soils as pile supported load transfer platform. Eng. Geol. 2010, 114, 34–44. [Google Scholar] [CrossRef]
- Liu, S.Y.; Du, Y.J.; Yi, Y.L.; Puppala, A.J. Field investigations on performance of T-shaped deep mixed soil cement column-supported embankments over soft ground. J. Geotech. Geoenviron. Eng. 2012, 138, 718–727. [Google Scholar] [CrossRef]
- Horpibulsuk, S.; Chinkulkijniwat, A.; Cholphatsorn, A.; Suebsuk, J.; Liu, M.D. Consolidation behavior of soil cement column improved ground. Comput. Geotech. 2012, 43, 37–50. [Google Scholar] [CrossRef]
- Voottipruex, P.; Suksawat, T.; Bergado, D.T.; Jamsawang, P. Numerical simulations and parametric study of SDCM and DCM piles under full scale axial and lateral loads. Comput. Geotech. 2011, 38, 318–329. [Google Scholar] [CrossRef]
- Jamsawang, P.; Boathong, P.; Mairaing, W.; Jongpradist, P. Undrained creep failure of a drainage canal slope stabilized with deep cement mixing columns. Landslides 2015, 13, 939–955. [Google Scholar] [CrossRef]
- Jamsawang, P.; Yoobanpot, N.; Thanasisathit, N.; Voottipruex, P.; Jongpradist, P. Three-dimensional numerical analysis of a DCM column-supported highway embankment. Comput. Geotech. 2016, 72, 42–56. [Google Scholar] [CrossRef]
- Cui, X.; Cao, Y.; Jin, Y. Three-Dimensional Analysis of Load Transfer Mechanism for Deep Cement Mixing Piled Embankment under Static and Cyclic Load. Sustainability 2023, 15, 6532. [Google Scholar] [CrossRef]
- Bergado, D.T.; Singh, N.; Sim, S.H.; Panichayatum, B.; Sampaco, C.L.; Balasubramaniam, A.S. Improvement of soft Bangkok clay using vertical geotextile band drains compared with granular piles. Geotext. Geomembr. 1990, 9, 203–231. [Google Scholar] [CrossRef]
- Katti, R.K.; Katti, A.R.; Naik, S. Monograph to Analysis of Stone Columns with and without Geosynthetic Encasement; CBIP Publication: New Delhi, India, 1993. [Google Scholar]
- Raithel, M.; Kempfert, H.G. Calculation models for dam foundations with geotextile coated sand columns. In Proceedings of the International Conference on Geotechnical & Geological Engineering, GeoEngg—2000, Melbourne, Australia, 19–24 November 2000. [Google Scholar]
- Raithel, M.; Kempfert, H.G.; Kirchner, A. Geotextile-encased columns (GEC) for foundation of a dike on very soft soils. In Proceedings of the Seventh International Conference on Geosynthetics, Nice, France, 22–27 September 2002; pp. 1025–1028. [Google Scholar]
- Malarvizhi, S.N.; Ilamparuthi, K. Load versus settlement of clay bed stabilized with stone and reinforced stone columns. In Proceedings of the GeoAsia–2004, Seoul, Republic of Korea, 21–23 June 2004; pp. 322–329. [Google Scholar]
- Ayadat, T.; Hanna, A.M. Encapsulated stone columns as a soil improvement technique for collapsible soil. Ground Improv. 2005, 9, 137–147. [Google Scholar] [CrossRef]
- Murugesan, S.; Karpurapu, R. Geosynthetic-encased stone columns: Numerical evaluation. Geotext. Geomembr. 2006, 24, 349–358. [Google Scholar] [CrossRef]
- Yoo, C. Performance of Geosynthetic-Encased Stone Columns in Embankment Construction: Numerical Investigation. J. Geotech. Geoenviron. Eng. 2010, 136, 1148–1160. [Google Scholar] [CrossRef]
- Keykhosropour, L.; Soroush, A.; Imam, R. 3D numerical analyses of geosynthetic encased stone columns. Geotext. Geomembr. 2012, 35, 61–68. [Google Scholar] [CrossRef]
- PLAXIS. PLAXIS 2D-Reference Manual. Bentley. 2020. Available online: https://communities.bentley.com/cfs-file/__key/communityserver-wikis-components-files/00-00-00-05-58/3113.PLAXIS2DCE_2D00_V20.02_2D00_2_2D00_Reference.pdf (accessed on 20 September 2023).
- Villard, P.; Huckert, A.; Briançon, L. Load transfer mechanisms in geotextile-reinforced embankments overlying voids: Numerical approach and design. Geotext. Geomembr. 2016, 44, 381–395. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).