Empirical Equations Expressing the Effects of Measured Suction on the Compaction Curve for Sandy Soils Varying Fines Content
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Setup
2.2.1. Suction Measurement Using Membrane Filter Method in Pressure Plate Apparatus (SWCC)
2.2.2. Suction Measurement Using Membrane Filter Method in Triaxial Apparatus
- (a)
- Sample preparation
- (b)
- Measurement procedure
3. Experimental Results and Discussion
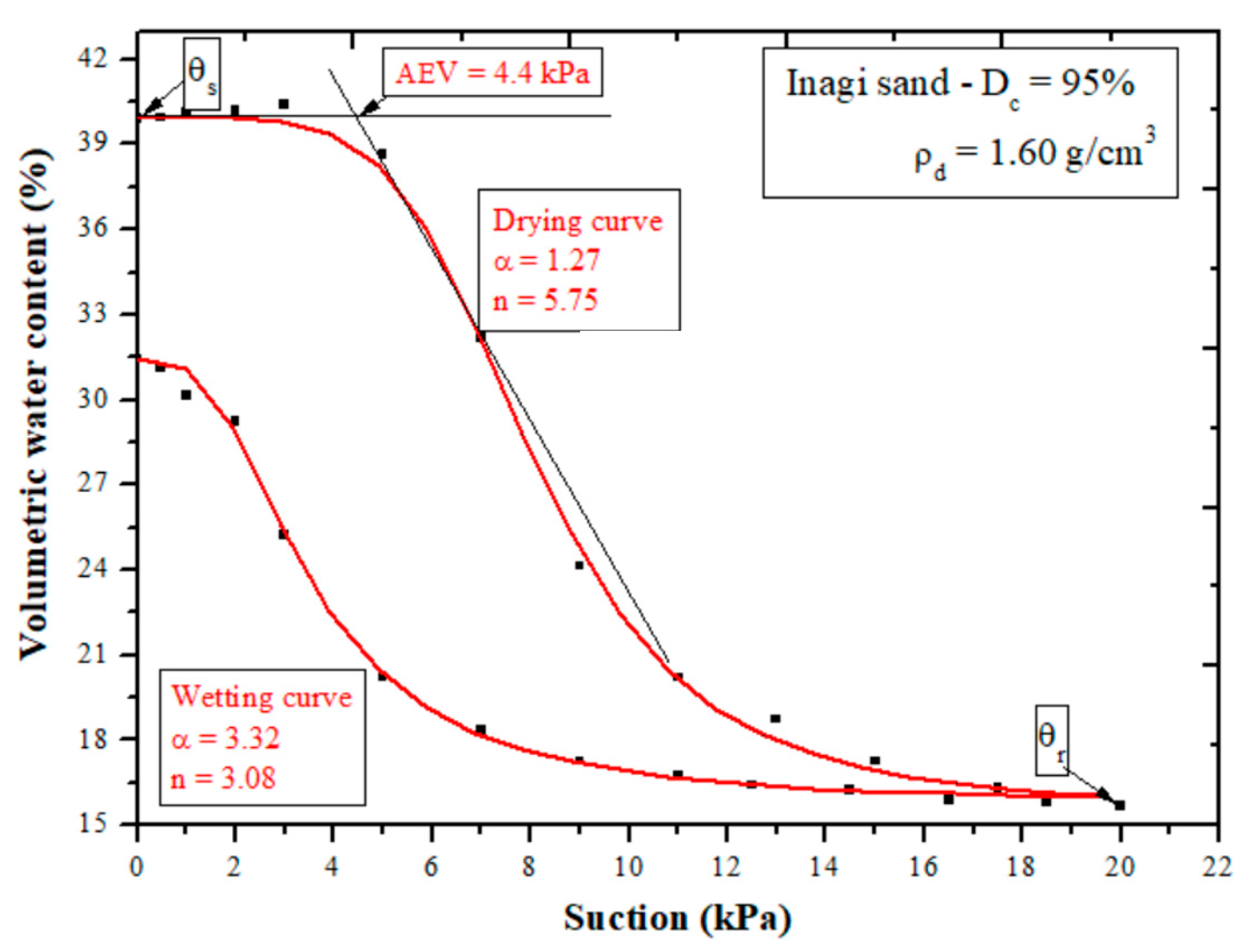
3.1. Measurement of Suction Using Pressure Plate Apparatus
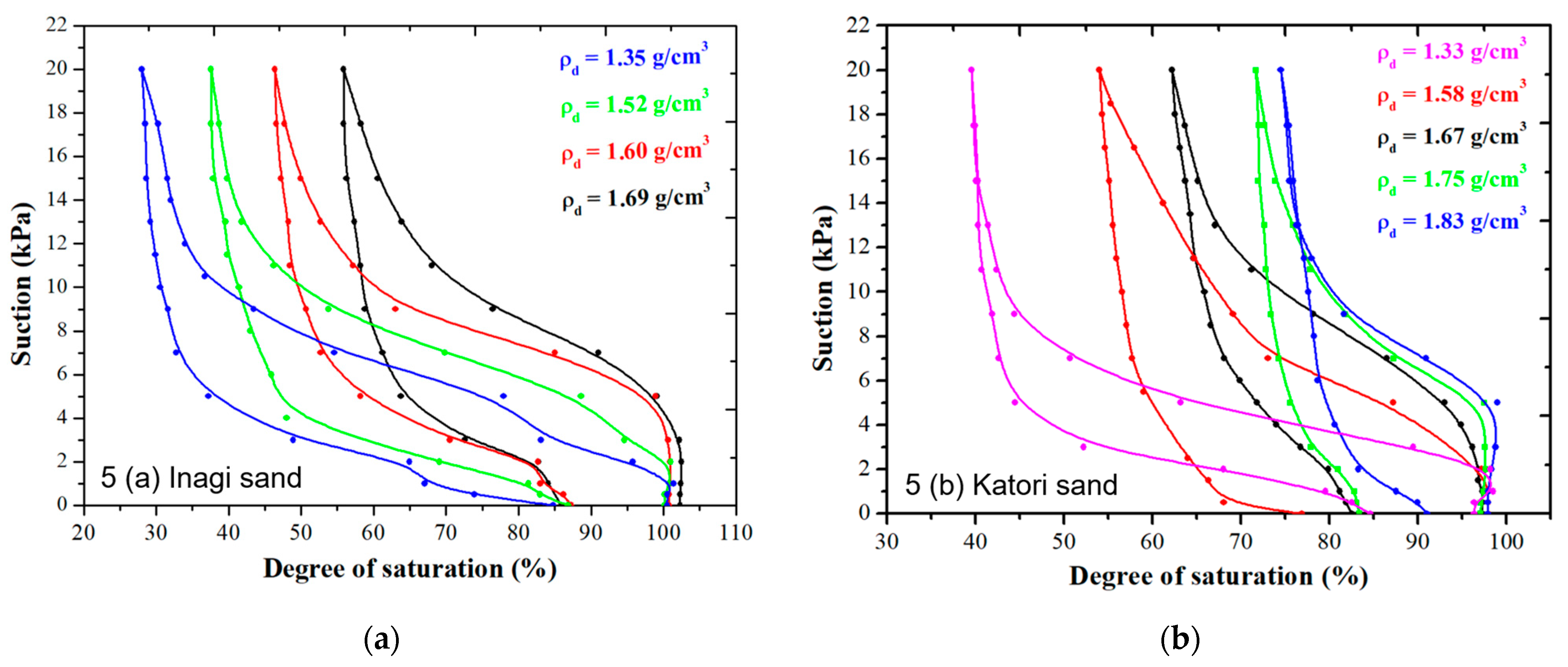
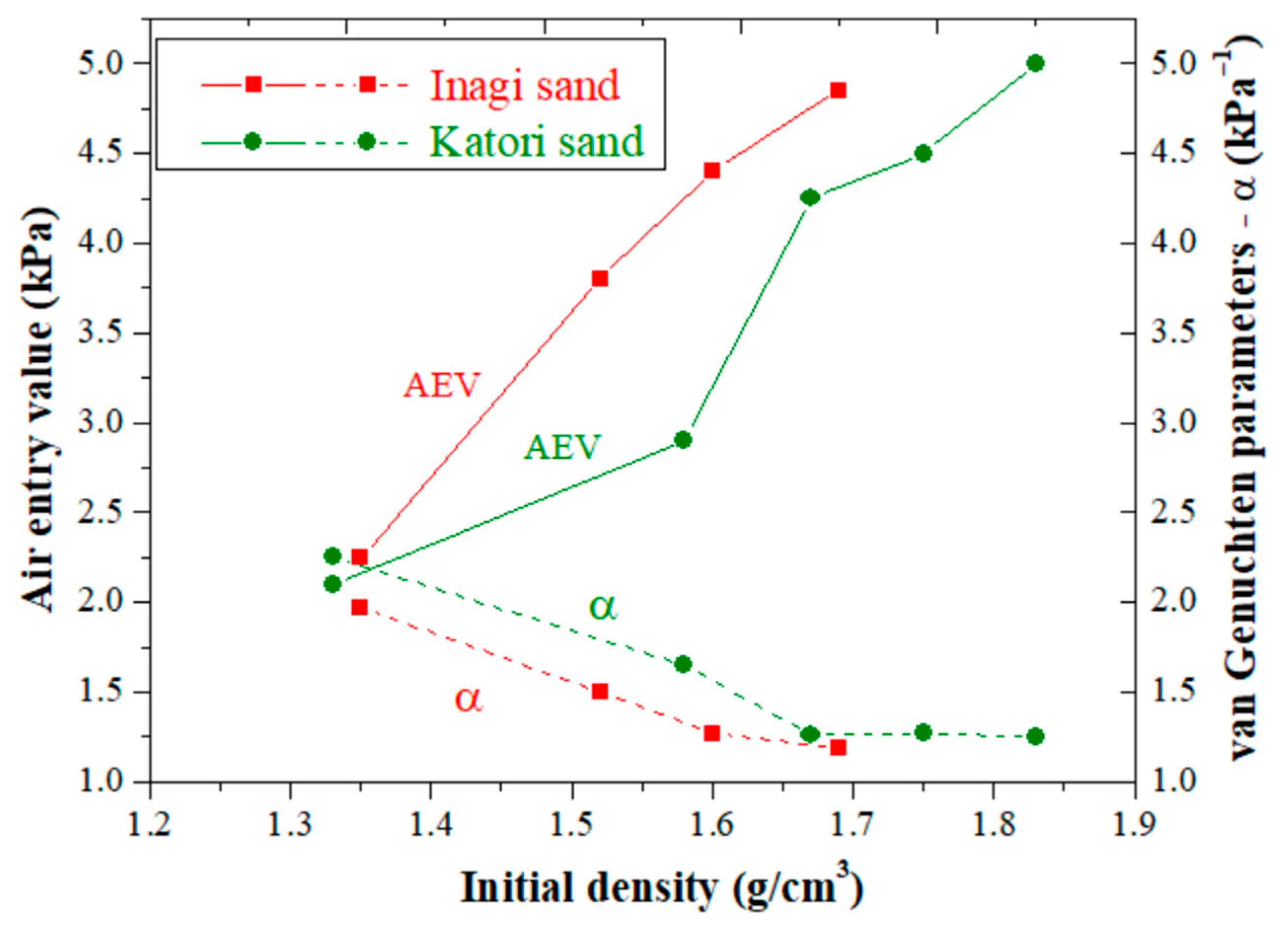
3.1.1. Effect of Initial Density of Sandy Soils on SWCC
3.1.2. Effect of Fines Content on SWCC
3.2. Measurement of Suction Using Triaxial Apparatus
4. Discussion
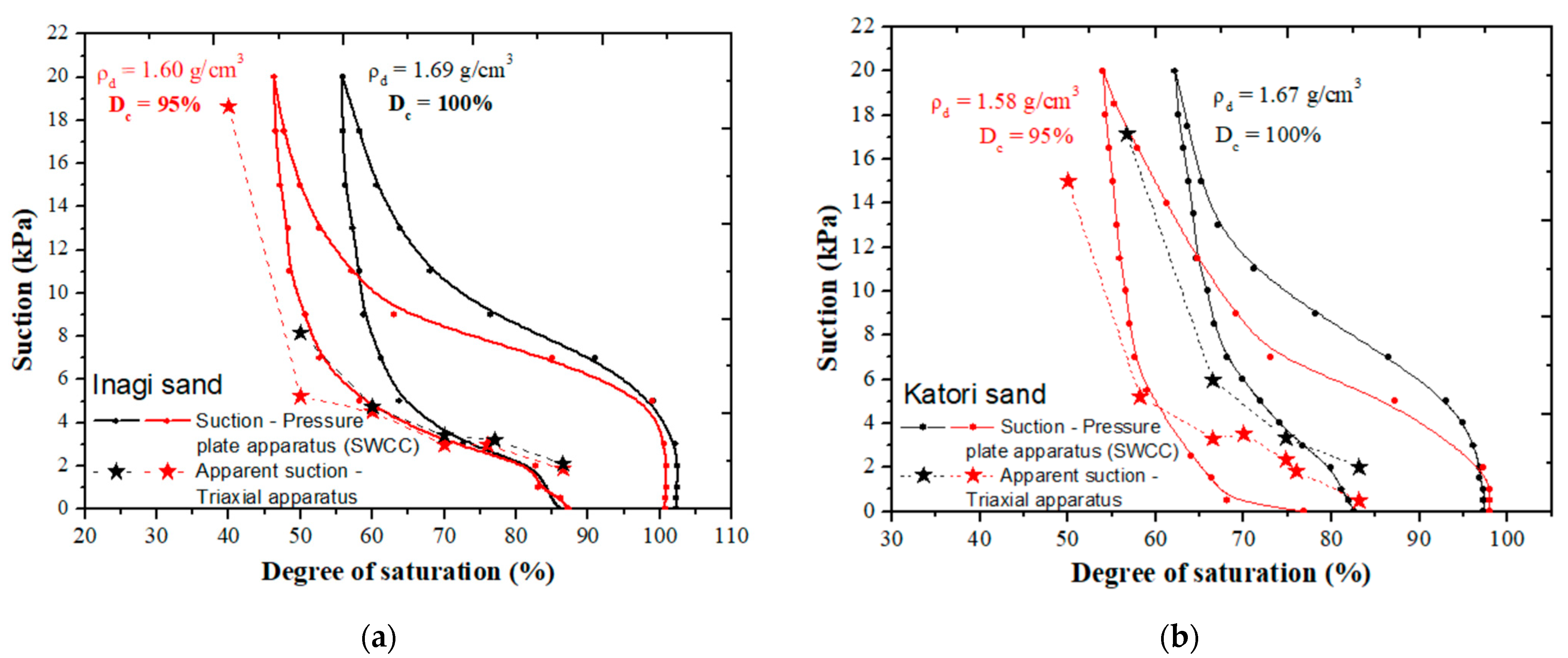
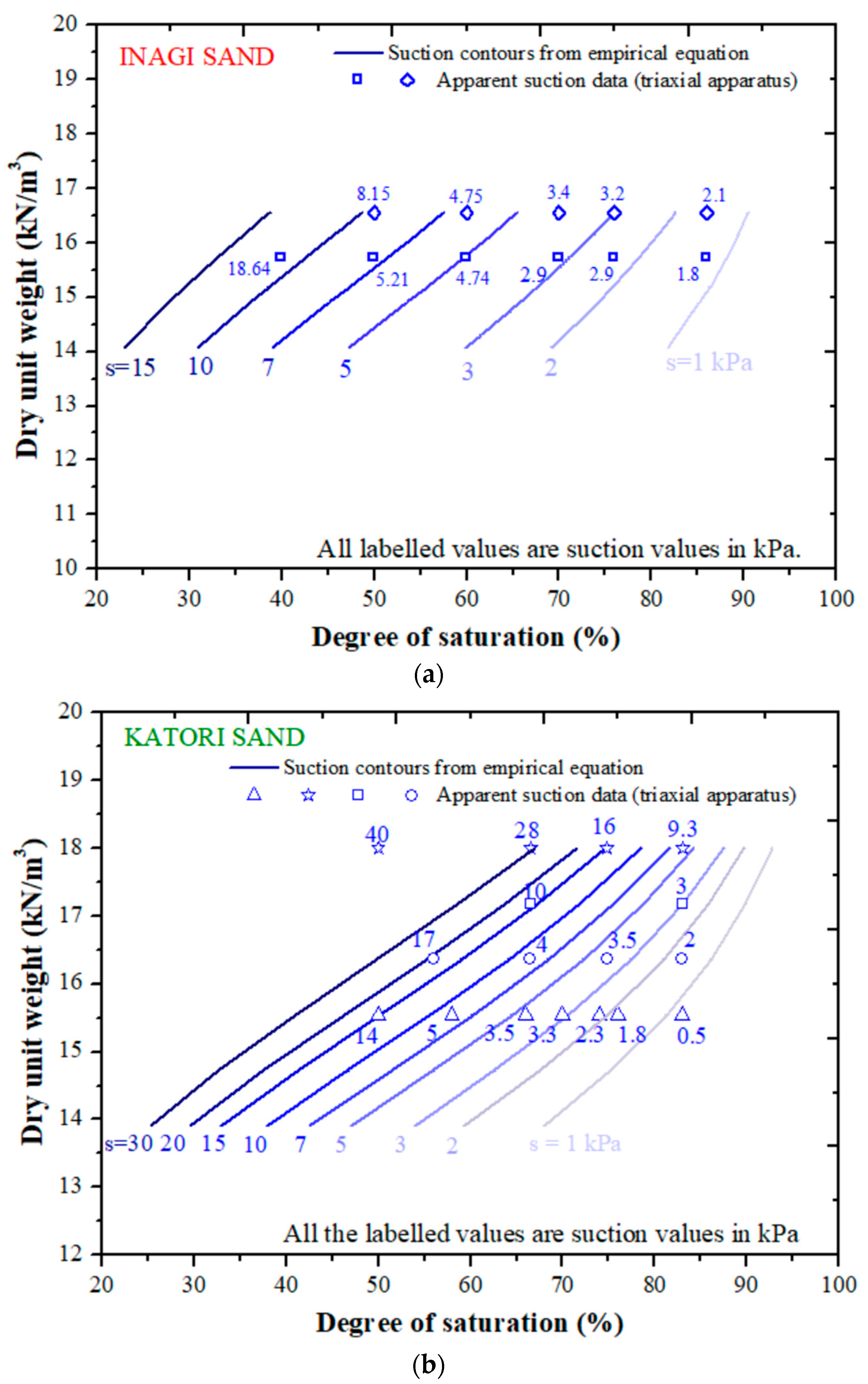
4.1. Comparison of Measured Suction from Triaxial Apparatus and SWCC
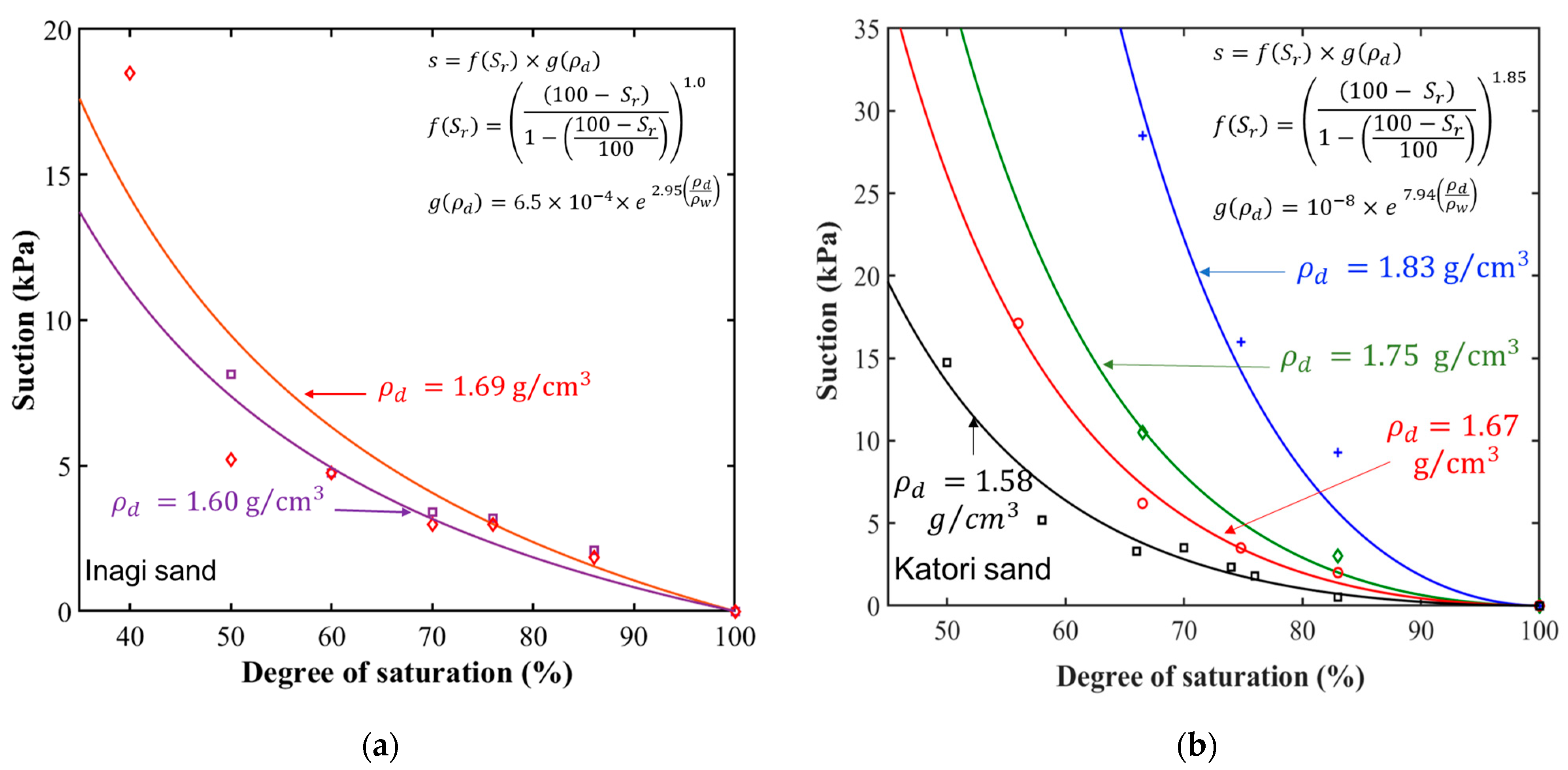
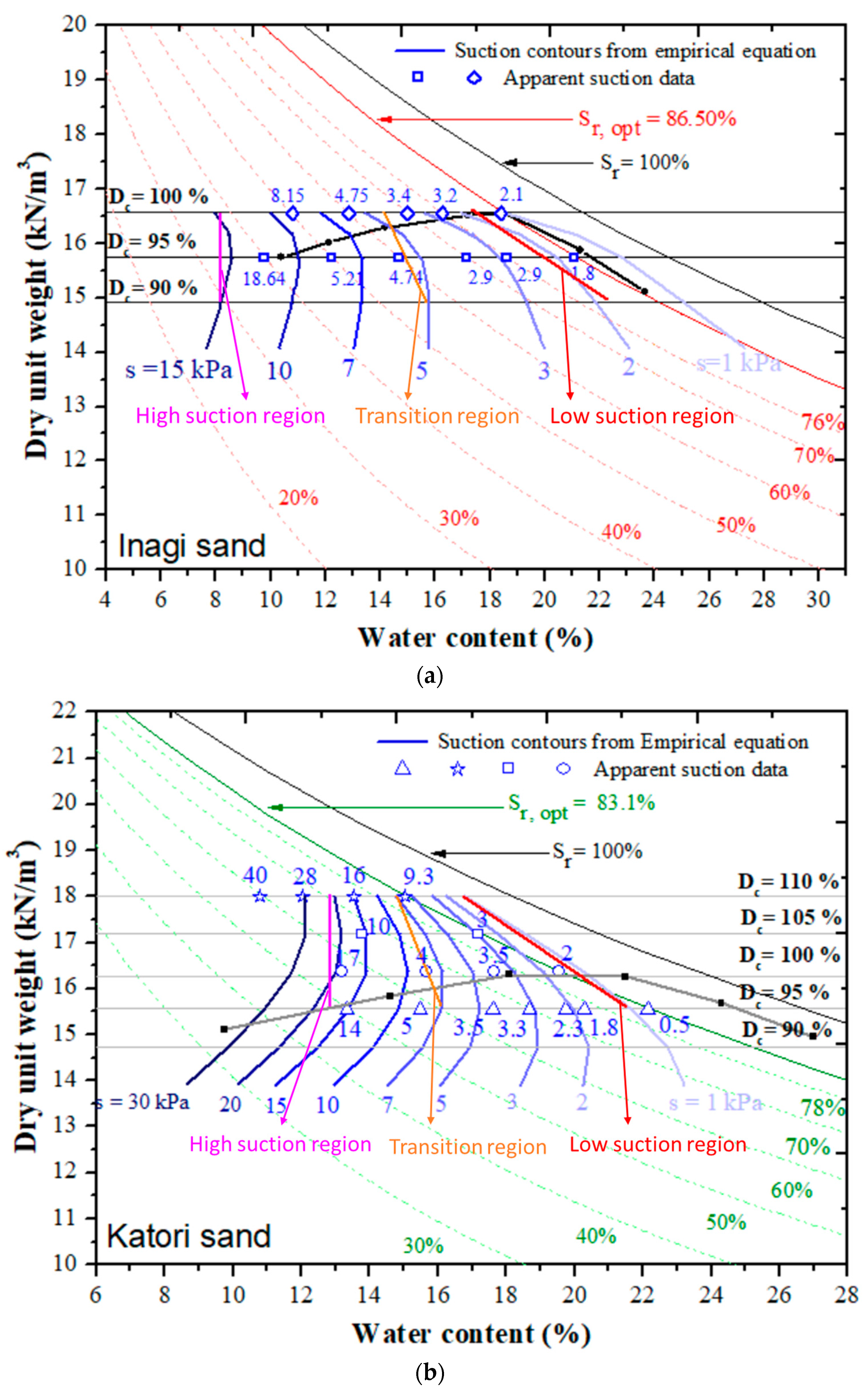
4.2. Empirical Relationship Derived to Obtain Suction Contours on Compaction Curve
4.3. Variation of Suction Contours along the Compaction Curve
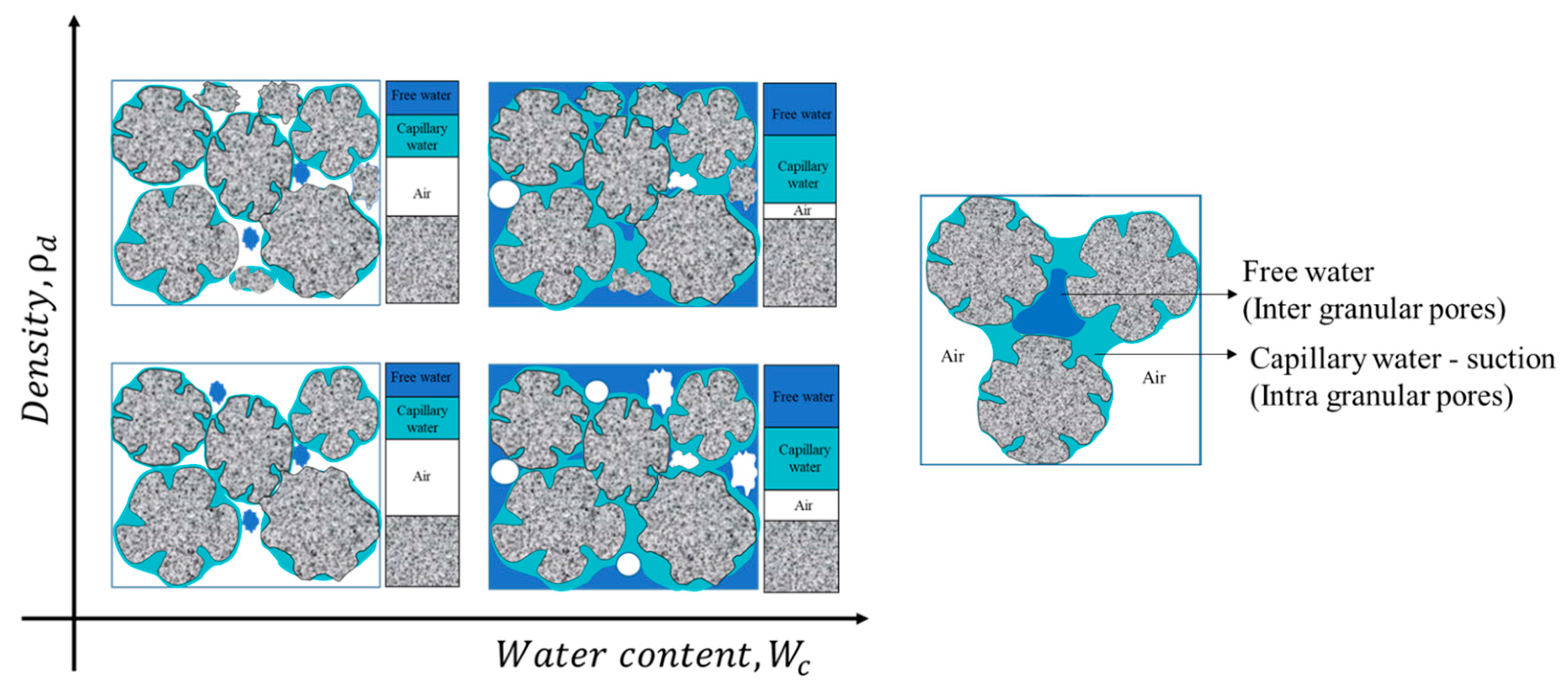
4.3.1. Effect of Density on Suction at Same Degree of Saturation
4.3.2. Effect of Density on Suction at Same Water Content
4.3.3. Effect of Suction on Compaction Energy Level
5. Conclusions
- The measurement of suction using the membrane filter method with a triaxial apparatus (apparent suction) is an efficient and reliable technique that replicates field conditions.
- With an increase in the initial density at the same degree of saturation, the suction value increases as the pore size and number of pores increases. Therefore, the air entry value increases with the increase in the initial dry density.
- Comparison of apparent suction with the imposed suction from the soil-water characteristic curve (SWCC) reveals that apparent suction closely follows the wetting curve of the SWCC. This suggests that the suction during field compaction is more closely related to the imposed suction from the minimum hysteresis range of the SWCC, which is the wetting curve.
- At high water contents, the suction decreases with increasing density, indicating that the compression of intergranular pores and an increase in capillary water in micropores dominate the changes in suction. However, at low water contents, the suction contours show minimal changes with increasing density, suggesting that the compression of air-filled pores and retention of capillary water in micropores remain relatively constant.
- At the same compaction energy level (CEL), the suction in compacted soil tends to increase as the water content decreases ( < ), which in turn makes compaction more difficult in the field. Additionally, it is crucial to note that at higher compaction efforts, even slight changes in the degree of saturation can lead to significant variations in apparent suction. This highlights the need for precise control of the degree of saturation during compaction at higher efforts to achieve the desired characteristics of the compacted soil.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tatsuoka, F.; Fujishiro, K.; Tateyama, K.; Kawabe, S.; Kikuchi, Y. Properties of Compacted Soil as a Function of Dry Density and the Degree of Saturation. In Proceedings of the 15th Asian Regional Conference on Soil Mechanics and Geotechnical Engineering (15 ARC), Fukuoka, Japan, 9–13 November 2015; pp. 247–252. [Google Scholar] [CrossRef]
- Tatsuoka, F.; Gomes Correia, A. Importance of Controlling the Degree of Saturation in Soil Compaction Linked to Soil Structure Design. Transp. Geotech. 2018, 17, 3–23. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Al-Mahbashi, A.M.; Al-Shamrani, M.A.; Moghal, A.A.B. Soil–Water Characteristic Curve and One-Dimensional Deformation Characteristics of Fiber-Reinforced Lime-Blended Expansive Soil. J. Mater. Civ. Eng. 2020, 32, 1–9. [Google Scholar] [CrossRef]
- Deng, D.; Wen, S.; Lu, K.; Li, L. Calculation Model for the Shear Strength of Unsaturated Soil under Nonlinear Strength Theory. Geomech. Eng. 2020, 21, 247. [Google Scholar]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Dai, G. Estimation of Tensile Strength of Sandy Soil from Soil–Water Characteristic Curve. Acta Geotech. 2020, 15, 3371–3381. [Google Scholar] [CrossRef]
- Cui, Y.J.; Delage, P. Yielding and Plastic Behaviour of an Unsaturated Compacted Silt. Geotechnique 1996, 46, 291–311. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Vanapalli, S.K. Shear Strength of Unsaturated Soils. Methods Soil Anal. Part 4 Phys. Methods 2018, 321, 329–361. [Google Scholar] [CrossRef]
- Hilf, J.W. An Investigation of Pore-Water Pressure in Compacted Cohesive Soils; University of Colorado at Boulder: Boulder, CO, USA, 1956. [Google Scholar]
- Vanapalli, S.K.; Nicotera, M.V.; Sharma, R.S. Axis Translation and Negative Water Column Techniques for Suction Control. Geotech. Geol. Eng. 2008, 26, 645–660. [Google Scholar] [CrossRef]
- Hedayati, M.; Hossain, M.S.; Mehdibeigi, A.; Thian, B. Real-Time Modeling of Moisture Distribution in Subgrade Soils. In Proceedings of the Geo-Congress 2014: Geo-Characterization and Modeling for Sustainability, Atlanta, GA, USA, 23–26 February 2014; pp. 3015–3024. [Google Scholar]
- Sun, D.; Sheng, D.; Xu, Y. Collapse Behaviour of Unsaturated Compacted Soil with Different Initial Densities. Can. Geotech. J. 2007, 44, 673–686. [Google Scholar] [CrossRef]
- Romero, E.; Gens, A.; Lloret, A. Water Permeability, Water Retention and Microstructure of Unsaturated Compacted Boom Clay. Eng. Geol. 1999, 54, 117–127. [Google Scholar] [CrossRef]
- Birle, E.; Heyer, D.; Vogt, N. Influence of the Initial Water Content and Dry Density on the Soil–Water Retention Curve and the Shrinkage Behavior of a Compacted Clay. Acta Geotech. 2008, 3, 191–200. [Google Scholar] [CrossRef]
- Salager, S.; Nuth, M.; Ferrari, A.; Laloui, L. Investigation into Water Retention Behaviour of Deformable Soils. Can. Geotech. J. 2013, 50, 200–208. [Google Scholar] [CrossRef]
- Lourenço, S.; Gallipoli, D.; Toll, D.; Evans, F.; Medero, G. Determination of the Soil Water Retention Curve with Tensiometers. In Experimental Unsaturated Soil Mechanics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 95–102. [Google Scholar]
- Murray, E.J.; Sivakumar, V. Unsaturated Soils: A Fundamental Interpretation of Soil Behaviour; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Toll, D.G.; Lourenço, S.D.N.; Mendes, J. Advances in Suction Measurements Using High Suction Tensiometers. Eng. Geol. 2012, 165, 29–37. [Google Scholar] [CrossRef]
- Nishimura. Earthquake-Induced Landslides. In Proceedings of the International Symposium on Earthquake-Induced Landslides, Kiryu, Japan, 7–9 November 2013. [Google Scholar] [CrossRef]
- Wang, H.; Koseki, J.; Nishimura, T.; Miyashita, Y. Membrane Filter Properties and Application of the Filter to Undrained Cyclic Triaxial Test of Unsaturated Materials. Can. Geotech. J. 2017, 54, 1196–1202. [Google Scholar] [CrossRef]
- Rs, L. Preparing Test Specimens Using Undercompaction. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 50. [Google Scholar] [CrossRef]
- Ishikawa, T.; Zhang, Y.; Tokoro, T.; Miura, S. Medium-Size Triaxial Apparatus for Unsaturated Granular Subbase Course Materials. Soils Found. 2014, 54, 67–80. [Google Scholar] [CrossRef]
- Wang, H.; Koseki, J.; Sato, T.; Chiaro, G.; Tan Tian, J. Effect of Saturation on Liquefaction Resistance of Iron Ore Fines and Two Sandy Soils. Soils Found. 2016, 56, 732–744. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A New Model for Predicting the Hydraulic Conductivity of Unsaturated Porous Media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Aitchison, G.D. Relationships of Moisture Stress and Effective Stress Functions in Unsaturated Soils. In Golden Jubilee of the International Society for Soil Mechanics and Foundation Engineering: Commemorative Volume; Institution of Engineers: Barton, ACT, Australia, 1985; pp. 20–25. [Google Scholar]
- Gallage, C.P.K.; Uchimura, T. Effects of Dry Density and Grain Size Distribution on Soil-Water Characteristic Curves of Sandy Soils. Soils Found. 2010, 50, 161–172. [Google Scholar] [CrossRef]
- Kimoto, S.; Oka, F.; Fukutani, J.; Yabuki, T.; Nakashima, K. Monotonic and Cyclic Behavior of Unsaturated Sandy Soil under Drained and Fully Undrained Conditions. Soils Found. 2011, 51, 663–681. [Google Scholar] [CrossRef]
- Kawai, K.; Karube, D.; Ashida, W.; Kado, Y. Modeling of Water Retention Curves with Effects of Void Ratio. Doboku Gakkai Ronbunshu 2000, 2000, 291–302. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Wu, L.; Wei, Y. Influence of Fine Content on the Soil–Water Characteristic Curve of Unsaturated Soils. Geotech. Geol. Eng. 2020, 38, 1371–1378. [Google Scholar] [CrossRef]
- Gu, C.; Zhan, Y.; Wang, J.; Cai, Y.; Cao, Z.; Zhang, Q. Resilient and Permanent Deformation of Unsaturated Unbound Granular Materials under Cyclic Loading by the Large-Scale Triaxial Tests. Acta Geotech. 2020, 15, 3343–3356. [Google Scholar] [CrossRef]
- Zheng, F.; Shao, S.; Wang, J.; Shao, S. Experimental Study on the Mechanical Behaviour of Natural Loess Based on Suction-Controlled True Triaxial Tests. KSCE J. Civ. Eng. 2020, 24, 2304–2321. [Google Scholar] [CrossRef]
- Nam, S.; Gutierrez, M.; Diplas, P.; Petrie, J. Determination of the Shear Strength of Unsaturated Soils Using the Multistage Direct Shear Test. Eng. Geol. 2011, 122, 272–280. [Google Scholar] [CrossRef]
- Tatsuoka, F.; Hashimoto, T.; Tateyama, K. Soil Stiffness as a Function of Dry Density and the Degree of Saturation for Compaction Control. Soils Found. 2021, 61, 989–1002. [Google Scholar] [CrossRef]
- Delage, P. Experimental Unsaturated Soil Mechanics. Vadose Zo. J. 2008, 9, 196. [Google Scholar] [CrossRef][Green Version]
- Wang, H.; Koseki, J.; Nishimura, T. Water Retention Characteristics of Iron Ore Fines. Can. Geotech. J. 2020, 57, 1427–1437. [Google Scholar] [CrossRef]
- Lloret, A.; Villar, M.V.; Sànchez, M.; Gens, A.; Pintado, X.; Alonso, E.E. Mechanical Behaviour of Heavily Compacted Bentonite under High Suction Changes. Geotechnique 2003, 53, 27–40. [Google Scholar] [CrossRef]
- Bradbury, M.H.; Baeyens, B. Nuclear Energy and Safety Research Department Porewater Chemistry in Compacted Re-Saturated MX-80 Bentonite: Physico-Chemical Characterisation and Geochemical Modelling Porewater Chemistry in Compacted Re-Saturated MX-80 Bentonite: Physico-Chemical Char; PSI Bericht 02-10; Paul Scherrer Institut: Villigen, Switzerland, 2002. [Google Scholar]
- Jacinto, A.C.; Villar, M.V.; Ledesma, A. Influence of Water Density on the Water-Retention Curve of Expansive Clays. Geotechnique 2012, 62, 657–667. [Google Scholar] [CrossRef]
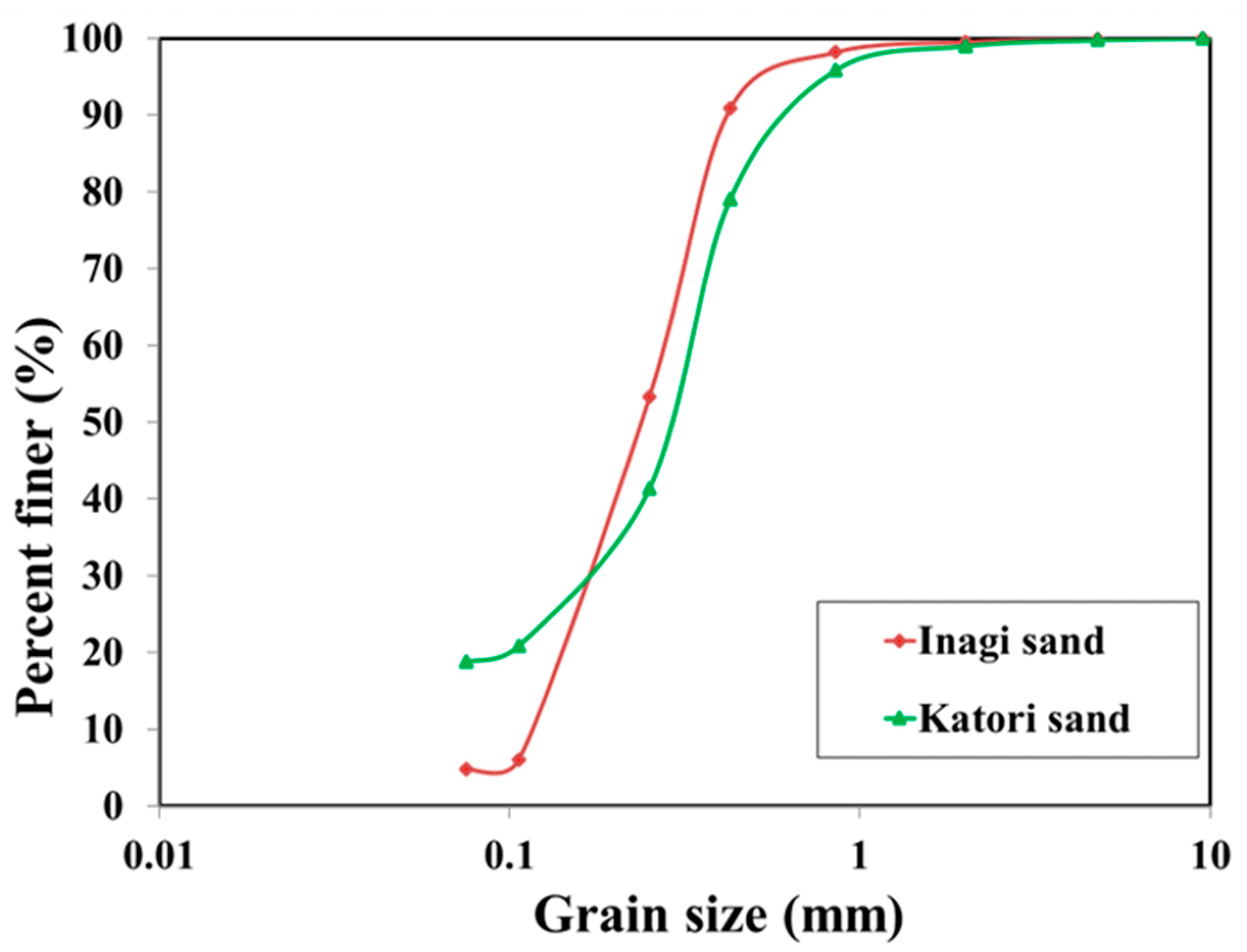
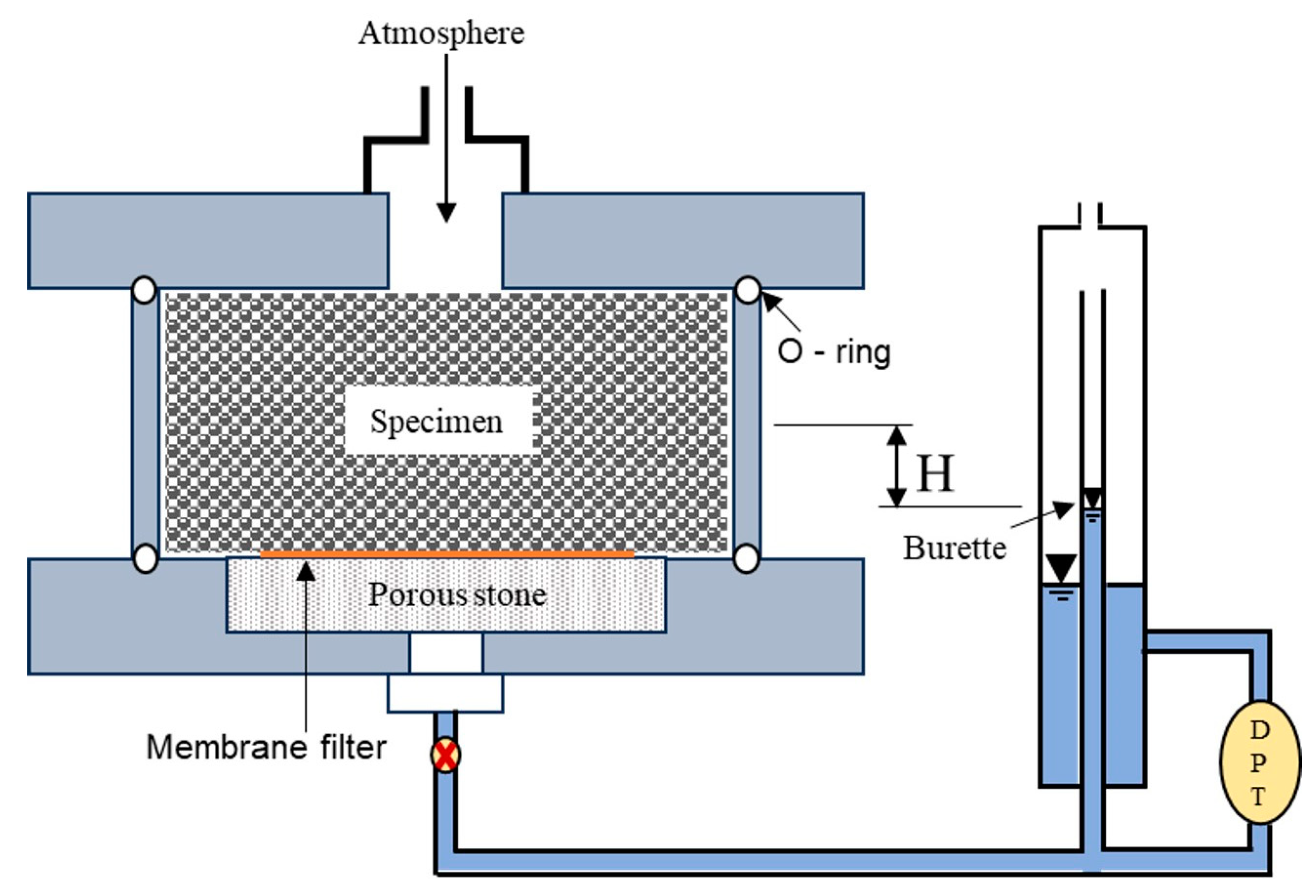
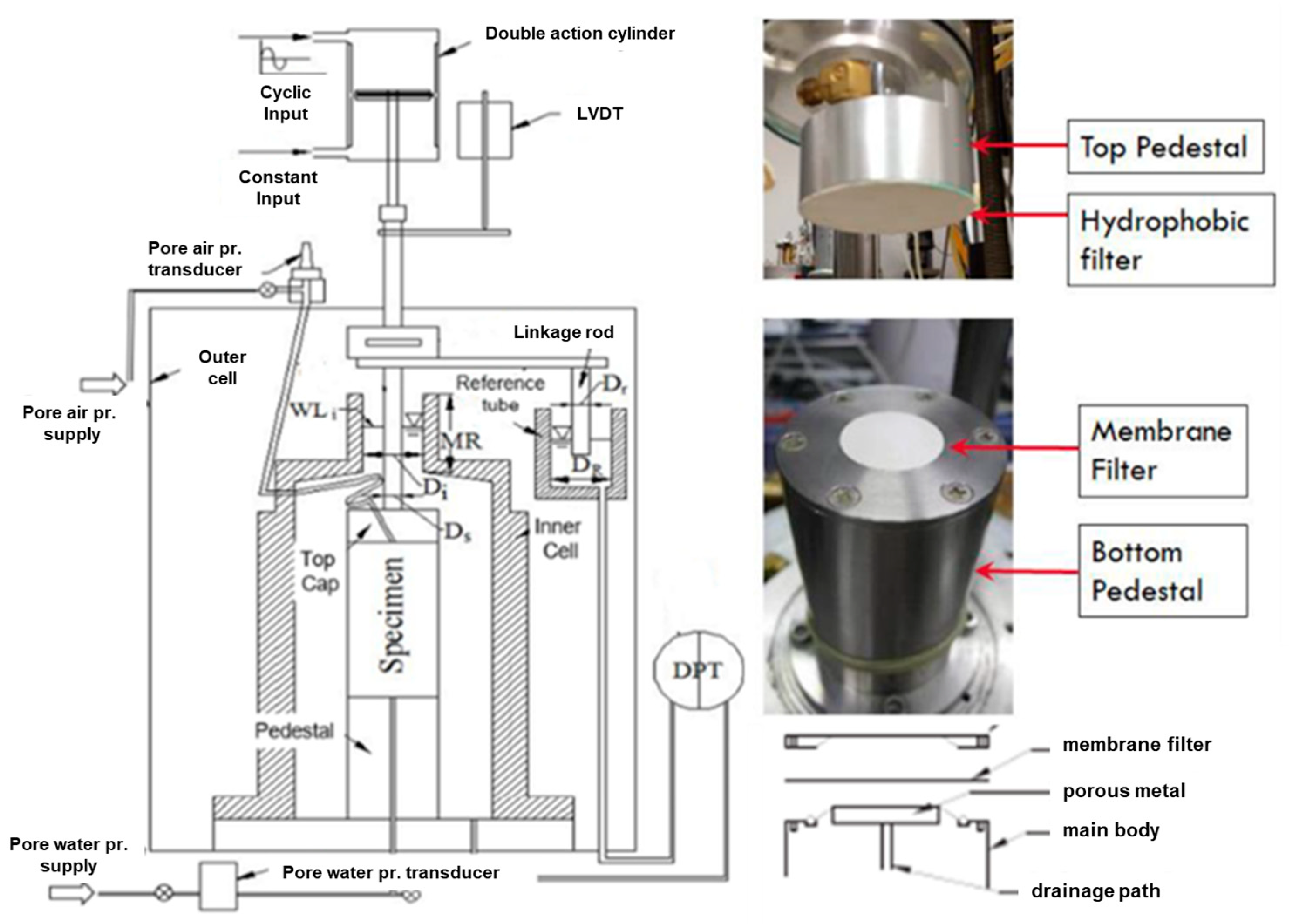


| Material | Inagi Sand | Katori Sand |
|---|---|---|
| Fines Content () | 4.75 | 18.80 |
| Specific Gravity, | 2.645 | 2.754 |
| (g/cm3) | 1.69 | 1.67 |
| (mm) | 0.12 | 0.07 |
| (mm) | 0.18 | 0.17 |
| (mm) | 0.28 | 0.33 |
| 0.96 | 1.14 | |
| ′ | 2.38 | 4.48 |
| () | 18.5 | 19.6 |
| () | 86.5 | 83.1 |
| Test Material | Fines Content | Specific Gravity | Void Ratio | Dry Density | Degree of Compaction | Van Genuchten Parameters [24] | Saturated Water Content | Residual Water Content | Air Entry Value | |
|---|---|---|---|---|---|---|---|---|---|---|
| (%) | (g/cm3) | (%) | (%) | (%) | AEV | |||||
| Inagi sand | 4.75 | 2.64 | 1.010 | 1.35 | 80 | 1.97 | 3.47 | 0.49 | 0.13 | 2.25 |
| 0.74 | 1.52 | 90 | 1.5 | 4.66 | 0.42 | 0.15 | 3.8 | |||
| 0.649 | 1.60 | 95 | 1.27 | 5.75 | 0.39 | 0.18 | 4.4 | |||
| 0.566 | 1.69 | 100 | 1.19 | 4.93 | 0.37 | 0.20 | 4.85 | |||
| Katori sand—F18 | 18.8 | 2.75 | 1.061 | 1.33 | 80 | 2.25 | 4.46 | 0.49 | 0.20 | 2.1 |
| 0.735 | 1.58 | 95 | 1.65 | 3.38 | 0.41 | 0.22 | 2.9 | |||
| 0.649 | 1.67 | 100 | 1.26 | 4.53 | 0.38 | 0.24 | 4.25 | |||
| 0.57 | 1.75 | 105 | 1.27 | 4.8 | 0.36 | 0.27 | 4.5 | |||
| 0.49 | 1.83 | 110 | 1.25 | 6.65 | 0.31 | 0.24 | 5 | |||
| Test Material | Fines Content | Specific Gravity | Void Ratio | Dry Density | Degree of Compaction | Degree of Saturation | Apparent Suction |
|---|---|---|---|---|---|---|---|
| (%) | (g/cm3) | (%) | (%) | (kPa) | |||
| Inagi sand | 4.75 | 2.64 | 0.649 | 1.60 | 95 | 40 | 18.64 |
| 0.649 | 1.60 | 95 | 50 | 5.21 | |||
| 0.649 | 1.60 | 95 | 60 | 4.74 | |||
| 0.649 | 1.60 | 95 | 70 | 2.99 | |||
| 0.649 | 1.60 | 95 | 76 | 2.98 | |||
| 0.649 | 1.60 | 95 | 86 | 1.85 | |||
| 0.566 | 1.69 | 100 | 50 | 8.15 | |||
| 0.566 | 1.69 | 100 | 60 | 4.75 | |||
| 0.566 | 1.69 | 100 | 70 | 3.4 | |||
| 0.566 | 1.69 | 100 | 76 | 3.2 | |||
| 0.566 | 1.69 | 100 | 86 | 2.1 | |||
| Katori sand—F18 | 18.8 | 2.75 | 0.735 | 1.58 | 95 | 83 | 0.5 |
| 0.735 | 1.58 | 95 | 76 | 1.8 | |||
| 0.735 | 1.58 | 95 | 74 | 2.34 | |||
| 0.735 | 1.58 | 95 | 70 | 3.5 | |||
| 0.735 | 1.58 | 95 | 66 | 3.3 | |||
| 0.735 | 1.58 | 95 | 58 | 5.2 | |||
| 0.735 | 1.58 | 95 | 50 | 14.75 | |||
| 0.649 | 1.67 | 100 | 83 | 2.0 | |||
| 0.649 | 1.67 | 100 | 74.8 | 3.5 | |||
| 0.649 | 1.67 | 100 | 66.5 | 6.2 | |||
| 0.649 | 1.67 | 100 | 56 | 17.12 | |||
| 0.57 | 1.75 | 105 | 83 | 3.0 | |||
| 0.57 | 1.75 | 105 | 66.5 | 10.5 | |||
| 0.49 | 1.83 | 110 | 83 | 9.3 | |||
| 0.49 | 1.83 | 110 | 74.8 | 16 | |||
| 0.49 | 1.83 | 110 | 66.5 | 28.5 | |||
| 0.49 | 1.83 | 110 | 58 | 43.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chowdepalli, B.; Watanabe, K. Empirical Equations Expressing the Effects of Measured Suction on the Compaction Curve for Sandy Soils Varying Fines Content. Geotechnics 2023, 3, 760-780. https://doi.org/10.3390/geotechnics3030042
Chowdepalli B, Watanabe K. Empirical Equations Expressing the Effects of Measured Suction on the Compaction Curve for Sandy Soils Varying Fines Content. Geotechnics. 2023; 3(3):760-780. https://doi.org/10.3390/geotechnics3030042
Chicago/Turabian StyleChowdepalli, Bhargavi, and Kenji Watanabe. 2023. "Empirical Equations Expressing the Effects of Measured Suction on the Compaction Curve for Sandy Soils Varying Fines Content" Geotechnics 3, no. 3: 760-780. https://doi.org/10.3390/geotechnics3030042
APA StyleChowdepalli, B., & Watanabe, K. (2023). Empirical Equations Expressing the Effects of Measured Suction on the Compaction Curve for Sandy Soils Varying Fines Content. Geotechnics, 3(3), 760-780. https://doi.org/10.3390/geotechnics3030042






