Abstract
This paper describes the relationship between bedrock depth (D) and site fundamental frequency (f0) in the Nakdonggang delta region in the southeastern part of the Korean peninsula. We collected borehole logs to confirm the thickness of the sediments and estimated the f0 at over 200 locations across the delta using the horizontal-to-vertical spectral ratio (HVSR) method. We developed an f0 map of the study area by spatially interpolating the f0 values using the Ordinary Kriging method. The bedrock depth in the main delta showed a power-law dependence on the f0. The derived f0–D model predicted much shallower bedrock depths compared with similar studies from other parts of the world. This was attributed to the fact that the Nakdonggang delta region is composed of relatively low Vs Holocene sediments. With an f0 map, the derived model could enable a quick estimation of the bedrock depth, which could help to determine the site class in the Nakdonggang delta region according to the Korean Seismic Design Standard (KDS 17 10 00).
1. Introduction
Ground motions can be amplified and lengthened due to the constructive interference and trapping of waves in sedimentary layers []. This phenomenon, known as site amplification effects, has been demonstrated by numerous case studies of historical earthquakes. Following the 1985 Mw 8.0 Mexico City earthquake, seismic stations installed on sedimentary sites recorded ground motions significantly larger than those installed on rocky sites []. Seed et al. [] suggested that, during the Loma Prieta earthquake (Mw 6.9, 1989), the damage was concentrated in the San Francisco Bay area due to the site amplification effect in the deep sedimentary layers consisting of marine deposits. During the Kocaeli Earthquake (Mw 7.4, 1999), many buildings collapsed in Avcilar, which is located around 150 km away from the epicenter. Karagoz et al. [] observed that the peak ground acceleration (PGA) was amplified by the deep sedimentary layer to four to five times larger than that of other stations installed on rock sites.
Observations from historical earthquakes have demonstrated that characterizing site amplification effects plays an important role in predicting the intensity of ground motions and that the design ground motions must account for the site effects. Ground motion amplification can be accounted for by either applying the correction factors specified in the seismic design codes or performing ground response analyses. Although code-based correction methods are generally more conservative, they are much more widely applied due to their simplicity in comparison with site-specific ground response analyses, which require a detailed characterization of the site’s dynamic properties and knowledge on the dynamic site response analysis [].
In the Korean Seismic Design Standard [], sites are classified based on the bedrock depth (D) and the average shear wave velocity of the soil layer (Vs, soil), as shown in Table 1. Different amplification factors are then applied to the design response spectrum according to the site classification. For example, the site class S1, corresponding to the rock site, only considers the amplification of the short-period ground motion. However, other classes consider the amplification of the long-period ground motion in the design response spectrum. Therefore, it is necessary to determine the bedrock depth and average shear wave velocity of each site to account for the site amplification effect according to the KDS 17 10 00 [].

Table 1.
Site classification criteria in KDS 17 10 00 [].
The D and Vs, soil for each site can be determined directly by performing a geotechnical investigation (i.e., drilling boreholes) and geophysical exploration. However, direct measurements are costly and time-consuming. The D and Vs, soil can also be determined from a pre-existing geotechnical investigation database, if a boring log exists near the target site. However, in the database, boring logs with stratigraphic data that reach the depth of the bedrock are scarce where it is deep, and the amount of geophysical data to confirm the Vs, soil are also insufficient. Therefore, it is necessary to develop an alternative approach that will enable a more convenient way of determining the site class.
For a uniform homogeneous soil layer, the relationship between the shear wave velocity (Vs), the thickness of the soil layer above the bedrock (D), and the natural frequency of the ground (f0) can be expressed by the following equation []:
which shows that f0, D, and Vs are related to each other, and it is also possible to determine the remaining parameter if two of them are known. However, sedimentary soils are always heterogeneous, and the Vs of soils is usually dependent on the effective confining pressure. A direct application of Equation (1) is not always guaranteed.
f0 = Vs/4D,
Previous studies have shown that the relationship between f0 and D can be expressed by a power-law model, which is shown in Equation (2) [,,,]:
where a and b are constants specific to the regional geologic characteristics. These models show that the constants a and b can be strongly dependent on the regional geologic characteristics, meaning that it is necessary to develop a region-specific model that considers the local geologic properties.
D = af0b,
The influence of site amplification would be significant in the study area due to the presence of widely distributed loose Holocene sediments, which are as deep as eighty meters. The goal of this study was to establish a relationship between the f0 and D in the Nakdonggang delta region, with which one can quickly estimate the bedrock depth and determine the seismic site class in accordance with KDS 17 10 00.
We estimated the f0 at multiple sites in our previous study using the microtremor horizontal to vertical spectral ratio (HVSR) method []. Additionally, we collected bedrock depth data from the geotechnical investigations that had been conducted in the study area. We developed a power-law model of the bedrock depth in the study area using a log-log regression of the collected f0 and D data. We then compared the model with similar studies conducted in other regions to investigate the difference in the f0–D correlation model based on regional characteristics.
2. Study Area
The Nakdonggang delta region is in the southeastern part of the Korean peninsula, as shown in Figure 1. It is the largest delta area in the Korean peninsula and is surrounded by various faults and mountains. An extensional basin was formed by a half-graben structure bounded by the Yangsan fault, as shown in Figure 1. The main delta is approximately 10 km wide and 20 km long, with an exposed land area of around 136 km2, a plains area, and several interdistributary islands []. The southeastern part of the Korean peninsula is known to have a higher seismic hazard compared with the rest of the country [].
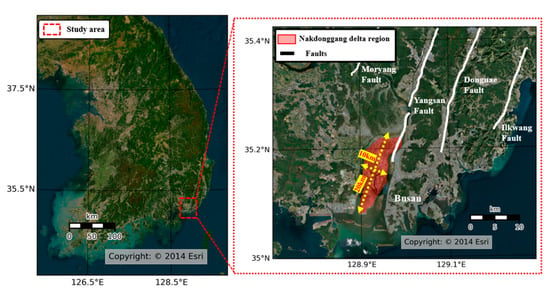
Figure 1.
Location of the Nakdonggang delta region in the Korean peninsula and the nearby faults.
The Nakdonggang delta area is characterized by layers of deltaic, marine, and fluvial sediments that cover a wide area, as shown in Figure 1. The maximum thickness of the sediments overlying the bedrock is approximately 80 m. Holocene sediments consist of a sandy layer (deltaic sediments) up to around 15 m below the ground surface, overlying the remaining layer, consisting of thick marine clay []. According to Ham et al. [], the study area was dominated by a fluvial environment during the late Pleistocene, due to low sea levels. Fluvial deposits, consisting of granular to fine sand and small amounts of gravel, were formed on top of the bedrock at a maximum observed depth of around 50 m. The sea level then gradually rose for a long period, leading to the formation of marine deposits containing a small amount of shells on top of the late Pleistocene fluvial deposits. The sea level then steadily decreased to its current level, resulting in the formation of the present sedimentary delta at the end of the Holocene. Therefore, it is expected that the ground dynamic characteristics at different depths may vary depending on the formative process, while it is also expected that layers that were deposited during the same era may have similar ground dynamic characteristics.
3. Methodology
3.1. Characterization of f0 Based on the HSVR Method
The HVSR method is a geophysical exploration method that provides a convenient way of estimating the fundamental vibration frequency (f0) of sedimentary soils. It was first proposed by Nogoshi and Igarashi [], and later, Nakamura [] argued that the 1D transfer function of a site can be defined through the horizontal-to-vertical Fourier spectral ratio of the microtremor. It has become popular since the 1990s and many researchers have effectively used HVSR for the characterization of site amplification properties [,,,].
The origin of HVSR peaks and their relationship with site response characteristics are still controversial. For example, Nogoshi and Igarashi [] suggested that the main contribution to ambient noise originates from Rayleigh waves and HVSR peaks represent the ellipticity of these Rayleigh waves. In contrast, Nakamura [] argued that HVSR peaks are mainly due to S-wave resonance within the surficial sedimentary layer. Other studies have pointed out that the ambient noise on the ground surface is composed of different types of waves, including body, Rayleigh, and Love waves, and their proportions vary depending on the site conditions and source characteristics [,]. Some studies have attempted to isolate Rayleigh waves from Love waves within noise recordings for a more reliable identification of site amplification properties [,,].
Nevertheless, many studies have confirmed that the peak frequency of microtremor HVSR generally corresponds to the fundamental frequency of the 1D transfer function of each site [,,,]. Bard [] explained that HVSR peaks are very close to the site fundamental frequencies at sites with a strong impedance contrast, because the vertical components of Rayleigh waves tend to vanish near the S-wave resonance frequency. We used the microtremor HVSR method to estimate the f0, and Figure 2 shows a typical example of an HVSR obtained in the study area.
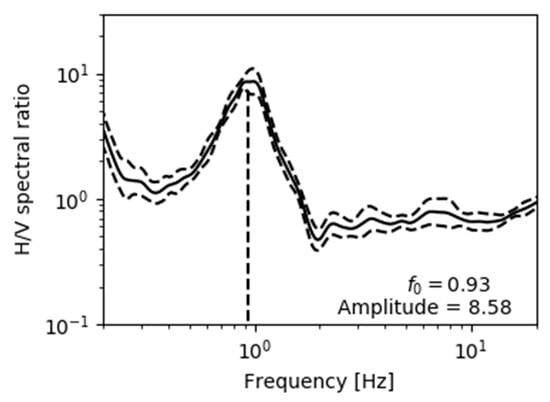
Figure 2.
An example of a horizontal-to-vertical spectral ratio calculated from microtremor data recorded at a location in the study area. Microtremor record was divided into windows of 180 s and HVSR was calculated for each window. The solid and dashed lines represent the mean and standard deviation, respectively.
To estimate the spatial distribution of the fundamental site frequencies in the study area, over 200 test locations were selected at spacings of about 1 km, as shown in Figure 3, and microtremor data were recorded for at least 1 hour at each location.
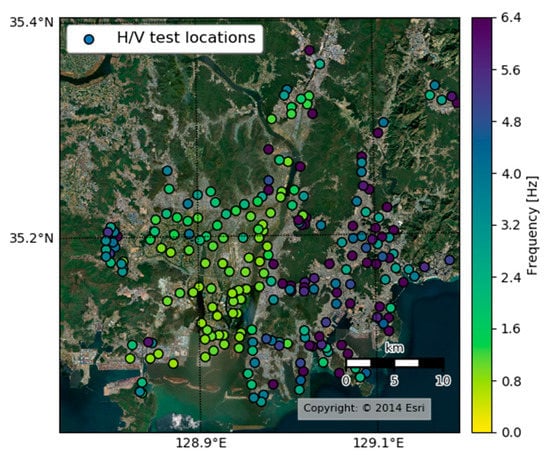
Figure 3.
HVSR test locations with spacings of about 1 km and obtained f0 values at each site.
The microtremor data were recorded using Raspberry Shake 3D (Raspberry Shake, S.A., Panama) and Trillium Compact 20 s seismometers (Nanometrics Inc., Canada), shown in Figure 4, with a sampling rate of 100 samples per second. Raspberry Shake 3D is a geophone-based velocity sensor with a flat response in 2 s to 50 Hz. Trillium Compact 20 s is a force feedback velocity seismometer with a flat response in 20 s to 100 Hz. We used both types to expedite our field work. We conducted a huddle test before the field work to ensure all the sensors produced consistent outputs. To ensure a good coupling, we fixed the seismic sensors on the ground by combining spikes with an aluminum plate. The seismometers were aligned to the magnetic north using a compass and levelled using built-in bullseye bubbles.

Figure 4.
(a) Raspberry Shake 3D, and (b) Trillium Compact 20 s seismometers deployed to collect the microtremor data.
We obtained the HVSR from the obtained microtremors using the Geopsy 2.10.1 software suite (https://www.geopsy.org (accessed on 7 July 2020)), applying the Konno-Ohmachi smoothing method [] with a smoothing constant of b = 40. Within the analysis, the recorded data were divided into multiple time windows of 180 s long and the frequency sampling was done logarithmically from 0.1 to 50 Hz. The value of the f0 was obtained from all time windows and, subsequently, the mean and standard deviation were calculated. Figure 3 also shows the f0 at the studied sites, obtained using the HVSR method described above. Most sites located inside or near the Nakdonggang delta region showed a low f0 of around 1 Hz, while others located near mountains showed higher values.
3.2. Bedrock Depth Obtained from Borehole Data
To derive the relationship between the f0 and D, we collected boring logs from the Korean geotechnical investigation database system (www.geoinfo.or.kr (accessed on 6 March 2023)) in the study area. Figure 5a shows the bedrock depth logged at each location and Figure 5b provides a typical example of the stratigraphy in the study area, which is consistent with the known sedimentation history of the study area, as suggested by Ham et al. []. The boring logs showed that the bedrock depth in the study area was predominantly around 60 m, while at some sites towards the south, it reached up to 90 m. Overall, there was a relatively large variability in the bedrock depth in the study area. Based on Figure 5b, it was also expected that there would be no significant impedance contrast until the bedrock is reached.
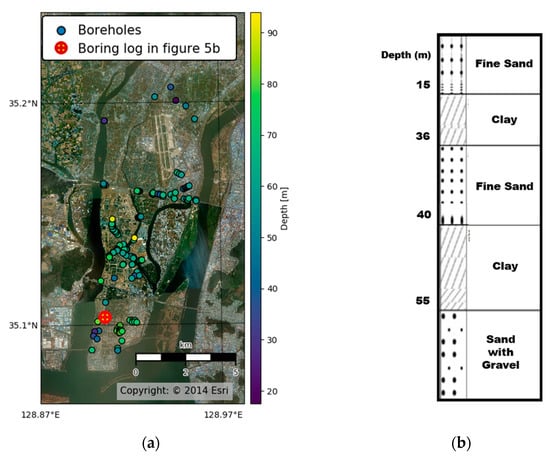
Figure 5.
(a) Locations of boreholes and the depth to the bedrock obtained from the Korean geotechnical investigation database system (www.geoinfo.or.kr) in the main delta region. (b) A typical example of collected stratigraphic data in the study area at the location shown in Figure 5a.
3.3. Estimation of f0 at Each Borehole by Spatial Interpolation
Based on the results of the HVSR, we created an f0 map of the Nakdonggang delta region (Figure 6a) to confirm the spatial distribution of the f0 in the study area. We used the Ordinary Kriging method to spatially interpolate the f0 data of the study area with intervals of around 30 m. We applied a variogram with 3.82, 5.32, and 12,492 as “Sill”, “Nugget”, and “Range”, respectively. The spatial distribution of the variance is illustrated in Figure 6b. Based on the f0 map of the Nakdonggang delta region, we can confirm that most of the study area had an f0 around 1 Hz and showed a relatively small variability compared with other areas.
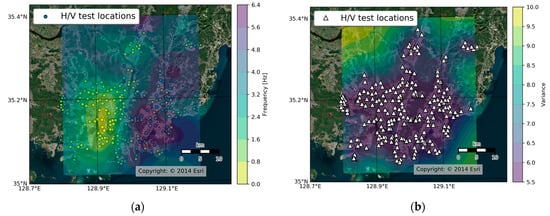
Figure 6.
(a) Fundamental site frequency map of the Nakdonggang delta region, developed by the Ordinary Kriging, and (b) distribution of variance by separated distance.
We then extracted the f0 values from the interpolation results (Figure 7a) within the main delta that were closest to each borehole location, in order to investigate the relationship between the f0 and bedrock depth at each site. Figure 7b shows the specific locations.
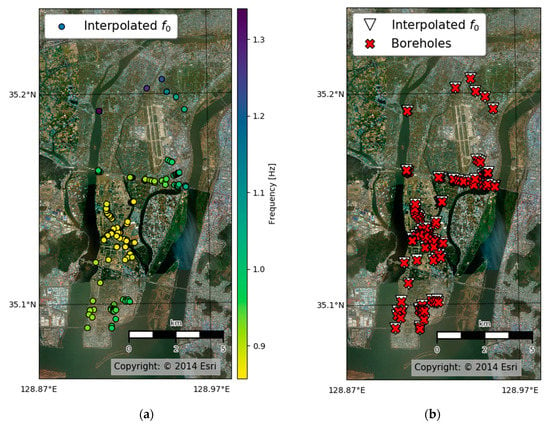
Figure 7.
(a) Specific locations of extracted f0 from the interpolation results, and (b) specific locations of used data.
4. Result and Discussions
Ibs-von Seht and Wohlenberg [] developed the correlation between the bedrock depth and f0 in the western Lower Rhine Embayment of Germany. Parolai et al. [] produced a similar model for the Cologne area (Germany). Jeong and Wotherspoon [] applied the same technique in the Waikato region (New Zealand) and their results were overall consistent with those of the two previous studies. Moon et al. [] derived the correlation between the f0 and D in the Bukit Timah granite formation (Singapore) and found that their model showed a much smaller negative exponent compared with other studies. The specific model parameters and conditions of each study are summarized in Table 2.

Table 2.
Correlation coefficients in Equation (2) and conditions of previous studies.
Using the bedrock depth from the borehole data and the interpolated f0, we derived a f0–D correlation model for the Nakdonggang delta region by performing a log-log regression analysis between the ln f0 and ln D, as shown in Equation (3):
which can be converted back into a power function, as shown in Equation (4):
ln D = (4.017 ± 0.026) − (1.315 ± 0.232) ln f0,
D = 55.5 f0−1.315.
The coefficient of determination from the regression was 0.2, which is relatively low. Equation (3) shows that the standard error for coefficient b was relatively large. We attribute this to the relatively narrow range of fundamental frequencies combined with the inherently large variability in the bedrock depth from the boring logs.
Figure 8 shows the results of this study in comparison with similar studies conducted in other parts of the world. Some of the previous studies have shown a good agreement with each other, but the results of this study indicate much shallower bedrock depths given the same frequency in comparison with others. This suggests that the bedrock depth would be overestimated if the results of previous studies were used in the study area. Among the previous studies, the slope of the Ibs-von Seht and Wohlenberg [] model was the closest to the result of this study; the slopes of other models, except for the Moon et al. [] model, also fell within the standard error of this study.
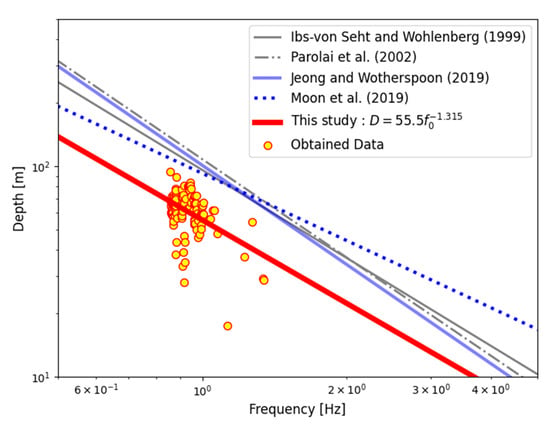
Figure 8.
Obtained data (yellow points) and derived the f0–D model of this study (red line) and f0–D models of previous studies [,,,].
However, coefficient a in Equation (4) from our study was much lower than that in all the other studies listed in Table 2. Coefficient a in Equation (4) gave the average estimate of the bedrock depth when f0 = 1, and a lower value would suggest a lower average Vs. Our results summarized in Table 2 and Figure 8 suggest that the Holocene sedimentary soils considered in this study showed a much lower average Vs compared with the previous studies considered.
We calculated the residuals between the predicted bedrock depths, obtained from the power-law model defined in Equation (4), and the bedrock depths obtained from the borehole data. In Figure 9, the red line and filled area represent the moving average and 67% confidence interval, respectively, which were calculated by applying windows of 24 data points. By trialing the moving average with different binning schemes, we confirmed that using windows of 24 points effectively represented the variations in the means and standard deviations of the residuals. Figure 9 shows that the power-law model of the bedrock depth derived in this study was consistent with the observation and the standard deviations of the residuals were generally smaller than 0.3. This suggests that a measurement of the f0 using the HVSR method could provide a quick estimate of the bedrock depth in the Nakdonggang delta region and valuable input for regional seismic hazard studies and regional-scale seismic performance assessments of structures [,,,]. However, the inconsistency between the empirical models demonstrated in Figure 8 suggests that the relationship between the f0 and bedrock depth is region-specific.
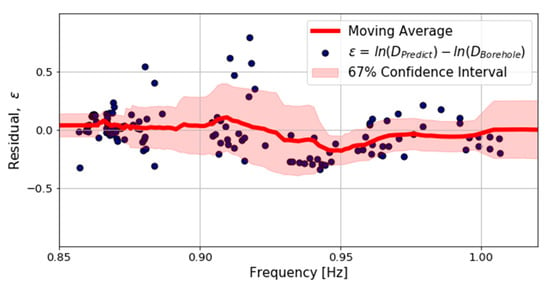
Figure 9.
Residuals between the predicted and obtained bedrock depth (points). The moving average of 24 points (red line) and 67% confidence interval (filled area) are also illustrated.
5. Conclusions
We estimated the f0 at over 200 locations using the HVSR method and collected geotechnical boring logs to determine the D in the Nakdonggang delta region in the southeastern part of the Korean Peninsula. We spatially interpolated the obtained f0 using the Ordinary Kriging method and developed an f0 map of the study area. We then derived an f0–D correlation model for the Nakdonggang delta region as a power-law function and compared it with previous studies from other regions. The conclusions from this study can be summarized as follows:
- The HVSRs from the collected microtremor show that most sites located in or near the Nakdonggang delta region show a low f0 of around 1 Hz, which corresponded to the fundamental mode vibration of the Holocene sediments. This suggests that the ground motions observed in this region would be rich in f ≥ 1 Hz due to the amplification in the fundamental and higher modes;
- Using the spatially interpolated f0 and D from the boring logs, we developed an f0–D correlation model. Our model predicted much shallower bedrock depths compared with those in previous studies, which was attributed to the relatively lower Vs of the Holocene sediments in the studied area. It also suggested that the relationship between the f0 and bedrock depth is region-specific;
- The predicted bedrock depth from the f0–D correlation model was in good agreement with the observations and the standard deviations of the residuals were generally smaller than 0.3. This suggests that a measurement of the f0 using the HVSR method could provide a quick estimate of the bedrock depth for determination of the site class in the Nakdonggang delta region.
Author Contributions
Conceptualization, J.K. and S.J.; methodology, J.K. and S.J.; formal analysis, J.K.; investigation, J.K, G.H., S.J. and D.K.; resources, S.J. and D.K.; data curation, J.K. and G.H.; writing—original draft preparation, J.K.; writing—review and editing, J.K., G.H., S.J. and D.K.; visualization, J.K.; supervision, S.J.; project administration, S.J.; funding acquisition, S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Ministry of Science and ICT (MSIT) (No. NRF-2020R1F1A1076539).
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors would like to acknowledge the contribution from Minji Kim and Taeik Kwon for helping to collect and analyze the microtremor data during the initial phase of this research. We are grateful to MOLIT for operating and maintaining GeoInfo geotechnical database.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Borcherdt, R.D. Effects of Local Geology on Ground Motion Near San Francisco bay. Bull. Seismol. Soc. Am. 1970, 60, 29–61. [Google Scholar]
- Singh, S.K.; Mena, E.; Castro, R. Some aspects of source characteristics of the 19 September 1985 Michoacan earthquake and ground motion amplification in and near Mexico City from strong motion data. Bull. Seismol. Soc. Am. 1988, 78, 451–477. [Google Scholar]
- Seed, R.B.; Dickenson, S.E.; Idriss, I.M. Principal Geotechnical Aspects of the 1989 Loma Prieta Earthquake. Soils Found. 1991, 31, 1–26. [Google Scholar] [CrossRef]
- Karagoz, O.; Chimoto, K.; Citak, S.; Ozel, O.; Yamanaka, H.; Hatayama, K. Estimation of shallow S-wave velocity structure and site response characteristics by microtremor array measurements in Tekirdag region, NW Turkey. Earth Planets Space 2015, 67, 176. [Google Scholar] [CrossRef]
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice-Hall: Hoboken, NJ, USA, 1996. [Google Scholar]
- Korean Design Standard (KDS) 17 10 00; Seismic Design Standard. Ministry of Land, Infrastructure and Transport: Sejong-si, Republic of Korea, 2018.
- Ibs-von Seht, M.; Wohlenberg, J. Microtremor Measurements Used to Map Thickness of Soft Sediments. Bull. Seismol. Soc. Am. 1999, 89, 250–259. [Google Scholar] [CrossRef]
- Jeong, S.; Wotherspoon, L.M. Development of a Waikato Basin T0 and depth model by the H/V spectral ratio method. In Proceedings of the 2019 Pacific Conference on Earthquake Engineering, Auckland, New Zealand, 4–6 April 2019; pp. 1–8. [Google Scholar]
- Moon, S.W.; Subramaniam, P.; Zhang, Y.; Vinoth, G.; Ku, T. Bedrock depth evaluation using microtremor measurement: Empirical guidelines at weathered granite formation in Singapore. J. Appl. Geophys. 2019, 171, 103866. [Google Scholar] [CrossRef]
- Parolai, S.; Bormann, P.; Milkereit, C. New Relationships between Vs, Thickness of Sediments, and Resonance Frequency Calculated by the H/V Ratio of Seismic Noise for the Cologne Area (Germany). Bull. Seismol. Soc. Am. 2002, 92, 2521–2527. [Google Scholar] [CrossRef]
- Kim, J.H. Characterization of Dynamic Site Properties in the Gimhae Plains Using the Microtremor Array Method and the Horizontal-to-Vertical Spectral Ratio Method. Master’s Thesis, Changwon National University, Changwon-si, Republic of Korea, 2023. [Google Scholar]
- Kwon, H. A Geomorphorphic Study of the Nakdong Delta. J. Korean Geogr. Soc. 1973, 8, 8–23. [Google Scholar]
- Park, S.; Hong, T.-K.; Rah, G. Seismic Hazard Assessment for the Korean Peninsula. Bull. Seismol. Soc. Am. 2021, 111, 2696–2719. [Google Scholar] [CrossRef]
- Kim, S.K.; Kim, Y.T.; Kim, J.H. The Guidelines for Designing Vertical Drain Boards in Deep Soft Ground. Geotech. Eng. 2014, 30, 15–24. [Google Scholar]
- Ham, A.; Shin, S.; Kim, J.; Jung, S.; Komal, S.; Cheong, D. Late Quaternary depositional environmental changes from the middle part of Nakdong River delta core sediments. J. Geol. Soc. Korea 2018, 54, 47–59. [Google Scholar] [CrossRef]
- Nogoshi, M.; Igarashi, T. On the Amplitude Characteristics of Microtremor (Part 2). J. Seismol. Soc. Jpn. 1971, 24, 26–40. [Google Scholar]
- Nakamura, Y. A Method for Dynamic Characteristics Estimation of Subsurface Using Microtremor on the Ground Surface. Railw. Tech. Res. Inst. Q. Rep. 1989, 30, 25–33. [Google Scholar]
- Lermo, J.; Chavez-Garcia, F.J. Site Effect Evaluation Using Spectral Ratios with Only One Station. Bull. Seismol. Soc. Am. 1993, 83, 1574–1594. [Google Scholar] [CrossRef]
- Rong, M.; Fu, L.; Wang, Z.; Li, X.; Carpenter, N.S.; Woolery, E.W.; Lyu, Y. On the Amplitude Discrepancy of HVSR and Site Amplification from Strong-Motion Observations. Bull. Seismol. Soc. Am. 2017, 107, 2873–2884. [Google Scholar] [CrossRef]
- Stanko, D.; Markušić, S.; Gazdek, M.; Sanković, V.; Slukan, I.; Ivančić, I. Assessment of the Seismic Site Amplification in the City of Ivanec (NW Part of Croatia) Using the Microtremor HVSR Method and Equivalent-linear Site Response Analysis. Geosciences 2019, 9, 312. [Google Scholar] [CrossRef]
- Xu, R.; Wang, L. The horizontal-to-vertical spectral ratio and its applications. EURASIP J. Adv. Signal Process. 2021, 2021, 75. [Google Scholar] [CrossRef]
- Bonnefoy-Claudet, S.; Cornou, C.; Bard, P.Y.; Cotton, F.; Moczo, P.; Kristek, J.; Fäh, D. H/V ratio: A tool for site effects evaluation. Results from 1-D noise simulations. Geophys. J. Int. 2006, 167, 827–837. [Google Scholar] [CrossRef]
- Lunedei, E.; Albarello, D. On the seismic noise wavefield in a weakly dissipative layered Earth. Geophys. J. Int. 2009, 177, 1001–1014. [Google Scholar] [CrossRef]
- Del Gaudio, V. Instantaneous polarization analysis of ambient noise recordings in site response investigations. Geophys. J. Int. 2017, 210, 443–464. [Google Scholar] [CrossRef]
- Fäh, D.; Kind, F.; Giardini, D. A theoretical investigation of average H/V ratios. Geophys. J. Int. 2001, 145, 535–549. [Google Scholar] [CrossRef]
- Poggi, V.; Fäh, D.; Burjanek, J.; Giardini, D. The use of Rayleigh-wave ellipticity for site-specific hazard assessment and microzonation: Application to the city of Lucerne, Switzerland. Geophys. J. Int. 2012, 188, 1154–1172. [Google Scholar] [CrossRef]
- Bard, P.Y. Microtremor measurements: A tool for site effect estimation. In The Effects of Surface Geology on Seismic Motion; Irikura, K., Kudo, K., Okada, H., Sasatani, T., Eds.; Balkema: Rotterdam, The Netherlands, 1999; Volume 3, pp. 1251–1279. [Google Scholar]
- Konno, K.; Ohmachi, T. Ground-motion characteristics estimated from spectral ratio between horizontal and vertical components of microtremor. Bull. Seismol. Soc. Am. 1998, 88, 228–241. [Google Scholar] [CrossRef]
- Gosar, A. Study on the applicability of the microtremor HVSR method to support seismic microzonation in the town of Idrija (W Slovenia). Nat. Hazards Earth Syst. Sci. 2017, 17, 925–937. [Google Scholar] [CrossRef]
- Martorana, R.; Capizzi, P.; D’Alessandro, A.; Luzio, D.; Di Stefano, P.; Renda, P.; Zarcone, G. Contribution of HVSR measures for seismic microzonation studies. Ann. Geophys. 2018, 61. [Google Scholar] [CrossRef]
- Pitilakis, K.D.; Anastasiadis, A.I.; Kakderi, K.G.; Manakou, M.V.; Manou, D.K.; Alexoudi, M.N.; Fotopoulou, S.D.; Argyroudis, S.A.; Senetakis, K.G. Development of comprehensive earthquake loss scenarios for a Greek and a Turkish city: Seismic hazard, geotechnical and lifeline aspects. Earthq. Struct. 2011, 2, 207–232. [Google Scholar] [CrossRef]
- Xu, J.G.; Feng, D.C.; Mangalathu, S.; Jeon, J.S. Data-driven rapid damage evaluation for life-cycle seismic assessment of regional reinforced concrete bridges. Earthq. Eng. Struct. Dyn. 2022, 51, 2730–2751. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).