Elastoplastic Integration Method of Mohr-Coulomb Criterion
Abstract
1. Introduction
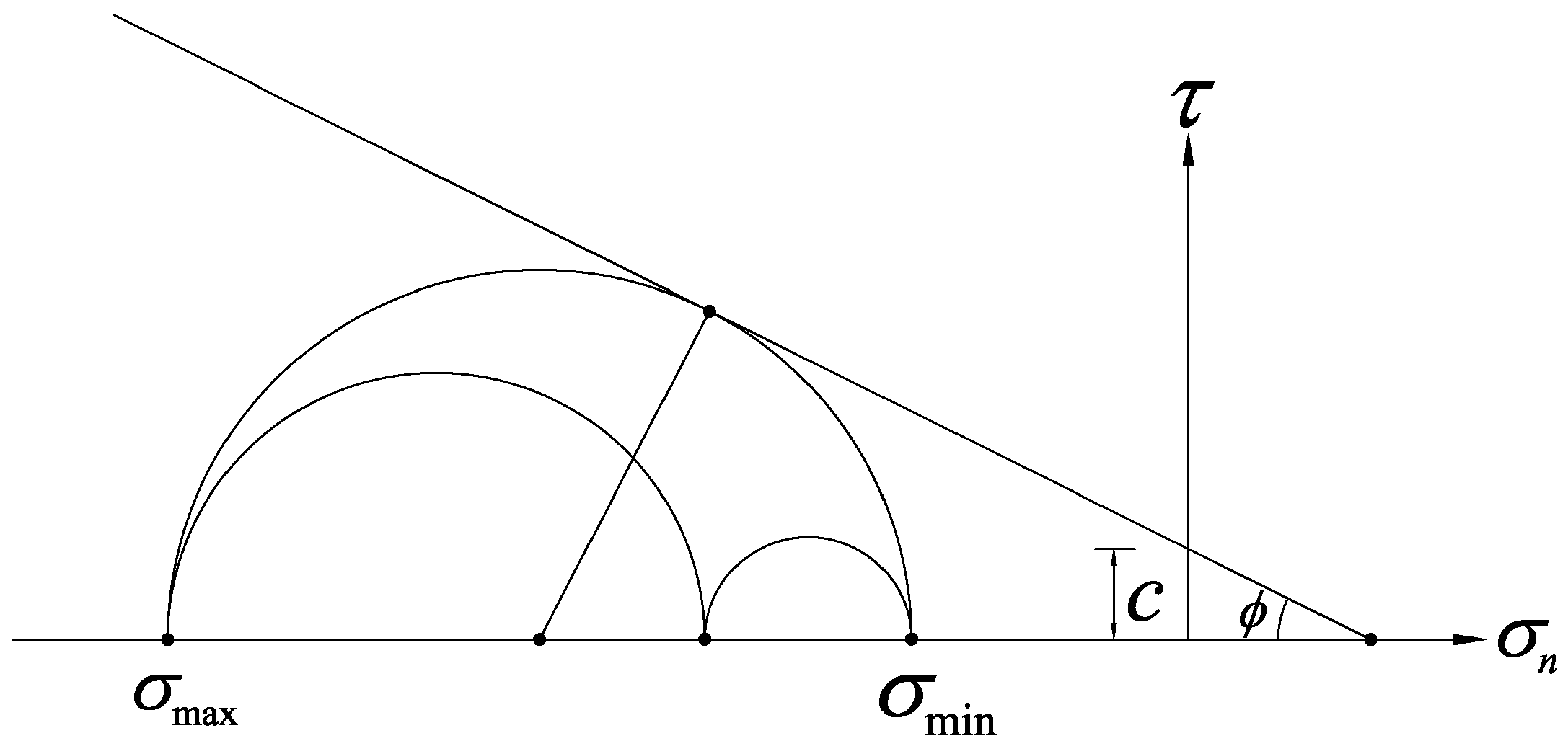
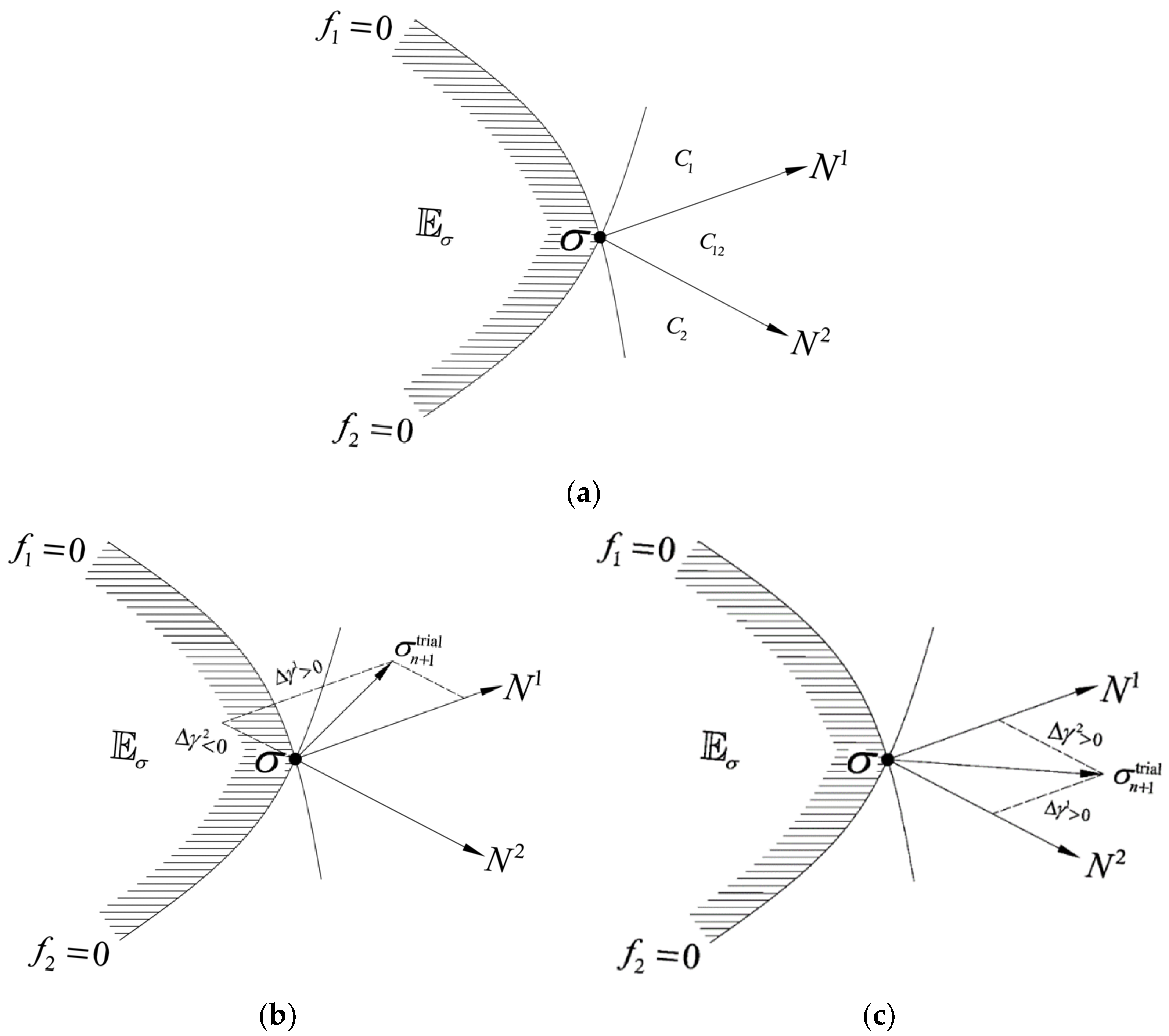
2. The Causes of Corner Problem of Mohr-Coulomb Criterion
3. Algorithm and Implementation
3.1. Constitutive Integral for Mohr-Coulomb Criterion
- 1
- Compute elastic predictor
- 2
- Check for plastic process
- 3
- Evaluate stress at iteration (k)
- 4
- Check convergence
- 5
- Computate plastic multiplier
- 6
- Update plastic strain
3.2. Partial Derivatives of Principal Stresses with Regard to Stress Components
- , , ,
- , , , etc.
- ,,,
- ,,,,, etc.
3.3. Algorithm PCA
4. Numerical Examples
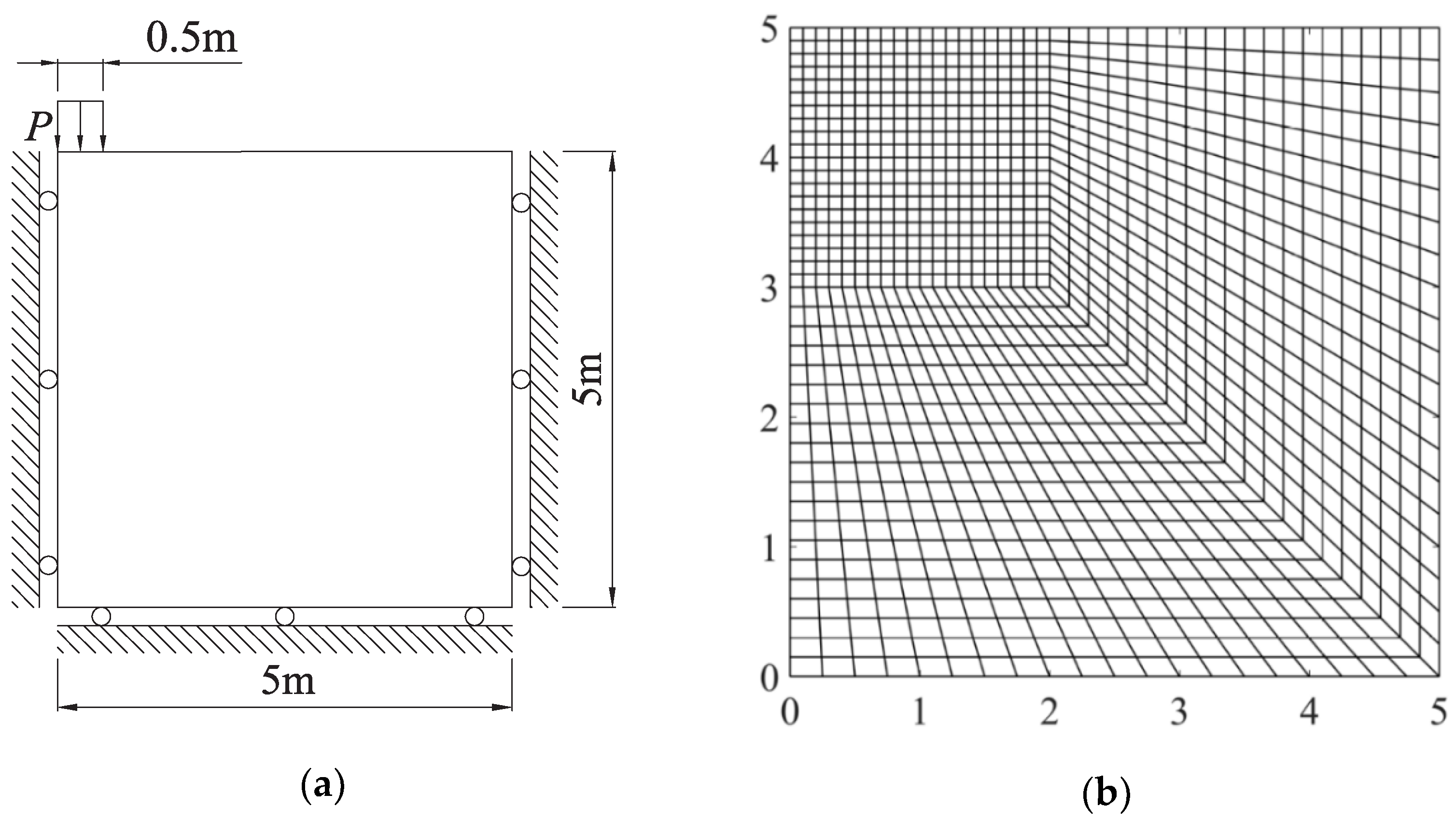
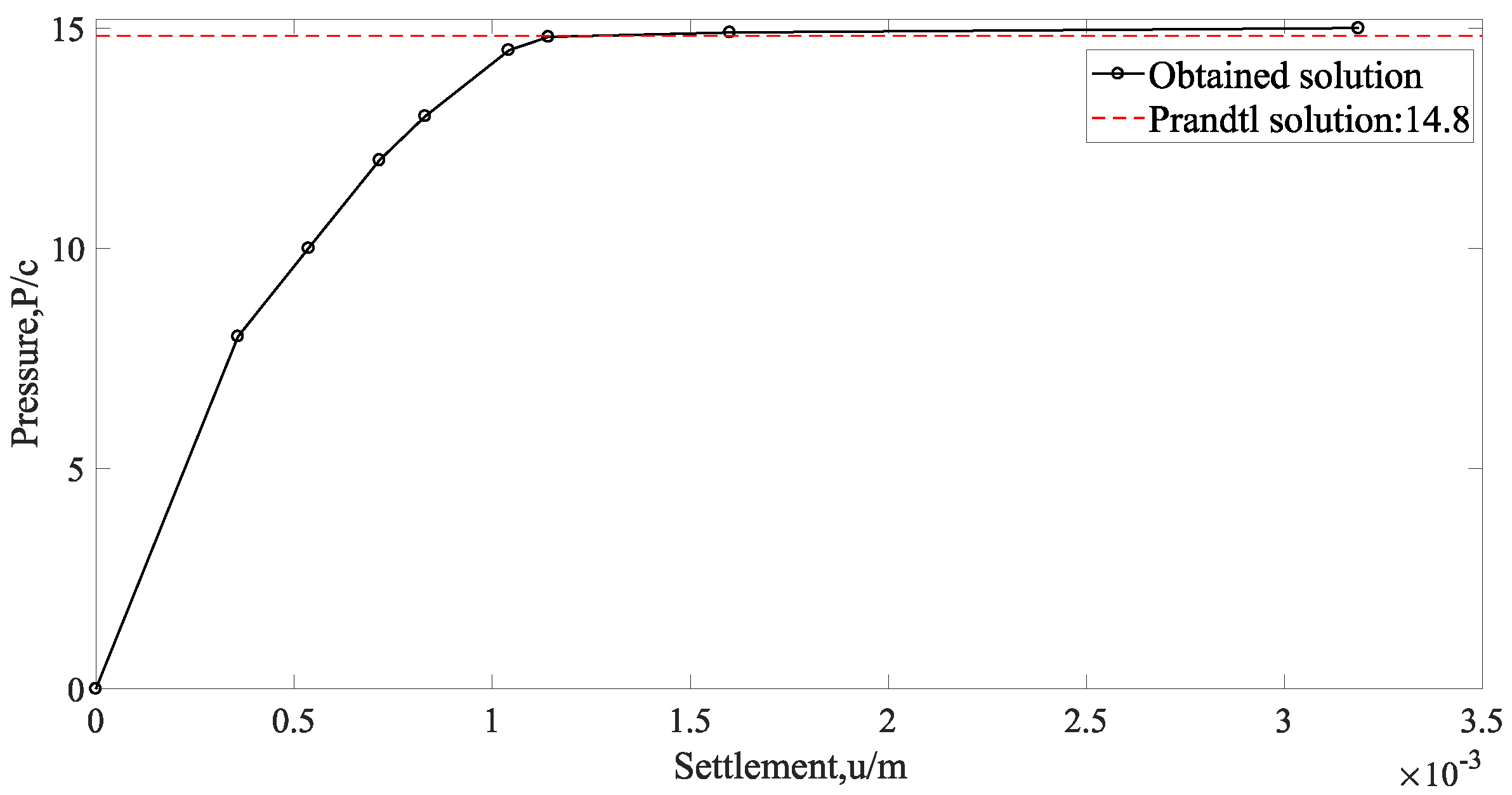
4.1. Strip Footing Collapse
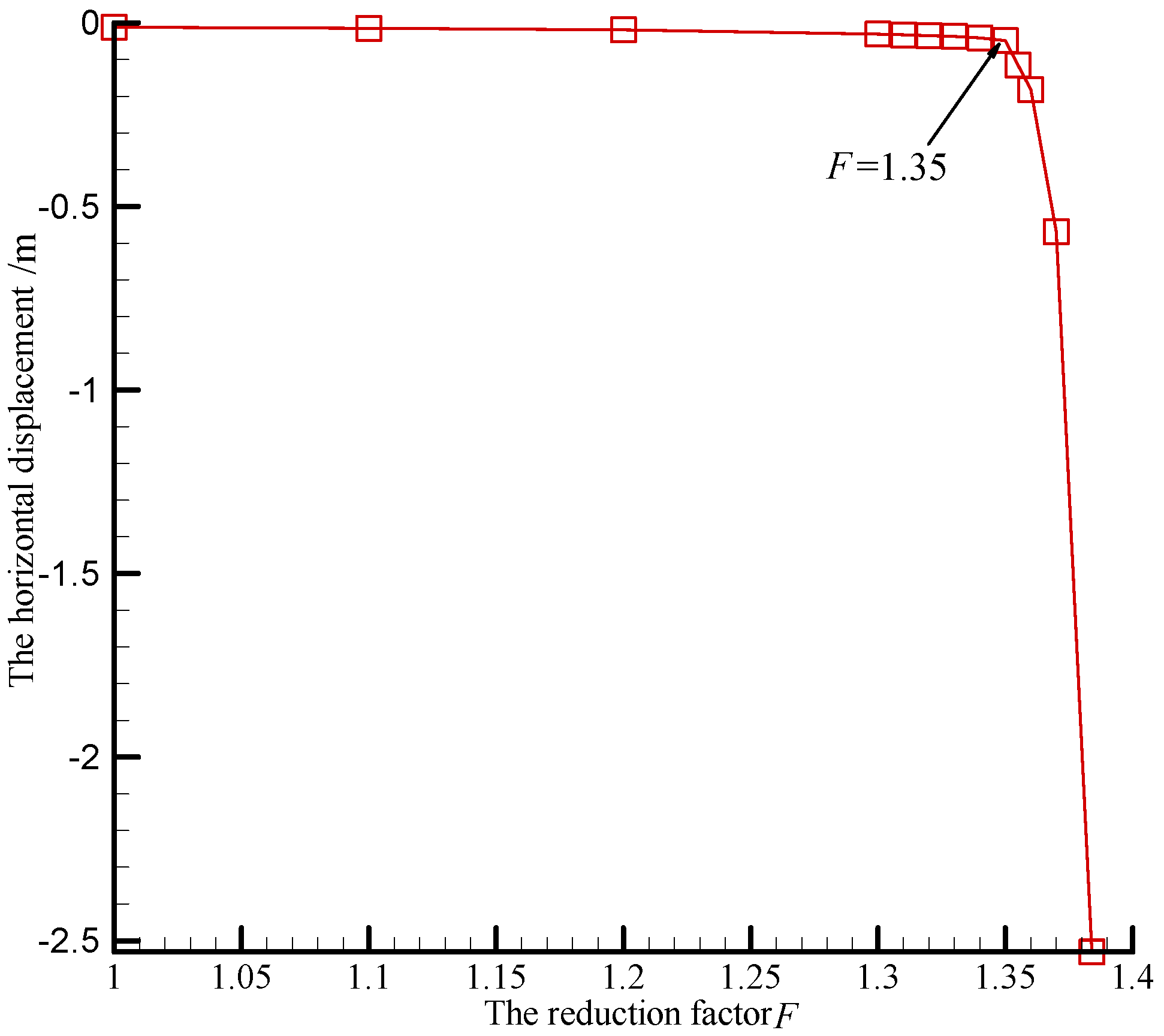
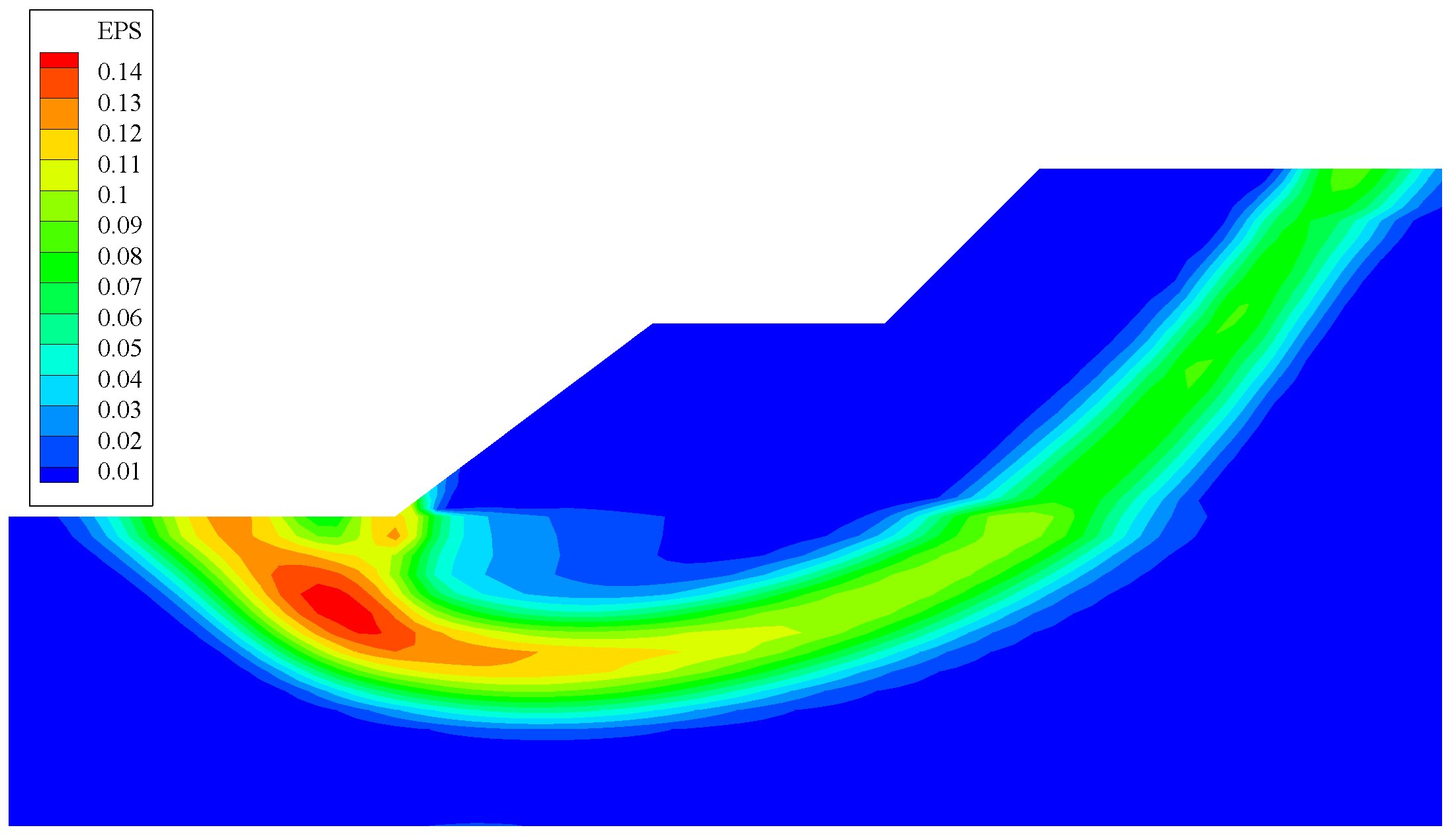
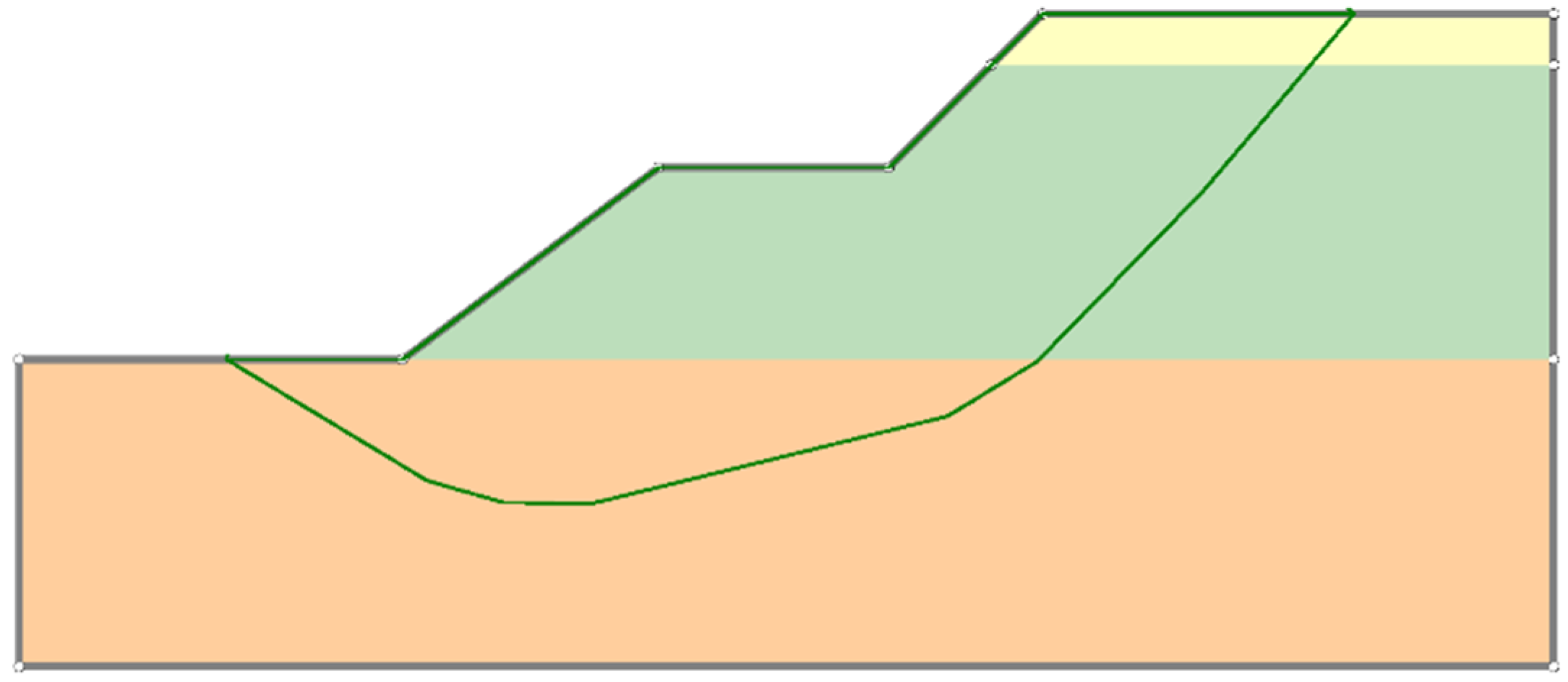
4.2. Slope Stability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Koiter, W.T. Stress-strain relations, uniqueness and variational theorems for elastic-plastic materials with a singular yield surface. Q. Appl. Math. 1953, 11, 350–354. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Valliappan, S.; King, I.P. Elasto-plastic solutions of engineering problems ‘initial stress’, finite element approach. Int. J. Numer. Methods Eng. 1969, 1, 75–100. [Google Scholar] [CrossRef]
- Hinton, E.; Owen, D.R.J. Finite Elements in Plasticity: Theory and Practice; Pineridge Press: Swansea, UK, 1980; pp. 20–45. [Google Scholar]
- Marques, J. Stress computation in elastoplasticity. Eng. Comput. 1984, 1, 42–51. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Pande, G.N. Some useful forms for isotropic yield surfaces for soils and rock mechanics. In Finite Elements in Geomechanics; Gudehus, G., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 1977; pp. 179–190. [Google Scholar]
- Sloan, S.W.; Booker, J.R. Removal of singularities in tresca and Mohr-Coulomb yield functions. Commun. Appl. Numer. Methods 1986, 2, 173–179. [Google Scholar] [CrossRef]
- Abbo, A.; Lyamin, A.; Sloan, S.; Hambleton, J. A C2 continuous approximation to the Mohr–Coulomb yield surface. Int. J. Solids Struct. 2011, 48, 3001–3010. [Google Scholar] [CrossRef]
- Larsson, R.; Runesson, K. Implicit integration and consistent linearization for yield criteria of the Mohr-Coulomb type. Mech. Cohesive -Frict. Mater. 1996, 1, 367–383. [Google Scholar] [CrossRef]
- Peric, D.; Neto, E.D.S. A new computational model for Tresca plasticity at finite strains with an optimal parametrization in the principal space. Comput. Methods Appl. Mech. Eng. 1999, 171, 463–489. [Google Scholar] [CrossRef]
- Neto, E.A.D.S.; Peri, D.; Owen, D.R.J. Computational Methods for Plasticity: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- de Borst, R. Integration of plasticity equations for singular yield functions. Comput. Struct. 1987, 26, 823–829. [Google Scholar] [CrossRef][Green Version]
- Pankaj, P.; Bićanić, N. Detection of multiple active yield conditions for Mohr-Coulomb elasto-plasticity. Comput. Struct. 1997, 62, 51–61. [Google Scholar] [CrossRef]
- Clausen, J.; Damkilde, L.; Andersen, L. An efficient return algorithm for non-associated plasticity with linear yield criteria in principal stress space. Comput. Struct. 2007, 85, 1795–1807. [Google Scholar] [CrossRef]
- Coombs, W.M.; Crouch, R.S.; Augarde, C.E. Reuleaux plasticity: Analytical backward Euler stress integration and consistent tangent. Comput. Methods Appl. Mech. Eng. 2010, 199, 1733–1743. [Google Scholar] [CrossRef][Green Version]
- Amouzou, G.; Soulaïmani, A. Numerical Algorithms for Elastoplacity: Finite Elements Code Development and Implementation of the Mohr–Coulomb Law. Appl. Sci. 2021, 11, 4637. [Google Scholar] [CrossRef]
- Zhao, R.; Li, C.; Zhou, L.; Zheng, H. A sequential linear complementarity problem for multisurface plasticity. Appl. Math. Model. 2021, 103, 557–579. [Google Scholar] [CrossRef]
- Simo, J.C.; Kennedy, J.G.; Govindjee, S. Non-smooth multisurface plasticity and viscoplasticity. Loading/unloading conditions and numerical algorithms. Int. J. Numer. Methods Eng. 1988, 26, 2161–2185. [Google Scholar] [CrossRef]
- Karaoulanis, F.E. Implicit Numerical Integration of Nonsmooth Multisurface Yield Criteria in the Principal Stress Space. Arch. Comput. Methods Eng. 2013, 20, 263–308. [Google Scholar] [CrossRef]
- Clausen, J.; Damkilde, L. An exact implementation of the Hoek–Brown criterion for elasto-plastic finite element calculations. Int. J. Rock Mech. Min. Sci. 2008, 45, 831–847. [Google Scholar] [CrossRef]
- Adhikary, D.P.; Jayasundara, C.T.; Podgorney, R.K.; Wilkins, A.H. A robust return-map algorithm for general multisurface plasticity. Int. J. Numer. Methods Eng. 2017, 109, 218–234. [Google Scholar] [CrossRef]
- Facchinei, F.; Pang, J.-S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- He, B. A Class of Projection and Contraction Methods for Monotone Variational Inequalities. Appl. Math. Optim. 1997, 35, 69–76. [Google Scholar] [CrossRef]
- Hill, R. The Mathematical Theory of Plasticity; Oxford University Press: London, UK, 1950; pp. 253–260. [Google Scholar]
- Vo, T.; Russell, A.R. Bearing capacity of strip footings on unsaturated soils by the slip line theory. Comput. Geotech. 2015, 74, 122–131. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Humpheson, C.; Lewis, R.W. Associated and nonassociated viscoplasticity in soil mechanics. Géotechnique 1975, 25, 671–689. [Google Scholar] [CrossRef]
- Naylor, D.J. Finite elements and slope stability. In Numerical Methods in Geomechanics; Springer: Dordrecht, The Netherland, 1981; pp. 229–244. [Google Scholar]
- Matsui, T.; San, K.-C. Finite Element Slope Stability Analysis by Shear Strength Reduction Technique. Soils Found. 1992, 32, 59–70. [Google Scholar] [CrossRef]
- Ugai, K.; Leshchinsky, D. Three-Dimensional Limit Equilibrium and Finite Element Analyses: A Comparison of Results. Soils Found. 1995, 35, 1–7. [Google Scholar] [CrossRef]
- Dawson, E.M.; Roth, W.H.; Drescher, A. Slope stability analysis by strength reduction. Géotechnique 1999, 49, 835–840. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Lane, P.A. Slope stability analysis by finite elements. Géotechnique 1999, 49, 387–403. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, D.F.; Li, C.G. Slope stability analysis based on elasto-plastic finite element method. Int. J. Numer. Methods Eng. 2005, 64, 1871–1888. [Google Scholar] [CrossRef]
- Zheng, H.; Sun, G.; Liu, D. A practical procedure for searching critical slip surfaces of slopes based on the strength reduction technique. Comput. Geotech. 2009, 16, 1–5. [Google Scholar] [CrossRef]


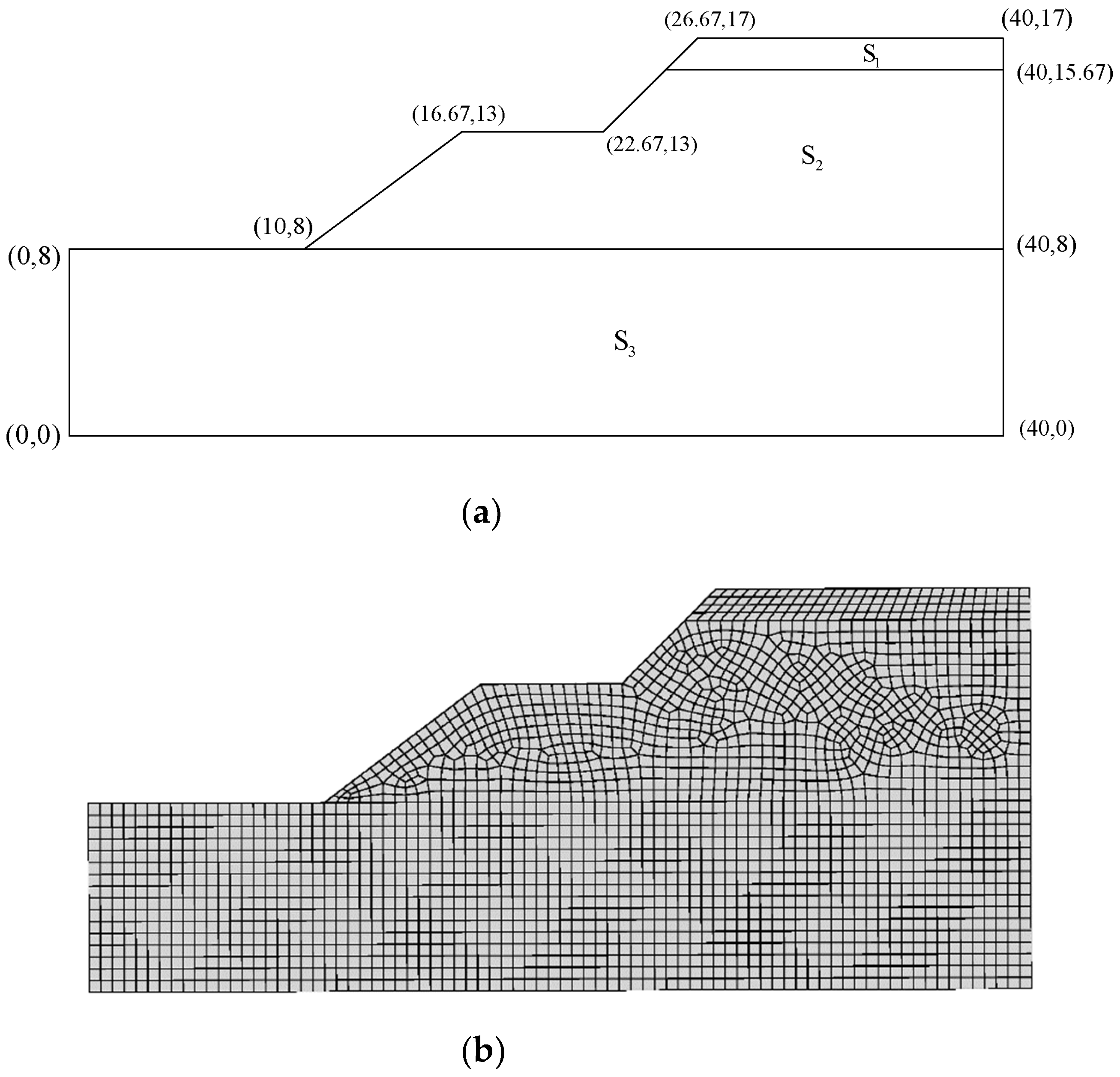
| Soil | |||||
|---|---|---|---|---|---|
| S1 | 18 | 4 | 0.4 | 10 | 13.6 |
| S2 | 19.2 | 4 | 0.38 | 20.8 | 15.1 |
| S3 | 17.5 | 35 | 0.42 | 16.1 | 9.3 |
| Number of Activated Surface | Time (Classic) | Time (Present) | Ratio |
|---|---|---|---|
| 1 | 1.692 | 1.373 | 1.232 |
| 2 | 2.438 | 1.464 | 1.665 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, T.; Lin, S.; Zheng, H.; Chen, Y. Elastoplastic Integration Method of Mohr-Coulomb Criterion. Geotechnics 2022, 2, 599-614. https://doi.org/10.3390/geotechnics2030029
Zhang T, Lin S, Zheng H, Chen Y. Elastoplastic Integration Method of Mohr-Coulomb Criterion. Geotechnics. 2022; 2(3):599-614. https://doi.org/10.3390/geotechnics2030029
Chicago/Turabian StyleZhang, Tan, Songtao Lin, Hong Zheng, and Yanjiang Chen. 2022. "Elastoplastic Integration Method of Mohr-Coulomb Criterion" Geotechnics 2, no. 3: 599-614. https://doi.org/10.3390/geotechnics2030029
APA StyleZhang, T., Lin, S., Zheng, H., & Chen, Y. (2022). Elastoplastic Integration Method of Mohr-Coulomb Criterion. Geotechnics, 2(3), 599-614. https://doi.org/10.3390/geotechnics2030029





