Cyclic Liquefaction Resistance of an Alluvial Natural Sand: A Comparison between Fully and Partially Saturated Conditions
Abstract
:1. Introduction
2. Material Definition
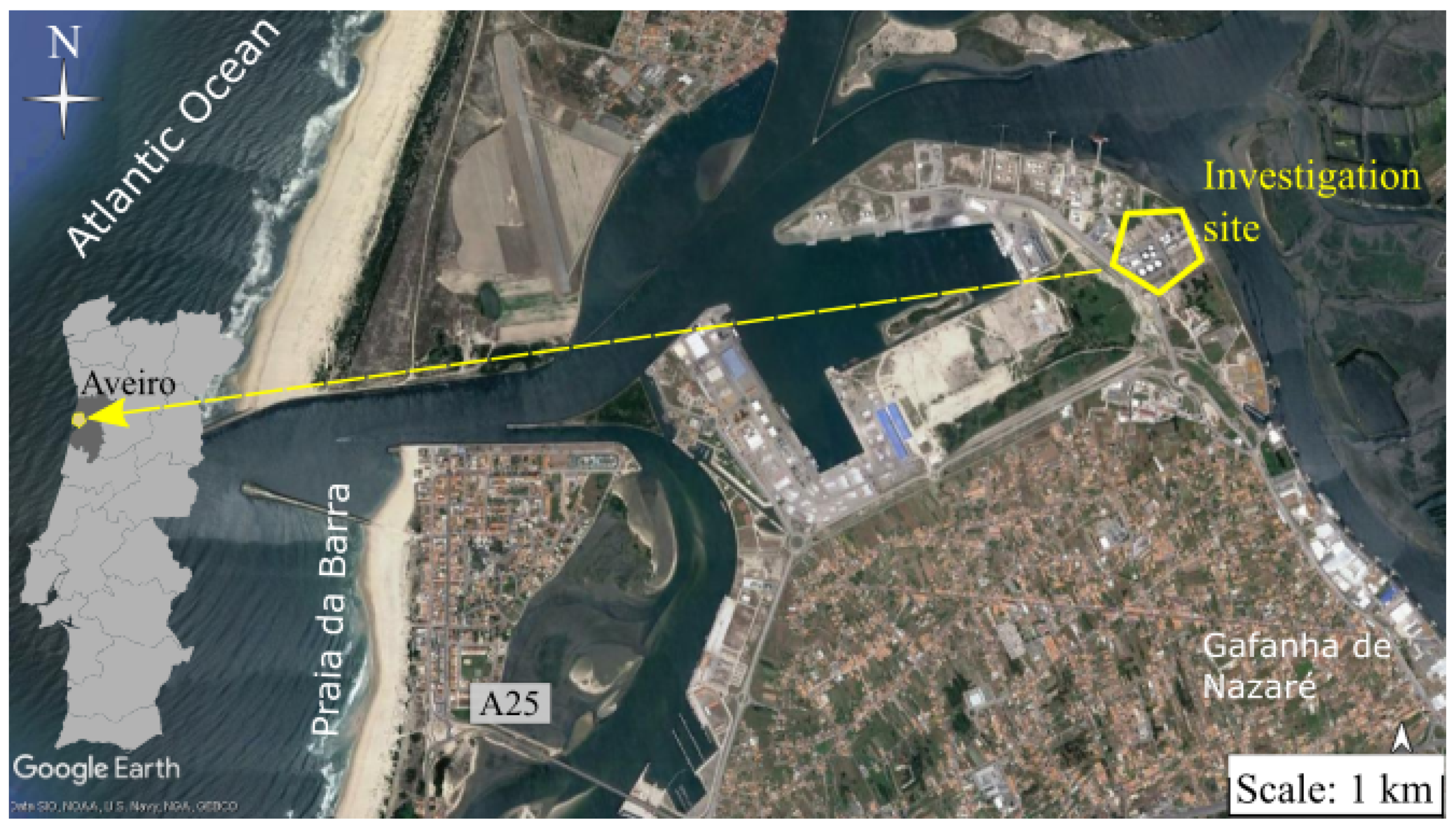
2.1. Experimental Site
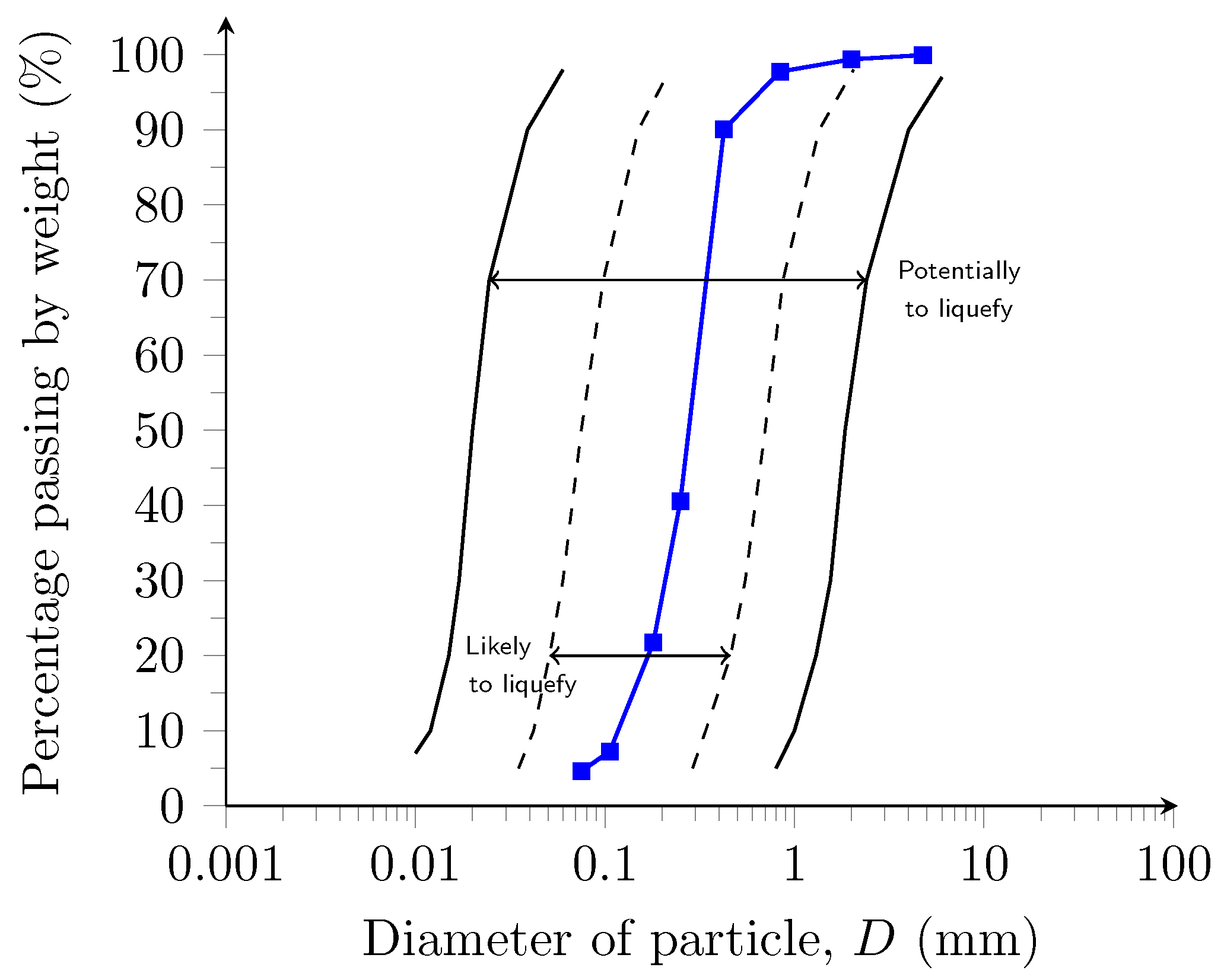
2.2. Soil Description
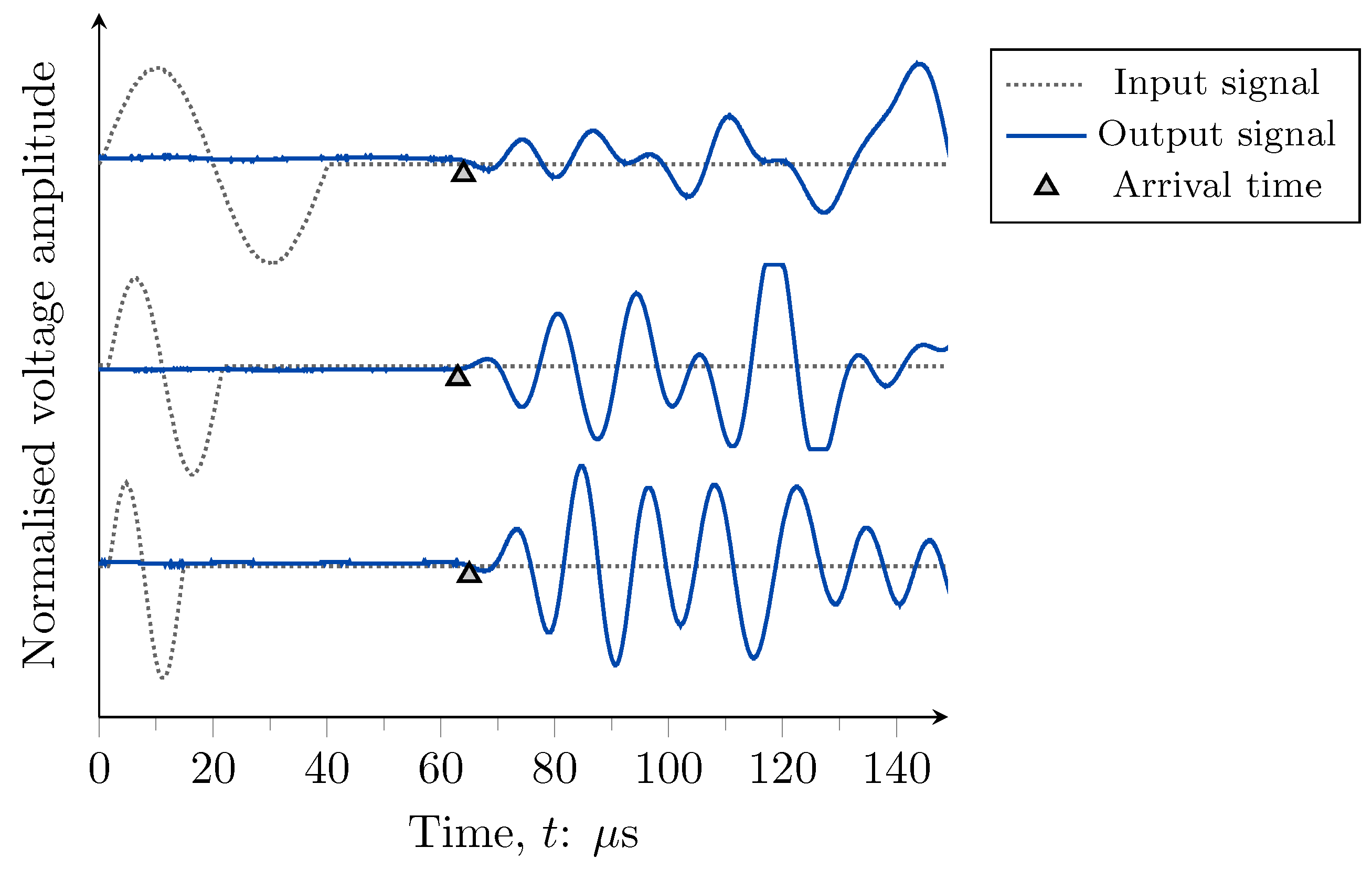
3. Experimental Methodology
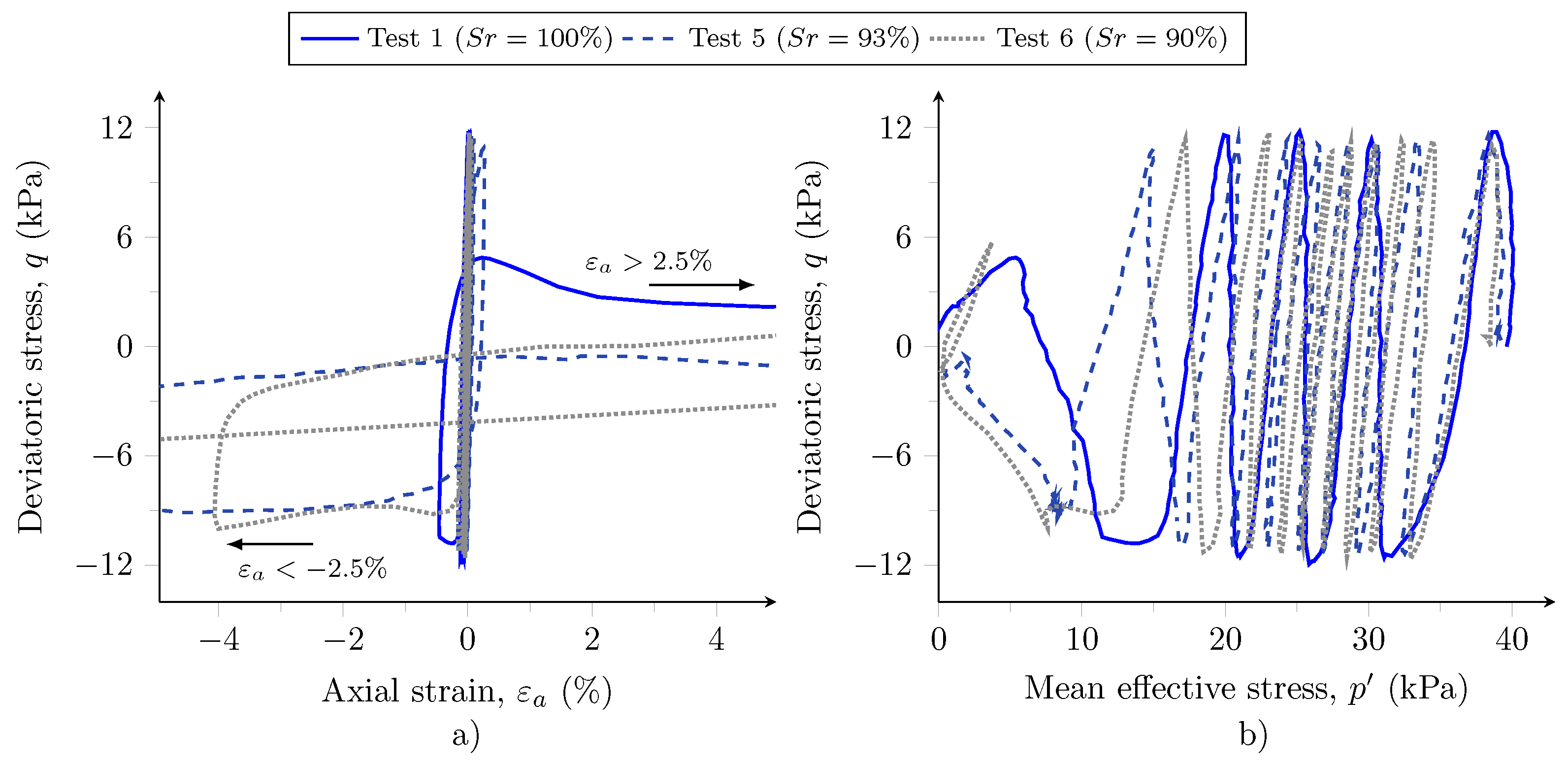
4. Analysis of Results and Discussion
5. Conclusions
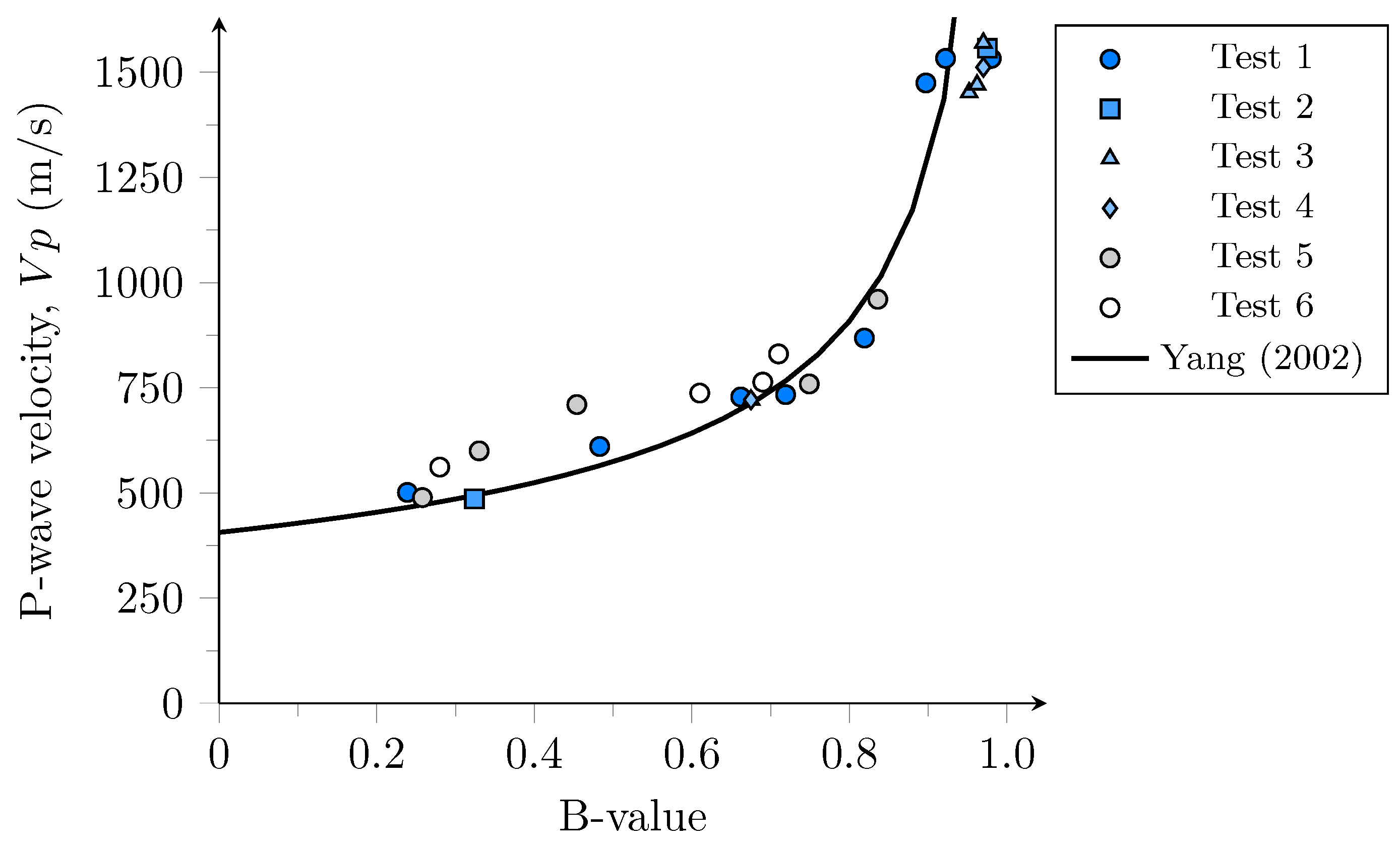
- The relationship between B-value and P-wave velocity of the studied soil fit well with the theoretical model proposed by Yang [31], providing an experimental approach for estimating and controlling the degree of saturation during triaxial testing.
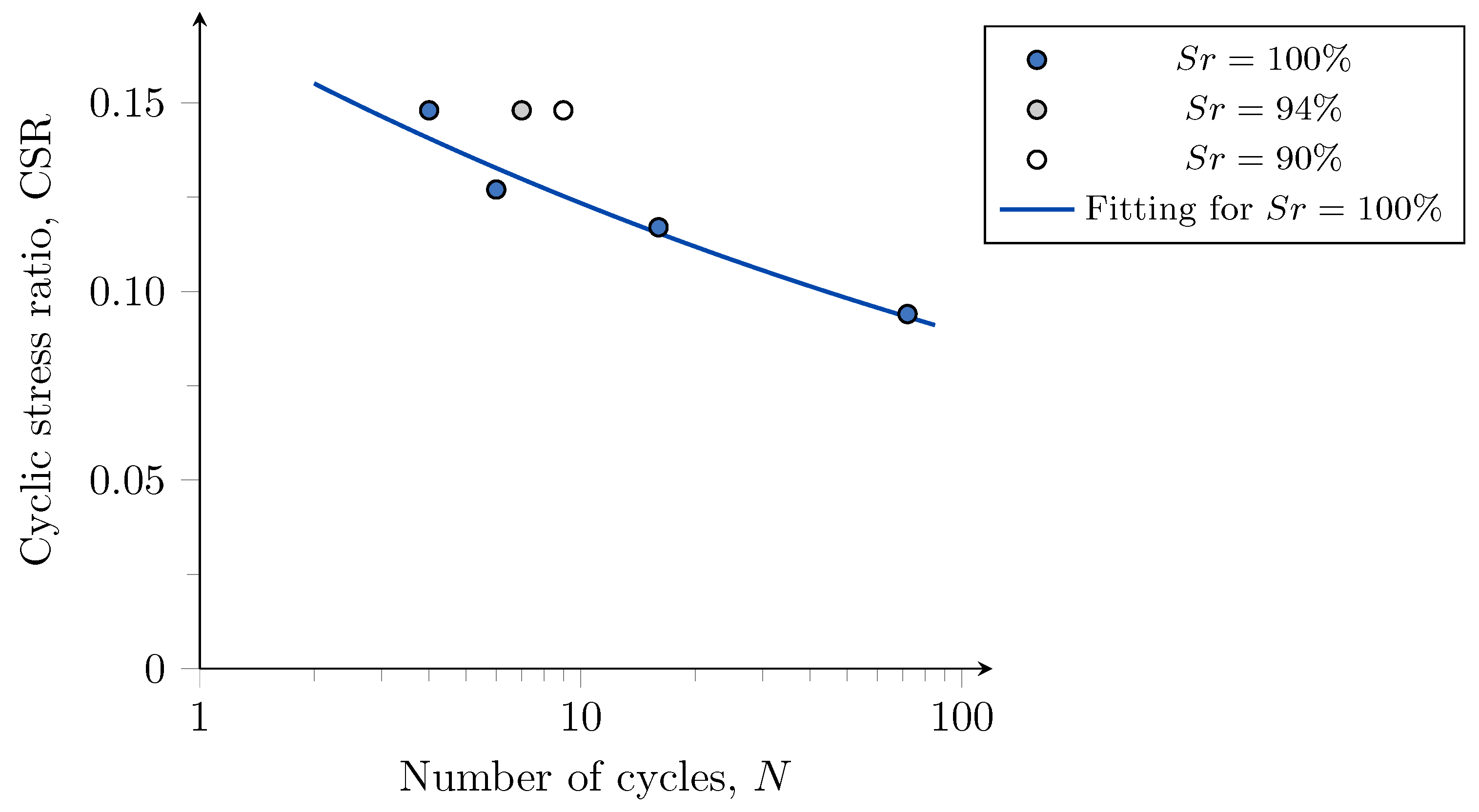
- The decrease in the degree of saturation of about 7% to 10% almost duplicated the number of cycles to trigger liquefaction of Aveiro sand in full saturation conditions. Such an increment was attributed to the compressibility of the air bubbles in the soil voids. The effects of matric suction are negligible because the low value of air entry (of about 2 kPa) of the studied soil—identified for degrees of saturation higher than 85%.
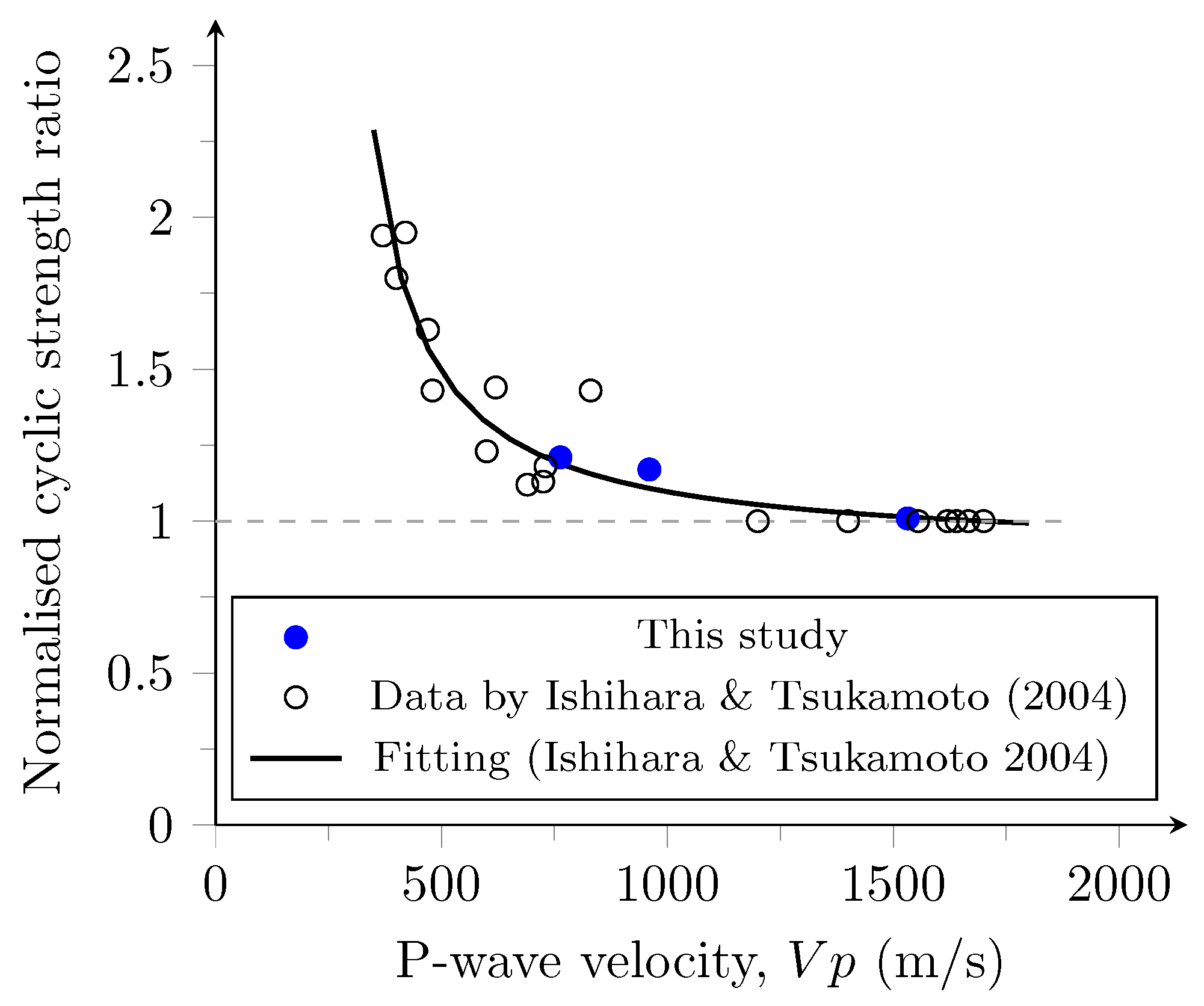
- The normalised cyclic strength ratio as a function of P-wave velocity adequately described the increment of liquefaction resistance with the decrease in the degree of saturation. Experimental data showed that the liquefaction resistance for and is 1.17 and 1.23 times higher than , respectively. Hence, such an approach provided a model suitable for comparisons of cyclic behaviour of the studied sand against other natural sands reported in the literature.
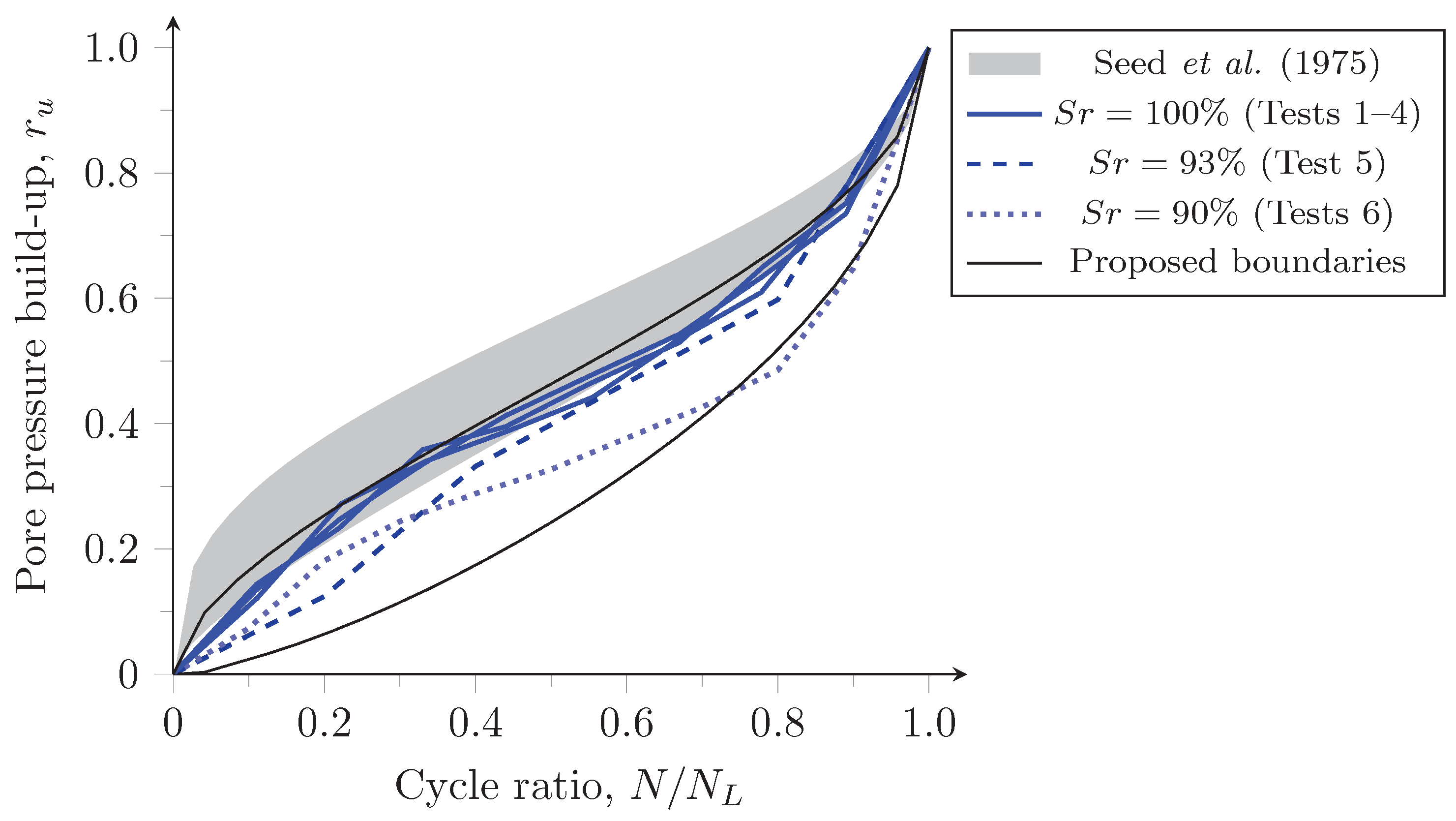
- The pore pressure evolution results, represented by the curves and , showed that the pore pressure build-up of the unsaturated soil specimens does not fit with the narrow zone suggested by Seed & Idriss [36]. Hence, and were recommended to describe the evolution of pore pressure build-up for the studied . This is a direct consequence of the presence of the air bubbles in the soil pores during cyclic loading.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lai, C.G.; Bozzoni, F.; Conca, D.; Famà, A.; Özcebe, A.G.; Zuccolo, E.; Meisina, C.; Bonì, R.; Bordoni, M.; Cosentini, R.M.; et al. Cosentini RM Technical guidelines for the assessment of earthquake induced liquefaction hazard at urban scale. Bull. Earthq. Eng. 2021, 19, 4013–4057. [Google Scholar] [CrossRef]
- Dashti, S.; Bray, J.D.; Pestana, J.M.; Riemer, M.; Wilson, D. Mechanisms of Seismically Induced Settlement of Buildings with Shallow Foundations on Liquefiable Soil. J. Geotech. Geoenviron. Eng. 2010, 136, 151–164. [Google Scholar] [CrossRef] [Green Version]
- Forcellini, D. Numerical simulations of liquefaction on an ordinary building during Italian (20 May 2012) earthquake. Bull. Earthq. Eng. 2020, 17, 4797–4823. [Google Scholar] [CrossRef]
- Huang, Y.; Wen, Z. Recent developments of soil improvement methods for seismic liquefaction mitigation. Nat. Hazards 2015, 76, 1927–1938. [Google Scholar] [CrossRef]
- Towhata, I. Liquefaction Mitigation Measures: A Historical Review. In Latest Developments in Geotechnical Earthquake Engineering and Soil Dynamics; Sitharam, T., Jakka, R., Kolathayar, S., Eds.; Springer: Singapore, 2021; pp. 41–86. [Google Scholar]
- Ravichandran, N. Fully coupled finite element model for dynamics of partially saturated soils. Soil Dyn. Earthq. Eng. 2009, 29, 1294–1304. [Google Scholar] [CrossRef]
- Lopez-Caballero, F.; Modaressi-Farahmand-Razavi, A. Numerical simulation of mitigation of liquefaction seismic risk by preloading and its effects on the performance of structures. Soil Dyn. Earthq. Eng. 2013, 49, 27–38. [Google Scholar] [CrossRef]
- Lopez-Caballero, F.; Modaressi-Farahmand-Razavi, A. Numerical simulation of liquefaction effects on seismic SSI. Soil Dyn. Earthq. Eng. 2008, 28, 85–98. [Google Scholar] [CrossRef] [Green Version]
- Elgamal, A.; Lu, J.; Forcellini, D. Mitigation of Liquefaction-Induced Lateral Deformation in a Sloping Stratum: Three-dimensional Numerical Simulation. J. Geotech. Geoenviron. Eng. 2009, 135, 1672–1682. [Google Scholar] [CrossRef]
- Tatsuoka, F.; Toki, S.; Miura, S.; Kato, H.; Okamoto, M.; Yamada, S.-I.; Yasuda, S.; Tanizawa, F. Some factors affecting cyclic undrained triaxial strength of sands. Soils Found. 1986, 26, 99–116. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Chu, J.; Liu, H. Undrained shear strength of desaturated loose sand under monotonic shearing. Soils Found. 2014, 54, 910–916. [Google Scholar] [CrossRef] [Green Version]
- Zeybek, A.; Madabhushi, G.S.P. Physical modelling of air injection to remediate liquefaction. Int. J. Phys. Model. Geotech. 2018, 18, 68–80. [Google Scholar] [CrossRef] [Green Version]
- Yegian, M.K.; Eseller-Bayat, E.; Alshawabkeh, A.; Ali, S. Induced-partial saturation for liquefaction mitigation: Experimental investigation. J. Geotech. Geoenviron. Eng. 2007, 134, 372–380. [Google Scholar] [CrossRef] [Green Version]
- Mele, L.; Tan Tian, J.; Lirer, S.; Flora, A.; Koseki, J. Liquefaction resistance of unsaturated sands: Experimental evidence and theoretical interpretation. Géotechnique 2019, 69, 541–553. [Google Scholar] [CrossRef]
- Molina-Gómez, F.; Bulla-Cruz, L.A.; Moreno-Anselmi, L.A.; Ruge, J.C.; Arévalo-Daza, C. Assessment of groundwater levelvariations using multivariate statistical methods. Ing. E Investig. 2019, 39, 36–42. [Google Scholar]
- Flora, A.; Bilotta, E.; Chiaradonna, A.; Lier, S.; Mele, L.; Pingue, L. A field trial to test the efficiency of induced partial saturation and horizontal drains to mitigate the susceptibility of soils to liquefaction. Bull. Earthq. Eng. 2021, 19, 3835–3864. [Google Scholar] [CrossRef]
- Rodrigues, C.; Amoroso, S.; Viana da Fonseca, A.; Cruz, N. Estudo do risco de liquefação das areias de Aveiro a partir de ensaios SCPTU e SDMT. In 14 Congresso Nacional de Geotecnia; UBI: Covilhã, Portugal, 2014. (In Portuguese) [Google Scholar]
- Eurocode 8—Design of Structures for Earthquake Resistance. Part 5: Foundations, Retaining Structures and Geotechnical Aspects; European Committee for Standardization: Brussels, Belgium, 2005; p. 229.
- Amoroso, S.; Rodrigues, C.; Viana da Fonseca, A.; Cruz, N. Liquefaction Evaluation of Aveiro Sands from SCPTU and SDMT Tests. In Proceedings of the 3rd International Conference on the Flat Dilatometer, Rome, Italy, 14–17 June 2015. [Google Scholar]
- Robertson, P.K. Interpretation of cone penetration tests—A unified approach. Can. Geotech. J. 2009, 46, 1337–1355. [Google Scholar] [CrossRef] [Green Version]
- Molina-Gómez, F.; Viana da Fonseca, A.; Ferreira, C.; Sousa, F.; Bulla-Cruz, L.A. Defining the soil stratigraphy from seismic piezocone data: A clustering approach. Eng. Geol. 2021, 287, 106111. [Google Scholar] [CrossRef]
- Tsuchida, H. Prediction and countermeasure against the liquefaction in sand deposits. In Seminar in the Port and Harbour Research Institute; Ministry of Transport of Japan: Yokosuka, Japan, 1970; pp. 3.1–3.2. (In Japanese) [Google Scholar]
- Ramos, C.; Ferreira, C.; Molina-Gómez, F.; Viana da Fonseca, A. Critical state lines of Portuguese liquefiable sands. E3S Web Conf. 2019, 92, 06003. [Google Scholar] [CrossRef]
- Cho, G.-C.; Dodds, J.; Santamarina, J.C. Particle Shape Effects on Packing Density, Stiffness, and Strength: Natural and Crushed Sands. J. Geotech. Geoenviron. Eng. 2006, 132, 591–602. [Google Scholar] [CrossRef] [Green Version]
- Viana da Fonseca, A.; Cordeiro, D.; Molina-Gómez, F. Recommended Procedures to Assess Critical State Locus from Triaxial Tests in Cohesionless Remoulded Samples. Geotechnics 2021, 1, 95–127. [Google Scholar] [CrossRef]
- Viana da Fonseca, A.; Ferreira, C.; Fahey, M. A Framework Interpreting Bender Element Tests, Combining Time-Domain and Frequency-Domain Methods. Geotech. Test. J. 2009, 32, 100974. [Google Scholar]
- Molina-Gómez, F.; Viana da Fonseca, A.; Ferreira, C.; Camacho-Tauta, J. Dynamic properties of two historically liquefiable sands in the Lisbon area. Soil Dyn. Earthq. Eng. 2020, 132, 106101. [Google Scholar] [CrossRef]
- D6836—Standard Test Methods for Determination of the Soil Water Chararcteristic Curve for Desorption Using a Hanging Column, Pressure Extractor, Chilled Mirror Hygrometer, and/or Centrifuge; ASTM International: West Conshohocken, PA, USA, 2016.
- Soares, M.; Viana da Fonseca, A. Factors Affecting Steady State Locus in Triaxial Tests. Geotech. Test. J. 2016, 36, 20150228. [Google Scholar] [CrossRef]
- Ferreira, C.; Díaz-Durán, F.; Viana da Fonseca, A.; Cascante, G. New approach to concurrent Vs and Vp measurements using bender elements. Geotech. Test. J. 2021, 44, 1801. [Google Scholar] [CrossRef]
- Yang, J. Liquefaction resistance of sand in relation to P-wave velocity. Géotechnique 2002, 52, 295–298. [Google Scholar] [CrossRef]
- Santamarina, J.C.; Klein, K.A.; Fam, M.A. Soils and Waves, 1st ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2001. [Google Scholar]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Tamura, S.; Tokimatsu, K.; Abe, A.; Sato, M. Effects of air bubbles on B-value and P-wave velocity of a partly saturated sand. Soils Found. 2002, 42, 121–191. [Google Scholar] [CrossRef] [Green Version]
- Ishihara, K.; Tsukamoto, Y. Cyclic strength of imperfectly saturated sands and analysis of liquefaction. Proc. Jpn. Acad. 2004, 80, 372–391. [Google Scholar] [CrossRef] [Green Version]
- Seed, H.B.; Idriss, I.M. Simplified procedure for evaluating liquefaction potential. J. Soil Mech. Found. Div. 1971, 97, 1249–1273. [Google Scholar] [CrossRef]



| Parameter | Type 1 | Type 2 |
|---|---|---|
| Seismic zone | 1.6 | 2.4 |
| 7.2 | 4.4 | |
| (m/s2) | 0.35 | 1.1 |
| 1 | 1 | |
| 0.35 | 1.1 | |
| Ground type | D | D |
| 2.00 | 2.00 | |
| S | 2.00 | 1.97 |
| (m/s2) | 0.70 | 2.16 |
| (g) | 0.70 | 0.22 |
| Parameter | Value |
|---|---|
| 2.67 | |
| 0.88 | |
| 0.53 | |
| FC (%) | 4.60 |
| (mm) | 0.23 |
| 2.31 | |
| 1.24 |
| Parameter | Symbol | Value |
|---|---|---|
| Sphericity | S | 0.70 |
| Roundness | R | 0.57 |
| Regularity | 0.64 |
| Test | Back-Pressure (kPa) | B-Value | (m/s) |
|---|---|---|---|
| 1 | 500 | 0.98 | 1532 |
| 2 | 500 | 0.98 | 1567 |
| 3 | 500 | 0.97 | 1570 |
| 4 | 150 | 0.98 | 1512 |
| 5 | 150 | 0.84 | 690 |
| 6 | 100 | 0.69 | 763 |
| Test | (%) | (%) | CSR | |
|---|---|---|---|---|
| 1 | 34 | 100 | 0.148 | 4 |
| 2 | 35 | 100 | 0.127 | 6 |
| 3 | 36 | 100 | 0.117 | 16 |
| 4 | 33 | 100 | 0.095 | 71 |
| 5 | 35 | 93 | 0.152 | 7 |
| 6 | 34 | 90 | 0.151 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cordeiro, D.; Molina-Gómez, F.; Ferreira, C.; Rios, S.; Viana da Fonseca, A. Cyclic Liquefaction Resistance of an Alluvial Natural Sand: A Comparison between Fully and Partially Saturated Conditions. Geotechnics 2022, 2, 1-13. https://doi.org/10.3390/geotechnics2010001
Cordeiro D, Molina-Gómez F, Ferreira C, Rios S, Viana da Fonseca A. Cyclic Liquefaction Resistance of an Alluvial Natural Sand: A Comparison between Fully and Partially Saturated Conditions. Geotechnics. 2022; 2(1):1-13. https://doi.org/10.3390/geotechnics2010001
Chicago/Turabian StyleCordeiro, Diana, Fausto Molina-Gómez, Cristiana Ferreira, Sara Rios, and António Viana da Fonseca. 2022. "Cyclic Liquefaction Resistance of an Alluvial Natural Sand: A Comparison between Fully and Partially Saturated Conditions" Geotechnics 2, no. 1: 1-13. https://doi.org/10.3390/geotechnics2010001
APA StyleCordeiro, D., Molina-Gómez, F., Ferreira, C., Rios, S., & Viana da Fonseca, A. (2022). Cyclic Liquefaction Resistance of an Alluvial Natural Sand: A Comparison between Fully and Partially Saturated Conditions. Geotechnics, 2(1), 1-13. https://doi.org/10.3390/geotechnics2010001






