Modeling of Seismic Energy Dissipation of Rocking Foundations Using Nonparametric Machine Learning Algorithms
Abstract
:1. Introduction
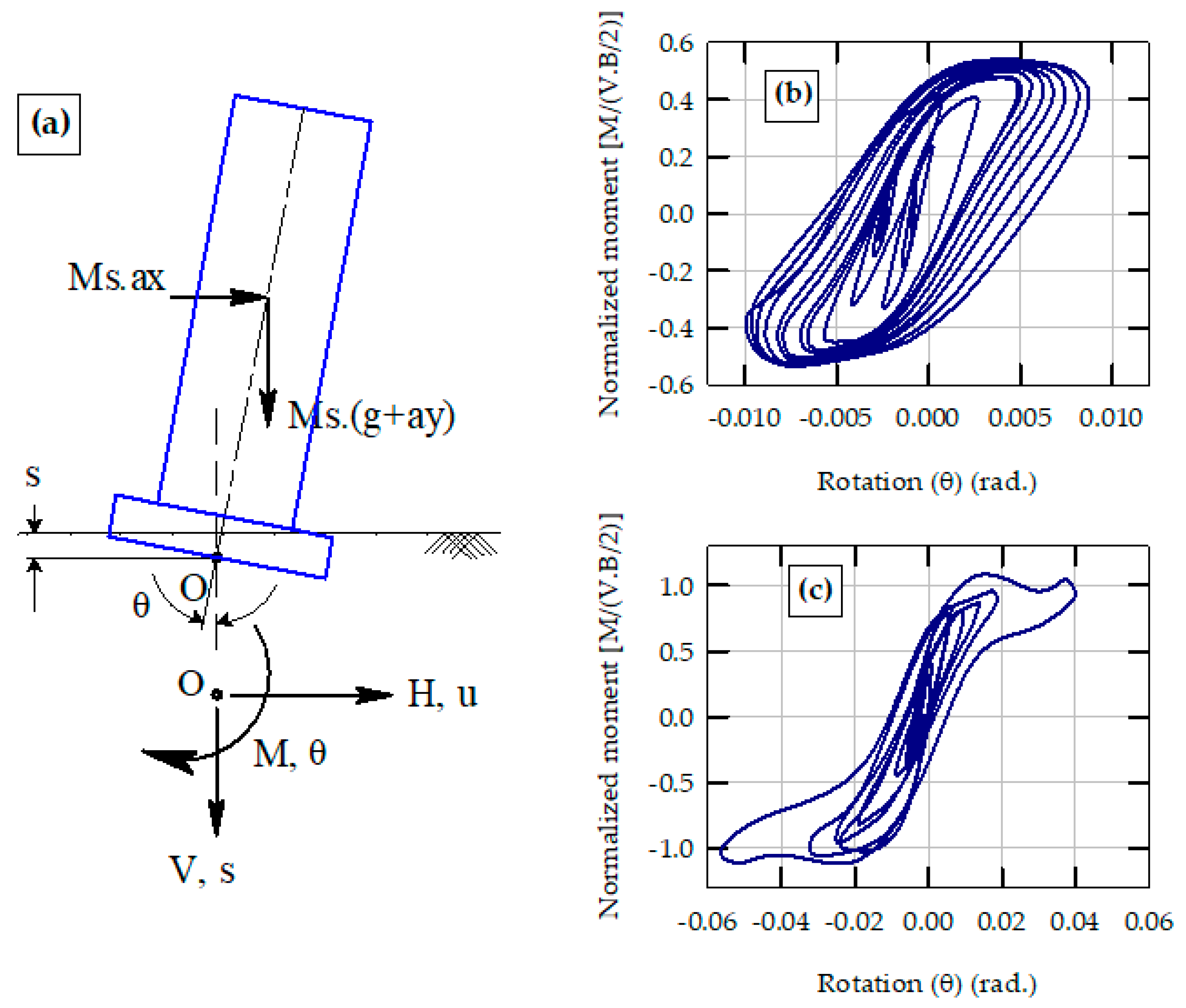
2. Background: Seismic Energy Dissipation of Rocking Shallow Foundations
3. Database, Input Features and Performance Parameter
3.1. Rocking Foundations Database
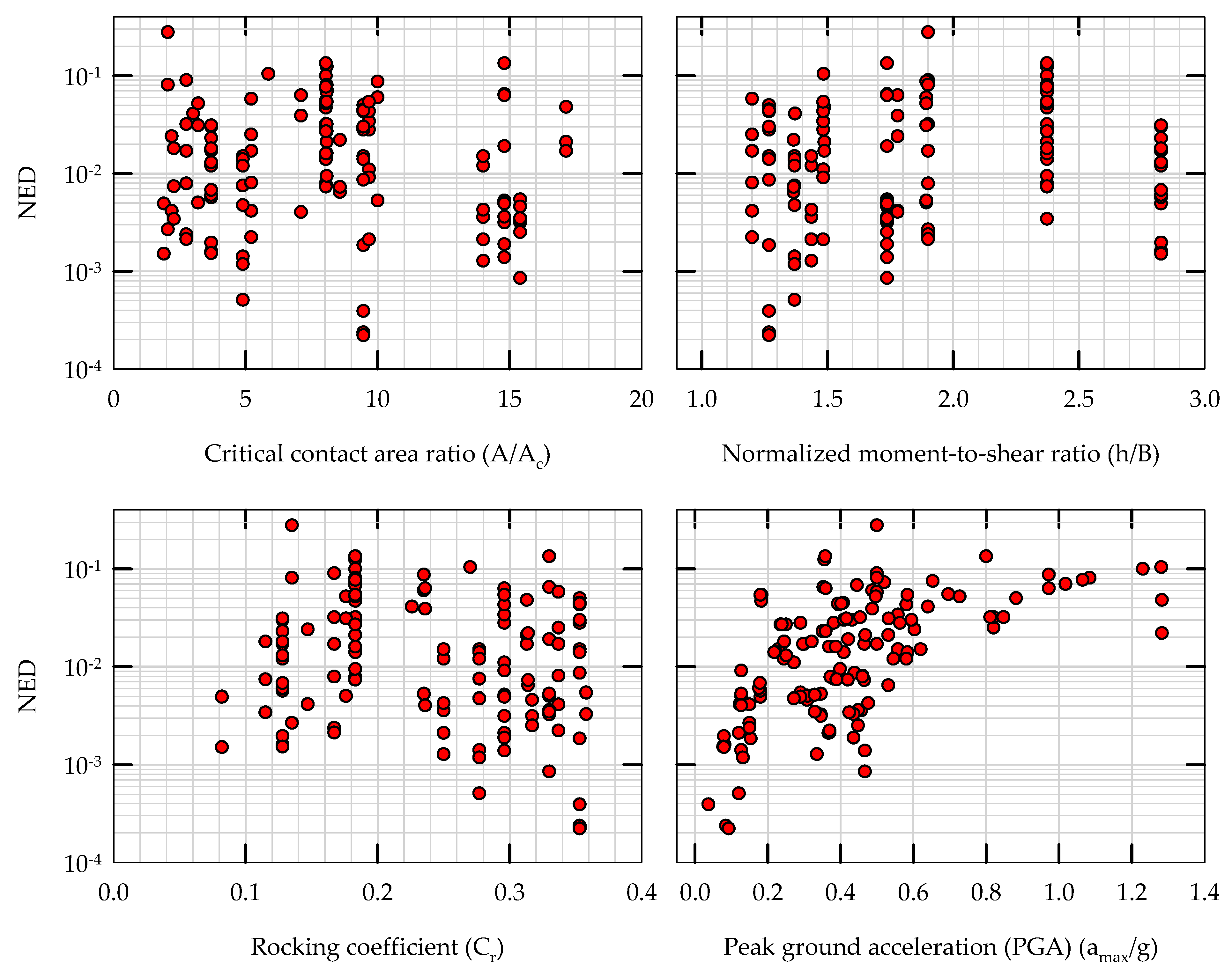
3.2. Input Features
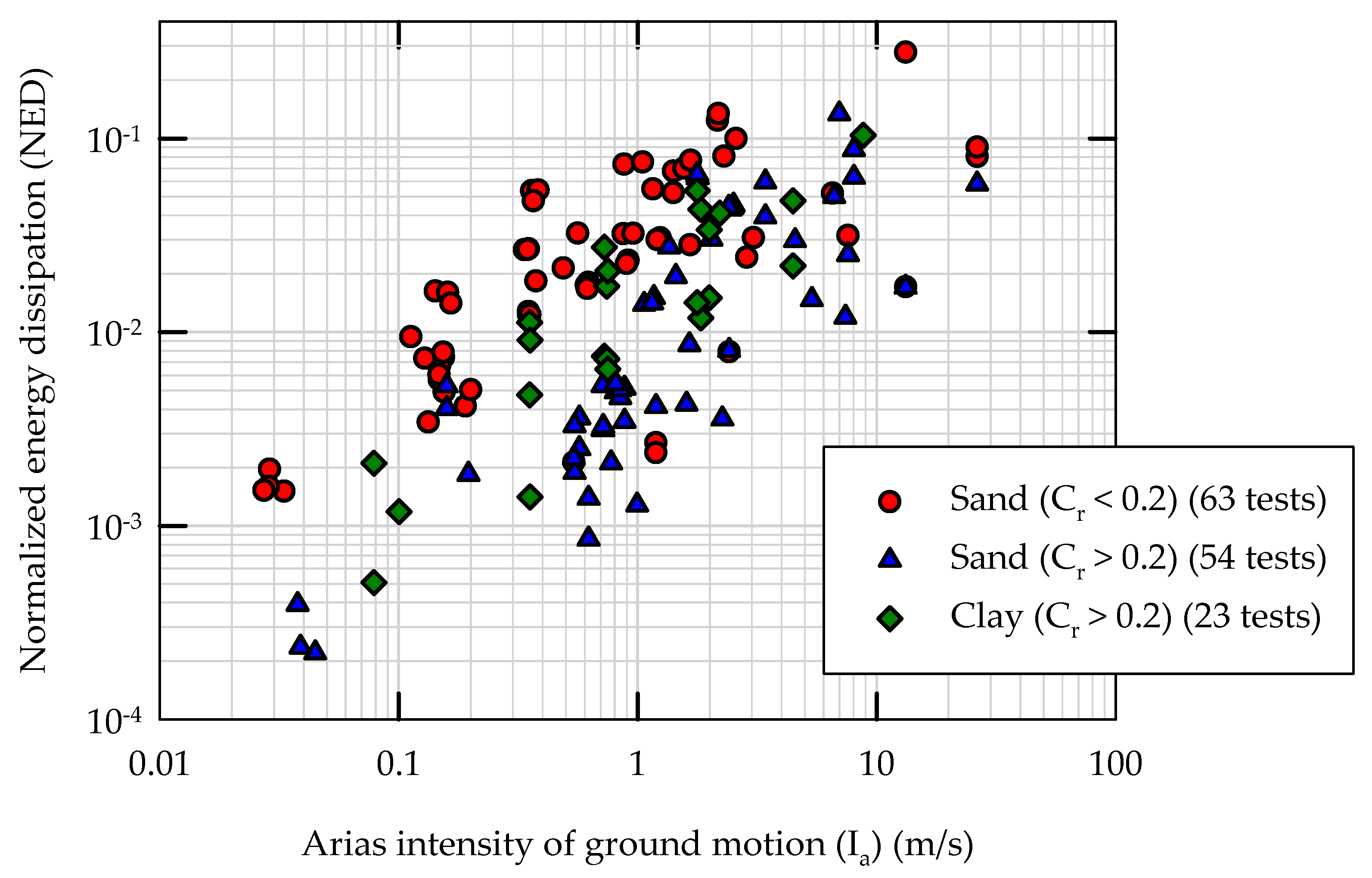
3.3. Performance Parameter: Normalized Energy Dissipation (NED)
3.4. Feature Transformation and Normalization
4. Machine Learning Algorithms
4.1. Weighted k-Nearest Neighbors Regression (KNN)
4.2. Support Vector Regression (SVR)
4.3. Decision Tree Regression (DTR)
5. Results and Discussion
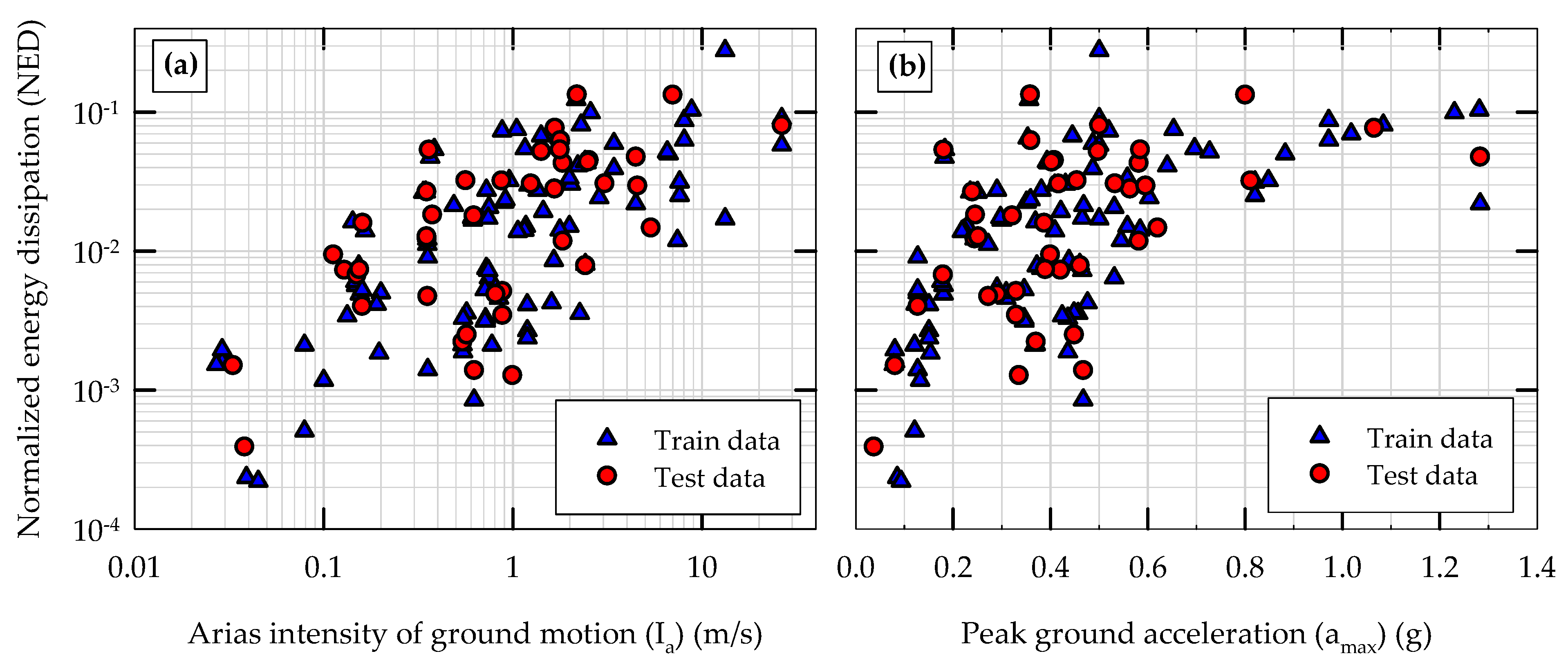
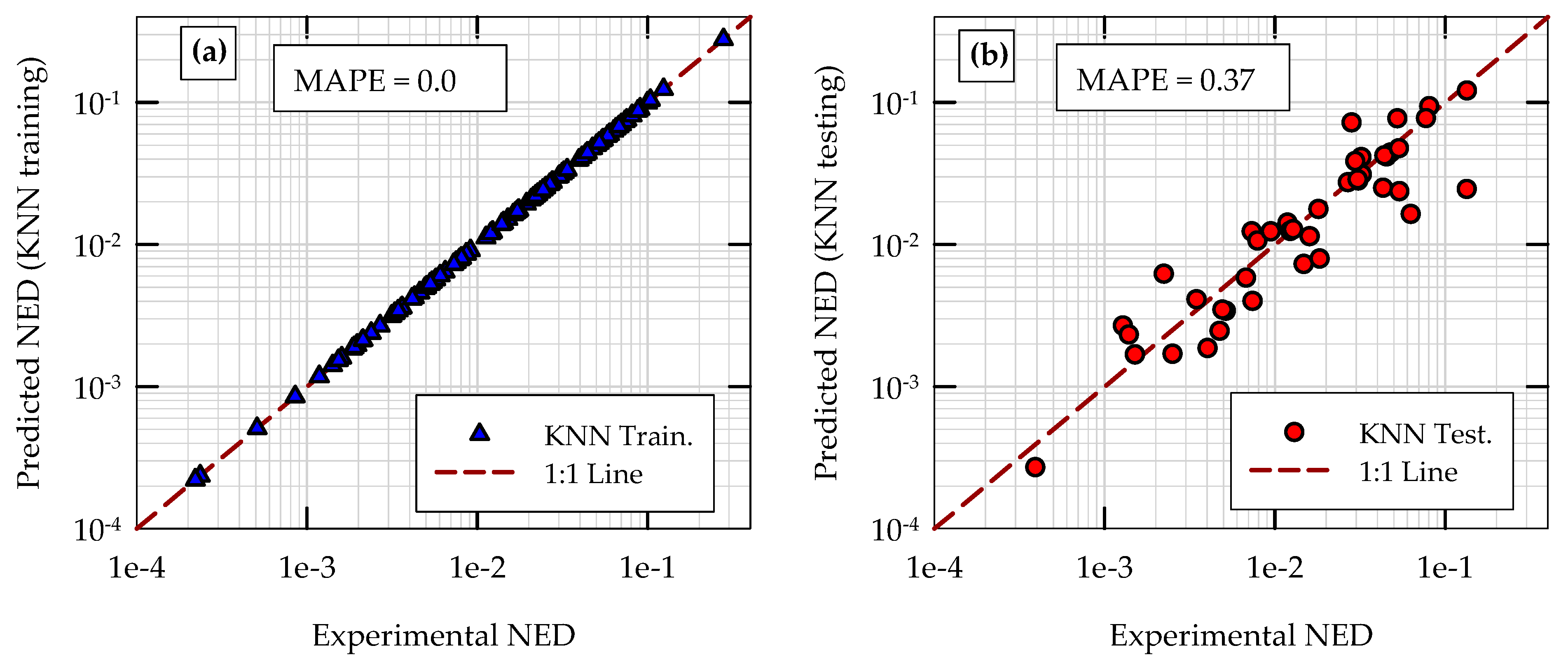
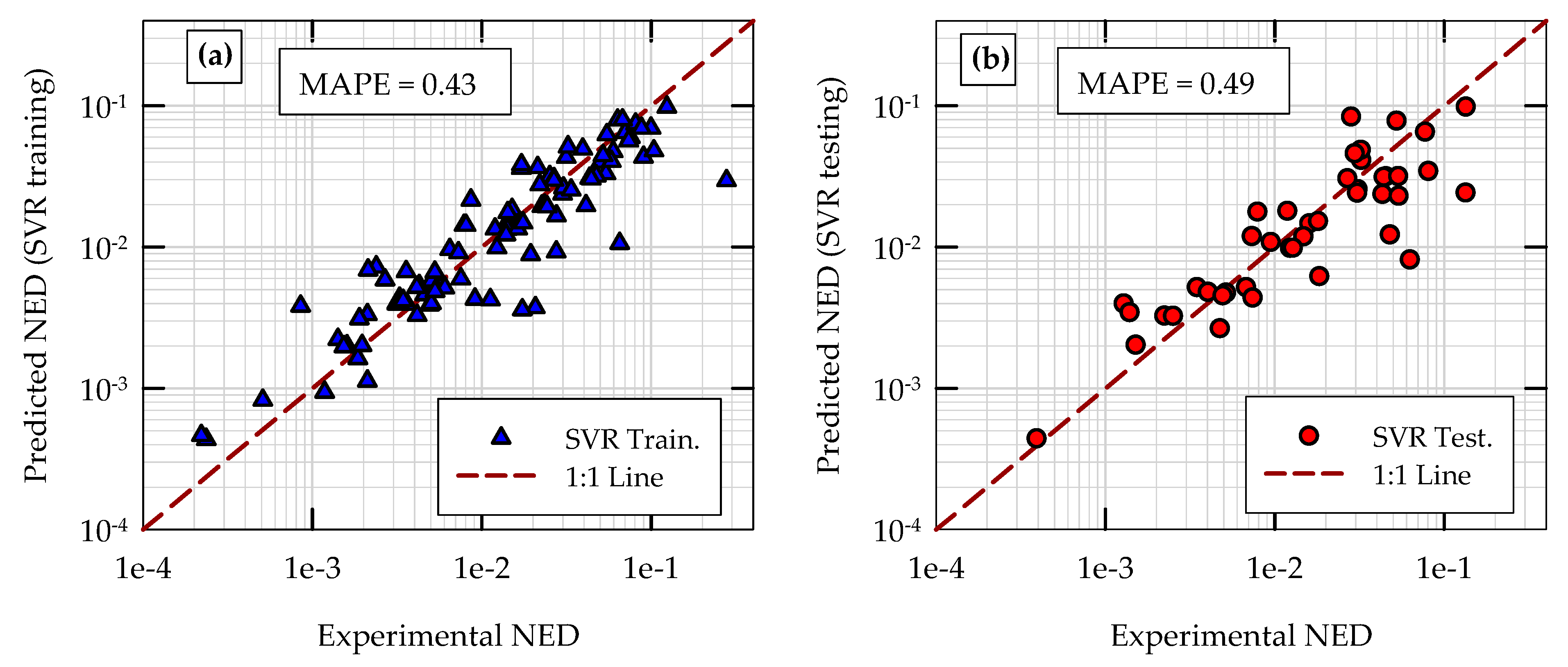
5.1. Initial Training and Testing of Models
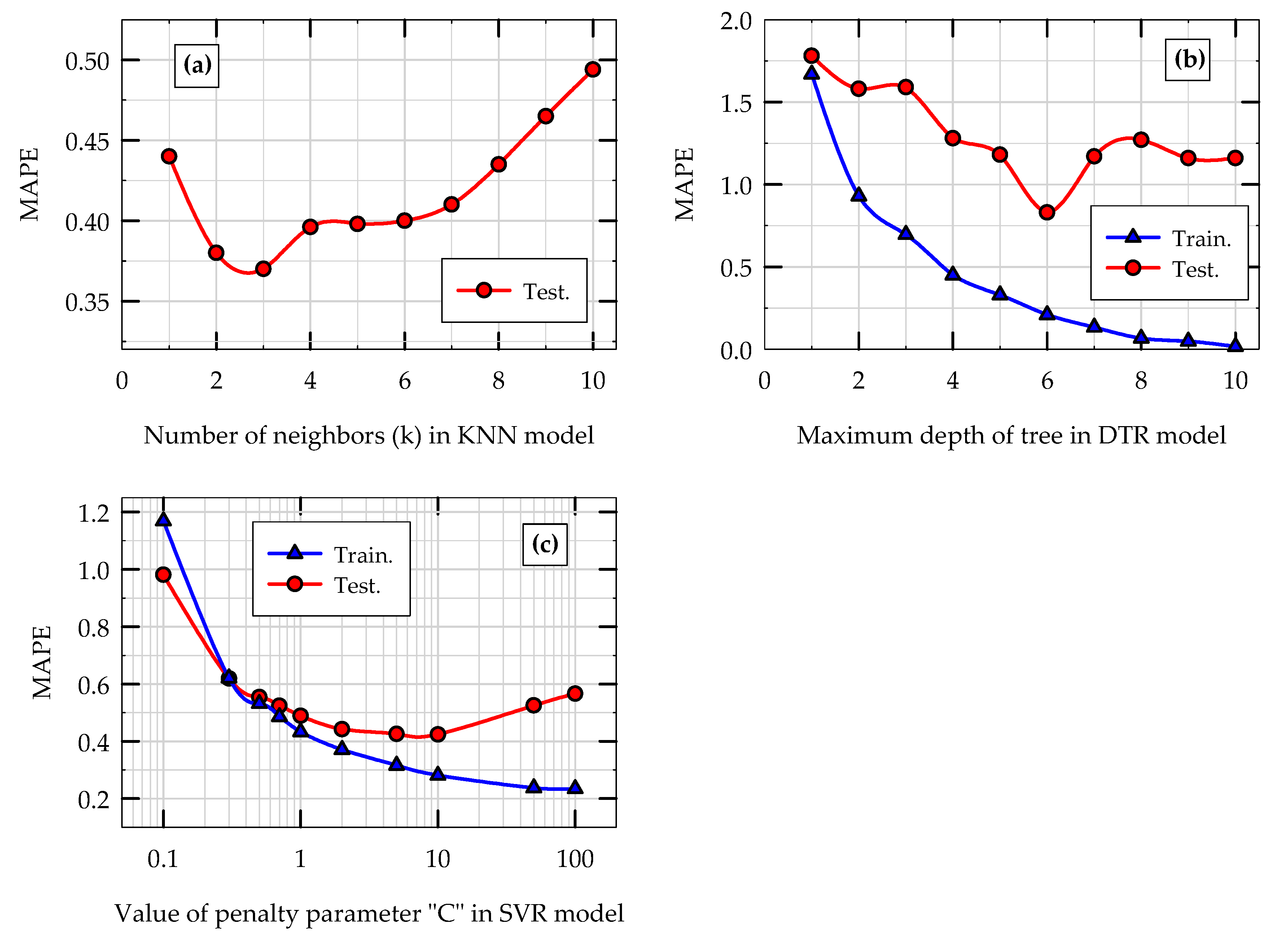
5.2. Hyperparameter Tuning of Models
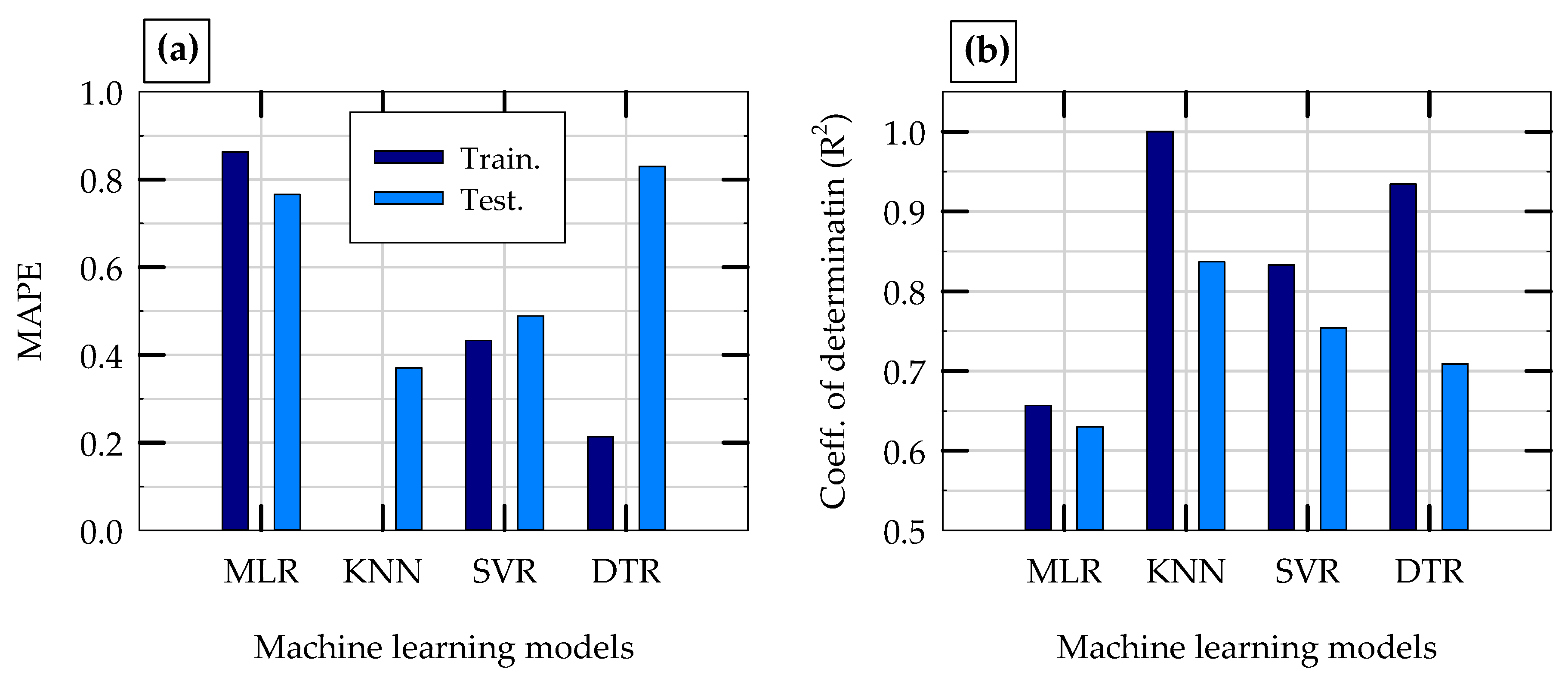
5.3. Comparison of Model Performances in Initial Training and Testing Phases
5.4. Repeated k-Fold Cross Validation Tests of Models
6. Discussion and Implications
7. Summary and Conclusions
7.1. Summary
7.2. Conclusions
- All three nonparametric machine learning models developed in this study (KNN, SVR and DTR) perform better than the parametric MLR model in capturing the complex relationship between NED and input features of rocking foundations.
- The overall performance of KNN and MLR models developed in this study are an improvement to the previously published results on the same topic, when the same experimental data with slightly different input features were used [58].
- Based on hyperparameter tuning of KNN, SVR and DTR models, k = 3, C = 1.0, and maximum depth of tree = 6, respectively, are found to be the optimum values for the respective hyperparameters for the problem considered.
- Among all four machine learning models developed in this study, KNN model consistently outperforms all other models in terms of accuracy of predictions. The average MAPE of KNN model in repeated 5-fold and 7-fold cross validations are 0.46 and 0.44, respectively. The second most accurate model is SVR, for which the corresponding average MAPE values are 0.54 and 0.52. On average, the accuracy of KNN model is about 16% higher than that of SVR model.
- Among all four machine learning models developed, SVR model is the most consistent in terms of training and testing errors as well as in terms of the variance in MAPE values in repeated k-fold cross validation tests. The total variance in MAPE of SVR model is 0.43 and 0.57 in repeated 5-fold and 7-fold cross validations, respectively. The second most consistent model in terms of total variance in MAPE is KNN, for which, the corresponding total variance in MAPE values are 0.62 and 0.69. On average, the variance of SVR model is about 27% smaller than that of KNN model.
- The DTR model has higher variance when compared to all other three models, however, the mean accuracy of DTR model is still better than that of the MLR model. The overall average MAPE values of DTR is 0.79, which is still better than the corresponding MAPE value of MLR model (0.90). The accuracy and variance of DTR model could be improved by combining multiple DTR models together using ensemble methods such as bagging and boosting.
- The data-driven predictive models developed in this study can be used in combination with other physics-based or mechanics-based models to complement each other in modeling of rocking behavior of shallow foundations in practical applications. One such recently emerged approach is theory-guided machine learning, where scientific knowledge is used as instructional guide to machine learning algorithms [67,68,69,70].
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Gajan, S.; Phalen, J.D.; Kutter, B.L.; Hutchinson, T.C.; Martin, G. Centrifuge modeling of load-deformation behavior of rocking shallow foundations. Soil Dyn. Earthq. Eng. 2005, 25, 773–783. [Google Scholar] [CrossRef]
- Gajan, S.; Kutter, B.L. Capacity, settlement, and energy dissipation of shallow footings subjected to rocking. J. Geotech. Geoenviron. Eng. 2008, 134, 1129–1141. [Google Scholar] [CrossRef] [Green Version]
- Shirato, M.; Kouno, T.; Asai, R.; Nakatani, S.; Fukui, J.; Paolucci, R. Large-scale experiments on nonlinear behavior of shallow foundations subjected to strong earthquakes. Soils Found. 2008, 48, 673–692. [Google Scholar] [CrossRef] [Green Version]
- Deng, L.; Kutter, B.L.; Kunnath, S.K. Centrifuge modeling of bridge systems designed for rocking foundations. J. Geotech. Geoenviron. Eng. 2012, 138, 335–344. [Google Scholar] [CrossRef]
- Drosos, V.; Georgarakos, T.; Loli, M.; Anastasopoulos, I.; Zarzouras, O.; Gazetas, G. Soil-foundation-structure interaction with mobilization of bearing capacity: Experimental study on sand. J. Geotech. Geoenviron. Eng. 2012, 138, 1369–1386. [Google Scholar] [CrossRef] [Green Version]
- Gelagoti, F.; Kourkoulis, R.; Anastasopoulos, I.; Gazetas, G. Rocking isolation of low-rise frame structures founded on isolated footings. Earthq. Eng. Struct. Dyn. 2012, 41, 1177–1197. [Google Scholar] [CrossRef]
- Anastasopoulos, I.; Loli, M.; Georgarakos, T.; Drosos, V. Shaking table testing of rocking—Isolated bridge pier on sand. J. Earthq. Eng. 2013, 17, 1–32. [Google Scholar] [CrossRef]
- Antonellis, G.; Gavras, A.G.; Panagiotou, M.; Kutter, B.L.; Guerrini, G.; Sander, A.; Fox, P.J. Shake table test of large-scale bridge columns supported on rocking shallow foundations. J. Geotech. Geoenviron. Eng. 2015, 141, 04015009. [Google Scholar] [CrossRef]
- Liu, W.; Hutchinson, T.; Gavras, A.; Kutter, B.L.; Hakhamaneshi, M. Seismic behavior of frame-wall-rocking foundation systems. II: Dynamic testing phase. J. Geotech. Geoenviron. Eng. 2015, 141, 04015060. [Google Scholar] [CrossRef]
- Ko, K.-W.; Ha, J.-G.; Park, H.-J.; Kim, D.-S. Centrifuge modeling of improved design for rocking foundation using short piles. J. Geotech. Geoenviron. Eng. 2019, 145, 04019031. [Google Scholar] [CrossRef]
- Sharma, K.; Deng, L. Characterization of rocking shallow foundations on cohesive soil using field snap-back tests. J. Geotech. Geoenviron. Eng. 2019, 145, 04019058. [Google Scholar] [CrossRef]
- Gavras, A.G.; Kutter, B.L.; Hakhamaneshi, M.; Gajan, S.; Tsatsis, A.; Sharma, K.; Kouno, T.; Deng, L.; Anastasopoulos, I.; Gazetas, G. Database of rocking shallow foundation performance: Dynamic shaking. Earthq. Spectra 2020, 36, 960–982. [Google Scholar] [CrossRef]
- Hakhamaneshi, M.; Kutter, B.L.; Gavras, A.G.; Gajan, S.; Tsatsis, A.; Liu, W.; Sharma, K.; Pianese, G.; Kouno, T.; Deng, L.; et al. Database of rocking shallow foundation performance: Slow-cyclic and monotonic loading. Earthq. Spectra 2020, 36, 1585–1606. [Google Scholar] [CrossRef]
- Gajan, S.; Soundararajan, S.; Yang, M.; Akchurin, D. Effects of rocking coefficient and critical contact area ratio on the performance of rocking foundations from centrifuge and shake table experimental results. Soil Dyn. Earthq. Eng. 2021, 141, 106502. [Google Scholar] [CrossRef]
- Kelly, T.E. Tentative seismic design guidelines for rocking structures. Bull. N. Z. Soc. Earthq. Eng. 2009, 42, 239–274. [Google Scholar] [CrossRef]
- Anastasopoulos, I.; Gazetas, G.; Loli, M.; Apostolou, M.; Gerolymos, N. Soil failure can be used for seismic protection of structures. Bull. Earthq. Eng. 2010, 8, 309–326. [Google Scholar] [CrossRef]
- Liu, W.; Hutchinson, T.C.; Kutter, B.L.; Hakhamaneshi, M.; Aschheim, M.A.; Kunnath, S.K. Demonstration of compatible yielding between soil-foundation and superstructure components. J. Struct. Eng. 2013, 139, 1408–1420. [Google Scholar] [CrossRef]
- Pecker, A.; Paolucci, R.; Chatzigogos, C.; Correia, A.A.; Figini, R. The role of non-linear dynamic soil-foundation interaction on the seismic response of structures. Bull. Earthq. Eng. 2014, 12, 1157–1176. [Google Scholar] [CrossRef]
- Kutter, B.L.; Moore, M.; Hakhamaneshi, M.; Champion, C. Rationale for shallow foundation rocking provisions in ASCE 41-13. Earthq. Spectra 2019, 32, 1097–1119. [Google Scholar] [CrossRef]
- American Society of Civil Engineers (ASCE). Seismic Evaluation and Retrofit of Existing Buildings; ASCE/SEI Standard 41-13; American Society of Civil Engineers: Reston, VA, USA, 2014. [Google Scholar] [CrossRef]
- Ntritsos, N.; Anastasopoulos, I.; Gazetas, G. Static and cyclic undrained response of square embedded foundations. Geotechnique 2015, 65, 805–823. [Google Scholar] [CrossRef]
- Kourkoulis, R.; Gelagoti, F.; Anastasopoulos, I. Rocking isolation of frames on isolated footings: Design insights and limitations. J. Earthq. Eng. 2012, 16, 374–400. [Google Scholar] [CrossRef]
- Gajan, S.; Raychowdhury, P.; Hutchinson, T.C.; Kutter, B.L.; Stewart, J.P. Application and validation of practical tools for nonlinear soil-foundation interaction analysis. Earthq. Spectra 2010, 26, 119–129. [Google Scholar] [CrossRef]
- Gajan, S.; Kayser, M. Quantification of the influences of subsurface uncertainties on the performance of rocking foundation during seismic loading. Soil Dyn. Earthq. Eng. 2019, 116, 1–14. [Google Scholar] [CrossRef]
- Allotey, N.; Naggar, M.H. Analytical moment-rotation curves for rigid foundations based on a Winkler model. Soil Dyn. Earthq. Eng. 2003, 23, 367–381. [Google Scholar] [CrossRef]
- Paolucci, R.; Shirato, M.; Yilmaz, M.T. Seismic behavior of shallow foundations: Shaking table experiments versus numerical modeling. Earthq. Eng. Struct. Dyn. 2008, 37, 577–595. [Google Scholar] [CrossRef]
- Raychowdhury, P.; Hutchinson, T.C. Performance evaluation of a nonlinear Winkler-based shallow foundation model using centrifuge test results. Earthq. Eng. Struct. Dyn. 2009, 38, 679–698. [Google Scholar] [CrossRef]
- Pelekis, I.; McKenna, F.; Madabhushi, S.P.G.; DeJong, M. Finite element modeling of buildings with structural and foundation rocking on dry sand. Earthq. Eng. Struct. Dyn. 2021, 50, 3093–3115. [Google Scholar] [CrossRef]
- Cremer, C.; Pecker, A.; Davenne, L. Cyclic macro-element of soil structure interaction: Material and geometrical nonlinearities. Int. J. Numer. Anal. Methods Geomech. 2001, 25, 1257–1284. [Google Scholar] [CrossRef]
- Gajan, S.; Kutter, B.L. Contact interface model for shallow foundations subjected to combined cyclic loading. J. Geotech. Geoenviron. Eng. 2009, 135, 407–419. [Google Scholar] [CrossRef]
- Chatzigogos, C.T.; Pecker, A.; Salencon, L. Macro element modeling of shallow foundations. Soil Dyn. Earthq. Eng. 2009, 29, 765–781. [Google Scholar] [CrossRef] [Green Version]
- Chatzigogos, C.T.; Figini, R.; Pecker, A.; Salencon, L. A macro element formulation for shallow foundations on cohesive and frictional soils. Int. J. Numer. Anal. Methods Geomech. 2011, 35, 902–931. [Google Scholar] [CrossRef]
- Gajan, S.; Godagama, B. Seismic performance of bridge-deck-pier-type-structures with yielding columns supported by rocking foundations. J. Earthq. Eng. 2019, 1–34. [Google Scholar] [CrossRef]
- Cavalieri, F.; Correia, A.A.; Crowley, H.; Pinho, R. Dynamic soil–structure interaction models for fragility characterization of buildings with shallow foundations. Soil Dyn. Earthq. Eng. 2020, 132, 106004. [Google Scholar] [CrossRef]
- OpenSees. Open System for Earthquake Engineering Simulations. Version 3.3.0.; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA; University of California: Berkeley, CA, USA, 2021; Available online: https://opensees.berkeley.edu/ (accessed on 1 September 2021).
- Forcellini, D. Seismic Assessment of a benchmark based isolated ordinary building with soil structure interaction. Bull. Earthq. Eng. 2018, 16, 2021–2042. [Google Scholar] [CrossRef]
- Deitel, P.; Deitel, H. Introduction to Python for Computer Science and Data Science, 1st ed.; Pearson Publishing: New York, NY, USA, 2020. [Google Scholar]
- Geron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools and Techniques to Build Intelligent Systems, 2nd ed.; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019. [Google Scholar]
- Daume, H., III. A Course in Machine Learning. Version 0.99; Self-Published: College Park, MD, USA, 2013; Available online: http://ciml.info (accessed on 1 September 2021).
- Brownlee, J. Machine Learning Algorithms from Scratch with Python. Machine Learning Mastery. Version v1.9. 2019. Available online: https://machinelearningmastery.com/ (accessed on 1 September 2021).
- Ebid, A.M. 35 years of (AI) in geotechnical engineering: State of the art. Geotech. Geol. Eng. 2021, 39, 637–690. [Google Scholar] [CrossRef]
- Jeremiah, J.J.; Abbey, S.J.; Booth, C.A.; Kashyap, A. Results of application of artificial neural networks in predicting geo-mechanical properties of stabilized clays—A review. Geotechnics 2021, 1, 144–171. [Google Scholar] [CrossRef]
- Yang, Y.; Rosenbaum, M.S. The artificial neural network as a tool for assessing geotechnical properties. Geotech. Geol. Eng. 2002, 20, 149–168. [Google Scholar] [CrossRef]
- Das, S.K.; Samui, P.; Khan, S.Z.; Sivakugan, N. Machine learning techniques applied to prediction of residual strength of clay. Cent. Eur. J. Geosci. 2011, 3, 449–461. [Google Scholar] [CrossRef]
- Mozumder, R.A.; Laskar, A.I. Prediction of unconfined compressive strength of geopolymer-stabilized clayey soils using artificial neural network. Comput. Geotech. 2015, 69, 291–300. [Google Scholar] [CrossRef]
- Ayeldeen, M.; Yuki, H.; Masaki, K.; Abdelazim, N. Unconfined compressive strength of compacted disturbed cement-stabilized soft clay. Int. J. Geosynth. Ground Eng. 2016, 2, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Salahudeen, A.B.; Ijimdiya, T.S.; Eberemu, A.O.; Osinubi, K.J. Artificial neural networks prediction of compaction characteristics of black cotton soil stabilized with cement kiln dust. J. Soft Comput. Civ. Eng. 2018, 2, 50–71. [Google Scholar]
- Priyadarshee, A.; Chandra, S.; Gupta, D.; Kumar, V. Neural models for unconfined compressive strength of kaolin clay mixed with pond ash, rice husk ash and cement. J. Soft Comput. Civ. Eng. 2020, 4, 85–120. [Google Scholar]
- Samui, P. Application of relevance vector machine for prediction of ultimate capacity of driven piles in cohesionless soils. Geotech. Geol. Eng. 2012, 30, 1261–1270. [Google Scholar] [CrossRef]
- Mohanty, R.; Das, S.K. Settlement of shallow foundations on cohesionless soils based on SPT value using multi-objective feature selection. Geotech. Geol. Eng. 2018, 36, 3499–3509. [Google Scholar] [CrossRef]
- Sakellariou, M.G.; Ferentinou, M.D. A study of slope stability prediction using neural networks. Geotech. Geol. Eng. 2005, 23, 419–445. [Google Scholar] [CrossRef]
- Samui, P.; Lansivaara, T.; Bhatt, M.R. Least square support vector machine applied to slope reliability analysis. Geotech. Geol. Eng. 2013, 31, 1329–1334. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I. Landslide susceptibility assessment using bagging ensemble based alternating decision trees, logistic regression and J48 decision trees methods: A comparative study. Geotech. Geol. Eng. 2017, 35, 2597–2611. [Google Scholar] [CrossRef]
- Qi, C.; Tang, X. Slope stability prediction using integrated metaheuristic and machine learning approaches: A comparative study. Comput. Ind. Eng. 2018, 118, 112–122. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Goh, S.H. Support vector machines: Their use in geotechnical engineering as illustrated using seismic liquefaction data. Comput. Geotech. 2007, 34, 410–421. [Google Scholar] [CrossRef]
- Hanna, A.M.; Ural, D.; Saygili, G. Neural network model for liquefaction potential in soil deposits using Turkey and Taiwan earthquake data. Soil Dyn. Earthq. Eng. 2007, 27, 521–540. [Google Scholar] [CrossRef]
- Njock, P.G.A.; Shen, S.-L.; Zhou, A.; Lyu, H.-M. Evaluation of soil liquefaction using AI technology incorporating a coupled ENN/t-SNE model. Soil Dyn. Earthq. Eng. 2020, 130, 105988. [Google Scholar] [CrossRef]
- Gajan, S. Application of machine learning algorithms to performance prediction of rocking shallow foundations during earthquake loading. Soil Dyn. Earthq. Eng. 2021, 151, 105988. [Google Scholar] [CrossRef]
- Deng, L.; Kutter, B.L.; Kunnath, S.K. Seismic design of rocking shallow foundations: Displacement-based methodology. J. Bridge Eng. 2014, 19, 04014043. [Google Scholar] [CrossRef]
- Deng, L.; Kutter, B.L. Characterization of rocking shallow foundations using centrifuge model tests. Earthq. Eng. Struct. Dyn. 2012, 41, 1043–1060. [Google Scholar] [CrossRef]
- Hakhamaneshi, M.; Kutter, B.L.; Deng, L.; Hutchinson, T.C.; Liu, W. New findings from centrifuge modeling of rocking shallow foundations in clayey ground. In Proceedings of the Geo-Congress 2012, Oakland, CA, USA, 25–29 March 2012. [Google Scholar]
- Tsatsis, A.; Anastasopoulos, I. Performance of rocking systems on shallow improved sand: Shaking table testing. Front. Built Environ. 2015, 1, 9. [Google Scholar] [CrossRef] [Green Version]
- Soundararajan, S.; Gajan, S. Effects of rocking coefficient on seismic energy dissipation, permanent settlement, and self-centering characteristics of rocking shallow foundations. In Proceedings of the Geo-Congress 2020, Minneapolis, MN, USA, 25–28 February 2020. [Google Scholar]
- Gajan, S.; Kutter, B.L. Effect of critical contact area ratio on moment capacity of rocking shallow foundations. In Proceedings of the Geotechnical Earthquake Engineering and Soil Dynamics IV, Sacramento, CA, USA, 18–22 May 2008. [Google Scholar]
- Gajan, S.; Kutter, B.L. Effects of moment-to-shear ratio on combined cyclic load-displacement behavior of shallow foundations from centrifuge experiments. J. Geotech. Geoenviron. Eng. 2009, 135, 1044–1055. [Google Scholar] [CrossRef]
- Kramer, S. Geotechnical Earthquake Engineering, 1st ed.; Prentice Hall Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Faghmous, J.; Banerjee, A.; Shekhar, S.; Steinbach, M.; Kumar, V.; Ganguly, A.R.; Samatova, N. Theory-guided data science for climate change. Computer 2014, 47, 74–78. [Google Scholar] [CrossRef]
- Wagner, N.; Rondinelli, J.M. Theory-guided machine learning in materials science. Front. Mater. 2016, 3, 28. [Google Scholar] [CrossRef] [Green Version]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-guided data science: A new paradigm for scientific discovery from data. arXiv 2017, arXiv:1612.08544. [Google Scholar] [CrossRef]
- Karpatne, A.; Watkins, W.; Read, J.; Kumar, V. Physics-guided neural networks (PGNN): An application in lake temperature modeling. arXiv 2018, arXiv:1710.11431. [Google Scholar]


| Input Feature | A/Ac | h/B | Cr | amax (g) | Ia (m/s) |
|---|---|---|---|---|---|
| Range | 1.9–17.1 | 1.2–2.83 | 0.08–0.36 | 0.04–1.28 | 0.03–26.4 |
| Mean | 8.17 | 1.89 | 0.24 | 0.43 | 2.31 |
| Std. dev. | 4.27 | 0.53 | 0.08 | 0.26 | 4.37 |
| Input Feature | A/Ac | h/B | Cr | amax (g) | Ia (m/s) |
|---|---|---|---|---|---|
| A/Ac | 1.0 | −0.39 | 0.66 | 0.13 | −0.18 |
| h/B | −0.39 | 1.0 | −0.86 | −0.11 | −0.2 |
| Cr | 0.66 | −0.86 | 1.0 | 0.07 | 0.02 |
| amax (g) | 0.13 | −0.11 | 0.07 | 1.0 | 0.34 |
| Ia (m/s) | −0.18 | −0.2 | 0.02 | 0.34 | 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajan, S. Modeling of Seismic Energy Dissipation of Rocking Foundations Using Nonparametric Machine Learning Algorithms. Geotechnics 2021, 1, 534-557. https://doi.org/10.3390/geotechnics1020024
Gajan S. Modeling of Seismic Energy Dissipation of Rocking Foundations Using Nonparametric Machine Learning Algorithms. Geotechnics. 2021; 1(2):534-557. https://doi.org/10.3390/geotechnics1020024
Chicago/Turabian StyleGajan, Sivapalan. 2021. "Modeling of Seismic Energy Dissipation of Rocking Foundations Using Nonparametric Machine Learning Algorithms" Geotechnics 1, no. 2: 534-557. https://doi.org/10.3390/geotechnics1020024
APA StyleGajan, S. (2021). Modeling of Seismic Energy Dissipation of Rocking Foundations Using Nonparametric Machine Learning Algorithms. Geotechnics, 1(2), 534-557. https://doi.org/10.3390/geotechnics1020024





