Results of Application of Artificial Neural Networks in Predicting Geo-Mechanical Properties of Stabilised Clays—A Review
Abstract
1. Introduction
1.1. Artificial Neural Network
1.2. Components of Artificial Neural Network
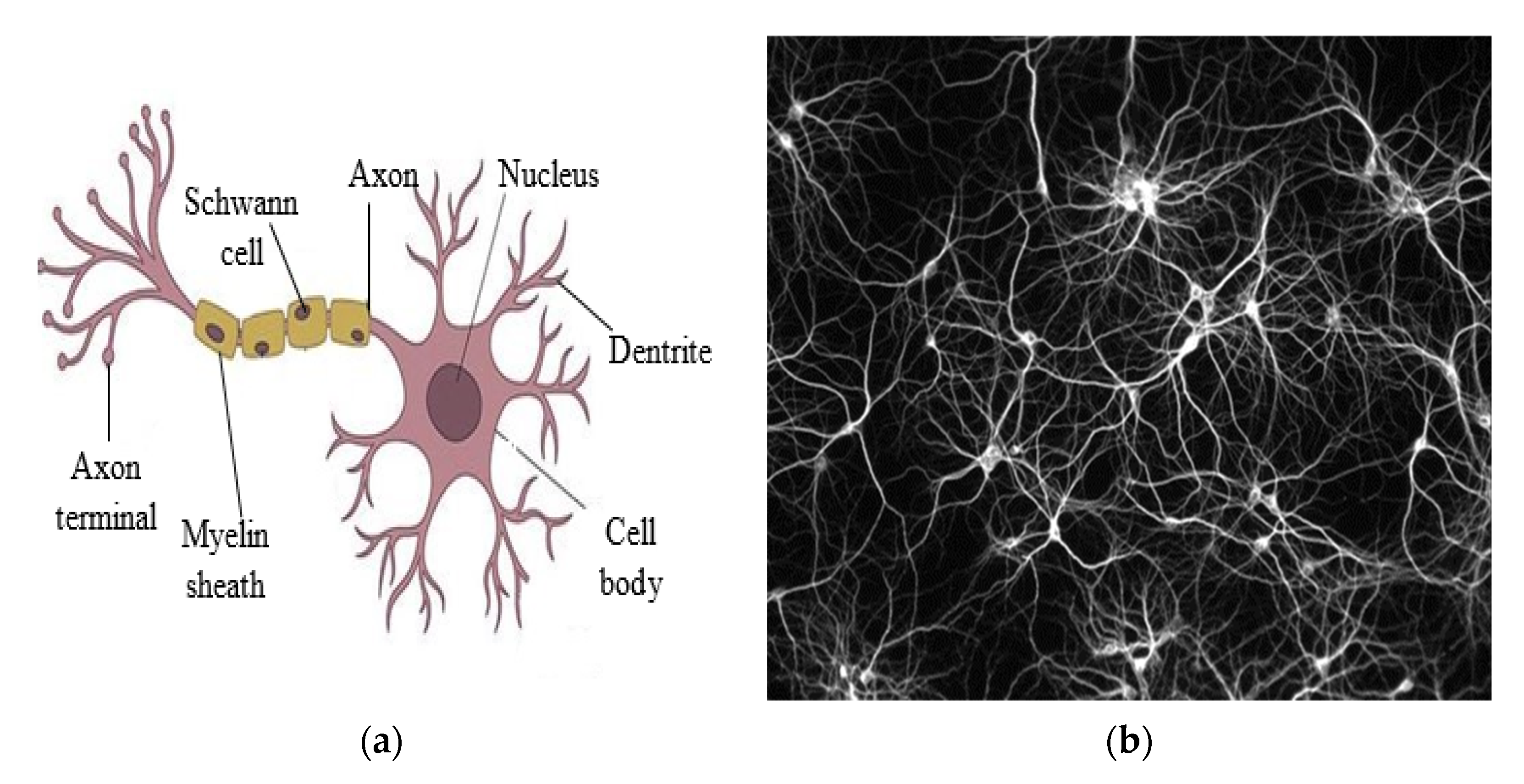
Neurons and Edges
2. Materials and Methods
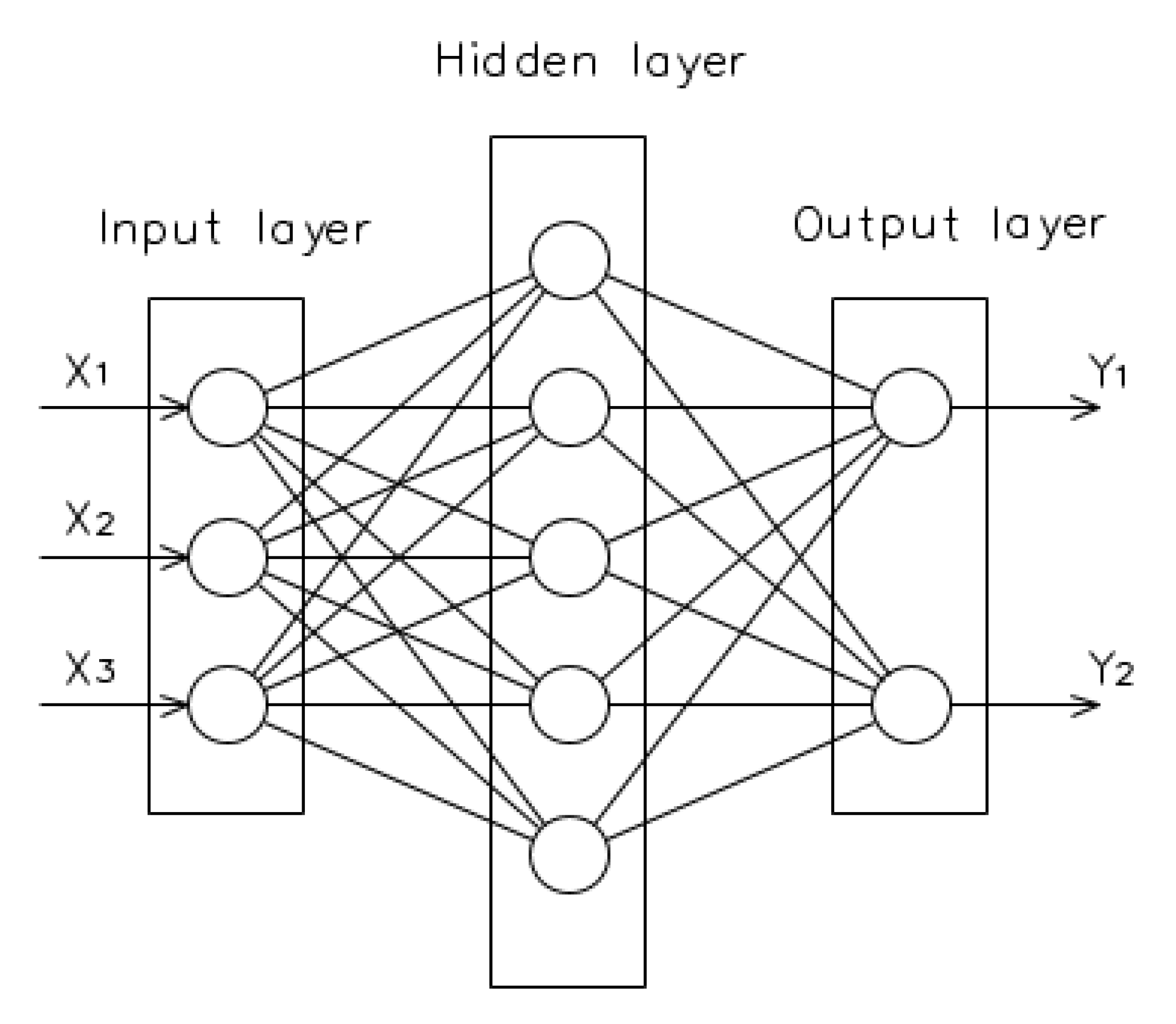
2.1. ANN Architecture
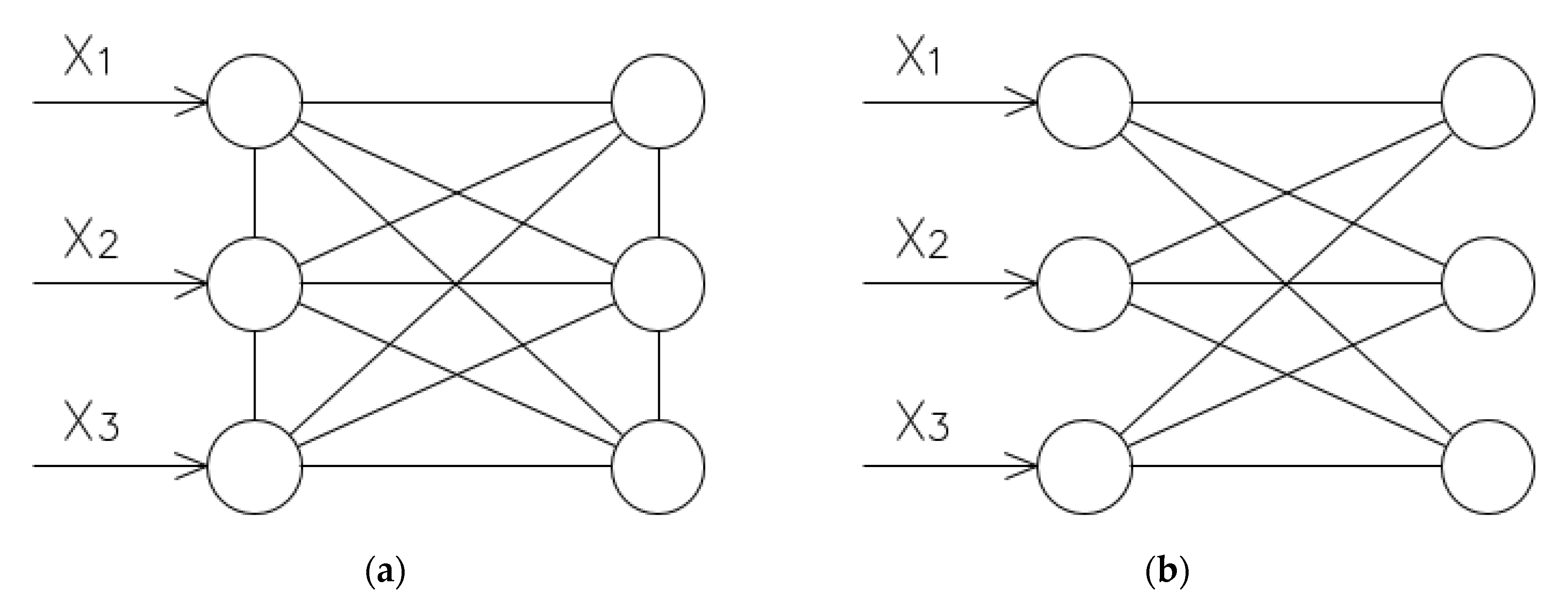
2.2. Feedforward and Recurring Networks
Data Preprocessing
3. Selecting Design Parameters for ANN in Soil Stabilisation
3.1. Training, Validation, and Testing
3.2. Estimating the Amount of Training Data
4. Application of ANN in Predicting the Properties of Stabilised Clays
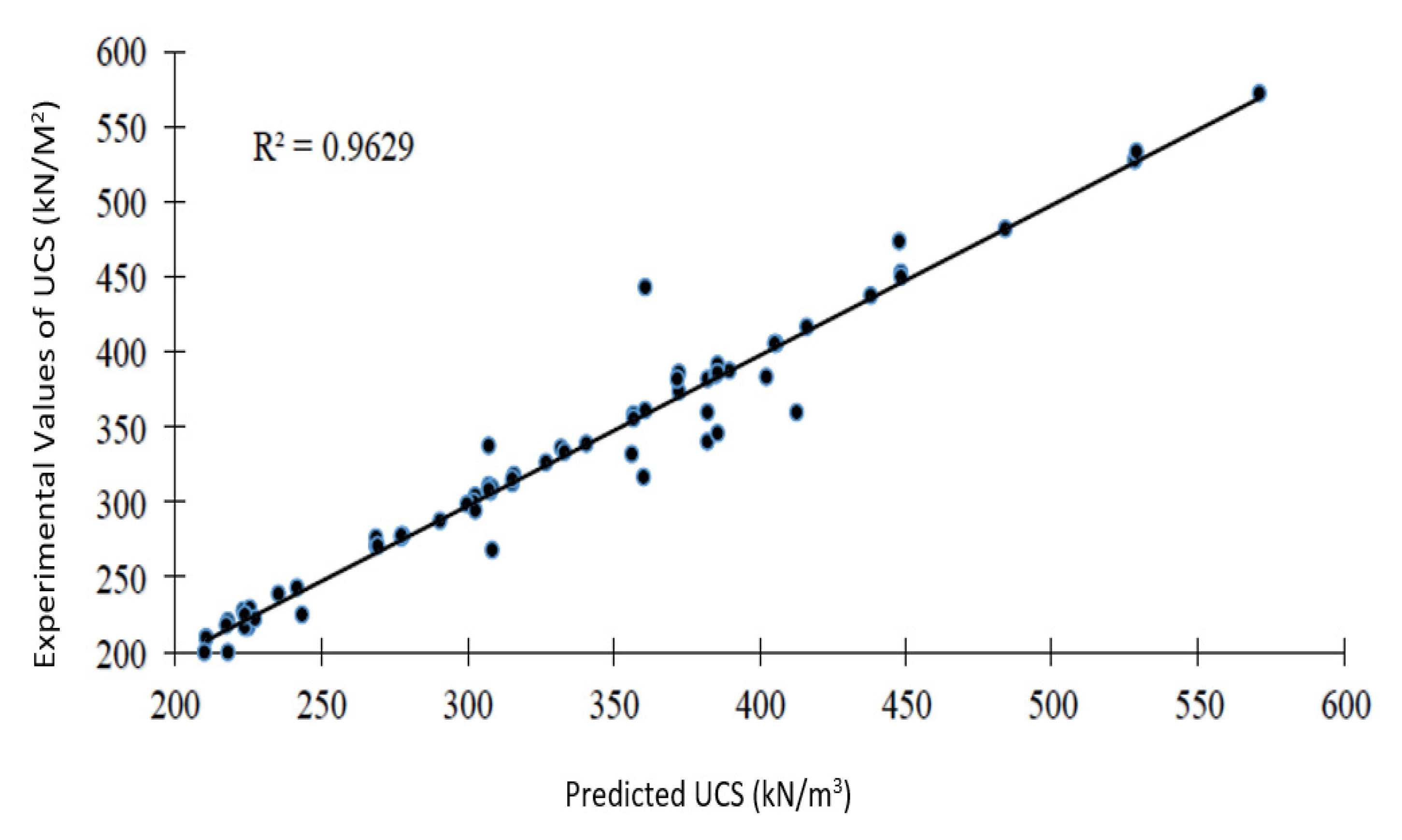
4.1. Unconfined Compressive Strength
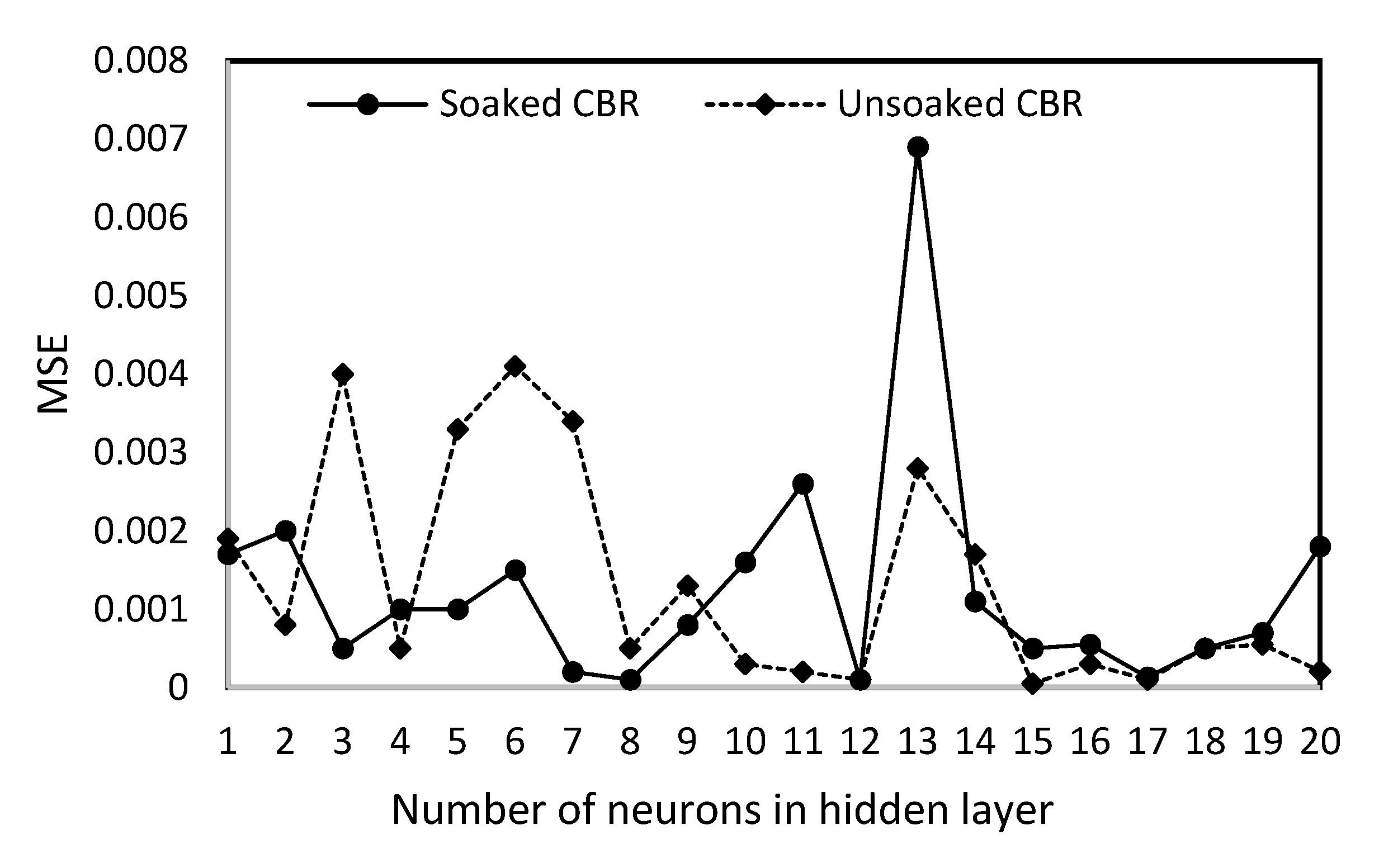
4.2. California Bearing Ratio
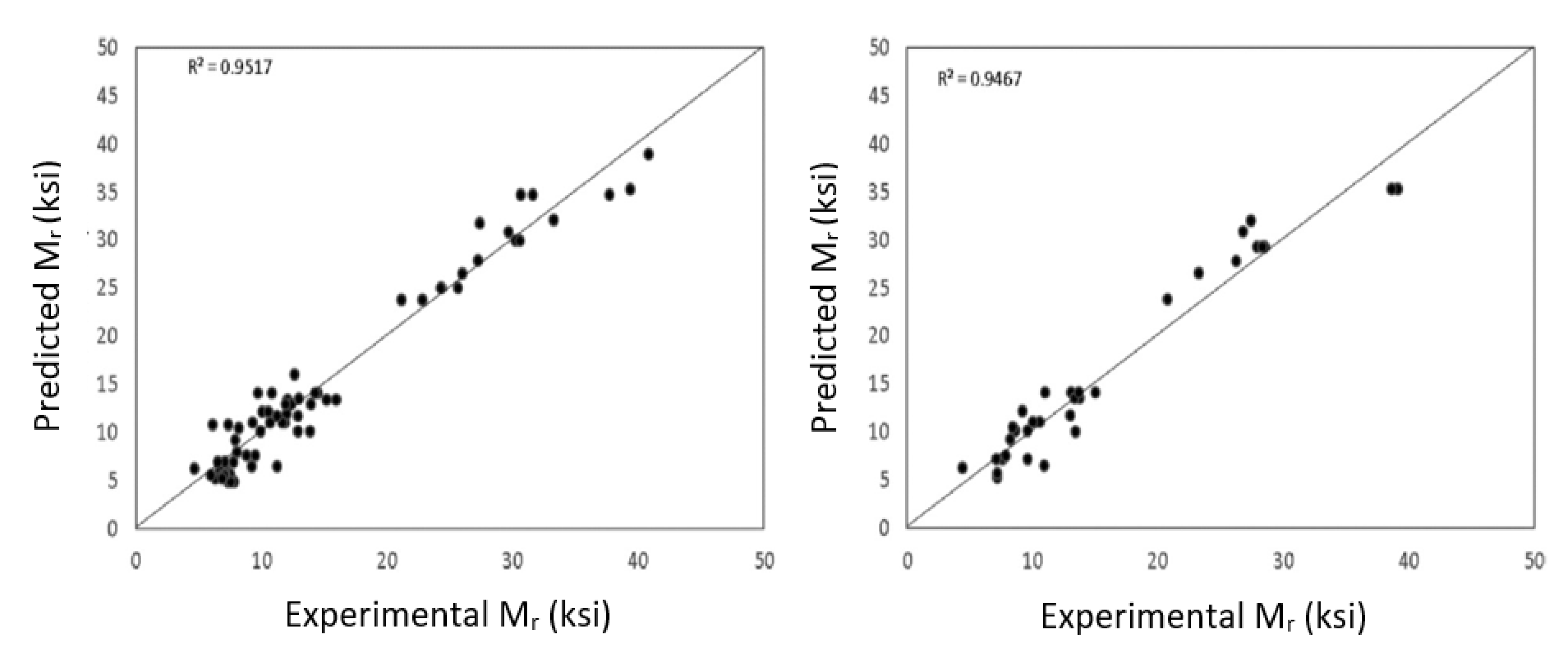
4.3. Permeability and Resilient Modulus
4.4. Plasticity Index and Compaction Characteristics
5. Discussions
6. Conclusions
- The advantages of the artificial neural over traditional regression analysis as applied to stabilisation have been highlighted in the foregoing sections. In a typical field stabilisation project, in order to improve the properties of expansive clays, experimental data are usually generated from several field and laboratory tests to monitor and ascertain the progress made in terms of improvement. These procedures are expensive and time-consuming and may be reduced to a minimum using ANN to predict the field response of the soils. In summary, the following conclusions are made.
- An artificial neural network is reliable and can be employed in modelling various properties of stabilised clays for easy prediction of soil response while eliminating the need for extensive experimental procedures.
- Backpropagation feedforward networks are the most used models in dealing with the problem of regression analysis for stabilisation of clays.
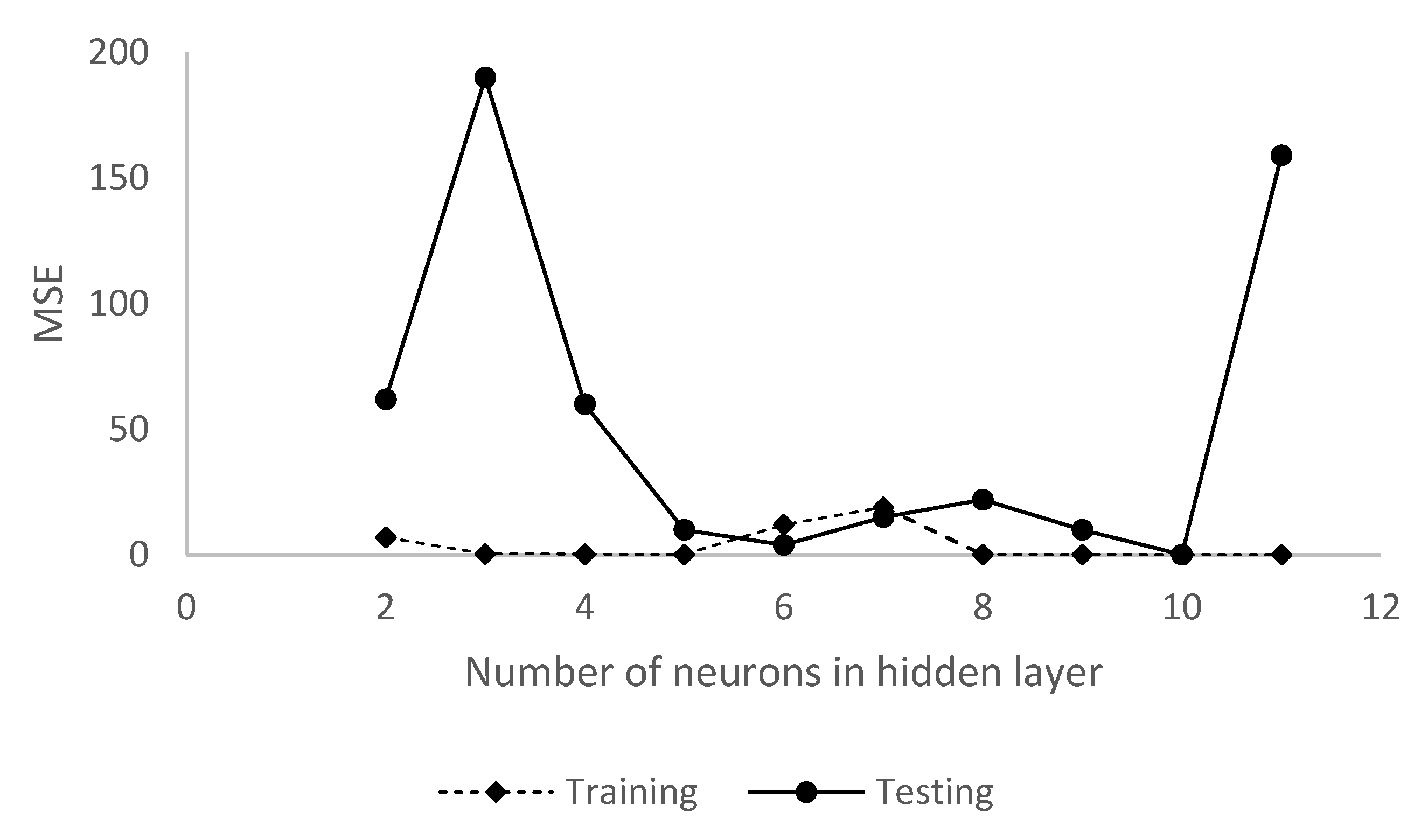
- An artificial neural network should be developed with a relatively substantial dataset to regression models with good correlation. Many of the studies in regression analysis of stabilised clays have used relatively small data sets, although the models have performed well. The ability of the models to generalize can be improved with a larger dataset which fields a wide range of possible soil behaviour for proper training of the model.
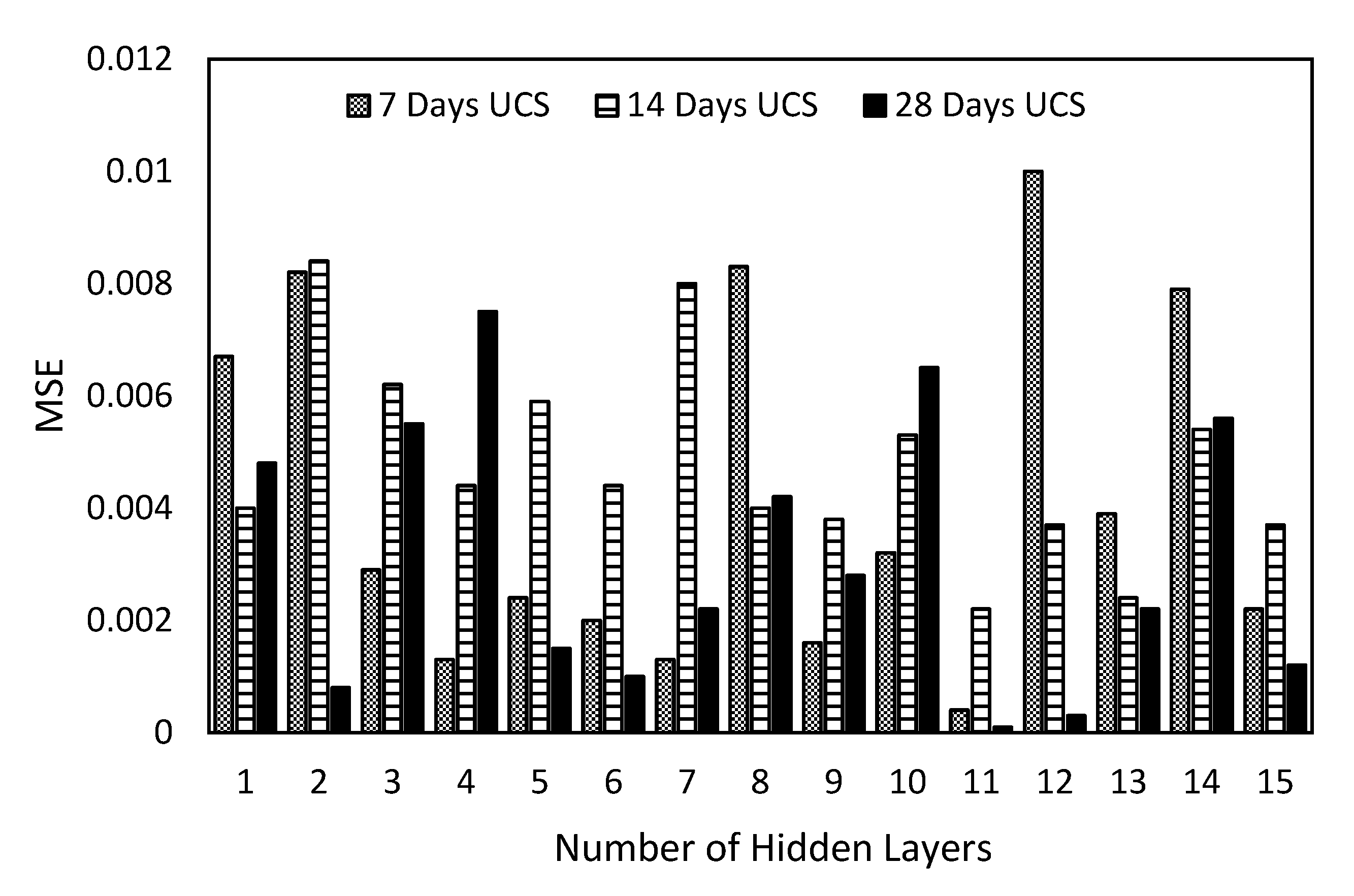
- Shallow networks made up of one hidden layer are the most used ANN architecture in developing predictive models for the prediction of geotechnical characteristics of stabilised clays and in modelling the response of stabilised expansive clays. The Levenberg–Marquardt training algorithm has been reported to be the most used among the studies reviewed.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gillott, J.E. Some clay-related problems in engineering geology in North America. Clay Miner. 1986, 21, 261–278. [Google Scholar] [CrossRef]
- Das, A.; Roy, S. Effect of Expansive Soil on Foundation and Its Remedies. Int. J. Innov. Res. Sci. Eng. Technol. 2014, 3, 92–95. [Google Scholar]
- Balasingam, M.; Farid, S. Interpretation of Geotechnical Properties of Cement Treated Soil; Washington State Department of Transportation (WSDOF): Olympia, WA, USA, 2008; pp. 77–122.
- Chew, S.H.; Kamruzzaman, A.H.M.; Lee, F.H. Physicochemical and Engineering Behavior of Cement Treated Clays. J. Geotech. Geoenvironmental Eng. 2004, 130, 696–706. [Google Scholar] [CrossRef]
- Abbey, S.J.; Eyo, E.U.; Oti, J.; Amakye, S.Y.; Ngambi, S. Mechanical Properties and Microstructure of Fibre-Reinforced Clay Blended with By-Product Cementitious Materials. Geosciences 2020, 10, 241. [Google Scholar] [CrossRef]
- Abbey, S.J.; Ngambi, S.; Olubanwo, A.O.; Tetteh, F.K. Strength and Hydraulic Conductivity of Cement and By–Product Cementitious Materials Improved Soil. Int. J. Appl. Eng. Res. 2018, 13, 8684–8694, ISSN 0973-4562. [Google Scholar]
- Eyo, E.U.; Ng’Ambi, S.; Abbey, S.J. Incorporation of a nanotechnology-based additive in cementitious products for clay stabilisation. J. Rock Mech. Geotech. Eng. 2020, 12, 1056–1069. [Google Scholar] [CrossRef]
- Eyo, E.U.; Ng’Ambi, S.; Abbey, S.J. Performance of clay stabilized by cementitious materials and inclusion of zeolite/alkaline metals-based additive. Transp. Geotech. 2020, 23, 100330. [Google Scholar] [CrossRef]
- Dongare, A.D.; Kharde, R.R.; Kachare, A.D. Introduction to Artificial Neural Network. Int. J. Eng. Innov. Technol. 2012, 2, 189–193, ISSN 2277-3754. [Google Scholar]
- Sharma, V.; Rai, S.; Anurag Dev, A. A Comprehensive Study of Artificial Neural Networks. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2012, 2, 278–284, ISSN 2277 128X. [Google Scholar]
- Vastrad, C. Performance Analysis of Neural Network Models for Oxazolines and Oxazoles Derivatives Descriptor Dataset. Int. J. Inf. Sci. Tech. 2013, 3, 1–15. [Google Scholar] [CrossRef]
- Stepniewska-Dziubinska, M.M.; Zielenkiewicz, P.; Siedlecki, P. Development and evaluation of a deep learning model for protein–ligand binding affinity prediction. Bioinformatics 2018, 34, 3666–3674. [Google Scholar] [CrossRef]
- Lal, B.; Tripathy, S.S. Prediction of dust concentration in open cast coal mine using artificial neural network. Atmos. Pollut. Res. 2012, 3, 211–218. [Google Scholar] [CrossRef]
- Chao, Z.; Ma, G.; Zhang, Y.; Zhu, Y.; Hu, H. The application of artificial neural network in geotechnical engineering. International Conference on Civil and Hydraulic Engineering (IConCHE). IOP Conf. Ser. Earth Environ. Sci. 2018, 189, 22054. [Google Scholar] [CrossRef]
- Nihat, S.I. Estimation of swell index of fine-grained soils using regression equations and artificial neural net-works. Sci. Res. Essay 2009, 4, 1047–1056. [Google Scholar]
- Rani, C.S.; Vaddi, P.K.; Togati, N.V.V.K. Artificial Neural Networks (ANN) for Prediction of Engineering Properties of Soils. Int. J. Innov. Technol. Explor. Eng. 2013, 3, 123–130, ISSN 2278-3075. [Google Scholar]
- Kalantary, F. and Kordnaeij, A. Prediction of compression index using artificial neural network. Sci. Res. Essays 2012, 7, 2835–2848. [Google Scholar] [CrossRef]
- Singh, V.; Bano, S.; Yadav, A.K.; Ahmad, S. Feasibility of Artificial Neural Network in Civil Engineering. Int. J. Trend Sci. Res. Dev. 2019, 3, 724–728. [Google Scholar] [CrossRef]
- Winston, P.H. Artificial Intelligence, 3rd ed.; Addison-Wesley Pub. Co.: Boston, MA, USA, 1992; ISBN 0-201-53377-4. [Google Scholar]
- Zell, A. Simulation of Neural Networks, 1st ed.; Addison-Wesley Pub. Co.: Boston, MA, USA, 2003; ISBN 978-3-89319-554-1. OCLC 249017987. [Google Scholar]
- Cal, Y. Soil classification by neural network. Adv. Eng. Softw. 1995, 22, 95–97. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Artificial Neural Networks-Based Settlement Prediction Formula for Shallow Foundations on Granular Soils. Aust. Geomech. 2002, 37, 45–52. [Google Scholar]
- Gunaydin, O.; Gokoglu, A.; Fener, M. Prediction of artificial soil’s unconfined compression strength test using statistical analyses and artificial neural networks. Adv. Eng. Softw. 2010, 41, 1115–1123. [Google Scholar] [CrossRef]
- Kerh, T.; Hu, Y.G.; Wu, C.H. Estimation of consolidation settlement caused by groundwater drawdown using artificial neural networks. Adv. Eng. Softw. 2003, 34, 559–568. [Google Scholar] [CrossRef]
- Reuter, U.; Sultan, A.; Reischl, D.S. A comparative study of machine learning approaches for modeling concrete failure surfaces. Adv. Eng. Softw. 2018, 116, 67–79. [Google Scholar] [CrossRef]
- Snyman, J. Practical Mathematical Optimization: An Introduction to Basic Optimisation Theory and Classical and New Gradient-Based Algorithms; Springer Science & Business Media: New York, NY, USA, 2005; ISBN 978-0-387-24348-1. [Google Scholar]
- Hinkelmann, K. Neural Networks. University of Applied Sciences Northwestern Switzerland School of Business. Available online: http://didattica.cs.unicam.it/lib/exe/fetch.php?media=didattica:magistrale:kebi:ay_1718:ke-11_neural_networks.pdf (accessed on 26 April 2021).
- Weisstein, E.W. Hyperbolic Tangent. MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/HyperbolicTangent.html (accessed on 26 April 2020).
- Squires, G.L. Practical Physics; Cambridge University Press (CUP): New York, NY, USA, 2001; ISBN 978-0-521-77940-1. [Google Scholar] [CrossRef]
- Mote, H.; Kumar, S.R.S. Use of Artificial Neural Network for Initial design of steel structures. IOP Conf. Ser. Mater. Sci. Eng. 2019, 660, 12064. [Google Scholar] [CrossRef]
- Sildir, H.; Aydin, E.; Kavzoglu, T. Design of Feedforward Neural Networks in the Classification of Hyperspectral Imagery Using Superstructural Optimization. Remote Sens. 2020, 12, 956. [Google Scholar] [CrossRef]
- Naidu, K.; Ali, M.S.; Abu Bakar, A.H.; Tan, C.K.; Arof, H.; Mokhlis, H. Optimized artificial neural network to improve the accuracy of estimated fault impedances and distances for underground distribution system. PLoS ONE 2020, 15, e0227494. [Google Scholar] [CrossRef] [PubMed]
- Renotte, C.; Wouwer, A.V.; Bogaertst, P.; Remy, M. Neural Network Applications in Non-linear Modelling of (Bio) chemical Processes. Meas. Control. 2001, 34, 197–201. [Google Scholar] [CrossRef]
- Zhang, T.; Fell, F.; Liu, Z.; Preusker, R.; Fischer, J.; He, M. Evaluating the performance of artificial neural network techniques for pigment retrieval from ocean color in Case I waters. J. Geophys. Res. Space Phys. 2003, 108, 3286. [Google Scholar] [CrossRef]
- Eyo, E.U.; Abbey, S.J. Machine learning regression and classification algorithms utilized for strength prediction of OPC/by-product materials improved soils. Constr. Build. Mater. 2021, 284. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Wald, A. Statistical Decision Functions; John Wiley & Sons: New York, NY, USA, 1950. [Google Scholar]
- Ikizler, S.B.; Aytekin, M.; Vekli, M.; Kocabas, F. Prediction of swelling pressures of expansive soils using artificial neural networks. Adv. Eng. Softw. 2009, 41, 647–655. [Google Scholar] [CrossRef]
- Ciresan, D.; Meier, U.; Masci, J.; Gambardella, L.M.; Schmidhuber, J. Flexible, High Performance Convolutional Neural Networks for Image Classification. Twenty-Second Int. Jt. Conf. Artif. Intell. 2011, 2, 1237–1242. [Google Scholar]
- Sushama, K.; Bindhu, L. ANN Based Prediction of Shear Strength of Soils from their Index Properties. Int. J. Earth Sci. Eng. 2015, 8, 2195–2202, ISSN 0974-5904. [Google Scholar]
- Murata, N.; Yoshizawa, S.; Amari, S. Learning curves, model selection and complexity of neural networks. In Advances in Neural Information Processing Systems 5; Jose Hanson, S., Cowan, J.D., Lee Giles, C., Eds.; Morgan Kaufmann: San Mateo, CA, USA, 1993; pp. 607–614. [Google Scholar]
- Maind, S.B.; Wankar, P. Research Paper on Basic of Artificial Neural Network. Int. J. Recent Innov. Trends Comput. Commun. 2014, 2, 96–100. [Google Scholar]
- Gareth, J. An Introduction to Statistical Learning: With Applications in R; Springer: New York, NY, USA, 2013; p. 176. ISBN 978-1461471370. [Google Scholar]
- Pathivada, S. Effects of Water-Cement Ratio on Deep Mixing Treated Expansive Clay Characteristics; The University of Texas at Arlington: Arlington, TX, USA, 2005. [Google Scholar]
- Lorenzo, G.A.; Bergado, D.T. Fundamental Parameters of Cement-Admixed Clay—New Approach. J. Geotech. Geoenvironmental Eng. 2004, 130, 1042–1050. [Google Scholar] [CrossRef]
- Turk, G.; Logar, J.; Majes, B. Modelling soil behaviour in uniaxial strain conditions by neural networks. Adv. Eng. Softw. 2001, 32, 805–812. [Google Scholar] [CrossRef][Green Version]
- Fan, J.; Wang, D.; Qian, D. Soil-cement mixture properties and design considerations for reinforced excavation. J. Rock Mech. Geotech. Eng. 2018, 10, 791–797. [Google Scholar] [CrossRef]
- Shahin, M.A.; Jaksa, M.B.; Maier, H.R. Artificial Neural Networks Application in Geotechnical Engineering. Aust. Geomech. 2001, 36, 49–62. [Google Scholar]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (The multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Mozumder, R.A.; Laskar, A.I. Prediction of unconfined compressive strength of geopolymer-stabilised clayey soils using artificial neural network. Comput. Geotech. 2015, 69, 291–300. [Google Scholar] [CrossRef]
- BRE. Low-Rise Buildings on Shrinkable Clay Soils: BRE Digest; CRC: London, UK, 1993; Volumes 240–242. [Google Scholar]
- Salahudeen, A.B.; Sadeeq, J.A.; Badamasi, A.; Onyelowe, K.C. Prediction of Unconfined Compressive Strength of Treated Expansive Clay Using Back-Propagation Artificial Neural Networks. Niger. J. Eng. Fac. Eng. Ahmadu Bello Univ. 2020, 27, 45–58, ISSN 0794–4756. [Google Scholar]
- BSI. BS 1377: 1990—Methods of Test. for Soils for Civil. Engineering Purposes; British Standards Institute: Milton Keynes, UK, 1990. [Google Scholar]
- BSI. BS 1924: 1990—Stabilised Materials for Civil. Engineering Purposes; British Standards Institute: Milton Keynes, UK, 1990. [Google Scholar]
- Priyadarshee, A.; Chandra, S.; Gupta, D.; Kumar, V. Neural Models for Unconfined Compressive Strength of Kaolin Clay Mixed with Pond Ash, Rice Husk Ash and Cement. J. Soft Comput. Civ. Eng. 2020, 4, 85–120. [Google Scholar] [CrossRef]
- Ayeldeen, M.; Yuki, H.; Masaki, K.; Abdelazim, N. Unconfined Compressive Strength of Compacted Disturbed Cement-Stabilised Soft Clay. Int. J. Geosynth. Ground Eng. 2016, 2, 1–10. [Google Scholar] [CrossRef]
- Ngo, H.T.T.; Pham, T.A.; Vu, H.L.T.; Giap, L.V. Application of Artificial Intelligence to Determined Unconfined Compressive Strength of Cement-Stabilized Soil in Vietnam. Appl. Sci. 2021, 11, 1949. [Google Scholar] [CrossRef]
- Tran, V.Q. Compressive Strength Prediction of Stabilized Dredged Sediments Using Artificial Neural Network. Adv. Civ. Eng. 2021, 2021. [Google Scholar] [CrossRef]
- Sabat, A.K. Prediction of California Bearing Ratio of a Stabilised Expansive Soil using Artificial Neural Network and Support Vector Machine. Electron. J. Geotech. Eng. 2015, 20, 981–991. [Google Scholar]
- Rajakumar, C.; Babu, G.R. Experimental study and neural network modelling of expansive sub grade stabilized with industrial waste by-products and geogrid. Mater. Today Proc. 2021, 46, 131–137. [Google Scholar] [CrossRef]
- Vinodhkumar, S.; Balaji, S. Artificial Neural Network Modelling and Economic Analysis of Black Cotton Soil Subgrade Stabilised with Flyash and Geotextile. Int. J. Earth Sci. Eng. 2016, 9, 81–86, ISSN 0974-5904. [Google Scholar]
- Belal, A.; Rahman, M.A.; Rafizul, I.M. Prediction of California Bearing Ratio of Stabilised Soil Using Artificial Neural Network. In Proceedings of the 3rd International Conference on Civil Engineering for Sustainable Development (ICCESD 2016), KUET, Khulna, Bangladesh, 12–14 February 2016; pp. 977–987, ISBN 978-984-34-0265-3. [Google Scholar]
- Salahudeen, A.B.; Sadeeq, J.A. California Bearing Ratio Prediction of Modified Black Clay Using Artificial Neural Networks. In Proceedings of the West Africa Built Environment Research (WABER) Conference 10th Anniversary Conference, Accra, Ghana, 5–7 August 2019; Laryea, S., Essah, E., Eds.; WABER: Johannesburg, South Africa, 2019. ISBN 978–9988–2–6010–1. [Google Scholar] [CrossRef]
- Vakili, A.H.; Davoodi, S.; Arab, A.; Razip, M.; Bin Selamat, M. Use of Artificial Neural Network in Predicting Permeability of Dispersive Clay Treated with Lime and Pozzolan. Int. J. Sci. Res. Environ. Sci. 2015, 3, 23–37. [Google Scholar] [CrossRef]
- Hanandeha, S.; Ardahb, A.; Abu-Farsakhc, M. Using artificial neural network and genetics algorithm to estimate the resilient modulus for stabilised subgrade and propose new empirical Formula. Transp. Geotech. 2020, 24, 100358. [Google Scholar] [CrossRef]
- Alavi, A.H.; Gandomi, A.H.; Mollahassani, A.; Heshmati, A.A.; Rashed, A. Modeling of maximum dry density and optimum moisture content of stabilised soil using artificial neural networks. J. Plant. Nutr. Soil Sci. 2010, 173, 368–379. [Google Scholar] [CrossRef]
- Salahudeen, A.B.; Ijimdiya, T.S.; Eberemu, A.O.; Osinubi, K.J. Artificial Neural Networks Prediction of Compaction Characteristics of Black Cotton Soil Stabilised with Cement Kiln Dust. J. Soft Comput. Civ. Eng. 2018, 2, 50–71. [Google Scholar]
- Bahmed, I.T.; Harichane, K.; Ghrici, M.; Boukhatem, B.; Rebouh, R.; Gadouri, H. Prediction of geotechnical properties of clayey soils stabilised with lime using artificial neural networks (ANNs). Int. J. Geotech. Eng. 2017, 13, 191–203. [Google Scholar] [CrossRef]
- Kamruzzaman, A.H.; Chew, S.H.; Lee, F.H. Structuration and destructuration behavior of cement-treated Singapore marine clay cement-treated Singapore marine clay. J. Geotech. Geoenviron. Eng. 2009, 135, 573–589. [Google Scholar] [CrossRef]
- Taskiran, T. Prediction of California bearing ratio (CBR) of fine grained soils by AI methods. Adv. Eng. Softw. 2010, 41, 886–892. [Google Scholar] [CrossRef]
- Radhakrishnan, G.; Kumar, M.A.; Raju, G.V.R.P. Influence of Chloride Compounds on the Swelling and Strength Properties of Expansive Subgrade Soil. J. Mech. Civ. Eng. IOSR-JMCE 2016, 13, 57–60. [Google Scholar]
- Ikeagwuani, C.C.; Nwonu, C.D. Emerging trends in expansive soil stabilisation: A review. J. Rock Mech. Geotech. Eng. 2019, 11, 423–440. [Google Scholar] [CrossRef]
- Eyo, E.; Ng’Ambi, S.; Abbey, S. Investigative Study of Behaviour of Treated Expansive Soil Using Empirical Correlations. In IFCEE 2018; American Society of Civil Engineers (ASCE): Orlando, FL, USA, 2018; pp. 373–384. [Google Scholar]
- Eyo, E.U.; Abbey, S.J.; Ngambi, S.; Ganjian, E.; Coakley, E. Incorporation of a nanotechnology-based product in cementitious binders for sustainable mitigation of sulphate-induced heaving of stabilised soils. Eng. Sci. Technol. Int. J. 2021, 24, 436–448. [Google Scholar] [CrossRef]



| Model | Dataset | Statistical Parameter | ||
|---|---|---|---|---|
| R2 | MSE | MAE (%) | ||
| ANN | Training data | 0.992 | 0.34 | 3.65 |
| Testing data | 0.964 | 1.50 | 8.34 | |
| MVR | Training data | 0.828 | 7.24 | 19.20 |
| Testing data | 0.808 | 8.04 | 19.26 | |
| Modified Plasticity Index | Volume Change Potential (VCP) |
|---|---|
| >60 | Very high |
| 40–60 | High |
| 20–40 | Medium |
| <20 | Low |
| Model | Dataset | Statistical Parameter | ||
|---|---|---|---|---|
| R2 | MSE | RSME | ||
| ANN | Training data | 0.9813 | 0.0395 | 0.1987 |
| Testing data | 0.9714 | 51.34 | 7.1651 | |
| MVR | 0.8870 | 68.7603 | 8.2921 | |
| Training Algorithm | R | MSE |
|---|---|---|
| Conscience bias learning function | 0.7693 | 7.08 |
| Gradient descent weight and bias learning function | 0.8991 | 3.98 |
| Gradient descent with momentum weight | 0.9163 | 6.66 |
| Levenberg–Marquardt function | 0.94317 | 0.49 |
| Hebb weight learning rule | 0.8761 | 2.4 |
| Training Algorithm | R | MSE |
|---|---|---|
| Quasi-Newton back propagation | 0.88712 | 1.083 × 10−4 |
| Bayesian regularisation back propagation | 0.85190 | 4.983 × 10−5 |
| Conjugate gradient back propagation with Powell–Beale restarts | 0.94122 | 3.776 × 10−7 |
| Conjugate gradient back propagation with Fletcher–Reeves updates | 0.81167 | 7.339 × 10−6 |
| Conjugate gradient back propagation with Polak–Ribiére updates | 0.85819 | 2.964 × 10−9 |
| Gradient descent back propagation | 0.94862 | 9.985 × 10−9 |
| Levenberg–Marquardt back propagation | 0.98695 | 8.0242 × 10−11 |
| One-step secant back propagation | 0.92335 | 1.388 × 1010 |
| Scaled conjugate gradient back propagation | 0.96904 | 1.946 × 10−6 |
| ANN Data | Network Architecture | Model Performance | References | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Soil Parameter Investigated | ANN Input Variables | No. of Data Used | No. of Training Data Used | No. of Testing Data Used | No. of Validation Data | No. of Hidden Layers | No. of Neurons in Hidden Layer | Training Algorithm Utilised | Training | Validation | Testing | |
| UCS | 8 Inputs. LL, PI, GGBS content, PFA content, Molarity, activator/binder ratio, Na/Al ratio, Si/Al ratio | 283 | 70% | 15% | 15% | 1 | 9 | Bayesian regularization | R = 0.996, MSE = 0.34, MAPE (%) = 3.65 | R = 0.982, MSE = 1.50, MAPE (%) = 8.34 | [50] | |
| UCS (7 days) | Gs, LS, CU, CC, LL, PL, OMC, MDD | 72 | 70% | 15% | 15% | 1 | 11 | - | R = 0.9782 | R = 0.996 | R = 0.9711 | [52] |
| UCS (14 days) | Gs, LS, CU, CC, LL, PL, OMC, MDD | 72 | 70% | 15% | 15% | 1 | 11 | - | R = 0.9824 | R = 0.9843 | R = 0.9615 | [52] |
| UCS (28 days) | Gs, LS, CU, CC, LL, PL, OMC, MDD | 72 | 70% | 15% | 15% | 1 | 11 | - | R = 0.9946 | R = 0.9992 | R = 0.9929 | [52] |
| UCS | Percentage of Clay, percentage of RHA, percentage of cement, percentage of PFA, curing duration(days) | 129 | 70% | 15% | 15% | 1 | 10 | Levenberg–Marquardt | R2 = 0.9813, MSE = 0.0395, RMSE = 0.1987 | R2 = 0.9714, MSE = 51.34, RMSE = 7.1651 | [55] | |
| UCS | Curing duration, compaction energy. | 80 | 70% | 15% | 15% | 2 | 8 in each layer | R2 = 0.924 | R2 = 0.908 | R2 = 0.889 | [56] | |
| UCS | ST, MC, We, CM, DI, L, CA, SV, D, MS, DS, CD, curing time (days), CT | 216 | 80% | 20% | 1 | 50 | Adam | R = 0.980 (Average), MAE = 115.29, RMSE = 231.2 | R = 0.925 (Average), MAE = 292.2, RMSE = 419.82 | [57] | ||
| UCS | Moisture content, cement (percentage), air foam(percentage) and waste fishing net content (percentage) | 51 | 70% | 30% | 2 | 12 and 10 neurons | Levenberg–Marquardt | R = 0.95, MAE = 3.9001, RMSE = 9.1948 | R = 0.94, MAE = 8.6535, RMSE = 10.3390 | [58] | ||
| CBR (28 days) | LL, PL, OMC and MDD | 49 | 70% | 30% | - | - | - | Differential evolution | R = 0.98 | R= 0.86 | [59] | |
| CBR (28 days) | LL, PL, OMC and MDD | 49 | 70% | 30% | - | - | - | Levenberg–Marquardt | R = 0.96 | R= 0.93 | [59] | |
| CBR (28 days) | LL, PL, OMC and MDD | 49 | 70% | 30% | - | - | - | Bayesian regularization | R = 0.96 | R= 0.93 | [59] | |
| CBR | Type of ash, mix proportion (percentage), LL, PL, MDD, OMC and number of geogrid layers | 210 | - | - | - | 1 | 7 | Levenberg–Marquardt | R = 0.94472 | R = 0.93327 | R = 0.94685 | [60] |
| CBR (28 days Soaked) | LL, PI, percentage of PFA, OMC, MDD and no. of geotextile layers | - | - | - | - | 1 | - | Levenberg–Marquardt | R = 0.99846 | R = 0.98508 | R = 0.92149 | [61] |
| CBR (28 days Soaked) | Percentage of RHA, percentage of lime, curing time (days), OMC and MDD | 48 | 70% | 15% | 15% | 1 | 12 | - | R = 0.9948 | R = 0.98909 | R = 0.98895 | [62] |
| CBR (Soaked) | PL, LL, GS, LS, CU, CC, OMC and MDD | 72 | 70% | 15% | 15% | 1 | 8 | - | R = 0.9988 | R = 0.9996 | R = 0.9976 | [63] |
| CBR (Unsoaked) | PL, LL, GS, LS, CU, CC, OMC and MDD | 72 | 70% | 15% | 15% | 1 | 17 | - | R = 0.9912 | R = 0.9993 | R = 0.9806 | [63] |
| Coefficient of permeability (K) | percentage passing 0.005 mm, PI, MDD, lime percentage, pozzolan percentage, Cd | 69 | 70% | 15% | 15% | 1 | 9 | R = 0.9968 | R = 0.98883 | R = 0.99405 | [64] | |
| Resilient Modulus (Mr) | Percentage of cement, percentage of lime, PI, percentage of silt, percentage of PFA, OMC, MC and clay | 125 | - | - | - | 1 | 9 | - | R = 0.9517 | - | R = 0.9467 | [65] |
| MDD | LL, PI, LS, clay-silt ratio, sand content, lime content, cement content, asphalt content in percentage | 192 | 52% | 24% | 24% | 1 | 18 | Gradient descent momentum | R2 = 0.9183, MSE = 0.28%, MAE = 4.44% | R2 = 0.9101, MSE = 0.26%, MAE = 4.24% | [66] | |
| OMC | LL, PI, LS, clay-silt ratio, sand content, lime content, cement content, asphalt content in percentage | 192 | 52% | 24% | 24% | 1 | 15 | Gradient descent momentum | R2 = 0.9025, MSE = 88.21%, MAE = 118.37% | R2 = 0.8916, MSE = 89.57%, MAE = 113.03% | [66] | |
| MDD | GS, LS, free swell, D10, D30, D60, CU, CC, LL, PL | 90 | 70% | 15% | 15% | 1 | 7 | R = 0.9946 | R = 0.9715 | R = 0.9754 | [67] | |
| OMC | GS, LS, free swell, D10, D30, D60, CU, CC, LL, PL | 90 | 70% | 15% | 15% | 1 | 5 | - | R = 0.9977 | R = 0.9779 | R = 0.8855 | [67] |
| Network Architecture | ANN Data | References | |||||
|---|---|---|---|---|---|---|---|
| No of Hidden Layers | No of Neurons in Hidden Layer | ANN Input Variables | No. of Network Parameters | No. of Data Used | No. of Training Data Used | Remarks | |
| 1 | 9 | 8 | 91 | 283 | 198 | Sufficient | [50] |
| 1 | 11 | 8 | 111 | 72 | 50 | May overfit | [52] |
| 1 | 11 | 8 | 111 | 72 | 50 | May overfit | [52] |
| 1 | 11 | 8 | 111 | 72 | 50 | May overfit | [52] |
| 1 | 10 | 5 | 71 | 129 | 90 | Sufficient | [55] |
| 2 | 8 in each layer | 2 | 105 | 80 | 56 | May overfit | [56] |
| 1 | 50 | 14 | 801 | 216 | 172 | May overfit | [57] |
| 2 | 12 and 10 | 4 | 201 | 51 | 36 | May overfit | [58] |
| - | - | 4 | - | 49 | 34 | No Remark | [59] |
| - | - | 4 | - | 49 | 34 | No Remark | [59] |
| - | - | 4 | - | 49 | 34 | No Remark | [59] |
| 1 | 7 | 7 | - | 210 | - | No Remark | [60] |
| 1 | - | 6 | - | - | - | No Remark | [61] |
| 1 | 12 | 5 | 85 | 48 | 34 | May overfit | [62] |
| 1 | 8 | 8 | 81 | 72 | 50 | May overfit | [63] |
| 1 | 17 | 8 | 171 | 72 | 50 | May overfit | [63] |
| 1 | 9 | 6 | 73 | 69 | 48 | May overfit | [64] |
| 1 | 9 | 8 | - | 125 | - | No Remark | [65] |
| 1 | 18 | 8 | 181 | 192 | 100 | May overfit | [66] |
| 1 | 15 | 8 | 151 | 192 | 100 | May overfit | [66] |
| 1 | 7 | 10 | 85 | 90 | 63 | May overfit | [67] |
| 1 | 5 | 10 | 61 | 90 | 63 | Sufficient | [67] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeremiah, J.J.; Abbey, S.J.; Booth, C.A.; Kashyap, A. Results of Application of Artificial Neural Networks in Predicting Geo-Mechanical Properties of Stabilised Clays—A Review. Geotechnics 2021, 1, 147-171. https://doi.org/10.3390/geotechnics1010008
Jeremiah JJ, Abbey SJ, Booth CA, Kashyap A. Results of Application of Artificial Neural Networks in Predicting Geo-Mechanical Properties of Stabilised Clays—A Review. Geotechnics. 2021; 1(1):147-171. https://doi.org/10.3390/geotechnics1010008
Chicago/Turabian StyleJeremiah, Jeremiah J., Samuel J. Abbey, Colin A. Booth, and Anil Kashyap. 2021. "Results of Application of Artificial Neural Networks in Predicting Geo-Mechanical Properties of Stabilised Clays—A Review" Geotechnics 1, no. 1: 147-171. https://doi.org/10.3390/geotechnics1010008
APA StyleJeremiah, J. J., Abbey, S. J., Booth, C. A., & Kashyap, A. (2021). Results of Application of Artificial Neural Networks in Predicting Geo-Mechanical Properties of Stabilised Clays—A Review. Geotechnics, 1(1), 147-171. https://doi.org/10.3390/geotechnics1010008








