Abstract
Approximately 82% of amputees prefer microprocessor knees (MPKs) to the passive alternatives. However, the cost of these devices makes them inaccessible for many patients. The aim of this research is to develop an affordable MPK that allows for stumble reduction and flexion dampening at a fraction of the cost of similar devices. The GKnee was developed by a sophisticated mathematical model that can effectively calculate geometric configuration and simulate forces transferred through a prosthetic knee at any given point through the gait cycle. With a median error of 6%, the mathematical model was developed to the point of reasonable accuracy for determining component placement and force interactions. The model served as a valuable tool to assist in the iterative design process of the GKnee, influencing component selection for the hydraulic system and frame design. This model was then validated using a compression rig and a mock GKnee prototype. The GKnee was then evaluated for its ability to perform under expected loading conditions, using compression testing and dynamic flexion testing. This research led to the development of a sub USD 500 microprocessor prosthetic, while remaining under 2.27 kg.
1. Introduction
Limb loss affects 36 to 58 million people globally, with transfemoral (TF) amputations affecting approximately 25% of that population and growing by 44,400 per year within the United States [1,2,3,4]. The emergence of dynamically adjusting microprocessor knees (MPKs) has greatly improved the gait for transfemoral amputee patients worldwide. MPKs can adjust to patient gait, even in mid-stride, and have shown reduced metabolic energy expenditure [5]. While the benefits of the MPKs include increased stability, biomechanical symmetry, other functional benefits, and even preference, these knees currently cost, on average, USD 20,000 to the prosthetist and nearly twice as much to the patient [6,7,8,9]. This price point is unreachable for 80% of the world’s population who earn less than USD 10 per day [10]. An affordable solution with the features of a high-end system is needed for most amputees in the world.
Previous work conducted in 2016 established the first iteration of a feasible low-cost, microprocessor-controlled knee device (E-Knee) for the current study to build upon [11,12]. The E-Knee was found to be a viable prototype that met low-cost, electronic-control design specifications and had comparable stability to commercial systems in qualitative and quantitative analysis.
The objective of this study was to create a ground-up design for the next iteration knee, using a mathematical model approach to allow for optimization of components and create a device with improved quality and functionality. The design work of this research is focused on improving a validated mechanical system from previous results while incorporating major changes [11,12]. Components and systems were evaluated and validated on an ongoing basis. Three major prototype iterations were completed, and the systems were evaluated for load-bearing capacity, pressure ratings, hydraulic fluid flow, dampening capabilities, and component cost.
2. Materials and Methods
This research aimed to combine the mechanical advantages presented by four-bar knee systems with an electro-hydraulic damper so that the prototype knee system (GKnee) could provide active control. Four-bar systems already have the innate advantages of increased toe clearance, reduced lateral sway, reduced hip rotation, and decreased risk of secondary injury [13,14,15]. The primary geometric design was based on the linkage from the LIMBS International M3 and was used in the previous E-Knee device discussed above [11]. The LIMBS M3 has innate stability to up to six degrees of flexion. This research intended to address the following limitations of the 2016 E-Knee system: restricted flexion range (90 degrees max), subpar dampening capabilities (could not arrest motion), elevated power requirements (mainly because of the solenoid), and union of the flexion stopping mechanism and the damper units. The desired device specifications are shown in Table 1.
Based on the previous E-Knee prototype, the damper remained an electro-hydraulic system. To address solenoid power requirements, the damper system was constrained to be actuated by a small servo. Thus, the damper would allow for the electronic control necessary in a microprocessor system. However, the microprocessor control system and other electronics were outside of the scope of this study. Components were selected based on the following criteria: stroke length, flow rate, and pressure response [11]. The intent was to use a force model from geometric analysis and optimize the system so that the damper could fully arrest flexion while the subject was running. The damper restricted flow, resulting in stance support that could hold up to three times the body weight of a 100 kg patient, ISO P5 [16]. From the literature, running puts up to two and a half times the body weight on the knee, and a safety factor of one-half the body weight was added [17].

Table 1.
Design specifications for the GKnee.
Table 1.
Design specifications for the GKnee.
| Criteria | Specification |
|---|---|
| Stability | Provide mechanism to arrest flexion. |
| Weight limit | Support patient of 100 kg. |
| Maintenance ease | Use retail parts commonly available. |
| Cost | Cost less than USD 500. |
| Variable cadence | Include mechanism for variable swing control. |
| Supportive yield for sitting down | Include mechanism for variable knee resistance. |
| Knee locking | Must have immediate effect from stability mechanism. |
| Redesign amount | Minimally redesign IM knee. |
| Degree of flexion | Minimum 120 degrees of flexion. |
| Weight | Weigh less than 2.27 kg (5 lb) [18]. |
2.1. Mathematical Model
The purpose of the mathematical model was to aid in the design process of the prosthetic components and optimization of the hydraulic system integration. The model was composed of two sections—the initial position problem and kinematic analysis. The initial position problem equations were used to find the position and angles of the links at any point in the gait cycle. The kinematic analysis calculated the reaction forces acting on the links by relating gait data to the individual links at their respective angles.
2.1.1. Initial Position Problem
The knee’s four-bar system consists of the following links: back link (L), upper block (T), kneecap (C), and lower block (B). As shown in Figure 1, the position of each link was detailed by four nodes situated at link attachment points to an axle. These nodes are P1 (back link and upper block), P2 (upper block and kneecap), P3 (kneecap and lower block), and P4 (lower block and back link). θ (angle between the back link and upper block), measured during flexion, serves as input to calculate θA, θL, and θC.
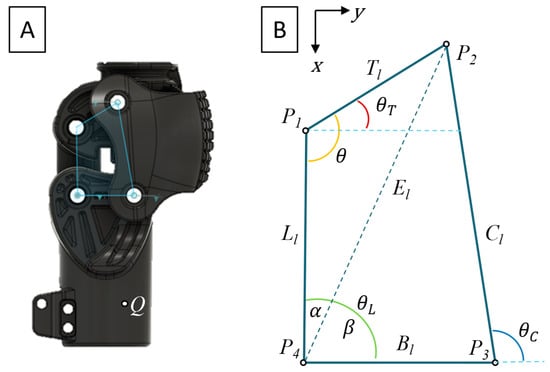
Figure 1.
(A) Side view of LIMBS IM prosthetic knee with four-bar overlay; (B) four-bar geometry with labeled links, angles, and nodes.
The calculations assume the back link (L) to be fixed and the length of the T (2.5 cm), C (5 cm), B (3 cm), and L (3.6 cm) to be constant. The origin of the coordinate system was assigned to node P1, and the B link was parallel to the positive x-axis. All three output angles are calculated in reference to the positive x-axis. The link E was the distance between P1 and P3, and α and β were the subdivisions of θL caused by this line. Figure 1 illustrates the knee’s four-bar system, its links, nodes, and angles relevant to initial position problem equations. Note that the subscript “l” denotes the length of that linkage. θT0 describes the initial angle of θT when at rest and is equal to 0.18π for this linkage.
P1 was chosen as the best top attachment point for the hydraulic piston because of the space requirements. The bottom attachment of the piston was chosen to be in the lower block, the x and y coordinates for the bottom attachment were set as variables Qx and Qy, respectively. Qx and Qy were user input values based on design modifications to the bottom block. For the knee to remain able to move freely during regular gait, the piston needs to have a variable length. A gait cycle was assumed to have a length of 1.2 s (approximation from the literature of healthy and amputee gaits) and a sample size of 1000 [19,20]. The length, angle, stroke, and velocity of the piston (Pl, Pa, Ps, and Pv, respectively) were calculated using the positional data of P1 through gait.
Because the system is a double-rocker linkage, meaning that both the back link and the kneecap do not complete full rotations and have constrained angles, continuous motion is not possible. These angle formulas were validated with CAD calculations on the linkage.
2.1.2. Kinematic Analysis
A kinematic analysis was developed to find appropriate internal attachment points and maximize the ratio between damper stroke and maximum force. A model of forces and moments acting through each link member was created using kinetic and kinematic gait data from Godest et al. and Winter [19,21]. A pseudo-static system was used to calculate the forces moving through the components at every time increment.
2.1.3. Free Body Diagram
The first step in analyzing the forces acting on the various linkages was establishing the free body diagram (FBD) and defining the various components in effect. Figure 2 shows the basic configuration of the forces. The analysis of the system was undertaken during static locking; therefore, the forces acting on the system from gait were two-dimensional vectors that were translated to the tibia from the GRFs. The tibia angle was used to translate the vertical GRF into a tibia vector. For this study, the analysis focused primarily on the force vector acting on the piston, which attached to the lower block on a rotating axle lower than shown. This was undertaken to appropriately select hydraulic components that could withstand gait. The lower block was fixed, and its posterior axle, denoted by a black dot in the figure below, was the point from which the forces were considered. The forces acting through the back link, piston, and kneecap are uniaxial because they are attached to rotating axles.
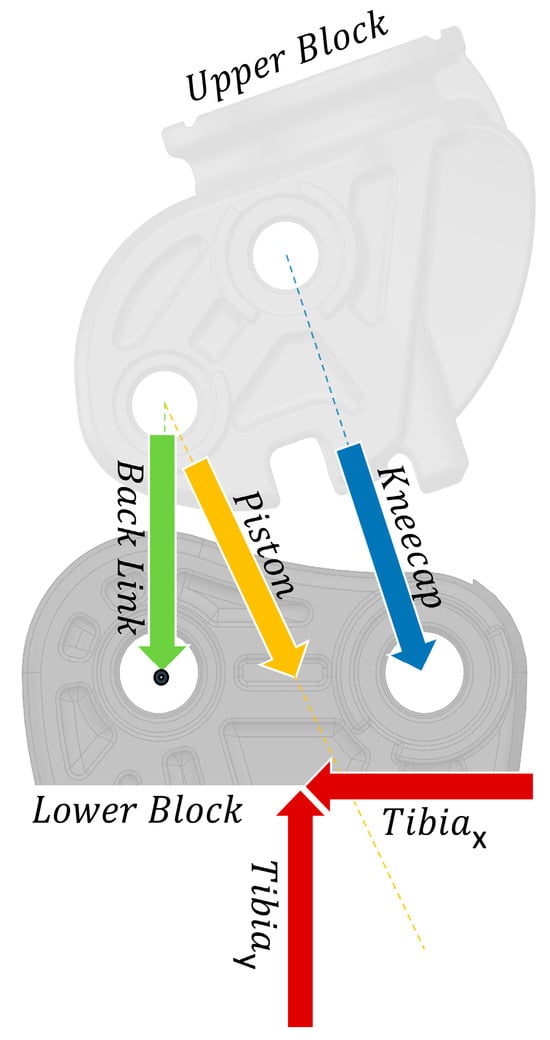
Figure 2.
Free body diagram (FBD) for the four-bar IM knee mechanism. Force vectors are indicated by arrows with dotted lines denoting linkage attachments.
2.1.4. Force Calculations
The objective of the knee design was to build a system that could resist loading during gait and stumble. Because the piston prevented further movement when it was locked into position, the forces acting through the system could be assumed to be static. Although static analysis simplified conditions, the system is a four-bar mechanism, which made the forces acting through the various linkages more difficult to determine initially.
Data from the literature was compiled to estimate the actual force requirement of a hydraulic piston. The data used were flexion angle (angle between tibia and femur), ground reaction forces (GRFs) in the x and y, and tibia angle in relation to the ground. The GRF in the x is the force parallel to the ground and GRF in the y is the force perpendicular to the ground. These two force components act on the foot of the prosthetic device as a reaction to the weight applied to the ground by the subject. The forces can be as high as 1.2× body weight during normal walking speed and can reach up to 2.5× body weight during running.
For the literature data to be useful in the mathematical model, the forces were translated to the components acting on the tibia segment of the prosthetic device. The GRF net force was found by adding the x and y GRF components. Then, the angle of the GRF net force was found and subtracted from the tibia angle to find the angle between the tibia and GRF. Using this angle, the tibia x (forces perpendicular to the tibia) and tibia y (forces parallel to the tibia) were found.
The calculated angle data was then used to relate the linkage angles during flexion to what is expected to occur during normal gait. θC is the angle between the positive x-axis and the cap link. θL is the angle between the positive x-axis and the back link. θP is the angle between the positive x-axis and the piston.
From the reference point, three equations were established: a sum of the moments, a sum of the forces in x, and a sum of the forces in y. Generalized equations can be seen below. These equations were calculated for a given load for all angles of the gait cycle. In these formulas, the letters representing the linkages are being used to display the force in each respective link. The primary force components were piston (P), tibia, kneecap (C), and back link (L). Bl represents the length of the lower block linkage, and Tibial represents the length of the tibia.
By solving for the forces acting on each of the links (P, C, and L), the max force acting on the piston during gait can be used as the required capacity for choosing the hydraulic system components. The forces solved were calculated for the initial 60% of gait encompassing heel strike to toe off. The following section consisting of the missing 40% of gait is called the “swing phase”, where the foot is not in contact with the ground; therefore, no forces are being transferred to the knee because of the subject’s weight. This reduces the range of flexion during gait to 0 to 38 degrees of flexion in a healthy individual. The max forces were calculated based on the following inputs: max forces on piston during gait, length of tibia, patient weight, factor of safety, and bottom attachment point.
2.1.5. Validation
The mathematical model was validated by constructing a knee frame with the same established dimensions and inserting an s-beam load cell in place of the piston. The knee frame was then inserted into a testing rig that had a pneumatic piston at the bottom and a load cell at the top. Because the GRF data were the known quantity, the knee was inserted upside down so that the force on the simulated tibia of the system would be read directly. The femur of the system would be pressed on by the pneumatic cylinder. At the start of both the femur and the tibia were axle joints that allowed the forces exerted to attempt to flex the knee. This rig setup can be seen in Figure 3.

Figure 3.
GKnee placed in the pneumatic compression testing rig locked at full extension.
A threaded bolt was used to adjust the faux piston length to set the knee to several different knee angles. At each set angle, the system was subjected to a loading cycle. The pneumatic cylinder applied force at a rate of 100 N/s and would hold at the set load for 30 s. During this time, the s-beam and the rig load cell were collecting data at 10 and 100 Hz, respectively. A commercial digital angle gauge (Johnson; accuracy: ±0.1 degrees) was used to collect the following angles: tibia, femur, and knee flexion. These were needed so that the mathematical model would apply the simulated GRFs to the knee at the appropriate angles.
At each set angle, the first load cycle was 200 N to settle the frame and remove any motion in the system. This angle value was recorded and became the set angle label. Loading cycles were conducted at 7, 12, 19, 24, 29, and 39 degrees. At each set angle, the true load cycles started at 1000 N and increased in steps of 200 N. The load cycles were discontinued after the s-beam read approximately 8000 N or the load angle reached 3000 N, which reflected the s-beam’s maximum load (1 imperial ton) and more than the maximum running weight of a 100 kg patient (~3000 N when including a factor of safety). The data were then used to validate both the accuracy of the mathematical model and quantitatively measure the forces that would be acting on the piston throughout the gait.
2.2. Components
Components were selected based on a variety of factors that related to the pressure requirements and balancing of various performance metrics. The approach of validation focused both on individual components but also included the validation tests of assembled systems. Additionally, the combined weight of the system was under consideration because of its effect on inertia and fatigue [22].
2.2.1. Selection Criteria
The force calculations were used to establish two parameters for the hydraulic system—the piston load and the piston attachment points. A balance had to be struck between the cylinder size, the maximum fluid pressure, and the flow rate of fluid. Additionally, the points of connection between the components could limit the flow rate and, thus, necessitate a higher-pressure system, which decreased the options for component selection. Source selection was mostly restricted to off-the-shelf components to reduce costs and improve maintenance ease. Based on preliminary data of knee angular velocity during gait, it was determined that the stroke speed of the cylinder would be at least 4 cm/s. Single- and double-acting cylinders were considered, but because the system was a damper, the additional functionality of a double was not beneficial.
Fluid flow rate and the valve actuation method were the primary considerations in selecting an appropriate valve for the system. The selected cylinders came with the condition of a flow rate of 7.11 L per minute (lpm). To increase or decrease dampening of the hydraulic system, the valve needed to have proportional control. Valve flow methods range from ball mechanisms to very small orifices, and actuation methods include mechanical and electrical inputs. Methods that allow large flow, such as ball valves, allow more fluid but would be more difficult to actuate. To reduce the power load on the future electronic system, mechanical proportional valves were chosen. These could be actuated using a small servo and required no continuous power to remain at specific dampening levels. Mechanical valves were evaluated on the following criteria: pressure rating (>20 MPa), flow rate (>7.11 lpm), and operating torque (<2.45 N·m). The operating torque limitation was established by finding a compact servo with the appropriate speed and voltage requirements. While pressure rating was a product specification, flow rate and operating torque often were not disclosed. Therefore, tests were conducted on the considered systems to validate their capability.
The oil considered for this system was transmission fluid. Although more advanced oils are available, this was analyzed because it was low cost and accessible throughout the world. Pressure drop calculations were performed to ensure the head loss of any connections or manifolds was not too great. The hydraulic system, when acting as a damper, was not applying force toward moving but, rather, restricting flow. As the fluid flowed out of the cylinder, it needed to be stored in a reservoir so that when the cylinder was extended again, the negative pressure would refill the cylinder. The primary specification of the reservoir was that it could hold at least the volume of fluid equal to that of the stroke of the cylinder during use.
2.2.2. Piston
Selection
The hydraulic pistons (Figure 4) are responsible for locking the knee and required a mounting interface to connect to the four-bar links. The Vektek and Bansbach pistons were both identified, offering opportunities for different designs based on their mounting styles.

Figure 4.
(A) Vektek threaded single-acting piston; (B) Bansbach double-acting piston.
The Vektek threaded single-acting piston has 25.4 mm of stroke and is capable of withstanding 34.5 MPa. This piston is threaded, which requires a mounting manifold; it also incorporates a SAE4 threaded port at the bottom, which allows the option to connect a pipe or to just have a manifold to direct fluid. The Bansbach double-acting piston was also identified, which incorporates clevis ends, reducing any requirement for additional machining, and uses a DN2 port. This piston was rated for 9 kN of extension force.
Validation
The mathematical model was used to calculate the force on the piston and, therefore, the pressure on the hydraulic system for the three-times body weight test of a 100 kg patient in recovery. Recovery in this case was set to a 20-degree knee angle, which is approximately 26% of a gait cycle before regular heel strike, and an 85-degree tibia angle, which is higher than typical during gait. It should be noted that this is a worst-case scenario simulation where not only is the subject running (2.5 times body weight on the system), but the safety factor is considered (0.5 times body weight on the system), and the subject is also stumbling at a drastic knee angle.
After the basic leak testing, the hydraulic system would be placed inside the complete prosthetic frame with a foot attached and a T-bar in place of the femur. The hydraulic system would then be locked while the knee was bent at an angle between 8 and 25 degrees. The testers would apply their body weights to simulate the moment that would occur when a patient applies body weight to a locked knee. The hydraulic system was observed for any leaking, as well as for deflection from the original locking angle. Because the system was designed and components selected to meet pressure parameters, the primary validation of this system was to confirm that the sealing of the system had been successful. Body weight (99.8 kg) was applied to the locked system at various angles. The researcher would balance on the system so that it bore the whole weight. The vertical weight was applied up to a 0.30 m offset, resulting in a 293.7 N·m moment when the knee was flexed to 30 degrees.
Following this, the knee would be placed into the compression rig with the fully assembled hydraulic system inside. The hydraulic system was to be capable of locking the knee while supporting a patient. This was up to 3000 N at up to 30 degrees of flexion. The knee was locked at varying angles ranging between 8 and 30 degrees, verified using a commercial digital angle gauge and compressed to 1000, 1500, 2000, 2500, and 3000 N with a rapid loading rate to simulate a stumble. The rapid loading rate was vital because a long and progressive load is not accurate to what would be experienced during a stumble. The knee angle was measured while testing to observe for deflection.
The Bansbach double-acting piston required different testing. Ideally, it could be tested using its own manifold as a complete system; however, due to machining limitations, another manifold could not be made. Regardless, a simple method was developed to test the piston orifice restriction (3.3 mm) during knee articulation. By comparison with manual extension and retraction, it could be determined whether the piston functioned on the same level as previous iterations.
2.2.3. Valve
Selection
The valve was the heart of the hydraulic system, as this component was responsible for manipulating the flow of fluid. It had to be capable of throttling or blocking the fluid flow, repeatedly. The first iteration valve was a ball valve, which could withstand pressures of up to 20.7 MPa. The second iteration valve was an Eaton MRV2-10 rotary valve, which improved restriction capabilities by directing fluid flow differently. It was rated for 21 MPa of pressure and had flow of up to 18.9 L/min. Key features that improved on the ball valve were the much lower breakaway torque, more proportionality in flow, and its cartridge shape. The shape allowed for a manifold assembly instead of several fittings.
Validation
To evaluate the torque required to turn the ball valve and, thus, aid in selecting a servo with enough capacity to do so, the valves were tested with a simple movement test. A bar was attached to the valve and weight was added until the valve began to turn (called breakaway torque). This was undertaken with both a 7 cm and an 11 cm lever arm, and the results were averaged. This test was also repeated for the rotary valve.
A key component to the hydraulic system selection was identifying the optimal fluid flow. Too much restriction would establish a base dampening force that would not allow the knee to move freely. The flow profile was established for each valve by using a flow sensor attached at the outlet of the valve and a water hose at the inlet. As each of the valves needs to be a bidirectional flow control valve, the set testing was repeated with the inlet and outlet switched. The flow profile allowed for estimation of the effective control range of each valve. The mathematical model was able to output the piston velocity during gait. This was used to estimate the expected maximum flow rate of the system required to achieve the desired angular velocity of the knee. By limiting the flow control valve to its effective range, the responsiveness of the valve was improved. Therefore, if a candidate valve did not have a manufacturer-provided datasheet, a flow test was conducted. The flow test established two specifications: the flow rate and flow control profile of the valve.
2.2.4. Reservoir
Selection
The first iteration reservoir is a HAWE bladder accumulator, capable of withstanding 50 MPa. This accumulator could hold approximately 13 cm3 of fluid, which was perfect for the Vektek cylinder based on its fluid displacement; however, it was expensive and weighed 0.3 kg. A different style of bladder made from silicone was custom molded to mimic the same fluid capacity through its elasticity but offered reductions in weight and cost. Both reservoirs, as shown in Figure 5, required mounting ports to be machined into a manifold.

Figure 5.
(A) HAWE diaphragm accumulator; (B) custom molded silicone bladder accumulator.
Validation
The objective of evaluating each reservoir was to determine if it was capable of holding 13 cm3 of fluid, its ability to cycle fluid in and out as the knee is actuated, and finally if it was able to sustain any pressure that it might experience through usage. Each reservoir was tested by attaching and plumbing it to its respective hydraulic manifold and piston. The piston was fully compressed and extended to validate that the reservoir could hold enough fluid. Following this, the reservoir was repeatedly cycled and monitored. When the full hydraulic system is locking the knee, the reservoir is not subjected to high pressure because of the valve. Regardless, the reservoir was observed during testing to ensure it did not leak, and this would be further evaluated in the manifold validation.
2.2.5. Manifold
Selection
Each manifold was designed around the Vektek threaded piston and served as an interface to connect each component of the system together, as shown in Figure 6. The first iteration manifold incorporated multiple components machined from 6061 T6 aluminum. There was a threaded manifold with an incorporated O-ring that directed flow from the piston to the ball valve. This was then connected to an additional manifold that connected to the accumulator.
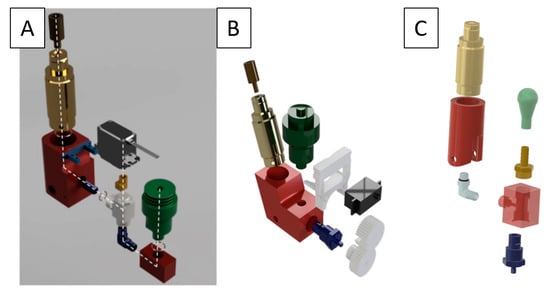
Figure 6.
(A) First iteration hydraulic system with ball valve; (B) second iteration system with rotary valve; (C) third iteration system with optimized configuration and molded bladder.
Calculations were conducted to estimate how hydraulic system performance could be improved by using a larger-diameter pipe connection between the piston and valve. These calculations aimed at seeing the fluid interaction when the piston applied a maximum force and how the fluid would react in that channel when increasing the pipe diameter to 10 mm. Assuming similar conditions with the aluminum roughness and fluid properties of the ATF, the Reynolds number results in 442, indicating laminar flow.
Using these data, a second iteration manifold was designed and streamlined the connections by only requiring one main manifold that all components would be connected to. It also improved the seals of the previous manifold by incorporating O-ring grooves. The inner diameter of the channel was also increased to allow for more laminar flow. The weight of this manifold was reduced to 0.44 kg.
Validation
The objective of evaluating each system was to determine if it was capable of its basic functional requirements, including fluid capacity, dynamics, and locking under simulated load. Evaluation of each system was conducted through various testing methods. The most basic form of testing was for fluid capacity and leaking. This was undertaken by plumbing each system with oil and cycling the piston by hand to evaluate that it was able to fully extend and compress. The next stage of testing was to test the valve’s ability to restrict fluid flow, which was also undertaken by closing the valve and attempting to compress the piston by hand. Throughout testing, the manifold iterations were observed for any failures related to leaking. If any leaking occurred, the root cause was investigated and addressed with either Teflon tape, machining modifications, or Loctite sealant. Finally, the systems were evaluated in the testing for the piston.
2.2.6. Frame
Selection
The frame of the prosthetic is the foundation for the device but must be designed to safely provide the necessary structure and volume to contain each system. The goal behind each design iteration was to improve on weight and costs while maintaining the strength requirements, as seen in Figure 7. The first iteration frame was a 12.7 mm thick 6061 T6 aluminum flat bar that connected with intermediate plates of aluminum to account for the change in width from the four-bar knee. This frame weighed 0.734 kg. It provided an area for attachment to a pylon at the bottom but, when loosened, caused the entire frame to become loose.

Figure 7.
Iterations of frames and corresponding assembly. (A) First iteration frame and assembly; (B) second iteration frame and assembly; (C) third iteration frame and assembly.
This assumes that the maximum force is 1 kN that is applied axially to the frame and the area is the cross-sectional area of the frame at its thinnest point, which is . Additionally, FEA simulations using Fusion 360 were implemented to estimate stress and minimum safety factors in order to highlight possible areas that needed redesign. These used the assumption that the load would be applied as pin supports on the frame.
The second iteration frame aimed to improve the design by reducing weight and reducing the extra pieces required by using a multi profile plate. It also incorporated an area for a pyramid adapter rather than pylon mount to allow for easy adjustments without complete disassembly of the frame. This frame was 0.68 kg in weight, which was achieved by reducing it to a thickness of 7.025 mm at the thinnest area (). Each iteration frame progressively became lighter and more compact.
The third iteration frame reduced the weight to 0.43 kg by using a 3.175 mm thick plate, thereby reducing the cross-sectional area to . This frame was evaluated using stress calculations and FEA simulation methods mentioned previously.
Validation
The knee was designed for a safety factor of 3 for a 100 kg patient. A pneumatic compression rig was used to simulate the knee loads during gait, as shown in Figure 3. The pneumatic piston simulates the person’s body weight, and attached to the piston is a steel bar that acts as a patient femur; then, the knee prototype is attached, another steel bar is attached to the bottom of the knee acting as the tibia, and a force sensor validates the load. The knee was locked by using an additional aluminum block that could be set to varying angles of flexion.
2.2.7. Assembly Validation
For load and cycling tests, assemblies were often tested as more complete systems. For instance, the hydraulic system was tested both in loading conditions and in cyclical velocity. These tests did not require the valves to change or the servos to move but tested the force-bearing and flexion-velocity functions.
System Angular Velocity
By attaching the foot of an assembled system to a bike pedal, the knee could be cycled to simulate a 100 steps/min cadence, which corresponds to an approximately 1.1 m/s gait speed falling within the norms of the literature cadence [23,24,25]. Though this task does not perfectly simulate human gait, the primary objective was to evaluate angular velocity capabilities in a cyclic environment. This was conducted for three minutes, and a video recording was processed with MATLAB dltdv8 software for dot tracking, which was then extrapolated into angular velocity tests. A sample of this data collection process is shown in Figure 8 below.

Figure 8.
GKnee attached to a bicycle with frame-by-frame marks (colored circles) from the dot tracking.
When tracking points, there were three locations required on the prosthetic assembly. One point was tracked on the ankle, one on the knee, and one point on the tibia bar. This way, calculations could be made comparing the change in knee flexion angle over time.
System Mechanical Load
Different variations of the pneumatic rig, shown in Figure 3, were used for the mathematical model validation, frame testing, and piston selection. During each of these trials, the frequency of the system load cell was 100 Hz, and the loading rate of the pneumatic piston was 100 N/s.
3. Results
The results below represent the validation of the mathematical model, which then drove the design of the physical system. Additionally, each component, including the frame, all parts within the hydraulic system, the electronics, and the fully assembled prototype, was investigated and validated with respect to the above-described methods.
3.1. Mathematical Model
Adhering to the methods described, the following force calculation models were created (shown below in Figure 9). From these calculations, it was determined that the piston needed to support a force up to 14,800 N. The forces shown are a theoretical simulation from a static evaluation of a 100 kg running patient.
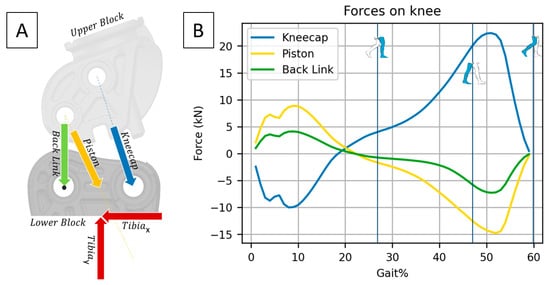
Figure 9.
Results of the force calculations for the damper attachment point. (A) FBD of the four-bar system; (B) simulated forces if piston had to perform a complete stop.
Figure 10 highlights both the validation of the mathematical model and a summary of the forces acting on the piston at various loads and angles. Note that angle 39 has been excluded from the figure below. Angles 29 and 39 began at 300 N and increased in 100 N steps until the limits had been reached because the normal 1000 N starting load already exceeded the measurement limitations. Despite this, angle 39 was at such extreme flexion that the test only had two data points and was therefore excluded.
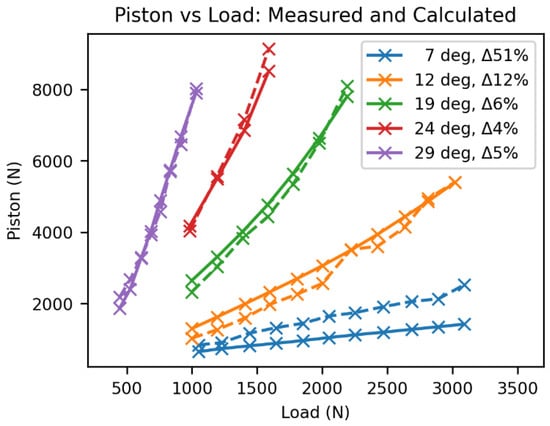
Figure 10.
Measured (solid line) and calculated (dashed line) forces acting on the piston during loading at various set angles. The difference error percentage is given between the two lines.
3.2. Valve Torque
The breakaway torques of the standard ball valve and the MRV2-10 Eaton rotary valve were 0.366 N·m and 0.0078 N·m, respectively. For the rotary valve, the plastic lever alone was enough to slowly turn the valve. This new data were very important because the previous servo was rated for 1.37 N·m, and this means a smaller, faster servo could be used as a replacement.
3.3. Hydraulic System
From calculations, the Vektek piston would only be subjected to 15.2 MPa of pressure, which is well within the limits of the piston. Based on the results of the flow analysis, the flow remains laminar until approximately 4 mm. This gave the indication that the manifold could be changed to reduce the inner diameter, or alternatively, a small diameter connecting pipe could be used instead.
The second iteration hydraulic system began leaking after the application of a simulated body weight. The pressure applied to the system caused the manifold to begin leaking out of the piston area. This leakage allowed for compression of the piston even when the valve was closed. This was presumed to be because of an O-ring failure; however, the manifold needed to be taken apart for analysis.
After analysis of the manifold, we realized a major flaw in the design. The groove for the O-ring was concentric to the channel connecting the piston to the accumulator, but this groove was not concentric to the face of the piston itself. This meant that an unequal pressure was being subjected to the O-ring, and it was not capable of sealing. A new manifold with corrections was machined and was found to hold pressure and has not leaked as before. A new issue presented itself, though, and that is that the internal O-ring that is around the valve, under pressure, extrudes into the hole where the accumulator threads and allows the fluid to seep into that hole, allowing the piston to compress. This happens at higher pressures, so we hope that under patient testing, this is unlikely to occur. The nature of this issue allows for the system to reset itself once the valve is cycled opened and closed.
The other manifold was repaired using a form of anaerobic flange sealant (Loctite) to seal the threads of the piston. The addition of Permatex high-performance thread sealant, which is rated to withstand upward of 70 MPa and temperatures up to 150 °C, was successful in keeping pressure and can be used as a method of sealing in the future.
The third iteration hydraulic system testing revealed significant failures in the machining of the manifold. The hydraulic system could not sustain loading even at the minimum load input of 1 kN. It was found that the system would briefly hold and then begin to completely compress.
Investigation found that the tolerances of the rotary valve were off by approximately 0.75 mm. Although this is less than 1 mm, the O-ring will not be properly compressed and cannot create an effective seal, allowing for fluid to bypass the closed valve, defeating the purpose of the valve.
The Bansbach piston had unfavorable results. After testing, it was discovered that the piston was very restrictive and was difficult to compress when inside the knee. Even by hand, it was obvious that this piston could not work for this application.
3.4. Angular Velocity
After converting the data into angular velocity, the knee had a peak velocity greater than 500 degrees per second. This is also in both extension and flexion, meaning the knee has effective mechanical capabilities. The resulting velocity is shown in Figure 11 below.
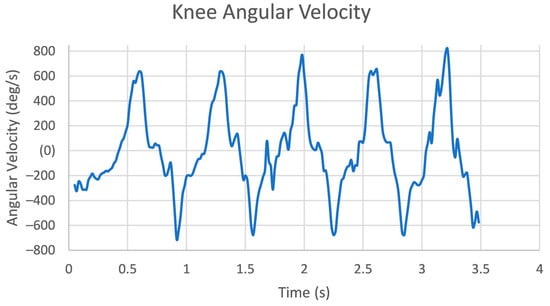
Figure 11.
Graph showing the resulting knee angular velocity during cycling test.
3.5. Frame
The 6061T6 aluminum has a yield strength of 241 MPa, and the max stress for iteration 1 was calculated to be 2.06 MPa. Iteration 2 was calculated to be 15 MPa of maximum stress. The simulations found that the frame had a minimum factor of safety of 14.1, which is above our goal of 3. The next iteration design experienced approximately 25 MPa of stress based on calculations, and the stress simulations found that the frame would be subjected to a maximum of 19.5 MPa and a safety factor of 12.7. When the prosthetic is assembled completely, there are much more complex joints being used, which allows the load to be distributed more across different components, relieving some of the stress across the individual frame pieces.
3.6. Cost and Weight
Combining the latest iteration of components into one assembled device, a breakdown of cost and weight was conducted. This breakdown assumes that the components of the knee were produced at a larger scale of 1000 prosthetics. Based on these assumptions, the final prosthetic weighs 2.12 kg and the component cost of this device is about USD 452. This weight is much more comparable to MPKs than the earlier iterations were, and the cost is significantly less than anything commercially available now.
4. Discussion
The largest multiplier on piston force loading is the knee angle during load. As Figure 11 demonstrates by the slight curvature of each line, the knee deformation past the set angle continues to increase the piston force. Based on the geometry of the four-bar mechanism, it was estimated that, near 23 degrees of flexion, the piston would become less effective at arresting flexion. This occurs because past this angle, minute angle increments of the back link and the piston attached cause substantially larger changes in overall knee flexion. Therefore, a limitation of the system is the ductility and tolerances. Further testing would be needed to isolate the sources of the ductility completely, but likely culprits are the kneecap and the axle joints. The kneecap is made from Delrin 100P (DuPont Wilmington, DE, USA), which has worked well for the M3 relief knee, but its flexibility in this case may be detrimental to arresting flexion in certain situations. The axle joints were precision machined into the frame, but the anterior axles do not go through the whole system but rather only pair the kneecap and the frame. A short axle has a much greater likelihood of movement because the contact points are more closely spaced.
The mathematical model showed consistent performance when compared to the s-beam force measurement. The four-bar mechanism of the system has innate stability up to approximately six degrees, and the model was consistent without error until it approached these angles of stability, which could be affected more by mechanical tolerance than what can be interpreted by the model. There is a limitation of using healthy gait and GRF data to model the forces acting through the piston during gait. Future work will include an amputee-specific GRF and kinematic standard on which to model the forces expected. Despite this, the model proved itself to be an effective tool for future iterations of the GKnee with the capability of optimizing geometry to improve device performance and strength.
4.1. Future Work
There is still room for improvement in the GKnee. A major component of the knee that can be improved is the hydraulic piston. The Bansbach double-acting piston mounting style offers an opportunity for weight and cost savings. To be able to give the GKnee to a patient, more development is needed to make it into a user-friendly system. This means developing an aesthetic case and a port for easy recharging of the battery. Since this is just a prototype, these are items that can be addressed in future iterations. However, the overall findings of this research do support the hypotheses that the knee will support a 100 kg patient and that the knee can swing at 500 deg/s, while remaining at a cost below USD 500.
4.2. Limitations
The focus of this research was the mechanical system of an MPK with a very restricted focus on electronic components. The GKnee must be subjected to ISO 10328 testing, which establishes loading conditions (force vectors, durations, etc.) for a simulated 100 kg patient with a fully extended knee system in both static and dynamic scenarios. Because such tests apply maximum loads and can take more than a month to complete, the time delay and potential destruction to the system were not considered worth the benefit. Largely due to the constraint of using commercially available hydraulic components, the GKnee has a very bulky and sub-optimal hydraulic system setup. There are opportunities to improve the system design, but it will likely require more custom designs and machining, which could drive up costs. These factors were improved with the final iteration but are still in need of development.
5. Conclusions
The results of this study provide the basis for an affordable microprocessor prosthetic knee to be manufactured at a low cost while maintaining similar features to advanced devices. MPKs have been in development for over 20 years; yet, the cost of these devices causes them to remain out of reach for patients who need them most. This study validated that a future improved GKnee can be provided to patients at a fraction of the cost. Using the mathematical model, the GKnee can be strengthened and tested under industry standards to one day become a competitor to similar devices.
Author Contributions
Conceptualization, L.G. and R.V.G.; methodology, L.G. and R.V.G.; software, L.G., G.B. and E.R.; validation, G.B. and E.R.; formal analysis, L.G. and G.B.; investigation, L.G., G.B. and E.R.; resources, L.G. and R.V.G.; data curation, L.G., G.B. and E.R.; writing—original draft preparation, L.G., E.R. and F.A.R.; writing—review and editing, L.G., G.B., E.R., F.A.R. and R.V.G.; visualization, L.G., G.B. and E.R.; supervision, L.G. and R.V.G.; project administration, R.V.G.; funding acquisition, L.G. and R.V.G. All authors have read and agreed to the published version of the manuscript.
Funding
Research reported in this paper was supported by the National Institute of General Medical Sciences of the National Institutes of Health under linked Award Numbers RL5GM118969, TL4GM118971, and UL1GM118970. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
This study did not generate additional data other than that shown. The primary data generation tool was the mathematical model, which has been described in detail.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study, in the collection, analyses, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results. The authors have no commercial interest in any of the components or the proposed device. L.G. has and R.V.G. had an association with LIMBS International, which is a 501(c)(3) nonprofit that distributes prosthetic systems, but they have no commercial investment in this proposed device nor in any of the discussed components.
References
- WHO. World Report on Disability; WHO: Geneva, Switzerland, 2011. [Google Scholar]
- Amputee Coalition. Amputee Statistics You Ought to Know. 2012. Available online: http://www.advancedamputees.com/amputee-statistics-you-ought-know (accessed on 3 February 2020).
- Ziegler-Graham, K.; MacKenzie, E.J.; Ephraim, P.L.; Travison, T.G.; Brookmeyer, R. Estimating the prevalence of limb loss in the United States: 2005 to 2050. Arch. Phys. Med. Rehabil. 2008, 89, 422–429. [Google Scholar] [CrossRef] [PubMed]
- Michael, J. Article on Amputee Demographics. 2001. Available online: http://www.oandp.com/news/jmcorner/2001-02/2.asp (accessed on 2 June 2017).
- Johansson, J.L.; Sherrill, D.M.; Riley, P.O.; Bonato, P.; Herr, H. A clinical comparison of variable-damping and mechanically passive prosthetic knee devices. Am. J. Phys. Med. Rehabil. Assoc. Acad. Physiatr. 2005, 84, 563–575. [Google Scholar] [CrossRef]
- Hafner, B.J.; Willingham, L.L.; Buell, N.C.; Allyn, K.J.; Smith, D.G. Evaluation of Function, Performance, and Preference as Transfemoral Amputees Transition From Mechanical to Microprocessor Control of the Prosthetic Knee. Arch. Phys. Med. Rehabil. 2007, 88, 207–217. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Villalpando, E.C.; Herr, H. Agonist-antagonist active knee prosthesis: A preliminary study in level-ground walking. J. Rehabil. Res. Dev. 2009, 46, 361–374. [Google Scholar] [CrossRef] [PubMed]
- Prinsen, E.C.; Nederhand, M.; Sveinsdóttir, H.; Prins, M.; van der Meer, F.; Koopman, H.; Rietman, J. The influence of a user-adaptive prosthetic knee across varying walking speeds: A randomized cross-over trial. Gait Posture 2017, 51, 254–260. [Google Scholar] [CrossRef] [PubMed]
- Hafner, B.J.; Smith, D.G. Differences in function and safety between Medicare Functional Classification Level-2 and -3 transfemoral amputees and influence of prosthetic knee joint control. J. Rehabil. Res. Dev. 2009, 46, 417–433. [Google Scholar] [CrossRef]
- Chen, S.; Ravallion, M. The Developing World is Poorer than We Thought, but No Less Successful in the Fight against Poverty. Q. J. Econ. 2010, 125, 1577–1625. [Google Scholar] [CrossRef]
- Galey, L.J. Development and Initial Testing of a Low-Cost, Electronic, Microprocessor-Controlled Prosthetic Knee. 2016. Available online: http://digitalcommons.utep.edu/dissertations/AAI10251518 (accessed on 9 May 2017).
- Galey, L.J.; Gonzalez, R.V. Design and Initial Evaluation of a Low-Cost Microprocessor-Controlled Above-Knee Prosthesis: A Case Report of 2 Patients. Prosthesis 2022, 4, 60–72. [Google Scholar] [CrossRef]
- Gard, S.A.; Childress, D.S.; Uellendahl, J.E. The Influence of Four-Bar Linkage Knees on Prosthetic Swing-Phase Floor Clearance. J. Prosthet. Orthot. 1996, 8, 34–40. [Google Scholar] [CrossRef]
- Gailey, R.; Allen, K.; Castles, J.; Kucharik, J.; Roeder, M. Review of secondary physical conditions associated with lower-limb amputation and long-term prosthesis use. J. Rehabil. Res. Dev. 2008, 45, 15–29. [Google Scholar] [CrossRef] [PubMed]
- Tang, P.C.Y.; Ravji, K.; Key, J.J.; Mahler, D.B.; Blume, P.A.; Sumpio, B. Let Them Walk! Current Prosthesis Options for Leg and Foot Amputees. J. Am. Coll. Surg. 2008, 206, 548–560. [Google Scholar] [CrossRef] [PubMed]
- ISO 10328:2006; Prosthetics-Structural Testing of Lower-Limb Prostheses—Requirements and Test Methods. International Organization for Standardization: Geneva, Switzerland, 2006.
- Keller, T.S.; Weisberger, A.M.; Ray, J.L.; Hasan, S.S.; Shiavi, R.G.; Spengler, D.M. Relationship between vertical ground reaction force and speed during walking, slow jogging, and running. Clin. Biomech. 1996, 11, 253–259. [Google Scholar] [CrossRef] [PubMed]
- Sup, F.; Bohara, A.; Goldfarb, M. Design and Control of a Powered Transfemoral Prosthesis. Int. J. Rob. Res. 2008, 27, 263–273. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A. Biomechanics and Motor Control of Human Movement, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1990. [Google Scholar]
- Selles, R.W.; Bussmann, J.B.J.; Wagenaar, R.C.; Stam, H.J. Effects of prosthetic mass and mass distribution on kinematics and energetics of prosthetic gait: A systematic review. Arch. Phys. Med. Rehabil. 1999, 80, 1593–1599. [Google Scholar] [CrossRef] [PubMed]
- Godest, A.C.; Beaugonin, M.; Haug, E.; Taylor, M.; Gregson, P.J. Simulation of a knee joint replacement during a gait cycle using explicit finite element analysis. J. Biomech. 2002, 35, 267–275. [Google Scholar] [CrossRef] [PubMed]
- Narang, Y.S.; Arelekatti, V.N.M.; Winter, A.G. The Effects of Prosthesis Inertial Properties on Prosthetic Knee Moment and Hip Energetics Required to Achieve Able-Bodied Kinematics. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 754–763. [Google Scholar] [CrossRef]
- Barr, A.E.; Lohmann Siegel, K.; Danoff, J.V.; McGarvey, C.L., III; Tomasko, A.; Sable, I.; Stanhope, S.J. Biomechanical comparison of the energy-storing capabilities of SACH and Carbon Copy II prosthetic feet during the stance phase of gait in a person with below-knee amputation. Phys. Ther. 1992, 72, 344–354. [Google Scholar] [CrossRef] [PubMed]
- Nolan, L.; Wit, A.; Dudziñski, K.; Lees, A.; Lake, M.; Wychowañski, M. Adjustments in gait symmetry with walking speed in trans-femoral and trans-tibial amputees. Gait Posture 2003, 17, 142–151. [Google Scholar] [CrossRef] [PubMed]
- Segal, A.D.; Orendurff, M.S.; Klute, G.K.; McDowell, M.L.; Pecoraro, J.A.; Shofer, J.; Czerniecki, J.M. Kinematic and kinetic comparisons of transfemoral amputee gait using C-Leg® and Mauch SNS® prosthetic knees. J. Rehabil. Res. Dev. 2006, 43, 857–870. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).