Lower Baskets and Smaller Balls Influence Mini-Basketball Players’ Throwing Motions

Abstract

Children have different anthropometrical size ratios in relation to ball and basket compared to adults, but usually compete on the same basket height and field. Therefore, they have to adapt their throwing technique, which might result in movement patterns unfavorable for long-term performance development. In this study, we analyze how children adapt their throwing techniques to different conditions. Seven basketball players (10.14 ± 1.12 years) completed a total of 60 throws, combining different ball sizes, basket heights, and distances. The throwing movements were captured by a 3D motion capture system. Accumulated distances between all time courses of angles, angular accelerations, and velocities served as similarity measures and were analyzed by cluster analysis, including purity measures. Considering all throws, a division into seven clusters separated each individual. For all subjects, distances accounted for the most changes in the throwing motion (purity 0.81–1). In the subclusters, the basket heights were not a decisive condition (purity 0.42–0.63). However, an increase in purity was found compared to the main clusters. Children seem to adapt their movement behavior primarily to throwing distances and subordinately to basket heights, which indicates that changing playing conditions (e.g., closer 3-point line, lower baskets) might be beneficial in mini-basketball.

1. Introduction

Shooting is the most popular action of mini-basketball players, accounting for 38.9% of all actions during game play and 40.4% in training sessions [1]. This indicates the enormous importance of throwing actions in mini-basketball, which also triggers the motivation of young, active players. However, since children have different size relationships to the ball and basket than adults, the affordances for successful movement execution increase enormously if these are not adjusted. To be able to successfully solve the movement task of shooting and to develop appropriate movement skills, the external conditions need to be adapted adequately. The integrated FTEM (foundations, talent, elite, mastery) framework development describes the refinement of movement as a crucial foundation, when it comes to long-term talent development [2]. Considering the size ratios of children (hand size to ball, body size to basket height), a disproportion becomes apparent. According to calculated “hand size-ball size ratios”, eleven-year-old children should actually play with a smaller and lighter ball of size “3” or “4” instead of a ball of size “5” as specified [3]. It has also been shown that children’s shooting percentage is higher on lower baskets and with smaller balls [4,5]. Additionally, children report greater confidence in throwing using appropriate equipment (lower baskets and smaller balls) which might benefit processes of motor learning [5]. Therefore, it is widely discussed to adapt sports equipment and rules to optimize performance development and talent promotion in youth basketball. Adjusted material for children has already been successfully introduced in other sports. In tennis, e.g., children dare more, hit more shots from a comfortable height and more winners, play more in a more forward position and volleys, and also force more errors when the net and court size were scaled [6]. In water polo, children also scored significantly more often (p < 0.05) in games on smaller goals than in games on large goals [7].

Basketball throwing technique of children also changes if they shoot at lower baskets [1,8]. The adjustment of the basket height increased the quality of the throwing execution. Lower baskets allow to position the forearms vertically facing the basket whereas children often tend to rotate the elbow outwards if the need to focus on generating high throwing power than on technique. Ortega-Toro and colleagues found that children otherwise could not successfully hit baskets at the regular height [9]. This study also showed that, due to the low height of the basket, the children did not throw the ball with both hands and increasingly switched to a one-handed throwing technique with a clearly recognizable throwing and supporting hand, as it is highly recommended [9]. When applying the regulations of adult basketball, it can be observed that adolescents often compensate for physical deficits with higher movement amplitudes, flatter flight curves, and throwing angles, as well as higher speeds, causing lower accuracies of the throws in the form of lower shooting percentages [10]. This happens if the movement impulse of the ball must be prioritized over throwing stability due to physical limitations in order to generate the necessary speed [10].

However, previous studies analyzed throwing techniques only based on single, discrete parameters and changes at specific key points in time. Thereby, information about the movement processing is lacking, and a conclusion on the quality or stability of the movement technique cannot be drawn. In order to obtain knowledge about the quality of the movements, a process-oriented approach is useful [11]. Using similarity measures in single-case analyses allows to assess and quantify the movement quality of individuals. Such approaches have already been successfully applied to identify individual movement in high performance sports [12]. In the long jump, this explorative method of pattern recognition was used to show structural changes in movement patterns as well as detect individual movement styles [11]. Cluster analysis is a suitable method for grouping movements in a larger data set. The similarities between the movements are then determined by a fitting distance measure. Subsequently, individual cases are combined into groups (clusters) that are homogeneous according to the established distance measure. Furthermore, the groups among them should be as dissimilar as possible [13]. This method is particularly advantageous as a large amount of data is produced when considering many variables over the entire course of the movement.

This study aims to bridge the research gap in movement analyses of youth basketball players. Based on a process-oriented approach, the kinematics of throwing movements in youth were analyzed to identify differences and adaptations of movement techniques depending on basket heights, throwing distances, and ball sizes.

2. Materials and Methods

Seven youth players (4 females: 11.0 ± 0.7 years, 1.52 ± 0.1 m, 40.0 ± 6.7 kg; 3 males: 9.0 ± 0.0 years, 1.40 ± 0.1 m, 34.3 ± 2.9 kg) participated in this study. They have been playing basketball for 2.7 ± 1.1 years and were throwing with the right hand, except for one player. All procedures were in line with the Declaration of Helsinki and approved by the local ethical committee (GEKTUDO_2021-28).

All participants completed five shots under twelve different conditions, which were a combination of two distances, three basket heights, and two ball sizes. To avoid possible effects of fatigue, a rest period of at least 3 min was provided between each change in conditions. Subjects received no explicit instructions regarding throwing technique or any feedback except for the outcome (scored or not).

With regard to previous studies [4,9,14], we decided on the free throw line (4.63 m) and a shorter distance (2.60 m). For basket heights, the rules of the German Basketball Association [15] were considered, leading to the three heights of 2.60 m, 2.85 m and 3.05 m. In addition, the regular size for mini-basketball (size 5 ≈ 470 g, 69 cm volume) and a smaller ball size 4 (≈290 g, 66 cm volume) were used.

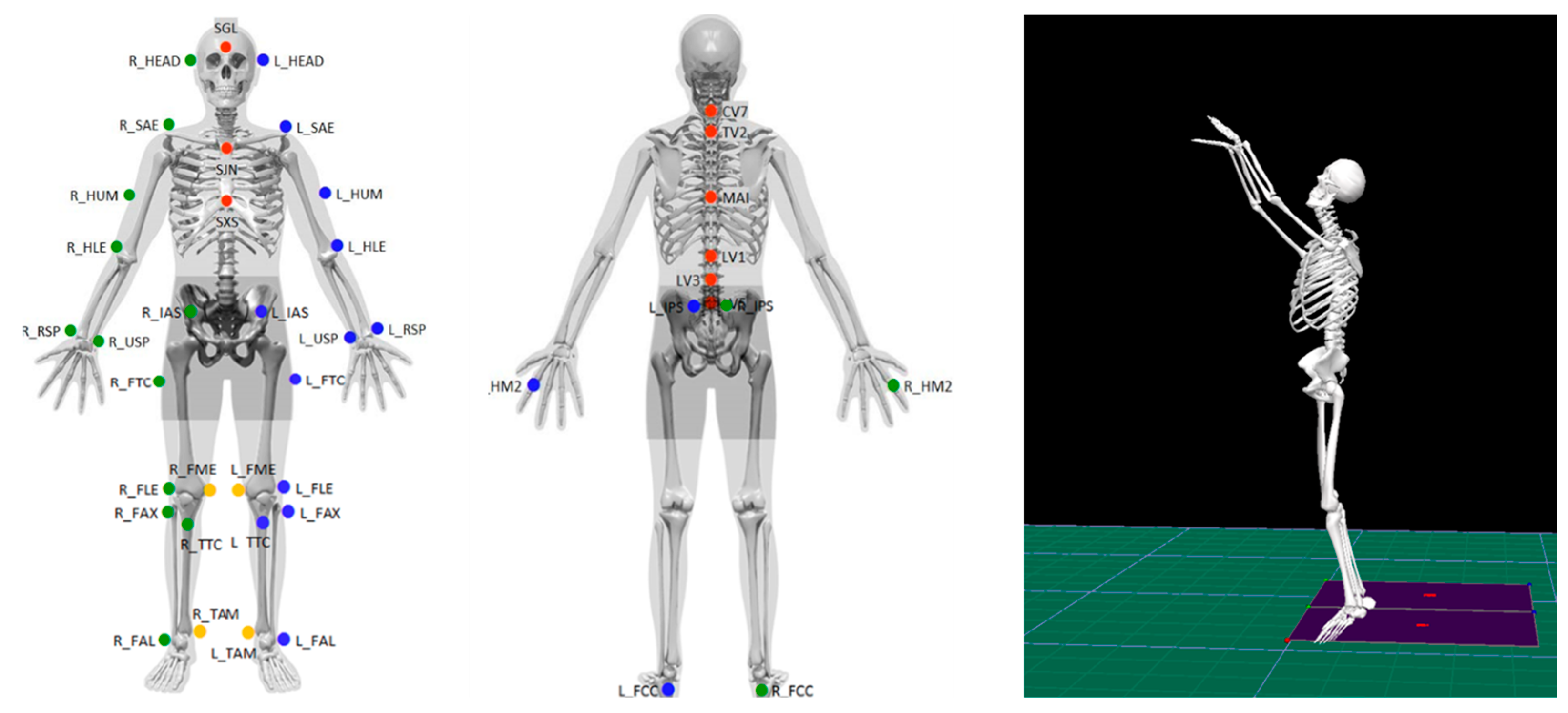
The children were guided through a warm-up for 10–15 min. The warm-up included running exercises as well as jump shots. After warm-up, reflective markers were attached to forty-seven anatomical landmarks based on a Cleveland marker set from a model used by Camargo et al. (2020) [16] (Figure 1). Each throwing motion was recorded by twelve high-speed cameras sampling at 120 Hz (Qualisys, Sweden).

The recorded marker trajectories were labeled, filtered with a 4th-order low-pass Butterworth filter with a cut-off frequency of 6 Hz, and processed further using the QTM software package (version 2019.1, build 4400, Qualisys, Sweden). The joint angles, joint velocities, and accelerations of the knees, hips, shoulders, elbows, and wrists were calculated during the entire motion sequence in Visual 3D (version 2021.11.3, C-Motion Inc., Germantown, MD, USA; Figure 1). The start and end of the motion sequence were defined by the beginning elevation of the ball (maximum elbow flexion) and the ball release (maximum extension of the elbow, plus 10 frames), respectively [10]. The time courses of all variables were normalized to the absolute maximum amplitude and to 100% time for the motion sequence described above, resulting in 101 data points with values between −1 and 1. So, comparability was ensured between different movement executions as well as the different variables. The three-dimensional Euclidean distances between the normalized trajectories were calculated from the differences at every 1% of the movement for each of the aforementioned variables. The sum of these distances served as a similarity metric for each throw when compared to each other. Cluster analysis was then used to identify groups of similar executions of the basketball shots. Hierarchical clustering combines subsets of data that are most similar. This is carried out iteratively, starting from single observations all the way to grouping all observations into one group, so any number of groups can be analyzed and evaluated. In order to quantify the similarity, the Ward method was used, which minimizes the within-group variance in each iteration [17]. A dendrogram visualizes the full hierarchical structure of the clustering. The height in the dendrogram depicts the similarity or dissimilarity, allowing an interpretation of the relative quality of the clusters. For further analysis, the purity of clusters considering a certain condition was calculated. It is defined as the sum of the absolute frequency of the most prevalent condition in each cluster divided by the total number of throws. In general, purity has an upper bound of 1 which represents a perfect separation of conditions within the clusters and a lower bound of 0 [18]. However, for interpreting purity, the number of conditions needs to be considered because an independent distribution of the conditions throughout the clusters produces the a priori relative frequency of the majority condition as the purity.

3. Results

Considering all throws (n = 395) of all subjects, the cluster analysis revealed two clusters (Figure 2). One contains all the performances of three subjects, and the other includes all the remaining subjects. Furthermore, a division into seven clusters perfectly separated the throwing techniques of each individual (Figure 2).

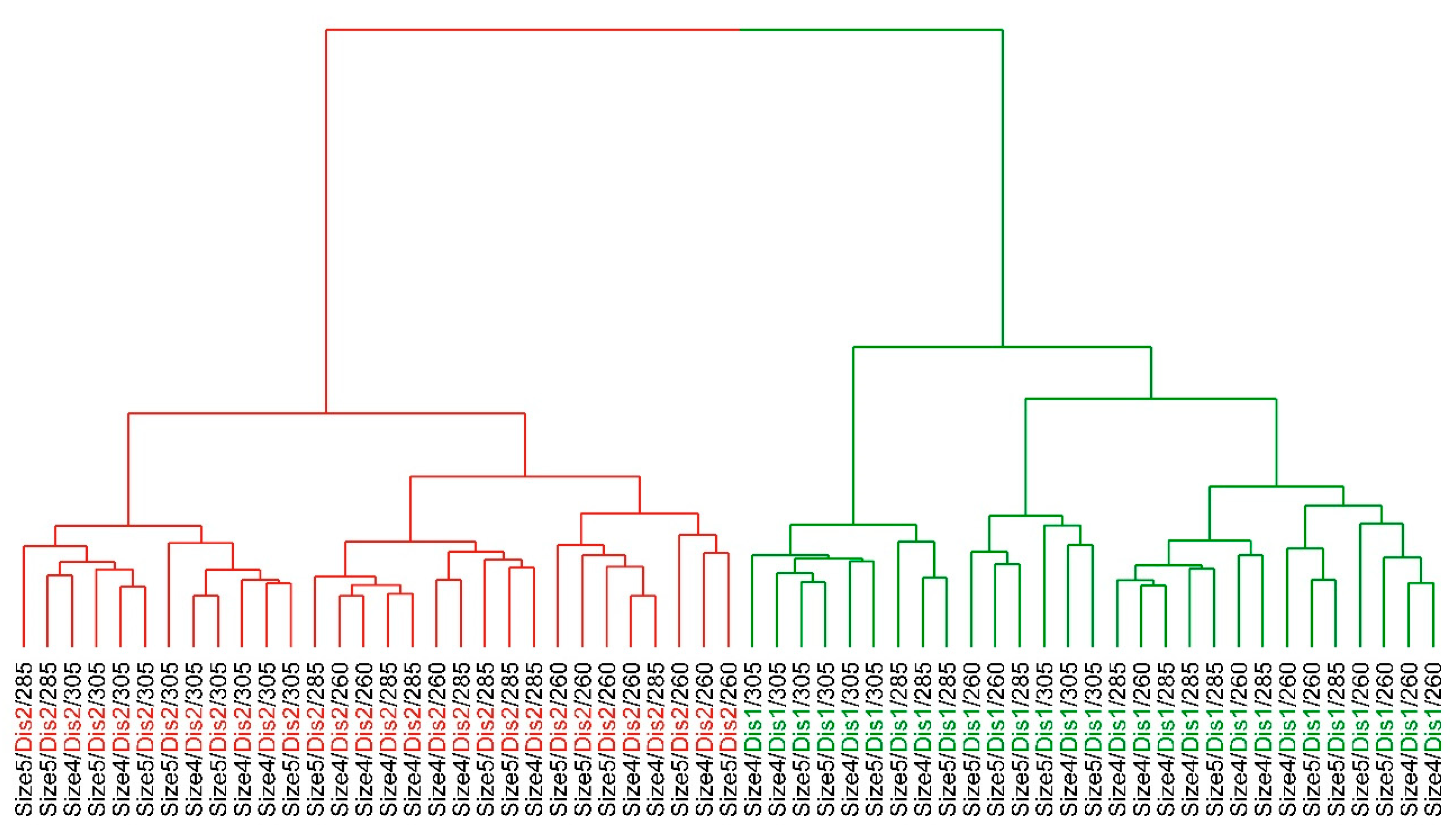
In the next step, we analyzed all throws from each subject separately. Figure 3 shows an example of a dendrogram of one subject in which two distinct main clusters are formed. These two clusters differentiate the 30 throws from the far distance (free throw line; Dis 2) and the 29 throws from the closer distance (Dis 1).

On a coarse level, two clusters can be identified that contain all throws from a specific distance. Further subclusters consist mainly of throws at the highest basket height (10 out of 12; respectively, 6 out of 9). Throws at the lower basket height are distributed over the remaining clusters. Ball sizes shown no distinct grouping. The exact distribution of all trials in the different clusters is displayed in Figure 4.

For all subjects, the dendrograms allowed optimal clustering into two or three main clusters. In these main clusters, the throwing condition distance showed the highest purity (0.81–1) in all subjects (see

Table 1. Purity in main clusters.

Subject/Condition	Distance	Basket Height	Ball Size
1	1	0.34	0.51
2	0.82	0.47	0.64
3	1	0.34	0.51
4	0.81	0.47	0.53
5	0.81	0.49	0.53
6	0.85	0.51	0.54
7	0.83	0.48	0.55

).

In five out of the seven subjects, subclusters could be identified. In these subclusters, the purity for basket height increases from 0.34–0.51 to 0.42–0.63 (

Table 2. Purity in subclusters.

Subject/Condition	Basket Height (3)	Ball Size
1	0.63	0.61
2	0.58	0.64
3	0.51	0.61
4	0.47	0.49
5	0.42	0.47
6	In main cluster	In main cluster
7	In main cluster	In main cluster

).

4. Discussion

When considering all variables from all subjects, seven neatly separated clusters can be identified. Each cluster represents one athlete and subsequently shows that the greatest influence on technique is, ultimately, individuality. Hence, our analyses indicate clearly that children within their age group already have individual movement techniques. Similar results have been published for adult athletes using a comparable approach [19]. Within subjects, movement patterns changed as the conditions became more difficult. Considering all subjects, distances accounted for the most changes in the throwing motion (purity 0.81–1). In the subclusters, the basket heights were not a decisive condition (purity 0.42–0.63). However, an increase in purity was found compared to the main clusters. In addition, lower values in purity are expected as we have three possible conditions. In the individual dendrograms, the highest basket height seems to be separated from the others, so at least 3.05 m high baskets caused changes in throwing motion. The throws with the two different ball sizes were equally distributed (purity 0.51–0.64), wherefore this factor had no influence. It can be concluded that the ball size did not represent a decisive condition. Therefore, children seem to adapt their movement behavior primarily to throwing distances and subordinately to basket heights. Ball sizes do not seem to have a considerable influence on their throwing performance.

A previous study by Satern (1993) also found significant differences in the mean values of kinematic parameters for two different throwing distances. Subjects showed decreased release angle and increased velocity of projection as shooting distance increased, indicating that throwing distance affects movement technique [14,20]. In line with this, we can verify by our approach that these adaptations are very stable and result in a characteristic variation of the throwing techniques, which manifests itself for the vast majority of trials under this condition. In addition, we show that the basket height also leads to specific technique changes in a subordinate way. On the other hand, our results are in line with Arias and colleagues, who showed that the ball size hardly affects the scoring rates [4].

Some of the subjects in our sample revealed clusters or subclusters with a heterogeneous distribution of the conditions. This might be explained by an already quite stable throwing technique, as for these subjects, all throws showed a high degree of similarity to each other. We assume that the better and more stable the children’s throwing technique is, the fewer changes in movement techniques are necessary to adapt to the different conditions. As a consequence, the differences in the similarity measures might be mainly due to movement variability independent of throwing distance and height as well as ball size, and the trials are heterogeneously assigned to different clusters. For mini-basketball players that already provide a comparable high level of expertise at these early stages, throwing at higher baskets from greater distances might not cause specific adaptations or motor learning-related changes in movement technique. For these players throwing under challenging conditions could be beneficial to further optimize skills and hence might be already applied in training.

5. Limitations

However, the sample size in this study is rather small and allows no generalization. Our interpretations should therefore be considered as preliminary assumptions that need to be confirmed in follow-up studies with larger groups of subjects. It would also be of particular interest to quantify the contribution of single or groups of variables to the changes in the complex movement pattern. This would allow for a detailed analysis of how youth players adapt the movements of their body segments in order to meet the requirements of the distinct throwing conditions. Furthermore, a comparison with adults’ throwing techniques would be beneficial to identify characteristics of the movement techniques that are favorable for the further development of youth basketball talents.

6. Conclusions

With regard to practical implications, we assume that throwing from different distances and on different basket heights causes specific adaptations of the movement techniques. These adaptations might be necessary because the children need to perform with higher strength and power to generate appropriate ball release parameters to hit a higher basket from a greater distance [10]. Qualitative observations of our results indicate that children in such situations exhibit greater rotation of the hip and shoulder or tend to jump forward. These short-term adaptations will very likely result in a modification of the throwing technique as an effect of learning when performed with a high number of repetitions. Hence, we therefore strongly recommend that children should throw at a lower basket (2.60–2.85 m) and from shorter distances to facilitate the acquisition of movement techniques that are beneficial to developing a high basketball expertise in later years/at a later age and avoid the necessity of relearning.