Modeling Particle-Doped Materials for Performance Improvement of Contact-Separation Triboelectric Nanogenerators
Abstract
1. Introduction
2. Numerical Procedures
3. Numerical Results
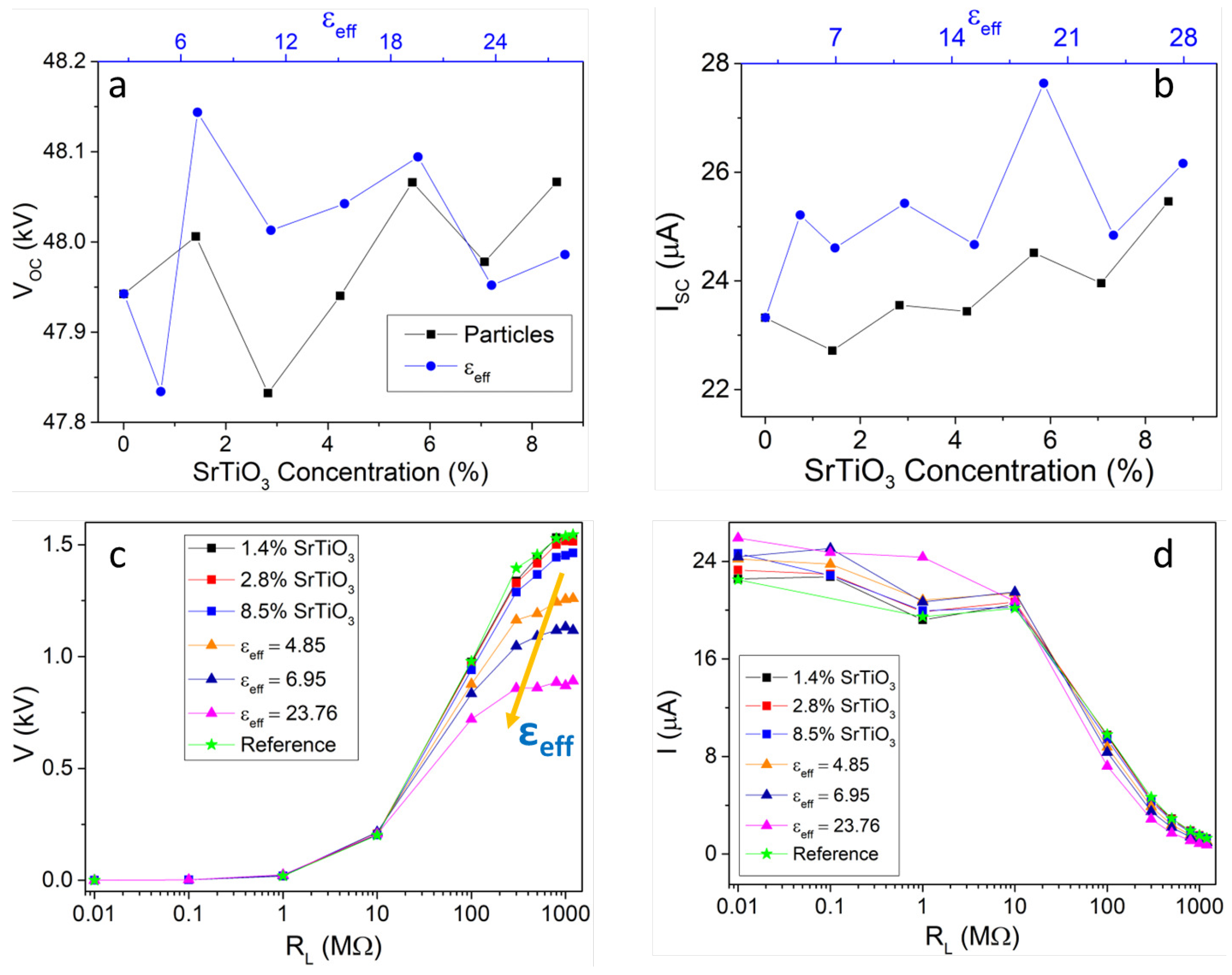
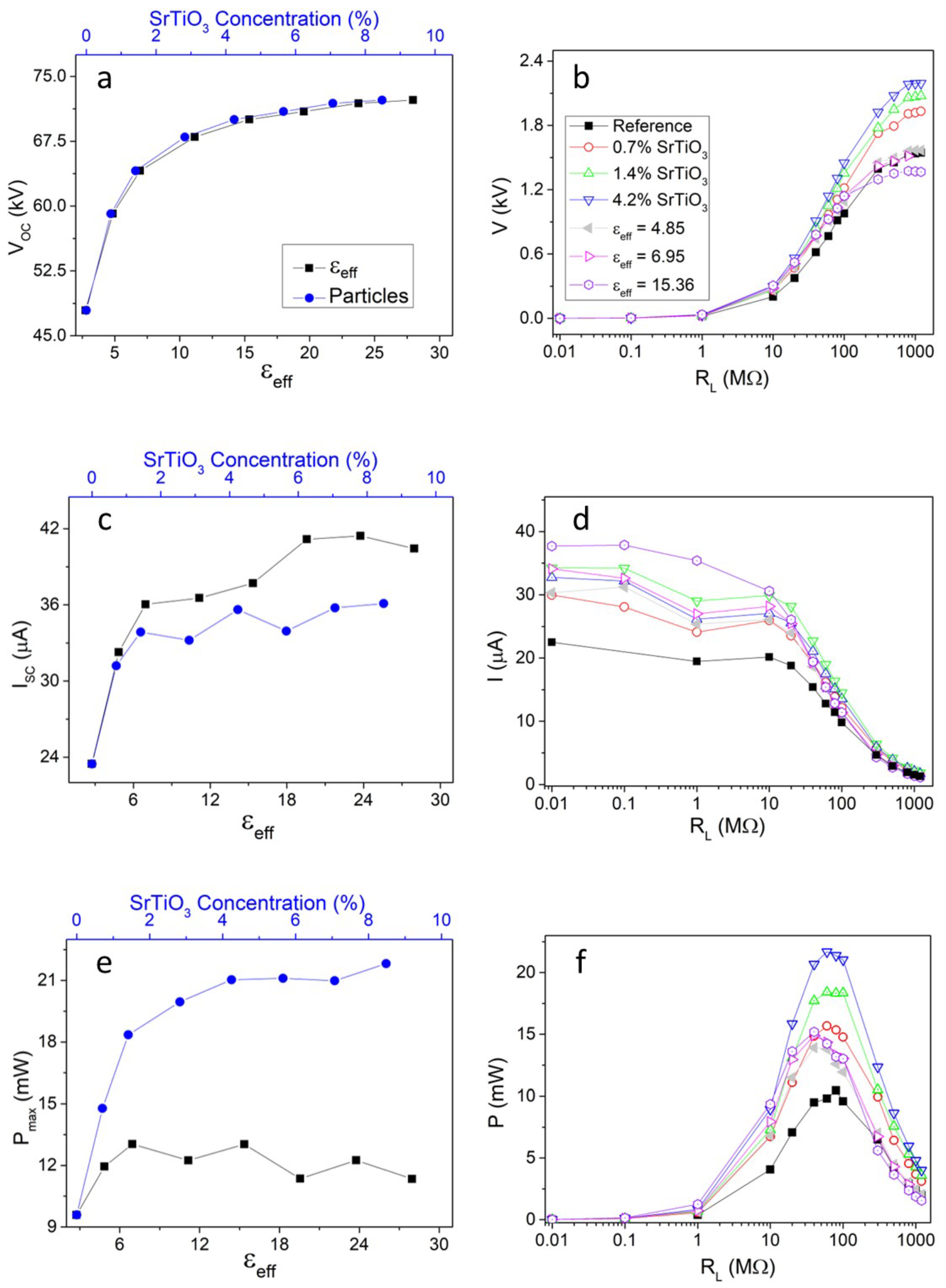
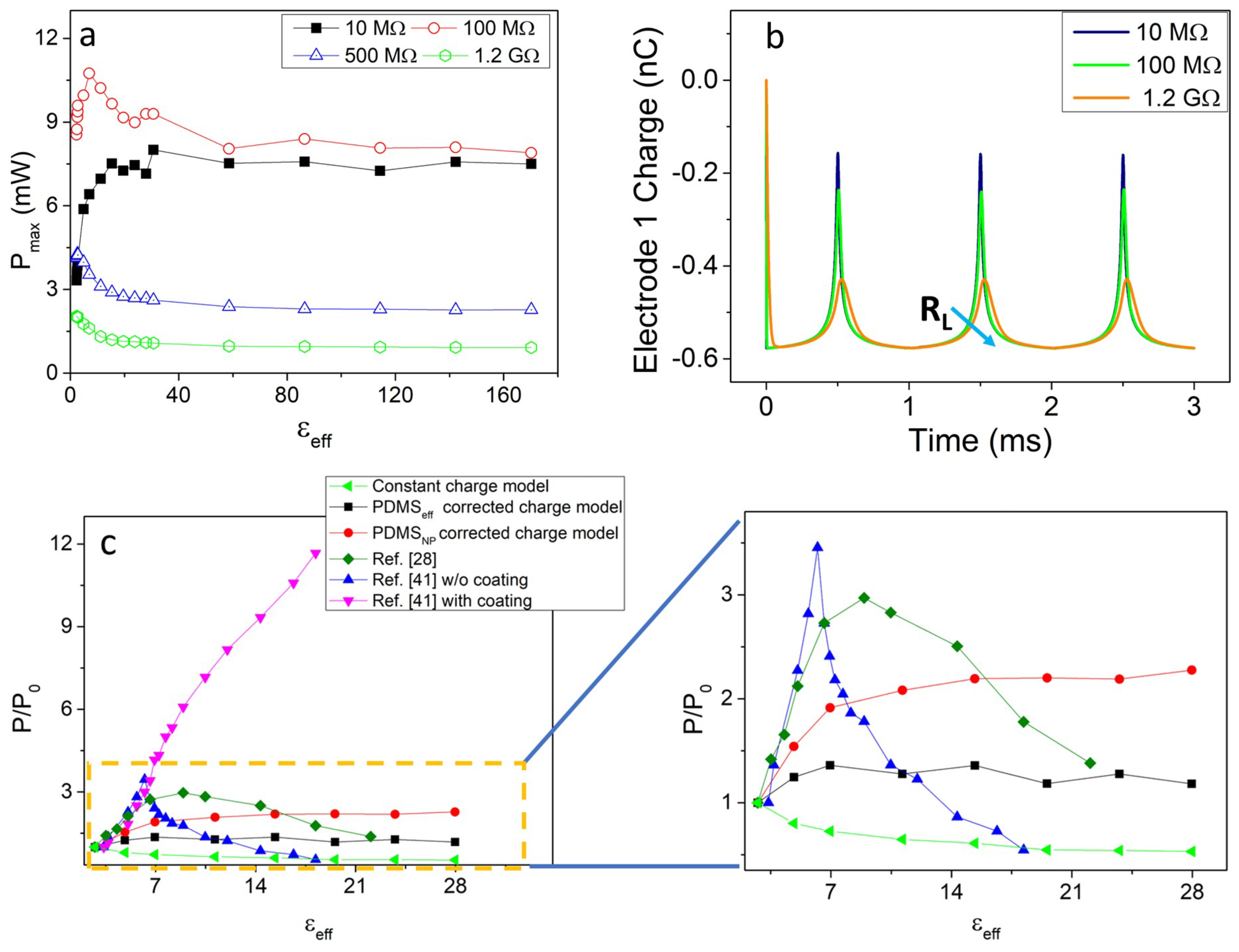
3.1. Constant Surface Charge Density Model
3.2. Varying Surface Charge Density
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Niu, S.; Wang, Z.L. Theoretical systems of triboelectric nanogenerators. Nano Energy 2014, 14, 161–192. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, J.; Yang, J. Recent Progress in Triboelectric Nanogenerators as a Renewable and Sustainable Power Source. J. Nanomater. 2016, 2016, 5651613. [Google Scholar] [CrossRef]
- Luo, J.; Wang, Z.L. Recent progress of triboelectric nanogenerators: From fundamental theory to practical applications. EcoMat 2020, 2, e12059. [Google Scholar] [CrossRef]
- Wu, C.; Wang, A.C.; Ding, W.; Guo, H.; Wang, Z.L. Triboelectric Nanogenerator: A Foundation of the Energy for the New Era. Adv. Energy Mater. 2019, 9, 1802906. [Google Scholar] [CrossRef]
- Liu, Z.; Ciais, P.; Deng, Z.; Lei, R.; Davis, S.; Feng, S.; Zheng, B.; Cui, D.; Dou, X.; Zhu, B.; et al. Near-real-time monitoring of global CO2 emissions reveals the effects of the COVID-19 pandemic. Nat. Commun. 2020, 11, 5172. [Google Scholar] [CrossRef] [PubMed]
- Technical, I.; Shukla, P.; Skea, J.; Slade, R.; van Diemen, R.; Haughey, E.; Malley, J.; Pathak, M.; Pereira, J.P. Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes In Terrestrial Ecosystems; Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2019; pp. 35–74. [Google Scholar]
- Toreti, A.; Bavera, D.; Acosta Navarro, J.; Cammalleri, C.; de Jager, A.; Di Ciollo, C.; Hrast Essenfelder, A.; Maetens, W.; Magni, D.; Masante, D.; et al. Drought in Europe—August 2022; Publications Office of the European Union: Luxembourg, 2022; JRC130493; p. 24. [Google Scholar] [CrossRef]
- Ma, M.; Kang, Z.; Liao, Q.; Zhang, Q.; Gao, F.; Zhao, X.; Zhang, Z.; Zhang, Y. Development, applications, and future directions of triboelectric nanogenerators. Nano Res. 2018, 11, 2951–2969. [Google Scholar] [CrossRef]
- Askari, H.; Hashemi, E.; Khajepour, A.; Khamesee, M.B.; Wang, Z.L. Towards self-powered sensing using nanogenerators for automotive systems. Nano Energy 2018, 53, 1003–1019. [Google Scholar] [CrossRef]
- Wang, S.; Lin, L.; Wang, Z.L. Triboelectric nanogenerators as self-powered active sensors. Nano Energy 2015, 11, 436–462. [Google Scholar] [CrossRef]
- Xia, K.; Zhu, Z.; Zhang, H.; Xu, Z. A triboelectric nanogenerator as self-powered temperature sensor based on PVDF and PTFE. Appl. Phys. A Mater. Sci. Process. 2018, 124, 520. [Google Scholar] [CrossRef]
- Rodrigues, C.; Nunes, D.; Clemente, D.; Mathias, N.; Correia, J.M.; Rosa-Santos, P.; Taveira-Pinto, F.; Morais, T.; Pereira, A.; Ventura, J. Emerging triboelectric nanogenerators for ocean wave energy harvesting: State of the art and future perspectives. Energy Environ. Sci. 2020, 13, 2657–2683. [Google Scholar] [CrossRef]
- Li, R.; Li, Y.; Zhao, Y.; Li, Y.; Li, Y. Harvest of ocean energy by triboelectric generator technology. Appl. Phys. Rev. 2018, 5, 031303. [Google Scholar] [CrossRef]
- Gonçalves, I.; Rodrigues, C.; Ventura, J. Sea State Adaptation Enhances Power Output of Triboelectric Nanogenerators for Tailored Ocean Wave Energy Harvesting. Adv. Energy Mater. 2023, 14, 2302627. [Google Scholar] [CrossRef]
- Rodrigues, C.; Gomes, A.; Ghosh, A.; Pereira, A.; Ventura, J. Power-generating footwear based on a triboelectric-electromagnetic-piezoelectric hybrid nanogenerator. Nano Energy 2019, 62, 660–666. [Google Scholar] [CrossRef]
- Dassanayaka, D.G.; Alves, T.M.; Wanasekara, N.D.; Dharmasena, I.G.; Ventura, J. Recent Progresses in Wearable Triboelectric Nanogenerators. Adv. Funct. Mater. 2022, 32, 2205438. [Google Scholar] [CrossRef]
- Liu, M.; Pu, X.; Jiang, C.; Liu, T.; Huang, X.; Chen, L.; Du, C.; Sun, J.; Hu, W.; Wang, Z.L. Large-Area All-Textile Pressure Sensors for Monitoring Human Motion and Physiological Signals. Adv. Mater. 2017, 29, 1–9. [Google Scholar] [CrossRef]
- Song, W.; Gan, B.; Jiang, T.; Zhang, Y.; Yu, A.; Yuan, H.; Chen, N.; Sun, C.; Wang, Z.L. Nanopillar Arrayed Triboelectric Nanogenerator as a Self-Powered Sensitive Sensor for a Sleep Monitoring System. ACS Nano 2016, 10, 8097–8103. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Cheng, J.; Wang, Z.; Ji, L.; Wang, Z.L. Triboelectric nanogenerators for human-health care. Sci. Bull. 2021, 66, 490–511. [Google Scholar] [CrossRef]
- Zheng, Q.; Shi, B.; Li, Z.; Wang, Z.L. Recent Progress on Piezoelectric and Triboelectric Energy Harvesters in Biomedical Systems. Adv. Sci. 2017, 4, 1700029. [Google Scholar] [CrossRef]
- Niu, S.; Wang, S.; Lin, L.; Liu, Y.; Zhou, Y.S.; Hu, Y.; Wang, Z.L. Theoretical study of contact-mode triboelectric nanogenerators as an effective power source. Energy Environ. Sci. 2013, 6, 3576–3583. [Google Scholar] [CrossRef]
- Niu, S.; Liu, Y.; Wang, S.; Lin, L.; Zhou, Y.S.; Hu, Y.; Wang, Z.L. Theory of Sliding-Mode Triboelectric Nanogenerators. Adv. Mater. 2013, 25, 6184–6193. [Google Scholar] [CrossRef]
- Niu, S.; Liu, Y.; Wang, S.; Lin, L.; Zhou, Y.S.; Hu, Y.; Wang, Z.L. Theoretical investigation and structural optimization of single-electrode triboelectric nanogenerators. Adv. Funct. Mater. 2014, 24, 3332–3340. [Google Scholar] [CrossRef]
- Chen, H.; Xu, Y.; Zhang, J.; Wu, W.; Song, G. Theoretical System of Contact-Mode Triboelectric Nanogenerators for High Energy Conversion Efficiency. Nanoscale Res. Lett. 2018, 13, 346. [Google Scholar] [CrossRef]
- Shao, J.; Jiang, T.; Tang, W.; Chen, X.; Xu, L.; Wang, Z.L. Structural figure-of-merits of triboelectric nanogenerators at powering loads. Nano Energy 2018, 51, 688–697. [Google Scholar] [CrossRef]
- Shao, J.; Willatzen, M.; Wang, Z.L. Theoretical modeling of triboelectric nanogenerators (TENGs). J. Appl. Phys. 2020, 128, 111101. [Google Scholar] [CrossRef]
- Callaty, C.; Gonçalves, I.; Rodrigues, C.; Ventura, J. Modeling the performance of contact-separation triboelectric nanogenerators. Curr. Appl. Phys. 2023, 50, 100–106. [Google Scholar] [CrossRef]
- Hossain, N.A.; Razavi, M.J.; Towfighian, S. Analysis of mechanical deformation effect on the voltage generation of a vertical contact mode triboelectric generator. J. Micromech. Microeng. 2020, 30, 045009. [Google Scholar] [CrossRef]
- Chen, J.; Guo, H.; He, X.; Liu, G.; Xi, Y.; Shi, H.; Hu, C. Enhancing Performance of Triboelectric Nanogenerator by Filling High Dielectric Nanoparticles into Sponge PDMS Film. ACS Appl. Mater. Interfaces 2016, 8, 736–744. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Deng, W.; Xu, J.; Chen, J. Engineering Materials at the Nanoscale for Triboelectric Nanogenerators. Cell Rep. Phys. Sci. 2020, 1, 100142. [Google Scholar] [CrossRef]
- Patsidis, A.C. Barium titanate/polydimethylsiloxane nano/ microcomposites fabrication, morphology, dielectric response and functionality. IET Nanodielectrics 2020, 3, 14–19. [Google Scholar] [CrossRef]
- Jang, S.; Oh, J.H. Rapid Fabrication of Microporous BaTiO3/PDMS Nanocomposites for Triboelectric Nanogenerators through One-step Microwave Irradiation. Sci. Rep. 2018, 8, 14287. [Google Scholar] [CrossRef]
- Tantraviwat, D.; Ngamyingyoud, M.; Sripumkhai, W.; Pattamang, P.; Rujijanagul, G.; Inceesungvorn, B. Tuning the Dielectric Constant and Surface Engineering of a BaTiO3/Porous PDMS Composite Film for Enhanced Triboelectric Nanogenerator Output Performance. ACS Omega 2021, 6, 29765–29773. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.J.; Lee, J.; Park, S.; Park, C.; Park, C.; Choi, H.J. Effect of the relative permittivity of oxides on the performance of triboelectric nanogenerators. RSC Adv. 2017, 7, 49368–49373. [Google Scholar] [CrossRef]
- Kim, J.; Ryu, H.; Lee, J.H.; Khan, U.; Kwak, S.S.; Yoon, H.J.; Kim, S.W. High Permittivity CaCu3Ti4O12 Particle-Induced Internal Polarization Amplification for High Performance Triboelectric Nanogenerators. Adv. Energy Mater. 2020, 10, 1903524. [Google Scholar] [CrossRef]
- Lee, J.W.; Ye, B.U.; Baik, J.M. Research Update: Recent progress in the development of effective dielectrics for high-output triboelectric nanogenerator. APL Mater. 2017, 5, 073802. [Google Scholar] [CrossRef]
- Chen, J.; Wang, J.; Xuan, W.; Dong, S.; Luo, J. Universal triboelectric nanogenerator simulation based on dynamic finite element method model. Sensors 2020, 20, 4838. [Google Scholar] [CrossRef] [PubMed]
- Hasan, S.; Kouzani, A.Z.; Adams, S.; Long, J.; Mahmud, M.A. Comparative study on the contact-separation mode triboelectric nanogenerator. J. Electrost. 2022, 116, 103685. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, W.; Hu, J.; He, W.; Yang, H.; Ling, C.; Xi, Y.; Wang, X.; Liu, A.; Hu, C. Two voltages in contact-separation triboelectric nanogenerator: From asymmetry to symmetry for maximum output. Nano Energy 2020, 69, 104452. [Google Scholar] [CrossRef]
- Rodrigues, C.; Pires, A.; Gonçalves, I.; Silva, D.; OIiveira, J.; Pereira, A.; Ventura, J. Hybridizing Triboelectric and Thermomagnetic Effects: A Novel Low-Grade Thermal Energy Harvesting Technology. Adv. Funct. Mater. 2022, 32, 2110288. [Google Scholar] [CrossRef]
- Zhou, Q.; Takita, R.; Ikuno, T. Improving the Performance of a Triboelectric Nanogenerator by Using an Asymmetric TiO2/PDMS Composite Layer. Nanomaterials 2023, 13, 832. [Google Scholar] [CrossRef]

| Parameter | Value |
|---|---|
| Velocity | m/s |
| Period | s |
| Number of periods (cycles) | 3 |
| Time per step | s |
| of nylon | C/m2 |
| of PDMS | C/m2 |
| of nylon | 4 |
| of PDMS | |
| Width/Height of the air box | 0.1 m |
| Height/thickness of nylon/PDMS/electrodes of cooper | m |
| Width of PDMS/nylon/electrodes of cooper | m |
| Maximum distance between nylon and PDMS surfaces | m |
| Minimum distance between planes | m |
| Concentration | |
|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Callaty, C.; Gonçalves, I.; Rodrigues, C.; Ventura, J. Modeling Particle-Doped Materials for Performance Improvement of Contact-Separation Triboelectric Nanogenerators. Nanoenergy Adv. 2024, 4, 147-155. https://doi.org/10.3390/nanoenergyadv4020009
Callaty C, Gonçalves I, Rodrigues C, Ventura J. Modeling Particle-Doped Materials for Performance Improvement of Contact-Separation Triboelectric Nanogenerators. Nanoenergy Advances. 2024; 4(2):147-155. https://doi.org/10.3390/nanoenergyadv4020009
Chicago/Turabian StyleCallaty, Carlos, Isabel Gonçalves, Cátia Rodrigues, and João Ventura. 2024. "Modeling Particle-Doped Materials for Performance Improvement of Contact-Separation Triboelectric Nanogenerators" Nanoenergy Advances 4, no. 2: 147-155. https://doi.org/10.3390/nanoenergyadv4020009
APA StyleCallaty, C., Gonçalves, I., Rodrigues, C., & Ventura, J. (2024). Modeling Particle-Doped Materials for Performance Improvement of Contact-Separation Triboelectric Nanogenerators. Nanoenergy Advances, 4(2), 147-155. https://doi.org/10.3390/nanoenergyadv4020009








