Abstract
Due to the unique electromechanical energy conversion capability of ferroelectric materials, they have been at the forefront of materials science for a variety of applications such as sensors, actuators and energy harvesting. Researchers have focused on exploring approaches to achieve improved ferroelectric performance, and to ensure that the available material systems are more environmentally friendly. This comprehensive review summarizes recent research progress on porous ceramics and highlights the variety of factors that are often ignored, namely the influence of porosity on the Curie temperature, and applications of porous ferroelectric materials with adjustable Curie temperature. Finally, the development trends and challenges of porous ferroelectric materials are discussed, aiming to provide new insights for the design and construction of ferroelectric materials.
1. Introduction
In modern society, scientists and experts are highlighting the need to pay attention to important challenges, where energy and the environment account for the largest share. While large scale low-emission power generation, such as nuclear, wind, and solar was once considered the primary approach to solve the energy crisis, the use of fragmented energy, which is often termed low-grade energy, is an alternative approach. In addition to large scale power, there is a need to provide low power for the large number of sensors that are required in our more connected society; defined as the Internet of Things (IoT).
One approach towards the development of fragmented energy is to employ smart materials, such as piezoelectric, pyroelectric and ferroelectric materials. A necessary condition for a material to be piezoelectric is that the crystal does not possess a center of symmetry. Of the 32 crystallographic point groups, 21 groups are non-centrosymmetric. Of these 21 groups, 20 groups can exhibit piezoelectricity and are termed piezoelectric since their polarization can change with stress. Among the 20 kinds of piezoelectric systems, 10 crystals are classed as pyroelectric since they have a unique unidirectional polar axis and have a spontaneous polarization that can change with temperature. Within the class of pyroelectrics, the polarization direction of some crystals can be changed by the application of an electric field, and these materials are classed as ferroelectric. All ferroelectrics, pyroelectrics, and piezoelectrics are also classed as dielectrics as a result of their low electrical conductivity [1].
Ferroelectric ceramics are polycrystalline materials formed by sintering crystals, which exhibit the piezoelectric effect. Due to the initial randomness of the orientation of the internal polycrystalline grains and ferroelectric domains, the orientation of the ferroelectric domains offset each other, and the material will not exhibit any piezoelectric effect from a macroscopic viewpoint. However, after a polarization treatment (termed poling) which involves the action of a strong direct electric field, the ferroelectric domains can be arranged in the direction close to the applied electric field, and the ferroelectric ceramics be macroscopically polarized, and a piezoelectric and pyroelectric effect can be observed.
Typical ferroelectric ceramic based piezoelectric materials include BaTiO3 [2] and Pb(Zr,Ti)O3 (PZT) [3]. BaTiO3 has the advantages of high dielectric constant and large electromechanical coupling coefficient, which was one of the earliest piezoelectric ceramics with practical value in transducer applications such as SONAR. Prior to the discovery of the ferroelectric characteristics of barium titanate, Rochelle salt and KH2PO4 were the primary form of ferroelectric used in transducer applications. When compared with piezoelectric single crystals, such as Rochelle salt, BaTiO3 piezoelectric ceramics have the advantages of ease of preparation, and can be formed into products with complex/arbitrary shape and any polarization direction since they can be poled after production. In 1947, the United States used BaTiO3 ceramics to manufacture pickups for phonographs [4] and today a variety of piezoelectric devices such as piezoelectric filters and transducers made from BaTiO3 ceramics continue to emerge. However, the Curie point (Tc) of BaTiO3 ceramics is relatively low, with Tc~120 °C [5], were the Tc represents the temperature at which the materials transforms from a non-centrosymmetric ferroelectric phase to a centrosymmetric paraelectric phase As a result, it can be relatively easy to approach the Curie point during operation, which can lead to depolarization and can cause the piezoelectric properties of BaTiO3 ceramics to vary greatly with both temperature and time, and therefore the materials cannot meet the requirements in some applications.
As an alternative, Pb(Zr,Ti)O3 (PZT) is a binary solid solution formed by antiferroelectric PbZrO3 and ferroelectric PbTiO3. Since the ionic radius of Ti4+ is similar to that of Zr4+, and the chemical properties are similar, PbZrO3 and PbTiO3 can form a continuous solid solution Pb(ZrxTi1−x)O3 (0 < x < 1) in any ratio, which has an ABO3-type perovskite structure. Near the composition x = 0.52, the tetragonal and trigonal phases of PZT piezoelectric ceramics are able to coexist and at this phase boundary, due to the low phase transition activation energy, the crystal phase structure can be transformed under the induction of a weak electric field. After a poling treatment, relatively good piezoelectric properties can be obtained. In addition, the Curie point of the Pb(ZrxTi1−x)O3 solid solution system varies between Tc~230–490 °C with the composition, which leads to a relatively thermally stable piezoelectric properties. The emergence of PZT piezoelectric ceramics has driven the rapid development of piezoelectric materials, and opened up a new era in the application of piezoelectric materials.
The materials described above are often used in their dense polycrystalline form. Recently, the production of ferroelectric ceramics in porous form have been examined in an attempt to improve their performance for a variety of pressure sensors, hydrophones and energy harvesters [6,7,8,9,10,11,12]. Previous work [13] has described the application prospects of porous ferroelectric materials in energy technologies, but lacks the exploration and summary of some intrinsic mechanisms of porous ferroelectric materials. Porous piezoelectric ceramics are a form of ceramic with deliberately introduced porosity, and compared with traditional dense piezoelectric ceramics, they can exhibit a number of many advantageous properties [14].
As shown in Figure 1, porous piezoelectric ceramics can be divided into 3-0 type, 3-1 type, 3-3 type and 2-2 type according to the different connection modes of the ceramic phase and the air phase [15]. Generally, the first number refers to the connection method of the piezoelectric ceramic phase, and the second number represents the connection mode of the air phase. The 3-0 and 3-3 type porous piezoelectric ceramics are both examples of foam ceramics. Among them, the pores in the 3-0 type porous piezoelectric ceramics are not connected to each other, and they are separated from each other by a continuous ceramic matrix, which is a closed-cell foam ceramic. The 3-1 type porous piezoelectric ceramics contain parallel pores evenly distributed and penetrating the ceramic body, which is a typical honeycomb structure ceramic. The pores of the 3-3 type porous piezoelectric ceramic are connected to each other, and the ceramic matrix is only contained in the pore edges, which is an open-pore (net-shaped) foam structure. The ceramic phase layer and the air phase layer of the 2-2 type porous piezoelectric ceramic are alternately arranged, which can be considered as a sandwich structure. According to the structural characteristics of the ceramic type, the processes for preparing porous piezoelectric ceramics are diverse.

Figure 1.
Schematic showing the potential connectivity of the porous ceramics, the first number denotes the connectivity of the ceramic phase, while the second number denotes the connectivity of the pore phase.
The field of piezoelectric materials has thoroughly studied [16], and a parameter of particular importance is the Curie point (Tc), which is used since piezoelectric properties were first discovered by the Curie brothers. For piezoelectric materials, the Curie point is the temperature at which the piezoelectric effect is lost, often due to a phase transition from a ferroelectric phase to a paraelectric phase. As early as 1880, the Curie brothers discovered that applying pressure or tensile force in a specific direction of a quartz crystal will lead to electric charges appearing on the crystal surface, and the density of the electric charges is proportional to the magnitude of the applied external force [17]. This was the first time that the positive piezoelectric effect of piezoelectric materials was discovered by researchers. Subsequently, the Curie brothers verified the inverse piezoelectric effect through experiments and obtained the direct and inverse piezoelectric coefficients of the quartz crystal [18]. Woldemar Voigt pointed out in 1894 that all crystalline media with non-centrosymmetric centers in the structure could be piezoelectric [19]. For a crystal with a symmetric center structure, regardless of whether an external force is applied, the centers of the positive and negative charges always overlap, therefore the crystal does not show polarity and produce a piezoelectric effect.
The Curie point is of interest since it reflects the operating temperature range of piezoelectric materials. A wide operating temperature range is often required for piezoelectric ceramics, coupled with excellent piezoelectric properties. However, to date, there are few reports on the effect of porosity on Curie point in porous piezoelectric materials and there are some contradictions in the data reported in the literature.
2. Preparation Method and Morphology of Porous Ferroelectrics
The preparation methods to create porous piezoelectric materials has developed rapidly in recent decades. In this section, the current mainstream preparation technology is summarized, where Figure 2 shows the process schematics and typical morphology formed by a variety of methods; this includes the replica template, burnt-out polymer spheres (BURPS), freeze casting, gel casting, and additive manufacturing. It should be noted first that porosity refers to the percentage of the pore volume in the bulk material to the total volume of the material in its natural state.
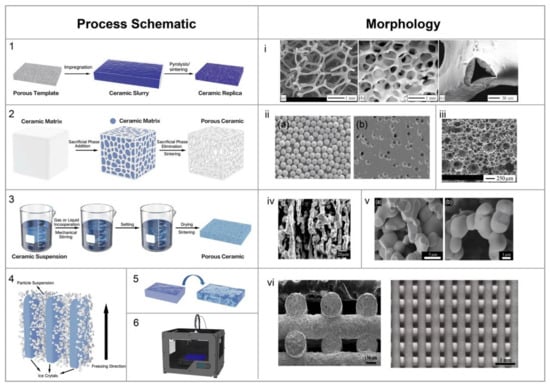
Figure 2.
Schematic of processes and their corresponding morphologies: (1, i) replica template [20], Reproduced with permission, Copyright 2006, Phil. Trans. R. Soc. A.; (2, ii) BURPS [21], Reproduced with permission, Copyright 2007, J. Eur. Ceram. Soc.; (3, iii) Direct Foaming [22], Reproduced with permission, Copyright 2010, J. Appl. Phys.; (4, iv) Freeze Casting [11], Reproduced with permission, Copyright 2017, J. Mater. Chem. A Mater.; (5, v) Gel Casting [22], Reproduced with permission, Copyright 2010, J. Appl. Phys.; (6, vi) Additive Manufacturing [23], Reproduced with permission, Copyright 2018, J. Am. Ceram. Soc.
2.1. Replica Template
The replica template method involves the immersion of a template material in a ceramic slurry, that fully absorbs the slurry, and then any excess absorbed slurry is removed by extrusion or centrifugation. Final removal of the template is achieved by drying and sintering in order to retain the porous structure [24]. In 1963, the US patent first reported the method of preparing porous ceramics using an organic-material based sponge impregnated ceramic slurry [25]. Currently, the most commonly used sponges are polyethylene, polyurethane, and cellulose. The microscopic morphology of the sponge, such as pore morphology and pore size distribution, directly determines the microscopic morphology and pore structure of the final sintered porous ceramic. In addition, the organic sponge needs to have an appropriate strength and elasticity to ensure that it can return to its original shape after being squeezed and centrifuged. Therefore, the use of sponge with the appropriate mechanical properties and morphology is a prerequisite for the preparation of high-quality porous ceramic foam using this process.
In 1978, Skinner used natural coral as a frame to manufacture 3-3 type PZT piezoelectric ceramic for the first time [26]: first, natural coral was vacuum immersed in a paraffin wax, and after the paraffin was cured, it was soaked in hydrochloric acid to remove the coral frame. The remaining paraffin wax was then used as a template for ceramic replication. This was achieved by the paraffin-based template being vacuum immersed in a PZT slurry to infill the template, and then heated to 300 °C to remove the paraffin replica and create the porous PZT ceramic green body. The green body is then sintered at a high temperature of 1280 °C, where a 3-3 type PZT piezoelectric ceramic can be obtained and the pores and ceramic are fully interpenetrating due to the coral structure. However, this process requires the use of natural coral as a template, which is not suitable for mass production, and the process itself involves multiple stages.
As shown in Figure 2i, porous ceramics prepared by the replica template method have an almost complete open-pore structure, and when porous high temperature ceramics (such as zirconia) are made in this form they suitable for filtering impurities in molten metals. At present, porous high-temperature ceramics are used for filtering molten metals to create high-quality ingots prior to casting. In 2003, Kara [27] prepared work on the formation of 3-3 type PZT piezoelectric ceramics with uniform pore distribution using polyethylene sponge as a template, and studied the effect of porosity on the properties of piezoelectric ceramics. When the porosity was 80 vol.%, the hydrostatic figure of merit (HFOM = dh.gh), which defines the suitability for underwater sonar applications, reached 15,095 × 10−15 Pa−1. The was approximately 50 times higher than that of the dense PZT piezoelectric ceramics. The advantage of the replication template method is that it can be used to prepare porous 3-3 piezoelectric ceramics with relatively high porosity, and by selecting templates with appropriate pore diameters and different shapes, and the relevant structural parameters can be easily adjusted. However, as Figure 2i shows, the porous ceramic prepared by this process is prone to stress concentrations due to the hollow frame formed by the loss of the polymer during burnout. As a result, the compressive strength can be relatively poor, generally only between 0.5–2 MPa, making it difficult to use as a material for stressed ultrasonic devices.
2.2. Burnt-Out Polymer Spheres (BURPS)
The burnt-out polymer spheres (BURPS) method, also known as sacrificial template method, involves mixing ceramic powder, a pore former and a binder uniformly to produce a green body. The pore former is then removed by a heat treatment and high temperature sintering to obtain the final porous product [28], as shown in Figure 2(2). Since the pore former will generate a large amount of gas during the combustion process, it is relatively easy to produce cracks during processing. Therefore, the porous ceramic prepared by the BURPS typically has a low porosity, generally between 5 vol.% and 45 vol.%, and many of the foam ceramics produced by this method have a 3-0 type closed-cell structure [28].
There are two types of pore formers: inorganic pore formers and organic pore formers. Inorganic pore formers include (NH4)2CO3, NH₄HCO₃, NH4Cl and other high-temperature decomposable salts, as well as coal powder, graphite, and carbon powder [29]. Organic pore formers are mainly high molecular polymers, organic acids and natural fibers [30]. The shape and size of the pore former particles determine the shape and size of the pores of the porous ceramic material. Researchers have studied the method of preparing 3-0 type PZT piezoelectric ceramics by dry pressing and forming with artificial organic (C5O2H8)n (PMMA) and natural organic dextrin as pore formers. The porous piezoelectric ceramics prepared by this method generally have a closed-cell structure, and the pores are not connected to each other. The porosity volume fraction levels are between 5% and 45%, and the hydrostatic figure of merit (HFOM = dh.gh) value is higher than 1500 × 10−15 Pa−1, which provides excellent sensitivity and signal to noise ratio.
BURPS is simple, mature, and easy to operate process. It is currently the most widely used piezoelectric ceramic preparation process. However, the pore-forming agent tends to leave unevenly distributed defects on the pore wall of the green body during the high-temperature ignition loss process, resulting in poor stability of the mechanical and electrical properties of the product, which restricts the application of this process.
2.3. Direct Foaming Method
The direct foaming method involves generating a large number of bubbles in a ceramic slurry, and then fixing and retaining the structure of the bubbles before the bubbles burst to obtain the porous ceramic green body [31]. The methods used include mechanical stirring, or adding a foaming agent to foam the ceramic suspension [32]. According to the type of foaming agent, it can be commonly divided into a physical foaming agent, inorganic foaming agent, or organic foaming agent. The physical foaming method aims to add an inert gas or low-boiling point liquid to the material to be foamed under high pressure, and then the material is heated, and the pressure reduced to make the gas separate, or allow the liquid to volatilize to foam the material. As a result, physical foaming agents are also called volatile foaming agents. During the foaming process, this type of foaming agent does not undergo any chemical reactions and only generates a large amount of gas to foam the material due to the changes in physical state. Commonly used physical foaming agents are N2, CO2, and H2. This kind of foaming agent, which has weak chemical activity, will not leave residue after foaming and have no adverse effect on the performance of porous ceramics. Low-boiling liquids are currently widely used physical foaming agents, such as pentane, isopentane, and hexane. Its advantages are a large volume gas generation, effective use of foaming agents, and little or no residue is left in the material system. Kim et al. [33] used gaseous CO2 as a foaming agent to prepare porous ceramics with a pore size of less than 30 µm and a porosity of 50 vol.%.
The inorganic foaming agent produces porous ceramics by heating or reacting with the original material to release a gas. After foaming, the volume of the porous material can even reach approximately 40 times larger than that of the original volume. The work of Schuster et al. [34] is an early example of the use of inorganic foaming agents to prepare high-performance porous ceramics, who used a mixture of sulfide and sulfate as a foaming agent to mix with clay materials, and directly heated and foamed without pretreatment to make porous ceramics.
Organic blowing agents mainly include azo compounds, sulfonyl hydrazide compounds, and nitroso compounds. The biggest feature of azo organic blowing agents is that they contain N=N structure in the molecule; the structure is unstable, and N2 can be released when exposed to heat source. The advantages of organic foaming agents are: (i) the bubbles are fine-scale and uniform in size; (ii) the decomposition temperature range is narrow and can be controlled; (iii) the diffusion rate of N2 in the material is small, and will not readily escape from the foam; therefore, the a high foaming efficiency is achieved; (iv) the organic chemical foaming agent is an exothermic foaming agent, which decomposes sharply when reaching a certain temperature, and the gas generation is relatively stable. The relationship between the amount of foaming agent and the foaming rate can be measured to improve the process.
2.4. Freeze Casting
Freeze casting, often termed the ice template method, is a method for manufacturing porous ceramics with a complex pore structure [35]. In the process, a homogeneous suspension is initially prepared, and the suspension is then slowly poured into the mold and frozen under a unidirectional temperature gradient; finally, the solidified solvent is sublimated in the freeze dryer [36]. In the frozen state, the solvent is not only the binder of the ceramic powder, but also the template for the formation of pores. The freeze casting method can be used to prepare porous ceramic products with a porosity of up to 90 vol.%, and the porosity can be controlled in a wide range. In addition to water [37], camphene [38], camphor [39] and other substances that are easy to crystallize at low temperatures and volatile at high temperatures can be used as solvents and templates.
Lee used a freeze casting to prepare 3-3 type piezoelectric ceramics: the ceramic powder was mixed with camphene solvent and then frozen and molded at low temperature, followed by freeze casting and sintering to obtain porous piezoelectric ceramics [40,41]. The porous piezoelectric ceramic prepared by this process has an interconnected pore structure with a pore size of approximately 10 μm. After testing, the porosity of the porous ceramic is between 50 vol.% and 82 vol.%, and the hydrostatic figure of merit (HFOM) reached a high value of dh.gh~35,650 × 10−15 Pa−1.
The microstructure and morphology of porous ceramics prepared by freezing casting mainly depend on the crystal morphology of the refrigerant. The use of water-based freezing casting will generate a layered directional pore structure, which is a typical 2-2 type structure. On using tert-butanol for freeze casting, highly aligned one-dimensional pores can be obtained due to the needle-like morphology of tert-butanol crystals. Freeze casting also provides good processing flexibility in controlling the morphology, microstructure and properties of porous ferroelectric ceramics. Compared with other manufacturing techniques, a highly aligned pore structure can be obtained by freezing casting. The porosity produced by freeze casting can be adjusted in a wide range, and a high level of porosity can be achieved [42,43].
2.5. Gel Casting
The gel casting method is a ceramic molding technology invented by Professors Jenny and Omatete of Oak Ridge National Laboratory in the United States in the late 1980s [44,45]. The molding process combines a traditional ceramic preparation process with polymer chemistry and provides a new technology that uses organic monomer polymers to shape the ceramic body. The process is as follows: firstly, ceramic powder is mixed with the organic monomer aqueous solution to prepare a ceramic slurry with high solid content and low viscosity. After adding the catalyst and initiator, the organic monomer aqueous solution is cross-linked and polymerized to form a three-dimensional network polymer gel, so that the ceramic slurry is solidified in situ into a ceramic body of a desired shape. In addition to polymerization and gelation, organic monomers also act as carriers for ceramic powder, completing the mold filling and molding curing processes, respectively [46]. Gel casting can overcome the shortcomings of traditional molding processes to produce ceramic parts with high strength, uniform composition, defect-free and complex shapes, and this process has the advantages of high efficiency, convenience, and is suitable for large-scale production, research, further development and utilization. It has been widely used in the manufacture of Al2O3 [47], Si3N4 [48], SiC [49], ZrO2 [50] and other components.
Based on the process of gel casting, Wang’s research group used tert-butanol (TBA) with low surface tension and high saturated vapor pressure to replace water as a solvent. Through their invented TBA-based gel casting, they successfully fabricated low-density, high-strength porous ceramic materials [51]. Among them, the porosity of porous alumina ceramics can reach 92 vol.%, the compressive strength exceeds 10 MPa, and the specific surface area can reach 14 m2/g. Since TBA leaves the green body during the drying process at only 50 °C, it ensures that the product has a uniform pore size distribution and stable electrical properties. At the same time, it overcomes the shortcomings of low body strength in the freeze-drying process. The prepared porous PZT piezoelectric ceramic has a porosity of 31vol.%–58 vol.%, a maximum HFOM value of dh.gh~23,000 × 10−15 Pa−1, and a minimum acoustic impedance of 3.0 MRayls, which can meet the requirements of underwater acoustic sensors. However, the high cost of the raw material TBA used in this process and the narrow porosity range of porous ceramics hinder its long-term development and wide application.
2.6. Additive Manufacturing
When manufacturing ferroelectric ceramics with complex porous structures through the above-mentioned methods, it is often necessary to design and produce complex and delicate molds, which may be expensive and time-consuming and present significant challenges in production. Additive manufacturing can produce complex structures without molds, and can realize a wide range of structures, thereby allowing the manufacture of porous ceramics with precisely controlled structures [52]. Among the available additive manufacturing methods, direct ink writing is the most commonly used method. Direct ink writing requires a freely moving nozzle and the additive manufacturing program will automatically layer the virtual model and accurately distribute the ink layer by layer to the substrate. It has already been used to produce piezoelectric materials with complex 3D shapes [53].
3. Characterization of Porous Piezoelectric Ceramics
The previous section discussed the preparation technology of porous ceramics. When the porous ceramic has the expected function, a specific required pore structure can be obtained by selecting a suitable method, so as to optimize the design and manufacture to meet the design and application purpose. Characterization of the porous material can allow researchers to understand the mechanism and application of porous piezoelectric materials. Whether the ceramics is porous or not, piezoelectric materials should exhibit the following main characteristics:
- (1)
- Electromechanical conversion characteristics: a high piezoelectric charge constant d33 is required (high charge per unit force, or high strain per unit electric field).
- (2)
- Mechanical properties: high mechanical strength and rigidity (stiffness), in particular for highly loaded applications.
- (3)
- Dielectric performance: a high resistivity, dielectric constant and dielectric strength to prevent breakdown when the driving electric field is applied.
- (4)
- Environmental adaptability: a good temperature and humidity stability, high Curie point, and wide operating temperature range is required.
- (5)
- Stability: The piezoelectric properties should not change significantly with time.
Among them, the Curie point of the material is closely related to stability and environmental adaptability. Compared with traditional dense piezoelectric ceramics, porous piezoelectric ceramics have a high fraction of secondary air phase. The presence of pores leads to porous ceramics exhibiting the characteristics of low density, low relative permittivity, low Young’s modulus, and low specific heat; the introduction of porosity also provide the ceramic with good thermal and sound insulation properties. Inevitably, as the porosity increases, the piezoelectric coefficient (such as d33) and pyroelectric coefficient (p) will decrease accordingly. However, some methods can be used to optimize the preparation process to greatly increase the polarization of the porous ceramic itself, thereby curbing this trend. As an example, this section summarizes the piezoelectric properties of multiple papers and lists them in Table 1, so that readers can understand the advantages of various porous piezoelectric ceramics concisely.
Definitions of key piezoelectric properties are summarized below.
- (1)
- d33 and d31 are the longitudinal and transverse piezoelectric charge coefficients, respectively,
- (2)
- g33 and g31 are the piezoelectric voltage constants that represent the electric field produced per unit stress.
- (3)
- is the relative permittivity at constant stress and is the permittivity of the free space.
- (4)
- Hydrostatic charge coefficient dh is a property that defines the hydrostatic actuation capability of the material; dh = d33 + 2d31.
- (5)
- Hydrostatic voltage coefficient is a property that the defines sensitivity of the hydrophone (electric field per unit hydrostatic stress).
- (6)
- Hydrostatic figure of merit HFOM = dh.gh, defines the suitability for underwater sonar applications and is an indicator of signal-to-noise ratio.
- (7)
- For energy harvesting application, the figure of merit in 33-mode is FOM33 = d33.g33 = .
- (8)
- The loss tangent (tanδ) is a parameter to describe energy dissipation. For dielectrics with small loss, the phase angle is small and tanδ ≈ 0. For porous ceramics, the loss tangent value is positively correlated with the porosity. Under an applied electric field, the electric field lines are concentrated in the pores of low permittivity, resulting in the dissipation of electrical energy and is not stored in the ceramic phase [21,54].
Generally, for a piezoelectric ceramic, the higher the degree of ceramic connectivity along the electric field, the greater the permittivity and piezoelectric coefficient, this will be discussed in more detail later.

Table 1.
Piezoelectric properties of porous ferroelectric materials.
Table 1.
Piezoelectric properties of porous ferroelectric materials.
| Composition | Method | Connectivity Mode | Porosity (vol.%) | Tc (°C) | d33 (pC/N) | dh (pC/N) | gh (10−3Vm/N) | dhgh (pm2/N) | ε33 [C2/(N·M2)] | tanδ | Ref |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BCZT | BURPS | 3-0 | 10~25 | 106 | 285~424 | 34~93 | ~10.2 | ~0.95 | 1026~2158 | 0.03~0.05 | [55] |
| PZT–PCN | 3-0 | 24~45.6 | - | 140~300 | - | 27~46 | 5.379 | 110~290 | - | [56] | |
| PZT | 3-0 | 35~54.5 | - | 161~312 | 35~180 | 16.1~31.1 | 0.554~5.753 | 241~1608 | - | [57] | |
| PZT | 3-0 | 5~45 | - | 208~350 | - | 5~40 | 0.35~5 | 300~1600 | - | [58] | |
| LNKN | 3-0 | 15~50 | 75~153 | - | - | - | - | - | [59] | ||
| PZT 95/5 | 3-0 | 4~16 | 220 | 66~71.2 | - | - | - | 220~310 | - | [21] | |
| PZT | 3-0 | 3~43 | - | ~450 | - | - | - | 450~1600 | - | [60] | |
| BCZT | 3-0 | 4~40 | - | - | - | - | - | - | - | [61] | |
| PZT | 3-0 | 1.8~59.4 | - | 90~142 | - | - | 0.1~0.5 | ~1300 | - | [62] | |
| PZT | 3-0 | 5~47 | - | - | - | - | - | 90~145 | ~0.015 | [63] | |
| BS–0.64PT | 3-0 | 9.4~43.9 | - | ~415 | - | - | - | 400~1500 | ~0.04 | [64] | |
| PZT | 3-0 | 10~50 | - | ~450 | - | - | - | - | - | [65] | |
| BST | 3-0 | ~29 | - | - | - | - | - | - | <0.05 | [66] | |
| PZT | 3-0 | 0.23~20.82 | - | 350~451 | - | - | - | - | - | [67] | |
| PZT-PCN | 3-0 | 12.56~45.57 | - | 185~356 | 46~74 | 6.5~43.5 | 0.481~2.732 | 182~1137 | - | [68] | |
| BZT | 3-0 | 5~21 | - | 38~154 | - | - | - | 1300~2100 | 0.03 | [69] | |
| BNT-BT | Freeze casting | 3-1 | 36 | - | 115~182 | - | - | - | - | - | [70] |
| PZT | 3-1 | 65.5~68 | - | 589~675 | - | - | - | - | - | [71] | |
| PZT | 3-1 | 36~67 | - | 170~400 | - | - | - | 427~969 | 0.025~0.19 | [72] | |
| PZT | 3-1 | 25~67 | - | 595~731 | - | - | - | - | - | [42] | |
| PZT–PZN | 3-1 | ~90 | - | 302~450 | 216~406 | 241~396 | 52.056~160.77 | 100~120 | - | [40] | |
| PZT–PZN | 3-1 | 50~82 | - | 380~475 | 259~298 | 34~118 | ~35.65 | 284~853 | - | [41] | |
| PZT | 2-2 | 28.1~68.7 | - | 608~690 | 244~330 | 8~28.3 | ~9.648 | 1400~3500 | - | [73] | |
| PZT | 2-2 | 20~60 | - | - | ~206 | ~83.5 | ~8.26 | ~2200 | - | [74] | |
| PZT | 2-2 | 25~45 | 210~229 | - | - | - | - | - | - | [75] | |
| PZT | 2-2 | 20~60 | - | ~460 | - | - | - | ~1400 | - | [11] | |
| PZT-PCN | 2-2 | 34 | - | ~639 | - | - | - | - | - | [76] | |
| NKNS | 2-2 | ~60.5 | 60~62.5 | ~130 | ~60 | ~58.7 | ~3.522 | ~1319 | - | [77] | |
| BT | 2-2 | 37~56 | - | ~134.5 | - | - | - | 580~1504 | - | [78] | |
| PZT | Gel casting | 3-3 | 23.9~57.6 | - | 454~588 | - | - | 5.964~22.299 | 502~2513 | - | [79] |
| PZT | 3-0 | 38.58~68.7 | - | 350~490 | - | 20.2~60.5 | 3.427~12.633 | 390.4~951.6 | - | [80] | |
| PZT | 3-3 | 36.4~56.2 | - | 415~504 | - | - | ~9.594 | 742~1566 | - | [81] | |
| PZT | 3-3 | 31.3~58.6 | - | 424~635 | - | - | 0.081~10.117 | 446~3418 | - | [82] | |
| PZT | 3-0/3-3 | 27.8~72.4 | - | 260~560 | 176~209 | 14.8~77.3 | ~15.236 | 400~3500 | - | [83] |
Definitions of piezoelectric materials are listed below: (1) PZT: PbZrx Ti1−xO3; (2) BCZT: Ba0.85Ca0.15Zr0.1Ti0.9O3; (3) LNKN: (Li, Na, K)NbO3; (4) BST: Ba1−xSrxTiO3; (5) BZT: BaZrxTi1−xO3; (6) BNT: Bi0.5Na0.5TiO3; (7) PZT-PCN: (x)Pb(ZrTi)O3-(1−x)Pb(CoNb)O3; (8) BZT: BaZrxTi1−xO3; (9) PZT-PZN: (x)Pb(ZrTi) O3-(1−x)Pb(ZnNb)O3; (10) NKNS: (NaK)(NbSb)O3; (11) BT: BaTiO3; (12) BS-PT: BiScO3–PbTiO3.
The above table shows various parameters of porous piezoelectric ceramics. A comparison of porous piezoelectric materials with dense materials will be presented in Figure 3.
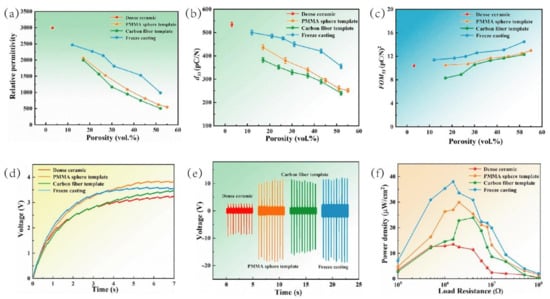
Figure 3.
Comparison of piezoelectric properties between porous and dense piezoelectric materials [84]: (a) relative permittivity; (b) d33; (c) FOM33; (d) time dependent charging curves; (e) output voltage; (f) output power density. Reproduced with permission, Copyright 2022, Ceram. Int.
Figure 3 compares some common parameters of porous piezoelectric materials with dense materials. Referring to the definition of the harvesting FOM33 = mentioned above it can be seen that the electrical energy produced by the piezoelectric device is highly dependent on the piezoelectric charge coefficient and dielectric constant. Piezoelectric materials with high piezoelectric charge coefficients and low dielectric constants can harvest more energy for an applied stress, and the introduction of porosity can significantly reduce the dielectric constant, while the piezoelectric charge coefficient only decreases slowly with an increase in porosity.
4. Mechanisms by Which Porosity Affects the Curie Temperature
The Curie point, Tc, is the transition temperature where a ferroelectric material loses its spontaneous polarization as it changes phase from a non-centrosymmetric ferroelectric phase to centrosymmetric paraelectric phase [85]. When the working temperature, T, is below the Curie point (T < Tc), the materials exhibit ferroelectric properties while when it is above the Curie point (T > Tc), the material is no longer ferroelectric, and the dielectric constant obeys the Curie-Weiss law. At T < Tc, the Tc is associated with the atomic displacement and described as ∝, where k is the Boltzmann constant, has the dimensions of a force constant, and is the atomic displacement [86]. According to this relationship between atomic displacement and Tc, experiments have shown that the smaller displacement of atoms resulted in a decrease of Tc [87]. There is also a simple theoretical relation defining the Curie point and the particle radius, R, of crystal: Tc ∝ 1/R [88]. Before this work, size effects on transition temperature of ferroelectric materials had been investigated both theoretically and experimentally. It was reported that as the particle size decreased, the Tc decreased [89]. Similarly, M.Kamel et al. later showed that the Tc shifted to a higher temperature with an increase in grain size [90]. In addition, there are many other factors affecting the transition temperature such as the composition of the material, the presence of dopants, external strain, pressure and the presence of an external dc electric field, which was systematically investigated using a thermodynamic approach to study the phase transition of ferroelectric crystals [91]. With respect to porous piezoelectric materials, the need to increase the Curie temperature is normally used to evaluate their working temperature for practical applications. A wide operating temperature range is necessary for all piezoelectric ceramics, coupled with high performance. However, to date, less work has been reported on the effects of the internal stress and the variation in lattice distortion (c/a ratio) with porosity, and its subsequent effect on the Curie point.
Hiroshima [92] reported in 1996 that the Curie point of a Pb1−xBaxNb2O6 material was affected by the preparation conditions, and ceramics with a large number of pores and cracks exhibited a higher Curie point compared to dense ceramics. In addition, fine-grained materials exhibit a higher Curie point compared to coarse-grained materials. When the free energy of the ferroelectric phase is smaller than the free energy of the paraelectric phase, a transition from the paraelectric phase to the ferroelectric phase occurs during cooling. During the phase transition, the crystal surfaces perpendicular to the c-axis of the paraelectric phase move outward and those parallel to the c-axis move inward. If an internal stress related is not generated during the phase transition, the phase transition occurs at the normal Curie point. However, when the movement of the crystal surface is hindered by the surrounding crystal grains, the level of internal stress will increase, resulting in an increasing of the free energy of the ferroelectric phase and a decrease of the Curie point since the ferroelectric phase is less stable. Alternatively, if the movement of the crystal surface is enhanced by any surrounding grains the Curie point will increase. Since pores, cracks, and grain boundaries can act to relax the state of internal stress in a material it is possible to understand why ceramics with a high fraction of porosity have a higher Curie point compared to the dense ceramic.
Similar observations in subsequent studies by other researchers supported his inference, although there have been different interpretations of results from a range of tested materials. The Curie point increased with an increase of the porosity, which was seen in both porous barium strontium titanate (BST) [93] and PZT [11] ceramics. Nie [94] stated that the reason why the Curie points increases with an increase of porosity is that stress can be amplified or concentrated in the pores. However, Okazaki [95] reported that the space charge electric field of lanthanum-doped lead zirconate titanate (PLZT) will increase with grain refinement and porosity reduction. When the grain size decreases, the surface area of the space charge layer increases, which in turn leads to an increase in the Curie point.
However, as Figure 4 shows, the results from other experiments have alternative conclusions. Keizer [96] found that, for a Pb1-αxLaxTiO3+x(1.5−α)(PLT) material, as the grain size of the PLT material decreased, the Curie point decreased accordingly, and this was because the smaller grain size led to an increase in the average compressive stress in the material which reduced the c/a ratio. Zhu [97] believed that the inter-grain stress increased with a decrease in grain size, and the decrease of the grain size in BaTiO3 ceramics will generate an internal compressive stress and therefore reduce the c/a ratio and its Curie point. For BaTiO3 ceramic samples with grain sizes of 5000 nm, 100 nm and 60 nm, the measured Tc were 128 °C, 120 °C and 111 °C, respectively. They suggested that since there is a volume increase during a cubic to tetragonal phase transition, the presence of an internal compressive stress helps to maintain and stabilize the paraelectric cubic structure and the BaTiO3 ceramic system is subjected to external pressure in a similar way to a system under hydrostatic pressure. A compressive pressure can therefore be viewed to favor a smaller volume lattice structure and a trend of a reduced c/a ratio, and a reduced Tc is therefore expected. Although their prediction of the relationship between grain size and Curie point is in contrast to Hiroshima, they believe that an increase in internal stress will lead to a decrease in Curie temperature. Samara [98], Schader [99], Jaffe [100] found that as the external pressure increases, the Curie temperature of the sample will also increase during the test. The mechanism of this phenomenon is consistent with that described by Zhu [98].
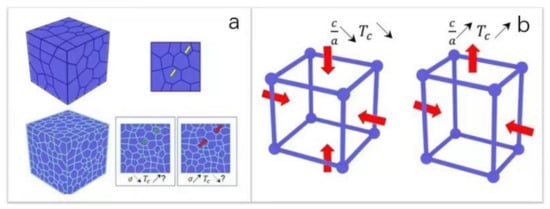
Figure 4.
Schematic of the mechanism affecting the Curie point and its contradictions: (a) from grain size aspect; (b) from lattice constant ratio aspect.
Hwang [101] and Yan [102] discovered doping with other elements or substitution of atomic positions in the crystal structure can affect the Curie point, although additives can also influence the state of internal stress. They provided a detailed explanation on the influence of compressive stress on the Curie temperature. The material studied was PZT-Ag composite material, and in their publications, they reported data describing the relationship between the Curie point of BaTiO3 and (Pb, La)(Zr, Ti)O3 and the amount of silver used in the composite [103,104,105]. According to previous reports [106,107,108,109], the Curie point decreased as the silver content increased and this phenomenon has been related to the substitution of silver in the perovskite crystal structure. However, the results of Hwang are contrary to these reports [106,107,108,109], and by incorporating silver particles into the material, the Curie temperature is increased. Therefore, the changes in Curie temperature observed in PZT-Ag composites cannot be explained by the substitution of silver into the perovskite crystal structure of PZT. Hae Jin Hwang believed that the Curie temperature is affected by the presence of an internal thermal stress which is produced as a result of the thermal expansion mismatch between the ceramic matrix and the silver particles. During the cooling process, a large thermal residual stress is introduced into the matrix grains and silver particles starting from the sintering temperature. The actual stress at any point of the matrix can be determined from the uniform average stress combined with the local stress generated by nearby particles. The internal thermal stress has two effects on the Curie point of PZT-Ag composites. The first effect is to broaden the phase change behavior. In PZT-Ag composites, silver particles are mainly located at the joints of multiple particles and if the c-axis of the PZT matrix grains is parallel to the radial direction of the surrounding silver grains, the grains transform at a higher temperature because the Curie point rises due to the expansion of the c-axis caused by the residual tensile stress. If the c-axis is perpendicular to the radial direction of the silver particle, the Curie point shifts to a lower temperature. Therefore, according to the relationship between the c-direction and the orientation of silver particles, the Curie temperature distribution of a single crystal grain is wider than the distribution without secondary dispersoid. The other effect of internal thermal stress is to lower the Curie points of perovskite ceramics. Although the residual thermal stress field is anisotropic, the average stress in the matrix is compressive and, as described in this section, the introduction compressive stress leads to a decrease in the Curie point. Therefore, the impact of a residual thermal stress cannot fully explain why the Curie point increases with an increase of silver content. When the polycrystalline ferroelectric is cooled to its transformation temperature, a single crystal grain is sandwiched by its adjacent crystal grains and internal stress is generated. However, the internal stress caused by this transformation can be alleviated by phenomena, such as the formation of the presence of pores or defects, the presence of grain boundary phases, or the 90° twinning in the crystallites. In particular, it has been indicated that the internal stress of piezoelectric ceramics decreases significantly with an increase in porosity. According to reports, the Curie point of some perovskite-type ceramics is a microstructure sensitive characteristic [94]. Yan found that if all sides of the crystal are subjected to uniform compressive stress, such as by a hydrostatic pressure, the ferroelectric to paraelectric phase transition is promoted from the tetragonal phase to the cubic phase, and the Curie temperature will move to a lower temperature; see left image in Figure 4b. When there is only a uniaxial stress applied, such as a compressive stress parallel to the a and b axes, or tensile stress parallel to the c axis, the value of c/a will increase accordingly, and the crystal is more inclined to remain tetragonal phase characteristics, resulting in an increase in the Curie temperature; see right image in Figure 4b. Differences are also expected for the application of a uniaxial stress, depending on the direction of the applied relative to the poling direction, or if the materials if poled or unpoled. This would be of interest to investigate for porous materials.
As Figure 4b shows, although there are contradictions in the discussion of various materials introduced above, the conclusion is that an increase in the internal stress the Curie temperature will decrease accordingly. The ability for porosity to reduce the internal compressive stress state provides scope for tailoring the Tc of ferroelectric materials.
5. Simulation of Porous Piezoelectric Ceramics
Through some optimization methods, porous piezoelectric ceramics can exhibit characteristics that cannot be achieved by dense ceramics. In addition to experimental testing, many researchers have also verified the superior performance of porous ceramics through computational simulation. These simulation results can be instructive for the design and manufacture of porous ferroelectric ceramics. This section therefore summarizes the porous ceramic modeling related to electric field distribution, mechanical properties, dielectric and piezoelectric properties.
5.1. Simulation of Electric Field Distribution
The polarization process of ferroelectric materials is critical. When the electric field that is applied during the polarization process reaches a certain strength, the initially randomly oriented domains can be aligned; the electric field at which domains align in the field direction is termed the coercive field (Ec). Compared with porous ferroelectric materials, dense ferroelectric materials have a relatively homogeneous electric field distribution since the permittivity is constant throughout the material. However, since the relative permittivity of the pores is much lower than that of ferroelectric ceramics, the introduction of pores will lead to an uneven distribution of the applied electric field, and the electric field will be concentrated in the low permittivity pores.
Since the porosity will significantly affect the electric field distribution in ceramics, it is necessary to study and quantify the electric field distribution in porous ceramics. To date, numerous studies have been conducted for this purpose. Gheorghiu et al. developed 3D porous ceramic models with different porosity levels by Finite Element Method (FEM) [110]. As shown in Figure 5a, the porosity of the ceramic model gradually increases from left to right. For an almost dense ferroelectric microstructure, the local field on the body is highly homogeneous (represented by green color), and its average value is almost equal to the externally applied field (voltage/thickness). For porous microstructures with porosity higher than 20%, the local electric field becomes highly inhomogeneous and is concentrated at the pores, as expected. In addition to the porosity, the pore morphology and orientation also affect the electric field distribution and degree of polarization. From the work of Stanculescu [66], they used the finite element method to focus on pore morphology and pore orientation on piezoelectric properties. From Figure 4b, the results show that the electric field of the porous structure with randomly distributed pores is much lower than that of the porous ceramics with aligned pores. When the ferroelectric ceramic structure is close to the ideal 2-2 lamellar structure, it is easier to fully pole the material if the pore channels are parallel to the electric field. This will lead to an increase in the polarization level and higher piezoelectric and pyroelectric characteristics. During the polarization process (poling), when the direction of the electric field is perpendicular to the aperture, in other words, if the porous ceramic is of type 3-1 or 3-3, the ceramic body tends to have a higher effective permittivity and intensity of polarization. If the ceramic body has a 2-2 structure and the electric field is perpendicular to the ceramic phase plane, the ceramic body will theoretically have the lowest effective permittivity and intensity of polarization. In addition, if the direction of applied electric field is consistent with the pore orientation, the minimum amount of unpoled area tends to be obtained. In summary, by artificially optimizing the structure of the porous ceramics, pore orientation and polarization process, the piezoelectric properties of the porous ceramics can be optimized.
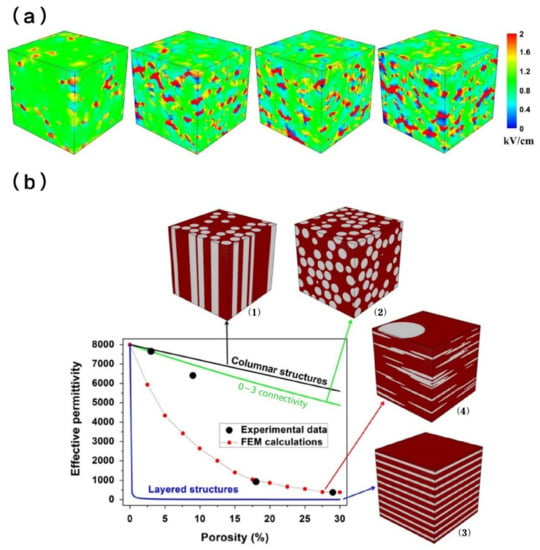
Figure 5.
Simulation of porous materials: (a) Effect of porosity on electric field distribution [110], Reproduced with permission, Copyright 2016, J. Am. Ceram.; (b) Influence of pore morphology on the electric field [66]. Reproduced with permission, Copyright 2015, J. Alloy. Compd.
5.2. Simulation of Dielectric and Piezoelectric Properties
Several studies have investigated the dielectric and piezoelectric properties of porous ferroelectric materials through computational simulation. Bosse et al. [111] developed a three-dimensional finite element model to characterize the influence of microstructure characteristics on the piezoelectric and dielectric properties of the 3-3 piezoelectric structure. By changing the aspect ratio of the porosity, the piezoelectric figures of merit, such as the hydrostatic piezoelectric charge coefficient (dh), hydrostatic piezoelectric voltage coefficient (gh), and hydrostatic figure of merit (dh.gh), can be significantly improved. Zhao et al. [112] simulated the piezoelectric properties of porous ferroelectric ceramics by phase field method. The simulation results, from Figure 6, indicate that a strong decrease in Pr of the highly porous ferroelectric is observed for the ferroelectric properties. As the porosity level increases, the relative permittivity and piezoelectric coefficient continue to decrease. The influence of porosity dominates, while the shape of the pores contributes less to and d33. Kargupta et al. [15] developed a finite element model to study the influence of porosity on 3-1 porous ferroelectric materials. This is consistent with Zhao’s results that the relative permittivity and piezoelectric coefficient of porous ceramics decrease monotonously with an increase of pore volume fraction.
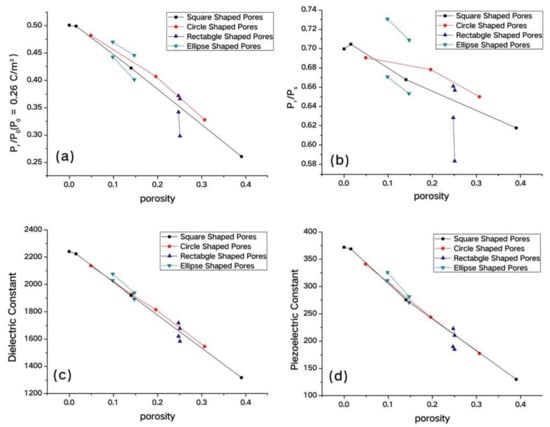
Figure 6.
The remnant polarization (a) rectangularity factor; (b) dielectric constant; (c) and piezoelectric coefficient; (d) versus porosity calculated for various shaped porous ceramics at different porosity levels [111]. Reproduced with permission, Copyright 2012, Acta Mater.
5.3. Simulation of Mechanical Properties
Considering the mechanical properties of piezoelectric ceramics, Kim et al. [113] simulated the materials using COMSOL Multiphysics V5.4 (COMSOL Inc., Stockholm, Sweden) and used atomic layer deposition (ALD) to deposit ZnO on a 3D epoxy template, and finally burnt off the epoxy template in the air to obtain a 3D-ZnO structure. As shown in Figure 7, their simulations showed that lateral expansion occurs when the structure is compressed in the z-direction, thus confirming that the Poisson’s ratio is greater than zero. The engineering elastic strain generated in the 3D hollow nanostructure is determined to be 0.030, which is 10 times larger the 0.003 of the dense structure. After unloading during the FEA simulation, the ZnO hollow nanostructure recovered 95.9%. They also indicated that the use of 3D hollow nanostructures in piezoelectric materials can not only improve the mechanical properties of the hollow nanostructures, but also effectively enhance the piezoelectric and pyroelectric response. Since ZnO has a relatively low piezoelectric coefficient in ceramic materials, the use of ceramic materials with higher piezoelectric coefficients and the same 3D hollow nanostructure provides a route to achieve improved piezoelectric coefficient results.
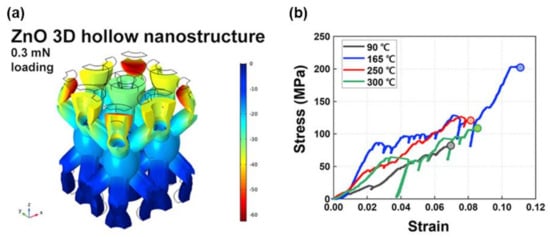
Figure 7.
Simulation results: (a) FEA simulation of 3D ZnO nanostructure [113]; (b) stress−strain plot of compression tests [113]. Reproduced with permission, Copyright 2020, Nano Energy.
6. Application of Porous Piezoelectric Ceramics
As a functional material with a wide range of application prospects, porous piezoelectric ceramics can benefit from its own structural characteristics, and these advantageous properties have led to researchers and industrial practitioners to design and develop porous piezoelectric ceramics with improved performance. As highlighted in the previous sections, porous piezoelectric ceramics can be optimized through a series of methods to achieve piezoelectric properties close to dense bodies and benefits in some properties such as the hydrostatic or energy harvesting figures of merit. Due to its porous structure, the specific surface area is much larger than that of the dense body and it also provides the materials with the properties of low permittivity, low density, low Young’s modulus, and low specific heat for an enhanced pyroelectric response. As Figure 8. shows, the combination of these characteristics can provide a variety of guiding ideas for the design and application of porous piezoelectric ceramics.
- (1)
- Energy Harvesting: Piezoelectric energy harvesting can capture the surrounding mechanical vibration energy and directly convert it into electrical energy through the piezoelectric effect. The energy obtained from environment mainly depends on the piezoelectric charge coefficient and relative permittivity. The introduction of porosity can sharply reduce the relative permittivity, while the piezoelectric charge coefficient decreases slowly with increased porosity. Previous studies have also shown that porous ferroelectric materials have a higher piezoelectric harvesting figure of merit factor than dense materials. Therefore, porous ferroelectric materials show great potential in piezoelectric energy harvesting applications. For example, by converting mechanical vibrations or temperature fluctuations and high energy density through piezoelectric and pyroelectric effects, the efficiency of piezoelectric materials can exceed electromagnetic generators with small size [114].
- (2)
- High-performance Sensors: Ferroelectric materials can also be used as sensors to detect force, pressures, and acceleration via the piezoelectric effect and heat via the pyroelectric effect. One advantage of piezoelectric sensors is that they do not require an external power supply and can act as “self-powered sensors”. Dense ceramic materials generally have a high relative permittivity, but as can be seen in Table 1, porous piezoelectric materials have the advantage of preparing high-sensitivity sensors due to their relatively low permittivity and high piezoelectric, pyroelectric and hydrostatic coefficients. The regulation of porosity tailor properties is therefore a feasible way to improve material properties and in recent years, porous ferroelectric composite materials have attracted widespread attention in sensing applications due to their high piezoelectric voltage coefficient and good mechanical flexibility. Porous piezoelectric materials have shown promising potential in wireless sensors [115], high-performance hydrophones [116], and strain measurement [117].
- (3)
- Since ferroelectric materials can directly convert mechanical energy into chemical energy or heat into chemical energy through piezoelectric potential induced by external mechanical force, porous nanostructured ferroelectric materials are being considered for use for catalysis due to the high specific surface area. The piezoelectric and thermoelectric catalysis of porous ceramics is used to treat organic dye wastewater due to their high efficiency and self-powered characteristics. In addition, porous ferroelectric composite materials composed of ferroelectric nanoparticles and polymers have shown great potential in catalytic applications due to the advantages of recyclability and reuse. The ability of porosity to tailor the Curie point is an advantage since piezocatalytic activity has been shown to improve near the Curie point [118,119].
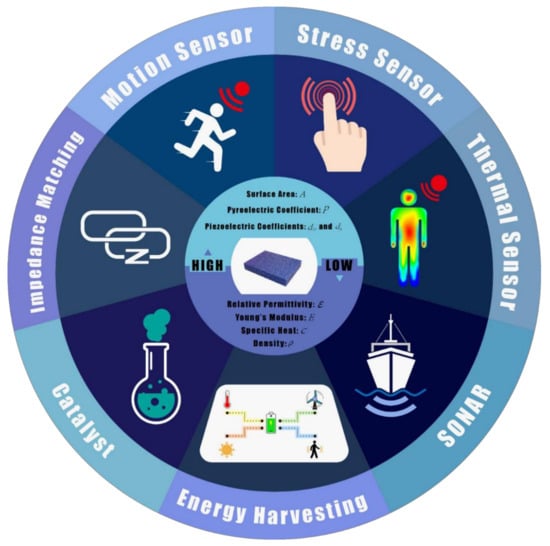
Figure 8.
Benefits of porous ferroelectrics and their potential applications.
7. Conclusions and Future Perspectives
Porous ferroelectric materials have attracted much attention due to their high sensitivity and harvesting figures of merit and their potential application in energy and sensing technologies. This article has reviewed the preparation methods, morphology, and characterization of porous ferroelectric materials, focuses on the mechanism that affects the state of internal stress and the Curie point of porous ferroelectric materials and highlights key simulations and applications that support the advantages of porous ceramics. In general, porous ferroelectric ceramics have low cost, large signal and energy output, and high controllability; they have potential for a large development space in performance and have a wide range of applications as transducers.
As mentioned above, porous piezoelectric ceramics can be generally classified into 3-0, 3-1, 3-3 and 2-2 type structures according to the connectivity of the pores. Among them, the 3-1 type and 2-2 type porous ferroelectric ceramics can improve the piezoelectric and pyroelectric energy harvesting performance by adjusting the orientation of the electric field and the pores. However, the brittleness of ceramics limits their applications. Porous ferroelectric polymers have good flexibility and biocompatibility, but their application prospects are also hindered by relatively low piezoelectric and pyroelectric coefficients. Therefore, porous ceramic-based ferroelectric composites combining the properties of both show great potential in sensing and energy harvesting applications.
There are various preparation methods for porous ceramic materials. The 3-1 type or 3-3 type porous ferroelectric ceramics obtained by freeze casting have a highly arranged pore structure, which makes their performance better than those produced by other methods. In addition, additive manufacturing is currently the most innovative method of fabrication because it is not limited by complex geometries and pore structures. Combining emerging manufacturing technologies with traditional technologies can also be a highly innovative endeavor. In addition, more in-depth explorations to discover the properties and internal mechanisms of porous materials in terms of state of internal stress, degree of tetragonality, domain structure and domain dynamics is also expected.
Author Contributions
Conceptualization, Y.Z. and X.Z.; writing—original draft preparation, X.Z.; writing—review and editing, C.B., Y.Z., J.Z. and Q.W.; supervision, K.Z. and D.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Academy of Medical Sciences GCRF fund (GCRFNGR2-10059); Key Research and Development Project of Hunan Province (No. 2020WK2004); National Natural Science Foundation of China (Nos. U19A2087, 52002404, 52102150); Overseas Talent Introduction Project of China, Hundred Youth Talents Program of Hunan.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Novak, I. Molecular isomorphism. Eur. J. Phys. 1995, 16, 151–153. [Google Scholar] [CrossRef]
- Selvarajan, S.; Alluri, N.R.; Chandrasekhar, A.; Kim, S.-J. BaTiO3 nanoparticles as biomaterial film for self-powered glucose sensor application. Sens. Actuators B Chem. 2016, 234, 395–403. [Google Scholar] [CrossRef]
- Proto, A.; Penhaker, M.; Bibbo, D.; Vala, D.; Conforto, S.; Schmid, M. Measurements of Generated Energy/Electrical Quantities from Locomotion Activities Using Piezoelectric Wearable Sensors for Body Motion Energy Harvesting. Sensors 2016, 16, 524. [Google Scholar] [CrossRef] [PubMed]
- Gray, R.B. Transducer and Method of Making the Same. U.S. Patent 2,486,560, 20 September 1946. [Google Scholar]
- Sakayori, K.; Matsui, Y.; Abe, H.; Nakamura, E.; Kenmoku, M.; Hara, T.; Ishikawa, D.; Kokubu, A.; Hirota, K.; Ikeda, T.I.T. Curie Temperature of BaTiO3. Jpn. J. Appl. Phys. 1995, 34, 5443. [Google Scholar] [CrossRef]
- Blank, T.A.; Eksperiandova, L.P.; Belikov, K.N. Recent trends of ceramic humidity sensors development: A review. Sens. Actuators B Chem. 2016, 228, 416–442. [Google Scholar] [CrossRef]
- Sanson, A.; Mercadelli, E.; Roncari, E.; Licheri, R.; Orrù, R.; Cao, G.; Merlone-Borla, E.; Marzorati, D.; Bonavita, A.; Micali, G.; et al. Influence of processing parameters on the electrical response of screen printed SrFe0.6Ti0.4O3-δ thick films. Ceram. Int. 2010, 36, 521–527. [Google Scholar] [CrossRef]
- Karmakar, S.; Kiran, R.; Singh Chauhan, V.; Vaish, R. Effect of Porosity on Energy Harvesting Performance of 0.5Ba(Ca0.8Zr0.2)O3-0.5(Ba0.7Ca0.3)TiO3 Ceramics: A Numerical Study. Energy Technol. 2020, 8, 1901302. [Google Scholar] [CrossRef]
- Martínez-Ayuso, G.; Friswell, M.I.; Adhikari, S.; Khodaparast, H.H.; Berger, H. Homogenization of porous piezoelectric materials. Int. J. Solids Struct. 2017, 113–114, 218–229. [Google Scholar] [CrossRef]
- Roscow, J.I.; Pearce, H.; Khanbareh, H.; Kar-Narayan, S.; Bowen, C.R. Modified energy harvesting figures of merit for stress- and strain-driven piezoelectric systems. Eur. Phys. J. Spec. Top. 2019, 228, 1537–1554. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, M.; Roscow, J.; Bao, Y.; Zhou, K.; Zhang, D.; Bowen, C.R. Enhanced pyroelectric and piezoelectric properties of PZT with aligned porosity for energy harvesting applications. J. Mater. Chem. A Mater. 2017, 5, 6569–6580. [Google Scholar] [CrossRef]
- Roscow, J.; Zhang, Y.; Taylor, J.; Bowen, C.R. Porous ferroelectrics for energy harvesting applications. Eur. Phys. J. Spec. Top. 2015, 224, 2949–2966. [Google Scholar] [CrossRef]
- Yan, M.; Xiao, Z.; Ye, J.; Yuan, X.; Li, Z.; Bowen, C.; Zhang, Y.; Zhang, D. Porous ferroelectric materials for energy technologies: Current status and future perspectives. Energy Environ. Sci. 2021, 14, 6158–6190. [Google Scholar] [CrossRef]
- Zhang, S.; Li, F.; Jiang, X.; Kim, J.; Luo, J.; Geng, X. Advantages and Challenges of Relaxor-PbTiO3 Ferroelectric Crystals for Electroacoustic Transducers—A Review. Prog. Mater. Sci. 2015, 68, 1–66. [Google Scholar] [CrossRef]
- Kargupta, R.; Venkatesh, T. Electromechanical response of porous piezoelectric materials. Acta Mater. 2006, 54, 4063–4078. [Google Scholar] [CrossRef]
- Settera, N.; Damjanovic, D. Ferroelectric thin films: Review of materials, properties, and applications. J. Appl. Phys. 2006, 100, 051606. [Google Scholar] [CrossRef]
- Curie, J.; Curie, P. Développement par compression de l’électricité polaire dans les cristaux hémièdres à faces inclinées. Bull. Soc. Minéral. 1880, 3, 90–93. [Google Scholar] [CrossRef]
- Curie, J.; Pierre, C. Contractions and expansions produced by voltages in hemihedral crystals with inclined faces. Comptes Rendus 1881, 93, 1137–1140. [Google Scholar]
- Woldemar, V. Beiträge zur molekularen Theorie der Piëzoelectricität. Ann. Phys. 1894, 51, 638–660. [Google Scholar]
- Colombo, P. Conventional and novel processing methods for cellular ceramics. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2006, 364, 109–124. [Google Scholar] [CrossRef]
- Zeng, T.; Dong, X.; Mao, C.; Zhou, Z.; Yang, H. Effects of pore shape and porosity on the properties of porous PZT 95/5 ceramics. J. Eur. Ceram. Soc. 2007, 27, 2025–2029. [Google Scholar] [CrossRef]
- Guo, R.; Wang, C.A.; Yang, A.K.; Fu, J.T. Enhanced piezoelectric property of porous lead zirconate titanate ceramics with one dimensional ordered pore structure. J. Appl. Phys. 2010, 108, 124112. [Google Scholar] [CrossRef]
- Nan, B.; Olhero, S.; Pinho, R.; Vilarinho, P.M.; Button, T.W.; Ferreira, J.M. Direct ink writing of macroporous lead-free piezoelectric Ba0.85Ca0.15Zr0.1Ti0.9O3. J. Am. Ceram. Soc. 2018, 102, 3191–3203. [Google Scholar] [CrossRef]
- Woyansky, J.S.; Scott, C.E.; Minnear, W.P. Processing of Porous Ceramics. Am. Ceram. Soc. Bull. 1992, 71, 1674–1682. [Google Scholar]
- Karl, S.; Somers, A.V. Method of Making Porous Ceramic Articles. U.S. Patent 3090094, 21 February 1963. [Google Scholar]
- Safari, A.; Halliyal, A.; Bowen, L.J.; Newnham, R.E. Flexible Composite Transducers. J. Am. Ceram. Soc. 2010, 65, 207–209. [Google Scholar] [CrossRef]
- Kara, H.; Ramesh, R.; Stevens, R.; Bowen, C.R. Porous PZT Ceramics for Receiving Transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 289–296. [Google Scholar] [CrossRef] [PubMed]
- Studart, A.R.; Gonzenbach, U.T.; Tervoort, E.; Gauckler, L.J. Processing Routes to Macroporous Ceramics: A Review. J. Am. Ceram. Soc. 2006, 89, 1771–1789. [Google Scholar] [CrossRef]
- Sanson, A.; Pinasco, P.; Roncari, E. Influence of pore formers on slurry composition and microstructure of tape cast supporting anodes for SOFCs. J. Eur. Ceram. Soc. 2008, 28, 1221–1226. [Google Scholar] [CrossRef]
- Sun, Y.; Tan, S.H.; Jiang, D.L. Synthesis of porous silicon carbide and its catalysis. J. Inorg. Mater. 2003, 18, 830–836. [Google Scholar]
- Pokhrel, A.; Seo, D.N.; Lee, S.T.; Kim, I.J. Processing of Porous Ceramics by Direct Foaming: A Review. J. Korean Ceram. Soc. 2013, 50, 93–102. [Google Scholar] [CrossRef]
- Wu, L.; Huang, Y.; Wang, Z.; Liu, L. Research Process of Foaming Technology For Preparing Porous Ceramics; China Ceramics: Jinan, China, 2010. [Google Scholar]
- Kim, Y.W.; Kim, S.H.; Kim, H.D.; Park, C.B. Processing of closed-cell silicon oxycarbide foams from a preceramic polymer. J. Mater. Sci. 2004, 39, 5647–5652. [Google Scholar] [CrossRef]
- Schuster; Chiari, B.V. Foamed Ceramic Element. U.S. Patent US4123285A, 1978. [Google Scholar]
- Deville, S.; Saiz, E.; Tomsia, A.P. Freeze casting of hydroxyapatite scaffolds for bone tissue engineering. Biomaterials 2006, 27, 5480–5489. [Google Scholar] [CrossRef]
- Deville, S. Freeze-Casting of Porous Ceramics: A Review of Current Achievements and Issues. Adv. Eng. Mater. 2010, 10, 155–169. [Google Scholar] [CrossRef]
- Fukasawa, T.; Ando, M.; Ohji, T.; Kanzaki, S. Synthesis of Porous Ceramics with Complex Pore Structure by Freeze—Dry Processing. J. Am. Ceram. Soc. 2010, 84, 230–232. [Google Scholar] [CrossRef]
- Yoon, B.H.; Koh, Y.H.; Park, C.S.; Kim, H.E. Generation of Large Pore Channels for Bone Tissue Engineering Using Camphene—Based Freeze Casting. J. Am. Ceram. Soc. 2007, 90, 1744–1752. [Google Scholar] [CrossRef]
- Araki, K.; Halloran, J.W. Room-Temperature Freeze Casting for Ceramics with Nonaqueous Sublimable Vehicles in the Naphthalene—Camphor Eutectic System. J. Am. Ceram. Soc. 2010, 87, 2014–2019. [Google Scholar] [CrossRef]
- Lee, S.H.; Jun, S.H.; Kim, H.E.; Koh, Y.H. Piezoelectric Properties of PZT-Based Ceramic with Highly Aligned Pores. J. Am. Ceram. Soc. 2008, 91, 1912–1915. [Google Scholar] [CrossRef]
- Lee, S.H.; Jun, S.H.; Kim, H.E.; Koh, Y.H. Fabrication of Porous PZT–PZN Piezoelectric Ceramics With High Hydrostatic Figure of Merits Using Camphene—Based Freeze Casting. J. Am. Ceram. Soc. 2007, 90, 2807–2813. [Google Scholar] [CrossRef]
- Xu, T.; Wang, C.-A. Control of pore size and wall thickness of 3-1 type porous PZT ceramics during freeze-casting process. Mater. Des. 2016, 91, 242–247. [Google Scholar] [CrossRef]
- Roscow, J.; Li, Y.; Hall, D. Residual stress and domain switching in freeze cast porous barium titanate. J. Eur. Ceram. Soc. 2022, 42, 1434–1444. [Google Scholar] [CrossRef]
- Jenny, M.A.; Omalete, O.O. Method for Molding Ceramic Powders Using a Water-Based Gel Casting Process. U.S. Patent US 5145908, 8 September 1992. [Google Scholar]
- Young, A.C.; Omatete, O.O.; Janney, M.A.; Menchhofer, P.A. Gelcasting of Alumina. J. Am. Ceram. Soc. 1991, 74. [Google Scholar] [CrossRef]
- Wu, J.M.; Lu, W.Z.; Liang, J. Microwave Dielectric Properties of 0.9Al2O3—0.1TiO2Ceramics Prepared by Aqueous Gelcasting. J. Inorg. Mater. 2010, 26, 102–106. [Google Scholar] [CrossRef]
- Wu, L.; Huang, Y.; Wang, Z.; Li, L. Controlled fabrication of porous Al2O3 ceramic by N,N′-dimethylformamide-based gel-casting. Scr. Mater. 2010, 62, 602–605. [Google Scholar] [CrossRef]
- Yu, J.; Wang, H.; Zhang, J. Neural network modeling and analysis of gel casting preparation of porous Si3N4 ceramics. Ceram. Int. 2009, 35, 2943–2950. [Google Scholar] [CrossRef]
- Ananthakumar, S.; Prabhakaran, K.; Hareesh, U.S.; Manohar, P.; Warrier, K.G.K. Gel casting process for Al2O3–SiC nanocomposites and its creep characteristics. Mater. Chem. Phys. 2004, 85, 151–157. [Google Scholar] [CrossRef]
- Yuan, L.; Liu, Z.; Hou, X.; Liu, Z.; Zhu, Q.; Wang, S.; Ma, B.; Yu, J. Fibrous ZrO2-mullite porous ceramics fabricated by a hydratable alumina based aqueous gel-casting process. Ceram. Int. 2019, 45, 8824–8831. [Google Scholar] [CrossRef]
- Chen, R.; Wang, C.A.; Huang, Y.; Ma, L.; Lin, W. Ceramics with Special Porous Structures Fabricated by Freeze-Gelcasting: Using tert-Butyl Alcohol as a Template. J. Am. Ceram. Soc. 2010, 90, 3478–3484. [Google Scholar] [CrossRef]
- Dommati, H.; Ray, S.S.; Wang, J.C.; Chen, S.S. A comprehensive review of recent developments in 3D printing technique for ceramic membrane fabrication for water purification. RSC Adv. 2019, 9, 16869–16883. [Google Scholar] [CrossRef]
- Morissette, S.L.; Lewis, J.A.; Clem, P.G.; Cesarano, J.; Dimos, D.B. Direct-Write Fabrication of Pb(Nb,Zr,Ti)O3 Devices: Influence of Paste Rheology on Print Morphology and Component Properties. J. Am. Ceram. Soc. 2010, 84, 2462–2468. [Google Scholar] [CrossRef]
- Penn, S.J.; Alford, N.M.; Templeton, A.; Wang, X.; Xu, M.; Reece, M.; Schrapel, K. Effect of Porosity and Grain Size on the Microwave Dielectric Properties of Sintered Alumina. J. Am. Ceram. Soc. 1997, 80, 1885–1888. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, M.; Roscow, J.; Bowen, C. Dielectric and piezoelectric properties of porous lead-free 0.5Ba(Ca0.8Zr0.2)O3-0.5(Ba0.7Ca 0.3)TiO3 ceramics. Mater. Res. Bull. 2019, 112, 426–431. [Google Scholar] [CrossRef]
- Abdullah, F.F.; Nemati, A.; Bagheri, R. Dielectric and piezoelectric properties of porous PZT–PCN ceramics sintered at different temperatures. Mater. Lett. 2015, 151, 85–88. [Google Scholar] [CrossRef]
- Zeng, T.; Dong, X.L.; Chen, H.; Wang, Y.L. The effects of sintering behavior on piezoelectric properties of porous PZT ceramics for hydrophone application. Mater. Sci. Eng. B 2006, 131, 181–185. [Google Scholar] [CrossRef]
- Zeng, T.; Dong, X.; Chen, S.; Yang, H. Processing and piezoelectric properties of porous PZT ceramics. Ceram. Int. 2007, 33, 395–399. [Google Scholar] [CrossRef]
- Wang, Q.; Chen, Q.; Zhu, J.; Huang, C.; Darvell, B.W.; Chen, Z. Effects of pore shape and porosity on the properties of porous LNKN ceramics as bone substitute. Mater. Chem. Phys. 2008, 109, 488–491. [Google Scholar] [CrossRef]
- Zhang, H.; Li, J.-F.; Zhang, B. Microstructure and electrical properties of porous PZT ceramics derived from different pore-forming agents. Acta Mater. 2007, 55, 171–181. [Google Scholar] [CrossRef]
- Zhang, Y.; Roscow, J.; Lewis, R.; Khanbareh, H.; Topolov, V.Y.; Xie, M.; Bowen, C.R. Understanding the effect of porosity on the polarisation-field response of ferroelectric materials. Acta Mater. 2018, 154, 100–112. [Google Scholar] [CrossRef]
- Roncari, E.; Galassi, C.; Craciun, F.; Capiani, C.; Piancastelli, A. A microstructural study of porous piezoelectric ceramics obtained by different methods. J. Eur. Ceram. Soc. 2001, 21, 409–417. [Google Scholar] [CrossRef]
- Praveenkumar, B.; Kumar, H.H.; Kharat, D.K. Study on microstructure, piezoelectric and dielectric properties of 3-3 porous PZT composites. J. Mater. Sci. Mater. Electron. 2006, 17, 515–518. [Google Scholar] [CrossRef]
- Tan, J.; Li, Z. Microstructures, dielectric and piezoelectric properties of unannealed and annealed porous 0.36BiScO3-0.64PbTiO3 ceramics. J. Mater. Sci. 2016, 51, 5092–5103. [Google Scholar] [CrossRef]
- Khansur, N.H.; Biggemann, J.; Stumpf, M.; Riess, K.; Fey, T.; Webber, K.G. Temperature-and Stress-Dependent Electromechanical Response of Porous Pb(Zr,Ti)O3. Adv. Eng. Mater. 2020, 22, 2000389. [Google Scholar] [CrossRef]
- Stanculescu, R.; Ciomaga, C.E.; Padurariu, L.; Galizia, P.; Horchidan, N.; Capiani, C.; Galassi, C.; Mitoseriu, L. Study of the role of porosity on the functional properties of (Ba,Sr)TiO 3 ceramics. J. Alloys Compd. 2015, 643, 79–87. [Google Scholar] [CrossRef]
- Li, J.-F.; Takagi, K.; Ono, M.; Pan, W.; Watanabe, R.; Almajid, A.; Taya, M. Fabrication and Evaluation of Porous Piezoelectric Ceramics and Porosity-Graded Piezoelectric Actuators. J. Am. Ceram. Soc. 2003, 86, 1094–1098. [Google Scholar] [CrossRef]
- Naeem, H.T. The influence of different pore forming agents on piezoelectric and dielectric properties of porous PZT-PCN ceramics. Mater. Today Proc. 2020, 20, 531–534. [Google Scholar] [CrossRef]
- Curecheriu, L.; Lukacs, V.A.; Padurariu, L.; Stoian, G.; Ciomaga, C.E. Effect of Porosity on Functional Properties of Lead-Free Piezoelectric BaZr0.15Ti0.85O3 Porous Ceramics. Materials 2020, 13, 3324. [Google Scholar] [CrossRef]
- Zhu, S.; Cao, L.; Xiong, Z.; Lu, C.; Gao, Z. Enhanced piezoelectric properties of 3-1 type porous 0.94Bi0.5Na0.5TiO3-0.06BaTiO3 ferroelectric ceramics. J. Eur. Ceram. Soc. 2018, 38, 2251–2255. [Google Scholar] [CrossRef]
- Guo, R.; Wang, C.-A.; Yang, A. Effects of pore size and orientation on dielectric and piezoelectric properties of 1–3 type porous PZT ceramics. J. Eur. Ceram. Soc. 2011, 31, 605–609. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, H.; Liu, X.; Sui, H.; Xiao, S. Structural design of PZT porous ceramics obtained via free-casting by ice-templating and performance exploration. Mater. Res. Bull. 2020, 127, 110862. [Google Scholar] [CrossRef]
- Guo, R.; Wang, C.-A.; Yang, A. Piezoelectric Properties of the 1-3 Type Porous Lead Zirconate Titanate Ceramics. J. Am. Ceram. Soc. 2011, 94, 1794–1799. [Google Scholar] [CrossRef]
- Zhang, Y.; Roscow, J.; Xie, M.; Bowen, C.R. High piezoelectric sensitivity and hydrostatic figures of merit in unidirectional porous ferroelectric ceramics fabricated by freeze casting. J. Eur. Ceram. Soc. 2018, 38, 4203–4211. [Google Scholar] [CrossRef]
- Zhang, Y.; Bao, Y.; Dou, Z.; Bowen, C.R. Porous PZT Ceramics with Aligned Pore Channels for Energy Harvesting Applications. J. Am. Ceram. Soc. 2015, 98, 2980–2983. [Google Scholar] [CrossRef]
- Schultheiß, J.; Roscow, J.I.; Koruza, J. Orienting anisometric pores in ferroelectrics: Piezoelectric property engineering through local electric field distributions. Phys. Rev. Mater. 2019, 3, 084408. [Google Scholar] [CrossRef]
- Dixit, P.; Seth, S.; Rawal, B.; Kumar, B.P.; Panda, H.S. Freeze casting of lamellar-structured porous lead-free (Na0.52K0.48)(Nb0.95Sb0.05)O3 piezoceramic with remarkable enhancement in piezoelectric voltage constant and hydrostatic figure of merit. J. Mater. Sci. Mater. Electron. 2021, 32, 5393–5403. [Google Scholar] [CrossRef]
- Roscow, J.I.; Zhang, Y.; Kraśny, M.J.; Lewis, R.W.C.; Taylor, J.; Bowen, C.R. Freeze cast porous barium titanate for enhanced piezoelectric energy harvesting. J. Phys. D Appl. Phys. 2018, 51, 225301. [Google Scholar] [CrossRef]
- Yang, A.K.; Wang, C.A.; Guo, R.; Huang, Y.; Nan, C.W. Effects of sintering behavior on microstructure and piezoelectric properties of porous PZT ceramics. Ceram. Int. 2010, 36, 549–554. [Google Scholar] [CrossRef]
- Liu, W.; Xu, J.; Lv, R.; Wang, Y.; Xu, H.; Yang, J. Effects of sintering behavior on piezoelectric properties of porous PZT ceramics. Ceram. Int. 2014, 40, 2005–2010. [Google Scholar] [CrossRef]
- Yang, A.K.; Wang, C.A.; Guo, R.; Huang, Y. Effects of porosity on dielectric and piezoelectric properties of porous lead zirconate titanate ceramics. Appl. Phys. Lett. 2011, 98, 152904. [Google Scholar] [CrossRef]
- Yang, A.; Wang, C.A.; Guo, R.; Huang, Y.; Nan, C.W. Porous PZT Ceramics with High Hydrostatic Figure of Merit and Low Acoustic Impedance by TBA-Based Gel-Casting Process. J. Am. Ceram. Soc. 2010, 93, 1427–1431. [Google Scholar] [CrossRef]
- Liu, W.; Xu, J.; Wang, Y.; Xu, H.; Xi, X.; Yang, J. Processing and Properties of Porous PZT Ceramics from Particle-Stabilized Foams via Gel Casting. J. Am. Ceram. Soc. 2013, 96, 1827–1831. [Google Scholar] [CrossRef]
- Yan, M.; Liu, S.; Xiao, Z.; Yuan, X.; Zhai, D.; Zhou, K.; Zhang, D.; Zhang, G.; Bowen, C.; Zhang, Y. Evaluation of the pore morphologies for piezoelectric energy harvesting application. Ceram. Int. 2022, 48, 5017–5025. [Google Scholar] [CrossRef]
- Damodaran, A.R.; Breckenfeld, E.; Chen, Z.; Lee, S.; Martin, L.W. Enhancement of Ferroelectric Curie Temperature in BaTiO3 Films via Strain-Induced Defect Dipole Alignment. Adv. Mater. 2014, 26, 6341–6347. [Google Scholar] [CrossRef]
- Abrahams, S.C.; Kurtz, S.K.; Jamieson, P.B. Atomic Displacement Relationship to Curie Temperature and Spontaneous Polarization in Displacive Ferroelectrics. Phys. Rev. 1968, 172, 551–553. [Google Scholar] [CrossRef]
- Huang, S.; Zeng, J.; Zheng, L.; Man, Z.; Ruan, X.; Shi, X.; Li, G. A novel piezoelectric ceramic with high Curie temperature and high piezoelectric coefficient. Ceram. Int. 2020, 46, 6212–6216. [Google Scholar] [CrossRef]
- Uchino, K.; Sadanaga, E.; Hirose, T. Dependence of the Crystal Structure on Particle Size in Barium Titanate. J. Am. Ceram. Soc. 1989, 72, 1555–1558. [Google Scholar] [CrossRef]
- Ishikawa, K.; Yoshikawa, K.; Okada, N. Size effect on the ferroelectric phase transition in PbTiO3 ultrafine particles. Phys. Rev. B 1988, 37, 5852–5855. [Google Scholar] [CrossRef]
- Kamel, T.M.; de With, G. Grain size effect on the poling of soft Pb(Zr,Ti)O3 ferroelectric ceramics. J. Eur. Ceram. Soc. 2008, 28, 851–861. [Google Scholar] [CrossRef]
- Su, Y.; Weng, G. The shift of Curie temperature and evolution of ferroelectric domain in ferroelectric crystals. J. Mech. Phys. Solids 2005, 53, 2071–2099. [Google Scholar] [CrossRef]
- Hiroshima, T.; Tanaka, K.; Kimura, T. Effects of Microstructure and Composition on the Curie Temperature of Lead Barium Niobate Solid Solutions. J. Am. Ceram. Soc. 1996, 79, 3235–3242. [Google Scholar] [CrossRef]
- Bao, Y.; Huang, B.; Zhou, K.; Roscow, J.; Bowen, C. Hierarchically structured lead-free barium strontium titanate for low-grade thermal energy harvesting. Ceram. Int. 2021, 47, 18761–18772. [Google Scholar] [CrossRef]
- Pu, Y.; Zhu, J.; Zhu, X.; Luo, Y.; Li, X.; Wang, M.; Jing, L.; Li, X.; Zhu, J.; Xiao, D. Enhanced Ferroelectric Properties of Intragranular-Porous Pb(Zr0.95Ti0.05)O3Ceramic Fabricated with Carbon Nanotubes. J. Am. Ceram. Soc. 2010, 93, 642–645. [Google Scholar]
- Okazaki, K.; Nagata, K. Effects of Grain Size and Porosity on Electrical and Optical Properties of PLZT Ceramics. J. Am. Ceram. Soc. 1973, 56, 82–86. [Google Scholar] [CrossRef]
- Keizer, K.; Burggraaf, A.J. Grain Size Effects on the Ferroelectric-Paraelectric Transition, the Dielectric Constant, and the Lattice Parameters in Lanthana-Substituted Lead Titanate. Phys. Stat. Solidi 1974, 26, 561–569. [Google Scholar] [CrossRef]
- Zhu, J.L.; Lin, S.; Feng, S.M.; Li, F.Y.; Wang, L.J.; Jin, C.Q.; Wang, X.H.; Li, L.T. The effects of high pressure on the ferroelectric properties of nano-BaTiO3 ceramics. J. Phys. Conf. Ser. 2008, 121, 162005. [Google Scholar] [CrossRef]
- Samara, G.A. Pressure Dependence Of The Ferroelectric Properties of Rochelle Salt. J. Phys. Chem. Solids 1964, 26, 121–131. [Google Scholar] [CrossRef]
- Schader, F.H.; Aulbach, E.; Webber, K.G.; Rossetti, G.A., Jr. Influence of uniaxial stress on the ferroelectric-to-paraelectric phase change in barium titanate. J. Appl. Phys. 2013, 113, 174103. [Google Scholar] [CrossRef]
- Jaffe, H.; Berlincourt, D.; McKee, J.M. Effect of Pressure on the Curie Temperature of Polycrystalline Ceramic Barium Titanate. Phys. Rev. 1957, 105, 57–58. [Google Scholar] [CrossRef]
- Hwang, H.J.; Nagai, T.; Ohji, T.; Sando, M.; Toriyama, M.; Niihara, K. Curie Temperature Anomaly in Lead Zirconate Titanate/Silver Composites. J. Am. Ceram. Soc. 1998, 81, 709–712. [Google Scholar] [CrossRef]
- Yan, H.; Li, C.; Zhou, J.; Zhu, W.; He, L.; Song, Y.; Yu, Y. Effects of A-Site (NaCe) Substitution with Na-Deficiency on Structures and Properties of CaBi4Ti4O15-Based High-Curie-Temperature Ceramics. Jpn. J. Appl. Phys. 2001, 40, 6501–6505. [Google Scholar] [CrossRef]
- Sato, Y.; Kanai, H.; Yamashita, Y. Effects of Silver and Palladium Doping on the Dielectric Properties of 0.9Pb(Mg1/3Nb2/3)O3–0.1 PbTiO3 Ceramic. J. Am. Ceram. Soc. 2010, 79, 261–265. [Google Scholar] [CrossRef]
- Ikushima, H.; Hayakawa, S. Electrical Properties of Ag-Doped Barium Titanate Ceramics. Jpn. J. Appl. Phys. 1965, 4, 328–336. [Google Scholar] [CrossRef]
- Maher, G.H. Effect of Silver Doping on the Physical and Electrical Properties of PLZT Ceramics. J. Am. Ceram. Soc. 2010, 66, 408–413. [Google Scholar] [CrossRef]
- Baxter, P.; Hellicar, N.J.; Lewis, B. Effect of Additives of Limited Solid Solubility on Ferroelectric Properties of Barium Titanate Ceramics. J. Am. Ceram. Soc. 2010, 42, 465–470. [Google Scholar] [CrossRef]
- Saburi, O. Semiconducting Bodies in the Family of Barium Titanates. J. Am. Ceram. Soc. 1961, 44, 54–63. [Google Scholar] [CrossRef]
- Ihrig, H. The phase stability of BaTiO3 as a function of doped 3d elements: An experimental study. J. Phys. C Solid State Phys. 2001, 13, 159. [Google Scholar] [CrossRef][Green Version]
- Fritz, I.J. Ultrasonic, dilatometric, and dielectric study of uniaxial-stress effects in a barium-calcium titanate ceramic. J. Appl. Phys. 1978, 49, 788–794. [Google Scholar] [CrossRef]
- Gheorghiu, F.; Padurariu, L.; Airimioaei, M.; Curecheriu, L.; Ciomaga, C.; Padurariu, C.; Mitoseriu, L. Porosity-dependent properties of Nb-doped Pb(Zr,Ti)O3ceramics. J. Am. Ceram. Soc. 2016, 100, 647–658. [Google Scholar] [CrossRef]
- Bosse, P.W.; Challagulla, K.S.; Venkatesh, T.A. Electromechanical response of piezoelectric foams: Effects of foam shape and porosity aspect ratio. Acta Mater. 2012, 60, 2111–2127. [Google Scholar] [CrossRef]
- Zhao, H.; Wu, P.; Du, L.; Du, H. Effect of the nanopore on ferroelectric domain structures and switching properties. Comput. Mater. Sci. 2018, 148, 216–223. [Google Scholar] [CrossRef]
- Kim, H.; Yun, S.; Kim, K.; Kim, W.; Ryu, J.; Nam, H.G.; Han, S.M.; Jeon, S.; Hong, S. Breaking the elastic limit of piezoelectric ceramics using nanostructures: A case study using ZnO. Nano Energy 2020, 78, 105259. [Google Scholar] [CrossRef]
- Bowen, C.R.; Taylor, J.; Leboulbar, E.; Zabek, D.; Chauhan, A.; Vaish, R. Pyroelectric materials and devices for energy harvesting applications. Energy Environ. Sci. 2014, 7, 3836–3856. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, M.; Zhu, Q.; Wang, F.; Su, H.; Li, H.; Diao, C.; Zheng, H.; Wu, Y.; Wang, Z.L. Performance enhancement of flexible piezoelectric nanogenerator via doping and rational 3D structure design for self-powered mechanosensational system. Adv. Funct. Mater. 2019, 29, 1904259. [Google Scholar] [CrossRef]
- Marselli, S.; Pavia, V.; Galassi, C.; Roncari, E.; Craciun, F.; Guidarelli, G.J. Porous piezoelectric ceramic hydrophone. Acoust. Soc. Am. 1999, 106, 733–738. [Google Scholar] [CrossRef]
- Xie, M.; Zhang, Y.; Krany, M.J.; Bowen, C.; Khanbareh, H.; Gathercole, N. Flexible and active self-powered pressure, shear sensors based on freeze casting ceramic-polymer composites. Energy Environ. Sci. 2018, 11, 2919–2927. [Google Scholar] [CrossRef] [PubMed]
- Phuong, P.T.T.; Zhang, Y.; Gathercole, N.; Khanbareh, H.; Bowen, C. Demonstration of Enhanced Piezo-Catalysis for Hydrogen Generation and Water Treatment at the Ferroelectric Curie Temperature. iScience 2020, 23, 101095. [Google Scholar] [CrossRef]
- Zhang, Y.; Phuong, P.T.T.; Roake, E.; Khanbareh, H.; Wang, Y.; Dunn, S.; Bowen, C. Thermal energy harvesting using pyroelectric-electrochemical coupling in ferroelectric materials. Joule 2020, 4, 301–309. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).