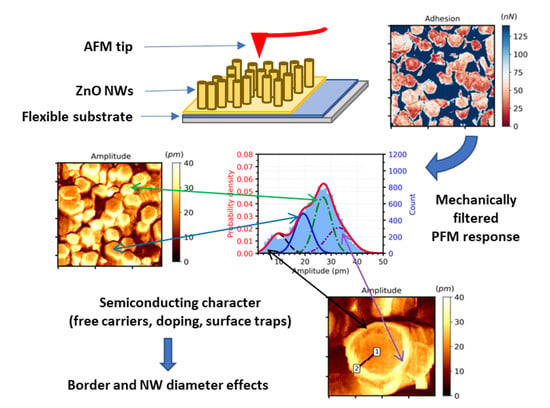
Size and Semiconducting Effects on the Piezoelectric Performances of ZnO Nanowires Grown onto Gravure-Printed Seed Layers on Flexible Substrates

Abstract

Zinc oxide (ZnO) nanogenerators have attracted increasing interest in the scientific community for use in energy harvesting and mechanical sensing applications. Understanding the interplay between piezoelectricity and semiconductor physics is fundamental to enhancing these devices’ performances, although direct characterization at the nanoscale is challenging. With this work, we present a new strategy to improve piezoresponse force microscopy (PFM) measurements and analysis. This strategy was applied to study the piezoelectric performances of ZnO nanowires grown on seed layers deposited by gravure printing onto flexible substrates. We demonstrate the influence of nanowire diameter and atomic force microscope (AFM) tip position on the piezoresponse amplitude. We also explain our results with simulations showing the importance of considering semiconducting properties in the analysis.

1. Introduction

In recent years, there has been a significant boost in development of portable and wearable electronic devices. However, the issue of powering the electronic devices has limited their widespread deployment, specifically in harsh and inaccessible environments. In this context, batteries have limited life and are a possible source of environmental pollution. Self-powered systems are suitable candidates to solve this problem, as such devices can harvest energy from their surroundings and become self-sustainable. Moreover, these self-powered systems can be used in harsh environments where battery operation and maintenance are complex [1,2,3]. Mechanical energy sources are readily available in most environments and can be harvested using piezoelectric transducers. For example, the mechanical vibrations around the human body in the form of muscle movements or within the circulatory system can be used to power body-implantable electronic systems [4].

Due to a sizeable piezoelectric response and increased failure stress compared to bulk in some semiconductor materials [5,6], nanowires have recently been used as a primary component to realize piezoelectric nanocomposites (also known as nanogenerators [1]). In particular, zinc oxide (ZnO) nanowires (NWs) are good candidates for the development of nanogenerators (NGs), thanks to their low cost, environment friendly, easy to process, lightweight, thermally stable and low-temperature fabrication process, allowing for the use of flexible substrates [7]. Recently, it has been demonstrated that ZnO NW-based NGs can produce a high output potential of the order of volts by applying a mechanical excitation [8,9,10,11,12,13]. However, most theoretical works considering semiconducting properties, such as doping level, in ZnO have not been able to account for this high piezoelectric response because the output potential decreases due to the screening effect of free electrons [14]. A surface Fermi-level pinning (SFLP) mechanism has been proposed as an intrinsic property of ZnO NWs to solve this contradiction [15]. In this context, PFM is an interesting tool to probe NW properties at the nanoscale in order to better understand the physics at stake in this system and to optimize performance. In particular, the influence of the top electrode present in macroscopic test benches can be eliminated. However, conventional scanning probe microscopy (SPM) measurements on nanoscale objects are challenging and thus rarely reported. Indeed, various artifacts, such as electrostatic effect [16], lateral NW bending by the tip during a scan, clamping, cantilever mechanical resonance signal amplification or cantilever buckling, can affect the piezoresponse [17]. In the present paper, we propose a new method to eliminate these experimental artefacts. We also report experimental observations of depletion effects, together with a consistent theoretical confirmation using finite element method (FEM)-based simulations. With this study, we confirm the theoretically predicted [18,19] influence of the NW diameter and the semiconducting character on piezoelectric properties, as well as the consistency of these results with different flexible substrates. In particular, the experiments reported in this study were carried out on NWs grown on gravure-printed ZnO seed layers. The seed layers were deposited on different electrodes and annealed at different times.

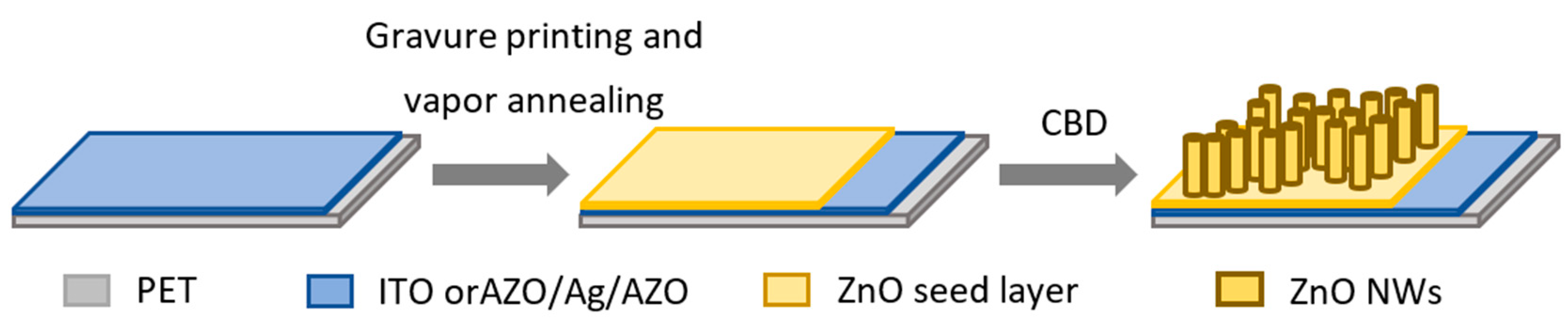
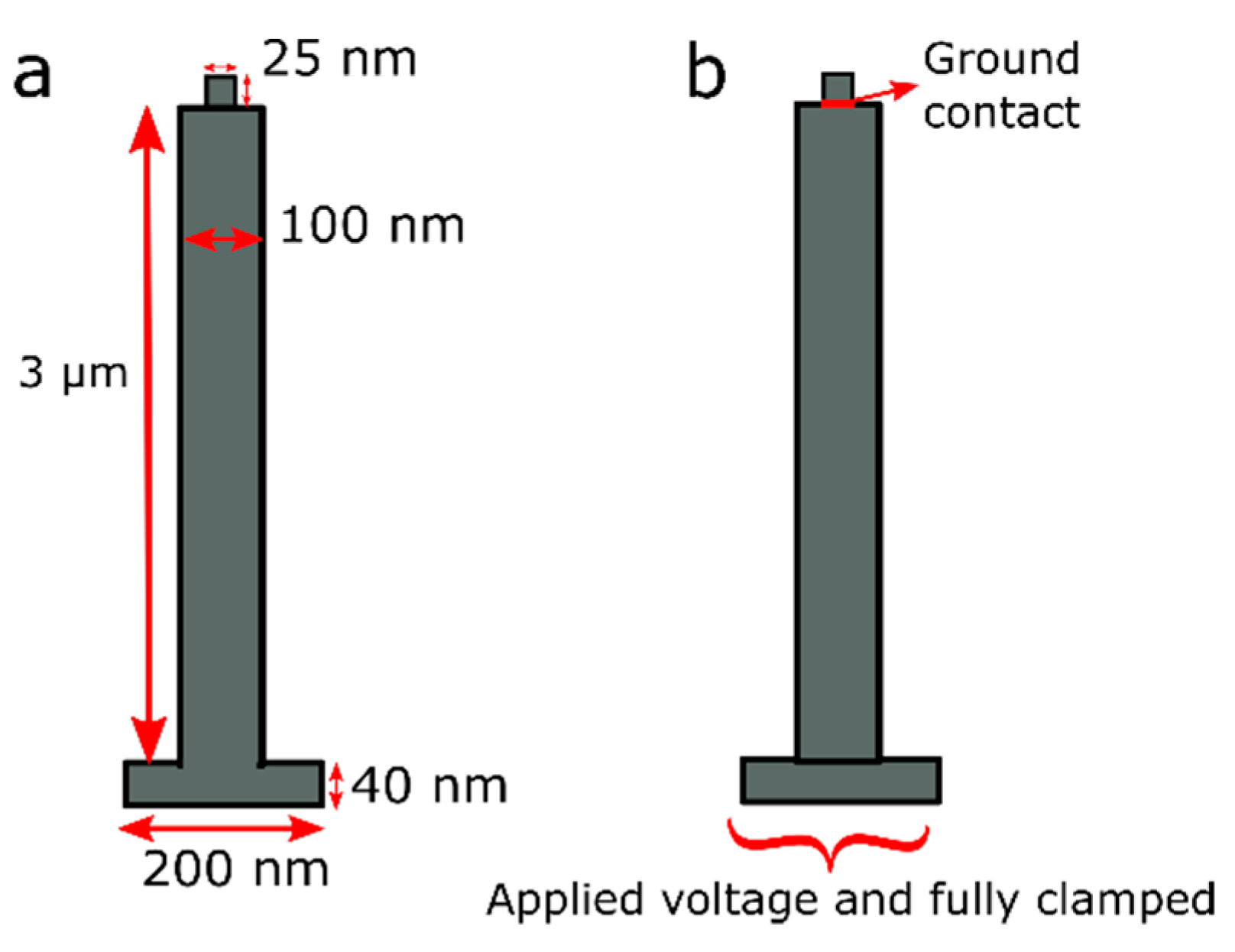
2. Experimental and Simulation Details

Two types of flexible substrates were used for the seed-layer deposition and the subsequent ZnO NW growth. The first substrate was commercial polyethylene terephthalate (PET)/indium tin oxide (ITO) (150 nm ITO on 125 µm PET). The second substrate was PET/aluminum-doped zinc oxide (AZO)/Silver (Ag)/AZO (150 nm AZO on 125 µm PET). A ZnO seed layer with a thickness of 55 ± 6 nm was deposited by gravure printing on top of the two substrates, following the method reported in [7]. Then, the samples were exposed to vapors of 1 M aqueous acetic acid solution in a closed oven at 50 °C for different annealing times (0, 1, 1.5 and 2.5 h) to induce morphological changes in the as-printed nanoparticulate seed layers [20]. The NWs were grown on the substrates with the seed layers using a precursor solution following the chemical bath deposition (CBD) process. An equimolar solution of 50 mM hexamethylenetetramine (HMT, ${\left({\mathrm{CH}}_2\right)}_6{\mathrm{N}}_4\left({\mathrm{CH}}_2\right)$, Sigma-Aldrich, St. Louis, MO, USA) and zinc nitrate hexahydrate ($\mathrm{Zn}{\left({\mathrm{NO}}_3\right)}_{2.6}{\mathrm{H}}_2\mathrm{O}$, Sigma-Aldrich, St. Louis, MO, USA) was prepared in 500 mL of deionized water (DI) at room temperature. The precursor solution was stirred for 20 min at 1000 rpm, then put to rest for 40 min before transferring the clear solution to glass bottles. Then, each ZnO seed layer substrate was clamped on glass slides using Kapton tape (3M, St. Paul, MN, USA) and placed face-down into the growth solution in the glass bottles. The hydrothermal growth process was carried out in an oven at 85 °C for 16 h. After the procedure, the substrates were rinsed with DI water and dried with N₂ gas. Figure 1 shows a schematic of the fabrication process.

We performed piezoresponse force microscopy (PFM, Bruker, Billerica, MA, USA) measurements with an atomic force microscope (AFM; Dimension Icon from Bruker, Billerica, MA, USA). An alternating bias voltage of 5 V was applied between the sample’s bottom electrode and the tip (grounded), and the sample’s deformations were recorded with the AFM tip. Platinum-coated silicon tips (PtSi-NCH from Bruker, Billerica, MA, USA) with a spring constant in the range of 43–50 N/m and a resonance frequency between 204 and 497 kHz were used. As in previous work [16,17,21], we noticed that this frequency varied depending on the cantilever or substrate. Therefore, we chose a PFM modulation frequency in the range of 5–50 kHz and ensured that the piezoresponse amplitude and phase were frequency-independent to avoid parasitic piezoelectric amplitude magnification. The significant stiffness of the tip also prevents cantilever buckling and significantly reduces electrostatic interference with the piezoresponse [16].

We took advantage of the spatial resolution of AFM to map the piezoresponse amplitude and phase as a function of the tip position. We also used a specific scanning mode (DataCube mode; see Supplementary Figure S1 in the Supplementary Materials) to avoid collisions and lateral bending of the vertically grown NWs with the tip. This issue could happen in the classical contact mode of PFM, which was not used in this study. Here, the absence of an insulating matrix between the NWs prevents clamping artifacts. PFM measurements were taken in three different regions (selected randomly) on each sample to verify their reproducibility, as shown in Figure S2. PFM measurements corresponding only to the ZnO NW top surface were extracted thanks to the ability of the PFM technique to record both mechanical and piezoelectric properties. A more significant tip–sample interaction force was measured when the tip was on the top surface of the NWs. This interaction force allows for filtering of the measurements performed on the top surface of the NWs only.

To qualitatively support our experimental PFM results, we performed 2D simulations using the finite element method with COMSOL Multiphysics software (version 5.6, COMSOL, Inc., Stockholm, Sweden). We followed the same strategy of static simulations implemented in previous reports on piezoelectric semiconductor materials to explain their piezoelectric response [17]. However, we added the semiconductor properties in our model, which was not considered previously [17]. Static simulations are well adapted to our experiments because the PFM amplitude is independent of the 5–50 kHz frequency range. Our simulations correspond to a snapshot of the oscillating motion of the ZnO NWs at their maximum amplitude. We neglected the mechanical tip–sample interaction and solved the piezoelectric and semiconducting coupled Equations (1) and (2):

$$\left[\sigma \right]=\left[c\right]\left[\epsilon \right]-{\left[e\right]}^T\left[E\right]$$

(1)

$$\left[D\right]=\left[e\right]\left[\epsilon \right]+\left[\kappa \right]\left[E\right]$$

(2)

where $\left[\sigma \right]$ is the stress matrix, [$\epsilon ] \mathrm{is}$ the strain matrix, [$E]$ is the electric field vector, [$D]$ is the electric displacement vector, $\left[c\right] \mathrm{is}$ the elasticity matrix, [$\kappa ]$ is the dielectric constant matrix and [e] is the piezoelectric coefficient matrix. The two matrices, $\left[e\right]$ and ${\left[e\right]}^T$, introduce the coupling between piezoelectric and semiconductor physics, which correspond to direct and inverse piezoelectric effects, respectively.

The simulated structure consists of a ZnO seed layer substrate and a ZnO NW with respective thicknesses of 40 nm and 3 μm and widths of 200 nm and 100 nm, corresponding to our samples. The AFM tip is modeled by a 25 × 25 nm square on top of the ZnO NW, as shown in Figure 2a. Our simulations took into account the semiconducting property of ZnO NWs. The local free carrier densities and the average doping concentrations are therefore included in the local density of charge $\left(\rho \right)$ in the Poisson equation:

$$\nabla ·D=\rho =q\left(p-n+N_d^{+}-N_A^{-}\right)$$

(3)

where $n$, $p$, $N_A^{-}$ and $N_d^{+}$ are the electrons, holes, acceptor atoms and donor atom densities, respectively. Electron and hole concentrations are functions of the local electric potential and the band structures of the ZnO material, respectively. For the electrical boundary conditions, a static voltage of 5 V was applied to the bottom substrate, as depicted in Figure 2b. In contrast, the potential at the interface between the probe and top surface of ZnO was set to zero. For the mechanical boundary conditions, the bottom side was fully clamped, whereas the rest of the side walls remained unclamped (see Figure 2b). The properties of ZnO used in our model are summarized in Table S1 in the Supplementary Materials.

3. Results and Discussion

3.1. Structural Characterization

After gravure printing of the ZnO seed layers, the samples were exposed or not to a vapor annealing treatment to investigate the effect of the seed layer morphology on the NW characteristics. Figure 3 shows SEM (FEGSEM, Leo 1530 Gemini by Zeiss, Oberkochen, Germany) and AFM (Veeco Dimension Digital Instruments Nanoscope IV, New York, NY, USA) top views of the gravure-printed ZnO seed layers exposed to different annealing times ranging between 0 and 2.5 h. The surface morphology of the ZnO seed layers exhibits a granular structure and grain growth phenomenon. There is a consequent reduction in the void areas between the grains themselves. As the annealing time increases, the grains enlarge, the contact points between the grains increase, seeds start bonding and the grain boundary melts after 2.5 h. In detail, the AFM phase images show that the untreated samples have a compact structure with seeds not uniformly sized and characterized by an imperfectly spherical shape. For the 1 h sintering treatment, the granular form appears to be better organized and more regular, with spherical-shaped seeds that are not uniformly sized. When the annealing time is increased to 1.5 h, the grains enlarge, and the neighboring seeds melt and form clusters randomly immersed into the regular granular structure.

When the treatment time is further increased to 2.5 h, several aggregates emerge that are intercalated with small grains. Thus, the clusters enlarge and enhance, and only the smaller structures still appear as grains. Thanks to the dissolution–reprecipitation mechanism resulting from the acidic vapor annealing, grain boundaries migration occurs, generating the observed grain growth phenomenon [20,22]. Because the grain boundary energy is anisotropic, the lower-energy boundary, i.e., the non-polar ZnO planes, tends to extend with increased annealing time [7,22,23,24,25,26].

Figure 4 shows scanning electron micrograph (SEM) top views of ZnO NWs grown on PET-ITO and PET-AZO substrates before (0 h) and after different annealing times (1, 1.5 and 2.5 h) on the ZnO seed layer. The NWs exhibit hexagonal shapes and are vertically aligned, regardless of the annealing time. In contrast, their radius is not homogeneous, as demonstrated by statistical analysis of AFM topographic images (see Figures S3–S7) and by a statistical study analyzing the topography of the AFM figures (see the following subsection) in three different places on each sample. The average NW radius slightly decreases as the annealing time increases—from 146 nm to 107 nm for PET-AZO and from 118 nm to 90 nm for PET-ITO. Although there are some errors due to the convolution between the AFM tip and the sample topography, which lead to a systematic overestimation of the NWs’ radii (see Figure S8), this does not affect the trends discussed here. As the NW radius is proportional to the size of the polar grains of the seed layer [27], non-polar surfaces may grow despite polar surfaces with the increase in annealing time. Therefore, acidic vapor annealing of the seed layer can eventually tune the NW characteristics. Finally, the AZO substrate probably also participates in the nucleation process of the NWs, forming a thicker seed layer, together with the printed ZnO layer. This may be the reason why ZnO NWs grow with larger diameters on the AZO substrate [28,29].

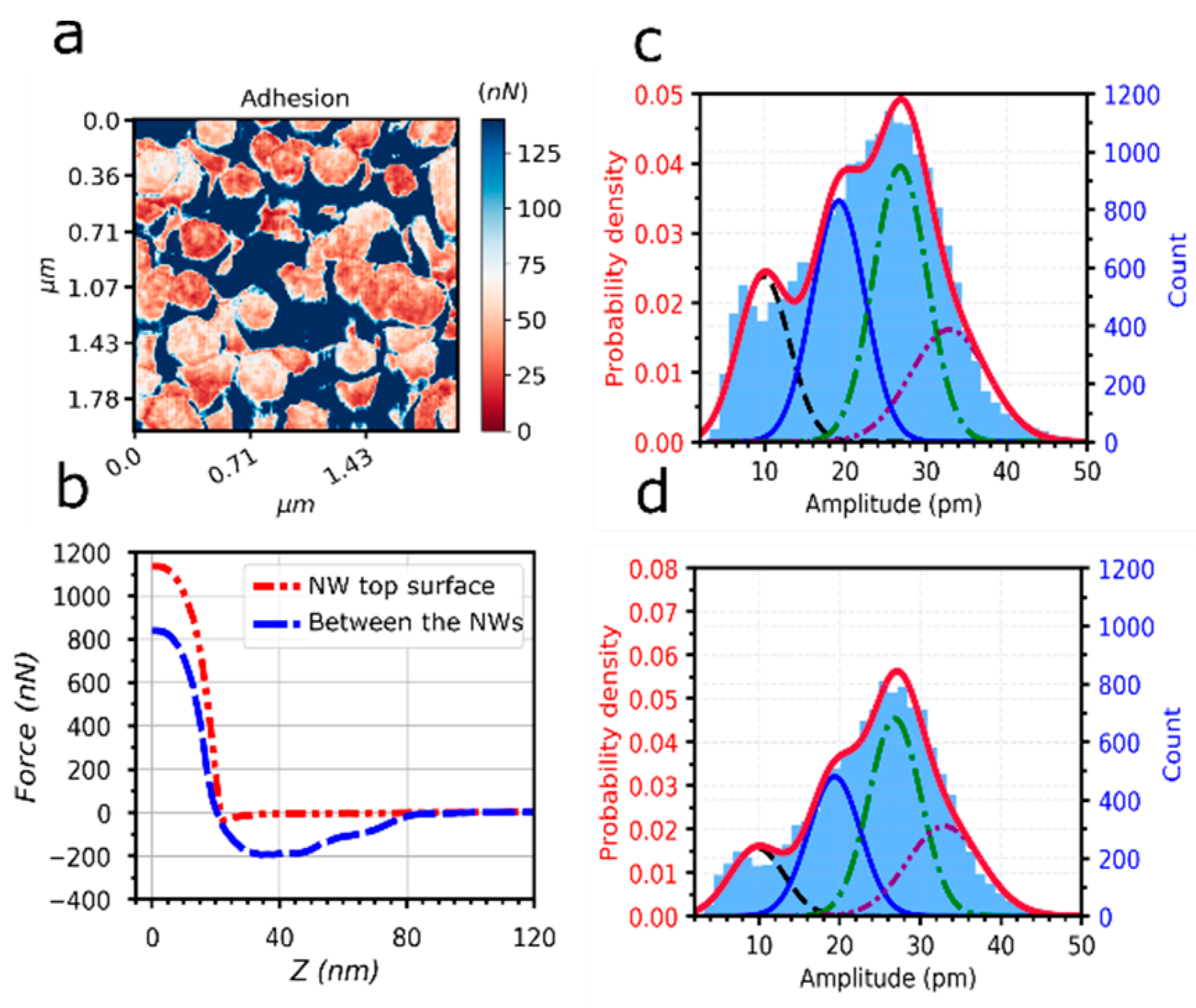
3.2. Piezoelectric Measurements

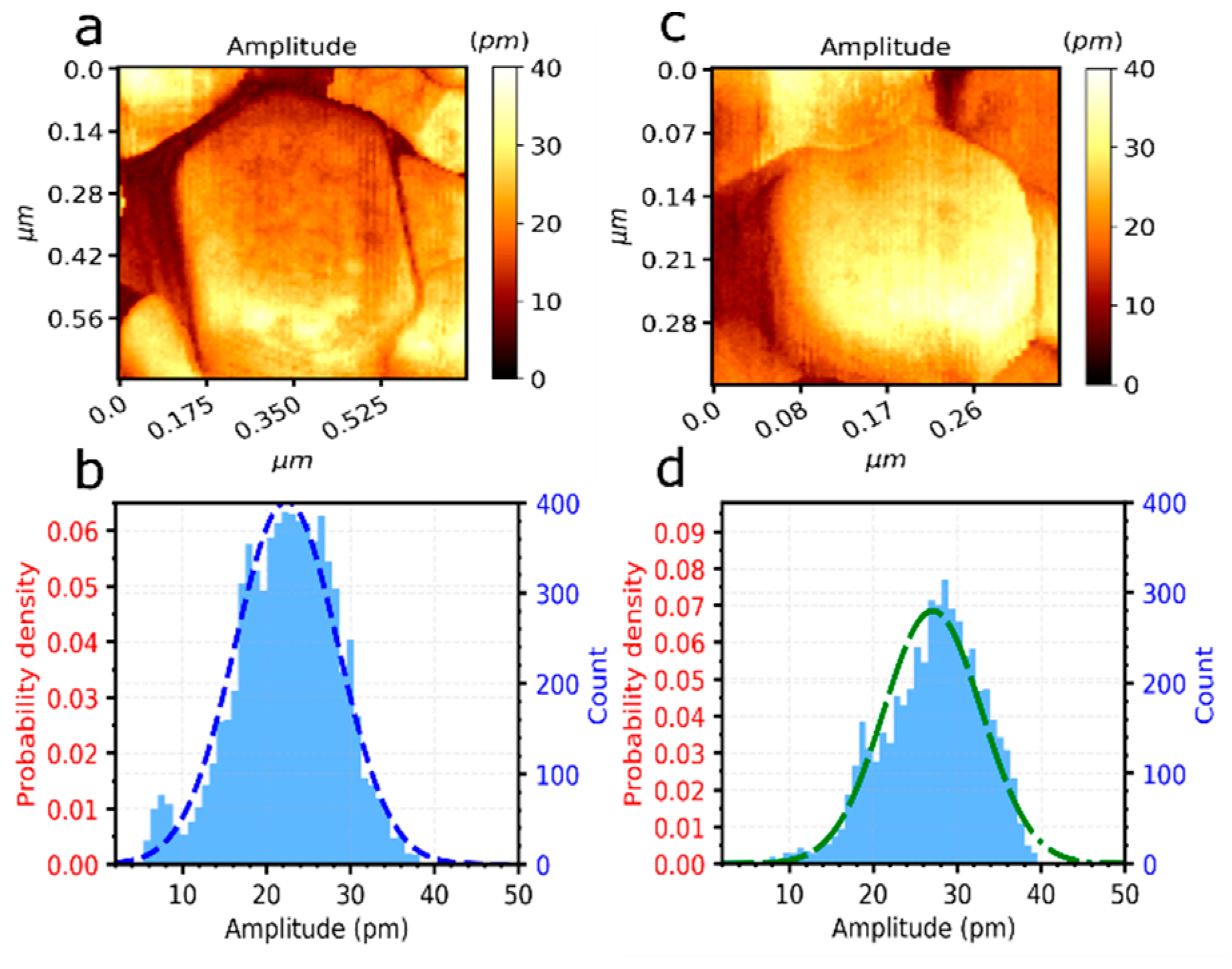
3.2.1. Extracting the Piezoelectric Properties of the NWs’ Top Surface

Figure 5 shows the piezoelectric measurements taken on NWs grown on PET-ITO (top panels) and PET-AZO (bottom panels) for a given annealing time (1 h). Panels (a) and (d) display the topography of the 2 × 2 µm areas investigated by PFM, panels (b) and (e) show the piezoresponse amplitude and panels (c) and (f) show its phase. The piezoelectric amplitude and phase maps evidence spatial inhomogeneity and single polarity. As for the samples treated for different annealing times, the results were similar (see Figures S3 and S4). Thus, this kind of measurement reflects the piezoelectric response of the whole sample not only on the top surface of the NWs but also on their wall sides when the tip is between two NWs.

A closer look at the adhesion force distribution (see Figure 6a) allows one to distinguish between the NW top surface and wall sides and, therefore, to extract the piezoelectric properties of the NW top surface only. Figure 6b shows a force–distance curve during tip withdrawal from the NW top surface and from the spaces among NWs. The adhesion force is the minimum of this curve and corresponds to the force required to disengage the tip. Figure 6a shows that a smaller force detaches the tip from the top surface of the NWs rather than from the side. This effect is associated with a more significant electrostatic interaction between the tip and the NW walls because the contact surface is larger in this configuration.

Figure 6c shows a histogram of the piezoresponse amplitude values measured in a 140 × 140 pixel 2D piezoelectric map on the right axis. This histogram is fitted with a mixture of four Gaussian curves to establish a frame of reference to compare with other samples. This fit corresponds to the probability density (left axis). By filtering these data with only the pixels corresponding to less than 80 nN adhesion, we obtained the histogram displayed in Figure 6d corresponding to the NW top surface only. This filtering process removes the pixels where the tip is in contact with the side walls of the NWs. This avoids a misinterpretation of the piezoelectric properties of the ZnO NWs, considering only purely vertical deformation. As a result of this filtering, the probability density of the smallest piezoresponse amplitude is reduced to half its initial value (see the peak of the black Gaussian curves in Figure 6c,d). Below, we discuss the origin of the four Gaussian curves used to fit the piezoresponse histogram.

3.2.2. Effect of NW Radius

Several PFM measurements with a higher resolution on a single ZnO NW were carried out to obtain a clear statistical interpretation of the amplitude value at a smaller scale. The piezoresponse amplitude maps of a wide NW (with a radius of around 200 nm) and a thin NW (with a radius of around 100 nm) are shown in Figure 7a,b, respectively. The amplitude signal is larger at the bottom edge of the wide NW, which is further discussed in Section 3.3. The piezoresponse amplitude histograms (Figure 7c,d) show that the amplitude peaked around 20 pm for the wide NW and at 25 pm for the thin NW, revealing a dependence of the piezoresponse amplitude on the NW radius.

For all the samples (grown on PET-ITO and PET-AZO substrates with different annealing times), the piezoresponse amplitude histograms (shown in Figures S5 and S6) can be fitted with four Gaussian curves. The resulting piezoresponse amplitudes of these four peaks are independent of the sample (see Figure S7). In particular, the green and blue peaks are located around 25 pm and 20 pm, respectively, as shown in Figure 7. We therefore attribute the green Gaussian curve peaking around 25 pm to thin NWs and the blue Gaussian curve peaking around 20 pm to wide NWs.

To the best of our knowledge, the present work is the first experimental report of the effect of NW size on the piezoresponse amplitude. Hence, this confirms the previous theoretical work that predicted enhancement of the piezoresponse with a reduction in the ZnO NW radius [18,19]. This effect could be related to an enhancement of the depletion region due to surface state defects or trap density due to the high surface–volume ratio of this type of structure [30].

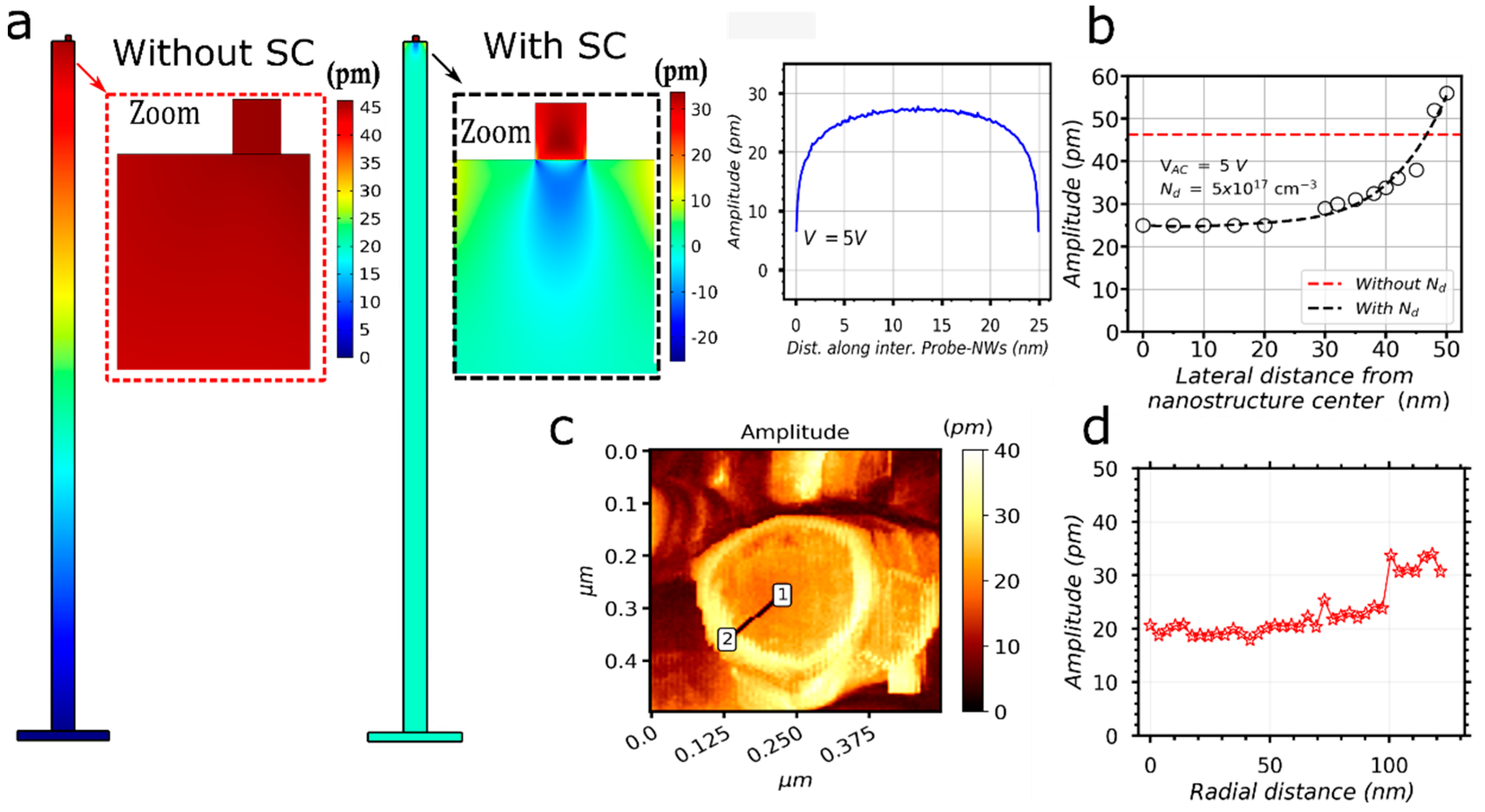
3.2.3. Border Effects

We interpret the peak with larger amplitudes (purple Gaussian curve) as a border effect related to the semiconducting character of the NWs. This effect appears when the AFM tip is at the edge of the NW and is accounted for by a theoretical model (see Section 3.3). As for the smaller peak (black Gaussian curve), we think it originated from an enhanced screening by free carriers, either due to locally smaller surface trap density or to free carrier tunnelling among adjacent NWs [31].

3.2.4. Comparison with Other Studies

The piezoresponse amplitudes corresponding to the wide and thin NWs (Figure 7b,d) are 20 pm and 25 pm, respectively, which is true for both types of substrates. The effective piezoelectric coefficient ($d_{33}^{eff}$) values of 4 pm/V and 5 pm/V were obtained by dividing the piezoelectric amplitude of the top surface of the ZnO NW by the applied AC voltage. These $d_{33}^{eff}$ values are in the same range of values reported using the same technique [32,33,34,35] or other techniques, such as nanoindentation [36] and piezometry [37]. The differences in the absolute values from the different references could be explained by the different conditions of the experiments, such as AFM tip stiffness and working frequency, as well as growth conditions of the samples and electrodes, leading to different semiconducting properties, such as doping and surface states. Finally, a dependence of $d_{33}^{eff}$ on the type of electrode has already been reported for ZnO [37,38]. In this work, we measured a similar or slightly larger piezoresponse amplitude in samples grown on AZO. However, they exhibited slightly wider NWs than those grown on ITO (see Figure S7). Given the effect of NW diameter demonstrated above, one would expect a lower piezoresponse. The observed experimental behavior can therefore be attributed to a slight improvement in the piezoelectric performances with AZO electrodes compared to ITO, exceeding the size effect in this range of diameters. The tilt could also have an effect in the piezoelectric performance of single NWs, although evaluated in another configuration exploiting the direct piezoelectric effect. Theoretical simulations predict that NWs tilted <10° would have lower performances (<14%) compared to perfectly vertical NWs [39]. This effect could also be present when exploiting the reverse piezoelectric effect (PFM) and could explain the differences in the performance of NWs grown on PET-ITO and PET-AZO. However, the effect of the substrate electrode and tilt need to be investigated further in a future study because fine control of the NW’s diameter, tilt and its homogeneity is required to disentangle the effect of NW diameter and of the substrate.

A homogeneous polarity is important when integrated in composite layers because a mixture of Zn and O phases could reduce the global piezoelectric response. The combination of both phases has been measured in some ZnO thin films [40]. The positive value of the piezoelectric phase (see Figure 5c,f) corresponds to the in-phase response and therefore to a Zn-polarity on the top surface of ZnO NWs [40], as reported in PFM measurements from in the literature (

Table 1. Comparison of $d_{33}^{exp}$ obtained from different ZnO structures and experimental methods.

ZnO Structure	Diameter (nm), Length (µm), Thickness (nm)	Substrate	Tip Stiffness (N/m)/Frequency (Hz)	$\left|{\mathit{d}}_{33}^{\mathit{e}\mathit{x}\mathit{p}}\right|(\mathbf{pm}/\mathbf{V})$	Polarity $\left(\mathbf{Sign}\mathbf{of}{\mathit{d}}_{33}^{\mathit{e}\mathit{x}\mathit{p}}\right)$	Method
NW [32]	150, 1.5, NC	Si/Au	8.8/40k	11.8	+	PFM
NW [36]	150, 2.3, NC	paper/PEDOT:PSS	NC/NC	9.8	NC	Nanoindentation
NW [33]	300, 2, NC	GaN	3/33k	7.5	+	PFM
NW [34]	150, 600, NC	Ag	40/15k	4.41	+	PFM
NW [35]	30, NC, NC	Glass/ITO, PET/ITO	5/15k	2.13 and 5.2	+	PFM
NW/PMMA composite [37]	80–160, 1.3–1.7	Pt, Au, Ti	NC/30–110	3, 3, 7–26	+	Piezometer
Bulk [41]	NC, NC, NC	NC	40/30–300k	9.93	+	PFM
Thin film [42]	NC, NC, 70	Glass/ITO	NC/NC	3–20	+	Current/charge
Thin film [40]	NC, NC, 1100	Si	45/7k	1.8–2.6	+/−	PFM
Single crystal [38]	5 × 5 × 5 mm3	ITO, Ag	NC/NC	0, 11	+	Impedance and direct piezoelectric measurements
NW (this work)	100–200, 3, NC	PET-ITO, PET-AZO	43–50/204–497k	4–5	+	PFM

NC: not communicated.

).

Finally, in contrast to all reported PFM experiments in Table 1, the PFM measurements presented in the present work were performed using DataCube mode. This mode prevents lateral bending of the NWs and does not require additional dielectric deposition and etching to make the sample compatible with the conventional contact PFM mode. Given the risks of contamination during this process and the experimental bias due to the presence of the deposited dielectric, DataCube mode turns out to be a major asset.

3.3. Simulation Results

To further investigate the piezoelectric amplitude response on ZnO’s top surface, we carried out finite element method (FEM) simulations to compute the electric field-induced displacement at the interface between the tip and a 2D nanostructure, as shown in Figure 8a. The positive value of this displacement means that the electric field goes in the same direction as the c-axis of the piezo structure. The c-axis is thus oriented upwards, corresponding to the Zn polarity observed in our measurements. When the square shaped tip is positioned at the center of the 2D nanostructure, the maximum piezo-induced displacement (in absolute value) at the tip–nanostructure interface reaches 25 pm. We also performed this simulation for the same system, except that we did not consider the semiconducting properties of ZnO (see Figure S8). We obtained a piezoresponse amplitude almost twice as large (around 46 pm). This significant difference demonstrates the strong influence of semiconducting properties (such as free carriers) on the piezoelectric performances of these structures.

We performed several numerical simulations by moving the top electrode step-by-step towards the edge of the nanostructure and computed the minimum amplitude value, along with the interface between the tip and the NW. In a model where the semiconducting properties are not considered, the piezoresponse amplitude is constant, irrespective of the AFM tip position. In contrast, when the semiconducting properties are included in the model, the piezoresponse amplitude increases when the AFM tip approaches the nanostructure edge, up to the system’s value without semiconducting properties (see Figure 8b). This increase in the piezoresponse amplitude at the edge of the nanostructure is experimentally observed in our measurements on NWs (see Figure 7a and Figure 8c,d). This suggests that the border effect and the lower piezoelectric-induced amplitude near the middle of the nanostructure can be explained by the semiconducting nature of the ZnO NWs. Although grain boundaries and surface defects were not included in these simulations, they could also affect the piezoelectric performance of the piezoelectric nanostructures. We expect the creation of a depletion layer from the bottom (due to grain boundaries at the seed layer) [43] and from all other surfaces (due to surface defects). They would reduce the screening effect caused by free charges [30]. The inclusion of these effects in future simulations will facilitate a better understand the correlation between semiconducting and piezoelectric properties at the nanoscale. The measurement of parameters such as doping and surface trap densities is also needed, as these parameters could differ from those reported in the literature, leading to completely different expected piezoelectric performances. More complex models are required to fully assess the role of the semiconducting nature in the piezoresponse amplitude of these nanostructures (i.e., 3D geometry and surface traps).

4. Conclusions

In this work, ZnO NWs were grown on PET-ITO and PET-AZO flexible substrates using the CBD method. Gravure printing was used for the deposition of the ZnO seed layers. Although the NW radii were not homogeneous on the different substrates, we observed a decrease in the average NW radius, probably due to the effect of the non-polar grain growth of the seed layer as the annealing time increased up to 2.5 h. The average radius was 146 nm to 107 nm for PET-AZO and 118 nm to 90 nm for PET-ITO. We measured the NWs’ piezoelectric response via piezoelectric force microscopy. We used the AFM force volume technique to avoid lateral bending of the NWs during PFM measurements. We proposed a new statistical method to extract the piezoelectric response only on the top surface of the NWs. We evidenced a dependence of the piezoelectric response on the radius of the NWs, exhibiting piezoresponse amplitude values from 20 pm (i.e., $d_{33}^{eff}$ of 4 pm/V) to 25 pm (i.e., $d_{33}^{eff}$ of 5 pm/V) for wide (about 200 nm diameter) and thin (about 100 nm diameter) NWs, respectively. Moreover, we observed an inhomogeneous piezoresponse amplitude on the NWs’ top surface, reaching up to 32 pm (i.e., $d_{33}^{eff}$ of 6 pm/V) on the edges due to border effects. These experimental trends were observed on both substrates and for all ZnO seed layer annealing times investigated herein. These trends are in agreement with those revealed by numerical simulations based on the finite element method, evidencing the decisive influence of the semiconducting properties (i.e., doping level) of the ZnO NWs on the piezoresponse. The present study provides a new method to simultaneously investigate the closely related piezoelectric and semiconducting properties at the nanoscale, which is of particular interest for the optimization of the new generation of nanostructured energy harvesters, sensors and self-powered electronic devices.