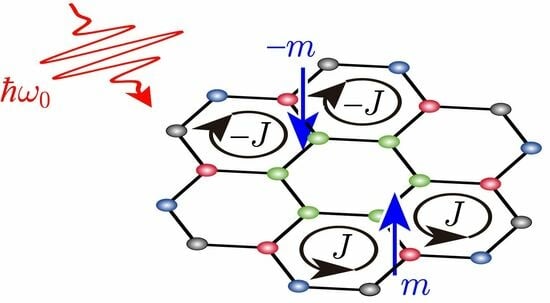
Photoproduction of Loop Currents in Coronene Isomers Without Any Applied Magnetic Field
Abstract
1. Introduction
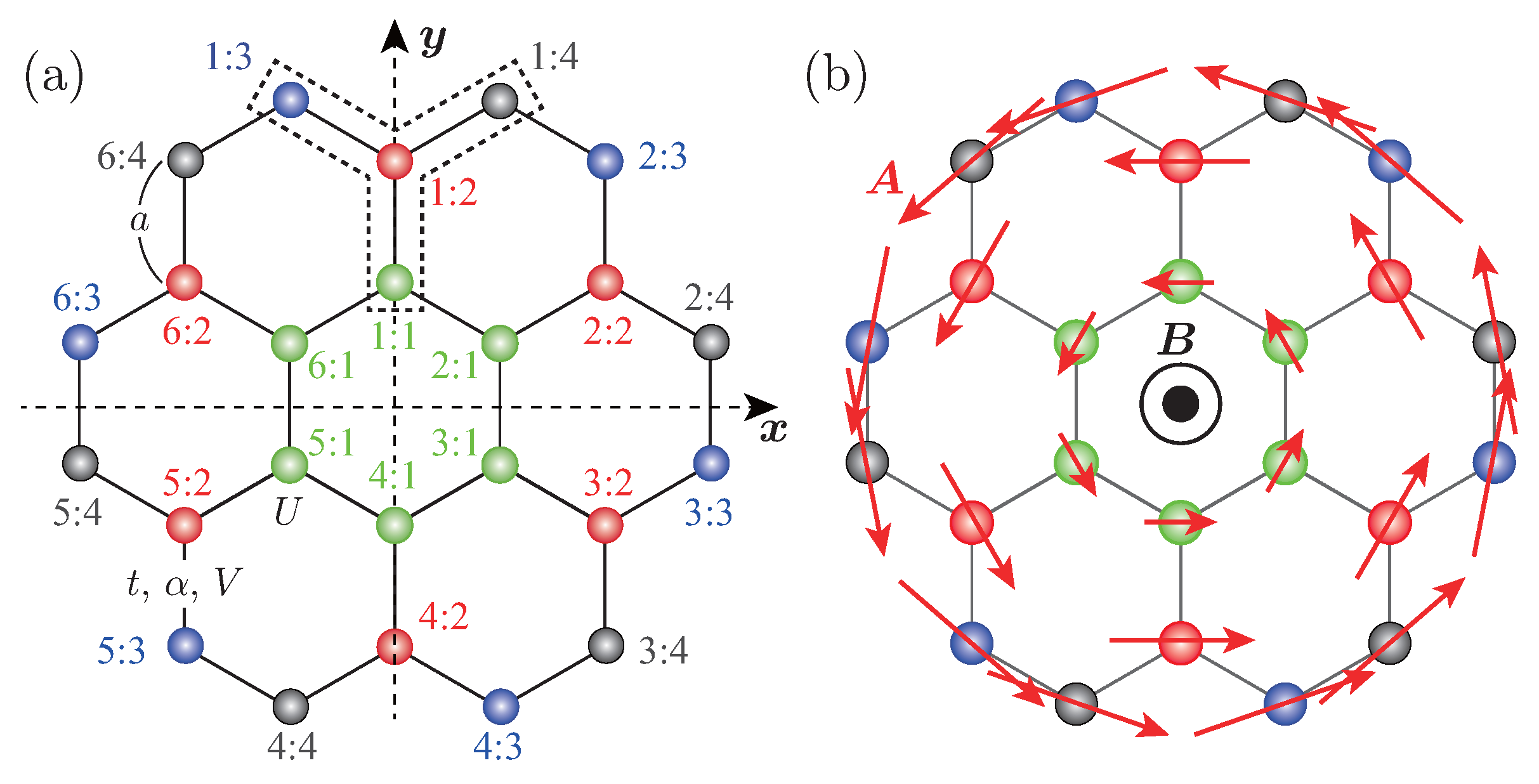
2. Model Hamiltonian
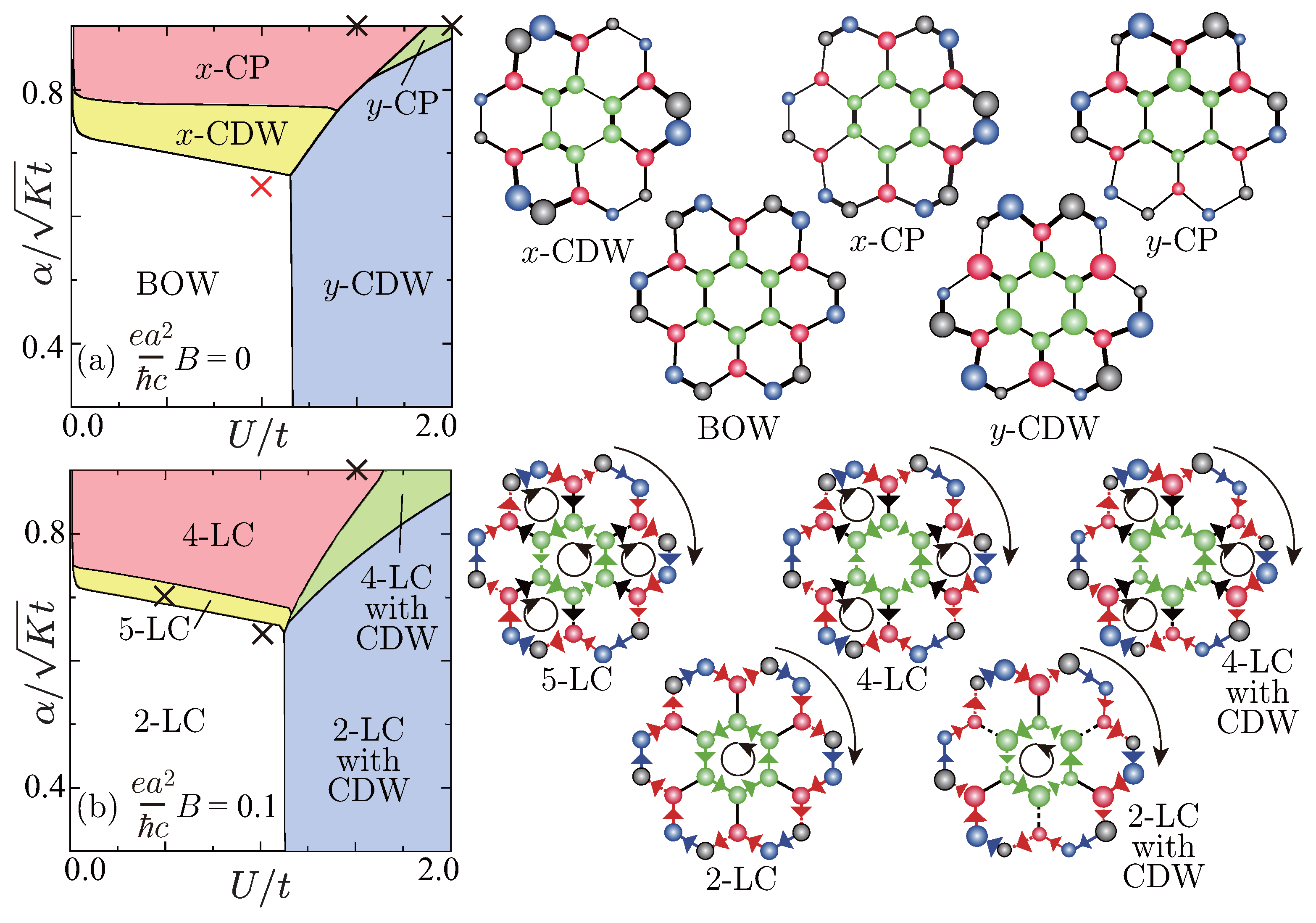
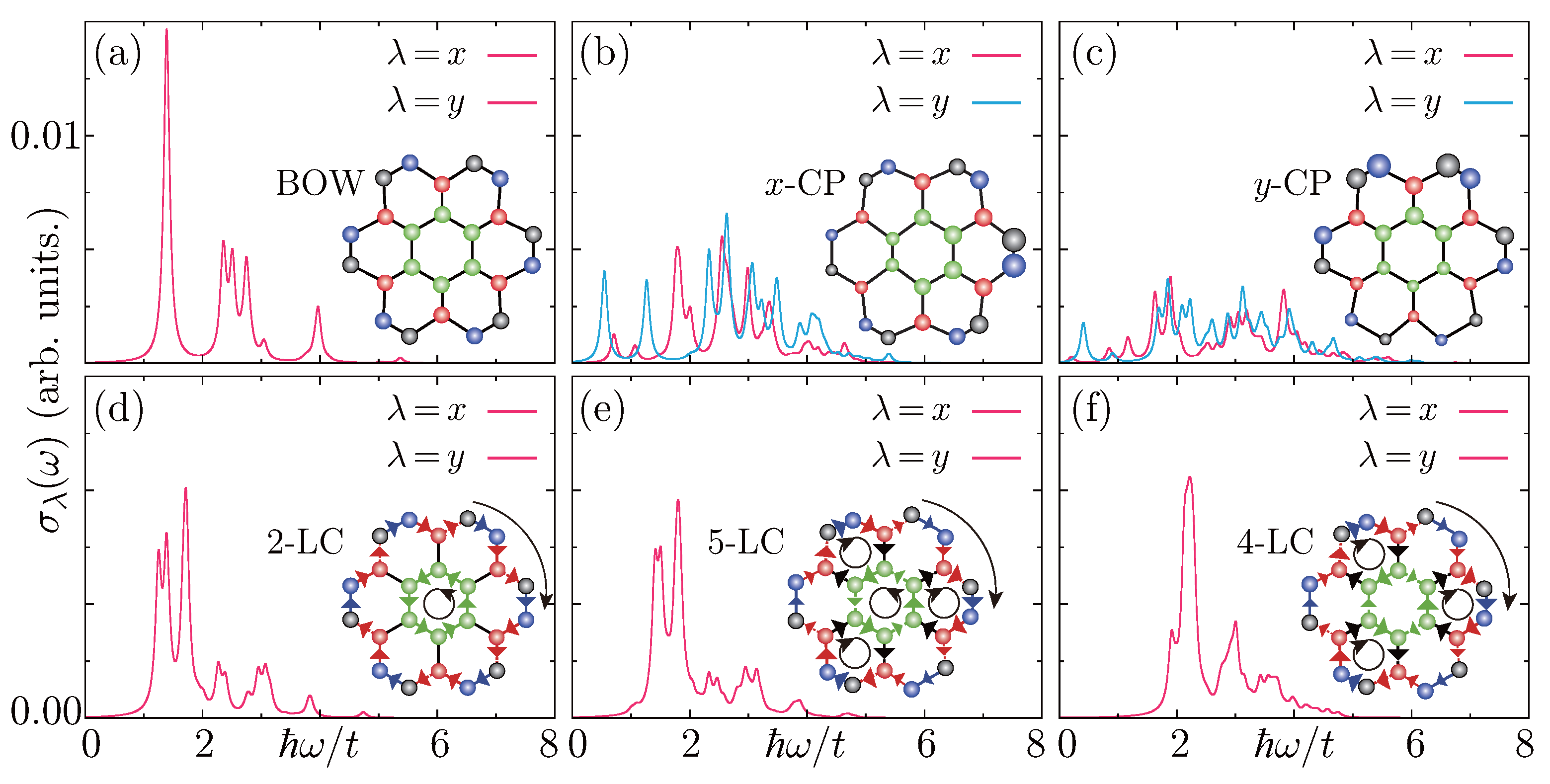
3. Ground-State Phase Varieties and Their Optical Features
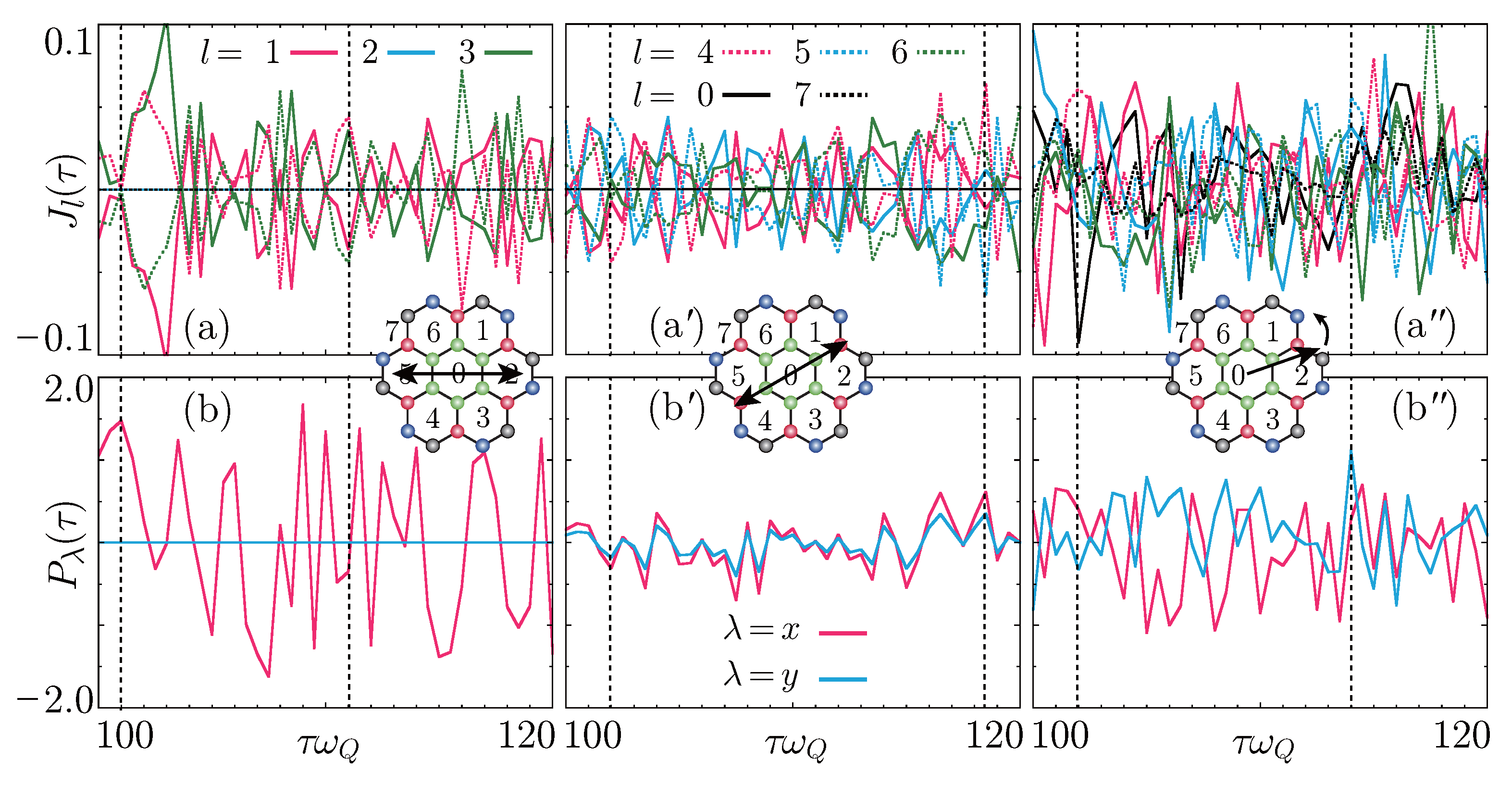
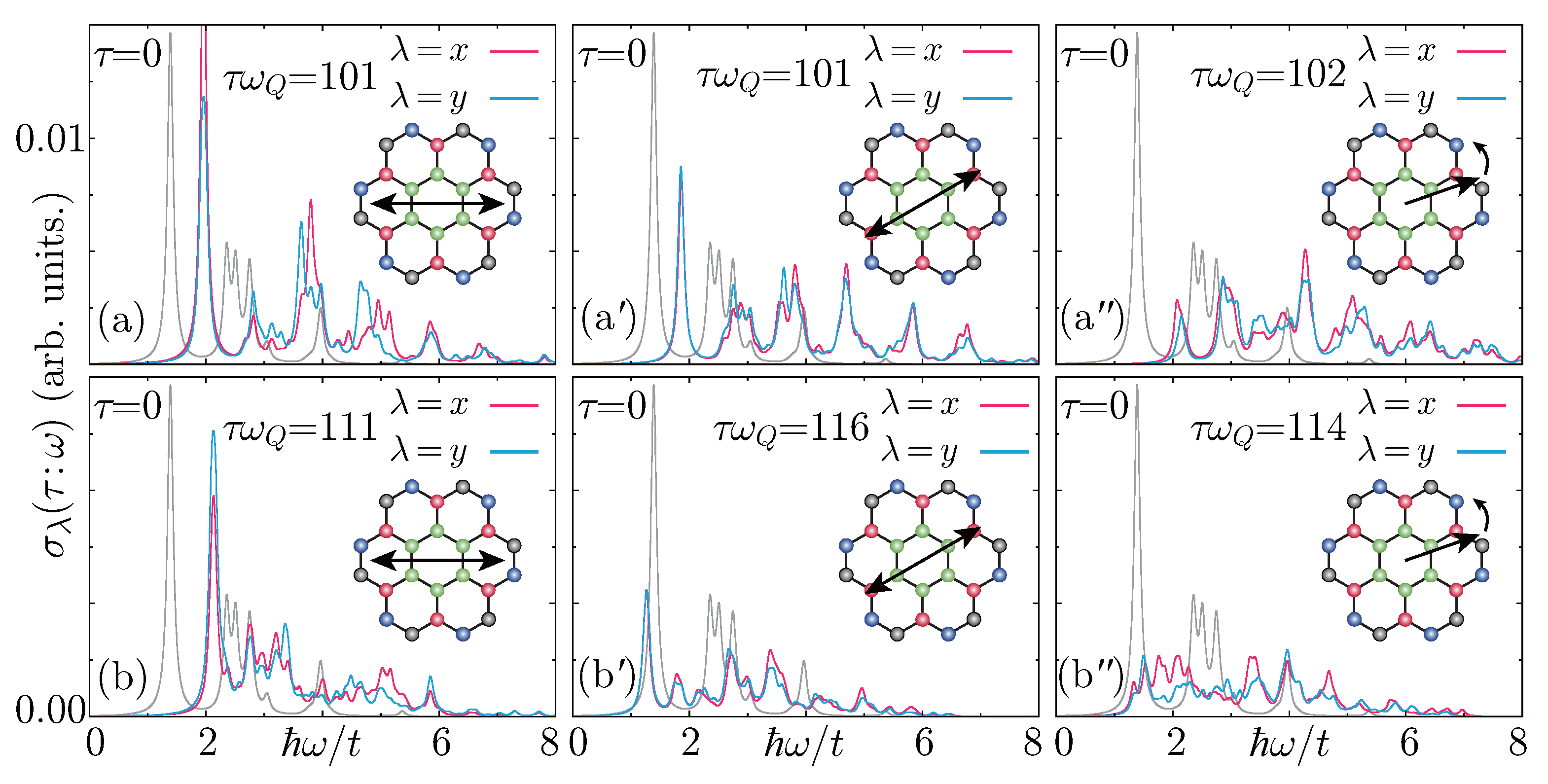
4. Light-Polarization-Dependent Dynamic Loop Currents
5. Summary and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pople, J.A. Molecular orbital theory of aromatic ring currents. Mol. Phys. 1958, 1, 175. [Google Scholar] [CrossRef]
- McWeeny, R. Ring currents and proton magnetic resonance in aromatic molecules. Mol. Phys. 1958, 1, 311. [Google Scholar] [CrossRef]
- Merino, G.; Heine, T.; Seifert, G. The induced Magnetic field in cyclic molecules. Chem. Eur. J. 2004, 10, 4367. [Google Scholar] [CrossRef] [PubMed]
- Gomes, J.A.N.F.; Mallion, R.B. Aromaticity and ring currents. Chem. Rev. 2001, 101, 1349. [Google Scholar] [CrossRef]
- Bühl, M. The relation between endohedral chemical shifts and local aromaticities in fullerenes. Chem. Eur. J. 1998, 4, 734. [Google Scholar] [CrossRef]
- Schulman, J.M.; Disch, R.L. Thermal and magnetic properties of coronene and related molecules. J. Phys. Chem. A 1997, 101, 9176. [Google Scholar] [CrossRef]
- Schleyer, P.V.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J. Nucleus-independent chemical shifts: A simple and efficient aromaticity probe. J. Am. Chem. Soc. 1996, 118, 6317. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W.; Jenneskens, L.W. Counter-rotating ring currents in coronene and corannulene. Angew. Chem. Int. Ed. 2001, 40, 362. [Google Scholar] [CrossRef]
- Balaban, A.T.; Bean, D.E.; Fowler, P.W. Patterns of ring current in coronene isomers. Acta. Chim. Solv. 2010, 57, 507. [Google Scholar]
- Randić, M.; Novič, M.; Vračko, M.; Vukičević, D.; Placšć, D. π-electron currents in polycyclic conjugated hydrocarbons: Coronene and its isomers having five and seven member rings. Int. J. Quant. Chem. 2012, 112, 972. [Google Scholar] [CrossRef]
- Kato, T.; Yoshizawa, K.; Yamabe, T. Jahn-Teller effects in the coronene anions and cations. J. Chem. Phys. 1999, 110, 249. [Google Scholar] [CrossRef]
- Kato, T.; Yamabe, T. Electron-intermolecular-phonon coupling and possible superconductivity in negatively charged coronene and corannulene. J. Chem. Phys. 2002, 117, 2324. [Google Scholar] [CrossRef]
- Devos, A.; Lannoo, M. Electron-Phonon coupling for aromatic molecular crystals: Possible consequences for their superconductivity. Phys. Rev. B 1998, 58, 8236. [Google Scholar] [CrossRef]
- Kosugi, T.; Miyake, T.; Ishibashi, S.; Arita, R.; Aoki, H. Abinitio electronic structure of solid coronene: Differences from and commonalities to picene. Phys. Rev. B 2011, 84, 020507(R). [Google Scholar] [CrossRef]
- Roth, F.; Bauer, J.; Mahns, B.; Büchner, B.; Kunpfer, M. Electronic structure of undoped and potassium-doped coronene investigated by electron energy-loss spectroscopy. Phys. Rev. B 2012, 85, 014513. [Google Scholar] [CrossRef]
- Kubozono, Y.; Mitamura, H.; Lee, X.; He, X.; Yamanari, Y.; Takahashi, Y.; Suzuki, Y.; Kaji, Y.; Eguchi, R.; Akaike, K.; et al. Metal-intercalated aromatic hydrocarbons: A new class of carbon-based superconductors. Phys. Chem. Chem. Phys. 2011, 13, 16476. [Google Scholar] [CrossRef]
- Malček, M.; Natalia, M.; Cordeiro, D.S. A DFT and QTAIM study of the adsorption of organic molecules over the copper-doped coronene and circumcoronene. Phys. E 2018, 95, 59. [Google Scholar] [CrossRef]
- Joyce, T.; Jaron, A. Ultrafast switching of persistent electron and hole ring currents in a molecule. Phys. Rev. A 2023, 108, 053114. [Google Scholar] [CrossRef]
- Kanno, M.; Kono, H.; Fujimura, Y. Laser-control of ultrafast π-electron ring currents in aromatic molecules: Roles of molecular symmetry and light polarization. Appl. Sci. 2018, 8, 2347. [Google Scholar] [CrossRef]
- Nobusada, K.; Yabana, K. Photoinduced electric currents in ring-shaped molecules by circularly polarized laser pulses. Phys. Rev. A 2007, 75, 032518. [Google Scholar] [CrossRef]
- Zhang, L.; Yamamoto, S. Photoinduced directional and bidirectional phase transitions in bistable linear polycyclic aromatic compounds. J. Phys. Soc. Jpn. 2014, 83, 064708. [Google Scholar] [CrossRef]
- Yamamoto, S. Photoinduced structural phase transitions in polyacene. J. Phys. Soc. Jpn. 2011, 80, 084713. [Google Scholar] [CrossRef]
- Hirano, Y.; Ono, Y. Photogeneration dynamics of a soliton pair in polyacetylene. J. Phys. Soc. Jpn. 1998, 67, 3835. [Google Scholar] [CrossRef]
- Hirano, Y.; Ono, Y. Photogeneration dynamics of nonlinear excitations in polyacetylene. J. Phys. Soc. Jpn. 2000, 69, 2131. [Google Scholar] [CrossRef]
- Subbaswamy, K.R.; Grabowski, M. Bond alternation, on-site Coulomb correlations, and solitons in polyacetylene. Phys. Rev. B 1981, 24, 2168. [Google Scholar] [CrossRef]
- Otsubo, K.; Wakabayashi, Y.; Ohara, J.; Yamamoto, S.; Matsuzaki, H.; Okamoto, H.; Nitta, K.; Uruga, T.; Kitagawa, H. Bottom-up realization of a porous metal-organic nanotubular assembly. Nat. Mater. 2011, 10, 291. [Google Scholar] [CrossRef]
- Funase, K.; Yamamoto, S. Competing ground states of metal-halide ladders. J. Phys. Soc. Jpn. 2006, 75, 044717. [Google Scholar] [CrossRef]
- Steiner, E.; Fowler, P.W.; Jenneskens, L.W.; Acocella, A. Visualisation of counter-rotating ring currents in kekulene. Chem. Commun. 2001, 659–660. [Google Scholar] [CrossRef]
- Yamamoto, S. Optical characterization of ground states of polyacene. Phys. Rev. B 2008, 78, 235205. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-Mechanical Theory of Irreversible Processes. I. General Theory and Simple Applications to Magnetic and Conduction Problems. J. Phys. Soc. Jpn. 1957, 12, 570. [Google Scholar] [CrossRef]
- Gammel, J.T.; Saxena, A.; Batistić, I.; Bishop, A.R. Two-band model for halogen-bridged mixed-valence transition-metal complexes. I. Ground state and excitation spectrum. Phys. Rev. B 1992, 45, 6408. [Google Scholar] [CrossRef] [PubMed]
- Ohara, J.; Yamamoto, S. Photocontrollable mixed-valent states in platinum-halide ladder compounds. Appl. Sci. 2018, 8, 2126. [Google Scholar] [CrossRef]
- Ohara, J.; Yamamoto, S. Photoinduced bidirectional magnetism against monodirectional electronics in square-antiprismatic octacyanometalates. J. Phys. Soc. Jpn. 2020, 89, 093706. [Google Scholar] [CrossRef]
- Yan, Y.H.; An, Z.; Wu, C.Q. Dynamics of polaron in a polymer chain with impurities. Eur. Phys. J. B 2004, 42, 157. [Google Scholar] [CrossRef]
- Nakanishi, S.; Tsukada, M. Quantum loop current in a C60 molecular bridge. Phys. Rev. Lett. 2001, 87, 126801. [Google Scholar] [CrossRef] [PubMed]
- Tsuji, N.; Takajo, S.; Aoki, H. Large orbital magnetic moments in carbon nanotubes generated by resonant transport. Phys. Rev. B 2007, 75, 153406. [Google Scholar] [CrossRef]
- Wang, B.; Chu, R.; Wang, J.; Guo, H. First-principal calculation of chiral current and quantum self-inductance of carbon nanotubes. Phys. Rev. B 2009, 80, 235430. [Google Scholar] [CrossRef]
- Tsukada, M.; Tagami, K.; Hirose, K.; Kobayashi, N. Theory of quantum conductance of aromatic and molecular bridges. J. Phys. Soc. Jpn. 2005, 74, 1079. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohara, J.; Yamamoto, S. Photoproduction of Loop Currents in Coronene Isomers Without Any Applied Magnetic Field. Solids 2024, 5, 640-650. https://doi.org/10.3390/solids5040043
Ohara J, Yamamoto S. Photoproduction of Loop Currents in Coronene Isomers Without Any Applied Magnetic Field. Solids. 2024; 5(4):640-650. https://doi.org/10.3390/solids5040043
Chicago/Turabian StyleOhara, Jun, and Shoji Yamamoto. 2024. "Photoproduction of Loop Currents in Coronene Isomers Without Any Applied Magnetic Field" Solids 5, no. 4: 640-650. https://doi.org/10.3390/solids5040043
APA StyleOhara, J., & Yamamoto, S. (2024). Photoproduction of Loop Currents in Coronene Isomers Without Any Applied Magnetic Field. Solids, 5(4), 640-650. https://doi.org/10.3390/solids5040043