Influence of Unidirectional Cyclic Loading on Bond between Steel Bars Embedded in Lightweight Aggregate Concrete
Abstract
:1. Introduction
- The position of the embedded reinforcing bar relative to the direction of the casting of concrete [8];
- The stress state of concrete around the steel bar [10];
- The amount of transverse reinforcement [11];
- The loading rate [12];
- The type and specific weight of lightweight aggregate [13];
- The characteristics of cyclic loading (amplitude, number of loading cycles, etc.) [14];
1.1. Effect of Lightweight Aggregate on Bond Strength
1.2. Effect of Cyclic Loading on Bond Strength
- D
- Sum of fatigue damage;
- nSi
- Number of load cycles belonging to the i-th stress (load) level;
- NRi
- Number of load cycles belonging to the i-th stress (load) level and resulting in failure;
2. Materials and Methods
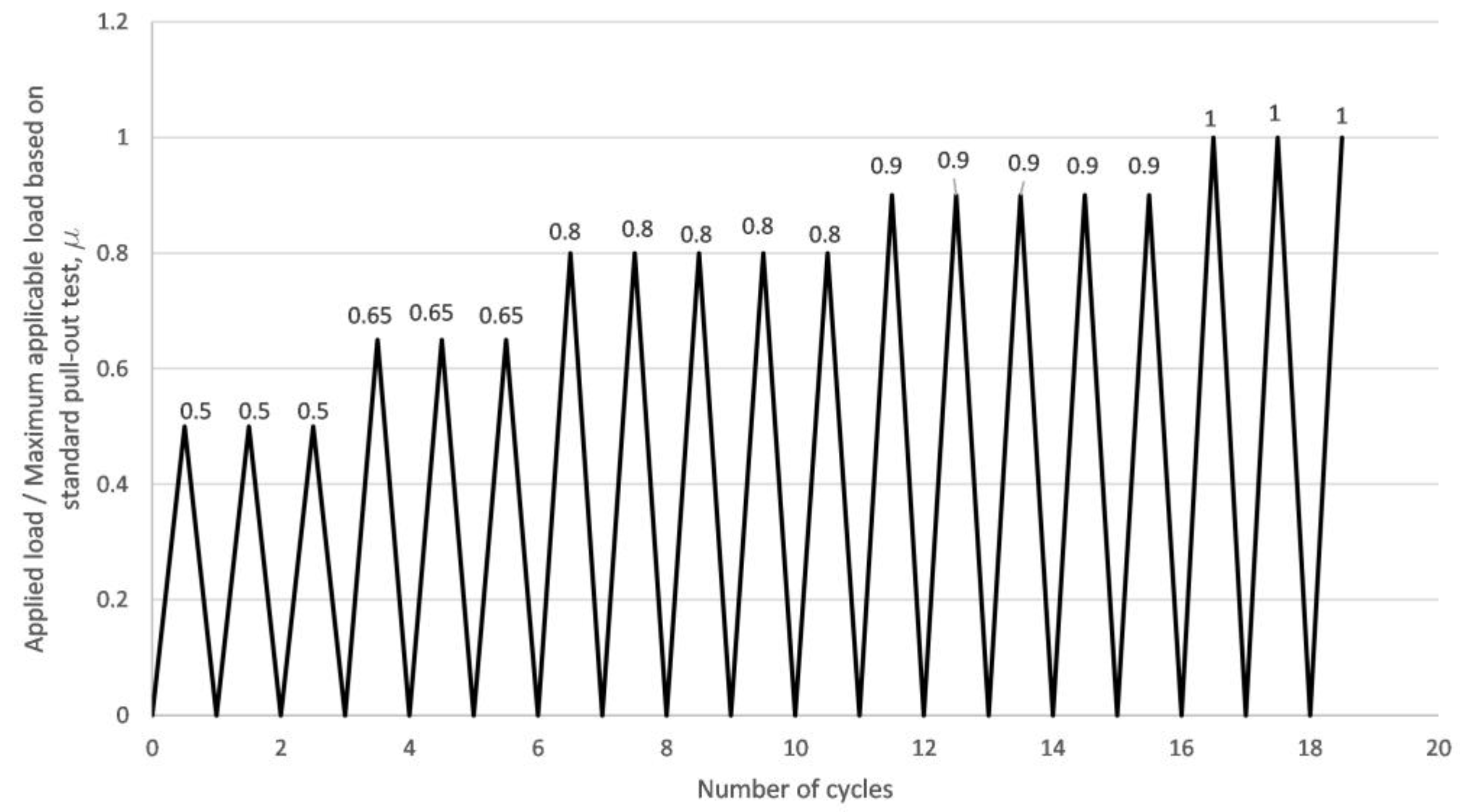
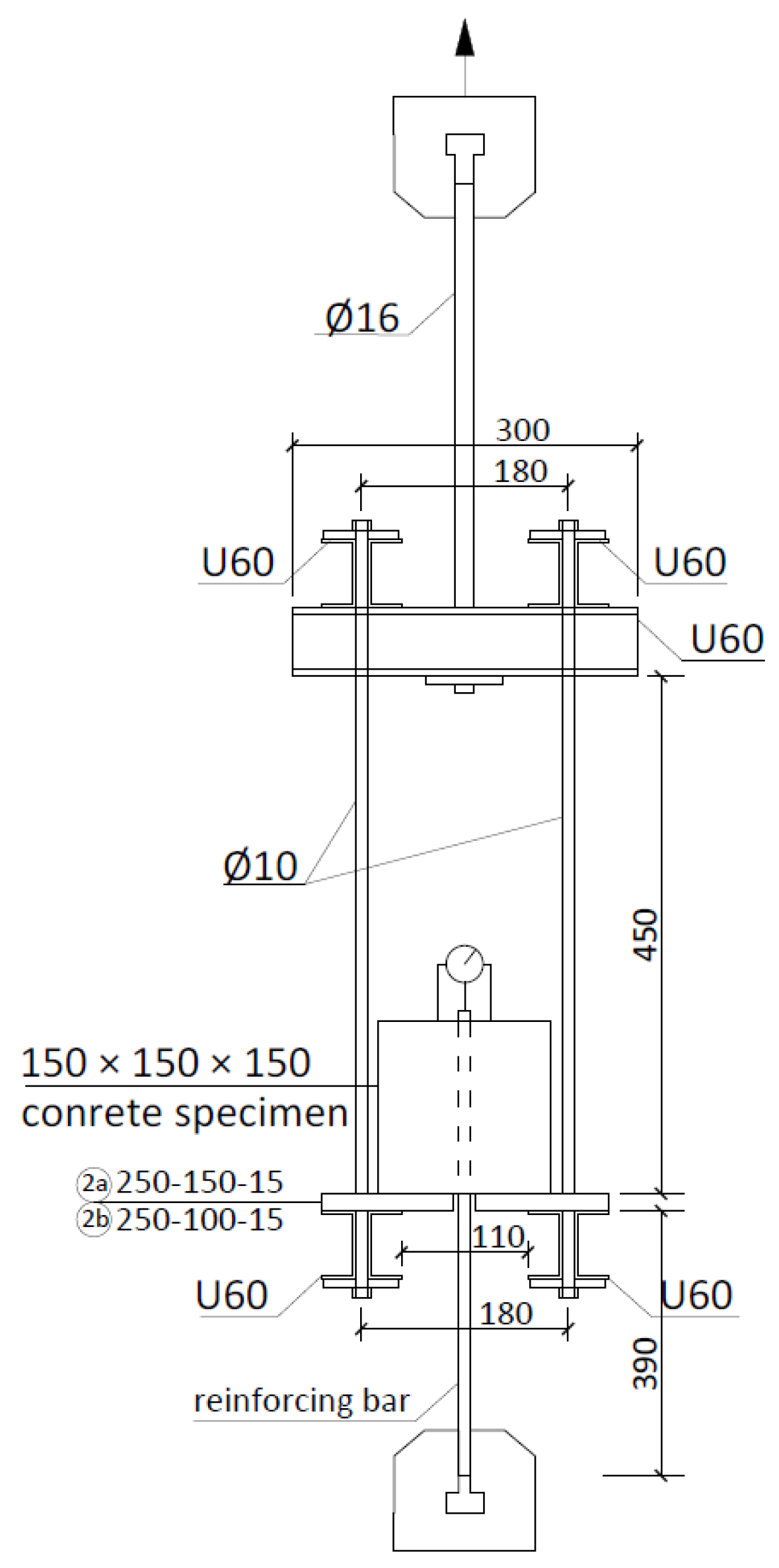
2.1. Pull-Out Test Setup
- The duration of test decreases compared to standard cyclic tests using monotonic cyclic load with μ = 0.5–0.6;
- The increment in slip as well as in dissipated energy can be well measured and evaluated at different load levels.
2.2. Test Program
2.3. Concrete Mixes
3. Results and Discussion
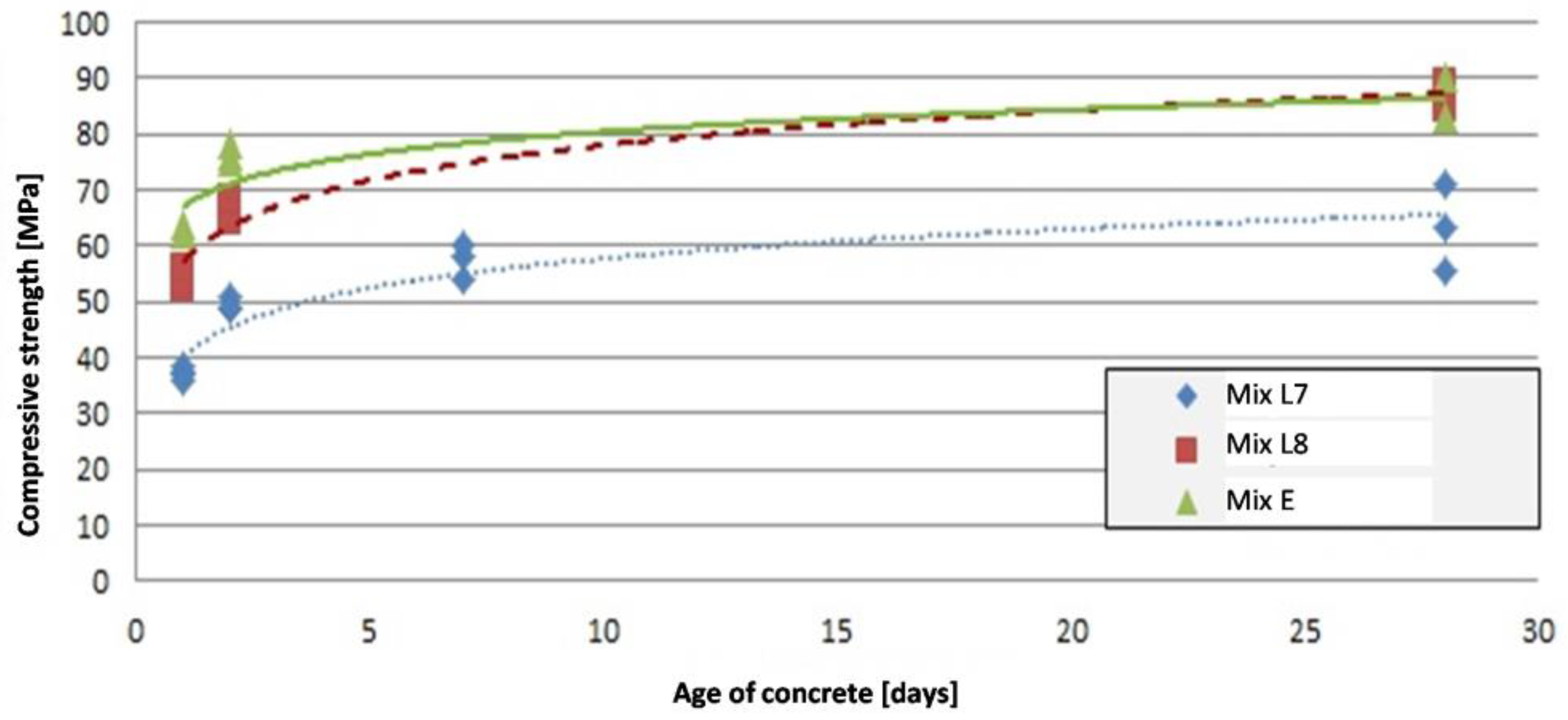
3.1. Compressive and Splitting-Tensile Strength
3.2. Standard Pull-Out Test
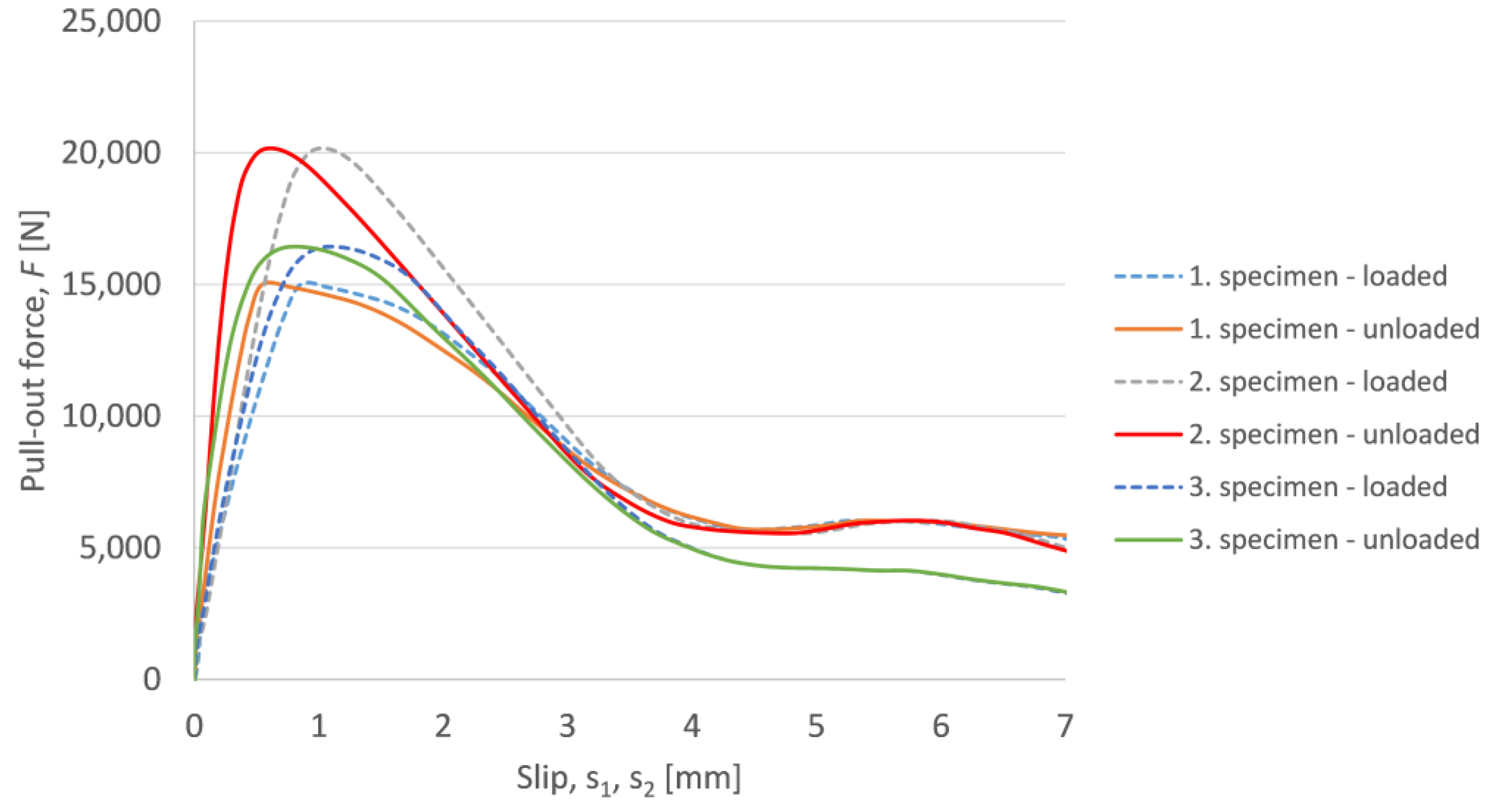
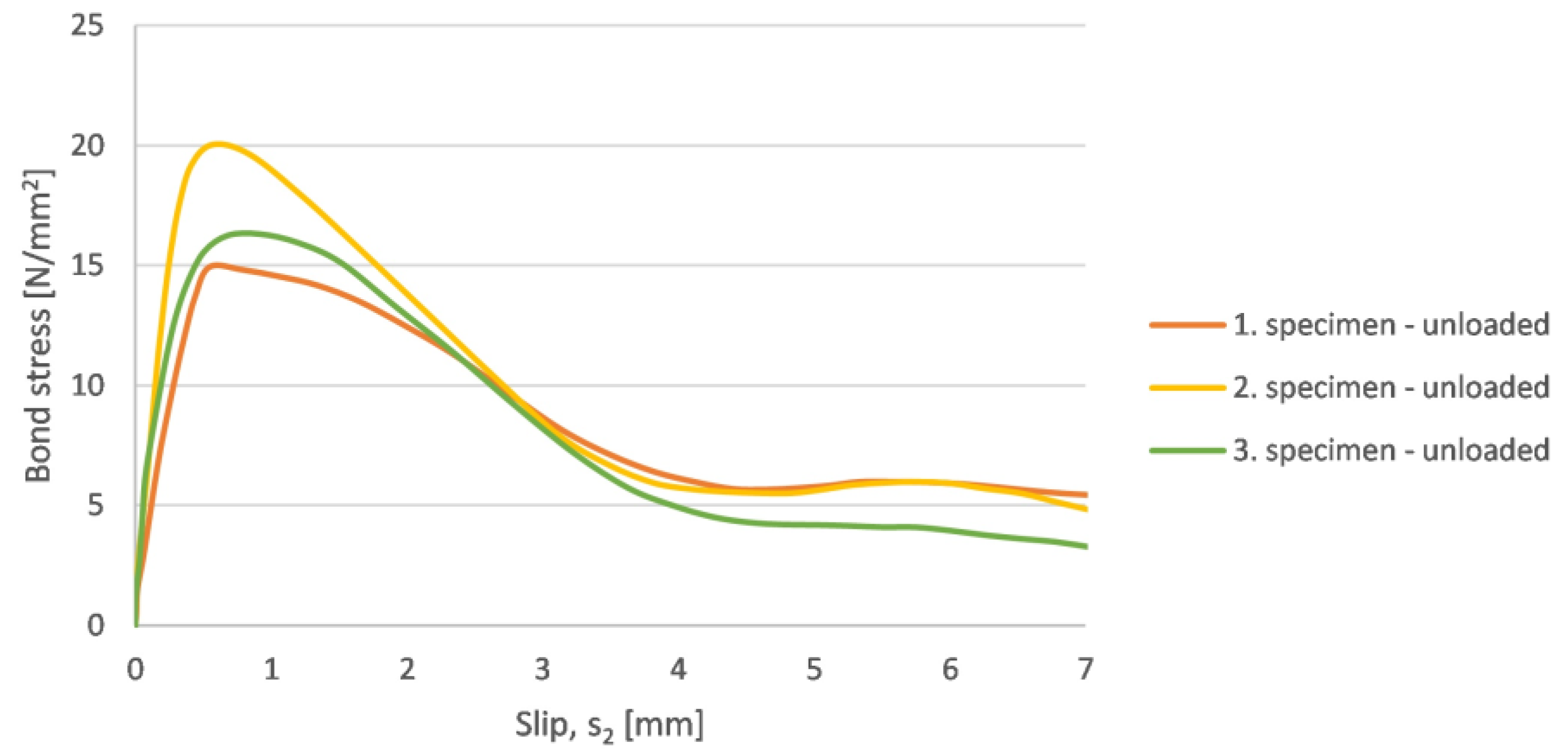
3.2.1. Standard Pull-Out Test of Lightweight Concrete
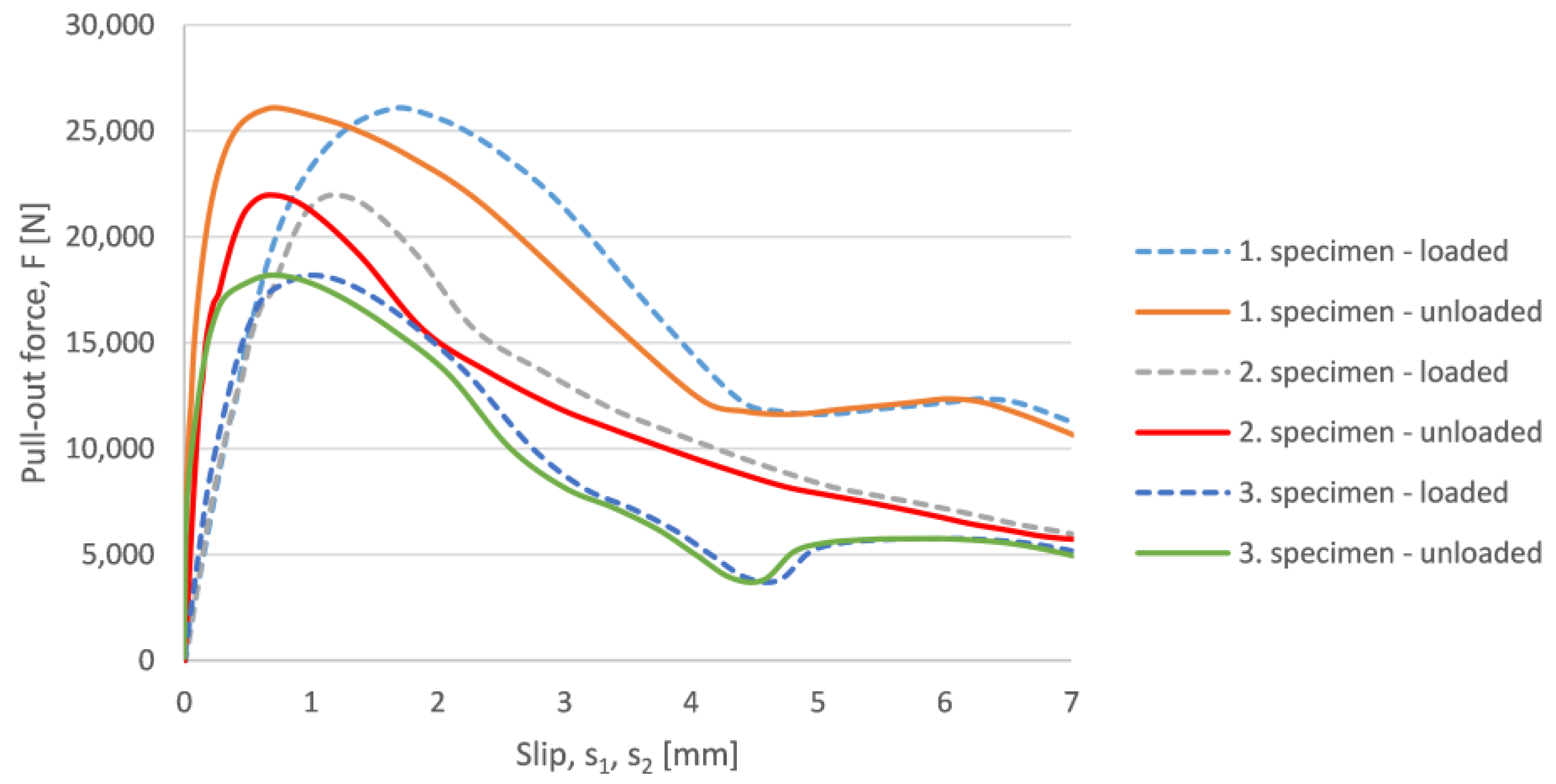
3.2.2. Standard Pull-Out Test of Normal Concrete
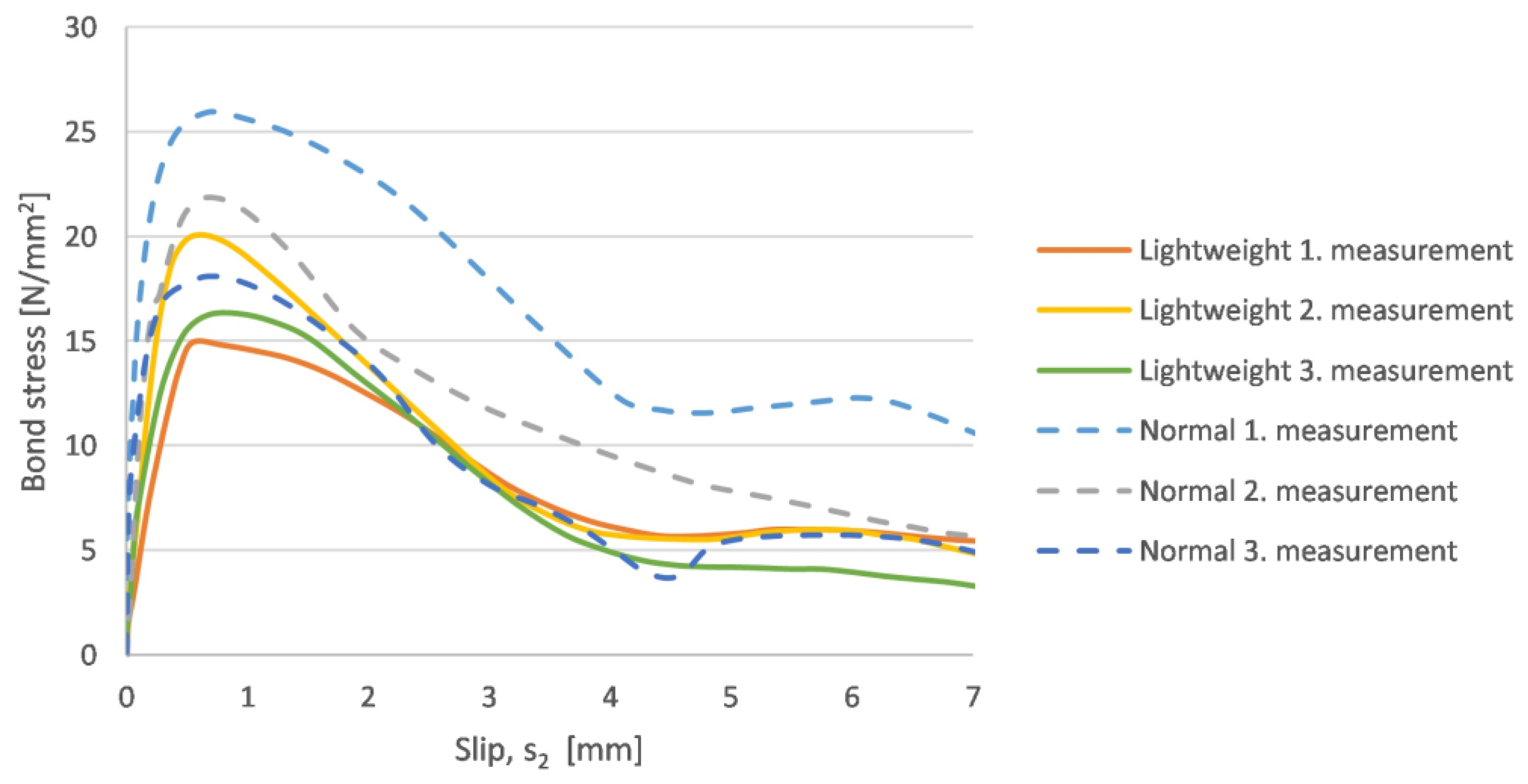
3.3. Comparison of the Normal and Lightweight Concrete Standard Pull-Out Tests
- The phenomenon is similar in both cases;
- The bond strength of NWAC is higher (in average about 5 N/mm2);
- The maximum slip of the unloaded surface (s2) is in the range of 0.5–1.0 mm for both concretes;
- The initial slope of the figure is higher in case of the normal concrete;
- The residual stresses are in the range of 5–10 N/mm2 for both concretes.
- The compressive strength is 20% lower in case of LWAC;
- The tensile strength of LWAC is 71% of the tensile strength of NWAC;
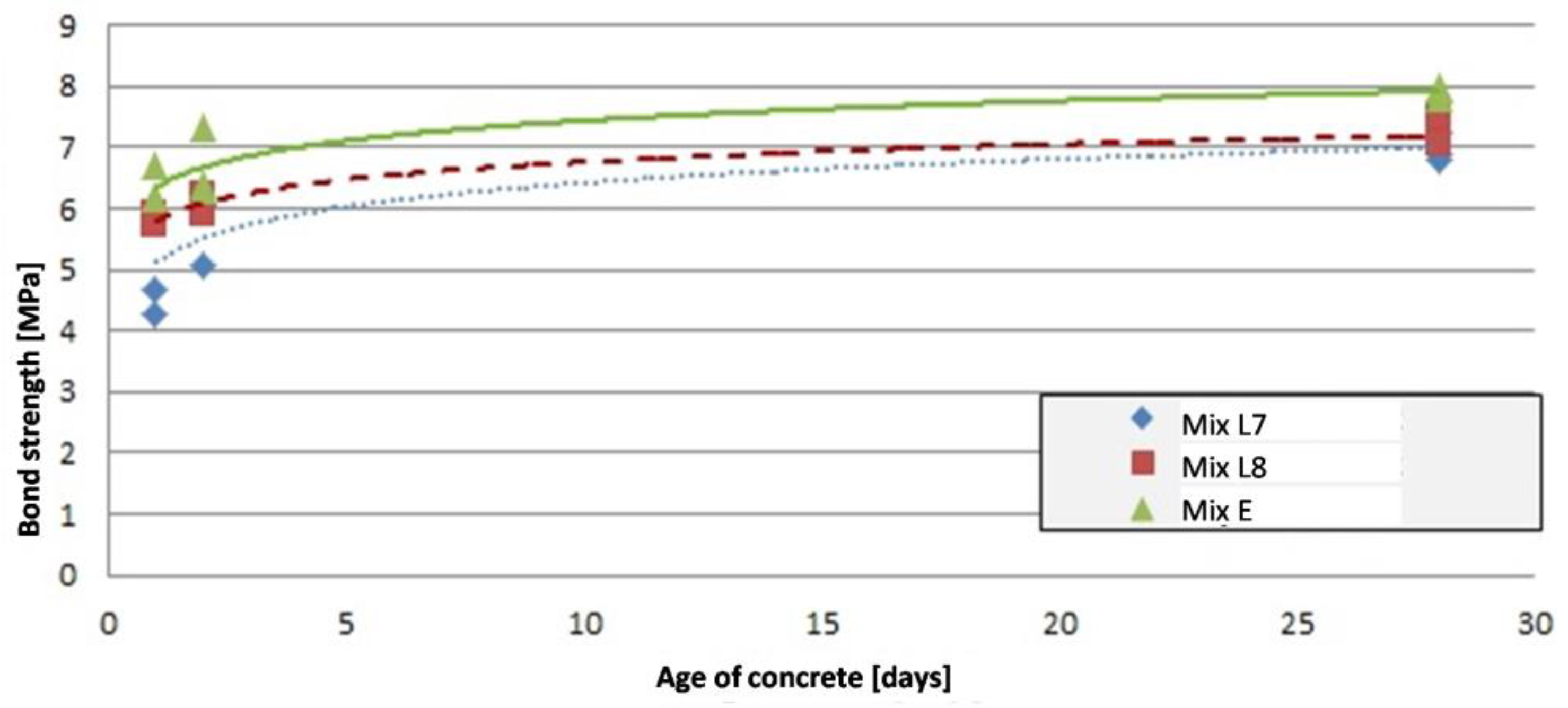
- The bond strength of LWAC is 22% lower compared to NWAC;
- The NWAC shows larger standard deviations in case of compressive strength and bond strength–
- The ratio of the bond strength in LWAC and in NWAC (77.87%) is between the values corresponding to the compressive (80.27%) and tensile (71.09%) strength. The bond strength is considered in the literature to be proportional to the tensile strength. The experiments show a higher ratio in case of bond strength (than in case of tensile strength) that can be explained by the different contact zone between the steel and the aggregates of normal and lightweight concrete.
3.4. Cyclic Pull-Out Test
3.4.1. Cyclic Pull-Out Test of LWAC
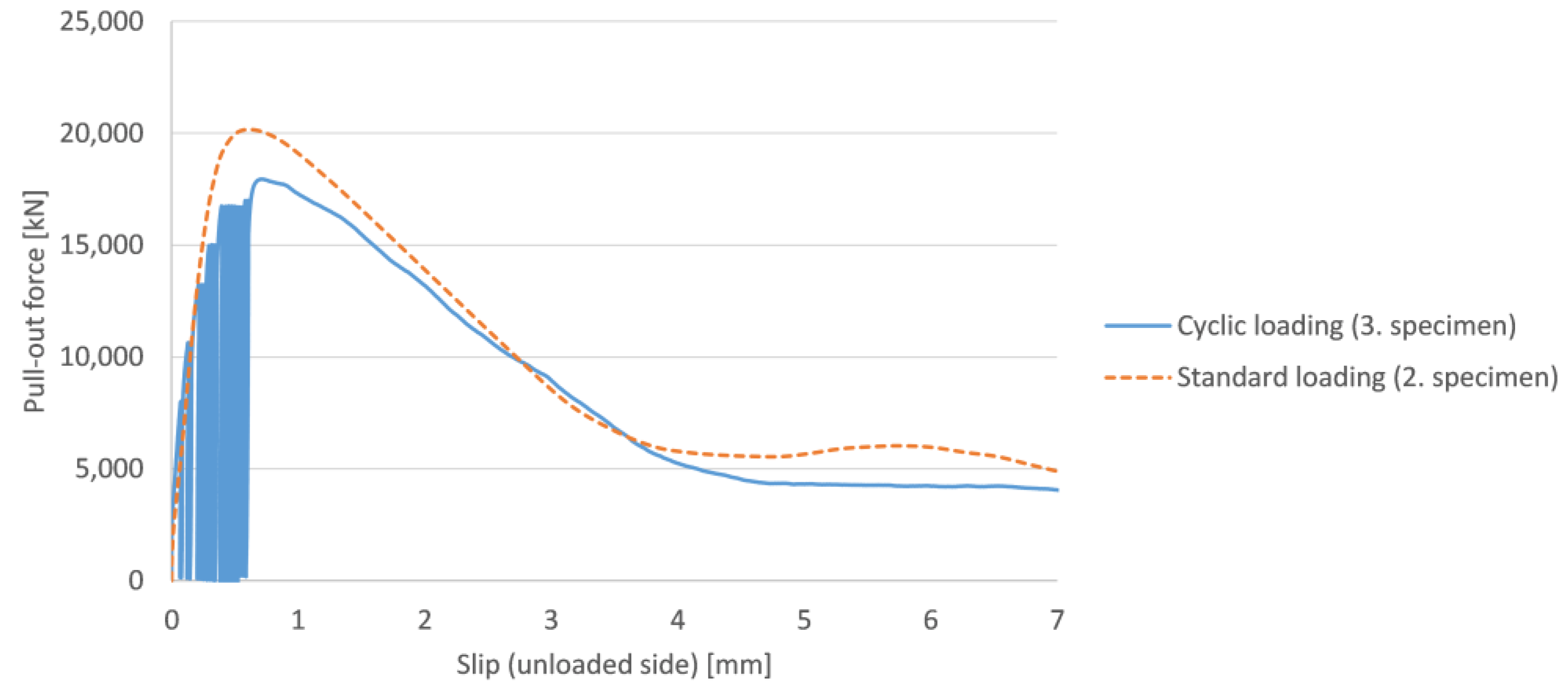
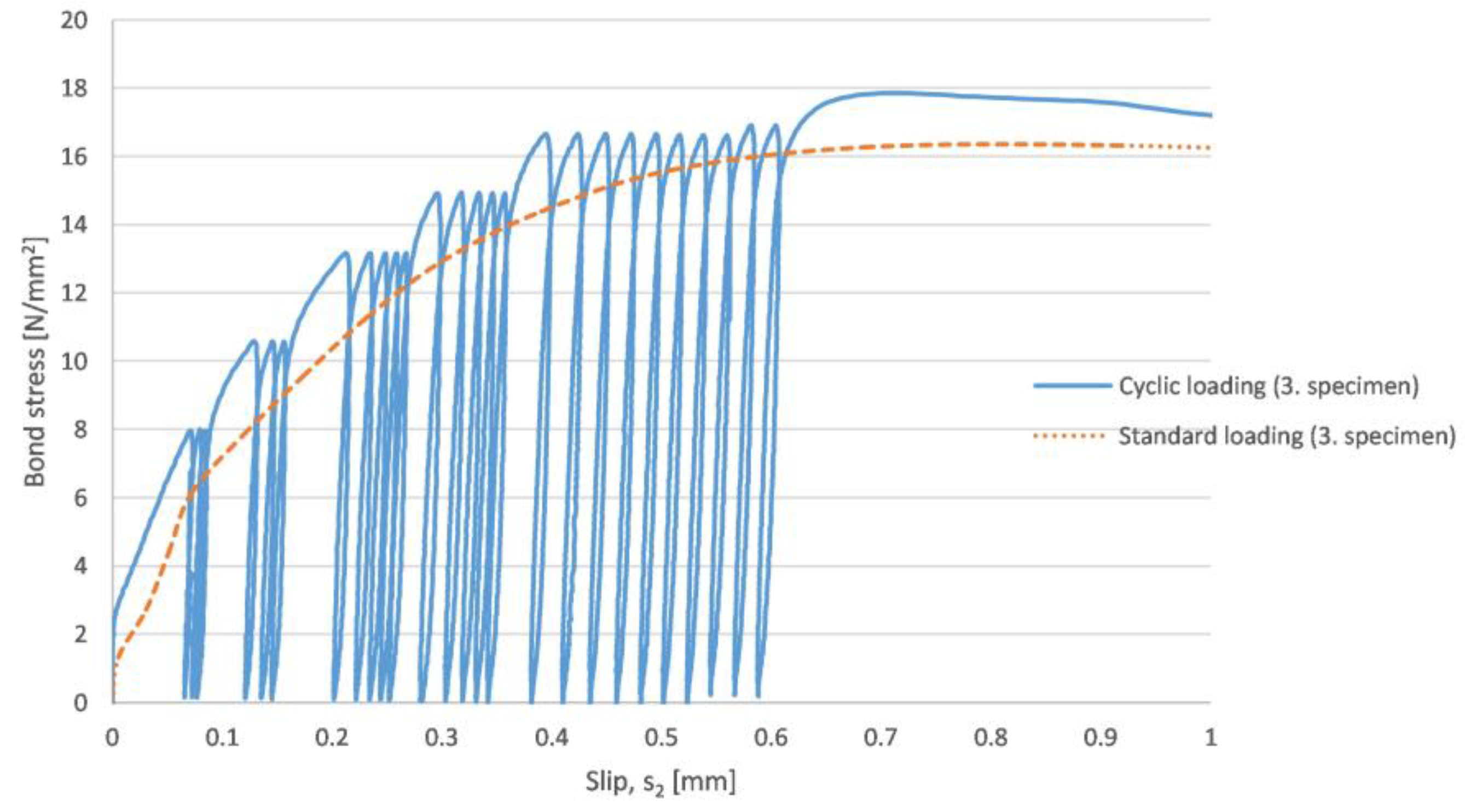
- The enveloping curve of the cyclic loading is similar to the standard pull-out test, but in the maximal load bearing capacity significant differences were observed. As a conclusion it can be stated that the force–slip curve of the cyclic loading always stays inside the figure of the standard pull-out test;
- At the unloaded surface under a given load level, no displacement was observable;
- It can be seen that always the first cycle of the given load level produces the largest displacement. After the first cycle at a given load level, the slips in every cycle (at a given load level) are similar to each other;
- The descending part of the cyclic loading curve is similar to the curve of the standard loading.
3.4.2. Cyclic Pull-Out Test of NWAC
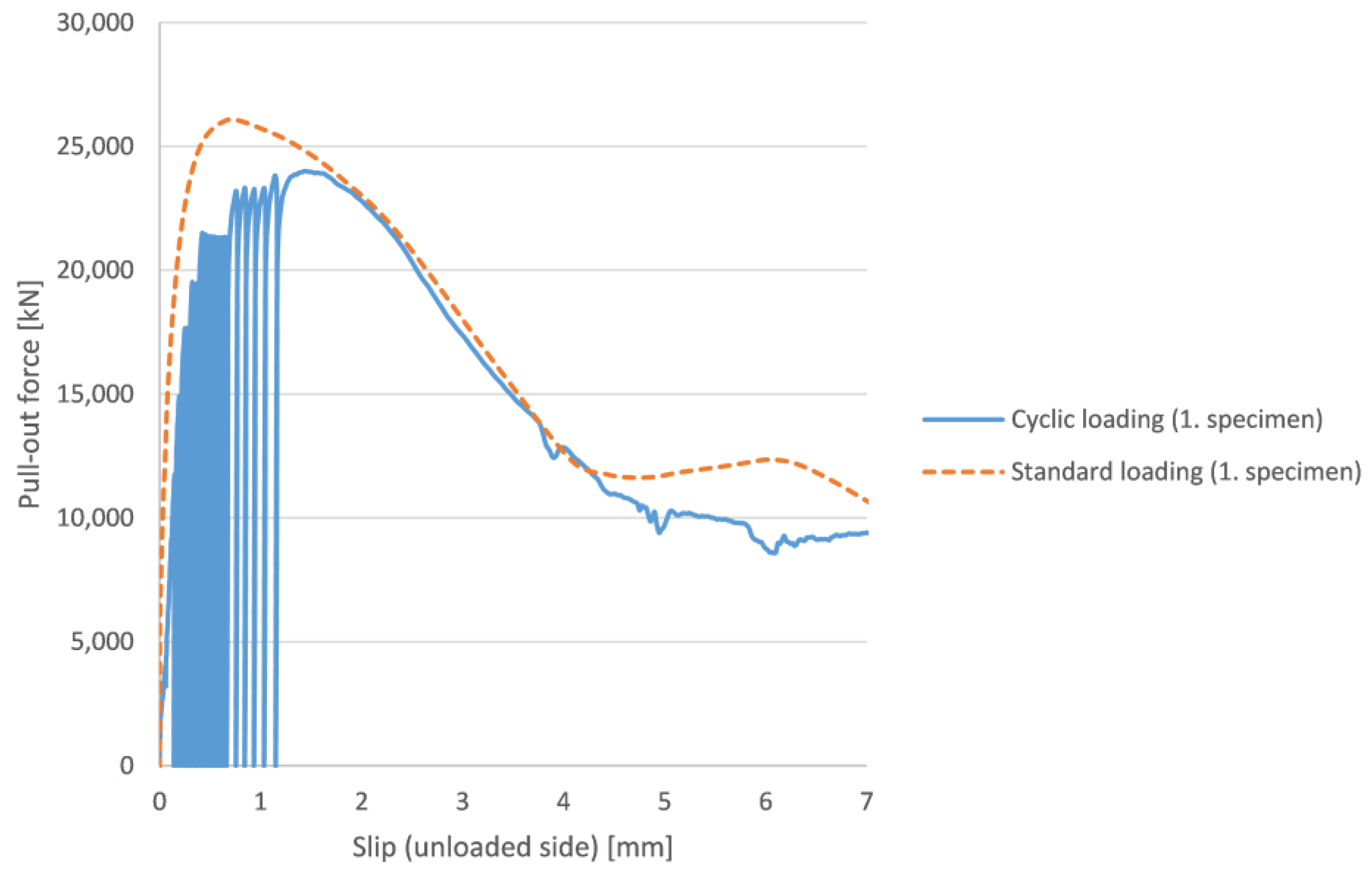
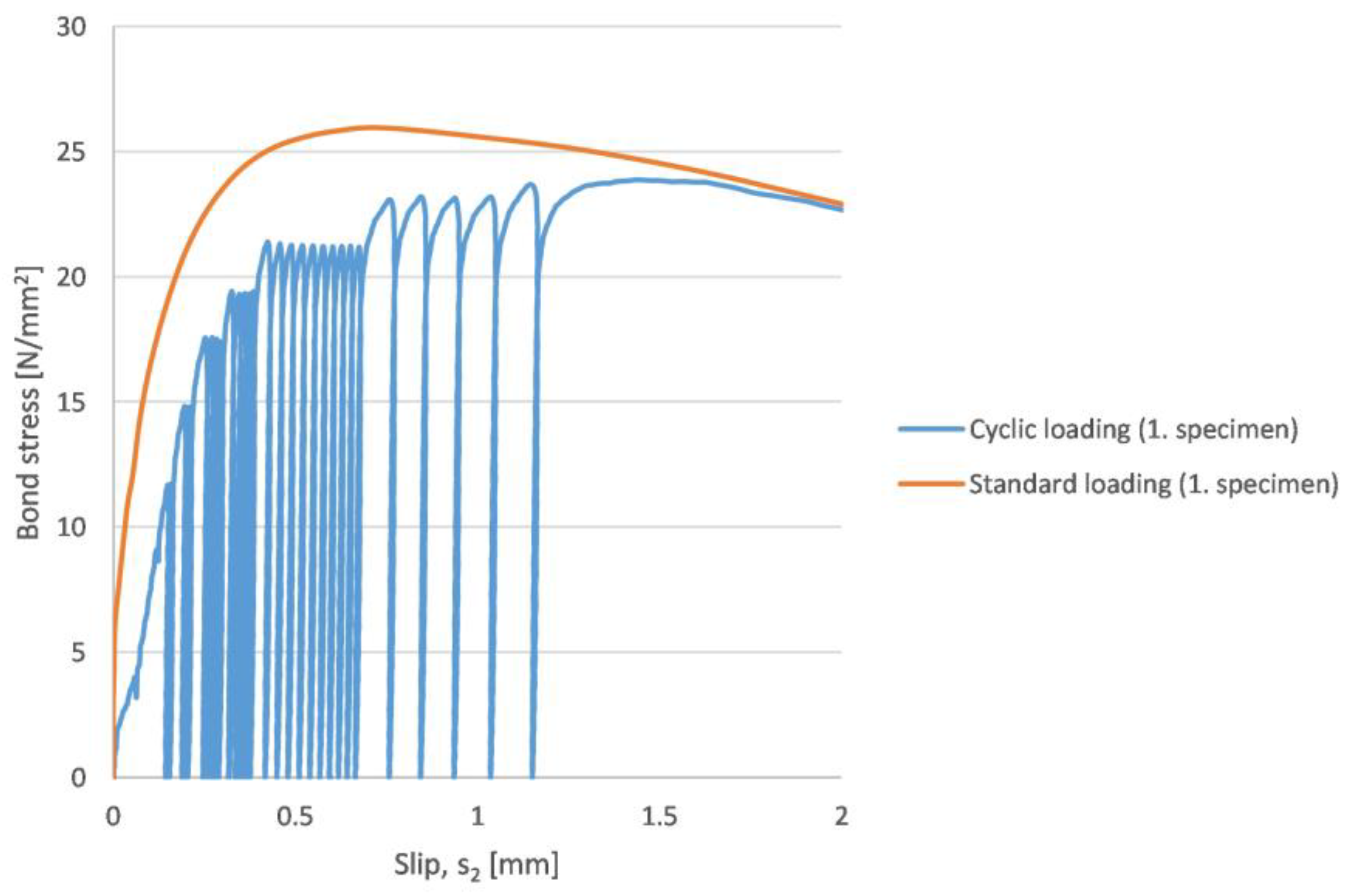
- The curve of the standard pull-out test envelopes the curve of the cyclic loading. In case of NWAC the standard bond stress–slip curve also envelopes the curve of the cyclic loading;
- It can be seen that the specimen can resist the maximum 26,000 N loading multiple times without failure. It is due to the short time period of this loading that there is not enough time for the development of microcracks. It can lead us to the conclusion that the number of cycles is a function of the loading rate. If one decreases the loading rate, the number of cycles (necessary for the failure) decreases in case of the same type of concrete;
- It can be seen that always the first cycle of the given load level produces the largest displacement. After the first cycle, the cycles in a given load level always become smaller and smaller. This is true only until the maximum bond stress is reached, after that, the first slip of the given load level is the smallest;
- The slip belonging to the maximum bond stress is shifting;
- The residual bond stress and the descending part of the figures (standard and cyclic) are not affected by the loading scenario, they are similar to each other;
- The slope of the (re)loading is always the same independently of the load level;
- The cyclic pull-out test causes plastic displacements (in case of NWAC and LWAC as well).
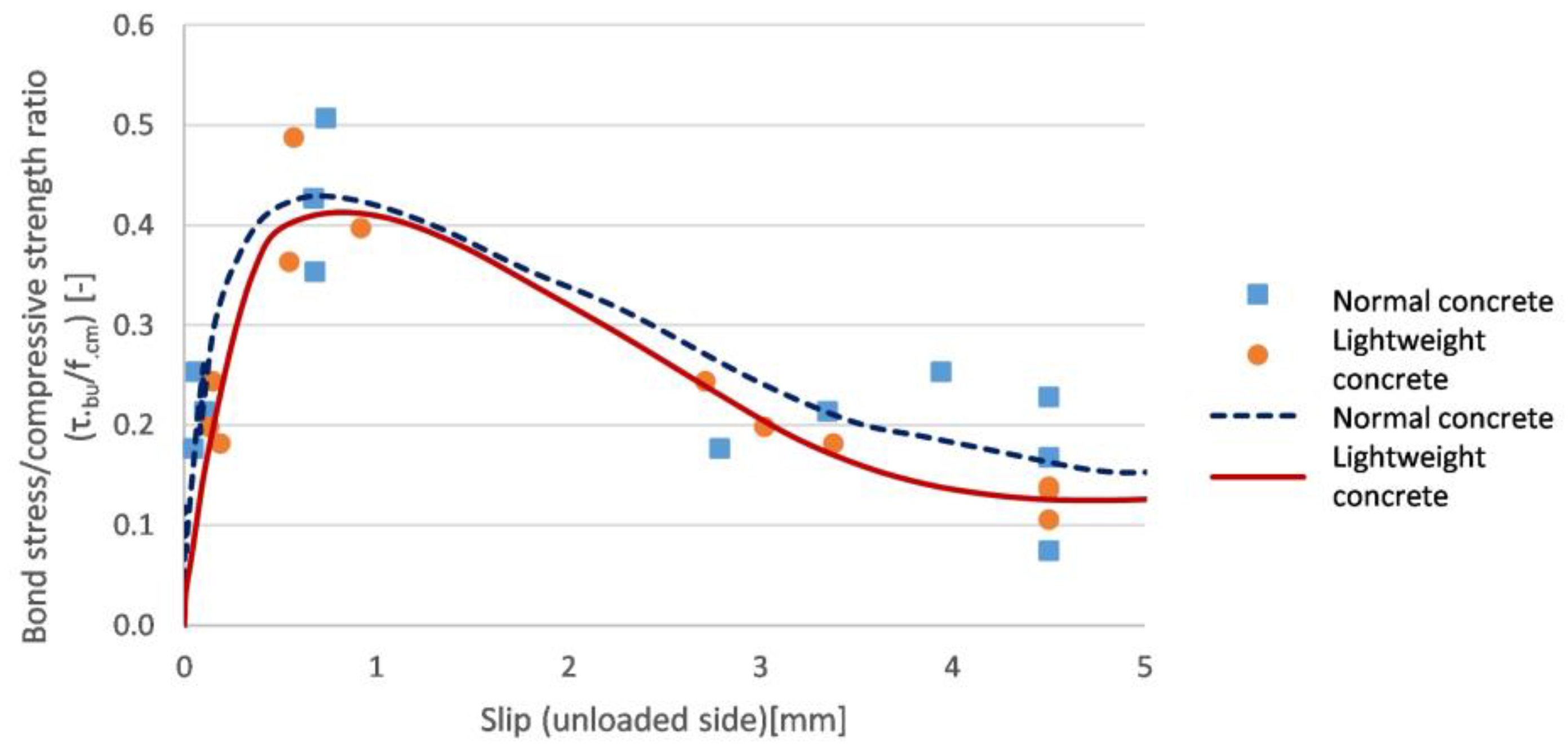
3.4.3. Comparison of the Results
- The maximum bond stress;
- Fifty percent of the maximum stress on the ascending and the descending part of the curve;
- The stress belonging to the 4.5 mm slip value to represent the residual stress. (The value of the slip was chosen arbitrarily based on the figures.)
- The discrete values show larger standard deviations in case of NWAC;
- The initial slope of the figure is less steep in the case of the LWAC;
- The average curve of the NWAC always envelops the curve of the lightweight concrete. It means that the energy absorption capacity of the NWAC is higher; however, the difference between the two curves is quite small.
- The difference of normal and lightweight concrete in maximum stress is less than 3%;
- At the ascending part of the curves, it can be observed that the lightweight concrete needs higher displacements to reach the same stress level as the normal weight concrete, which can cause difficulties in case of design for serviceability.
4. Conclusions
- The concrete mix with the lightweight aggregate resulted in a 20% lower compressive strength, and a 29% lower splitting-tensile strength compared to the normal weight aggregate concrete mix. This showed sufficient correlation with the values calculated with the expressions of the Eurocode and Model Code;
- Based on the fracture surface of the lightweight samples subjected to the splitting-tensile strength test, it could be stated that the mortar and the aggregate both took part in the load bearing;
- The pull-out bond stress and slip values results showed a higher standard deviation compared to the ones of the compression and bending-tensile strength tests;
- It was observed for both mixes, that the bond stress–slip diagram showed a good correlation with each other (in shape); moreover, it could be seen that the failure mode was the same for all samples;
- The standard pull-out test did not show a significant difference in shape between the normal and lightweight aggregate concrete mixes until the maximum bond stress was reached. After that, the difference remained small and, in contrast to our expectations, the lightweight concrete did not show a more rigid behaviour;
- The bond stress—slip figure of the standard pull-out test covered (enveloped) properly the same figure of the cyclic pull-out test in the case of NWAC. In the case of LWAC, this was not true for all specimens;
- Both concrete types were able to resist the maximum pull-out force multiple times in the case of cyclic loading. It was possible because there was no time for the formation/further development of cracks or the redistribution of stresses. In the case of cyclic loading, not only was the loading rate was important, but the time while the maximum load was applied on the sample influenced the results;
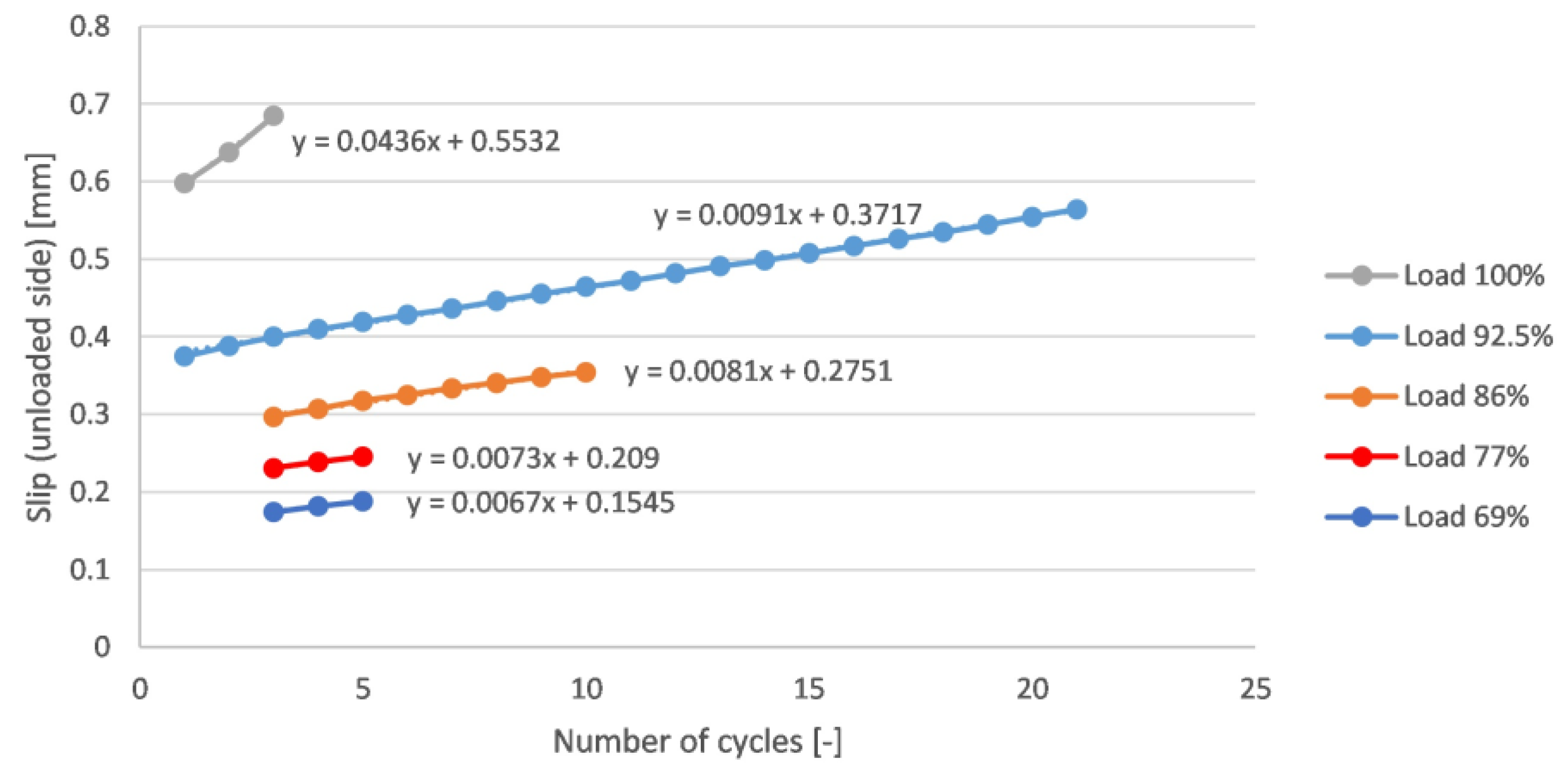
- For cyclic bond tests carried out at low load levels (50–80% of maximum bond stress), always the first cycle produced the largest slip; however, for a high load level (90% of maximum bond stress) the slip in the subsequent cycles gradually intensified;
- For cyclic bond tests, the accumulating slip versus the cycle number relationship could be well described by a linear for all load levels; however, the inclination of these lines increased with the load level;
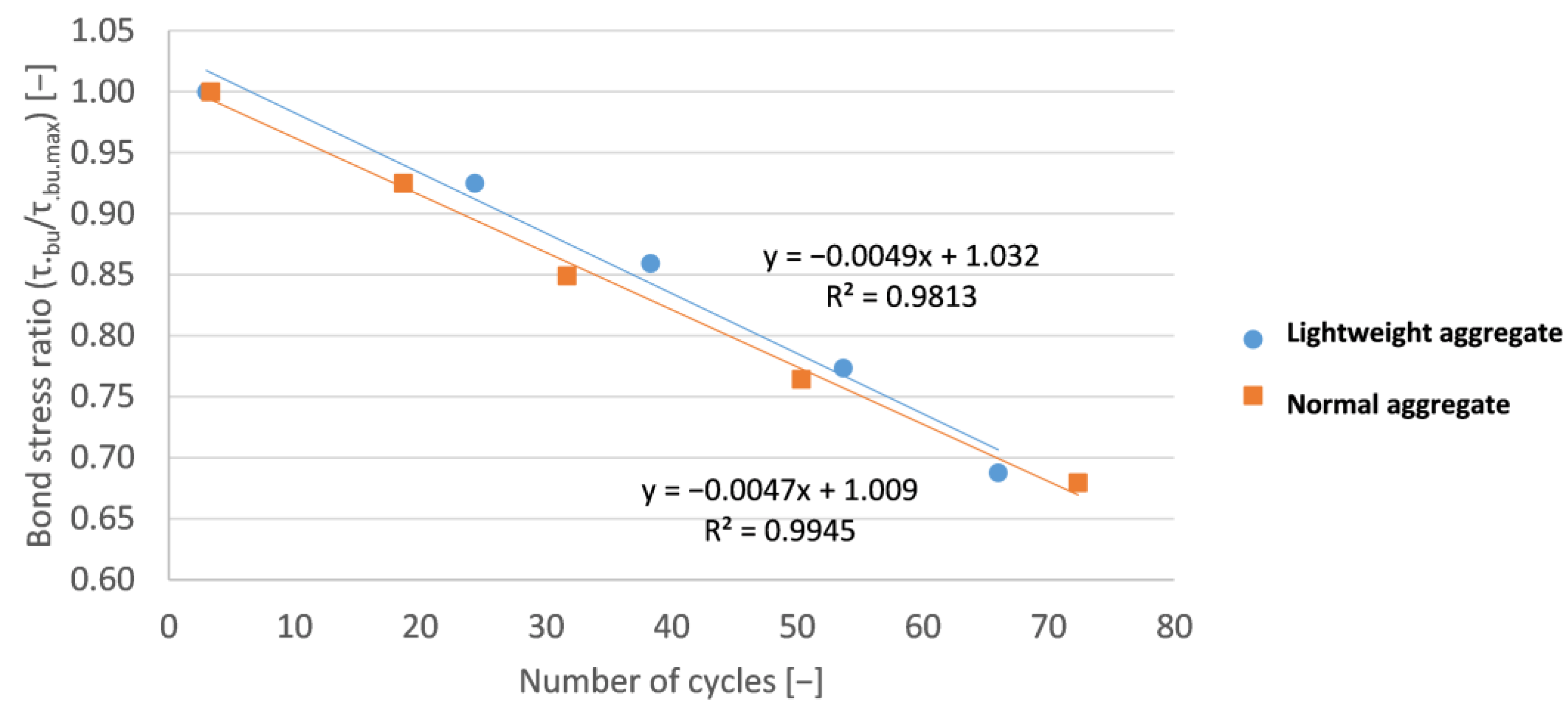
- In the case of a low cycle number fatigue, there was no significant difference between the pull-out bond test results of the normal and lightweight aggregate concrete;
- In the standards, only limited data can be found on bond strength in case of cyclic loading.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kovács, T.; Nemes, R. Bond between strands and high-strength lightweight aggregate concrete. In Proceedings of the 11th CCC Congress Hainburg, Hainburg, Austria, 2 October 2015. [Google Scholar]
- Farina, I.; Moccia, I.; Salzano, C.; Singh, N.; Sadrolodabaee, P.; Colangelo, F. Compressive and Thermal Properties of Non-Structural Lightweight Concrete Containing Industrial Byproduct Aggregates. Materials 2022, 15, 4029. [Google Scholar] [CrossRef] [PubMed]
- Bogas, J.A.; Cunha, D. Non-structural lightweight concrete with volcanic scoria aggregates for lightweight fill in building’s floors. Constr. Build. Mater. 2017, 135, 151–163. [Google Scholar] [CrossRef]
- Dilli, M.E.; Atahan, H.N.; Sengül, C. A comparison of strength and elastic properties between conventional and lightweight structural concretes designed with expanded clay aggregates. Constr. Build. Mater. 2015, 101, 260–267. [Google Scholar] [CrossRef]
- Wang, X.F.; Fang, C.; Kuang, W.Q.; Li, D.W.; Han, N.X.; Xing, F. Experimental study on early cracking sensitivity of lightweight aggregate concrete. Constr. Build. Mater. 2017, 136, 173–183. [Google Scholar] [CrossRef]
- Ganesan, N.; Indira, P.V.; Sabeena, M.V. Bond stress slip response of bars embedded in hybrid fibre reinforced high performance concrete. Constr. Build. Mater. 2014, 50, 108–115. [Google Scholar] [CrossRef]
- Wang, L.; Yi, J.; Xia, H.; Fan, L. Experimental study of a pull-out test of corroded steel and concrete using the acoustic emission monitoring method. Constr. Build. Mater. 2016, 122, 163–170. [Google Scholar] [CrossRef]
- Vos, E. Influence of Loading Rate and Radial Pressure on Bond in Reinforced Concrete: A Numerical and Experimental Approach. Ph.D. Thesis, Delft University Press, Delft, The Netherlands, 1983. [Google Scholar]
- Bilek, V.; Bonczková, S.; Hurta, J.; Pytlík, D.; Mrovec, M. Bond Strength Between Reinforcing Steel and Different Types of Concrete. Procedia Eng. 2017, 190, 243–247. [Google Scholar] [CrossRef]
- Eligehausen, R.; Popov, E.P.; Bertero, V.V. Local Bond Stress-Slip Relationships of Deformed Bars under Generalized Excitations; Report No. UCB/EERC 83-19; University of California: Berkeley, CA, USA, 1982. [Google Scholar]
- Morita, S.; Fuji, S. Bond capacity of deformed bars due to splitting of surrounding concrete. Bond. Concr. 1982, 331–341. [Google Scholar]
- Vos, E.; Reinhardt, H.W. Bond stress-slip behaviour of deformed bars, plain bars and strands under impact loading. In Bond in Concrete; Applied Science Publishers: London, UK, 1982; 173p. [Google Scholar]
- Al-Shannag, M.J.; Charif, A. Bond behavior of steel bars embedded in concretes made with natural lightweight aggregates. J. King Saud Univ. Eng. Sci. 2017, 29, 365–372. [Google Scholar] [CrossRef]
- Lundgren, K. Pull-out tests of steel-encased specimens subjected to reversed cyclic loading. Mater. Struct. 2012, 33, 450–456. [Google Scholar] [CrossRef]
- Fathi, H.; Farhang, K. Effect of cyclic loadings on heated self-compacting concrete. Constr. Build. Mater. 2014, 69, 26–31. [Google Scholar] [CrossRef]
- Baea, B.-I.; Choi, H.-K.; Choi, C.-S. Bond stress between conventional reinforcement and steel fibre reinforced reactive powder concrete. Constr. Build. Mater. 2016, 112, 825–835. [Google Scholar] [CrossRef]
- Sinha, B.P.; Gerstle, K.H.; Tulin, L.G. Stress–strain relations for concrete under cyclic loading. ACI Struct. J. 1964, 61, 195–211. [Google Scholar]
- Li, X.; Zhao, J.; Zhang, X. A mechanical bond model for reinforcing bar in concrete subjected to monotonic and reversed cyclic loading. J. Build. Eng. 2021, 44, 102912. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Y.; Zhu, Z.; Sha, S.; Lv, C. Experimental study on the cyclic bond behavior of corroded rebar based on modified beam test. J. Build. Eng. 2022, 47, 103834. [Google Scholar] [CrossRef]
- Fathi, H.; Dabbagh, H. Damage mechanism of SCC under cyclic loading with different speed. Constr. Build. Mater. 2015, 101, 252–259. [Google Scholar] [CrossRef]
- Park, R.; Paulay, T. Reinforced Concrete Structure; Wiley: Hoboken, NJ, USA, 1975. [Google Scholar]
- Boulekbache, B.; Hamrat, M.; Chemrouk, M.; Amziane, S. Flexural behaviour of steel fibre-reinforced concrete under cyclic loading. Constr. Build. Mater. 2016, 126, 253–262. [Google Scholar] [CrossRef]
- Lin, H.; Ožbolt, Y.Z.J. The bond behavior between concrete and corroded steel bar under repeated loading. Eng. Struct. 2017, 140, 390–405. [Google Scholar] [CrossRef]
- Caratelli, A.; Meda, A.; Rinaldi, Z. Monotonic and cyclic behaviour of lightweight concrete beams with and without steel fiber reinforcement. Constr. Build. Mater. 2016, 122, 23–35. [Google Scholar] [CrossRef]
- Bogas, J.A.; Gomes, M.G.; Real, S. Bonding of steel reinforcement in structural expanded clay lightweight aggregate concrete: The influence of failure mechanism and concrete composition. Constr. Build. Mater. 2014, 65, 350–359. [Google Scholar] [CrossRef]
- Robins, P.J.; Standish, I.G. Effect of lateral pressure on bond of reinforcing bars in concrete. Int. J. Adhes. Adhes. 1982, 2, 129–133. [Google Scholar] [CrossRef]
- American Concrete Institute. Guide for Structural Lightweight-Aggregate Concrete in Specifications for Structural Concrete; ACI 301-05; American Concrete Institute: Indianapolis, IN, USA, 2014. [Google Scholar]
- Zhou, H.; Lu, J.; Xv, X.; Dong, B.; Xing, F. Effects of stirrup corrosion on bond–slip performance of reinforcing steel in concrete: An experimental study. Constr. Build. Mater. 2015, 93, 257–266. [Google Scholar] [CrossRef]
- Zhou, H.; Liang, X.; Xiaolin, Z.; Jinlong, L.; Feng, X.; Liu, M. Variation and Degradation of Steel and Concrete Bond Performance with Corroded Stirrups. Constr. Build. Mater. 2017, 138C, 56–68. [Google Scholar] [CrossRef]
- Fib Bulletins 51, 52 and 53: Structural Concrete Textbook on Behaviour, Design and Performance, 2nd ed.; Beton- und Stahlbetonbau: Berlin, Germany, 2010. [CrossRef]
- Rehm, G.; Eligehausen, R. Bond of Ribbed Bars under High-Cycle Repeated Loads. ACI J. 1979, 76, 297–309. [Google Scholar]
- Balázs, G.L.; Koch, R.; Harre, W. Verbund von Stahl in Beton unter Betriebsbeanspruchung. In Proceedings of the Deutscher Ausschuss für Stahlbeton–30, Forschungskolloquium, Stuttgart, Germany, 24–25 March 1994; pp. 167–176. [Google Scholar]
- Balázs, G.L. Fatigue of Bond. ACI Mater. J. 1991, 88, 620–629. [Google Scholar]
- Balázs, G.L.; Koch, R. Bond Characteristics under Reversed Cyclic Loading. Otto Graf J. 1995, 6, 47–62. [Google Scholar]
- RILEM; CEB; FIP. Bond test for reinforcing steel. Mater. Struct. 1973, 6, 96–105. [Google Scholar]
- EN 10080:2005; Steel for the Reinforcement of Concrete—Weldable Reinforcing Steel—General. BSI: London, UK, 2005.
- Windisch, A. A Modified Pull-out Test and New Evaluation Methods for a More Real Local Bond-Slip Relationship. Mater. Struct. 1985, 18, 181–184. [Google Scholar] [CrossRef]
- Chao, S.-H. Bond Characterization of Reinforcing Bars and Prestressing Strands in High Performance Fiber Reinforced Cementious Composites under Monotonic and Cyclic Loading. Ph.D. Thesis, University of Michigan, ProQuest Dissertations Publishing, Ann Arbor, MI, USA, 2005. [Google Scholar]
- EN 12390-3:2009; Testing Hardened Concrete. Part 3: Compressive Strength of Test Specimens. European Committee for Standardization: Brussels, Belgium, 2009.
- EN 12390-5:2010; Testing Hardened Concrete. Part 5: Flexural Strength of Test Specimens. European Committee for Standardization: Brussels, Belgium, 2010.
- Maree, A.F.; Riad, K.H. Analytical and experimental investigation for bond behaviour of newly developed polystyrene foam particles’ lightweight concrete. Eng. Struct. 2014, 58, 1–11. [Google Scholar] [CrossRef]



| Pull-Out Tests | Strength Tests | |||
|---|---|---|---|---|
| Standard Loading | Cyclic Loading | Compression Strength | Splitting Tensile Strength | |
| Lightweight (LWAC) | 3 | 3 | 4 | 3 |
| Normal weight (NWAC) | 3 | 3 | 5 | 3 |
| Total | 12 | 9 | 6 | |
| Components | Normal Weight Concrete (NWAC) Mix | Lightweight Concrete (LWAC) Mix |
|---|---|---|
| (kg) | (kg) | |
| Cement (CEM II/A-S 42.5 R) | 360 | 360 |
| Water (v/c = 0.5) | 180 | 180 |
| Coarse aggregate: Quartz gravel (NWAC: 4/16 mm fraction) or Liapor HD 5n (LWAC: 4/8 mm fraction) | 1193 | 450 |
| Fine aggregate: Quartz sand (0/4 mm fraction) | 646 | 646 |
| Lightweight Concrete | ||||||||
|---|---|---|---|---|---|---|---|---|
| Compressive Strength | Splitting Tensile Strength | |||||||
| Specimen | Density | Max. Force | Strength | Specimen | Density | Max. Force | Strength | |
| (kg/m3) | (kN) | (N/mm2) | (kg/m3) | (kN) | (N/mm2) | |||
| LWAC1 | JL-K-11 | 1783 | 957 | 42.03 | JL-KH-11 | 1735 | 186 | 2.62 |
| LWAC2 | JL-K-12 | 1736 | 927 | 41.09 | JL-KH-12 | 1741 | 193 | 2.72 |
| LWAC3 | JL-K-22 | 1782 | 950 | 41.83 | JL-KH-22 | 1756 | 170 | 2.40 |
| LWAC4 | JL-K-21 | 1779 | 903 | 39.40 | - | - | - | - |
| Average | 1770 | 41.09 | 1744 | 2.58 | ||||
| Normal Weight Concrete | ||||||||
|---|---|---|---|---|---|---|---|---|
| Compressive Strength | Splitting Tensile Strength | |||||||
| Specimen | Density | Max. Force | Strength | Specimen | Density | Max. Force | Strength | |
| (kg/m3) | (kN) | (N/mm2) | (kg/m3) | (kN) | (N/mm2) | |||
| NWAC1 | JL-N-11 | 2383 | 1176 | 52.06 | JL-NH-11 | 2363 | 263 | 3.68 |
| NWAC2 | JL-N-12 | 2364 | 1219 | 53.29 | JL-NH-21 | 2379 | 246 | 3.47 |
| NWAC3 | JL-N-21 | 2350 | 1075 | 47.49 | JL-NH-22 | 2355 | 266 | 3.73 |
| NWAC4 | JL-N-22 | 2354 | 1075 | 47.75 | - | - | - | - |
| NWAC5 | JL-N-23 | 2333 | 1266 | 55.34 | - | - | - | - |
| Average | 2357 | 51.19 | 2366 | 3.63 | ||||
| Lightweight Concrete | Slip (At Max. Force) | Max. Force | Bond Stress |
|---|---|---|---|
| (mm) | (N) | (N/mm2) | |
| 1. Specimen | 0.547 | 15,010 | 14.93 |
| 2. Specimen | 0.570 | 20,149 | 20.04 |
| 3. Specimen | 0.919 | 16,402 | 16.32 |
| Average | 17,187 | 17.10 | |
| Standard deviation | 2170 | 2.16 | |
| Normal Concrete | Slip (At Max. Force) | Max. Force | Bond Stress |
|---|---|---|---|
| (mm) | (N) | (N/mm2) | |
| 1. Specimen | 0.737 | 26,087 | 25.95 |
| 2. Specimen | 0.673 | 21,969 | 21.85 |
| 3. Specimen | 0.680 | 18,173 | 18.08 |
| Average | 22,076 | 21.96 | |
| Standard deviation | 3232 | 3.21 | |
| Type of Concrete | Statistical Data | Compressive Strength | Splitting-Tensile Strength | Bond Strength |
|---|---|---|---|---|
| (N/mm2) | (N/mm2) | (N/mm2) | ||
| Lightweight | Average | 41.09 | 2.58 | 17.10 |
| Std. deviation | 1.04 | 0.21 | 2.16 | |
| Normal | Average | 51.19 | 3.63 | 21.96 |
| Std. deviation | 3.10 | 0.18 | 3.21 | |
| Lightweight compared to normal weight concrete (%) | ||||
| (%) | Average | 80.27 | 71.09 | 77.87 |
| Std. deviation | 33.48 | 120.38 | 67.29 | |
| Type of Concrete | f.cm | 1. Specimen | 2. Specimen | 3. Specimen | Average | ||||
|---|---|---|---|---|---|---|---|---|---|
| s2 | τ.bu/f.cm | s2 | τ.bu/f.cm | s2 | τ.bu/f.cm | s2 | τ.bu/f.cm | ||
| (N/mm2) | (mm) | (-) | (mm) | (-) | (mm) | (-) | (mm) | (-) | |
| NWAC | 51.19 | 0.061 | 0.25 | 0.106 | 0.21 | 0.047 | 0.18 | 0.072 | 0.21 |
| 0.737 | 0.51 | 0.673 | 0.43 | 0.680 | 0.35 | 0.697 | 0.43 | ||
| 3.939 | 0.25 | 3.349 | 0.21 | 2.788 | 0.18 | 3.359 | 0.21 | ||
| 4.500 | 0.23 | 4.500 | 0.17 | 4.500 | 0.07 | 4.500 | 0.16 | ||
| LWAC | 41.09 | 0.189 | 0.18 | 0.147 | 0.24 | 0.129 | 0.20 | 0.155 | 0.21 |
| 0.547 | 0.36 | 0.570 | 0.49 | 0.919 | 0.40 | 0.679 | 0.41 | ||
| 3.379 | 0.18 | 2.714 | 0.24 | 3.021 | 0.20 | 3.038 | 0.21 | ||
| 4.500 | 0.14 | 4.500 | 0.14 | 4.500 | 0.11 | 4.500 | 0.13 | ||
| yend | 0.679 | [mm] | |||
|---|---|---|---|---|---|
| Load History | Parameters | Number of Cycles | Bond Strength/Compressive Strength Ratio | ||
| a | b | Calculated | Rounding (to Bottom) | ||
| (N) | (-) | (mm) | (-) | (-) | (-) |
| 8594 | - | - | - | - | 0.43 |
| 11,172 | - | - | - | - | 0.56 |
| 13,750 | 0.0067 | 0.1545 | 78.27 | 78 | 0.69 |
| 15,468 | 0.0073 | 0.209 | 64.37 | 64 | 0.77 |
| 17,187 | 0.0081 | 0.2751 | 49.85 | 49 | 0.86 |
| 18,500 | 0.0091 | 0.3717 | 33.76 | 33 | 0.93 |
| 20,000 | 0.0436 | 0.5532 | 2.88 | 2 | 1.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovács, T.; Gyurkó, Z.; Jakab, L.; Nemes, R. Influence of Unidirectional Cyclic Loading on Bond between Steel Bars Embedded in Lightweight Aggregate Concrete. Solids 2022, 3, 397-415. https://doi.org/10.3390/solids3030028
Kovács T, Gyurkó Z, Jakab L, Nemes R. Influence of Unidirectional Cyclic Loading on Bond between Steel Bars Embedded in Lightweight Aggregate Concrete. Solids. 2022; 3(3):397-415. https://doi.org/10.3390/solids3030028
Chicago/Turabian StyleKovács, Tamás, Zoltán Gyurkó, Levente Jakab, and Rita Nemes. 2022. "Influence of Unidirectional Cyclic Loading on Bond between Steel Bars Embedded in Lightweight Aggregate Concrete" Solids 3, no. 3: 397-415. https://doi.org/10.3390/solids3030028
APA StyleKovács, T., Gyurkó, Z., Jakab, L., & Nemes, R. (2022). Influence of Unidirectional Cyclic Loading on Bond between Steel Bars Embedded in Lightweight Aggregate Concrete. Solids, 3(3), 397-415. https://doi.org/10.3390/solids3030028






