Towards Recognition of Scale Effects in a Solid Model of Lattices with Tensegrity-Inspired Microstructure
Abstract
:1. Introduction
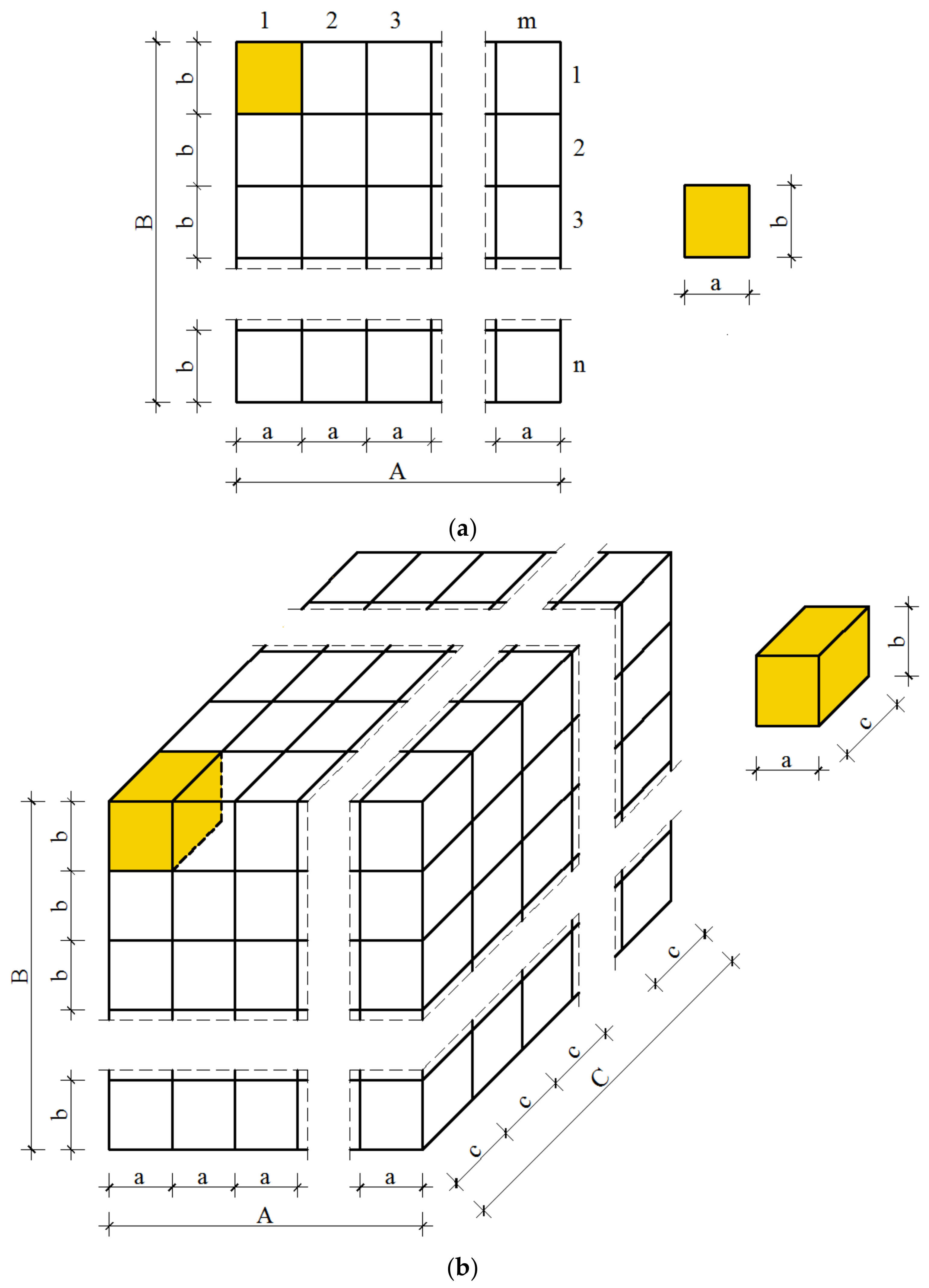
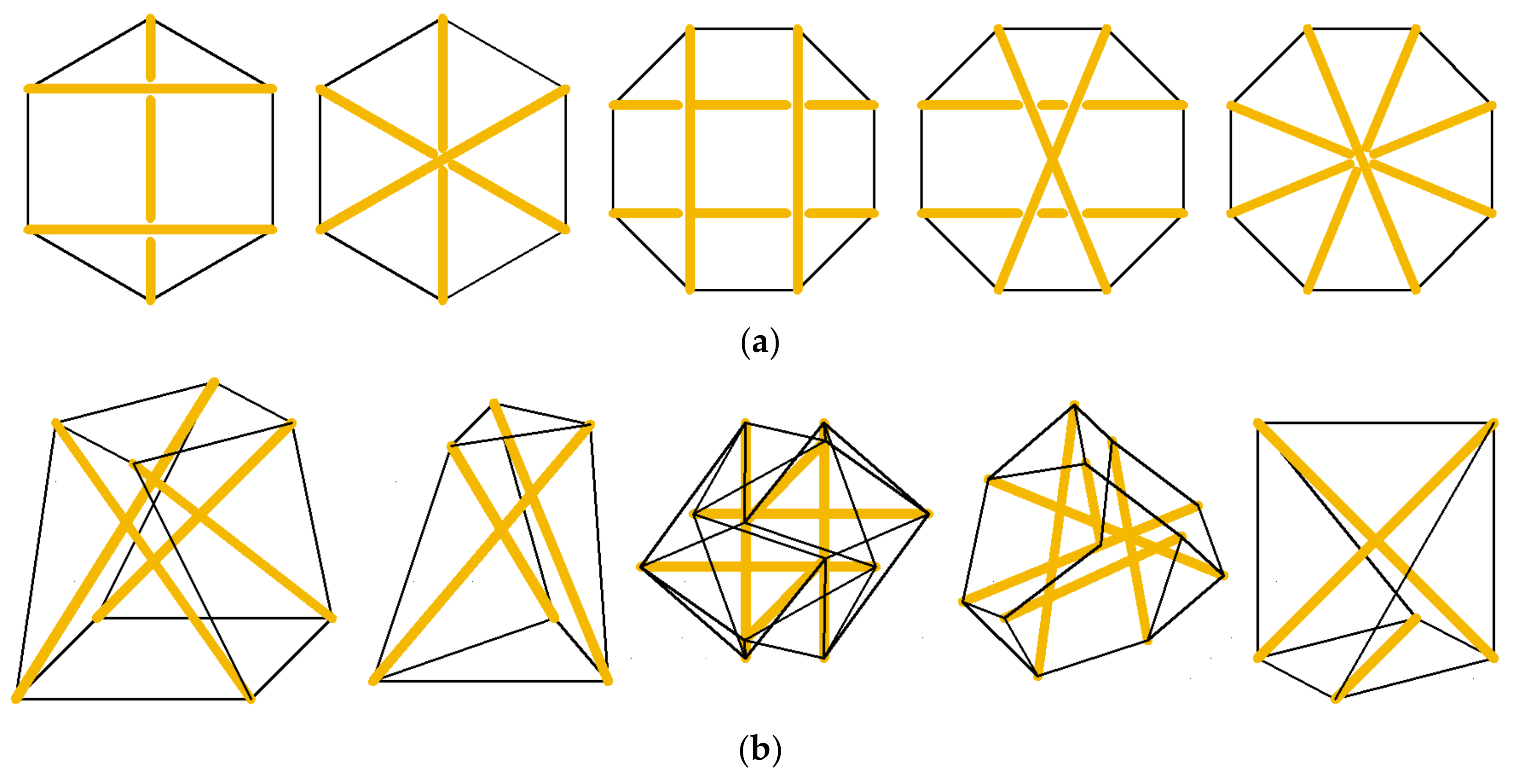
2. Lattices with Tensegrity-Inspired Microstructure
3. Enhanced Solid Model—Size Effect
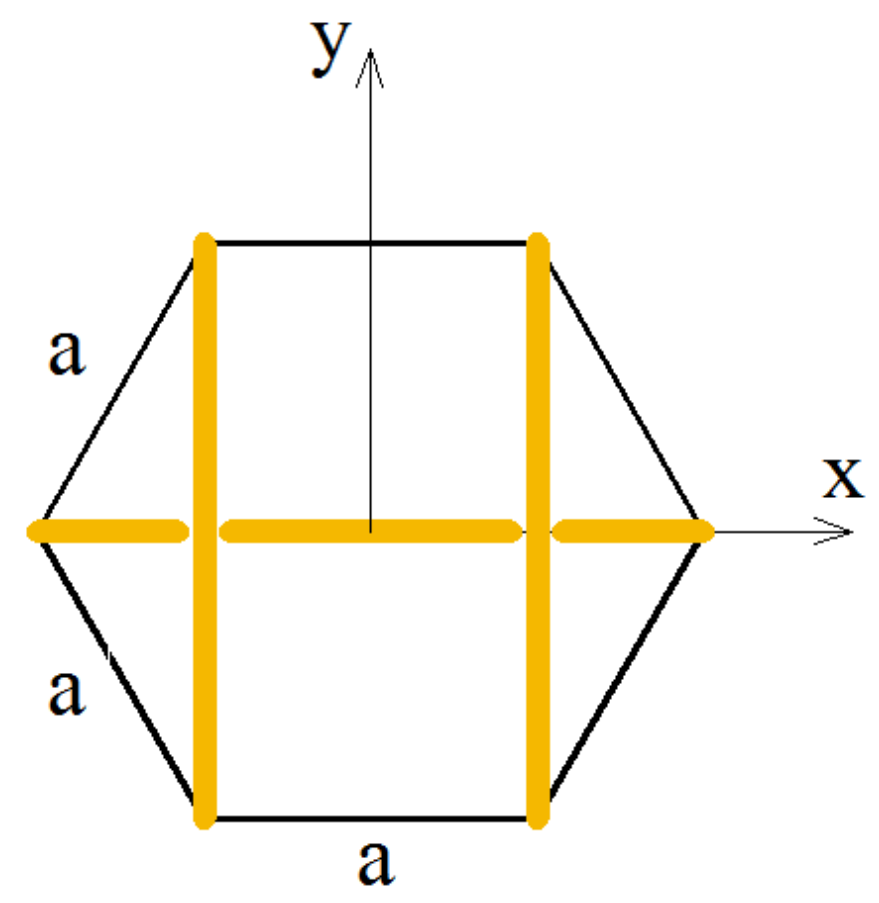
3.1. 2D Hexagonal Tensegrity Module
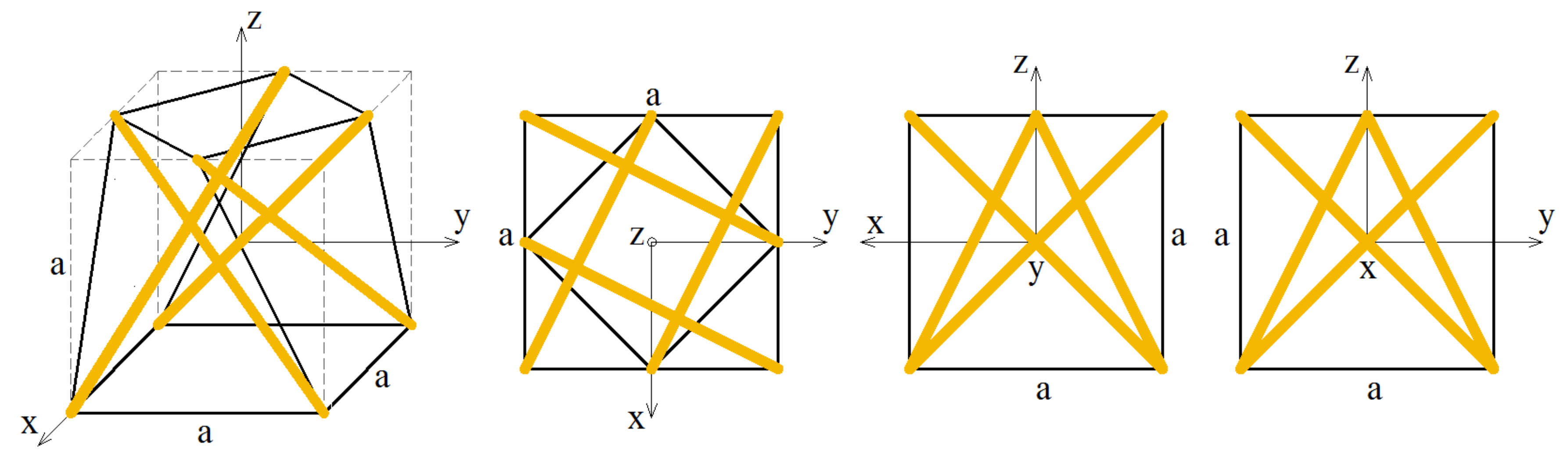
3.2. 3D 4-Strut Simplex Tensegrity Module
4. Conclusions and Future Work
- Substitute elasticity matrices coefficients depend on the cable to strut stiffness ratio as well as on the self-stress level.
- Coupling of the first and second gradient terms is identified.
- The scale effect can be observed.
- It is possible to determine the variability (sensitivity) of individual lattice or unit cell first gradient deformation states and to control them to a certain extent using geometric and self-stress parameters. They can be selected so that the second gradient coefficient is as small as possible, or even zero.
- The extended solid model can be used for evaluation of unusual mechanical properties of tensegrity lattices.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Skelton, R.E.; de Oliveira, M.C. Tensegrity Systems; Springer: New York, NY, USA, 2009. [Google Scholar]
- Motro, R. Tensegrity: Structural Systems for the Future; Kogan Page Science: London, UK, 2003. [Google Scholar]
- Wroldsen, A.S. Modelling and Control of Tensegrity Structures. Ph.D. Thesis, Department of Marine Technology, Norwegian University of Science and Technology, Trondheim, Norway, 2007; 208p. [Google Scholar]
- Calladine, C.R.; Pellegrino, S. First-order infinitesimal mechanisms. Int. J. Solids Struct. 1991, 27, 505–515. [Google Scholar] [CrossRef]
- Gilewski, W.; Al Sabouni-Zawadzka, A. On possible applications of smart structures controlled by self-stress. Arch. Civ. Mech. Eng. 2015, 15, 469–478. [Google Scholar] [CrossRef]
- Adam, B.; Smith, I.F.C. Self-diagnosis and self-repair of an active tensegrity structure. J. Struct. Eng. 2007, 133, 1752–1761. [Google Scholar] [CrossRef]
- Al Sabouni-Zawadzka, A.; Gilewski, W. Inherent smartness of tensegrity structures—Structural elements applications. In Proceedings of the International Association for Shell and Spatial Structures (IASS), Amsterdam, The Netherlands, 17–20 August 2015. [Google Scholar]
- Al Sabouni-Zawadzka, A.; Gilewski, W. Inherent smartness of tensegrity structures. Appl. Sci. 2018, 8, 787. [Google Scholar] [CrossRef] [Green Version]
- Obara, P.; Kłosowska, J.; Gilewski, W. Truth and myths about 2D tensegrity trusses. Appl. Sci. 2019, 9, 179. [Google Scholar] [CrossRef] [Green Version]
- Gilewski, W.; Al Sabouni-Zawadzka, A. Equivalent mechanical properties of tensegrity truss structures with self-stress included. Eur. J. Mech. Solids 2020, 83, 103998. [Google Scholar] [CrossRef]
- Fraternali, F.; Carpentieri, G.; Amendola, A.; Skelton, R.E.; Nesterenko, V.F. Multiscale tenability of solitary wave dynamics in tensegrity metamaterials. Appl. Phys. Lett. 2014, 105, 201903. [Google Scholar] [CrossRef] [Green Version]
- Fabbrocino, F.; Carpentieri, G.; Amendola, A.; Penna, R.; Fraternali, F. Accurate numerical methods for studying the nonlinear wave-dynamics of tensegrity metamaterials. Eccomas Procedia Compdyn 2017, 3911–3922. [Google Scholar] [CrossRef] [Green Version]
- Amendola, A.; Krushynska, A.; Daraio, C.; Pugno, N.M.; Fraternali, F. Tuning frequency band gaps of tensegrity mass-spring chains with local and global prestress. Int. J. Solids Struct 2018, in press. [Google Scholar] [CrossRef]
- Wang, Y.T.; Liu, X.N.; Zhu, R.; Hu, G.K. Wave propagation in tunable lightweight tensegrity metastructure. Sci. Rep. 2018, 8, 11482. [Google Scholar] [CrossRef]
- De Tommasi, D.; Marano, G.C.; Puglisi, G.; Trentadue, F. Optimal complexity and fractal limits of self-similar tensegrities. Proc. R. Soc. A 2016, 471, 20150250. [Google Scholar] [CrossRef] [Green Version]
- De Tommasi, D.; Marano, G.C.; Puglisi, G.; Trentadue, F. Morphological optimization of tensegrity-type metamaterials. Compos. Part B 2017, 115, 182–187. [Google Scholar] [CrossRef]
- Modano, M.; Mascolo, I.; Fraternali, F.; Bieniek, Z. Numerical and analytical approaches to the self-equilibrium problem of class teta = 1 tensegrity metamaterials. Front. Mech. 2018, 5, 5. [Google Scholar]
- Fraternali, F.; Carpentieri, G.; Amendola, A. On the mechanical modeling of the extreme softening/stiffening response of axially loaded tensegrity prisms. J. Mech. Phys. Solids 2015, 74, 136–157. [Google Scholar] [CrossRef] [Green Version]
- Rimoli, J.J.; Pal, R.K. Mechanical response of 3-dimensional tensegrity lattices. Compos. Part B 2017, 115, 30–42. [Google Scholar] [CrossRef]
- Salahsoor, H.; Pal, R.K.; Rimoli, J.J. Material symmetry phase transitions in the three-dimensional tensegrity metamaterial. J. Mech. Phys. Solids 2018, 119, 382–399. [Google Scholar] [CrossRef]
- Zhang, L.Y.; Li, S.X.; Zhu, S.X.; Zhang, B.Y.; Xu, G.K. Automatically assembled large-scale tensegrities by truncated regular polyhedral and prismatic elementary cells. Compos. Struct. 2018, 184, 30–40. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, D.; Dobah, Y.; Scarpa, F.; Fraternali, F.; Skelton, R.E. Tensegrity cell mechanical metamaterial with metal rubber. Appl. Phys. Lett. 2018, 113, 031906. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Zhang, Q.; Dobah, J.; Scarpa, F.; Fraternali, F.; Skelton, R.E.; Zhang, D.; Hong, J. Meta-tensegrity: Design of a tensegrity prism with metal rubber. Compos. Struct. 2018, 206, 644–657. [Google Scholar] [CrossRef] [Green Version]
- Al Sabouni-Zawadzka, A.; Gilewski, W. Smart metamaterial based on the simplex tensegrity pattern. Materials 2018, 11, 673. [Google Scholar] [CrossRef] [Green Version]
- Milton, G.; Cherkaev, A.V. Which elasticity tensors are realizable? J. Eng. Mater. Technol. 1995, 117, 483–493. [Google Scholar] [CrossRef]
- Kadic, M.; Buckmann, T.; Stenger, N.; Thiel, M. On the practicability of pentamode mechanical metamaterials. Appl. Phys. Lett. 2012, 100, 191901. [Google Scholar] [CrossRef] [Green Version]
- Al Sabouni-Zawadzka, A. Extreme mechanical properties of regular tensegrity unit cells in 3D lattice metamaterials. Materials 2020, 13, 4845. [Google Scholar] [CrossRef] [PubMed]
- Al Sabouni-Zawadzka, A.; Gilewski, W. Soft and stiff simplex tensegrity lattices as extreme smart metamaterials. Materials 2019, 12, 187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bathe, K.J. Finite Element Procedures in Engineering Analysis; Prentice Hall: New York, NY, USA, 1996. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method. Vol. 1. The Basis; Elsevier Butterworth-Heinemann: London, UK, 2000. [Google Scholar]
- Lewiński, T. On algebraic equations of elastic trusses, frames and grillages. J. Theor. Appl. Mech. 2001, 39, 307–322. [Google Scholar]
- Pełczyński, J.; Gilewski, W. Algebraic formulation for moderately thick elastic frames, beams, trusses, and grillages within Timoshenko theory. Math. Probl. Eng. 2019, 7545473. [Google Scholar] [CrossRef]
- Pełczyński, J.; Gilewski, W. An extension of algebraic equations of elastic trusses with self-equilibrated system of forces. In Proceedings of the ECCM6, Proceedings of the ECFD7, Glasgow, UK, 11–15 June 2018; R. Owen, R., de Borst, R., Reese, J., Pearce, C., Eds.; CIMNE: Barcelona, Spain, 2018; pp. 4343–4348. [Google Scholar]
- Kasprzak, A.; Gilewski, W. 3D continuum model of tensegrity modules with the effect of self0stress. In Proceedings of the WCCM XI, ECCM V, Barcelona, Spain, 20–25 July 2014. [Google Scholar]
- Pal, R.K.; Ruzzene, M.; Rimoli, J. A continuum model for nonlinear lattices under large deformations. Int. J. Solids Struct. 2016, 96, 300–319. [Google Scholar] [CrossRef]
- Pal, R.K.; Rimoli, J.; Ruzzene, M. Effect of large deformation pre-loads on the wave properties of hexagonal lattice. Smart Mat. Struct. 2016, 25, 054010. [Google Scholar] [CrossRef]
- Green, A.E.; Zerna, W. Theoretical Elasticity; Oxford University Press: Oxford, UK, 1968. [Google Scholar]
- Chadwick, P.; Vianello, M.; Cowin, S. A new proof that the number of linear elastic symmetries is eight. J. Mech. Phys. Solids 2001, 49, 2471–2492. [Google Scholar] [CrossRef]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Rat. Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Mindlin, R.D. Second gradient of strain and surface-tension in linear elasticity. Int. J. Solids Struct. 1965, 1, 417–438. [Google Scholar] [CrossRef]
- Eringen, A.C. Microcontinuum field theories I: Foundations of Solids; Springer: New York, NY, USA, 1999. [Google Scholar]
- Polyzos, D.; Fotadis, D.I. Derivation of Mindlin’s first and sedond strain gradient elastic theory via simple lattice and continuum models. Int. J. Solids Struct. 2012, 49, 470–480. [Google Scholar] [CrossRef] [Green Version]
- Askes, H.; Aifantis, E.C. Gradient elasticity in statics and dynamics: An overview of formulation, length scale identification procedures, finite element implementations and new results. Int. J. Solids Struct. 2011, 48, 1962–1990. [Google Scholar] [CrossRef]
- Forest, S.; Sab, K. Stress gradient continuum theory. Mech. Res. Comm. 2012, 40, 16–25. [Google Scholar] [CrossRef]
- Pellegrino, S. Structural computations with the singular value decomposition of the equilibrium matrix. Int. J. Solids Struct. 1993, 30, 3029–3035. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gilewski, W.; Sabouni-Zawadzka, A.A. Towards Recognition of Scale Effects in a Solid Model of Lattices with Tensegrity-Inspired Microstructure. Solids 2021, 2, 50-59. https://doi.org/10.3390/solids2010002
Gilewski W, Sabouni-Zawadzka AA. Towards Recognition of Scale Effects in a Solid Model of Lattices with Tensegrity-Inspired Microstructure. Solids. 2021; 2(1):50-59. https://doi.org/10.3390/solids2010002
Chicago/Turabian StyleGilewski, Wojciech, and Anna Al Sabouni-Zawadzka. 2021. "Towards Recognition of Scale Effects in a Solid Model of Lattices with Tensegrity-Inspired Microstructure" Solids 2, no. 1: 50-59. https://doi.org/10.3390/solids2010002
APA StyleGilewski, W., & Sabouni-Zawadzka, A. A. (2021). Towards Recognition of Scale Effects in a Solid Model of Lattices with Tensegrity-Inspired Microstructure. Solids, 2(1), 50-59. https://doi.org/10.3390/solids2010002




