Geotechnical Design of Barrier Pillar Between Boxcut and Underground Mining for Shallow Dipping Orebodies: A Case Study
Abstract
1. Introduction
2. Engineering Background
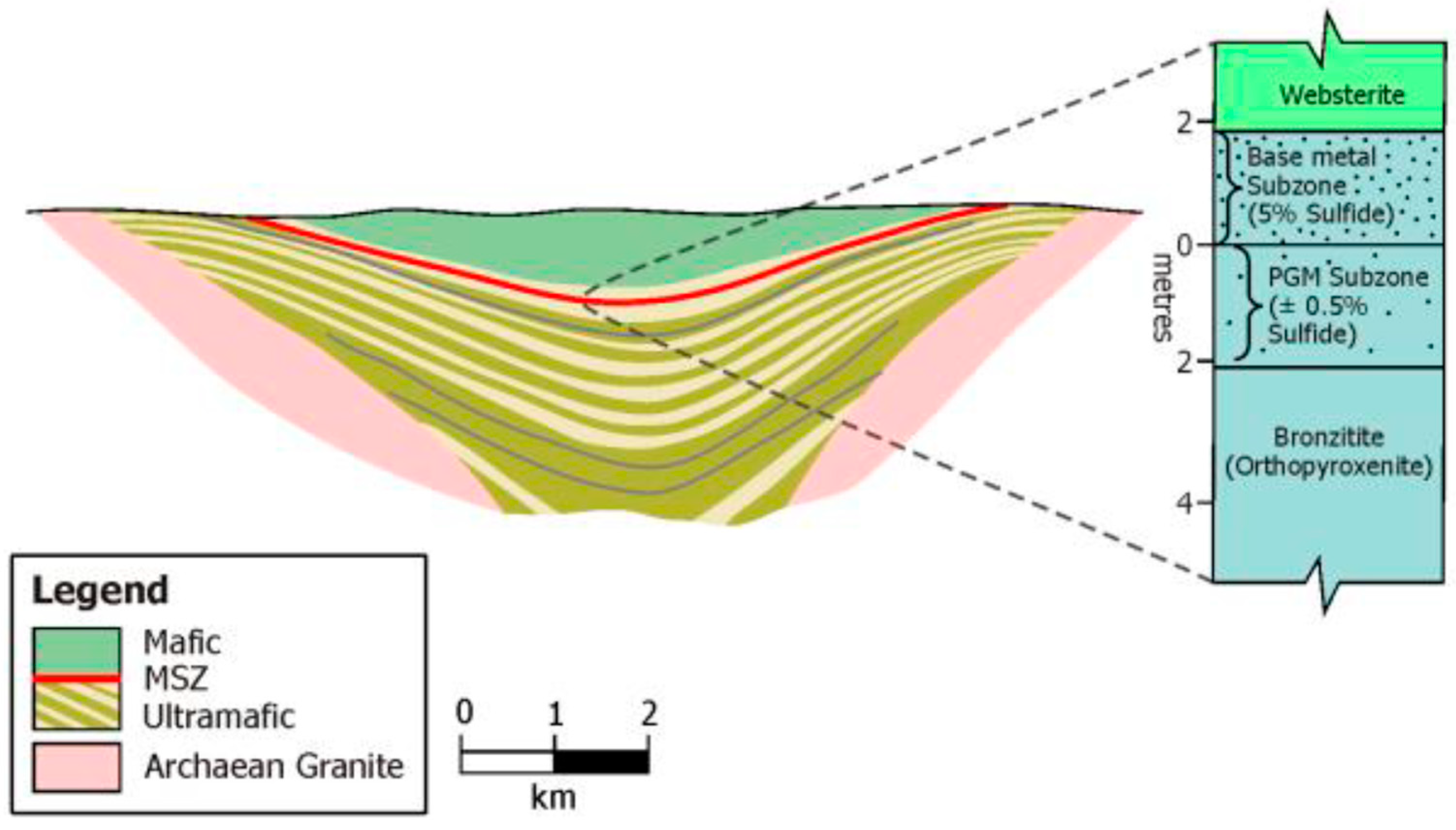
2.1. Regional Geology
2.2. Case Study Mine Geology and Structures
2.3. Rock Strength and Rock Mass Classification
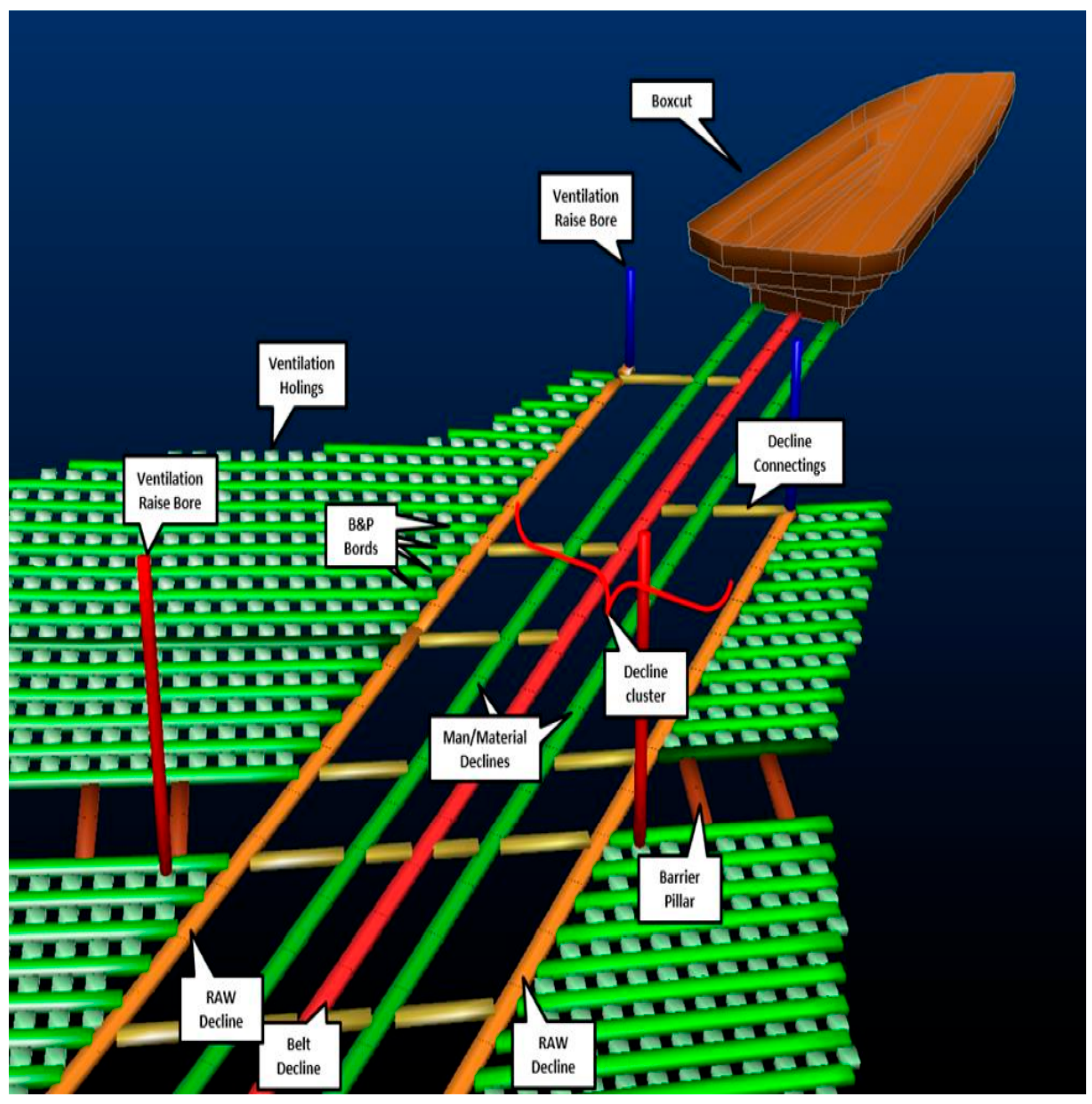
2.4. Planned Mining Method
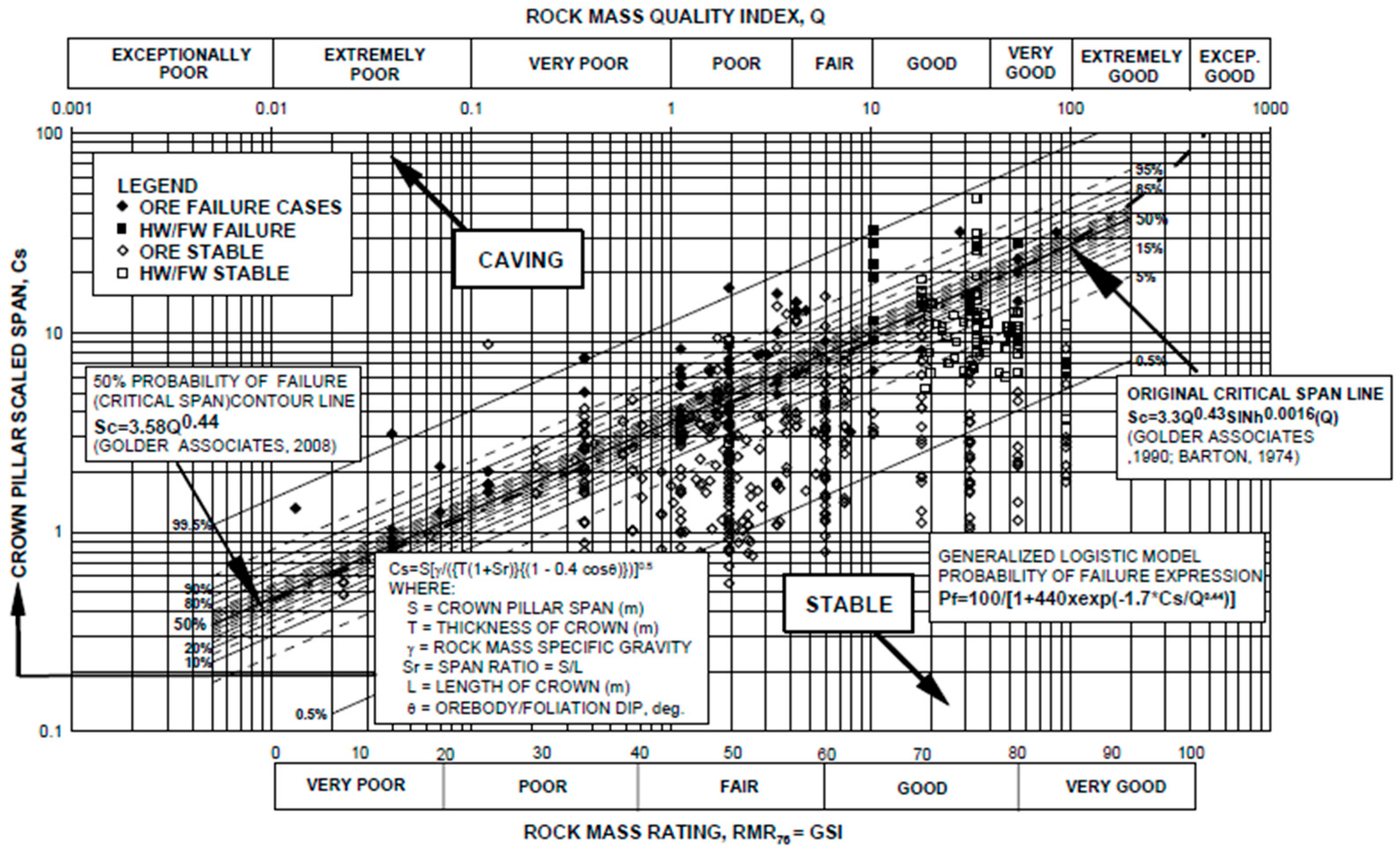
3. Empirical Analysis Method
4. Numerical Modelling
4.1. Failure Criterion
4.2. Model Description
4.3. Boundary Conditions
4.4. Numerical Analysis
5. Results and Discussion
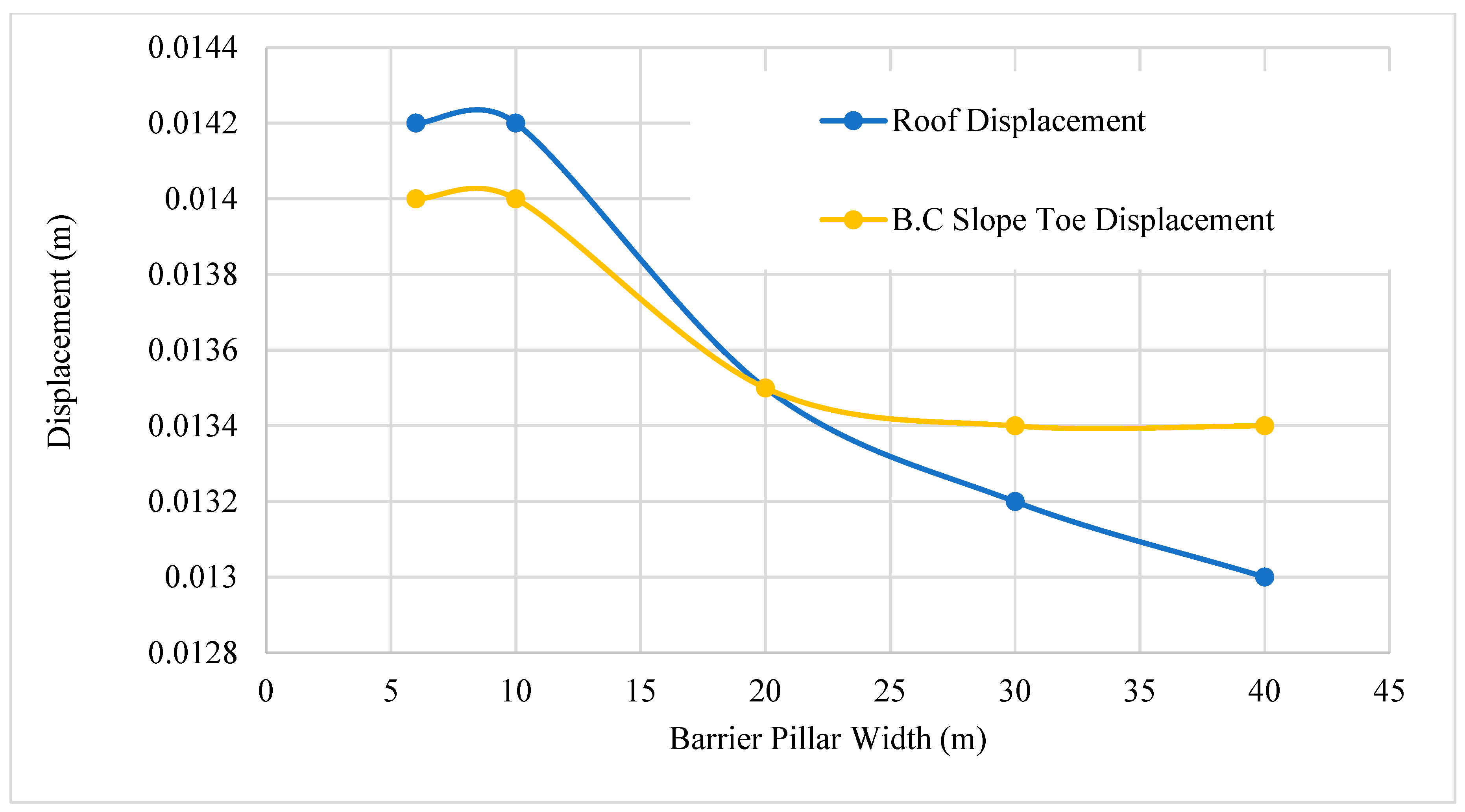
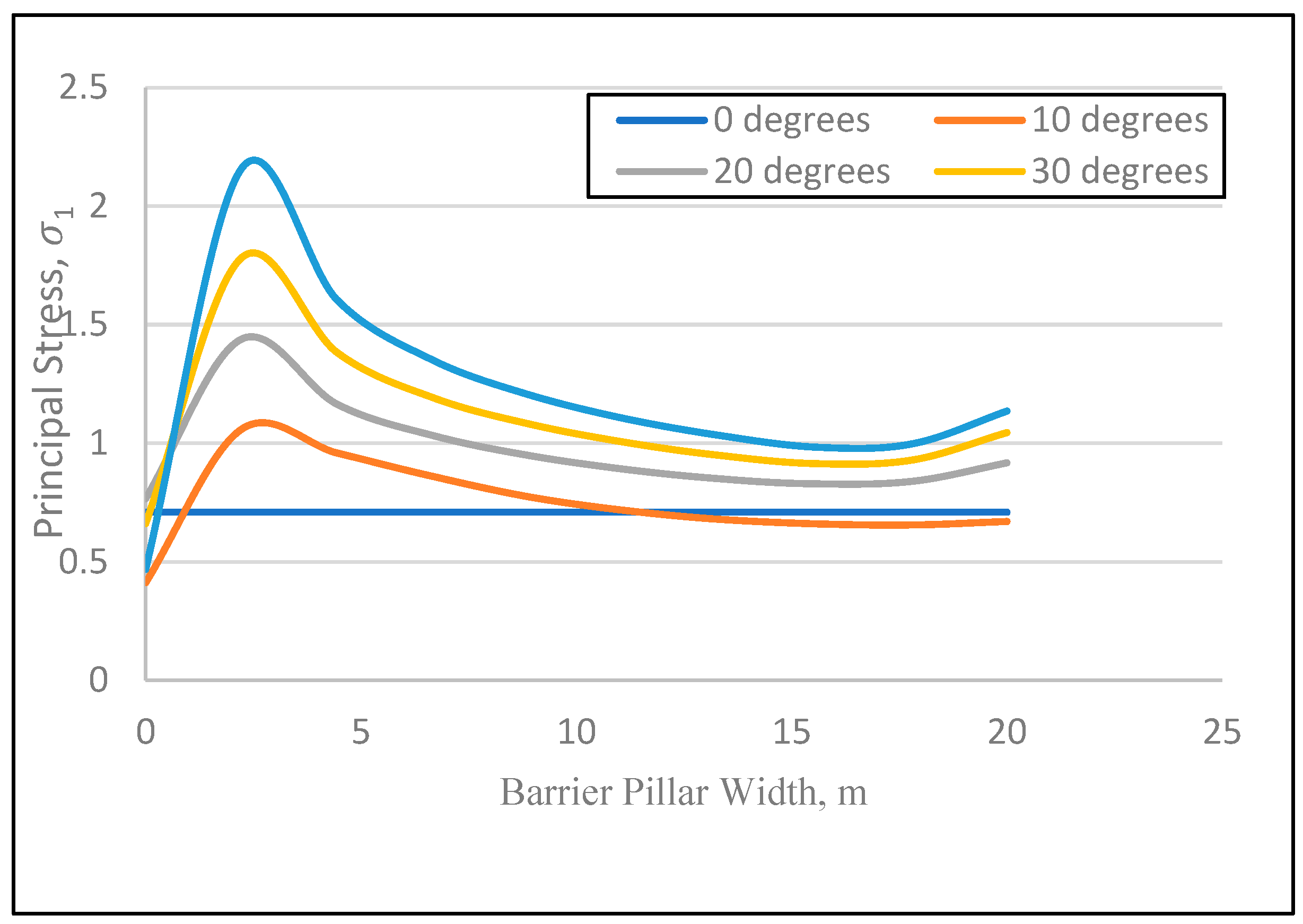
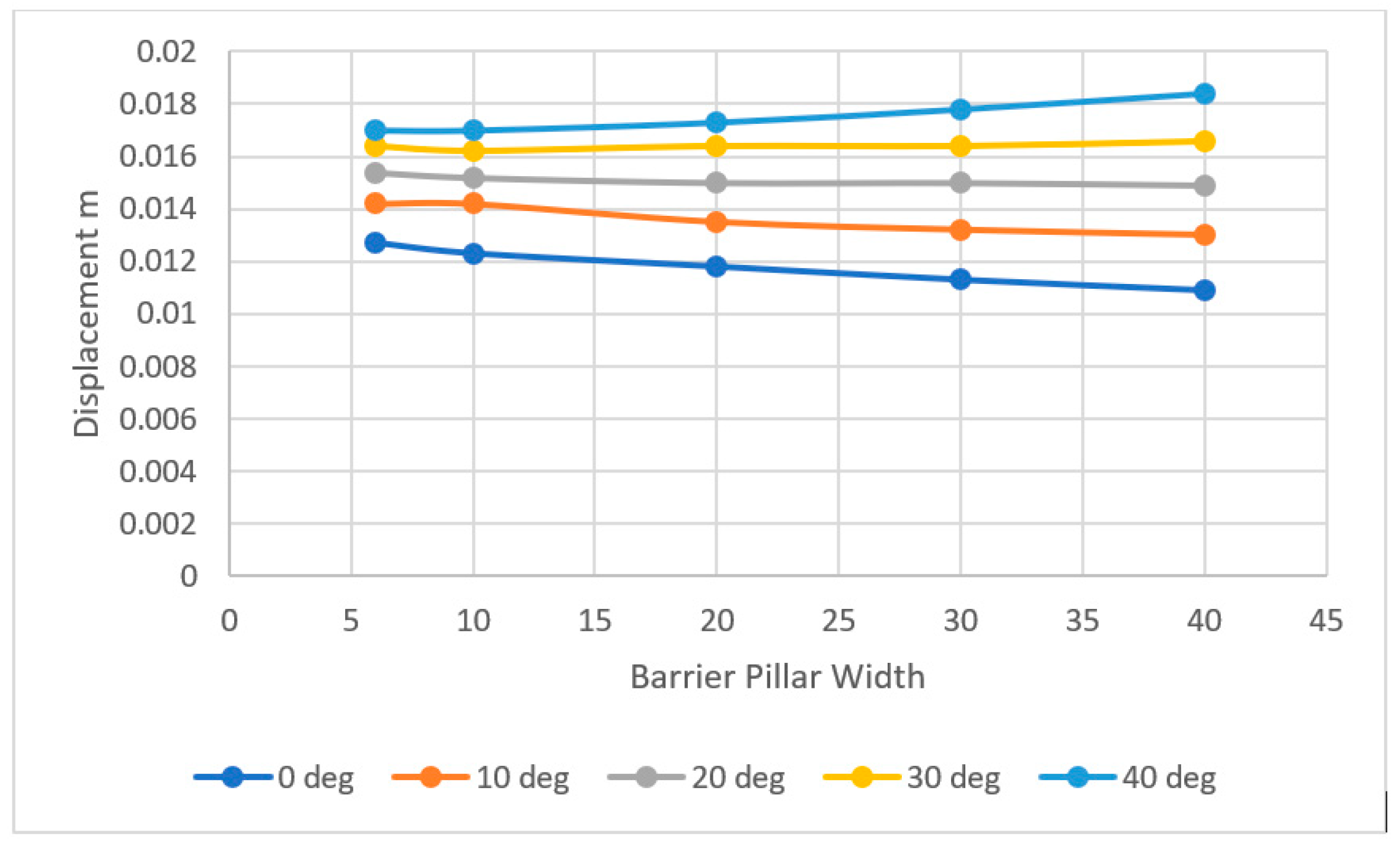
5.1. Effect of Barrier Pillar Width
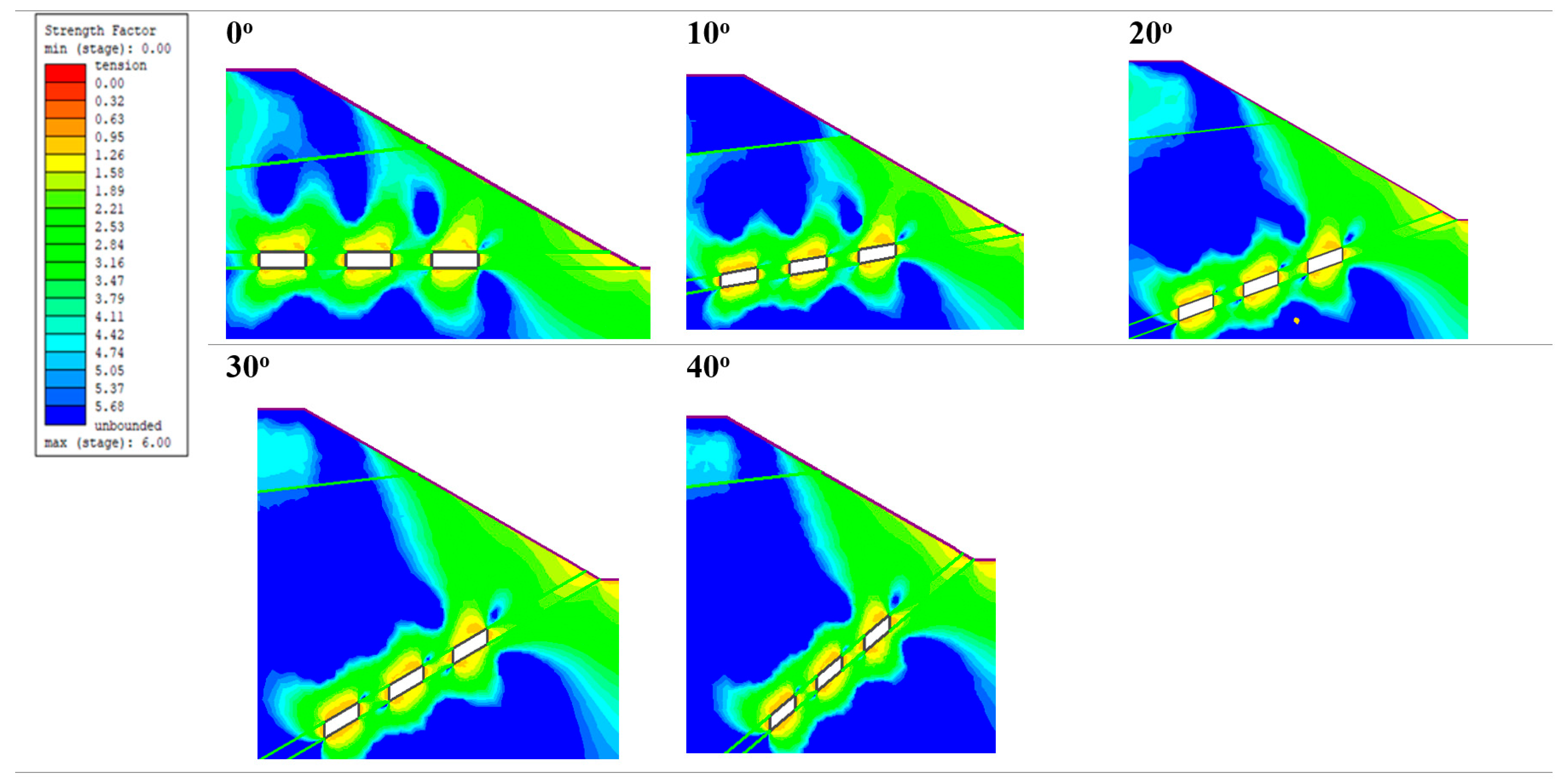
5.2. Effect of Orebody Dip Angle on the Barrier Pillar
5.3. Effect of Rock Mass Conditions on Barrier Pillar Width
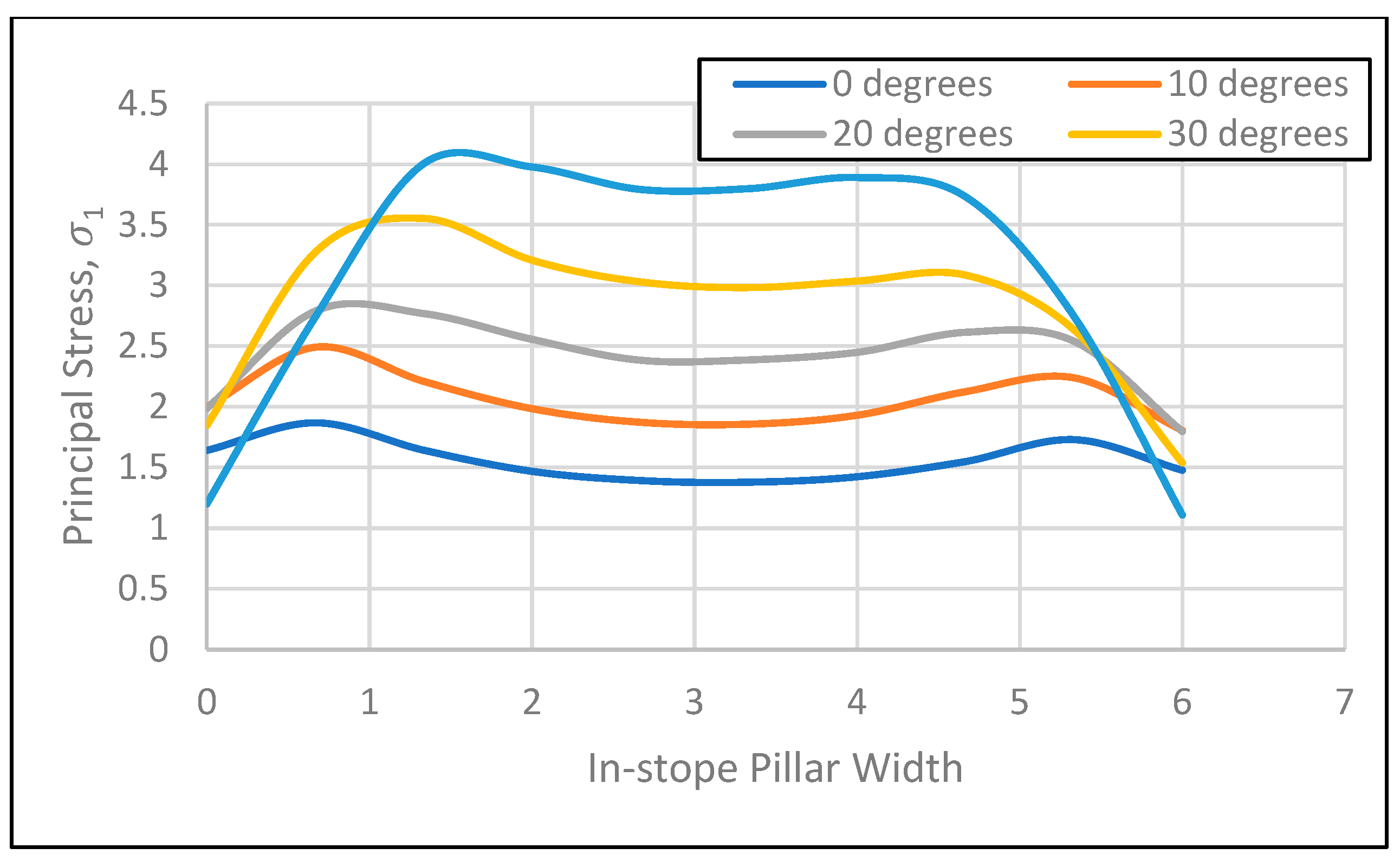
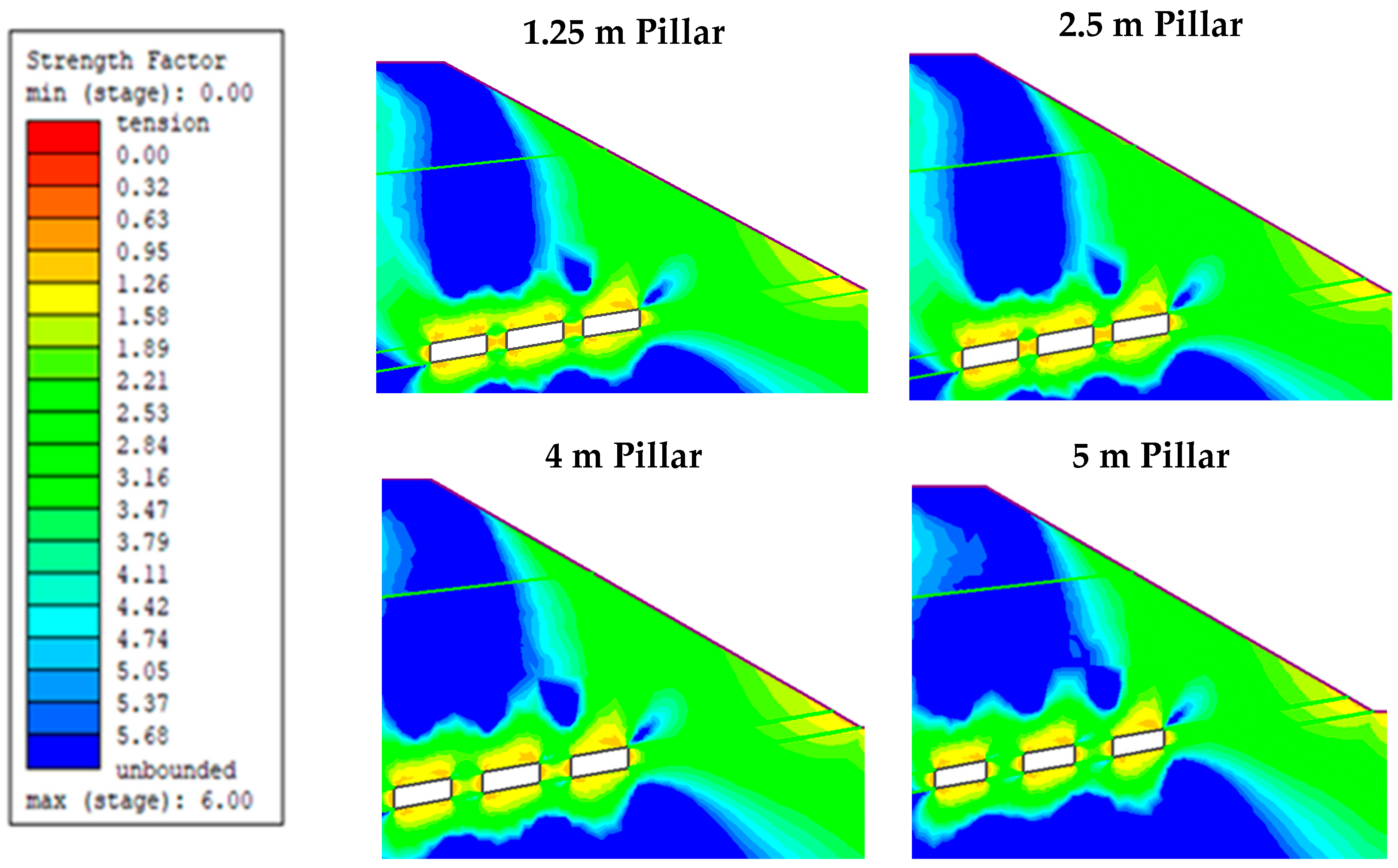
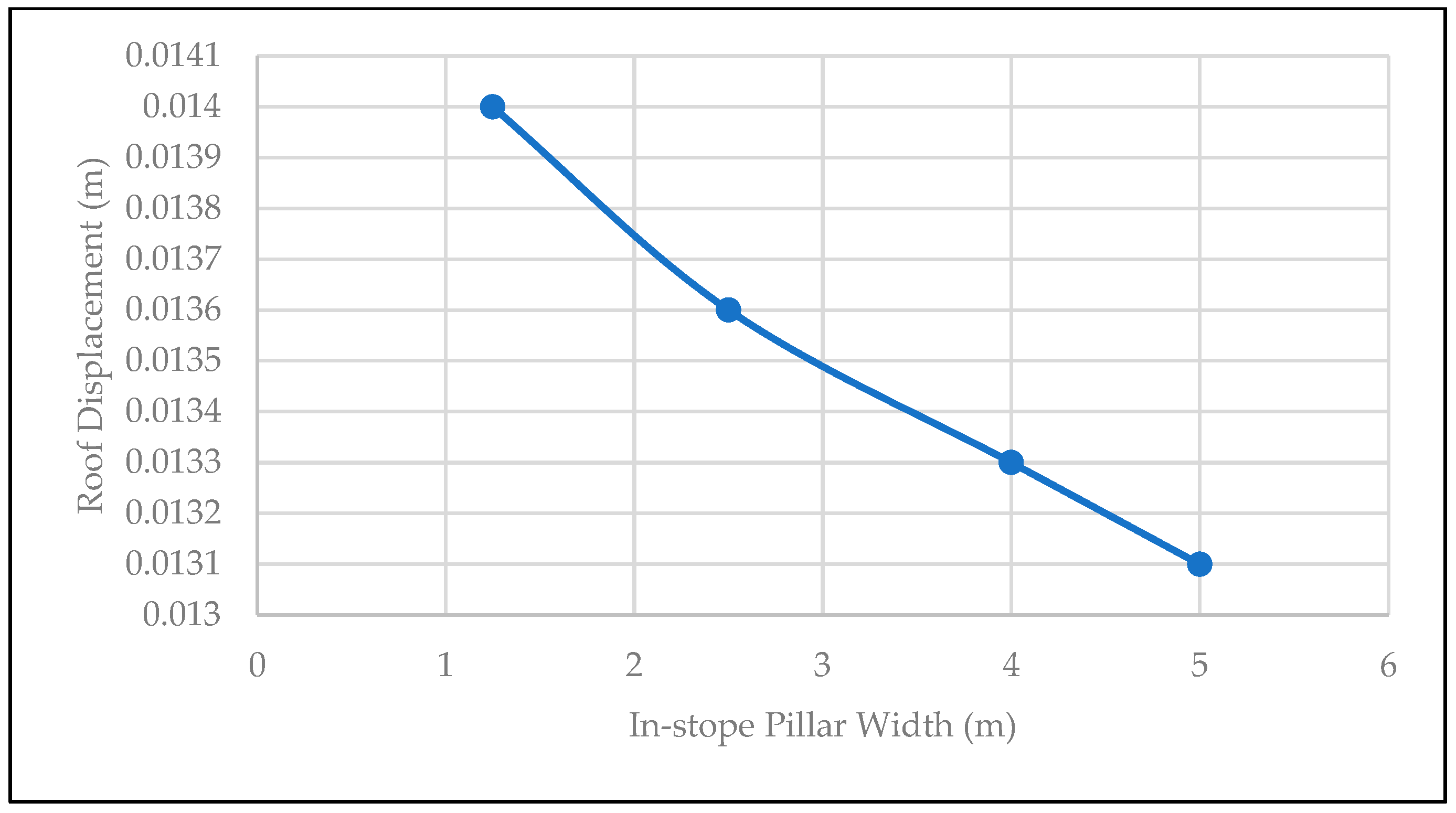
5.4. In-Stope Pillar Width Optimization of the Room and Pillar at the Case Study Mine
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dunn, M.J.; Parrott, T.T.; Wesseloo, J. Mine Portal Design: Considerations, Methods and Practices; Australian Centre for Geomechanics: Crawley, WA, Australia, 2023; pp. 237–254. [Google Scholar]
- Yardmci, A. Crown Pillar Optimization for Surface to Underground Mine Transition in Erzincan/Bizmisen Iron Mine. In Proceedings of the 50th U.S. Rock Mechanics/Geomechanics Symposium, Houston, TX, USA, 26–29 June 2016. [Google Scholar]
- Ozbay, M.U.; Ryder, J.A.; Jager, A.J. The Design of Pillar Systems as Practised in Shallow Hard-Rock Tabular Mines in South Africa. J. S. Afr. Inst. Min. Metall. 1995, 95, 7–18. Available online: https://www.saimm.co.za/Journal/v095n01p007.pdf (accessed on 14 July 2025).
- Mark, C. Empirical Methods for Coal Pillar Design. In Proceedings of the Second International Workshop on Coalpillar Mechanics and Design, Vail, CO, USA, 6 June 1999. [Google Scholar]
- Carter, T.G. Guidelines for Use of the Scaled Span Method for Surface Crown Pillar Stability Assessment; Ontario Ministry of Northern Development and Mines: Sudbury, ON, Canada, 2014. [Google Scholar]
- Zhao, X.; Li, L.; Tang, C.; Zhang, H. Stability of Boundary Pillars in Transition from Open Pit to Underground Mining. J. Cent. South Univ. 2012, 19, 3256–3265. [Google Scholar] [CrossRef]
- Kumar, H.; Deb, D.; Chakravarty, D. Design of Crown Pillar Thickness Using Finite Element Method and Multivariate Regression Analysis. Int. J. Min. Sci. Technol. 2017, 27, 955–964. [Google Scholar] [CrossRef]
- Dintwe, T.K.M.; Sasaoka, T.; Shimada, H.; Hamanaka, A.; Moses, D.N.; Peng, M.; Fanfei, M.; Liu, S.; Ssebadduka, R.; Onyango, J.A. Numerical Simulation of Crown Pillar Behaviour in Transition from Open Pit to Underground Mining. Geotech. Geol. Eng. 2022, 40, 2213–2229. [Google Scholar] [CrossRef]
- Das, A.J.; Mandal, P.K.; Paul, P.S.; Sinha, R.K. Generalised Analytical Models for the Strength of the Inclined as Well as the Flat Coal Pillars Using Rock Mass Failure Criterion. Rock Mech. Rock Eng. 2019, 52, 3921–3946. [Google Scholar] [CrossRef]
- Kabwe, E. Stability Analysis of Pillars in an Inclined Airleg Stope Under Static Loading Conditions. Geotech. Geol. Eng. 2024, 42, 1541–1572. [Google Scholar] [CrossRef]
- Dzimunya, N.; Fujii, Y.; Li, Z.; Amagu Amagu, C. Assessing Pillar Design Strategies in Hard Rock Room-and-Pillar Mining: A Review and Case Studies from the Great Dyke of Zimbabwe. Min. Metall. Explor. 2025, 42, 685–704. [Google Scholar] [CrossRef]
- Oberthür, T.; Melcher, F.; Buchholz, P.; Locmelis, M. The Oxidized Ores of the Main Sulphide Zone, Great Dyke, Zimbabwe: Turning Resources into Minable Reserves-Mineralogy Is the Key. J. S. Afr. Inst. Min. Metall. 2013, 113, 191–201. [Google Scholar]
- Wilson, A.H.; Prendergast, M.D. Platinum-Group Element Mineralisation in the Great Dyke, Zimbabwe, and Its Relationship to Magma Evolution and Magma Chamber Structure. S. Afr. J. Geol. 2001, 104, 319–342. [Google Scholar] [CrossRef]
- Chaumba, J.B.; Musa, C.T. Formation of the Main Sulfide Zone at Unki Mine, Shurugwi Subchamber of the Great Dyke, Zimbabwe: Constraints from Petrography and Sulfide Compositions. Geosphere 2020, 16, 685–710. [Google Scholar] [CrossRef]
- Li, C.; Ripley, E.M.; Oberthür, T.; Miller, J.D.; Joslin, G.D. Textural, Mineralogical and Stable Isotope Studies of Hydrothermal Alteration in the Main Sulfide Zone of the Great Dyke, Zimbabwe and the Precious Metals Zone of the Sonju Lake Intrusion, Minnesota, USA. Miner. Deposita 2008, 43, 97–110. [Google Scholar] [CrossRef]
- Carter, T.G. A New Approach to Surface Crown Pillar Design. In Proceedings of the 16th Canadian Rock Mechanics Symposium or the Sympodum Canadien de Mecaniques des Roches, Sudbury, ON, Canada, 15–19 June 1992. [Google Scholar]
- Hutchinson, D.J.; Phillips, C.; Cascante, G. Risk Considerations for Crown Pillar Stability Assessment for Mine Closure Planning. Geotech. Geol. Eng. 2002, 20, 41–64. [Google Scholar] [CrossRef]
- Enslin, Q.; Bosman, J.D. Pillar Stability Assessment Methodology for Massive Mines. In Proceedings of the SANIRE Symposium 2024, Muldersdrift, South Africa, 13–14 June 2024. [Google Scholar]
- Barton, N.; Lien, R.; Lunde, J. Engineering Classification of Rock Masses for the Design of Tunnel Support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Jing, L. A Review of Techniques, Advances and Outstanding Issues in Numerical Modelling for Rock Mechanics and Rock Engineering. Int. J. Rock Mech. Min. Sci. 2003, 40, 283–353. [Google Scholar] [CrossRef]
- Zhang, W.; Dai, B.; Liu, Z.; Zhou, C. Modeling Discontinuous Rock Mass Based on Smoothed Finite Element Method. Comput. Geotech. 2016, 79, 22–30. [Google Scholar] [CrossRef]
- Lemos, J.V. Discontinuum Modelling in Rock Engineering. Soils Rocks 2013, 36, 137–156. [Google Scholar] [CrossRef]
- Vyazmensky, A.; Elmo, D.; Stead, D.; Rance, J. Numerical Analysis of the Influence of Geological Structures on the Development of Surface Subsidence Associated with Block Caving Mining. In Proceedings of the 5th Conference and Exhibition on Mass Mining, Lulea, Sweden, 9–11 June 2008. [Google Scholar]
- Osthus, D.; Godinez, H.C.; Rougier, E.; Srinivasan, G. Calibrating the Stress-Time Curve of a Combined Finite-Discrete Element Method to a Split Hopkinson Pressure Bar Experiment. Int. J. Rock Mech. Min. Sci. 2018, 106, 278–288. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. The Hoek–Brown Failure Criterion and GSI—2018 Edition. J. Rock Mech. Geotech. Eng. 2019, 11, 445–463. [Google Scholar] [CrossRef]
- Kaiser, P.K.; Kim, B.; Bewick, R.P.; Valley, B. Rock Mass Strength at Depth and Implications for Pillar Design. Min. Technol. 2011, 120, 170–179. [Google Scholar] [CrossRef]
- Brown, E.T.; Potvin, Y.; Carter, J.; Dyskin, A.; Jeffrey, R. Estimating the Mechanical Properties of Rock Masses; Australian Centre for Geomechanics: Crawley, WA, Australia, 2008; pp. 3–22. [Google Scholar]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek-Brown Failure Criterion—2002 Edition. In Mining and Tunnelling Innovation and Opportunity: NARMS-TAC 2002, Proceedings of the 5th North American Rock Mechanics Symposium and 17th Tunnelling Association of Canada Conference, Toronto, ON, Canada, 7–10 July 2002. Available online: https://www.rocscience.com/assets/resources/learning/hoek/Hoek-Brown-Failure-Criterion-2002.pdf (accessed on 14 July 2025).
- Bahrani, N.; Kaiser, P.K. Influence of Degree of Interlock on Confined Strength of Jointed Hard Rock Masses. J. Rock Mech. Geotech. Eng. 2020, 12, 1152–1170. [Google Scholar] [CrossRef]
- Munemo, P. Prediction of Ground Instability for Coinciding Mining Operations. Master’s Thesis, University of the Witwatersrand, Johannesburg, South Africa, 2021. [Google Scholar]
- Napa-García, G.F.; Câmara, T.R.; Navarro Torres, V.F. Optimization of Room-and-Pillar Dimensions Using Automated Numerical Models. Int. J. Min. Sci. Technol. 2019, 29, 797–801. [Google Scholar] [CrossRef]




| Rock Type | Unit Weight (MN/m3) | Poisson’s Ration | Young’s Modulus (GPa) | UCS (MPa) | Hoek–Brown Parameters | ||||
|---|---|---|---|---|---|---|---|---|---|
| GSI | mi | mb | s | a | |||||
| Gabbro Norite | 0.029 | 0.3 | 100 | 201 | 50 | 20 | 3.354 | 0.00387 | 0.506 |
| Websterite | 0.033 | 0.25 | 125 | 225 | 43 | 27 | 3.526 | 0.00178 | 0.509 |
| MSZ | 0.033 | 0.24 | 65 | 170 | 40 | 22 | 2.581 | 0.00127 | 0.511 |
| Bronzitite | 0.029 | 0.29 | 30.2 | 199 | 45 | 25 | 3.506 | 0.00221 | 0.508 |
| Class | Probability of Failure % | Minimum Factor of Safety | Maximum Scaled Span, Cs (=Sc) | ESR (Barton et al., [19]) | Design Guidelines for Pillar Acceptability/Serviceable Life of Crown Pillar | ||||
|---|---|---|---|---|---|---|---|---|---|
| Expectancy | Years | Public Access | Regulatory Position on Closure | Operating Surveillance Required | |||||
| A | 50–100 | <1 | 11.31Q0.44 | >5 | Effectively zero | <0.5 | Forbidden | Totally unacceptable | Ineffective |
| B | 20–50 | 1.0 | 3.58Q0.44 | 3 | Very, very short-term (temporary mining purposes only); unacceptable risk of failure for temporary civil tunnel portals | 1.0 | Forcibly Prevented | Not acceptable | Continuous sophisticated monitoring |
| C | 10–20 | 1.2 | 2.74Q0.44 | 2 | Very short-term (quasi-temporary stope crowns; undesirable risk of failure for temporary civil works) | 2–5 | Actively prevented | High level of concern | Continuous monitoring with instruments |
| D | 5–10 | 1.5 | 2.33Q0.44 | 1.6 | Short-term (semi-temporary crowns, e.g., under non-sensitive mine infrastructure) | 5–10 | Prevented | Moderate level of concern | Continuous simple monitoring |
| E | 1.5–5 | 1.8 | 1.84Q0.44 | 1.3 | Medium-term (semi-permanent crowns, possibly under structures) | 15–20 | Discouraged | Low to moderate level of concern | Conscious superficial monitoring |
| F | 0.5–1.5 | 2.0 | 1.12Q0.44 | 1 | Long-term (quasi-permanent crowns, civil portals, near-surface sewer tunnels) | 50–100 | Allowed | Of limited concern | Incidental superficial monitoring |
| G | <0.5 | >>2 | 0.69Q0.44 | 0.8 | Very long-term (permanent crowns over civil tunnels) | >100 | Free | Of no concern | None required |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ncube, B.; Shimada, H.; Sasaoka, T.; Hamanaka, A.; Kawano, K.; Onyango, J.A. Geotechnical Design of Barrier Pillar Between Boxcut and Underground Mining for Shallow Dipping Orebodies: A Case Study. Mining 2025, 5, 56. https://doi.org/10.3390/mining5030056
Ncube B, Shimada H, Sasaoka T, Hamanaka A, Kawano K, Onyango JA. Geotechnical Design of Barrier Pillar Between Boxcut and Underground Mining for Shallow Dipping Orebodies: A Case Study. Mining. 2025; 5(3):56. https://doi.org/10.3390/mining5030056
Chicago/Turabian StyleNcube, Benedict, Hideki Shimada, Takashi Sasaoka, Akihiro Hamanaka, Koki Kawano, and Joan Atieno Onyango. 2025. "Geotechnical Design of Barrier Pillar Between Boxcut and Underground Mining for Shallow Dipping Orebodies: A Case Study" Mining 5, no. 3: 56. https://doi.org/10.3390/mining5030056
APA StyleNcube, B., Shimada, H., Sasaoka, T., Hamanaka, A., Kawano, K., & Onyango, J. A. (2025). Geotechnical Design of Barrier Pillar Between Boxcut and Underground Mining for Shallow Dipping Orebodies: A Case Study. Mining, 5(3), 56. https://doi.org/10.3390/mining5030056