Numerical Investigation of Ultra-Long Gravity Heat Pipe Systems for Geothermal Power Generation at Mount Meager
Abstract
1. Introduction
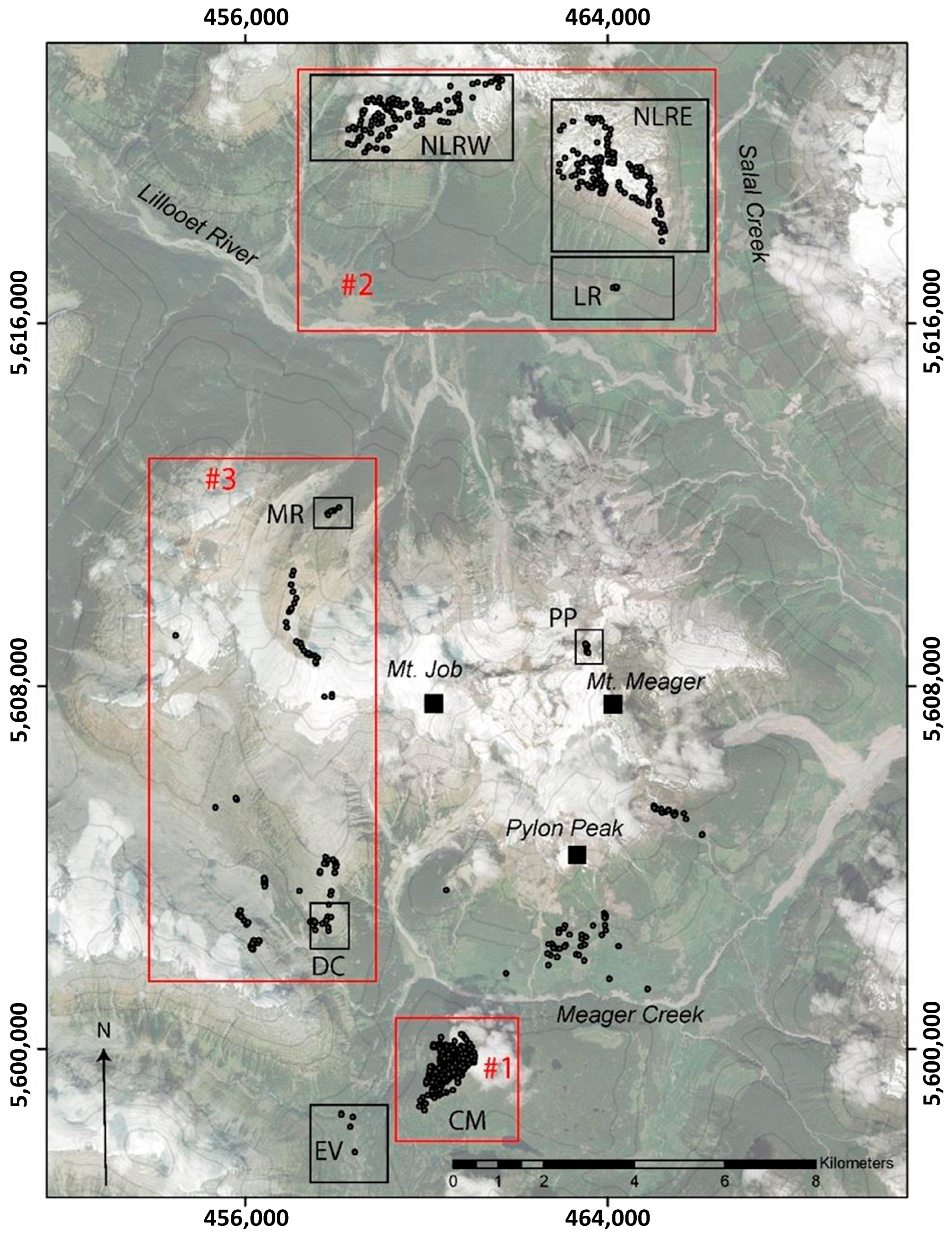
2. Mt Meager Geothermal Resources and Wellbore Assessment
3. Heat Pipe Technology Scheme Selection and Design Optimization
3.1. Principle of Closed Super-Long Gravity Heat Pipe
3.2. Working Fluid Selection and Performance Analysis
3.3. Structural Parameter Optimization of the Heat Pipe
4. Thermal Performance Simulation and Validation
4.1. Thermal Performance Simulation Framework
4.2. Steady-State Simulation Validation Results
4.2.1. Test Matrix Design for Simulation
4.2.2. Numerical Simulation Methods and Boundary Conditions
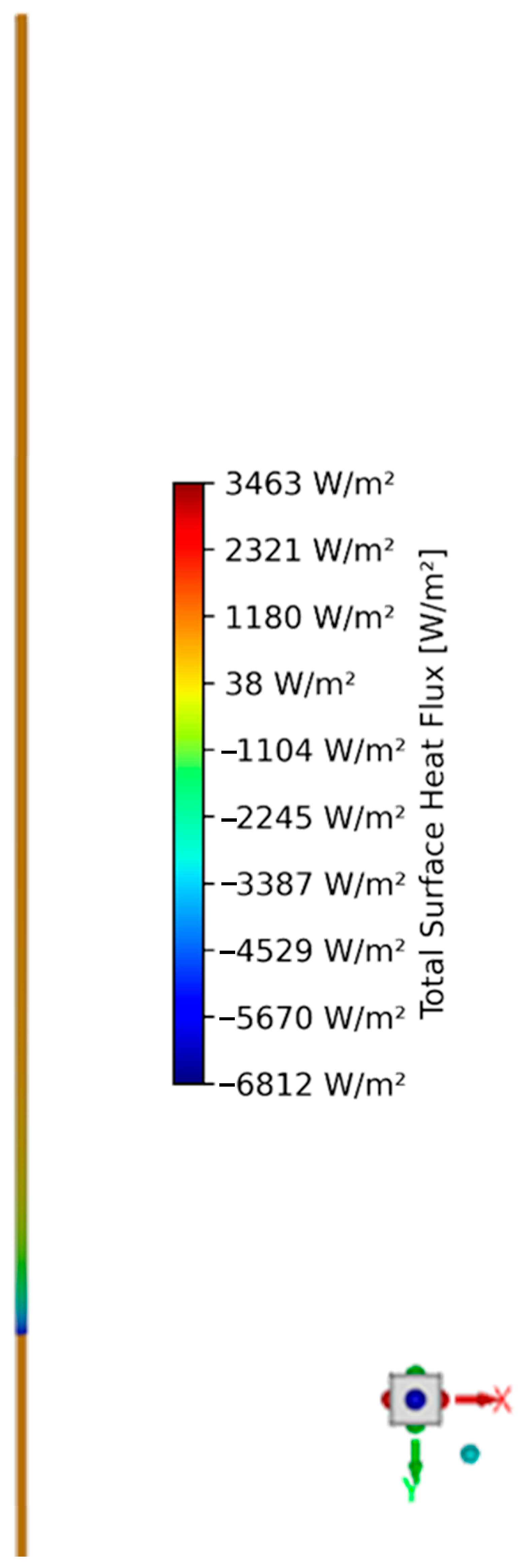
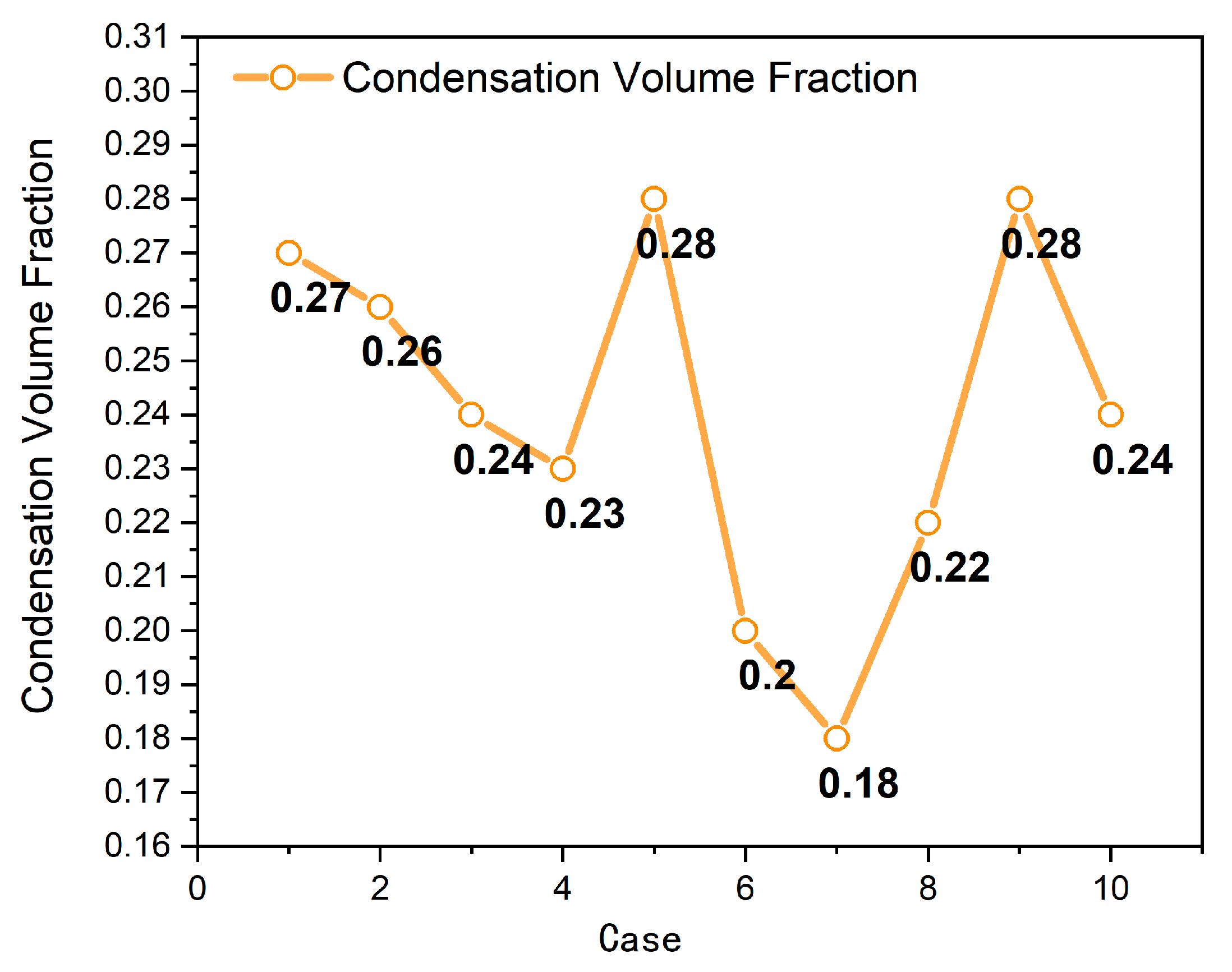
4.2.3. Steady-State Simulation Results and Model Validation
4.2.4. Comparison with Published Field-Scale Results
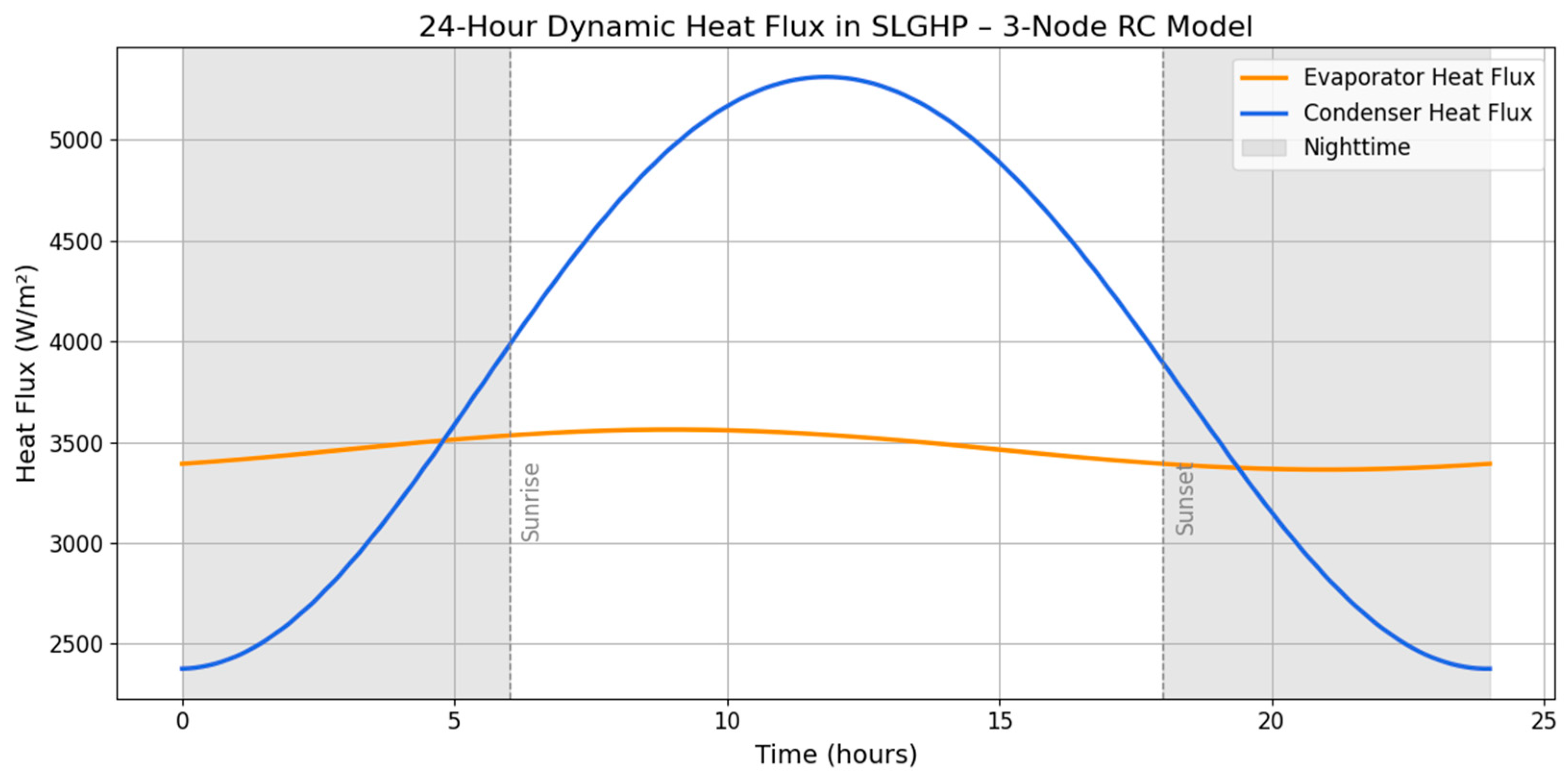
4.3. Dynamic Thermal Performance Analysis
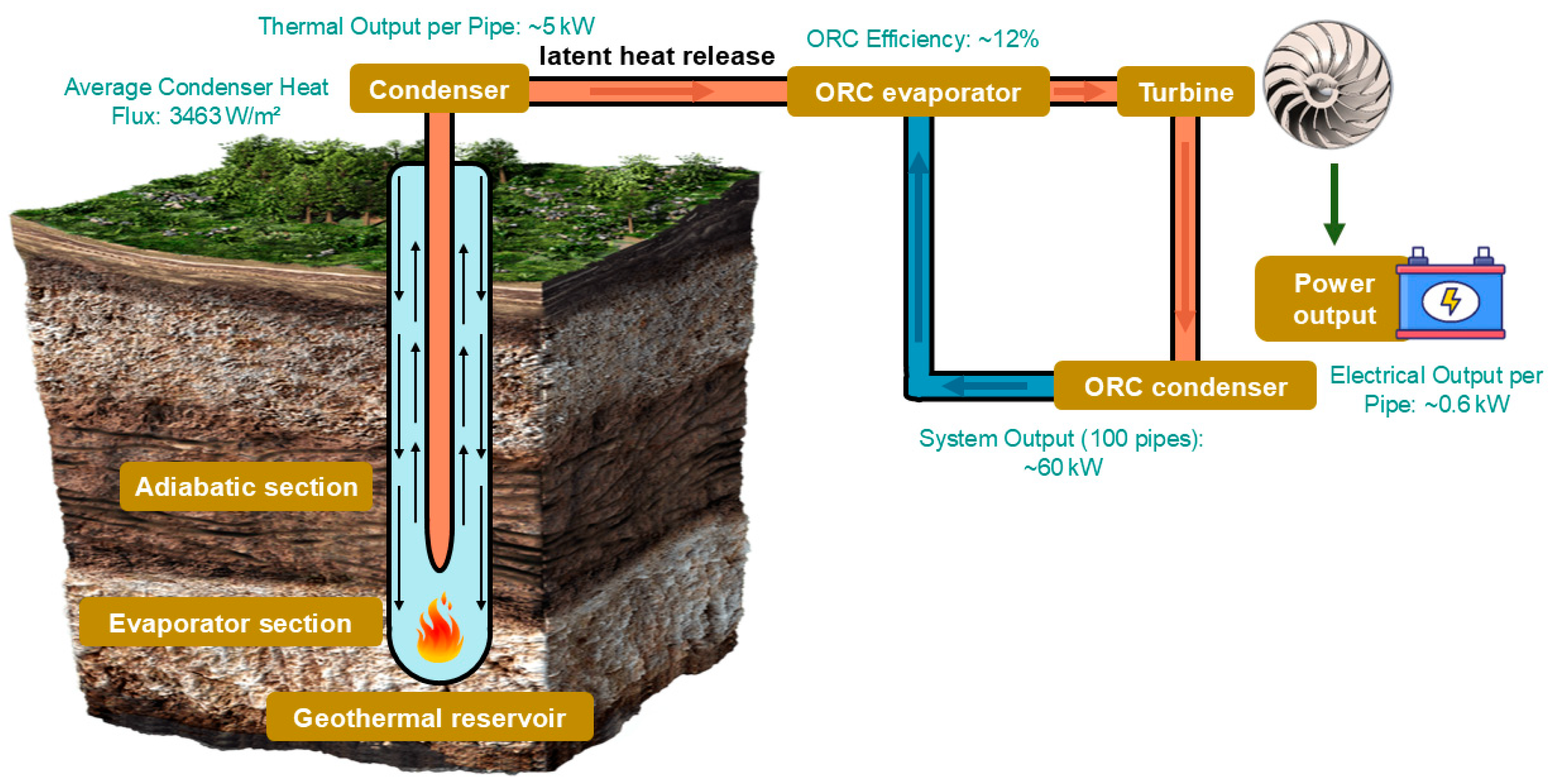
4.4. Power Generation Potential and System Concept
5. System Engineering Challenges and Economic Feasibility Discussion
5.1. Investment Cost
5.2. Operation Cost Model
5.3. Revenue Model
5.4. Sensitivity Analysis of Economic Parameters
5.5. Coupling Thermal Performance with Economic Outcomes
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
1D TRN Python Code for Heat Flux Estimation
| import numpy as np # ---------------------------- # Input Parameters (SI Units) # ---------------------------- L = 1200 # [m] Pipe length (based on Case 1 configuration) r_i = 0.038 # [m] Inner radius of 76 mm pipe (ID) r_o = r_i + 0.003 # [m] Outer radius assuming 3 mm wall thickness r_inf = r_o * 1.01 # [m] Far-field boundary for radial conduction (slightly > r_o) k_wall = 16 # [W/m·K] Thermal conductivity of 304 stainless steel (pipe wall) k_geo = 2.5 # [W/m·K] Thermal conductivity of surrounding formation (Mount Meager data) h_cond = 15.083 # [W/m2·K] Convective HTC at condenser surface (from CFD) T_bottom = 260 + 273.15 # [K] Deep reservoir temperature T_top = 35 + 273.15 # [K] Surface condenser temperature # Outer surface area of the SLGHP A_outer = 2 * np.pi * r_o * L # [m2] # ---------------------------- # Thermal Resistance Calculations # ---------------------------- R_geo = np.log(r_inf / r_o) / (2 * np.pi * k_geo * L) # Rock formation conduction resistance R_wall = np.log(r_o / r_i) / (2 * np.pi * k_wall * L) # Pipe wall conduction resistance R_cond = 1.0 / (h_cond * A_outer) # Condenser-side convective resistance R_total = R_geo + R_wall + R_cond # [K/W] Overall thermal resistance # ---------------------------- # Heat Transfer Calculations # ---------------------------- Q_total = (T_bottom−T_top) / R_total # [W] Total heat transfer rate q_flux = Q_total / A_outer # [W/m2] Surface heat flux density # ---------------------------- # Output Result # ---------------------------- print(f"Estimated heat flux by 1D TRN model (Case 1): {q_flux:.1f} W/m2") |
Appendix B
Python Simulation Code of the 3-Node RC Thermal Network Model
| import numpy as np import matplotlib.pyplot as plt # ---------------------------- # Time Vector: 24-hour period # ---------------------------- t = np.linspace(0, 24, 1000) # [hours] # ---------------------------- # Node 1—Geothermal Source # ---------------------------- T_ground = 260 # [°C] Constant geothermal source temperature # ---------------------------- # Node 2—Working Fluid in Evaporator Section # ---------------------------- T_fluid_steady = 100 # [°C] Steady-state temperature from CFD C_eff = 1.5 # Damping coefficient for thermal inertia T_fluid = T_fluid_steady + 2 * np.sin(2 * np.pi * (t−3) / 24) * np.exp(−C_eff * 0.1) # ---------------------------- # Node 3—Ambient Air at Condenser # ---------------------------- T_env = −12.5 + 7.5 * np.sin(2 * np.pi * (t−6) / 24) # [°C] Diurnal ambient temperature h = 35 + 15 * np.sin(2 * np.pi * (t−6) / 24) # [W/m2·K] Convective heat transfer coefficient # ---------------------------- # Heat Flux Calculations # ---------------------------- q_cond = h * (T_fluid−T_env) # Condenser heat flux [W/m2] q_evap = 3463 + 100 * np.sin(2 * np.pi * (t−3) / 24) # Evaporator heat flux [W/m2] # ---------------------------- # Plotting # ---------------------------- plt.figure(figsize=(12, 6)) plt.plot(t, q_evap, label='Evaporator Heat Flux', color='darkorange', linewidth=2.5) plt.plot(t, q_cond, label='Condenser Heat Flux', color='royalblue', linewidth=2.5) # Add nighttime shading (0–6 and 18–24 hours) plt.axvspan(0, 6, color='gray', alpha=0.2, label='Nighttime') plt.axvspan(18, 24, color='gray', alpha=0.2) # Annotate sunrise and sunset plt.axvline(6, color='gray', linestyle='--', linewidth=1) plt.axvline(18, color='gray', linestyle='--', linewidth=1) plt.text(6.2, max(q_evap)*0.96, 'Sunrise', rotation=90, va='top', fontsize=12, color='gray') plt.text(18.2, max(q_evap)*0.96, 'Sunset', rotation=90, va='top', fontsize=12, color='gray') # Axis labels and title plt.xlabel('Time (hours)', fontsize=14) plt.ylabel('Heat Flux (W/m2)', fontsize=14) plt.title('24-Hour Dynamic Heat Flux in SLGHP – 3-Node RC Model', fontsize=16) # Font sizes and legend plt.xticks(fontsize=12) plt.yticks(fontsize=12) plt.legend(loc='upper right', fontsize=12) plt.grid(True) plt.tight_layout() # Display the plot plt.show() |
References
- Barbier, E. Geothermal energy technology and current status: An overview. Renew. Sustain. Energy Rev. 2002, 6, 3–65. [Google Scholar] [CrossRef]
- Reinsch, T.; Dobson, P.; Asanuma, H.; Huenges, E.; Poletto, F.; Sanjuan, B. Utilizing supercritical geothermal systems: A review of past ventures and ongoing research activities. Geotherm. Energy 2017, 5, 16. [Google Scholar] [CrossRef]
- Lewis, T.J.; Souther, J.G. Meager Mountain, B.C.: A Possible Geothermal Energy Resource; Energy, Mines and Resources Canada, Earth Physics Branch: Ottawa, ON, Canada, 1978. [Google Scholar]
- Geoscience, B.C. Garibaldi Geothermal Volcanic Belt Project Summary; Technical Report; Geoscience BC: Vancouver, BC, Canada, 2017; Available online: https://www.geosciencebc.com (accessed on 6 July 2025).
- Allen, S. Searching for Mount Meager’s Geothermal Heart. In Eos–Science Updates; American Geophysical Union: Washington, DC, USA, 2023; Available online: https://eos.org/science-updates/searching-for-mount-meagers-geothermal-heart (accessed on 25 August 2025).
- Evans, K.F.; Zappone, A.; Kraft, T.; Deichmann, N.; Moia, F. A survey of the induced seismic responses to fluid injection in geothermal and CO2 reservoirs in Europe. Geothermics 2012, 41, 30–54. [Google Scholar] [CrossRef]
- Majer, E.L.; Baria, R.; Stark, M.; Oates, S.; Bommer, J.; Smith, B.; Asanuma, H. Induced seismicity associated with Enhanced Geothermal Systems. Geothermics 2007, 36, 185–222. [Google Scholar] [CrossRef]
- Miller, S. Modeling enhanced geothermal systems and the essential nature of large-scale changes in permeability at the onset of slip. Geofluids 2015, 15, 338–349. [Google Scholar]
- Kelly, J.; McDermott, C. Numerical modelling of a deep closed-loop geothermal system: Evaluating the Eavor-Loop. AIMS Geosci. 2022, 8, 175–212. [Google Scholar] [CrossRef]
- Liu, L.; Yu, H.-L.; Wang, Y.-Y.; Wang, H.-B.; Zhu, B.-Z.; Sun, Y.-L.; Huang, L.-Y.; Wu, S.-C. Exploitation of Geothermal Energy by Installing Gravity Heat Pipe in Abandoned Oil and Gas Wells. In Proceedings of the International Field Exploration and Development Conference 2021, Singapore, 1–3 November 2021; Lin, J.E., Ed.; Springer Nature: Singapore, 2022; pp. 3604–3617. [Google Scholar]
- Ma, W.; Chen, Y.; Wang, Y.; Yang, C.; Yang, C.; Xiao, C.; Liu, G. Multi-parameter design and optimization of enhanced geothermal system based on unit effective permeable area. Appl. Therm. Eng. 2023, 225, 120184. [Google Scholar] [CrossRef]
- Nemec, P. Gravity in Heat Pipe Technology. In Gravity-Geoscience Applications, Industrial Technology and Quantum Aspect; IntechOpen: London, UK, 2018. [Google Scholar][Green Version]
- Anand, R.S.; Li, A.; Huang, W.; Chen, J.; Li, Z.; Ma, Q.; Jiang, F. Super-long gravity heat pipe for geothermal energy exploitation—A comprehensive review. Renew. Sustain. Energy Rev. 2024, 193, 114286. [Google Scholar] [CrossRef]
- Gselman, U.; Peršak, V.; Goričanec, D. Numerical Analysis of Low-Enthalpy Deep Geothermal Energy Extraction Using a Novel Gravity Heat Pipe Design. Sustainability 2024, 16, 6660. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Huang, W.; Ma, Q.; Li, A.; Wang, B.; Sun, H.; Jiang, F. Super-long gravity heat pipe geothermal space heating system: A practical case in Taiyuan, China. Energy 2024, 299, 131521. [Google Scholar] [CrossRef]
- Geoscience, B.C. Garibaldi Geothermal Energy Project-Phase 1; Geoscience BC: Vancouver, BC, Canada, 2021. [Google Scholar]
- Geological Survey of Cananda Geothermal Measurements in the Mount Meager Area, British Columbia, Canada; Geological Survey of Canada: Ottawa, ON, Canada, 2022.
- Chai, Y.; Chen, Z.; Yin, S. A Preliminary Analysis of In-Situ Stress at Mount Meager by Displacement Discontinuity Method with Topography and Tectonics Considered. Energies 2023, 16, 1397. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Zheng, B.-C.; Wang, Q.; Li, S.-S. Study on the thermal storage performance of a gravity-assisted heat-pipe thermal storage unit with granular high-temperature phase-change materials. Energy 2015, 81, 754–765. [Google Scholar]
- Chen, J.; Huang, W.; Cen, J.; Li, Z.; Li, F.; Li, A.; Sun, H.; Lin, W.; Ma, Q.; Jiang, F. Operational characteristics of the super-long gravity heat pipe for geothermal energy exploitation. Appl. Therm. Eng. 2024, 236, 121530. [Google Scholar]
- Rahbar, K.; Mahmoud, S.; Al-Dadah, R.K.; Moazami, N.; Mirhadizadeh, S.A. Review of organic Rankine cycle for small-scale applications. Energy Convers. Manag. 2017, 134, 135–155. [Google Scholar] [CrossRef]
- C.A.I. Technologies. Heat Pipe Systems Brochure; Version 3; C.A.I. Technologies: Sheffield, UK, 2019. [Google Scholar]
- Gao, T.; Long, X.; Xie, H.; Sun, L.; Wang, J.; Li, C.; Gao, M.; Xia, E. A review of advances and applications of geothermal energy extraction using a gravity-assisted heat pipe. Geothermics 2024, 116, 102856. [Google Scholar]
- DiPippo, R. Geothermal Power Plants: Principles, Applications, Case Studies and Environmental Impact, 4th ed.; Butterworth-Heinemann: Amsterdam, The Netherlands, 2015; pp. 1–762. [Google Scholar]
- Gallup, D.L. Production engineering in geothermal technology: A review. Geothermics 2009, 38, 326–334. [Google Scholar] [CrossRef]
- DiPippo, R. Geothermal Power Plants: Principles, Applications, Case Studies and Environmental Impact; Butterworth-Heinemann: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Choi, Y.-S.; Nešic, S. Corrosion Behavior Of Carbon Steel In Supercritical CO2-Water Environments. In Proceedings of the CORROSION 2009, Atlanta, GA, USA, 22–26 March 2009; pp. 1–20. [Google Scholar]
- Zarrouk, S.J.; Moon, H. Efficiency of geothermal power plants: A worldwide review. Geothermics 2014, 51, 142–153. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H.; Wang, Y.; Zhu, Y. CFD simulation of dynamic heat transfer behaviors in super-long thermosyphons for shallow geothermal application. Appl. Therm. Eng. 2020, 174, 115295. [Google Scholar] [CrossRef]
- DiPippo, R. Geothermal Power Plants: Principles, Applications and Case Studies; Butterworth-Heinemann: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Ochsner, K. Geothermal Heat Pumps: A Guide for Planning and Installing; Earthscan: Abingdon, UK, 2008. [Google Scholar]
- Abdulshaheed, A.A.; Wang, P.; Huang, G.; Zhao, Y.; Li, C. Filling Ratio Optimization for High-Performance Nanoengineered Copper-Water Heat Pipes. J. Therm. Sci. Eng. Appl. 2021, 13, 051025. [Google Scholar]
- Lu, X.; Liu, J.; Tong, X.; Dai, R.; Xiao, Y.; Deng, J. Experimental investigation on thermal performance of gravity heat pipe with different pipe configurations. Case Stud. Therm. Eng. 2025, 65, 105695. [Google Scholar]
- Renaud, X.; Zarrouk, S. In Supercritical CO2 as Heat Transmission Fluid in Deep Closed-Loop Geothermal Systems: A Review. In Proceedings of the Stanford Geothermal Workshop, Standford, CA, USA, 12–14 February 2018. [Google Scholar]
- Rajasekar, K.; Raja, B. Heat and mass transfer characteristics during spray drying of Na2Fe0.6Mn0.4PO4F/C cathode material for Na-ion batteries. Appl. Therm. Eng. 2023, 221, 119838. [Google Scholar] [CrossRef]
- Wu, W.; Yang, X.; Zhang, G.; Chen, K.; Wang, S. Experimental investigation on the thermal performance of heat pipe-assisted phase change material based battery thermal management system. Energy Convers. Manag. 2017, 138, 486–492. [Google Scholar] [CrossRef]
- Cai, C.; Wang, Y.; Fang, J.; Chen, H.; Zheng, Q.; Zhang, H. Multiple aspects to flight mission performances improvement of commercial turbofan engine via variable geometry adjustment. Energy 2023, 263, 125693. [Google Scholar] [CrossRef]
- Barthwal, M.; Rakshit, D. No fins attached? Numerical analysis of internal–external fins coupled PCM melting for solar applications. Appl. Therm. Eng. 2022, 215, 118911. [Google Scholar] [CrossRef]
- Li, J.; Qiao, L.; Chen, M.; Song, D.; Zeng, X. Metal oxide nanofluid-enhanced closed-loop pulsating heat pipes considering the characteristics of base solution: Thermal performance improvement for battery thermal management in cryogenics. Energy 2025, 333, 137409. [Google Scholar] [CrossRef]
- Adepoju, Y.; Shor, R.; Chen, Z. Geothermal Energy Development in the Canadian Cordillera, a Case Study. GRC Trans. 2020, 44, 768–783. [Google Scholar]
- Tartière, T.; Astolfi, M. A World Overview of the Organic Rankine Cycle Market. Energy Procedia 2017, 129, 2–9. [Google Scholar] [CrossRef]
- Tocci, L.; Pal, T.; Pesmazoglou, I.; Franchetti, B. Small Scale Organic Rankine Cycle (ORC): A Techno-Economic Review. Energies 2017, 10, 413. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, X.; Wu, D.; Huang, X.; Wang, X.; Yang, Y.; Wen, C. A comparative study on design and performance evaluation of Organic Rankine Cycle (ORC) under different two-phase heat transfer correlations. Appl. Energy 2023, 350, 121724. [Google Scholar] [CrossRef]
- Teodoriu, C.; Falcone, G. Comparing completion design in hydrocarbon and geothermal wells: The need to evaluate the integrity of casing connections subject to thermal stresses. Geothermics 2009, 38, 238–246. [Google Scholar] [CrossRef]
- Walraven, D.; Laenen, B.; D’haeseleer, W. Minimizing the levelized cost of electricity production from low-temperature geothermal heat sources with ORCs: Water or air cooled? Appl. Energy 2015, 142, 144–153. [Google Scholar] [CrossRef]
- Pethurajan, V.; Sivan, S.; Joy, G.C. Issues, comparisons, turbine selections and applications–An overview in organic Rankine cycle. Energy Convers. Manag. 2018, 166, 474–488. [Google Scholar] [CrossRef]



| Case | Working Fluid | Pipe Diameter (mm) | Pipe Length (m) | Filling Ratio (%) | Material |
|---|---|---|---|---|---|
| 1 | H2O | 76 | 1200 | 40 | 304 SS |
| 2 | H2O | 90 | 1200 | 40 | 304 SS |
| 3 | H2O | 114 | 1200 | 40 | 304 SS |
| 4 | H2O | 90 | 600 | 40 | 304 SS |
| 5 | H2O | 90 | 2000 | 40 | 304 SS |
| 6 | NH3 | 76 | 1200 | 40 | 304 SS |
| 7 | CO2 | 76 | 1200 | 40 | 304 SS |
| 8 | H2O | 90 | 1200 | 30 | 304 SS |
| 9 | H2O | 90 | 1200 | 50 | 304 SS |
| 10 | H2O | 90 | 1200 | 40 | Aluminum |
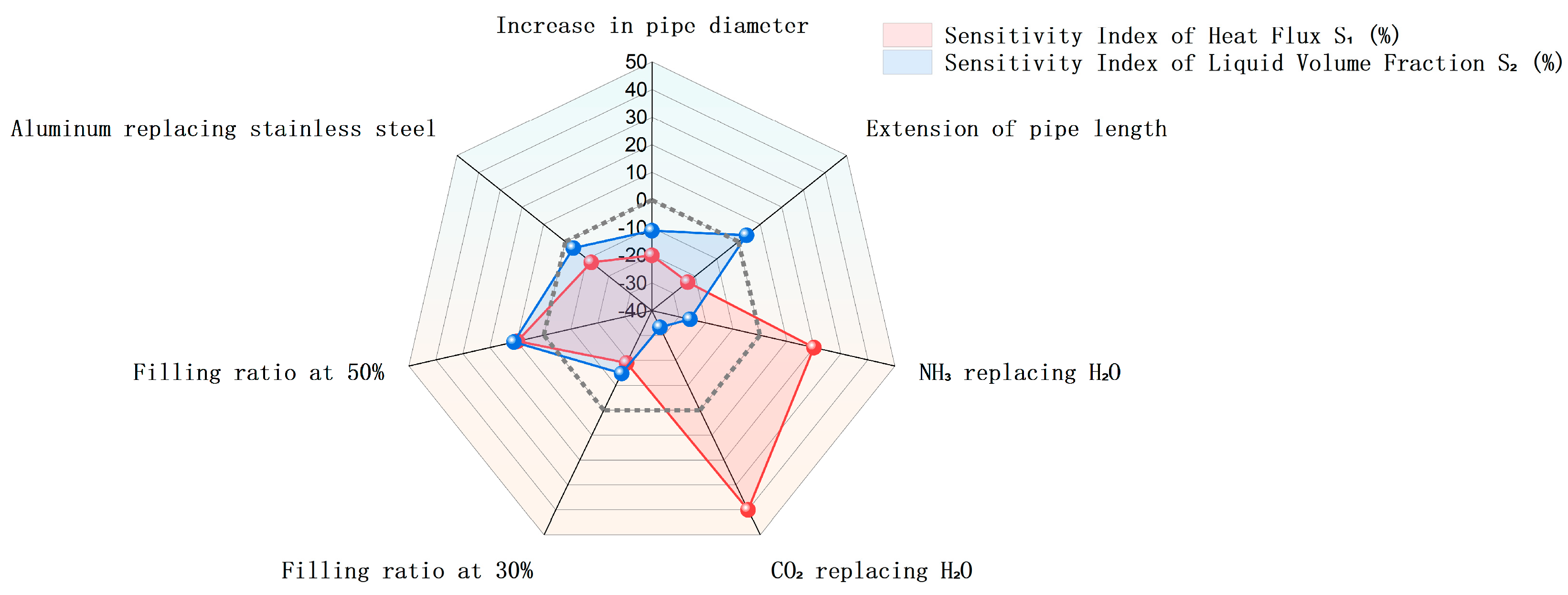
| Parameter | Δ Heat Flux (W/m2) | Sensitivity Index of Heat Flux (%) | Δ Liquid Volume Fraction | Sensitivity Index of Liquid Volume Fraction (%) |
|---|---|---|---|---|
| Increase in pipe diameter | −1362.4 | −20 | −0.03 | −11.1 |
| Extension of pipe length | −1600.8 | −23.5 | 0.01 | 3.7 |
| NH3 replacing H2O | 1362.4 | 20 | −0.07 | −25.9 |
| CO2 replacing H2O | 2724.8 | 40 | −0.09 | −33.3 |
| Filling ratio at 30% | −1294.3 | −19 | −0.04 | −14.8 |
| Filling ratio at 50% | 632.6 | 9.8 | 0.03 | 11.1 |
| Aluminum replacing stainless steel | −817.4 | −12 | −0.01 | −3.7 |
| Parameter | Base Case | Range Tested | NPV Impact (±) | Payback Period Impact (±) |
|---|---|---|---|---|
| Electricity Price (CAD/kWh) | 0.09 | 0.05–0.15 | ±42% | ±3.6 years |
| Drilling Cost (CAD/m) | 5400 | 4000–7000 | ±35% | ±2.1 years |
| ORC Efficiency (%) | 12 | 10–16 | ±12% | ±1.0 year |
| Discount Rate (%) | 6 | 4–10 | ±8% | ±0.6 year |
| Case | Heat Flux (W/m2) | Net Output per Pipe (kW) | Total Output (100 Pipes) (kW) | Capital Cost per kW (CAD) | NPV Impact |
|---|---|---|---|---|---|
| Case 1 (H2O, baseline) | 3463 | 0.6 | 60 | 3000 | Base |
| Case 7 (CO2) | 4850 | 0.84 | 84 | 2400 | +42% |
| Case 5 (longer pipe) | 2650 | 0.46 | 46 | 3800 | −30% |
| Case 9 (50% fill) | 6445 | 0.75 | 75 | 2700 | +15% |
| Case 10 (aluminum) | 5395 | 0.5 | 50 | 3300 | −12% |
| Parameter | Category | Normalized Sensitivity Score (0–1) | Direction of Influence | Recommended Design Implication |
|---|---|---|---|---|
| Working Fluid Type (CO2 vs. H2O) | Technical | 1 | ↑ Heat Flux, ↓ Liquid Hold-up | Prefer CO2 for high-output scenarios if stability is manageable |
| Pipe Length (2000 m vs. 1200 m) | Technical and Economic | 0.85 | ↓ Heat Flux, ↑ Cost | Limit length to ≤1200 m for optimized balance |
| Drilling Cost | Economic | 0.82 | ↓ NPV | Explore multi-pipe in single borehole to reduce per-unit cost |
| Electricity Price | Economic | 0.78 | ↑ NPV | Consider long-term PPAs or carbon credits |
| Filling Ratio | Technical | 0.62 | Non-linear | Optimal range: 40–50% |
| Pipe Diameter | Technical | 0.55 | ↓ Heat Flux | Avoid oversized diameter unless targeting low-flow zones |
| ORC Efficiency | Economic | 0.3 | ↑ NPV | Acceptable between 12–14% |
| Discount Rate | Economic | 0.2 | ↓ NPV | Use ≤ 6% in risk-adjusted models |
| Pipe Material (Al vs. SS) | Technical | 0.18 | ↓ Performance | Prefer SS304/316L for thermal stability |
| Working Fluid Type (CO2 vs. H2O) | Technical | 1 | ↑ Heat Flux, ↓ Liquid Hold-up | Prefer CO2 for high-output scenarios if stability is manageable |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, Y.; Cui, W.; Ren, A.; Asgarpour, S.; Yin, S. Numerical Investigation of Ultra-Long Gravity Heat Pipe Systems for Geothermal Power Generation at Mount Meager. Mining 2025, 5, 55. https://doi.org/10.3390/mining5030055
Chai Y, Cui W, Ren A, Asgarpour S, Yin S. Numerical Investigation of Ultra-Long Gravity Heat Pipe Systems for Geothermal Power Generation at Mount Meager. Mining. 2025; 5(3):55. https://doi.org/10.3390/mining5030055
Chicago/Turabian StyleChai, Yutong, Wenwen Cui, Ao Ren, Soheil Asgarpour, and Shunde Yin. 2025. "Numerical Investigation of Ultra-Long Gravity Heat Pipe Systems for Geothermal Power Generation at Mount Meager" Mining 5, no. 3: 55. https://doi.org/10.3390/mining5030055
APA StyleChai, Y., Cui, W., Ren, A., Asgarpour, S., & Yin, S. (2025). Numerical Investigation of Ultra-Long Gravity Heat Pipe Systems for Geothermal Power Generation at Mount Meager. Mining, 5(3), 55. https://doi.org/10.3390/mining5030055






