Enhancing Comminution Process Modeling in Mineral Processing: A Conjoint Analysis Approach for Implementing Neural Networks with Limited Data

Abstract

Mineral processing is a crucial stage in the mining process, involving comminution and concentration stages. Comminution is modeled using various ore variables and operational parameters, representing a complex system. An alternative to simplifying the complexity of these stages is adopting machine learning (ML) techniques; however, ML often requires a substantial amount of data for effective training and validation. The conjoint analysis methodology was used to develop a procedure for discretizing input variables and reducing the data needed for training neural networks, requiring only 77 different scenarios. Using the results from a comminution plant simulator built in Matlab Simulink, neural networks were trained to predict the key output parameters, such as the water consumption, energy consumption, operational parameters, and particle size generated by the plant. The predictive capability of the neural networks was excellent, achieving R² > 0.99 in all cases. The networks were tested with a new set of scenarios to assess their response to values not categorized in the discretization process, achieving R² > 0.98. However, the prediction capability was lost for out-of-range input variables. This approach is attractive for developing easy-to-implement ML tools capable of representing complex systems without needing large amounts of input data, thereby simplifying the modeling process in mineral processing.

1. Introduction

Mineral processing involves numerous variables and parameters, making the modeling of these stages highly complex. Alternatively, machine learning (ML) offers a way to simplify the modeling and simulation processes; however, a large amount of data is typically required to train and validate these tools. By using categorization techniques, it may be possible to reduce the amount of data needed to build effective ML tools. In this work, the traditional conjoint analysis method was adapted to discretize variables that influence comminution processes by categorizing them into different levels and generating an orthogonal design to obtain a series of scenarios. These scenarios were then used to simulate the operation of a comminution plant, characterizing its response, and the results were used to train artificial neural networks that can represent the plant’s response in a simplified manner. Finally, the possibility of adapting such techniques to simplify the characterization and analysis of complex systems, such as mineral-processing stages, is discussed.

1.1. Mineral Processing

Mineral processing is the process of separating commercially valuable minerals. It involves several steps designed to physically or chemically separate the minerals from the waste rock or gangue [1]. The main stages in mineral processing include a particle size reduction to liberate the mineral and concentration processes like flotation to produce a final product enriched with the mineral of interest. Achieving an adequate final concentrate requires rigorous control of the particle size reduction or comminution stages [2]. Comminution processes consist of crushing and grinding stages, where size classifiers, such as screens and hydrocyclones, are used to control the particle size sent to subsequent stages [3]. Currently, the most commonly used technologies in crushing processes include jaw crushers, gyratory crushers, and cone crushers, among others. Similarly, there are various technologies and equipment for the grinding stages, such as conventional ball mills, SAG mills, and high-pressure grinding rolls, among others [4]. These pieces of equipment are selected based on the type of ore being processed and the requirements of the designed mineral-processing plant.

Typically, crushing is performed in the absence of water, while grinding requires the use of water to make the process more efficient, which, among other advantages, helps reduce the energy consumed by the process [5,6,7]. This is extremely important, considering that the comminution stages are highly energy-intensive [8,9]. Water and energy are critical inputs for carrying out the comminution stages, and therefore, the proper and rational use of these resources is essential for the sustainable development of mining operations [10,11]. In this regard, it is crucial to have tools that accurately estimate the consumption of these resources based on the treated ore and the operational conditions of the comminution stages.

Currently, there are validated and widely accepted models that represent comminution and particle size classification operations. Comminution models are primarily based on population balances, while classification models are empirical [12,13,14,15]. These models serve as the foundation for simulation tools implemented in various software platforms [16,17,18,19]. In a previous work [20], mineral-processing models were implemented in Matlab’s Simulink, resulting in a robust simulator capable of capturing the full behavior of a plant, generating predictions of the particle size distributions, the residence time distributions, the concentrate and tailing composition, a blending estimation, and the water and energy consumption, among other outputs. Additionally, using this simulator, it was possible to develop operational strategies to reduce the water consumption by integrating meteorological information into the mining planning process [21]. The versatility of this tool allows for the accurate and reliable representation of any mineral-processing plant configuration, making it a valid instrument for representing a real-world operation.

1.2. Machine Learning Applications in the Mining Industry

Machine learning (ML) is increasingly being used in mineral processing to enhance the predictability, optimize the performance, and strengthen maintenance practices [22]. This approach enables the creation of material ‘fingerprints’, which help forecast the processing behavior and identify the root causes of variability [23]. In flotation processes, ML techniques are now central to monitoring and optimizing operations, with deep learning networks gaining traction for froth image analyses [24]. Additionally, ML methods are valuable in processing remote sensing data for mineral exploration, facilitating geological mapping and the development of mineral prospectivity maps [25]. Nonetheless, significant challenges remain, such as data scarcity, characterizing rare events, and modeling complex processes [22]. Overcoming these barriers calls for innovative learning approaches, the incorporation of phenomenological models, the development of reliable sensors, and the training of skilled personnel [22]. Despite these hurdles, ML continues to show substantial potential for enhancing the efficiency in mineral processing and success in exploration.

Machine learning and neural networks have emerged as powerful tools for addressing various challenges in mining, particularly those related to predictive modeling, process optimization, and managing the vast amounts of data generated in mining operations. In essence, ML refers to a subset of artificial intelligence (AI) that allows computers to learn from data and make predictions or decisions without being explicitly programmed. Neural networks, a key ML technique, are inspired by the human brain’s structure and excel at recognizing patterns in complex, non-linear data. These capabilities make ML and neural networks particularly suited for the mining industry, where processes such as ore grade estimations, equipment failure predictions, and energy consumption optimization require the analysis of large, intricate datasets [26].

In a study conducted by Avalos et al. [27], an approach based on long short-term memory (LSTM) networks was proposed to predict the operational relative hardness in semi-autogenous grinding (SAG) mills using real-time operational data. The study emphasized the ability of LSTM to capture temporal relationships by leveraging variables such as the energy consumption and feed tonnage. The model achieved an accuracy of over 93% in predicting the operational hardness. This model significantly enhances the efficiency of comminution process control, which is crucial for mining operations that depend on optimizing energy consumption and operational efficiency [27].

Posteriorly, Avalos and Ortiz [28] introduced a novel technique for simulating complex geostatistical patterns using recursive convolutional neural networks (RCNNs). Their method leverages CNNs’ ability to extract features from training images and applies them recursively to simulate two-dimensional and three-dimensional geological structures. This approach demonstrates a superior accuracy and flexibility when compared to traditional multiple-point statistics (MPS) methods, particularly in handling spatial complexity. Their study also emphasized the potential of deep learning to improve geological simulations, offering a promising direction for future applications in geosciences.

In another study, Lee et al. [29] explored the use of artificial neural networks (ANNs) to predict the particle size distribution (PSD) of grinding products. Their approach employed a kinetic model to generate training data, which improved the model’s accuracy. After fine-tuning the model with experimental data, the coefficient of determination reached 0.99, indicating highly precise predictions of the particle size distribution. This method offers an efficient and accurate alternative to traditional grinding techniques, which are typically more time-consuming and costly [29].

The study presented by Kwanghui [30] applied an ensemble ML approach to predict the efficiency of multi-stage froth flotation for complex lead–zinc ores. The authors used both neural networks and random forest models to analyze flotation data, achieving a high accuracy in predicting the grade and yield across different flotation stages. The model successfully outperforms traditional methods, offering significant insights for optimizing the flotation processes in mining operations.

Amoako et al. [31] developed a hybrid ML model combining artificial neural networks and support vector regression (SVR) to enhance the prediction accuracy of rock fragmentation in blasting operations. By leveraging variables such as the explosive properties, geometric parameters, and rock characteristics, the model outperformed traditional methods like the Kuz–Ram model. This hybrid approach achieved a higher predictive accuracy with a significant improvement in the R² value and a notable reduction in the mean square error (MSE), demonstrating its potential in optimizing the blasting design efficiency.

The study by Al-Bakri and Sazid [32] explored the application of artificial neural networks in predicting and optimizing blast-induced impacts, such as flyrock, ground vibrations, and back-break, in mining operations. The authors highlighted the inefficiency of traditional blasting, where only 30% of the explosive energy is used for rock fragmentation, while the rest leads to environmental and safety concerns. ANN models show superior predictive capabilities, optimizing blast operations by reducing undesirable effects and improving the overall efficiency, despite the need for more research on multi-impact predictions.

In another topic related to mining operations and safety, Vallejos and McKinnon [33] used neural networks and logistic regression to classify microseismic events as blasting operations based on the seismic source parameters. Using training data, they achieved an accuracy of over 95% in classifying seismic records as blasts. On the same topic, Vallejos and Estay [34] employed spatio-temporal clustering methodologies to identify and monitor areas with a higher microseismic risk and identify seismic sequences.

On a broader perspective, Jung and Choi [35] examined ML applications in mining, focusing on mineral exploration, exploitation, and reclamation. By analyzing 109 papers from 2011–2020, their study found that ML applications have increased significantly since 2018, with support vector machines and deep learning models being the most utilized. The key evaluation metrics include the root mean square error and the coefficient of determination. Their review highlights the potential of ML for improving the operational efficiency in the mining industry.

A more recent systematic review [26] provides a comprehensive overview of how deep learning (DL) techniques are applied across different stages of the mining process, including exploration, extraction, and reclamation. It emphasizes that, despite the slower adoption of deep learning in mining compared to other industries, recent advancements have shown great potential. The review categorizes existing studies based on DL architectures, such as convolutional neural networks (CNNs) and recurrent neural networks (RNNs), highlighting their use in geotechnical mapping, fault detection, and ore classification. The authors identified significant gaps in the availability of large, publicly accessible datasets and the need for more diverse sensor data in mining. Recommendations for future research include an improved generalization of models, adversarial testing, and the broader integration of DL in mining automation.

1.3. Conjoint Analysis

A conjoint analysis is a research tool used to assess the market potential, predict the market share, and forecast the sales of new or improved products and services [36,37,38]. The process involves estimating utilities for varying levels of product features and simulating marketplace preferences for established, improved, and/or new products. A conjoint analysis is widely used in marketing research for new product development, pricing, branding, market simulations, and market segmentation [36,38,39]. It has evolved from traditional rating- or ranking-based methods to a choice-based conjoint analysis, making it a versatile tool for studying discrete choice behavior [36].

There are different types of conjoint analysis models, including the following:

Traditional conjoint analysis: Widely used for measuring consumer preferences for product or service features, but limited by integrating a small number of attributes [40].

Choice-based conjoint analysis: A general experimental method to study individual’s discrete choice behavior, not limited to classical applications in marketing, and can be applied to study research questions from related disciplines [36].

Hierarchical information integration: A variation of a conjoint analysis that resolves the limitations arising in a traditional conjoint analysis and establishes ways to proceed in complex situations with many attributes [41].

However, a conjoint analysis has its limitations, such as complexity, as a traditional conjoint analysis is limited to handling a small number of attributes, while complex decision-making processes often involve between 10 and 20 relevant criteria [40]. Additionally, experiments with a conjoint analysis can face issues with information overload, which may impact the validity of the results [41]. Furthermore, the predictive power of conjoint applications can be compromised by response biases and measurement errors, potentially affecting the accuracy of the models [42].

A conjoint analysis can be represented using an orthogonal design, which generates an experimental plan that captures the possible combinations of categorized variables. An orthogonal design refers to a type of experimental design where the factors being studied are independent and uncorrelated, which is crucial in various fields such as statistics, coding theory, and computer experiments [43,44,45]. The orthogonal design ensures that the factors being studied are independent and uncorrelated. Various methods and algorithms have been proposed for constructing orthogonal designs, which are included as part of commercial software.

This research addresses a critical limitation in the application of ML to mineral processing: the substantial data requirements that often render ML methods impractical for small and medium-sized operations. By leveraging a conjoint analysis to discretize and categorize input variables, this study presents a novel approach that requires a minimal amount of data for effective neural network training. This methodology allows for the accurate modeling of complex comminution processes while overcoming the traditional data and resource barriers associated with ML applications in mineral processing.

2. Materials and Methods

2.1. Models Used in Simulation

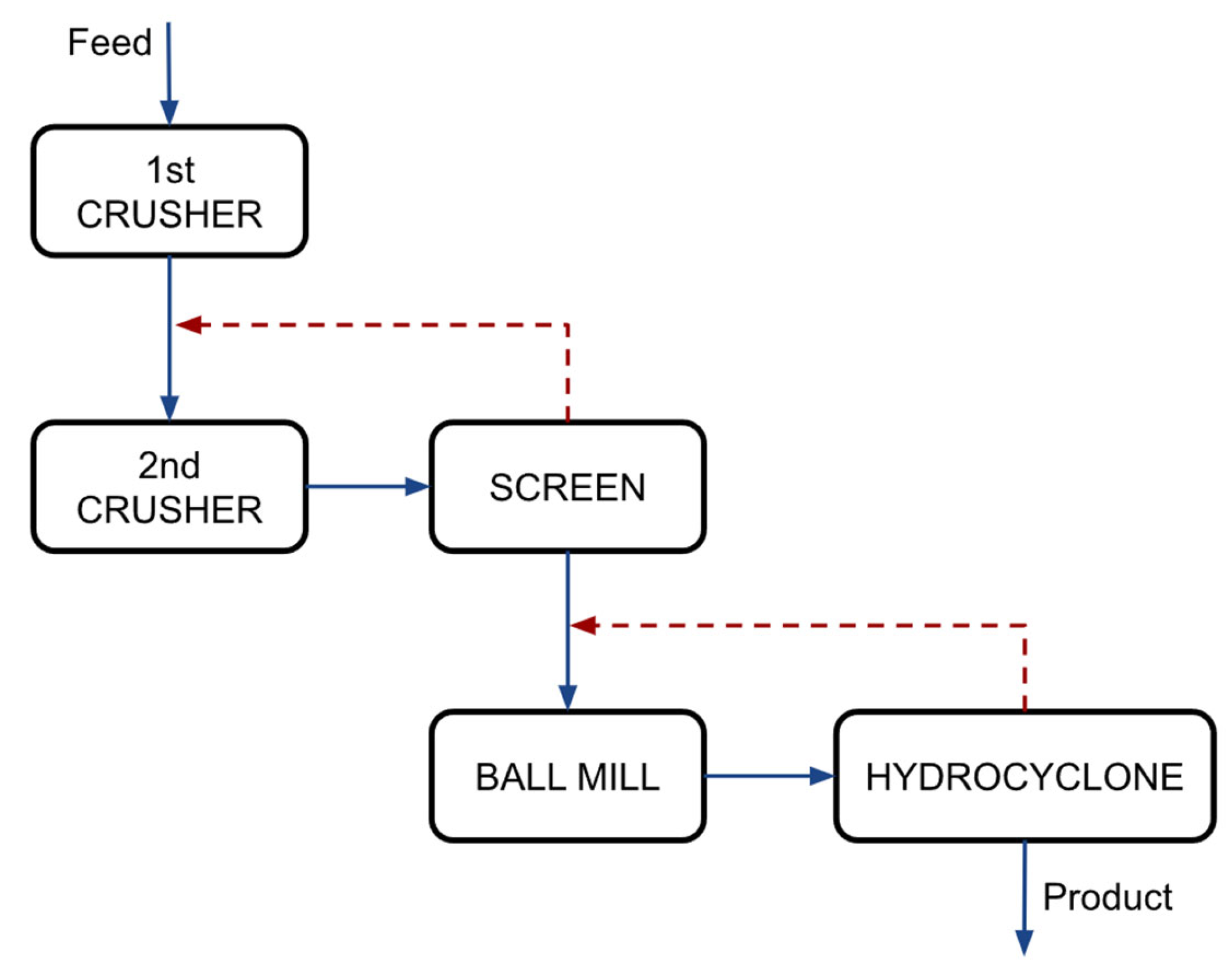
The methodology implemented to obtain results was based on the use of a comminution plant simulator. The plant consisted of two crushing stages with screening classification and a conventional grinding stage with hydrocyclone classification, as shown in Figure 1. The first crushing stage operated in an open circuit with a gyratory crusher (feed opening of 1000 mm), while the second stage utilized a cone gyratory crusher (feed opening of 350 mm) paired with a screen for size classification at 51 mm. Lastly, the setup included a ball mill (measuring 3.5 × 4.5 m) followed by a size classification stage consisting of five hydrocyclones, each with a diameter of 76 cm.

It was assumed that the feed to the plant followed a Rosin–Rammler distribution, where the complete size distribution can be constructed using the following expression [46]:

$$Y=1-exp{\left(-{\displaystyle \frac{x}{x_0}}\right)}^n$$

(1)

where $Y$ is the cumulative fraction of material by weight less than size $x$; $n$ is the uniformity constant; and $x_0$ is the characteristic particle size. In this way, the parameters $n$ and $x_0$ become input variables for the simulation process.

The energy consumed in the comminution processes was calculated using the Bond equation, which relates the hardness of the ore to the size reduction capacity of the equipment through the following expression [47]:

$$P_C=10·G_S·W_i·\left({\displaystyle \frac{1}{\sqrt{P_{80}}}}-{\displaystyle \frac{1}{\sqrt{F_{80}}}}\right)$$

(2)

where $P_C$ is the power consumption expressed in [kW]; $G_S$ is the fresh material flow in [t/h]; $W_i$ is the work index in [kWh/t]; and $F_{80}$ and $P_{80}$ are the feed and product characteristic sizes in [μm].

The models implemented in the simulation are presented in

Table 1. Models used in the comminution plant simulation.

Model/Stage	Crushing	Ball Grinding	References
Fragmentation	Population Balance	Population Balance	[12,13,48,49,50]
Classification	Karra	Plitt	[14,15]

. These models are based on population balances for comminution processes and empirical models for size classification. The detailed formulation of the models is described in a previous work [20]. These models are widely accepted and used to simulate operations in mineral processing, being part of the commercially available simulators currently in use. The simulation was carried out in Matlab Simulink R2024a due to its advantage of easily connecting stages, making it possible to implement complex systems with material recirculation.

Once the simulator was built, it was possible to manipulate the input variables and parameters to capture the plant’s response. The input variables and the operational results of interest provided by the simulator are indicated in

Table 2. Input variables for the simulation and output variables provided by the simulation.

Input Variables	Characteristic particle size X0	Uniformity constant	Work index	Feed flow	Ore density	1st crusher setting	2nd crusher setting	Mill speed	Solid concentration by weight	Hydrocyclone feed pressure
Output Variables	1st crusher P80 size	1st crusher energy consumption	2nd crusher P80 size	2nd crusher circulating load	2nd crusher energy consumption	Mill P80 size	Mill energy consumption	Circuit P80 size	Mill circulating load	Makeup water

. The simulator generated a series of other operational results that allowed the plant’s performance to be characterized; however, in this work, we used those presented in Table 2 for simplicity to exemplify the adjustment of the methodology.

2.2. Conjoint Analysis Implementation

It was necessary to explore the response space for the various output variables provided by this tool to implement neural network tuning based on the mineral-processing simulator. Due to the considerable number of identified input variables, characterizing the simulator’s response can be very resource-intensive. The conjoint analysis technique was used to reduce the number of scenarios needed to characterize the simulator’s response.

The selection of input parameters for the neural network model was grounded in their critical influence on the mineral-processing and comminution stages within the mining industry. The key parameters, including the feed granulometry, the slope of the granulometric curve, the mineral hardness, the feed flow rate, the mineral density, the primary and secondary crusher discharge settings, the mill rotation speed, the solids concentration, and the feed pressure, were chosen due to their direct impact on system performance. These variables were identified through a combination of industry relevance and simulated process scenarios, generating a comprehensive dataset of representative scenarios. This approach ensured that the model captured a broad range of operational conditions, enhancing its predictive accuracy and applicability across diverse processing settings.

The operational range of the input variables and operational parameters was defined based on typical data reported in the literature [47,51,52,53,54,55]. Then, a discretization of these variables was defined, generating 5 categories for each of them. This was a crucial step because the variables are continuous, and the conjoint analysis method requires discrete categories. The ranges and discretization of the variables are presented in

Table 3. Categorization of operational ranges for input variables in the comminution plant simulation.

Variables	Very Low	Low	Medium	High	Very High
Particle size distribution X0 [mm]	750	925	1100	1275	1450
Particle size distribution n	0.8	0.9	1.0	1.1	1.2
Work index [kWh/t]	9	11	13	15	17
Feed flow [t/h]	1000	1100	1200	1300	1400
Ore density [t/m3]	2.0	2.25	2.5	2.75	3
1st crusher setting [cm]	5	10	15	20	25
2nd crusher setting [cm]	1	2	3	4	5
Percent of critical mill speed [%]	70	72.5	75	77.5	80
Solids concentration by weight [%]	57	59	61	63	65
Hydrocyclone feed pressure [kPa]	50	87.5	125	162.5	200

.

Since 10 variables were defined with 5 categories each, the possible combinations amounted to more than 9.7 million. Using the orthogonal design tool in the SPSS software (version IBM SPSS 27.0) [56], a reduced number of scenarios was generated, ensuring the representation of each category of the input variables and capturing their variation within the defined ranges. In this way, a sample of 77 scenarios from the total possible combinations was established, provided as Supplementary Data to this work in Table S1.

2.3. Network Architecture and Training Justification

The neural network structure used in this study consisted of a single hidden layer with 10 neurons, along with an output layer. This architecture was selected to optimize the computational efficiency and enable faster model training and evaluation—important factors for industrial applications, especially in the mining sector. Prior research shows that a single hidden layer is often sufficient to capture complex, non-linear relationships in predictive tasks within similar fields. Al-Bakri et al. [32] reviewed the recent studies on blast-induced rock fragmentation using ANNs, noting that many solutions successfully employ a single hidden layer. For example, Dimitraki et al. [57] utilized 5 neurons in the hidden layer and achieved a high predictive accuracy (R² = 0.88), while Rosales-Huamani et al. [58] used 13 neurons, reaching an accuracy of R² = 0.87. These findings underscore that single-layer networks can effectively capture complex data patterns with minimal depth, thereby reducing the risk of overfitting and computational costs.

To determine the most effective training approach, three algorithms were tested: Levenberg–Marquardt, Bayesian regularization, and scaled conjugate gradient. The dataset was split into 70% for training, 15% for validation, and 15% for testing. Bayesian regularization, however, inherently optimized without requiring a separate validation set, making it particularly suitable for achieving strong generalization while preventing overfitting. Among the tested methods, Bayesian regularization showed the lowest average error and a superior generalization performance, proving to be robust across diverse operational scenarios, while the other methods exhibited higher cross-validation error rates, especially under extreme operational conditions.

In conclusion, the combination of a single hidden layer and Bayesian regularization training offered an optimal balance between the predictive accuracy and the computational efficiency. This architecture and training strategy ensured that the model is highly applicable in real-world, time-sensitive mining operations, providing reliable, efficient predictions in a challenging industrial context.

3. Results

In this study, continuous variables were discretized into five levels (very low, low, medium, high, and very high) to simplify the input space and optimize computational resources while preserving essential distinctions between operational states. This choice allowed the model to maintain its predictive accuracy by capturing the most relevant aspects of each variable’s influence on the process outcomes without overwhelming the model with excessive detail. Selecting an appropriate number of discretization levels is crucial: too few levels creates the risk of oversimplifying the input data and omitting important nuances, while overly granular levels could lead to increased computational demands without substantial gains in accuracy.

For practitioners, we recommend aligning the granularity of discretization with the significance and variability of each variable. Variables that have a substantial impact on process outcomes may benefit from finer discretization, whereas others can be grouped into broader categories. This approach helps ensure a balance between the computational efficiency and the model fidelity.

3.1. Neural Network Fitting

The neural network training process is exemplified in Figure 2, where the fit of the training, validation, test, and overall fit for a neural network predicting the water consumption is shown. It can be observed that the neural network fit well with the data generated by the simulation, an effect that was replicated for each of the remaining defined output variables.

To evaluate the fit quality of the neural networks, the behavior of six output variables representing the operational efficiency of the proposed comminution circuit was analyzed. These variables included the makeup water, energy consumption, circulating load, and characteristic particle sizes (P₈₀) resulting from each comminution stage. Figure 3 presents the neural network predictions contrasted with the values obtained from the simulations for the output variables. The fit measured by the coefficient of determination (R²) provided very high values for each of the variables, demonstrating a high predictive capability of the neural networks. These results allow for the precise estimation of the particle size evolution generated in each of the comminution stages, as well as the consumption of inputs such as water and energy. Additionally, the circulating load generated in the grinding circuit was reported as an operational control parameter, verifying that the neural network can characterize this behavior.

3.2. Predictions for Uncategorized Input Variable Values

To verify the effectiveness of the created neural networks, a new random set of scenarios was generated, where the input variables took values that were not categorized as part of the conjoint analysis. This was implemented because, in practice, the input variables are continuous and can take any value within the defined validity ranges. The new scenarios are provided as Supplementary Data to this work in Table S2. This additional test set allowed us to examine the model’s ability to generalize beyond the training data, focusing on both the accuracy and robustness. The neural networks, trained using the Bayesian regularization method, achieved a high precision, with determination coefficients (R²) consistently exceeding 0.99 and a minimal mean squared error (MSE) across all the key output variables. These results underscore the model’s effectiveness in replicating the system’s behavior under new operational scenarios, confirming its reliability and strong predictive capacity within the predefined operational boundaries.

The simulator and neural networks were executed using these values, and the results are presented in Figure 4. To simplify the analysis, the particle size behavior was exemplified through the P₈₀ generated by the entire circuit, understanding that the results for the crushing stages are analogous. The results show that the neural networks correctly predicted the system’s behavior represented by the simulator, even when tested with values that were not categorized for training. This demonstrates that it is possible to successfully train neural networks to capture the behavior of a comminution plant by using a variable discretization process that reduces the amount of input information and decreases the number of scenarios needed for their construction.

3.3. Sensitivity Analysis for Out-of-Range Input Variable Values

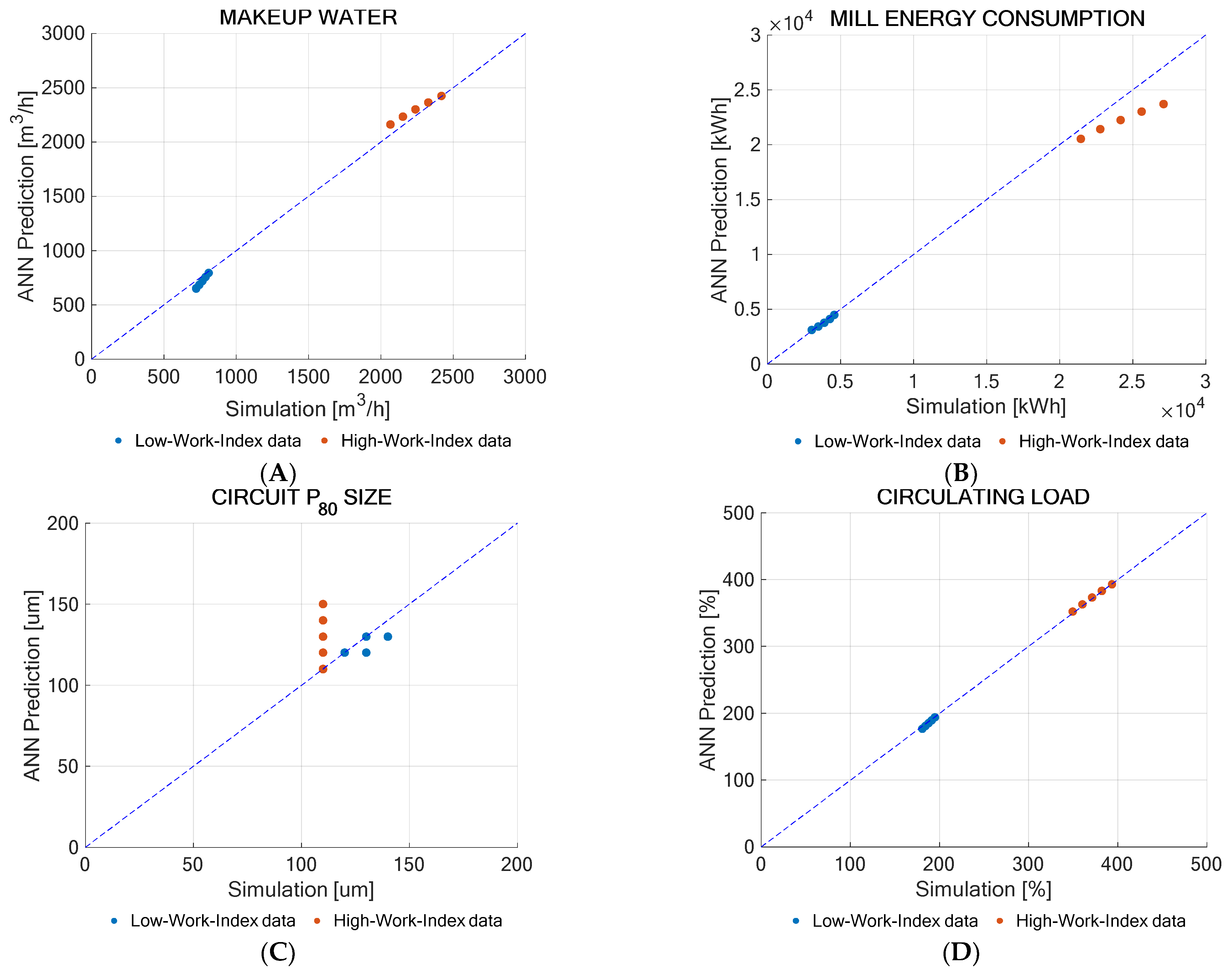
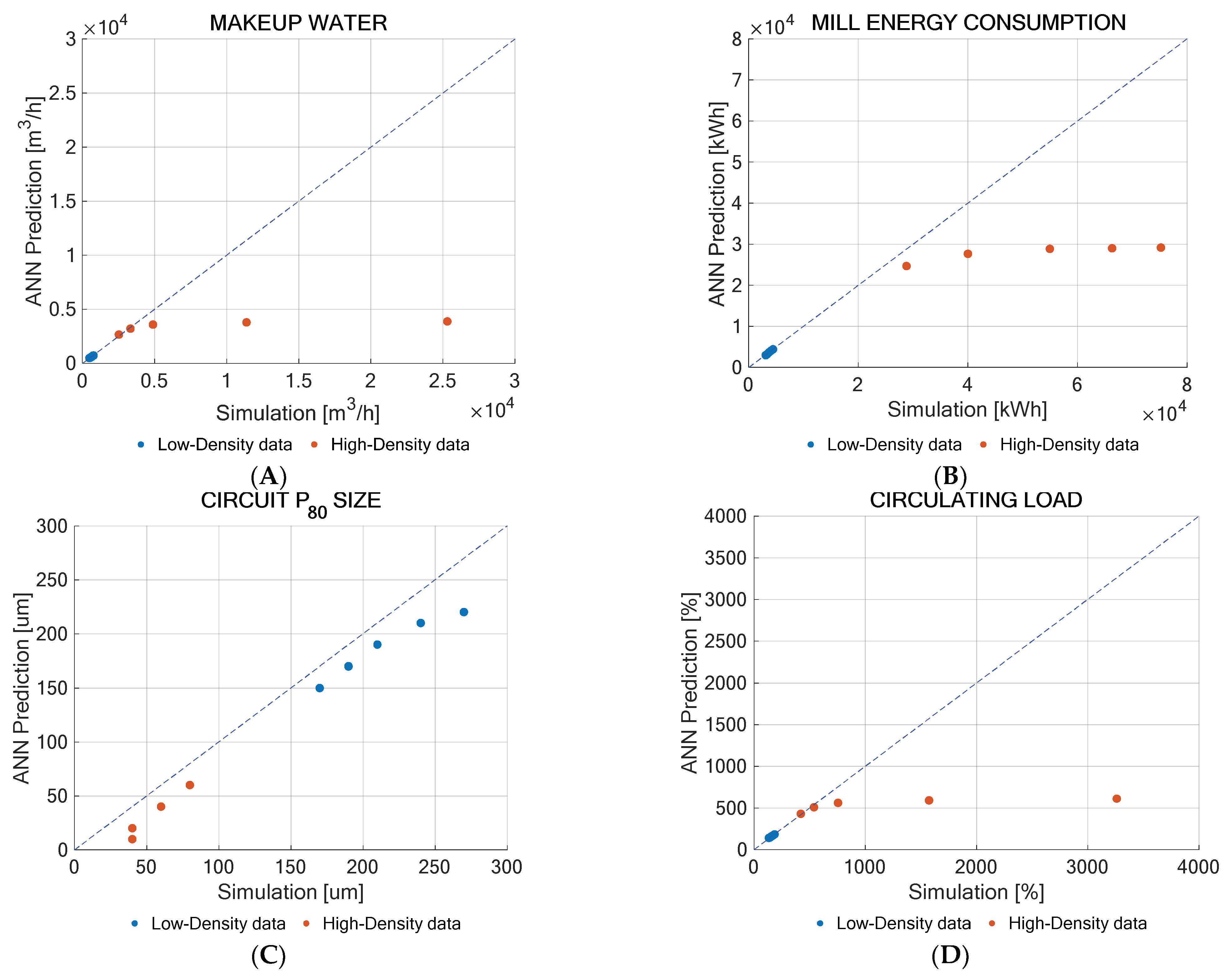
The aim was to explore whether the neural networks can capture the comminution plant’s behavior when the input variable values are outside the established training ranges. To achieve this, a sensitivity analysis of the neural networks was conducted using variables with values below the lower limit and above the upper limit of the established range. The sensitivity analysis was performed based on the work index and the ore density variables to exemplify the neural networks’ response. The input values used for the sensitivity analysis are presented in

Table 4. Input variable values of work index and ore density for sensitivity analysis.

Low Work Index Values [kWh/t]	High Work Index Values [kWh/t]	Low Ore Density Values [t/m3]	High Ore Density Values [t/m3]
4	18	1.1	3.5
5	19	1.2	4
6	20	1.4	4.5
7	21	1.6	5
8	22	1.8	5.5

. The sensitivity analysis results for the work index and the ore density are presented in Figure 5 and Figure 6, respectively.

The makeup water and circulating load predictions still aligned with the simulation values. However, in the case of the mill energy, the neural network failed to predict it accurately when tested with high work index values, underestimating the results obtained by the simulation. Additionally, the prediction of the particle size generated by the circuit was poor and not accurately represented by the neural network, showing no discernible trend toward fitting.

For the ore density variation, the neural networks preserved their predictive capability only for the output variables of the makeup water, mill energy, and circulating load when tested with low-density values. In cases of very high densities, the neural network’s fit was completely lost. For the particle size, although a fitting trend was observed, the neural network underestimated the values obtained by the simulator, leading to the conclusion that an adequate fit was not achieved.

In general terms, it was observed that, when testing the neural networks with input values outside the established training ranges, the predictive capability was deficient and did not reflect the behavior of the comminution plant. Therefore, it was established that the validity of the neural networks is limited to the training ranges, and it is not advisable to extend their use to conditions beyond these limits.

4. Discussion

This study used neural networks as a first approach to address the modeling problem in the context of comminution processes. Given the complexity and novelty of this problem, the research team chose to explore the neural network approach to understand the system’s behavior and its operational parameters. As this understanding progresses, future research could incorporate other machine learning techniques, such as random forest and support vector machines, to assess their accuracy and efficiency in comparison with this initial approach. It is noteworthy that this is the first work to address the specific modeling problem of comminution processes using a simulator and detailed parameters through machine learning methods, as no prior published results exist on this application.

These results show that it is possible to generate predictive neural networks for the behavior of a complex comminution plant. This process can be accomplished by adapting the conjoint analysis technique and discretizing and categorizing the input variables to generate an orthogonal experimental design. This approach reduces the number of scenarios needed to train the neural networks, allowing for a good fit between the input data (simulations) and the predictions made by the neural networks. This outcome is significant because it demonstrates that, with a small sample of the plant’s response, it is possible to reliably model its behavior.

This methodology allows results to be obtained on the consumption of inputs such as the makeup water and the energy used in size-reduction processes. This information could be used to estimate the expected consumption for processing a given ore precisely and promptly by evaluating the neural networks with input values associated with a planned feed. Additionally, it is possible to predict the particle sizes generated at each stage of the plant, enabling the tracking of particle size evolution as the ore progresses through the plant, thereby providing information that can be used to improve or optimize operations.

In this regard, when applied to a real mineral-processing plant, it is estimated that generating or collecting an exhaustive amount of data on the plant’s response is not necessary. Instead, the key is to adequately select data that represents the plant’s variability. Thus, it is suggested that the quality of the data is more important than its quantity. This observation is significant for the evaluation of small to medium-sized plants, where financial resources may be a limiting factor for process characterization and the implementation of ML tools. Therefore, using the conjoint analysis method could be an efficient and easy-to-implement alternative for diagnostic, control, and operational improvement purposes.

As observed in the results, the generalization of the neural network outcomes was only valid within the range of the values established for the input variables. Based on this, it is recommended to create a robust geometallurgical characterization of all the variables associated with the ore to be processed, covering the entire range of values encountered in operation. This information can be incorporated into the block model representing the exploited deposit and used as temporal data to feed a processing plant. In this way, developing neural networks that are specifically valid for each mining deposit would be possible.

In this study, additional tests were conducted with input values outside the trained operational range to assess the neural network’s generalization capabilities under extreme conditions. While the network demonstrated a high predictive accuracy within the trained range, its performance declined when tested with out-of-range values, leading to an underestimation of the mill energy and less precise particle size predictions. This outcome aligns with typical neural network behavior, as models trained within specific data ranges often lack reliability when extrapolated beyond those boundaries. Therefore, while the neural network model is highly accurate and dependable within the predefined operational parameters, its applicability under extreme conditions is limited, emphasizing the need to respect the defined training range for optimal performance.

This type of study based on a conjoint analysis can be easily extended to other stages of the mining process, such as extraction operations, processing, concentration, tailings disposal, etc. The tool used proved to be versatile and user-friendly for characterizing complex systems through variable discretization. Thus, it opens the possibility of representing complex mining systems through the interaction between stages of the production process, intending to provide a robust representation using ML tools.

Additionally, it is important to consider that simulation tools based on mineral-processing modeling often consume significant computational resources due to the large number of variables and parameters involved in the models. As a more comprehensive representation of the plant is required, more stages than those addressed in this work may be included, further complicating the simulation system and consuming more resources. In this context, ML offers an alternative for generating simple models that consume fewer computational resources, which could be significant for conducting quick and reliable analyses for control or process optimization purposes.

The proposed methodology is expected to yield neural network models capable of accurately predicting critical outputs, such as the water and energy consumption, the particle size distribution, and the circulating load, achieving a high coefficient of determination (R² > 0.98). By utilizing a conjoint analysis to reduce the data volume required, this study anticipates that this approach will enable the effective modeling of comminution processes, even with limited datasets. This data-efficient technique is particularly advantageous for small to medium-sized operations, where resources for extensive data collection may be limited. Moreover, while the neural networks are expected to perform well within their defined input ranges, this study acknowledges that the predictive capability may decrease when applied to scenarios beyond these training boundaries, highlighting the importance of adhering to the established range for reliable outcomes.

5. Conclusions

The conjoint analysis method was successfully adapted to discretize and categorize the variables involved in a complex comminution system, which includes crushing, grinding, and size classification stages. Using this technique, an orthogonal experimental design was developed and used to obtain the system’s response, referencing a comminution plant simulator. With these data, predictive neural networks were trained for various output variables, including the most relevant ones: the makeup water, energy consumption, particle size, and circulating load.

The neural networks achieved a high level of fit, accurately predicting the values reported by the simulator. Scenarios with input variable values that were not categorized during training were tested to assess the predictive capability of the neural networks. The results successfully predicted the behavior of the comminution plant. Additionally, a sensitivity analysis using values outside the training range confirmed that the neural networks are only valid within the specified range of input variables.

The methodology used proved effective in representing complex processes. Based on this, a conjoint analysis can be projected as a tool to characterize any mining and metallurgical processes with minimal input data or limited information volume. In this context, it is considered feasible for use in small to medium-sized operations, which often have limited financial resources for conducting an exhaustive characterization of the mineral to be processed.

In future work, it is planned to continue exploring this technique to adapt it to other stages of the mining process, integrate them, and generate interactions between these stages. This approach could provide an integrated view of the entire mining value chain through a simple, predictive tool that is less demanding in terms of resource consumption.