Enhancing Load-Bearing Capacity of Weak Soils Using Geosynthetics: A Finite Element Analysis
Abstract
1. Introduction
- Which model of geosynthetics will be effective for soil improvement?
- In what classification of soils will the use of geosynthetics have better effects?
- What depth is optimal for burying geosynthetics in order to have the highest soil bearing capacity?
- What effect will the changes in the length of geosynthetics have on the soil bearing capacity?
- Numerical Modeling of Geotextiles: this research utilizes advanced finite element analysis (FEA) through Abaqus to simulate the interaction between geotextiles and soil, providing a high-fidelity model that accounts for complex stress distributions.
- Influence on Soil Failure Mechanisms: this study investigates how geotextile placement alters soil rupture mechanisms, particularly in weak soils commonly found in mining applications.
- Impact of Geotextile Embedment Depth: by varying the depth at which geotextiles are embedded, this research quantifies the effect on load-bearing capacity, offering precise recommendations for optimal depth in different soil types.
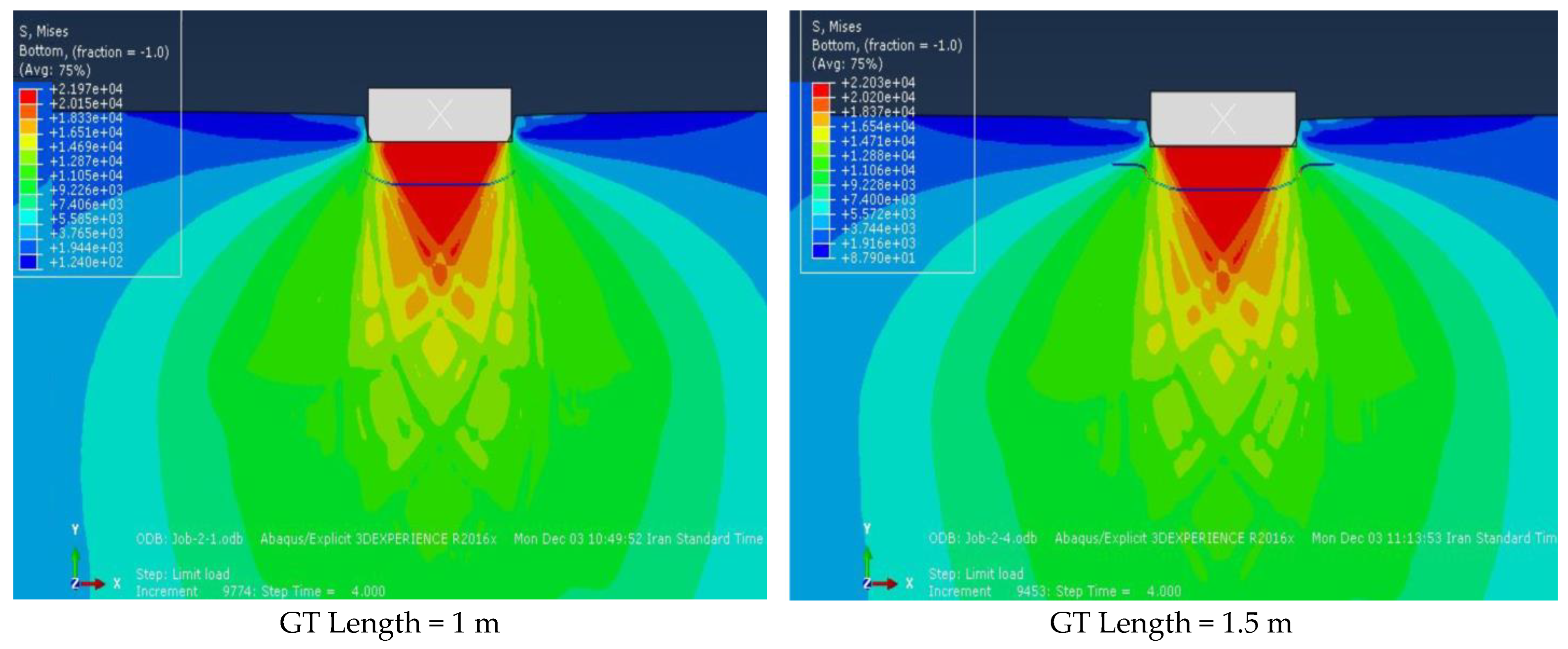
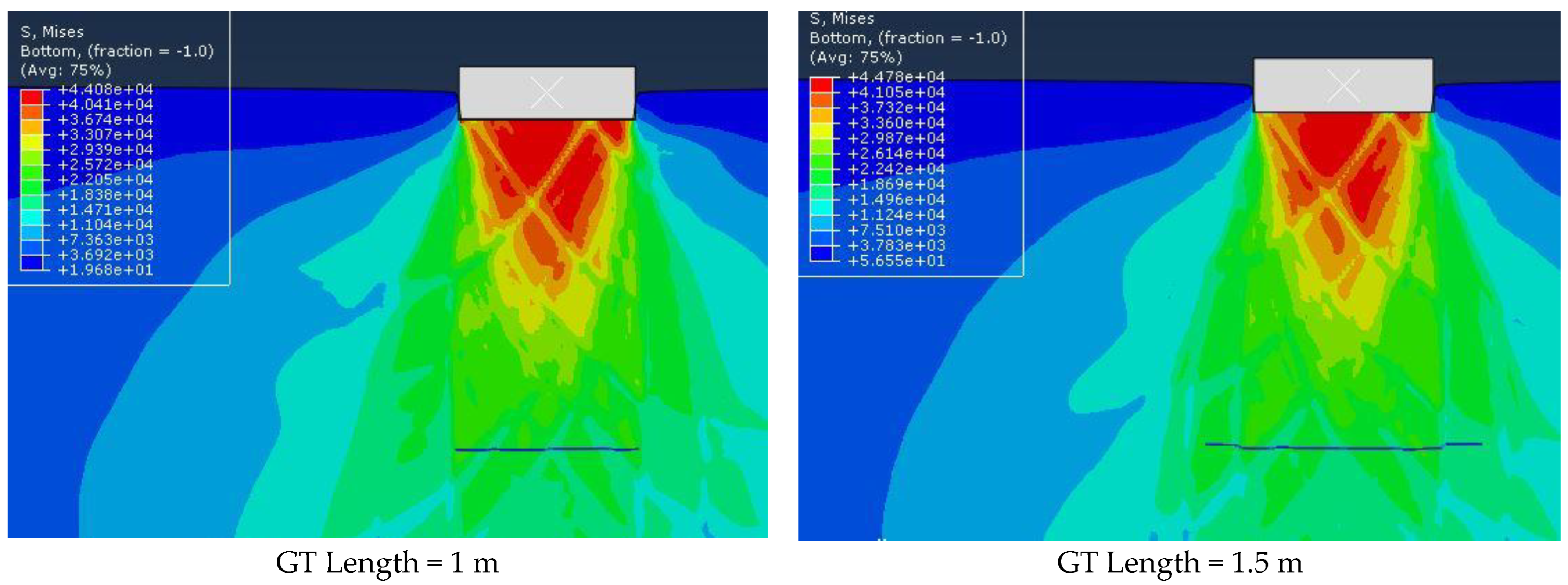
- Effect of Geotextile Length on Bearing Capacity: this study systematically examines how changes in geotextile length influence bearing capacity, identifying critical lengths that maximize soil stabilization.
- Variation in Soil Types: a comparative analysis of different soil types (ML, SM, SW) is conducted to determine how soil composition affects the performance of geotextiles.
- Determination of Optimal Geotextile Placement: this research provides specific guidelines for the optimal burial depth and length of geotextiles tailored to different soil conditions, contributing to safer and more efficient geotechnical practices in mining.
2. Materials and Methods
2.1. Material Specifications
2.2. Creating Model Geometry
2.3. Assembly of Parts
2.4. Loading, Boundary Conditions, and Meshing
3. Numerical Model
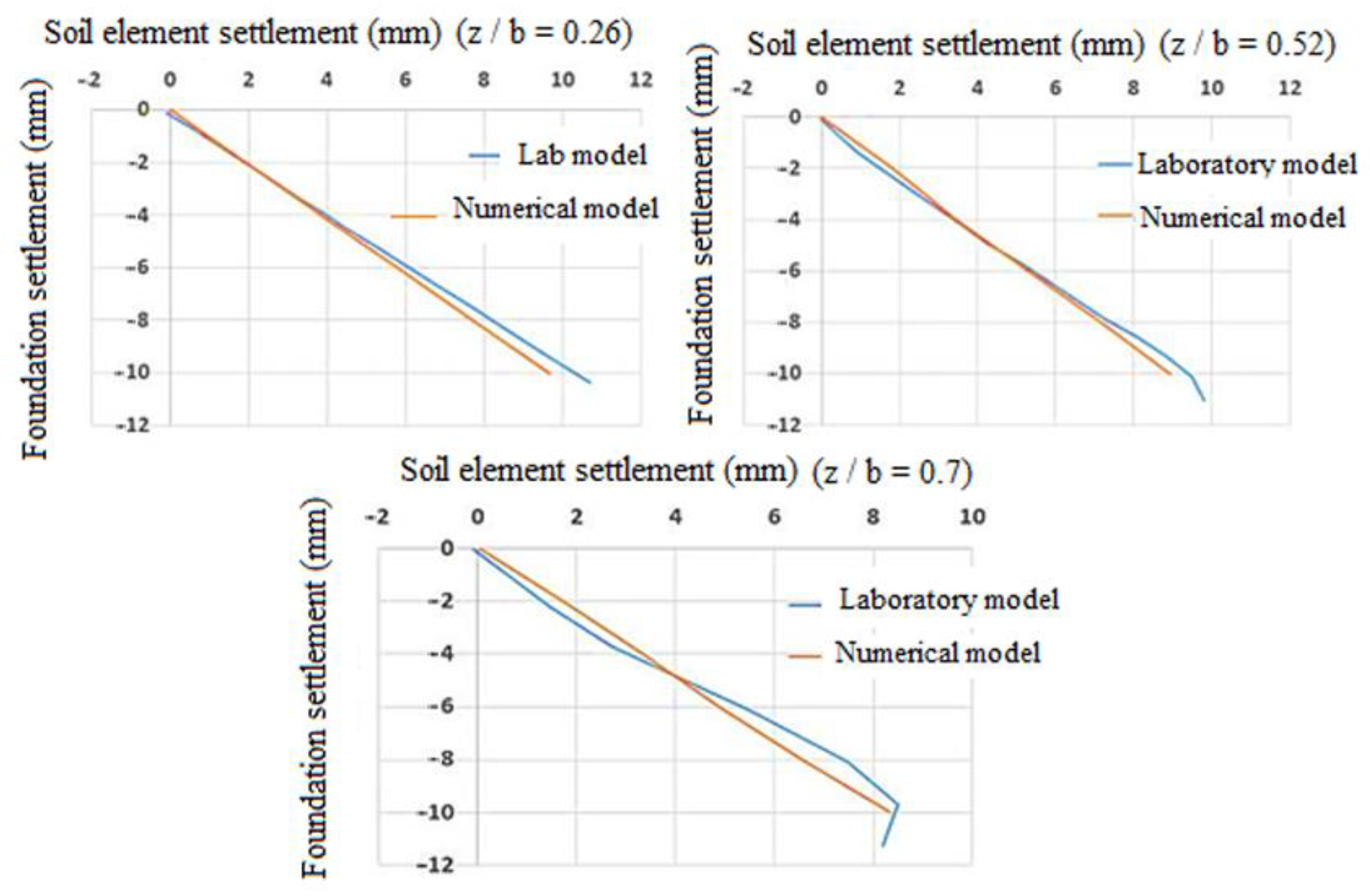
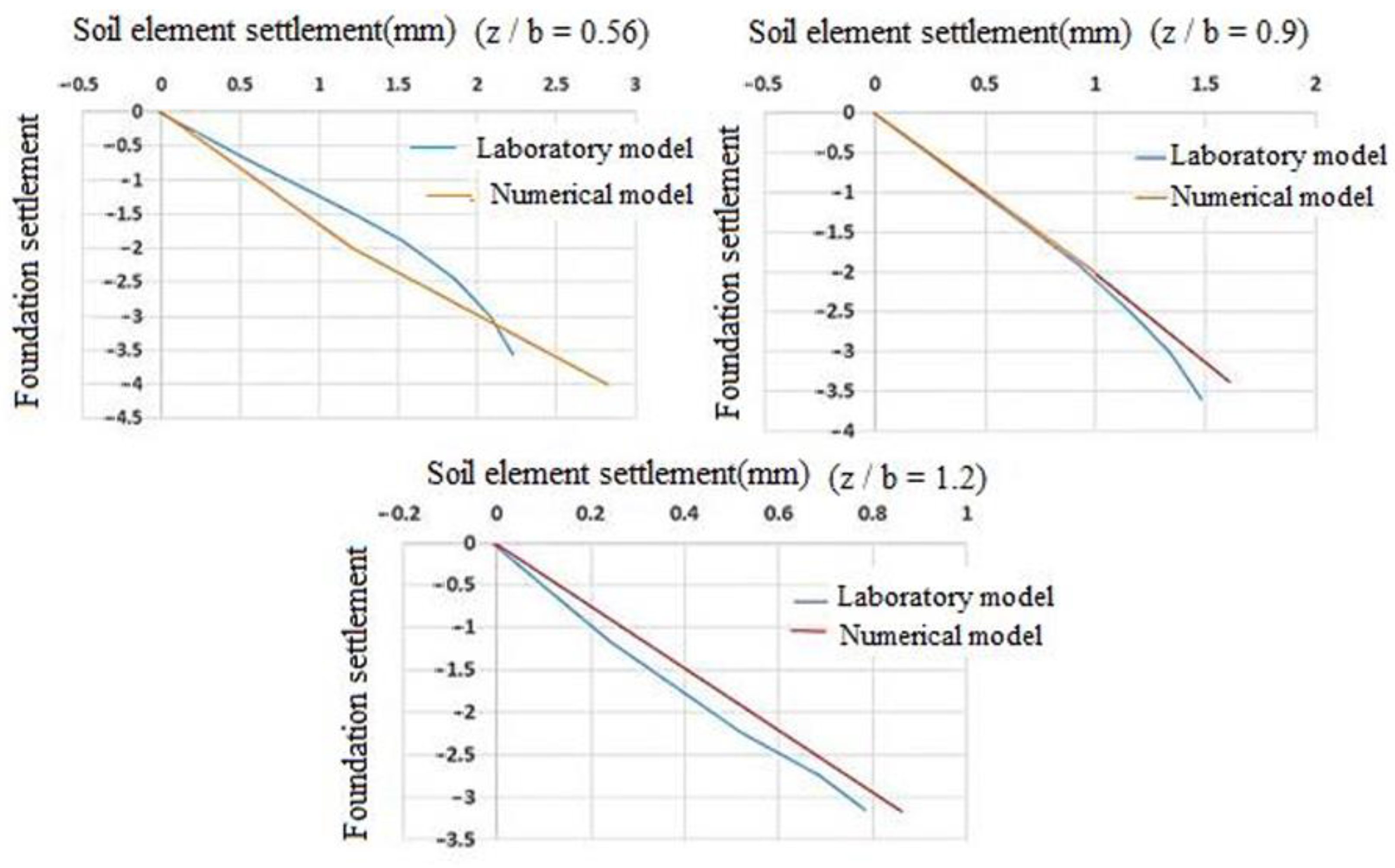
3.1. Validation of the Base Numerical Model
3.2. Numerical Material Specifications in the Base Model
3.3. Comparison of Experimental and Numerical Model Results
3.4. Model Planning
4. Results and Discussion
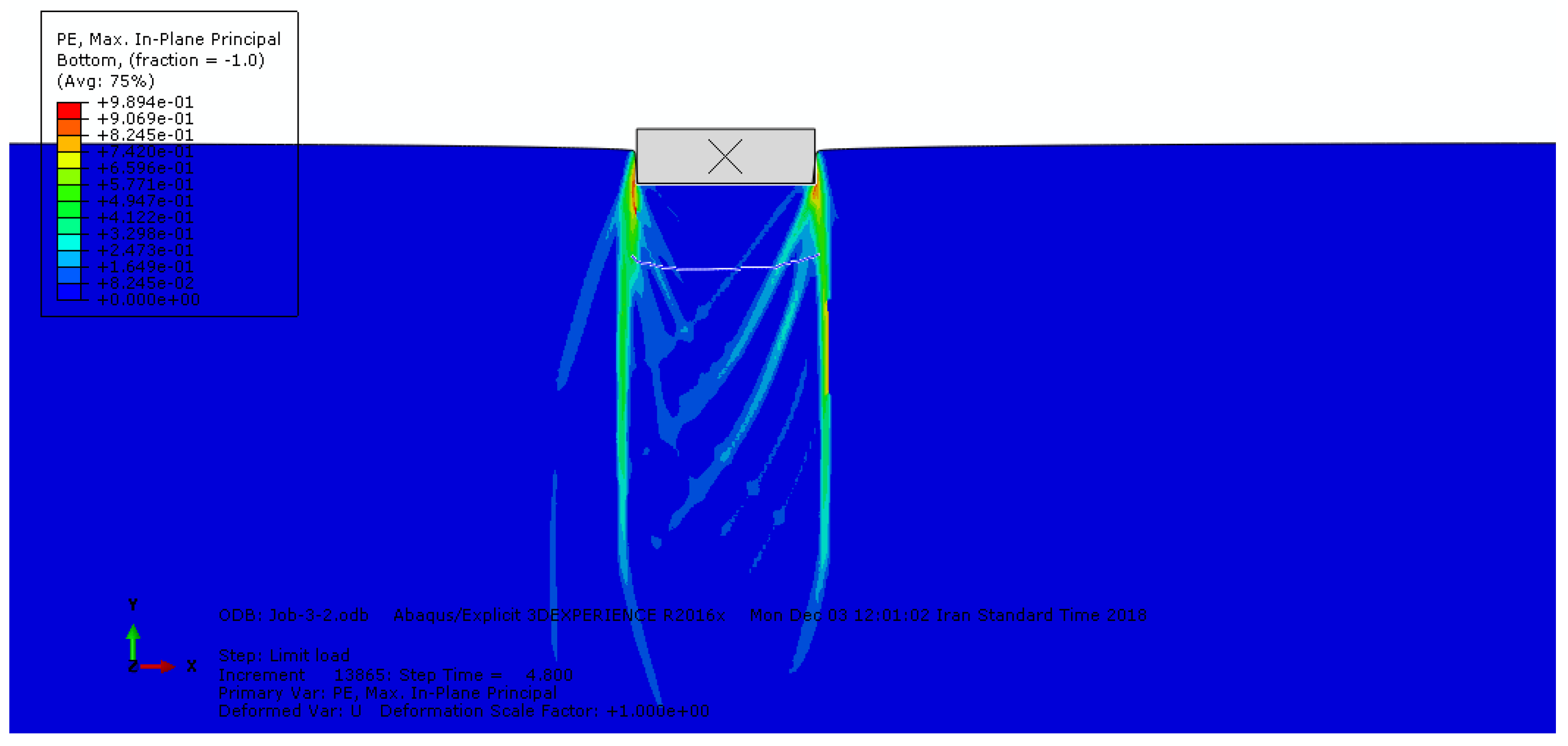
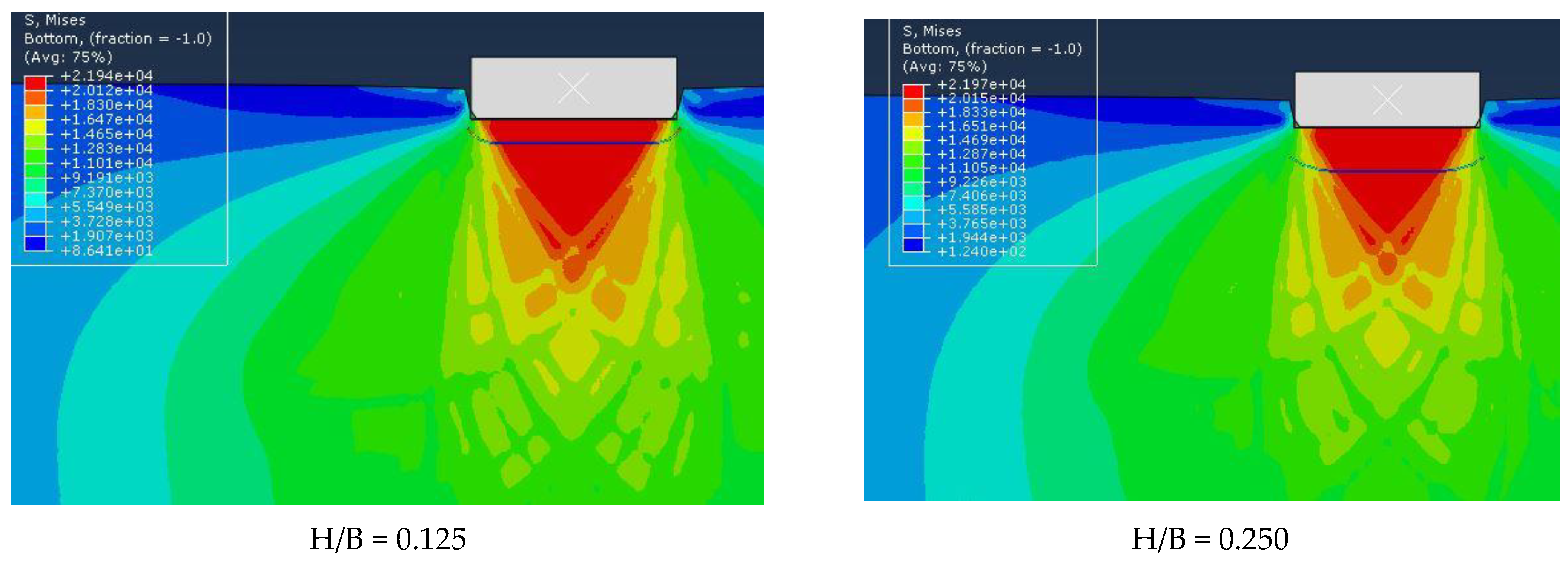
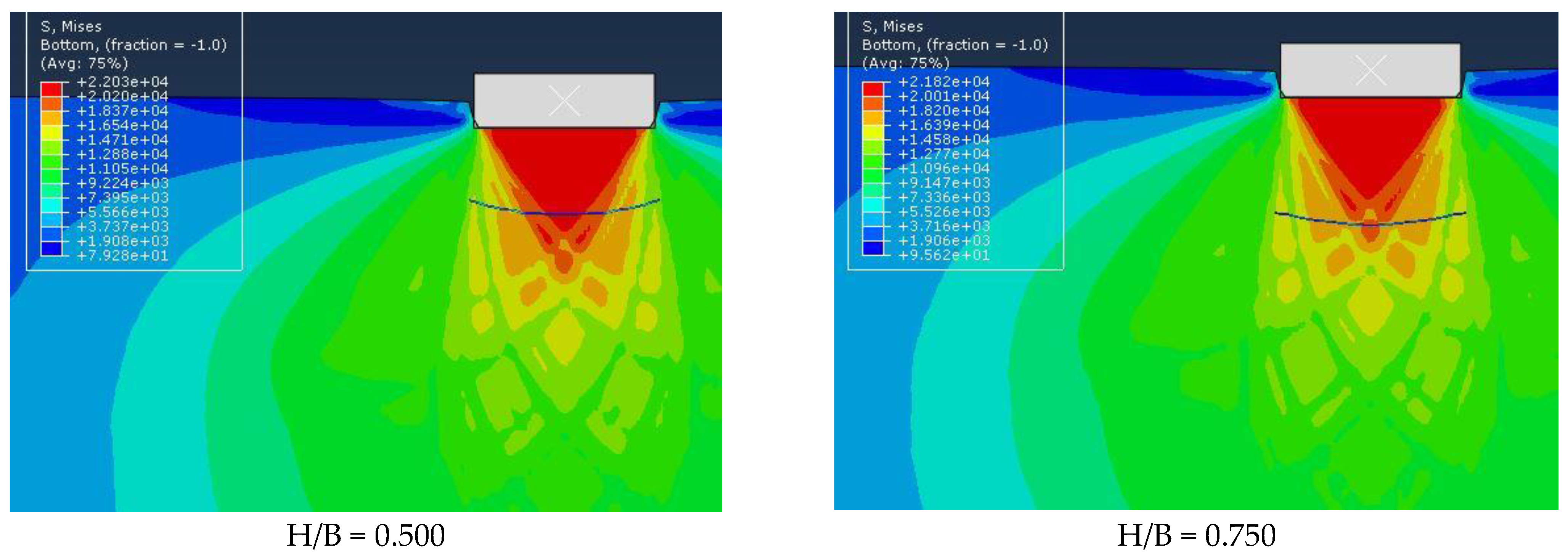
4.1. Mechanism of Soil Rupture
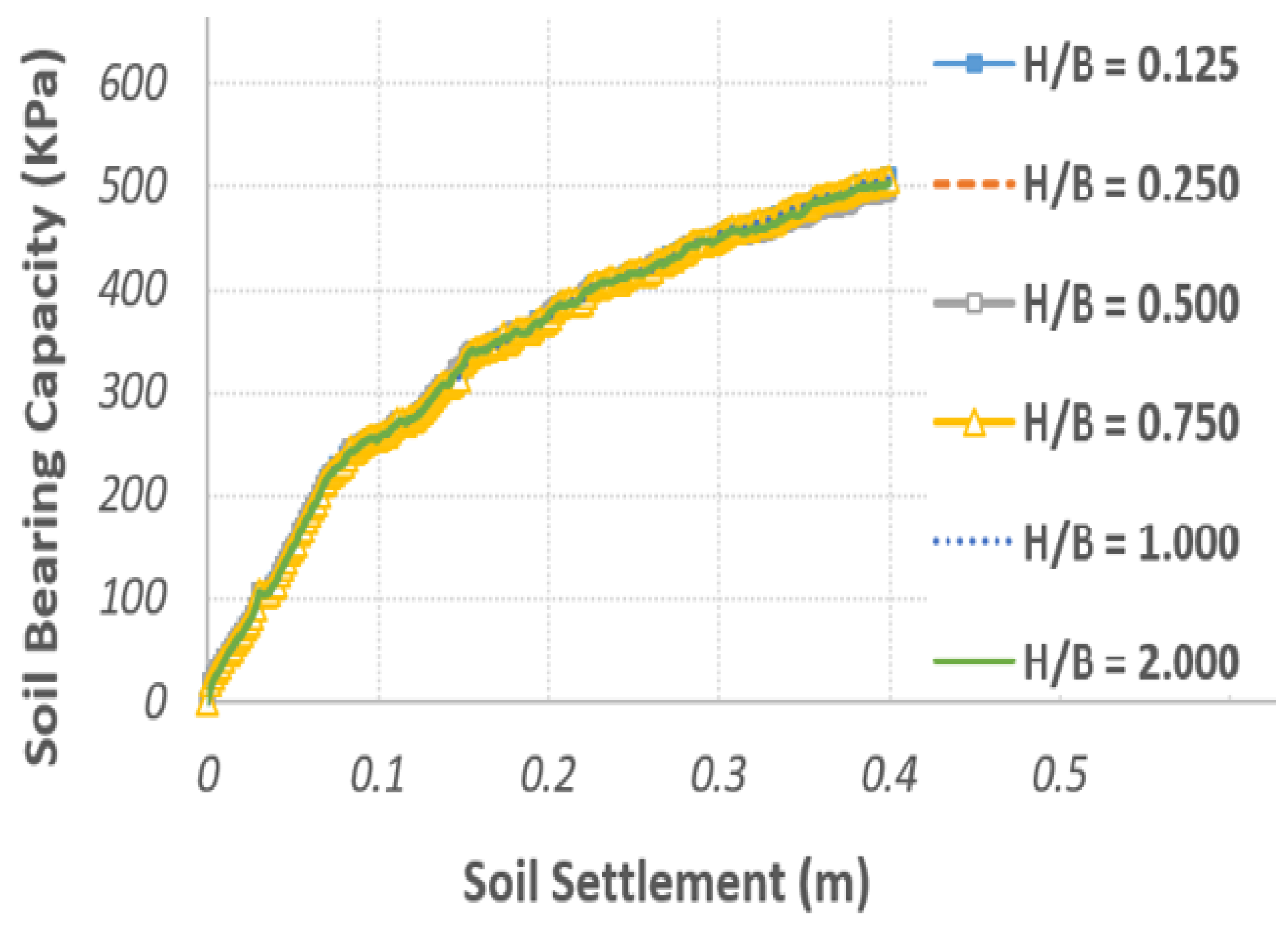
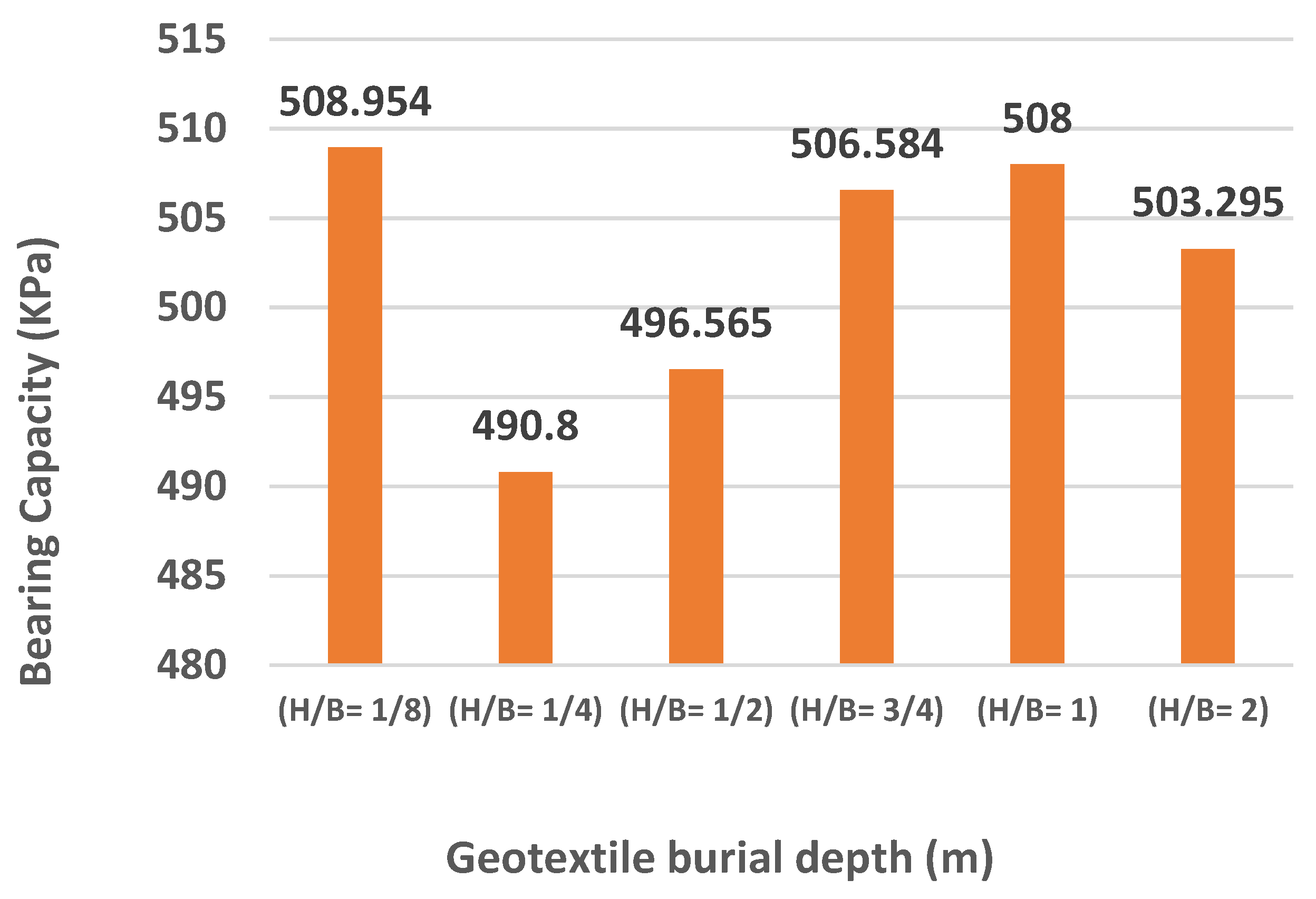
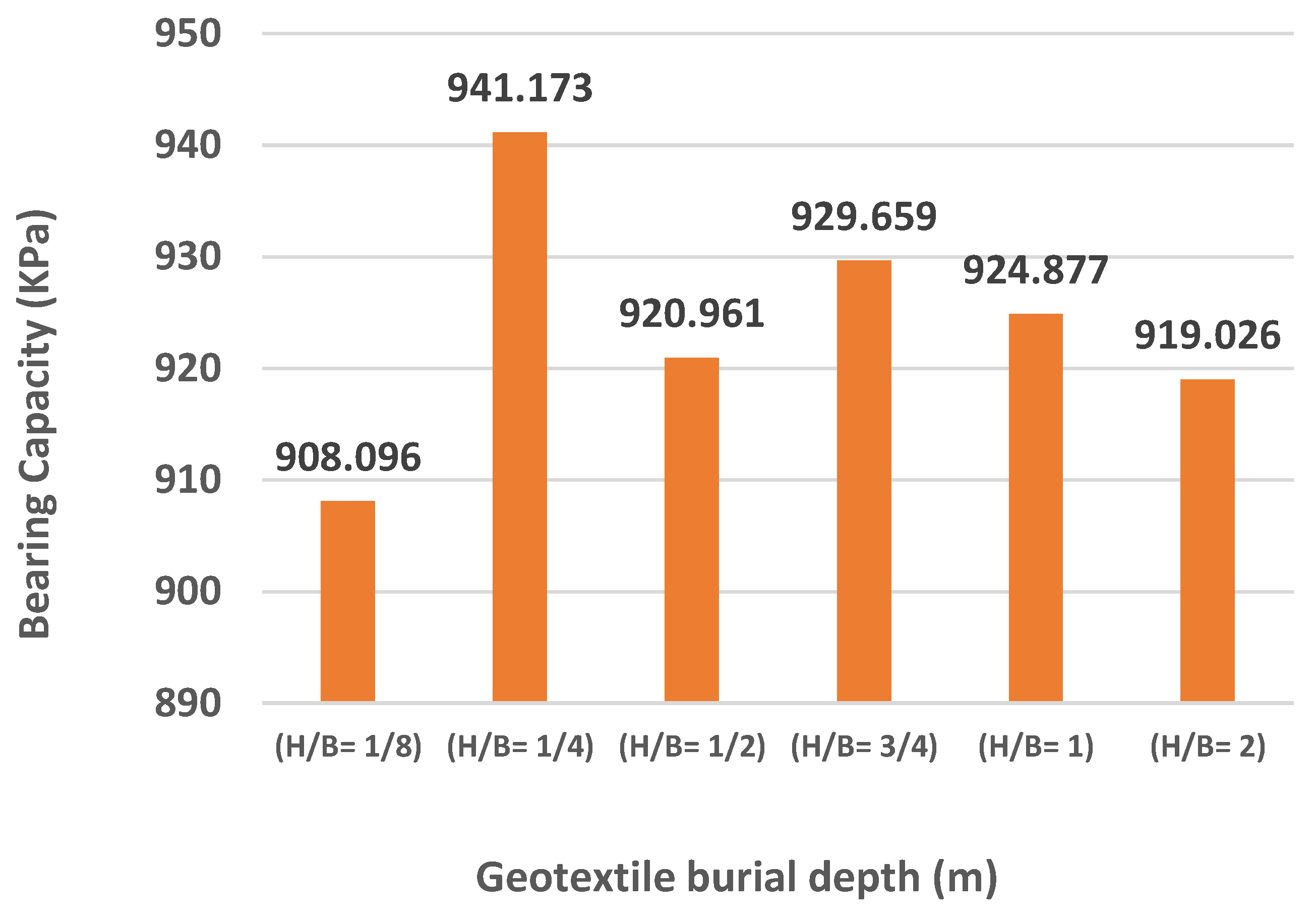
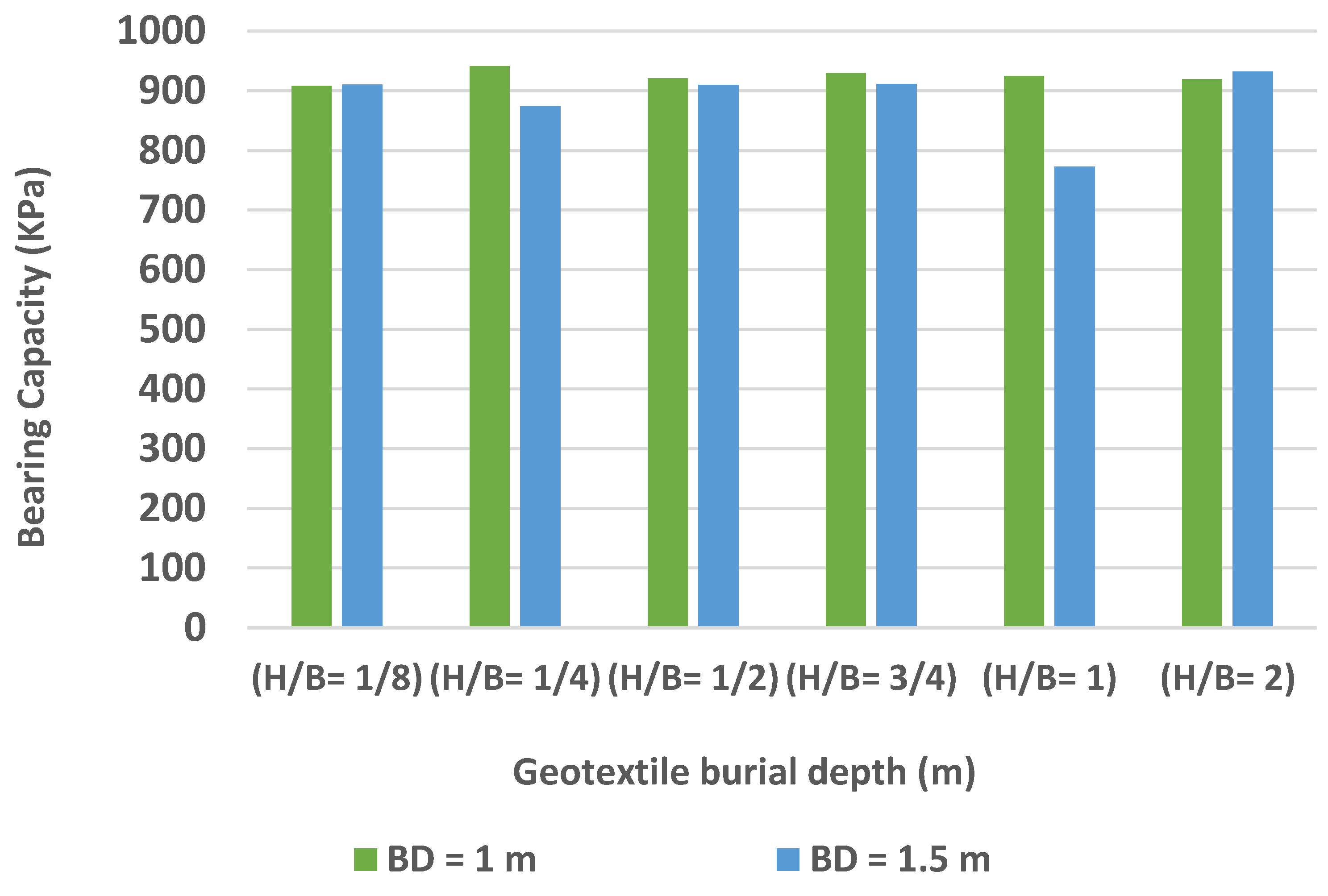
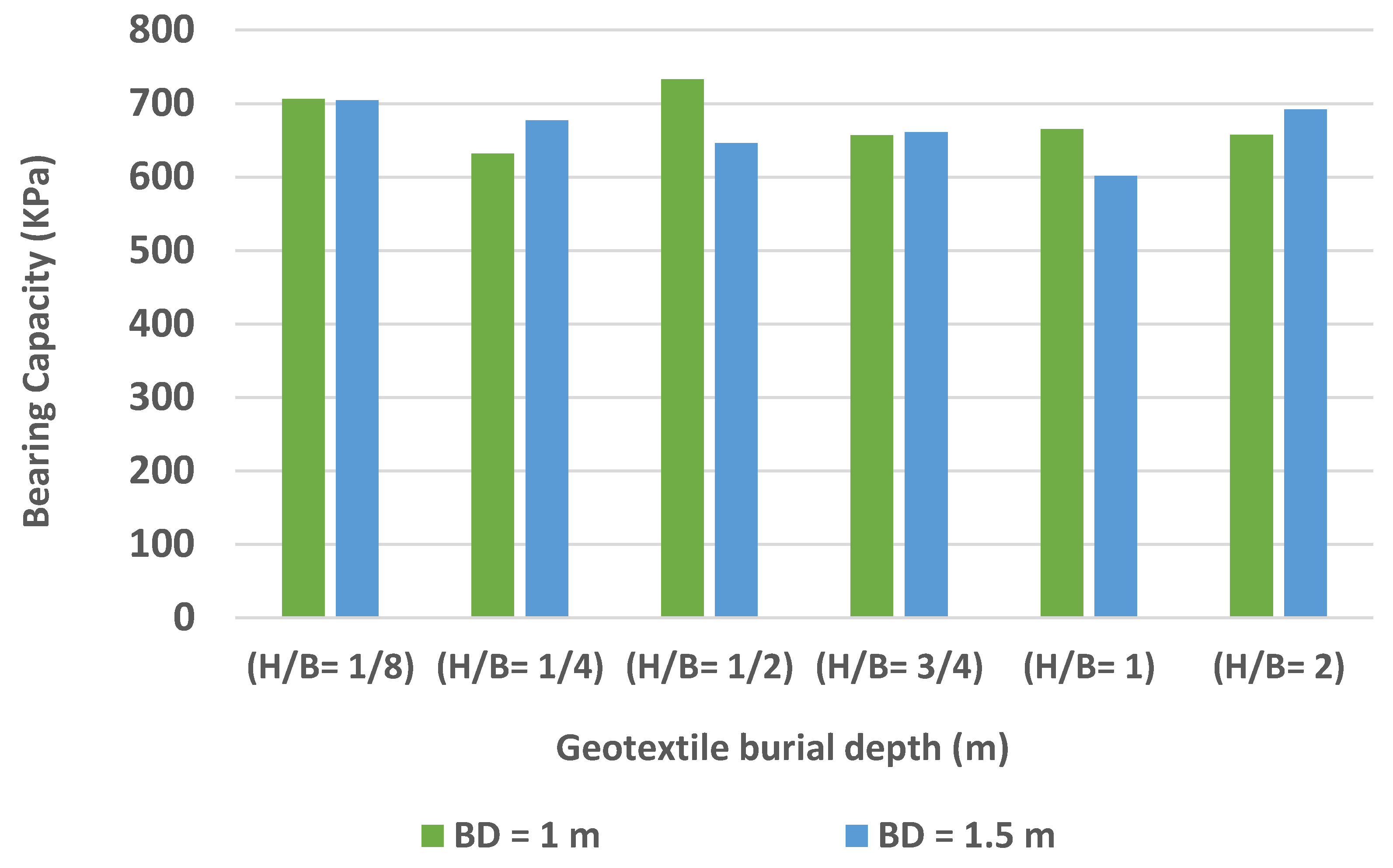
4.2. Qualitative Investigation of the Effect of Geotextile Burial Depth on Bearing Capacity
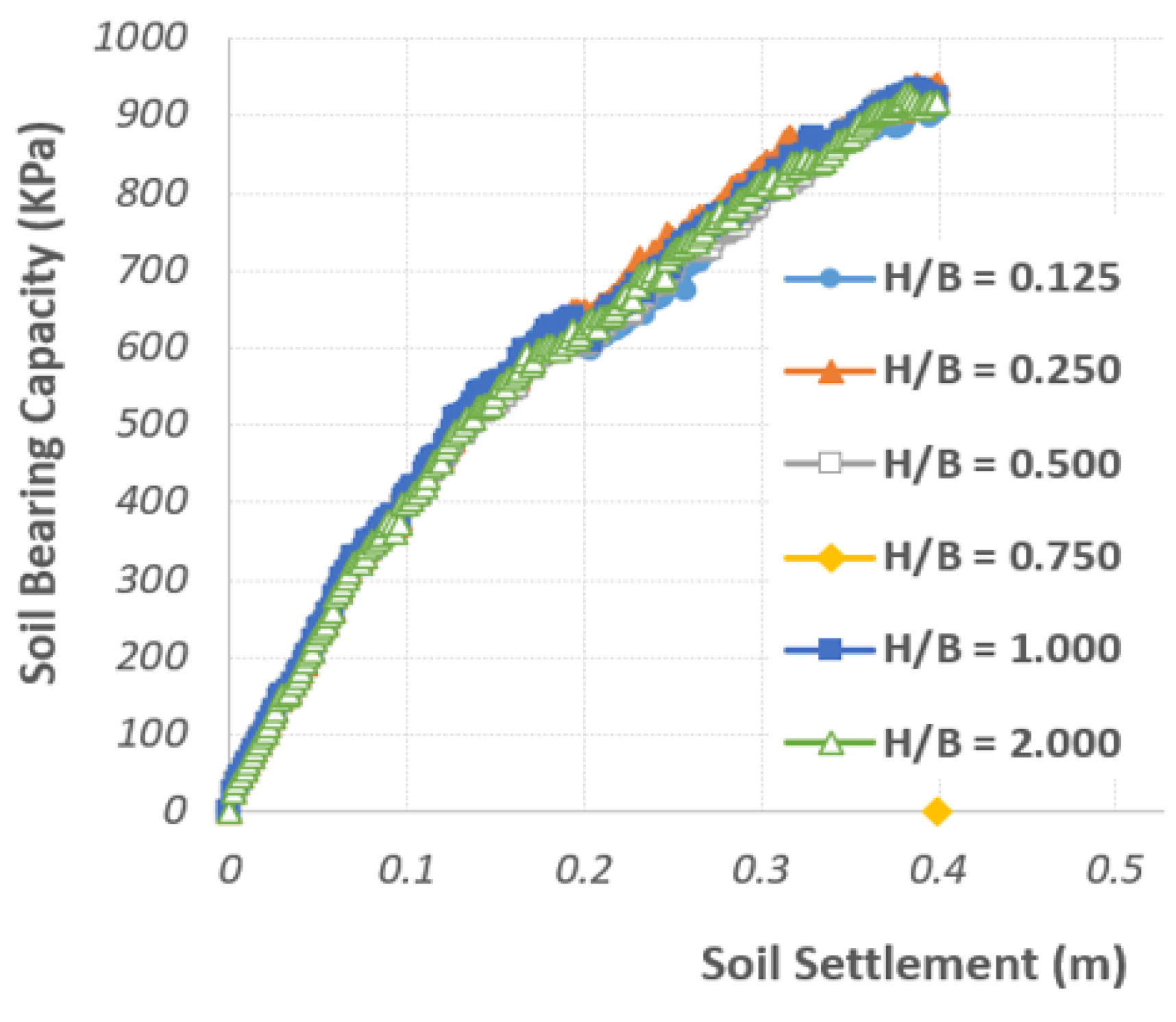
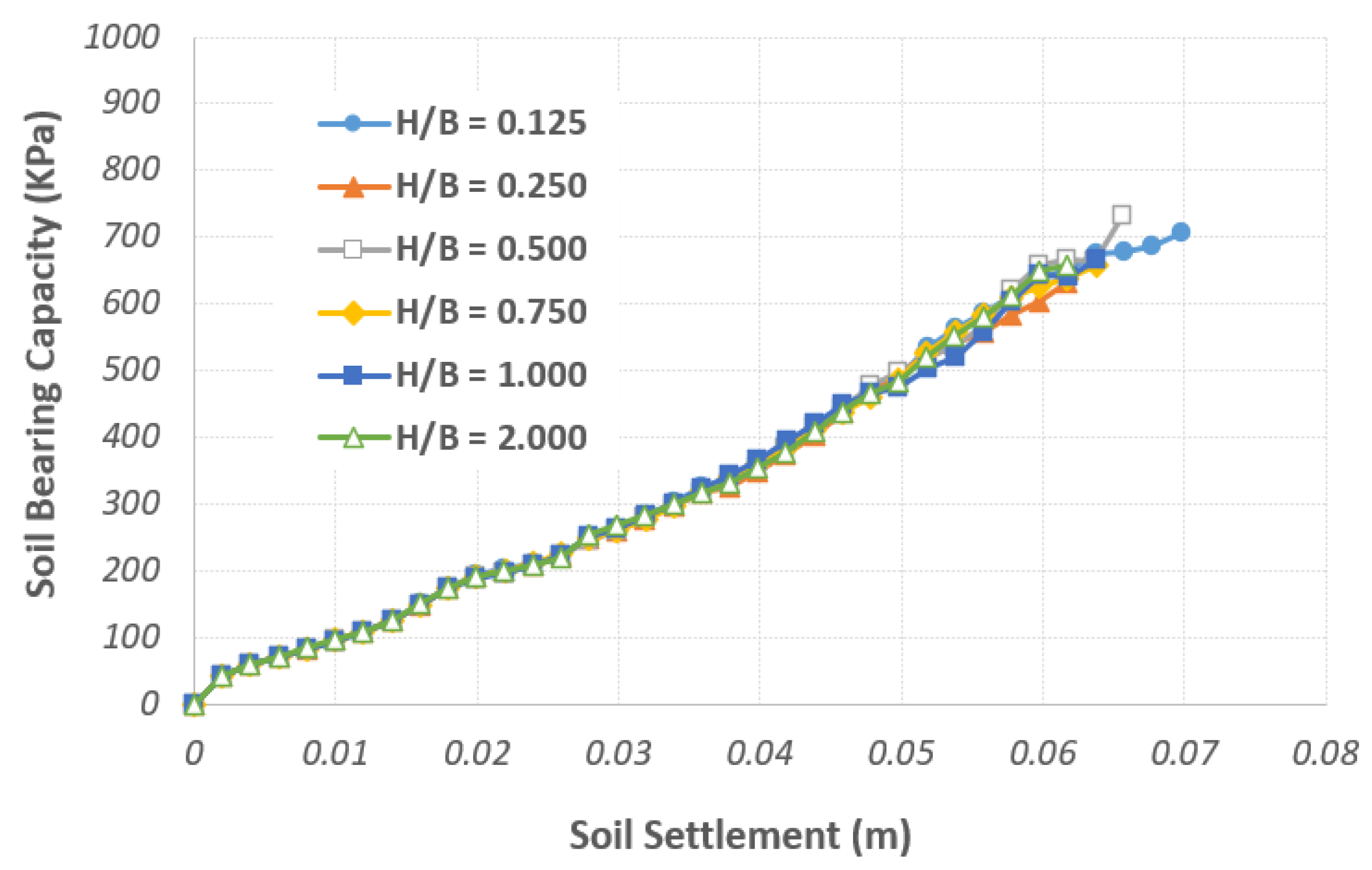
4.3. Quantitative Study of the Effect of Geotextile Burial Depth on Bearing Capacity
4.4. Qualitative Investigation of the Effect of Geotextile Length on Bearing Capacity
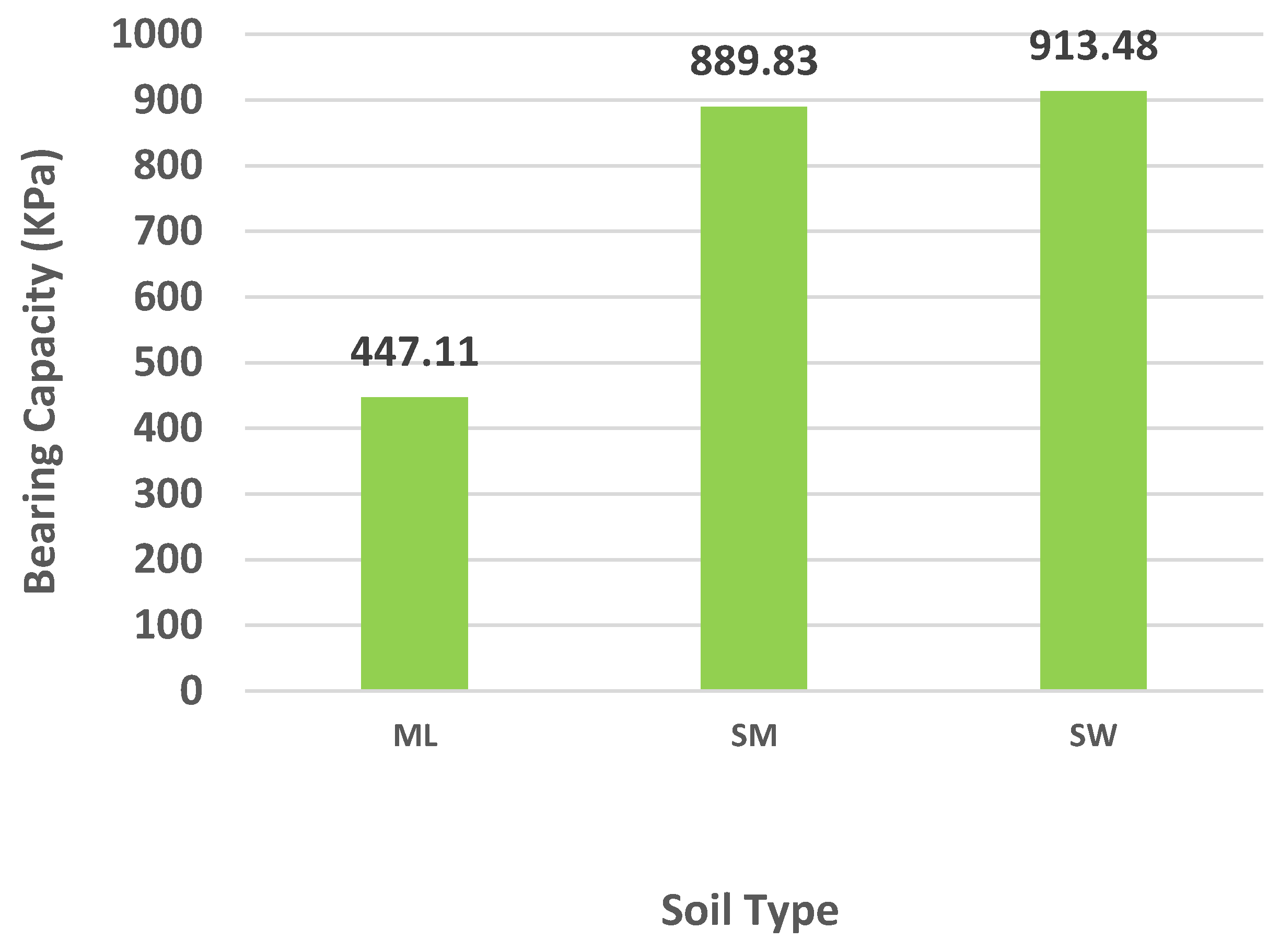
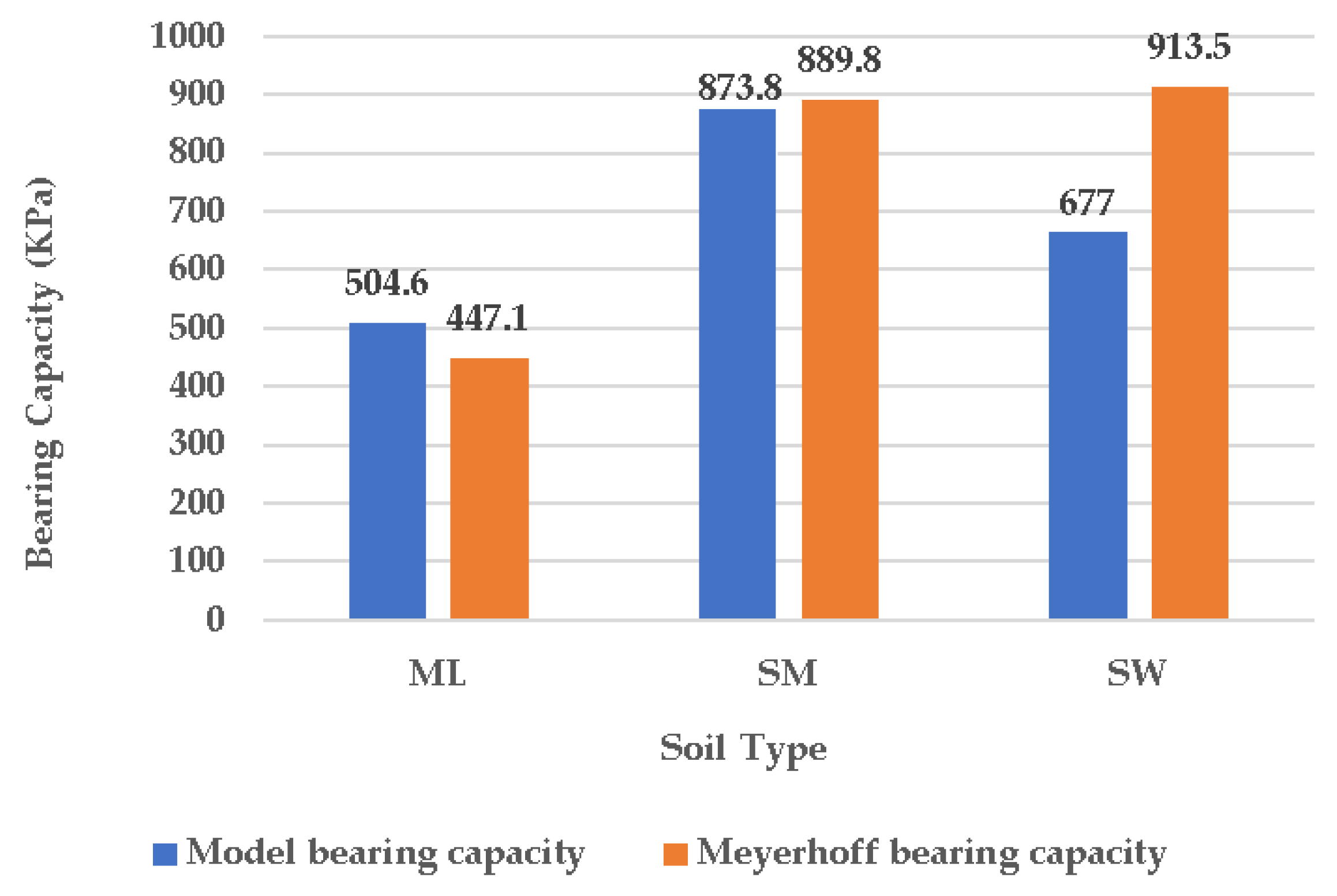
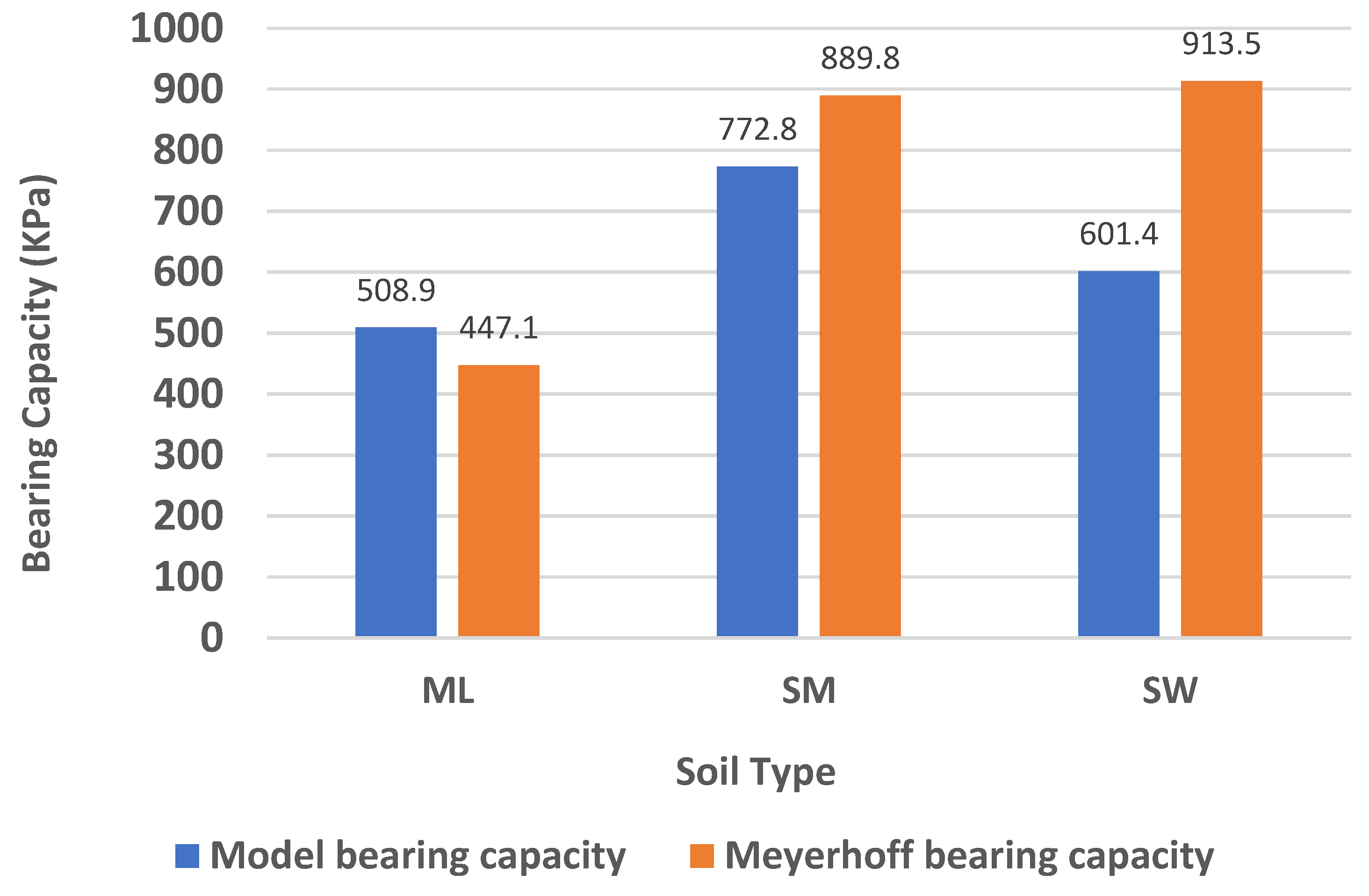
4.5. Effect of Soil Type on Bearing Capacity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Test Number | Geotextile Deployment Specifications | Soil Characteristics | |||||
|---|---|---|---|---|---|---|---|
| H/B | B (m) | H (cm) | C (KPa) | Φ | Υ (kg/m3) | E (KPa) | |
| 1 | - | - | - | 10 | 30 | 1478 | 1.40 × 104 |
| 1 | 0.125 | 1 | 12.5 | 40 | 15 | 1400 | 1.00 × 105 |
| 2 | 0.125 | 1 | 12.5 | 25 | 30 | 1740 | 1.50 × 104 |
| 3 | 0.125 | 1 | 12.5 | 0.10 | 40 | 1950 | 2.40 × 104 |
| 4 | 0.083 | 1.5 | 12.5 | 40 | 15 | 1400 | 1.40 × 104 |
| 5 | 0.083 | 1.5 | 12.5 | 25 | 30 | 1740 | 1.00 × 105 |
| 6 | 0.083 | 1.5 | 12.5 | 0.10 | 40 | 1950 | 2.40 × 104 |
| 7 | 0.250 | 1 | 25 | 40 | 15 | 1400 | 1.00 × 105 |
| 8 | 0.250 | 1 | 25 | 25 | 30 | 1740 | 1.50 × 104 |
| 9 | 0.250 | 1 | 25 | 0.10 | 40 | 1950 | 2.40 × 104 |
| 10 | 0.167 | 1.5 | 25 | 40 | 15 | 1400 | 1.00 × 105 |
| 11 | 0.167 | 1.5 | 25 | 25 | 30 | 1740 | 1.50 × 104 |
| 12 | 0.167 | 1.5 | 25 | 0.10 | 40 | 1950 | 2.40 × 104 |
| 13 | 0.500 | 1 | 50 | 40 | 15 | 1400 | 1.00 × 105 |
| 14 | 0.500 | 1 | 50 | 25 | 30 | 1740 | 1.50 × 104 |
| 15 | 0.500 | 1 | 50 | 0.10 | 40 | 1950 | 2.40 × 104 |
| 16 | 0.333 | 1.5 | 50 | 40 | 15 | 1400 | 1.00 × 105 |
| 17 | 0.333 | 1.5 | 50 | 25 | 30 | 1740 | 1.50 × 104 |
| 18 | 0.333 | 1.5 | 50 | 0.10 | 40 | 1950 | 2.40 × 104 |
| 19 | 0.750 | 1 | 75 | 40 | 15 | 1400 | 1.00 × 105 |
| 20 | 0.750 | 1 | 75 | 25 | 30 | 1740 | 1.50 × 104 |
| 21 | 0.750 | 1 | 75 | 0.10 | 40 | 1950 | 2.40 × 104 |
| 22 | 0.500 | 1.5 | 75 | 40 | 15 | 1400 | 1.00 × 105 |
| 23 | 0.500 | 1.5 | 75 | 25 | 30 | 1740 | 1.50 × 104 |
| 24 | 0.500 | 1.5 | 75 | 0.10 | 40 | 1950 | 2.40 × 104 |
| 25 | 1.000 | 1 | 100 | 40 | 15 | 1400 | 1.00 × 105 |
| 26 | 1.000 | 1 | 100 | 25 | 30 | 1740 | 1.50 × 104 |
| 27 | 1.000 | 1 | 100 | 0.10 | 40 | 1950 | 2.40 × 104 |
| 28 | 0.667 | 1.5 | 100 | 40 | 15 | 1400 | 1.00 × 105 |
| 29 | 0.667 | 1.5 | 100 | 25 | 30 | 1740 | 1.50 × 104 |
| 30 | 0.667 | 1.5 | 100 | 0.10 | 40 | 1950 | 2.40 × 104 |
| 31 | 2.000 | 1 | 200 | 40 | 15 | 1400 | 1.00 × 105 |
| 32 | 2.000 | 1 | 200 | 25 | 30 | 1740 | 1.50 × 104 |
| 33 | 2.000 | 1 | 200 | 0.10 | 40 | 1950 | 2.40 × 104 |
| 34 | 1.333 | 1.5 | 200 | 40 | 15 | 1400 | 1.00 × 105 |
| 35 | 1.333 | 1.5 | 200 | 25 | 30 | 1740 | 1.50 × 104 |
| 36 | 1.333 | 1.5 | 200 | 0.10 | 40 | 1950 | 2.40 × 104 |
| Test Number | Geotextile Deployment Specifications | Soil Characteristics | Bearing Capacity (KPa) | |||||
|---|---|---|---|---|---|---|---|---|
| H/B | B (m) | H (cm) | C (KPa) | Φ | Υ (kg/m3) | E (KPa) | ||
| 1 | - | - | - | 10 | 30 | 1478 | 1.40 × 104 | 388.847 |
| 1 | 0.125 | 1 | 12.5 | 40 | 15 | 1400 | 1.00 × 105 | 508.9540 |
| 2 | 0.125 | 1 | 12.5 | 25 | 30 | 1740 | 1.50 × 104 | 908.0960 |
| 3 | 0.125 | 1 | 12.5 | 0.10 | 40 | 1950 | 2.40 × 104 | 706.1300 |
| 4 | 0.083 | 1.5 | 12.5 | 40 | 15 | 1400 | 1.40 × 104 | 502.3580 |
| 5 | 0.083 | 1.5 | 12.5 | 25 | 30 | 1740 | 1.00 × 105 | 910.1440 |
| 6 | 0.083 | 1.5 | 12.5 | 0.10 | 40 | 1950 | 2.40 × 104 | 704.3690 |
| 7 | 0.250 | 1 | 25 | 40 | 15 | 1400 | 1.00 × 105 | 490.8000 |
| 8 | 0.250 | 1 | 25 | 25 | 30 | 1740 | 1.50 × 104 | 941.1730 |
| 9 | 0.250 | 1 | 25 | 0.10 | 40 | 1950 | 2.40 × 104 | 632.1840 |
| 10 | 0.167 | 1.5 | 25 | 40 | 15 | 1400 | 1.00 × 105 | 504.6220 |
| 11 | 0.167 | 1.5 | 25 | 25 | 30 | 1740 | 1.50 × 104 | 873.8600 |
| 12 | 0.167 | 1.5 | 25 | 0.10 | 40 | 1950 | 2.40 × 104 | 677.0650 |
| 13 | 0.500 | 1 | 50 | 40 | 15 | 1400 | 1.00 × 105 | 496.5650 |
| 14 | 0.500 | 1 | 50 | 25 | 30 | 1740 | 1.50 × 104 | 920.9610 |
| 15 | 0.500 | 1 | 50 | 0.10 | 40 | 1950 | 2.40 × 104 | 733.3540 |
| 16 | 0.333 | 1.5 | 50 | 40 | 15 | 1400 | 1.00 × 105 | 507.5590 |
| 17 | 0.333 | 1.5 | 50 | 25 | 30 | 1740 | 1.50 × 104 | 909.8120 |
| 18 | 0.333 | 1.5 | 50 | 0.10 | 40 | 1950 | 2.40 × 104 | 646.2090 |
| 19 | 0.750 | 1 | 75 | 40 | 15 | 1400 | 1.00 × 105 | 506.5840 |
| 20 | 0.750 | 1 | 75 | 25 | 30 | 1740 | 1.50 × 104 | 929.6590 |
| 21 | 0.750 | 1 | 75 | 0.10 | 40 | 1950 | 2.40 × 104 | 656.7460 |
| 22 | 0.500 | 1.5 | 75 | 40 | 15 | 1400 | 1.00 × 105 | 507.7100 |
| 23 | 0.500 | 1.5 | 75 | 25 | 30 | 1740 | 1.50 × 104 | 911.2680 |
| 24 | 0.500 | 1.5 | 75 | 0.10 | 40 | 1950 | 2.40 × 104 | 660.8910 |
| 25 | 1.000 | 1 | 100 | 40 | 15 | 1400 | 1.00 × 105 | 508.0010 |
| 26 | 1.000 | 1 | 100 | 25 | 30 | 1740 | 1.50 × 104 | 924.8770 |
| 27 | 1.000 | 1 | 100 | 0.10 | 40 | 1950 | 2.40 × 104 | 665.3290 |
| 28 | 0.667 | 1.5 | 100 | 40 | 15 | 1400 | 1.00 × 105 | 508.9090 |
| 29 | 0.667 | 1.5 | 100 | 25 | 30 | 1740 | 1.50 × 104 | 772.7800 |
| 30 | 0.667 | 1.5 | 100 | 0.10 | 40 | 1950 | 2.40 × 104 | 601.3890 |
| 31 | 2.000 | 1 | 200 | 40 | 15 | 1400 | 1.00 × 105 | 503.2950 |
| 32 | 2.000 | 1 | 200 | 25 | 30 | 1740 | 1.50 × 104 | 919.0260 |
| 33 | 2.000 | 1 | 200 | 0.10 | 40 | 1950 | 2.40 × 104 | 657.1950 |
| 34 | 1.333 | 1.5 | 200 | 40 | 15 | 1400 | 1.00 × 105 | 492.3850 |
| 35 | 1.333 | 1.5 | 200 | 25 | 30 | 1740 | 1.50 × 104 | 931.7800 |
| 36 | 1.333 | 1.5 | 200 | 0.10 | 40 | 1950 | 2.40 × 104 | 692.0160 |
| Test Number | Geotextile Deployment Specifications | Soil Characteristics | Bearing Capacity (KPa) | Meyerhof Bearing Capacity (KPa) | |||||
|---|---|---|---|---|---|---|---|---|---|
| H/B | B (m) | H (cm) | C (KPa) | Φ | Υ (kg/m3) | E (KPa) | |||
| 1 | - | - | - | 10 | 30 | 1478 | 1.40 × 104 | 388.847 | 306.03 |
| 1 | 0.125 | 1 | 12.5 | 40 | 15 | 1400 | 1.00 × 105 | 508.9540 | 447.1100 |
| 2 | 0.125 | 1 | 12.5 | 25 | 30 | 1740 | 1.50 × 104 | 908.0960 | 889.8300 |
| 3 | 0.125 | 1 | 12.5 | 0.10 | 40 | 1950 | 2.40 × 104 | 706.1300 | 913.4800 |
| 4 | 0.083 | 1.5 | 12.5 | 40 | 15 | 1400 | 1.40 × 104 | 502.3580 | 447.1100 |
| 5 | 0.083 | 1.5 | 12.5 | 25 | 30 | 1740 | 1.00 × 105 | 910.1440 | 889.8300 |
| 6 | 0.083 | 1.5 | 12.5 | 0.10 | 40 | 1950 | 2.40 × 104 | 704.3690 | 913.4800 |
| 7 | 0.250 | 1 | 25 | 40 | 15 | 1400 | 1.00 × 105 | 490.8000 | 447.1100 |
| 8 | 0.250 | 1 | 25 | 25 | 30 | 1740 | 1.50 × 104 | 941.1730 | 889.8300 |
| 9 | 0.250 | 1 | 25 | 0.10 | 40 | 1950 | 2.40 × 104 | 632.1840 | 913.4800 |
| 10 | 0.167 | 1.5 | 25 | 40 | 15 | 1400 | 1.00 × 105 | 504.6220 | 447.1100 |
| 11 | 0.167 | 1.5 | 25 | 25 | 30 | 1740 | 1.50 × 104 | 873.8600 | 889.8300 |
| 12 | 0.167 | 1.5 | 25 | 0.10 | 40 | 1950 | 2.40 × 104 | 677.0650 | 913.4800 |
| 13 | 0.500 | 1 | 50 | 40 | 15 | 1400 | 1.00 × 105 | 496.5650 | 447.1100 |
| 14 | 0.500 | 1 | 50 | 25 | 30 | 1740 | 1.50 × 104 | 920.9610 | 889.8300 |
| 15 | 0.500 | 1 | 50 | 0.10 | 40 | 1950 | 2.40 × 104 | 733.3540 | 913.4800 |
| 16 | 0.333 | 1.5 | 50 | 40 | 15 | 1400 | 1.00 × 105 | 507.5590 | 447.1100 |
| 17 | 0.333 | 1.5 | 50 | 25 | 30 | 1740 | 1.50 × 104 | 909.8120 | 889.8300 |
| 18 | 0.333 | 1.5 | 50 | 0.10 | 40 | 1950 | 2.40 × 104 | 646.2090 | 913.4800 |
| 19 | 0.750 | 1 | 75 | 40 | 15 | 1400 | 1.00 × 105 | 506.5840 | 447.1100 |
| 20 | 0.750 | 1 | 75 | 25 | 30 | 1740 | 1.50 × 104 | 929.6590 | 889.8300 |
| 21 | 0.750 | 1 | 75 | 0.10 | 40 | 1950 | 2.40 × 104 | 656.7460 | 913.4800 |
| 22 | 0.500 | 1.5 | 75 | 40 | 15 | 1400 | 1.00 × 105 | 507.7100 | 447.1100 |
| 23 | 0.500 | 1.5 | 75 | 25 | 30 | 1740 | 1.50 × 104 | 911.2680 | 889.8300 |
| 24 | 0.500 | 1.5 | 75 | 0.10 | 40 | 1950 | 2.40 × 104 | 660.8910 | 913.4800 |
| 25 | 1.000 | 1 | 100 | 40 | 15 | 1400 | 1.00 × 105 | 508.0010 | 447.1100 |
| 26 | 1.000 | 1 | 100 | 25 | 30 | 1740 | 1.50 × 104 | 924.8770 | 889.8300 |
| 27 | 1.000 | 1 | 100 | 0.10 | 40 | 1950 | 2.40 × 104 | 665.3290 | 913.4800 |
| 28 | 0.667 | 1.5 | 100 | 40 | 15 | 1400 | 1.00 × 105 | 508.9090 | 447.1100 |
| 29 | 0.667 | 1.5 | 100 | 25 | 30 | 1740 | 1.50 × 104 | 772.7800 | 889.8300 |
| 30 | 0.667 | 1.5 | 100 | 0.10 | 40 | 1950 | 2.40 × 104 | 601.3890 | 913.4800 |
| 31 | 2.000 | 1 | 200 | 40 | 15 | 1400 | 1.00 × 105 | 503.2950 | 447.1100 |
| 32 | 2.000 | 1 | 200 | 25 | 30 | 1740 | 1.50 × 104 | 919.0260 | 889.8300 |
| 33 | 2.000 | 1 | 200 | 0.10 | 40 | 1950 | 2.40 × 104 | 657.1950 | 913.4800 |
| 34 | 1.333 | 1.5 | 200 | 40 | 15 | 1400 | 1.00 × 105 | 492.3850 | 447.1100 |
| 35 | 1.333 | 1.5 | 200 | 25 | 30 | 1740 | 1.50 × 104 | 931.7800 | 889.8300 |
| 36 | 1.333 | 1.5 | 200 | 0.10 | 40 | 1950 | 2.40 × 104 | 692.0160 | 913.4800 |
| Test Number | Geotextile Deployment Specifications | Soil Characteristics | Bearing Capacity (KPa) | Meyerhof Bearing Capacity (KPa) | Settlement (m) | Possible Rupture Mechanism | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| H/B | B (m) | H (cm) | C (KPa) | Φ | Υ (kg/m3) | E (KPa) | |||||
| 1 | - | - | - | 10 | 30 | 1478 | 1.40 × 104 | 388.847 | 306.03 | 0.1177 | General shear |
| 1 | 0.125 | 1 | 12.5 | 40 | 15 | 1400 | 1.00 × 105 | 508.9540 | 447.1100 | 0.3994 | Local shear |
| 2 | 0.125 | 1 | 12.5 | 25 | 30 | 1740 | 1.50 × 104 | 908.0960 | 889.8300 | 0.3995 | Local shear |
| 3 | 0.125 | 1 | 12.5 | 0.10 | 40 | 1950 | 2.40 × 104 | 706.1300 | 913.4800 | 0.0698 | General shear |
| 4 | 0.083 | 1.5 | 12.5 | 40 | 15 | 1400 | 1.40 × 104 | 502.3580 | 447.1100 | 0.3959 | Local shear |
| 5 | 0.083 | 1.5 | 12.5 | 25 | 30 | 1740 | 1.00 × 105 | 910.1440 | 889.8300 | 0.3994 | Local shear |
| 6 | 0.083 | 1.5 | 12.5 | 0.10 | 40 | 1950 | 2.40 × 104 | 704.3690 | 913.4800 | 0.0638 | General shear |
| 7 | 0.250 | 1 | 25 | 40 | 15 | 1400 | 1.00 × 105 | 490.8000 | 447.1100 | 0.3990 | Local shear |
| 8 | 0.250 | 1 | 25 | 25 | 30 | 1740 | 1.50 × 104 | 941.1730 | 889.8300 | 0.3992 | Local shear |
| 9 | 0.250 | 1 | 25 | 0.10 | 40 | 1950 | 2.40 × 104 | 632.1840 | 913.4800 | 0.0617 | General shear |
| 10 | 0.167 | 1.5 | 25 | 40 | 15 | 1400 | 1.00 × 105 | 504.6220 | 447.1100 | 0.3991 | Local shear |
| 11 | 0.167 | 1.5 | 25 | 25 | 30 | 1740 | 1.50 × 104 | 873.8600 | 889.8300 | 0.3993 | Local shear |
| 12 | 0.167 | 1.5 | 25 | 0.10 | 40 | 1950 | 2.40 × 104 | 677.0650 | 913.4800 | 0.0617 | General shear |
| 13 | 0.500 | 1 | 50 | 40 | 15 | 1400 | 1.00 × 105 | 496.5650 | 447.1100 | 0.3991 | Local shear |
| 14 | 0.500 | 1 | 50 | 25 | 30 | 1740 | 1.50 × 104 | 920.9610 | 889.8300 | 0.3992 | Local shear |
| 15 | 0.500 | 1 | 50 | 0.10 | 40 | 1950 | 2.40 × 104 | 733.3540 | 913.4800 | 0.0657 | General shear |
| 16 | 0.333 | 1.5 | 50 | 40 | 15 | 1400 | 1.00 × 105 | 507.5590 | 447.1100 | 0.3992 | Local shear |
| 17 | 0.333 | 1.5 | 50 | 25 | 30 | 1740 | 1.50 × 104 | 909.8120 | 889.8300 | 0.3992 | Local shear |
| 18 | 0.333 | 1.5 | 50 | 0.10 | 40 | 1950 | 2.40 × 104 | 646.2090 | 913.4800 | 0.0617 | General shear |
| 19 | 0.750 | 1 | 75 | 40 | 15 | 1400 | 1.00 × 105 | 506.5840 | 447.1100 | 0.3992 | Local shear |
| 20 | 0.750 | 1 | 75 | 25 | 30 | 1740 | 1.50 × 104 | 929.6590 | 889.8300 | 0.3993 | Local shear |
| 21 | 0.750 | 1 | 75 | 0.10 | 40 | 1950 | 2.40 × 104 | 656.7460 | 913.4800 | 0.0637 | General shear |
| 22 | 0.500 | 1.5 | 75 | 40 | 15 | 1400 | 1.00 × 105 | 507.7100 | 447.1100 | 0.3992 | Local shear |
| 23 | 0.500 | 1.5 | 75 | 25 | 30 | 1740 | 1.50 × 104 | 911.2680 | 889.8300 | 0.3991 | Local shear |
| 24 | 0.500 | 1.5 | 75 | 0.10 | 40 | 1950 | 2.40 × 104 | 660.8910 | 913.4800 | 0.0617 | General shear |
| 25 | 1.000 | 1 | 100 | 40 | 15 | 1400 | 1.00 × 105 | 508.0010 | 447.1100 | 0.3993 | Local shear |
| 26 | 1.000 | 1 | 100 | 25 | 30 | 1740 | 1.50 × 104 | 924.8770 | 889.8300 | 0.3994 | Local shear |
| 27 | 1.000 | 1 | 100 | 0.10 | 40 | 1950 | 2.40 × 104 | 665.3290 | 913.4800 | 0.0637 | General shear |
| 28 | 0.667 | 1.5 | 100 | 40 | 15 | 1400 | 1.00 × 105 | 508.9090 | 447.1100 | 0.3990 | Local shear |
| 29 | 0.667 | 1.5 | 100 | 25 | 30 | 1740 | 1.50 × 104 | 772.7800 | 889.8300 | 0.2950 | Local shear |
| 30 | 0.667 | 1.5 | 100 | 0.10 | 40 | 1950 | 2.40 × 104 | 601.3890 | 913.4800 | 0.0598 | General shear |
| 31 | 2.000 | 1 | 200 | 40 | 15 | 1400 | 1.00 × 105 | 503.2950 | 447.1100 | 0.3992 | Local shear |
| 32 | 2.000 | 1 | 200 | 25 | 30 | 1740 | 1.50 × 104 | 919.0260 | 889.8300 | 0.3992 | Local shear |
| 33 | 2.000 | 1 | 200 | 0.10 | 40 | 1950 | 2.40 × 104 | 657.1950 | 913.4800 | 0.0617 | General shear |
| 34 | 1.333 | 1.5 | 200 | 40 | 15 | 1400 | 1.00 × 105 | 492.3850 | 447.1100 | 0.3991 | Local shear |
| 35 | 1.333 | 1.5 | 200 | 25 | 30 | 1740 | 1.50 × 104 | 931.7800 | 889.8300 | 0.3992 | Local shear |
| 36 | 1.333 | 1.5 | 200 | 0.10 | 40 | 1950 | 2.40 × 104 | 692.0160 | 913.4800 | 0.0967 | General shear |
References
- Benndorf, J.; Restrepo, D.A.; Merkel, N.; John, A.; Buxton, M.; Guatame-Garcia, A.; Dalm, M.; De Waard, B.; Flores, H.; Möllerherm, S.; et al. TRIM4Post-Mining: Transition Information Modelling for Attractive Post-Mining Landscapes—A Conceptual Framework. Mining 2022, 2, 248–277. [Google Scholar] [CrossRef]
- Elmouttie, M.; Hodgkinson, J.; Dean, P. Prediction of Mining Conditions in Geotechnically Complex Sites. Mining 2021, 1, 279–296. [Google Scholar] [CrossRef]
- Kavvadas, M.; Roumpos, C.; Servou, A.; Paraskevis, N. Geotechnical Issues in Decommissioning Surface Lignite Mines—The Case of Amyntaion Mine in Greece. Mining 2022, 2, 278–296. [Google Scholar] [CrossRef]
- Wu, X.; Liu, Z. Advances in Deformation and Permeability Evolution during Creep of Rocks. Geotechnics 2022, 2, 317–334. [Google Scholar] [CrossRef]
- Ghaychi Afrouz, S.; Westman, E.; Dehn, K.; Weston, B. Underground Rock Mass Behavior Prior to the Occur-rence of Mining Induced Seismic Events. Geotechnics 2022, 2, 765–780. [Google Scholar] [CrossRef]
- Banu, S.; Attom, M.; Abed, F.; Vandanapu, R.; Astillo, P.V.; Al-Lozi, N.; Khalil, A. Numerical Analysis of the Ulti-mate Bearing Capacity of Strip Footing Constructed on Sand-over-Clay Sediment. Buildings 2024, 14, 1164. [Google Scholar] [CrossRef]
- Rowe, R.K.; Fan, J. The Application of Geosynthetics in Tailings Storage Facilities: A General Review. Mining 2024, 4, 447–468. [Google Scholar] [CrossRef]
- Yerro, A.; Ceccato, F. Soil–Water–Structure Interactions. Geotechnics 2023, 3, 301–305. [Google Scholar] [CrossRef]
- Taghavi, S.A.; Jalali, F.M.; Moezzi, R.; Khaksar, R.Y.; Wacławek, S.; Gheibi, M.; Annuk, A. Numerical Analysis of Bearing Capacity in Deep Excavation Support Structures: A Comparative Study of Nailing Systems and Helical Anchors. Eng 2024, 5, 657–676. [Google Scholar] [CrossRef]
- Lopes, M.J.; Lopes, M.L. Soil-Geosynthetic Interaction—Influence of Soil Particle Size and Geosynthetic Struc-ture. Geosynth. Int. 1999, 6, 261–282. [Google Scholar] [CrossRef]
- Avesani Neto, J.O.; Bueno, B.S.; Futai, M.M. A Bearing Capacity Calculation Method for Soil Reinforced with a Geocell. Geosynth. Int. 2013, 20, 129–142. [Google Scholar] [CrossRef]
- Müller, W.W.; Saathoff, F. Geosynthetics in Geoenvironmental Engineering. Sci. Technol. Adv. Mater. 2015, 16, 34605. [Google Scholar] [CrossRef]
- Zarrabinia, M.; Yeganeh Khaksar, R. Numerical investigation of the performance of the foundation improved with geotextile on soft clay soil. In Proceedings of the 11th National Congress on Civil Engineering, Shiraz, Iran, 1–2 May 2019. [Google Scholar]
- Tavassoli Rad, H.; Yeganeh Khaksar, R. Numerical investigation of the effect of geotextile properties on the bearing capacity and lateral stability of embankment walls. In Proceedings of the 12th National Congress on Civil Engineering, Tabriz, Iran, 27–28 May 2020. [Google Scholar]
- Juraszek, J.; Gwóźdź-Lasoń, M.; Logoń, D. FBG Strain Monitoring of a Road Structure Reinforced with a Geosynthetic Mattress in Cases of Subsoil Deformation in Mining Activity Areas. Materials 2021, 14, 1709. [Google Scholar] [CrossRef]
- Lawton, E.C.; Khire, M.V.; Fox, N.S. Reinforcement of Soils by Multioriented Geosynthetic Inclusions. J. Geotech. Eng. 1993, 119, 257–275. [Google Scholar] [CrossRef]
- Kawalec, J.; Grygierek, M.; Koda, E.; Osiński, P. Lessons Learned on Geosynthetics Applications in Road Structures in Silesia Mining Region in Poland. Appl. Sci. 2019, 9, 1122. [Google Scholar] [CrossRef]
- Tanasă, F.; Nechifor, M.; Ignat, M.-E.; Teacă, C.-A. Geotextiles—A Versatile Tool for Environmental Sensitive Applications in Geotechnical Engineering. Textiles 2022, 2, 189–208. [Google Scholar] [CrossRef]
- Koerner, R.M.; Hwu, B.-L.; Wayne, M.H. Soft Soil Stabilization Designs Using Geosynthetics. Geotext. Geomembr. 1987, 6, 33–51. [Google Scholar] [CrossRef]
- Hatami, K.; Bathurst, R.J. Development and Verification of a Numerical Model for the Analysis of Geosynthetic-Reinforced Soil Segmental Walls under Working Stress Conditions. Can. Geotech. J. 2005, 42, 1066–1085. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, G.; Zhang, J.-M. Centrifuge Model Tests of Geotextile-Reinforced Soil Embankments during an Earthquake. Geotext. Geomembr. 2011, 29, 222–232. [Google Scholar] [CrossRef]
- Rashidian, V.; Naeini, S.A.; Mirzakhanlari, M. Laboratory Testing and Numerical Modelling on Bearing Capacity of Geotextile-Reinforced Granular Soils. Int. J. Geotech. Eng. 2018, 12, 241–251. [Google Scholar] [CrossRef]
- Panigrahi, B.; Pradhan, P.K. Improvement of Bearing Capacity of Soil by Using Natural Geotextile. Int. J. Geo-Eng. 2019, 10, 9. [Google Scholar] [CrossRef]
- Ouria, A.; Mahmoudi, A.; Sadeghpour, H. Effect of the Geotextile Arrangement on the Bearing Capacity of a Strip Footing. Int. J. Geosynth. Ground Eng. 2020, 6, 36. [Google Scholar] [CrossRef]
- Sinha, P.; Anusha Raj, K.; Kumar, S.; Singh, D. Mechanical Behavior of Geotextile and Geogrids on Soil Stabilization: A Review. In Recent Advances in Mechanical Engineering; Manik, G., Kalia, S., Verma, O.P., Sharma, T.K., Eds.; Springer Nature: Singapore, 2023; pp. 299–308. ISBN 9789811921872. [Google Scholar]
- Abid, M.S.; Rathod, D.; Vanapalli, S.K. Bearing Capacity of Annulus Stone Column Double-Encapsulated with Geotextiles. Int. J. Geomech. 2023, 23, 4022281. [Google Scholar] [CrossRef]
- Aliasgharzadeh, M.; Yousefzadehfard, M.; Atrchian, M.; Bayat, M. Experimental Study on Pullout Capacity of Geocell and Geotextile-Reinforced Horizontal Plate Anchors Embedded in Granular Soil. Int. J. Geosynth. Ground Eng. 2023, 9, 6. [Google Scholar] [CrossRef]
- Helwany, S. Applied Soil Mechanics: With ABAQUS Applications, 1st ed.; Wiley: Hoboken, NJ, USA, 2007; ISBN 9780471791072/9780470168097. [Google Scholar]
- Hajialilue, B.M.; Katebi, H.; Behrouz, S.F. Behavior Investigation of Reinforced and Unreinforced Sand below Strip Foundation Using PIV. J. Civ. Eng. Ferdowsi 2012, 23, 103–114. [Google Scholar]
- Aksu Alcan, B.; Çelik, S. The Effect of Different Fiber Reinforcement on Bearing Capacity under Strip Foundation on the Sand Soil: An Experimental Investigation. Appl. Sci. 2023, 13, 9769. [Google Scholar] [CrossRef]
- Mishra, J.; Panigrahi, R. Mini-Review on Structural Performance of Fiber Reinforced Geopolymer Concrete. Int. J. Innov. Technol. Interdiscip. Sci. 2020, 3, 435–442. [Google Scholar] [CrossRef]
- Zhu, H.-H.; Zhang, C.-C.; Tang, C.-S.; Shi, B.; Wang, B.-J. Modeling the Pullout Behavior of Short Fiber in Rein-forced Soil. Geotext. Geomembr. 2014, 42, 329–338. [Google Scholar] [CrossRef]
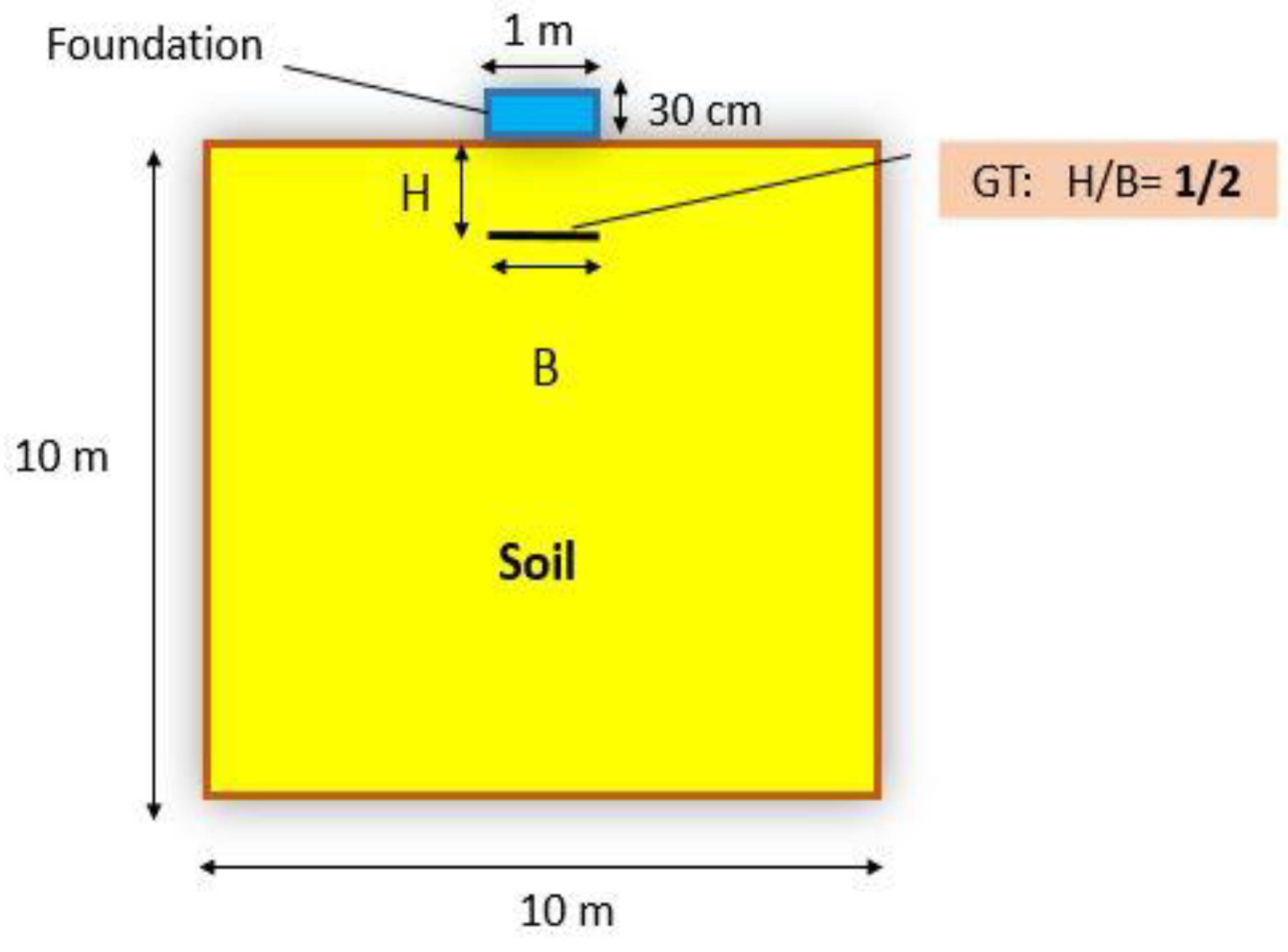
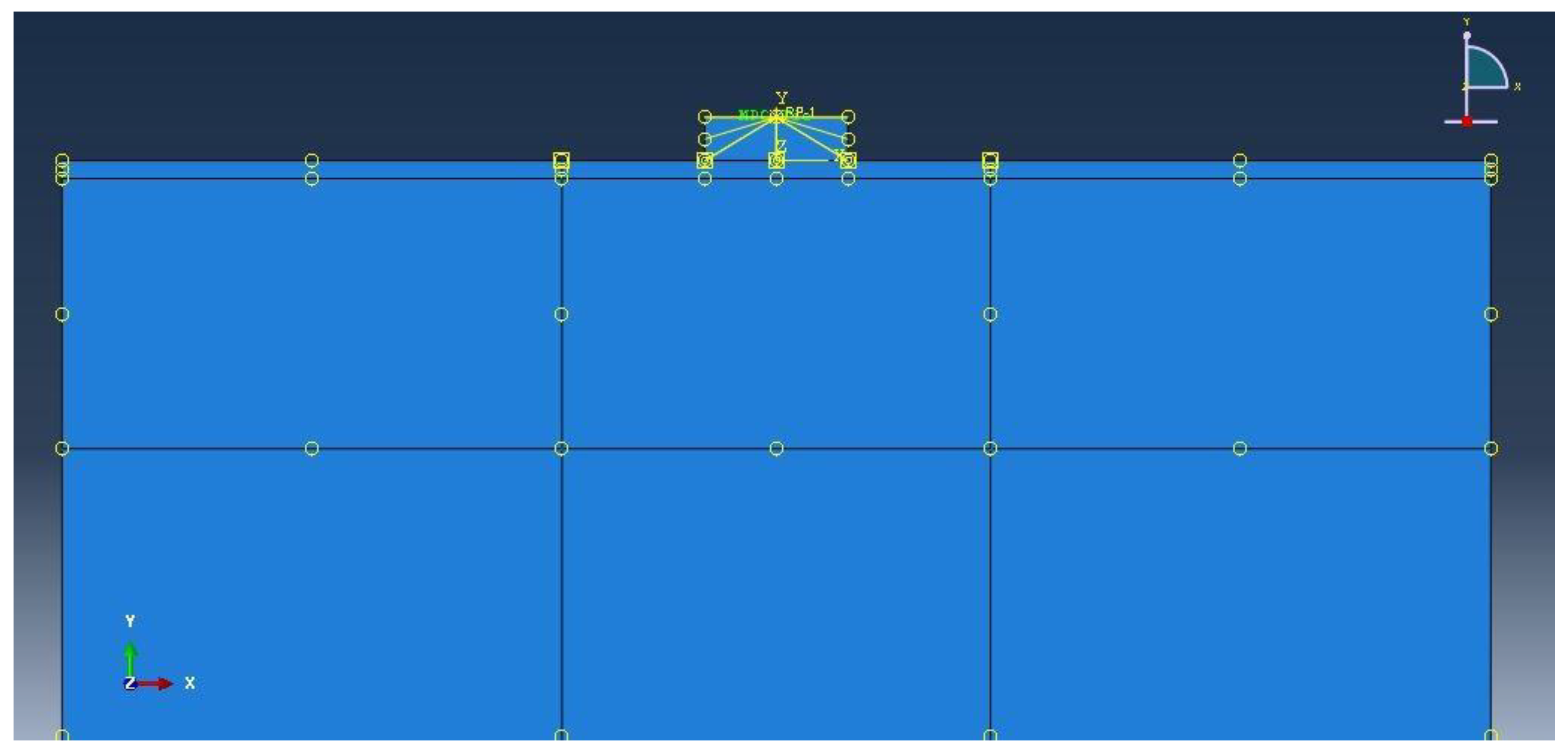
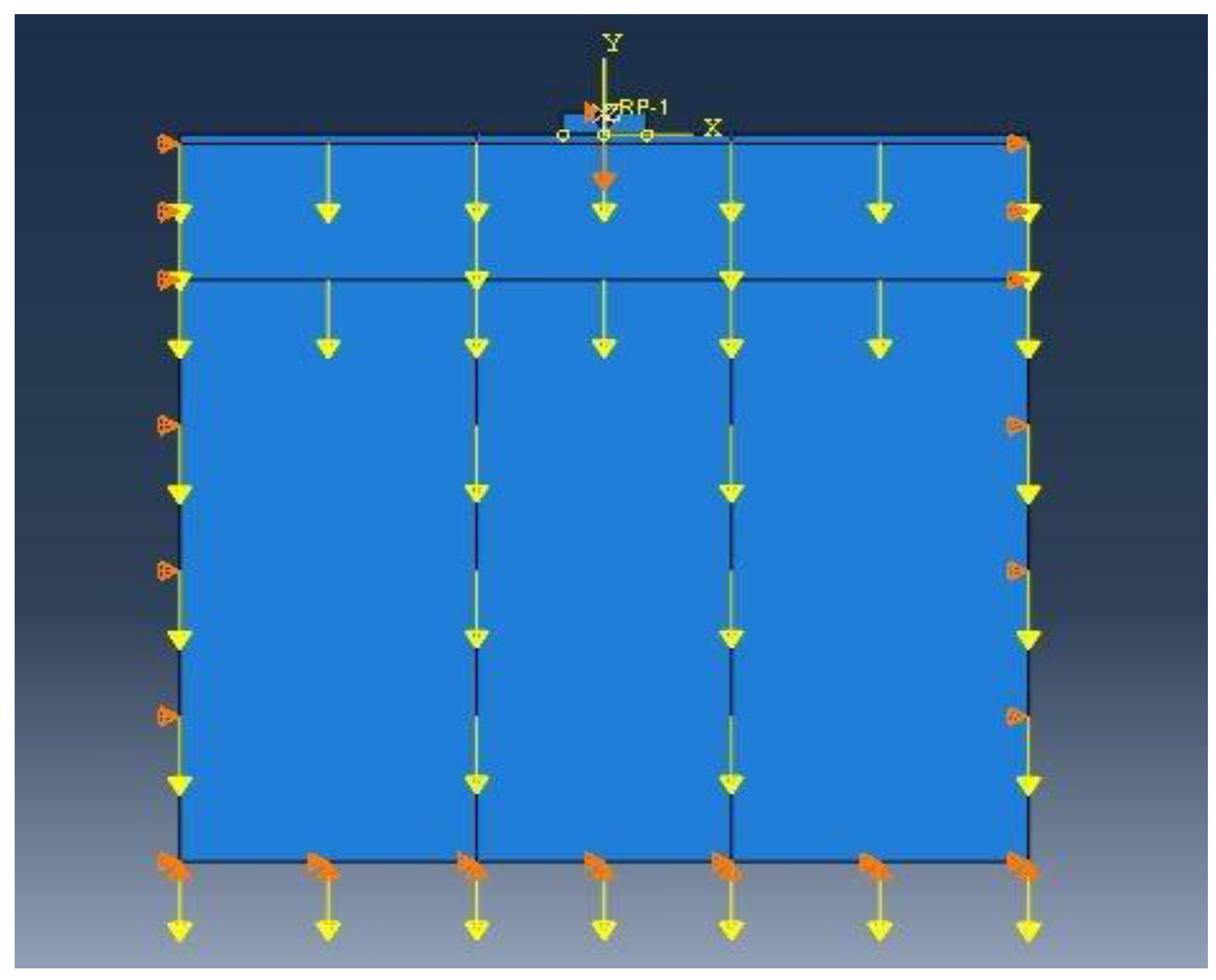
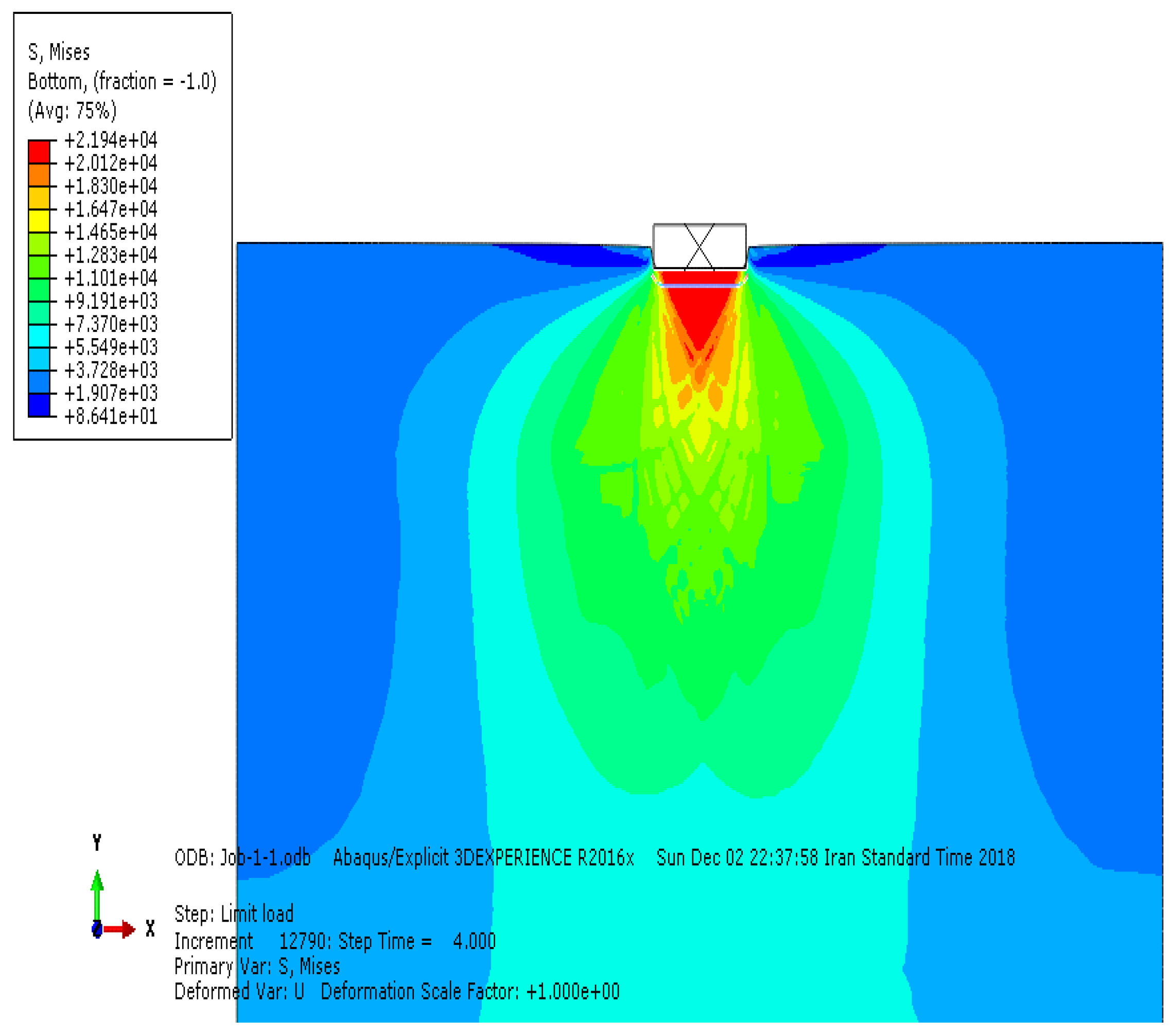
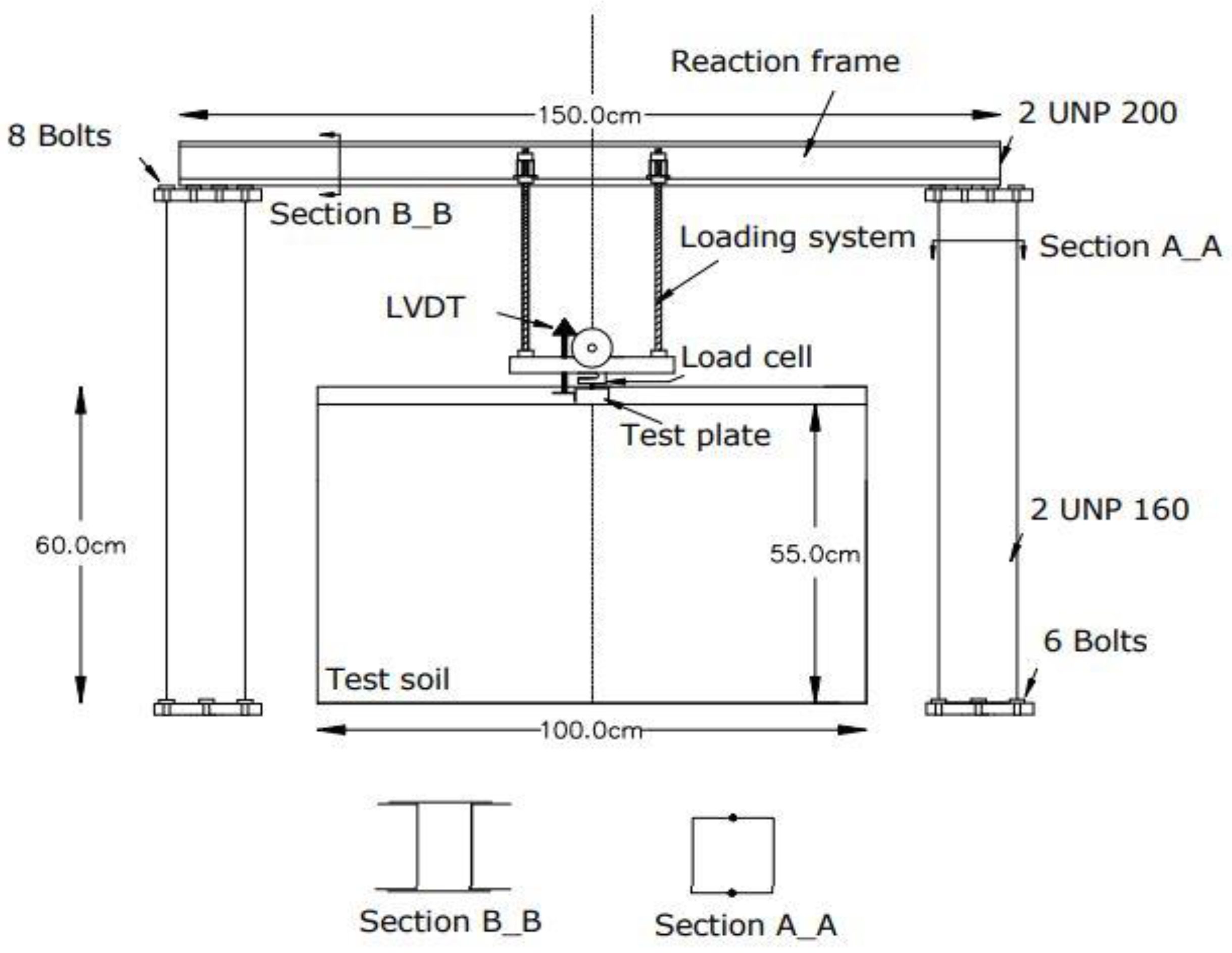
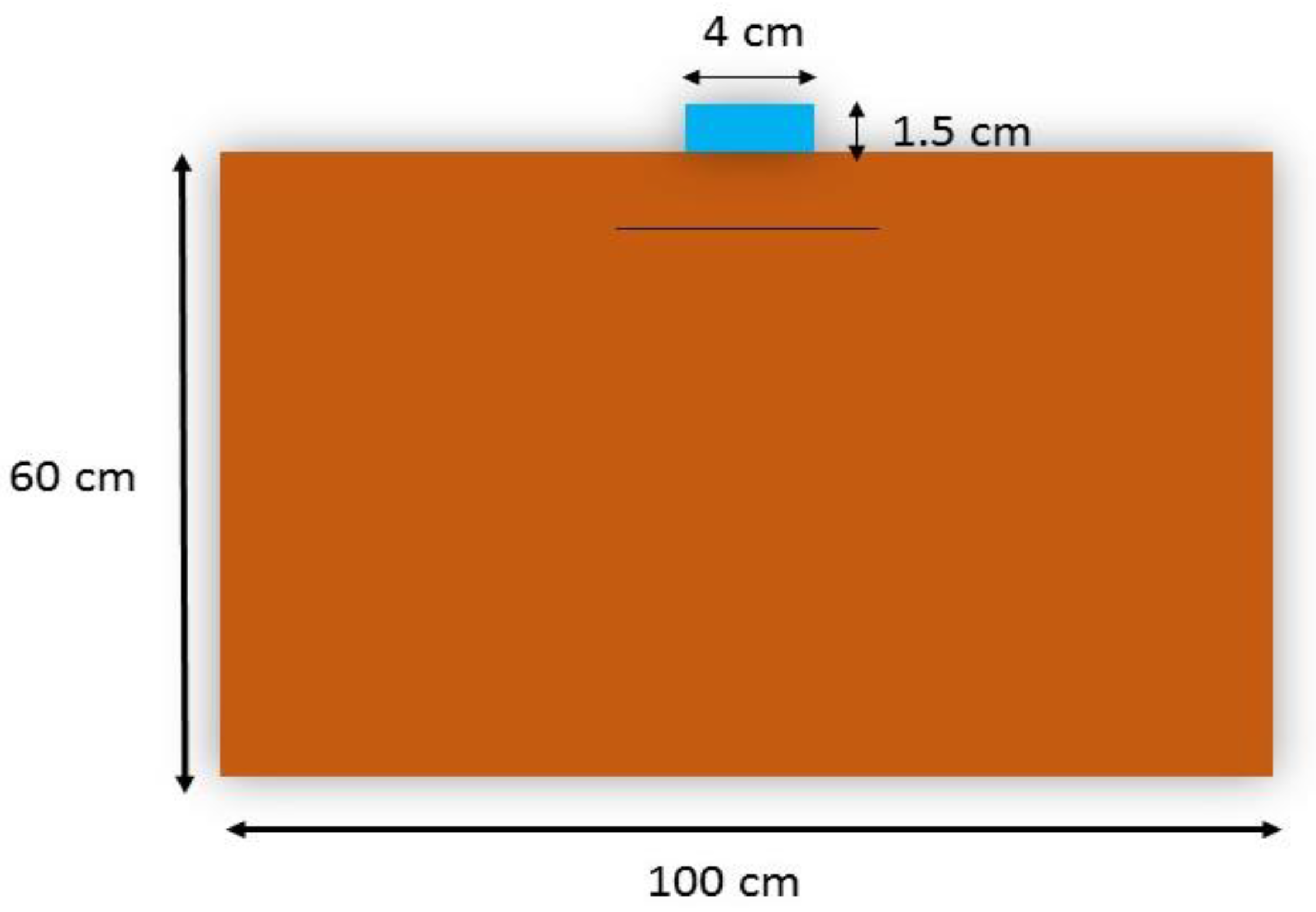
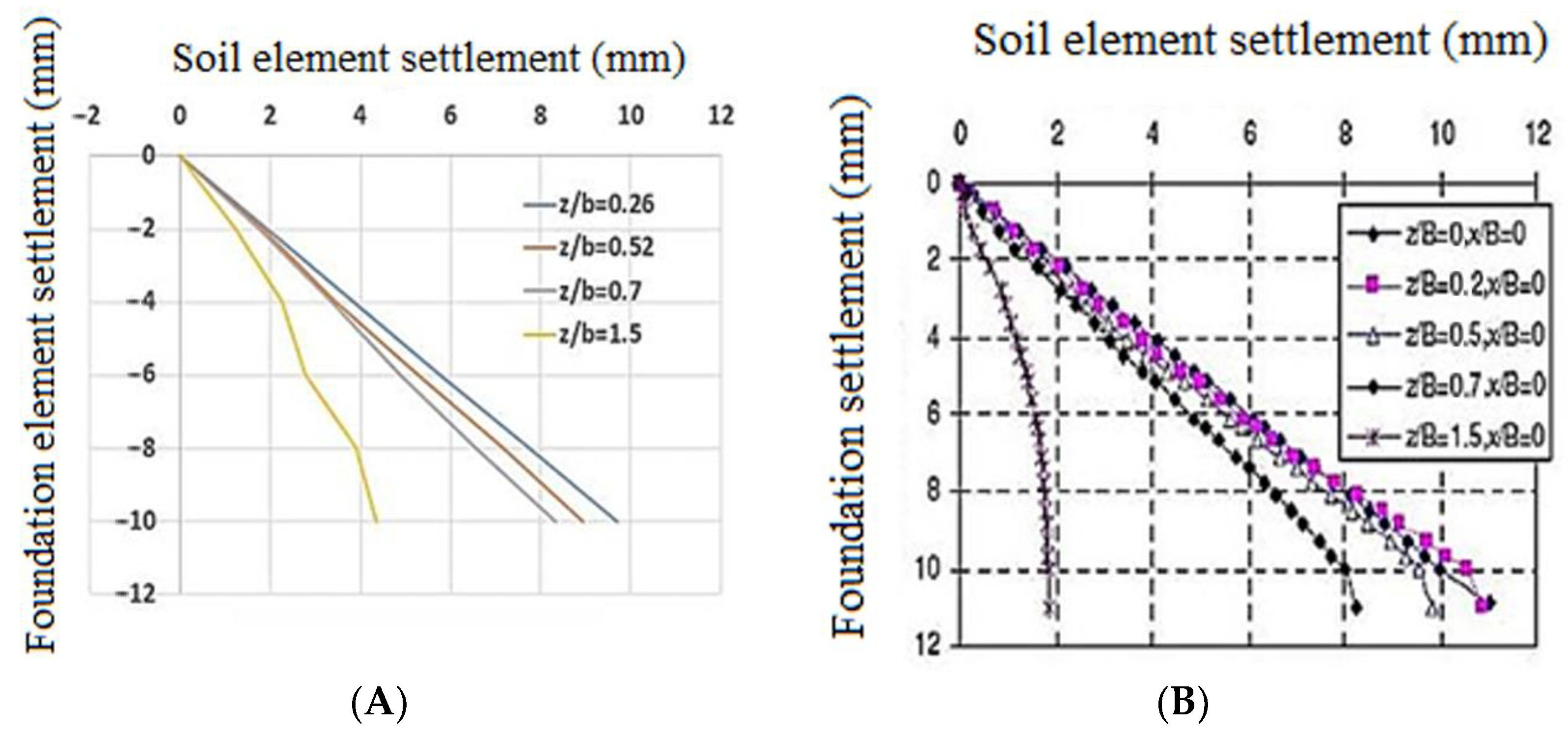








| Soil Type | Class | Φ (°) | C (KPa) | γ (kg/m3) | E (KPa) | μ | Dr (%) |
|---|---|---|---|---|---|---|---|
| Fine-grain | ML | 15 | 40 | 1400 | 10 × 104 | 0.1 | 15 |
| Granular | SM | 30 | 25 | 1740 | 15 × 104 | 0.2 | 30 |
| Granular | SW | 40 | 0,10 | 1950 | 24 × 104 | 0.3 | 80 |
| Model | Maximum Strain (%) | Tensile Resistance Force (N) | Thickness (m) | Weight per m2 (Kg) |
|---|---|---|---|---|
| G-150 | 60 | 340 | 0.0016 | 0.150 |
| Plastic Strain | Modulus of Elasticity (KPa) | Maximum Tensile Stress (KPa) | Density (kg/m3) |
|---|---|---|---|
| 60% | 354.17 | 212.50 | 93.75 |
| Density (kg/m3) | 1400 | Dilation Angle | 0.01 |
|---|---|---|---|
| Modulus of elasticity (KPa) | 10 × 104 | Cohesion (KPa) | 40 |
| Poisson’s ratio | 0.1 | Plastic strain | 5% |
| Internal friction angle | 15 |
| Density (kg/m3) | 93.75 | Maximum Tensile Stress (KPa) | 212.50 |
|---|---|---|---|
| Modulus of elasticity (KPa) | 354.17 | Plastic strain | 60% |
| Poisson’s ration | 0.02 |
| Name of the Analysis | Type of Analysis | Duration (s) |
|---|---|---|
| Initial | (Initial) | 0 |
| Geostatic | Dynamic-explicit | 1 |
| Limit load | Dynamic-explicit | 8 |
| Name | Type | Place of Effect |
|---|---|---|
| Geotextile installation in the prescribed depth | Embedded region | Geotextile surface with soil |
| Solidifying the foundation | Rigid body | Foundation |
| Type of Load and Settlement | Amount of Load and Settlement |
|---|---|
| Soil and foundation weight | 1400 (kg/m2) |
| Foundation settlement control | 40 cm |
| Initial geostatic stress at Z = 0 | 0 |
| Initial geostatic stress at Z = 10 | 14,000 (kg/m2) |
| Meshing Area | Approximate Number of Elements |
|---|---|
| Upper and lower bar of soil geometry | 240 |
| Side strips of soil geometry | 200 |
| Foundation environment | 1 |
| Geotextile tape | 40 |
| Soil Type | Classification | Φ (°) | C (Pa) | γ (kg/m3) | E (Pa) | μ | Dr (%) |
|---|---|---|---|---|---|---|---|
| Granular | SP | 30 | 9810 | 1478 | 1.3734 × 107 | 0.3 | 10% (loose) |
| Granular | SP | 28 | 981 | 1596 | 2.3544 × 107 | 0.3 | −70% (dense) |
| Unit weight (Kg/m2) | 0.3 |
| Thickness (m) | 0.0016 |
| Maximum tensile strength (N/m) | 12,959.6 |
| Elongation in the maximum stretch position (%) | 50 |
| Density (kg/m3) | 187.5 |
| Modulus of elasticity (Pa) | 1.617 × 107 |
| Yield stress (Pa) | 8.102 × 106 |
| Poisson’s ratio | 0.02 |
| Soil Type | ML | SM | SW |
|---|---|---|---|
| Bearing capacity (KPa) | 438.38 | 873.84 | 895.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rad, H.T.; Jalali, F.M.; Gheibi, M.; Khaksar, R.Y.; Annuk, A.; Moezzi, R. Enhancing Load-Bearing Capacity of Weak Soils Using Geosynthetics: A Finite Element Analysis. Mining 2024, 4, 777-805. https://doi.org/10.3390/mining4040044
Rad HT, Jalali FM, Gheibi M, Khaksar RY, Annuk A, Moezzi R. Enhancing Load-Bearing Capacity of Weak Soils Using Geosynthetics: A Finite Element Analysis. Mining. 2024; 4(4):777-805. https://doi.org/10.3390/mining4040044
Chicago/Turabian StyleRad, Hassan Tavassoli, Farhad Mahmoudi Jalali, Mohammad Gheibi, Reza Yeganeh Khaksar, Andres Annuk, and Reza Moezzi. 2024. "Enhancing Load-Bearing Capacity of Weak Soils Using Geosynthetics: A Finite Element Analysis" Mining 4, no. 4: 777-805. https://doi.org/10.3390/mining4040044
APA StyleRad, H. T., Jalali, F. M., Gheibi, M., Khaksar, R. Y., Annuk, A., & Moezzi, R. (2024). Enhancing Load-Bearing Capacity of Weak Soils Using Geosynthetics: A Finite Element Analysis. Mining, 4(4), 777-805. https://doi.org/10.3390/mining4040044








