Abstract
The undercutting process is a technique employed to initiate the caving of the ore mass in block caving, achieved by creating a basal cut on the block scheduled to be submerged. The effective execution of the undercutting process involves numerous variables, such as the undercut height and the vertical section’s undercut geometry, whose influence has often been overlooked. This research presents a methodology for determining the undercut height in a post-undercutting scenario, including variables such as the undercut level design, the extraction level design, and the air gap. Integral to this methodology is a parameterization that estimates the undercut height, from which design abacuses can be created to aid the assessment of present and future operations for any block/panel caving operation that employs the post-undercutting variant. Additionally, two examples demonstrate the application of this methodology, revealing how alterations in the dimensions of the crown pillar and drawbells significantly influence the undercut height. The calculation methodology outlined in this document delivers an undercutting height, providing an evaluation methodology for ongoing operations. Consequently, any height exceeding this suggests a conservative approach, potentially offering an opportunity for design improvement and alignment with the described parameters.
1. Introduction
Undercutting refers to the methodology employed to initiate the movement of the ore body in caving mining using blasting [1,2]. This blasting destabilizes the base of the rock mass, allowing the caveback to collapse. There are different undercutting designs that have been implemented [2,3], with various geometries and results. Specifically, Brown [2] identifies the height of the undercut as a significant factor influencing the success of caving. If the undercut performed is of substandard quality, a loss in the productive area could occur due to damage or collapse at the production level [4,5,6,7,8]. Subsequently, this could require the reinstallation of support, causing delays to the initial production plans. Such hindrances jeopardize the success of the exploitation method, leading to an increase in costs.
In cave mining, three common types of undercutting strategies have been applied [2,3,7,9]: post-undercutting, pre-undercutting, and advanced undercutting. The distinctions between these undercutting strategies are based on the sequences used for the construction of production and undercut levels, and the initiation of undercutting. For example, at the current levels of the El Teniente mine, hydraulic fracturing has been used ahead of undercutting [10] to facilitate operations under high-stress conditions, aiding in seismicity control. This methodology has even been applied below the production level [11]. Alternatively, at the Newcrest mine, undercutting has been carried out from the production level to reduce costs and timelines and enhance the safety of this stage at high depths [12]. Also, confined blasting over the undercutting was used to increase the initial productivity [13].
The types of undercutting can be classified as high or low undercut, depending on the height of the area to be blasted. Among the advantages of a high undercut, Brown [2] suggests it makes breaking easier due to the free face available. The risk of not achieving complete breakage is greater with low undercuts due to the high confinement. Additionally, a small number of deviated shots can exacerbate the confinement problem. Disadvantages identified with high undercutting include the following: (1) the longer hole drilling can have an impact on irregularities in the caveback, resulting in poor fragmentation and poor caving; (2) high undercutting increases global costs due to more drilling and explosives being required [14]; (3) with advanced subsidence, problems related to the removal of the swelling material can also occur. Table 1 presents a summary of the main advantages and disadvantages of the types of undercutting based on the undercut geometry: high undercutting, narrow undercutting, and narrow inclined undercutting.

Table 1.
Advantages and disadvantages of different undercut geometries.
Flores and Karzulovic [20] conducted a bibliographic and specialized technical review concerning undercut height, highlighting that the effect of this parameter on caving initiation is often overlooked. Recommendations typically focus solely on the open undercut area required in terms of the hydraulic radius [21,22]. Additionally, through analyzing a database of various mines exploited via block/panel caving, Flores and Karzulovic suggest that it is not possible to establish a relationship between undercut height, block height, or the distance between drifts. This height exhibits variations between 3 and 42 m with an average of 9.2 and a coefficient of variation of 0.77. In particular, low undercut heights have been commonly applied in secondary ore [16].
In terms of low undercut heights, the following observations have been made [20]: The height should be defined based on the mean rock size to maximize the weakening of the rock mass and on the coarse sizes (d85) to reduce the risk of remnant rock pillars. If the planar undercut height is less than 10% of the undercut area, it may produce high-stress concentrations in the undercut level (UCL) pillars. The undercut height must be high enough to prevent the eventual accumulation of coarse rock fragments between drawbells. In general, the author suggests avoiding the use of a low undercut height in primary rock.
Henríquez [15] compared three undercut heights through gravitational flow experiments to evaluate their productivity. In Henriquez’s study, the tonnage extracted, the emergence of coarse material, and hang-up events were evaluated at the beginning of the life of the drawpoints. Higher undercut heights increase productivity in early stages due to the low incidence of hang-ups, finer fragmentation and low stresses [23,24,25]. However, the interaction between extraction ellipsoids decreases in the initial stages as a result of finer material for very high undercutting (40 m), which could affect the mining recovery of the method. Henríquez concluded that, of the three alternatives evaluated, the undercut height of 20 m is the most recommended in terms of productivity and costs. In terms of stress distribution, Hormazabal et al. [16] studied the influence of undercut height on stress distribution using numerical modeling. In this work, it was noticed that as the undercut height decreased, stresses tended to concentrate at the front of the undercut.
A literature review on undercutting height suggests that, currently, there is no defined trend or criteria for determining the optimal height for block/panel caving mining exploited using post-undercutting. Though the undercutting height must be factored into the mining design when determining the size of the extraction layout, the crown pillar, and the drawbell design, decisions are made based on operational experience. Therefore, establishing a methodology for estimating the undercutting height, above which caving is guaranteed without the risk of poor propagation, remaining pillars, or hang-ups, would be beneficial. This study presents an initial approach and rules to estimating the undercutting height for block-caving mining operations using post-undercutting.
2. Methodology
Figure 1 shows the proposed methodology to determine the undercut height. This methodology is considered appropriate for the prefeasibility engineering stage. Initially, the design of the extraction level must be determined, for which common steps are indicated. Then, the minimum height of air gap necessary to generate caving propagation is defined. The angle of repose (or flow angle [26]) must also be estimated. In this work, the assumption that the minimum height of the air gap for caving propagation is equivalent to 3 times the d80 (primary fragmentation) is used, considering that the minimum hydraulic radius (Laubscher methodology [21] or another) is already met. Finally, the undercut height is determined considering the geometry of the crown pillar, the minimum height of the air gap, and the angle of repose.
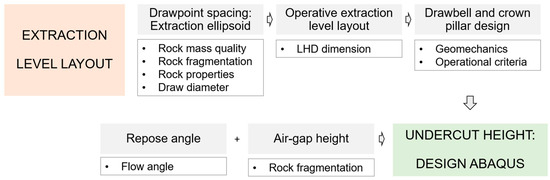
Figure 1.
Proposed methodology for defined the undercutting height based on the extraction level design, repose angle and air gap.
Undercut Conceptual Model
The undercutting height (Hsoc) is defined as the vertical distance between the floor of the undercut level and the roof of the blasted-block rock. One of the main criteria to consider is that the undercut height must be such that it exceeds the height of the cone formed by the repose angle of the broken ore [26] measured from the floor of the undercut level. In this zone, there is the remaining broken ore, limited by the projection of the repose angle and the crown pillar geometry (Figure 2).
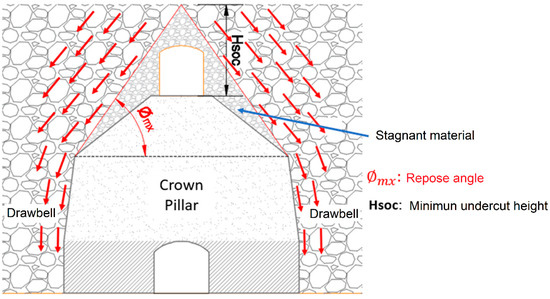
Figure 2.
Conceptual model used to define the undercut required; red vectors represent broken material flow direction due to ore draw. The stagnant material forms a cone of material that must be overcome.
To determine the most appropriate undercut height for each operation, it is key to consider the size of expected primary ore fragmentation, the selected extraction level layout, and the design of the undercut and extraction level. Fragmentation can be directly related to the air gap that ensures cave propagation. Considering these variables, it is possible to estimate the undercut height to ensure successful caving.
The presence of the air gap will depend on the extraction speed and the rate of caving. As a working assumption, it was postulated that the space required to ensure the propagation of caving is achieved when the air gap reaches three times the size of the primary fragmentation. This criterion can be utilized to evaluate the undercut geometry and its impact on the propagation of subsidence. In our evaluations, we included the air gap as a function of primary fragmentation for the simulations conducted with FlowSim BC.
Figure 3 shows the main geometric parameters required to estimate the minimum undercutting height. Among these parameters are variables associated with the undercut and extraction levels. The design presented in Figure 3 corresponds to a general scheme of a mining design for post-undercutting. The design also includes the conceptualization of the undercut height delimited by the projection of the repose angle of the broken ore from the brow of the drawbell and the inclusion of the air gap height (HAG) as an input to be used.
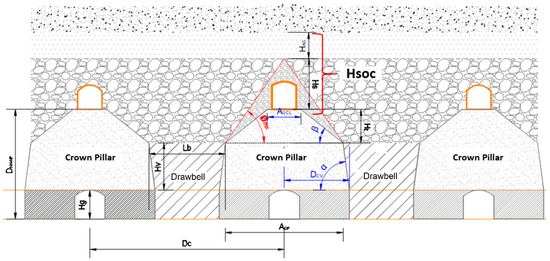
Figure 3.
Profile view of the main geometrical parameters that are required to define the minimum undercutting height.
Equation (1) provides the undercut height estimation using the design variables shown in Figure 3. These variables can be summarized in three main categories, which will define the undercut height and are used to propose Equation (2): the width of the crown pillar, the height of the drawbell chute (upper section), and the air gap, all three of which come from the expected primary fragmentation.
In Equations (1) and (2), is the distance between drifts [m], is the crown pillar width at the top [m], is the drawbell length at the top [m], is the undercut apex [m], is the distance between the production drift and the drawpoint brow [m], is the repose angle of the broken ore [°], is the angle of the drawpoint brow [°], is the angle of the drawbell wall [°], is the distance between levels (extraction and undercut) [m], is the drift height [m], is the height of the drawpoint brow [m], is the height of the drawbell chute [m], : is the minimum undercutting height [m], is the air gap height [m], and is the undercut height [m].
3. Undercutting Height Design Chart
Design charts can be determined, using Equations (1) and (2), that facilitate the estimation of the undercutting height from an already-defined drawbell and crown pillar. This chart can be applied to quickly evaluate whether the undercut height being considered to initiate subsidence in new productive sectors equals or exceeds the already-defined undercut height. In general, in mines mined by the block/panel caving method, the heights of the drawbell chute are at values of 2 m, 3 m, 4 m and 5.5 m, while the width of the crown pillar varies between 12 m and 21 m.
The impact of the height of the drawbell chute and the width of the crown pillar on the undercutting height can be seen in Figure 4. Here, the crown pillar width has a greater impact on the undercut height because of the larger base. The larger the base of the pillar, the greater its height will have to be for the same angle of repose because it increases the distance between opposite drawpoints (along the crown pillar).
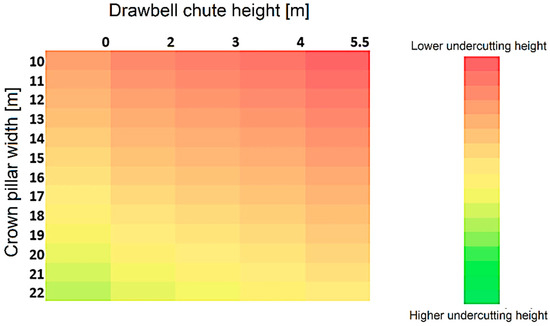
Figure 4.
Influence of the variables of crown pillar width and chute height on the undercut height required.
Considering Equations (1) and (2) and the main dimensions of the crown pillar and drawbells, design charts can be constructed. Three scenarios are used to facilitate the estimation based on the expected primary fragmentation: fine, medium, and coarse fragmentation (Figure 5, Figure 6 and Figure 7, respectively). Figure 5 presents the chart built for fine fragmentation that considers broken ore below 0.5 m. On the other hand, Figure 7 presents the chart built for coarse fragmentation that considers broken ore over 1 m (d80). These graphs allow the undercutting height to be defined quickly for satisfactory performance in the proposed mine design. An example application is presented in the next section.
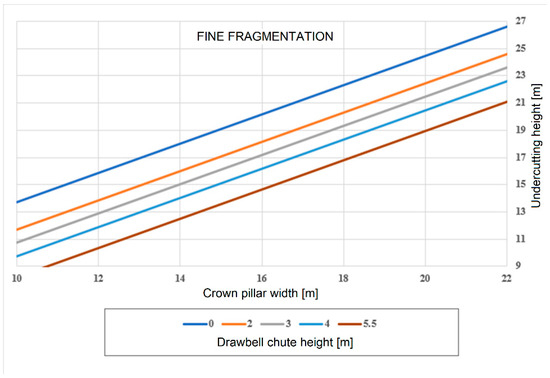
Figure 5.
Undercutting height chart for fine fragmentation.
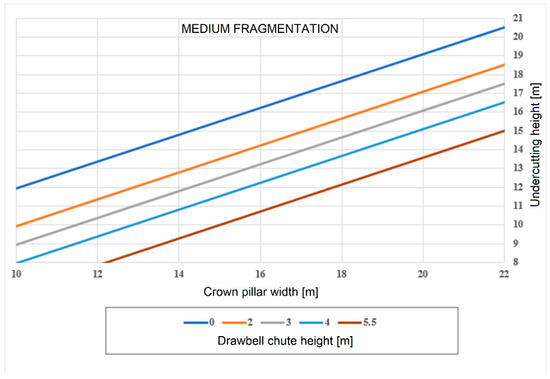
Figure 6.
Undercutting height chart for medium fragmentation.
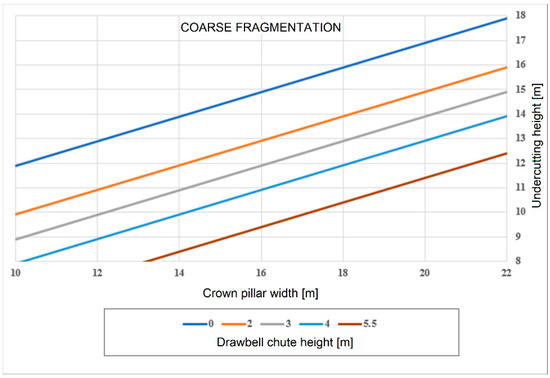
Figure 7.
Undercutting height chart for coarse fragmentation.
4. Application
As an example, two cases are presented below in which the proposed graphs were applied to determine the undercut height according to the particular and typical conditions of mining design and rock fragmentation.
4.1. Example of Application 1
Let us consider a panel caving mine that will be exploited through post-undercutting, requiring the design of a drawbell built from the production level and from the undercut level. Part of the mine design includes radial drill holes (drilled from the undercut level), which will also connect with the drawbell through the construction of the drawbell chute.
The mine considers two sectors with different extraction layouts (Figure 8): a 16 × 32 El Teniente layout type and a 20 × 32 El Teniente layout type with different drawbell geometries. For the first design (16 × 32), the drawbells have a straight brow, and for the other, the drawbells have an inclined brow. The mining design is defined to increase the height of the drawbell for the 20 × 32 layout. This decreases the height of the drawbell chute. A medium primary fragmentation (approximate d80 of 1 m) is expected with a repose angle of 55°.
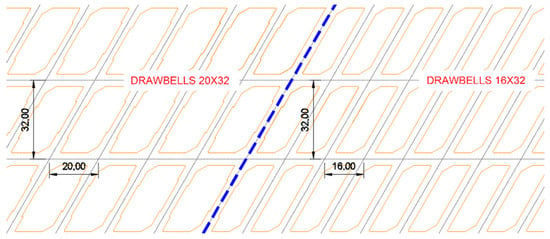
Figure 8.
Plan view of the extraction level layout of case 1. The blue line represents the design interface. Units are in meters.
Figure 9 shows the drawbell and crown pillar geometries for both layouts. The main differences are the distance between the extraction drifts and the drawbell length. Figure 9 also shows the differences in drawbell geometries and draw cone above the apex. In Table 2, the different geometric parameters used in this example are presented. In general, larger dimensions are associated with the greater spacing layout.
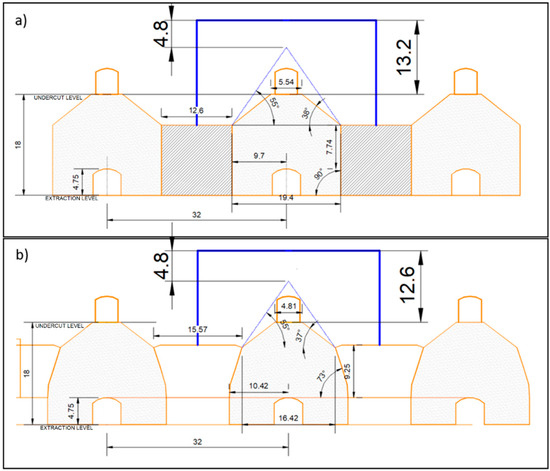
Figure 9.
Profile view of mine design of the example of application 1. (a) Layout 16 × 32. (b) Layout 20 × 32. Units are in meters.

Table 2.
Design parameters used in case 1.
From Equations (1) and (2), the dimensions of the crown pillar and the height of the drawbell chute are obtained for both layouts (indicated in Table 3), and from these, the undercutting height is determined as shown in Figure 10. The undercutting height is similar for both cases because the crown pillar and drawbell changed in similar proportions, not greatly affecting the undercutting height. For this particular case and to be conservative, maintaining a single height of 13.2 m would be recommended.

Table 3.
Result of crown pillar, drawbell chute, and undercutting height for case 1 using the proposed methodology.
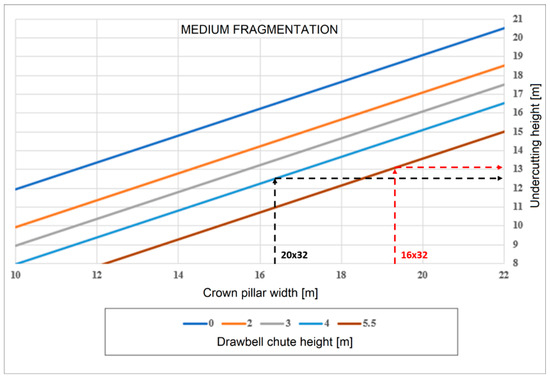
Figure 10.
Example of application of the undercutting height chart—medium fragmentation.
4.2. Example of Application 2
Now, we will consider the case of a block caving mine exploited using post-undercutting. In this case, the crown pillar must be strengthened due to the geomechanical problems in the rock mass to avoid future damage above the extraction level. For this, the option of a high drawbell with a straight brow is evaluated. Figure 11 shows a profile view perpendicular to the production drifts. In this design, the drawbell length increases above the gallery of the undercut level. Once the drawbell and drilled ring are blasted, the ore starts flowing due to ore extraction. Then, the repose angle delimits the zone where the fragmented ore moves towards the drawbell.
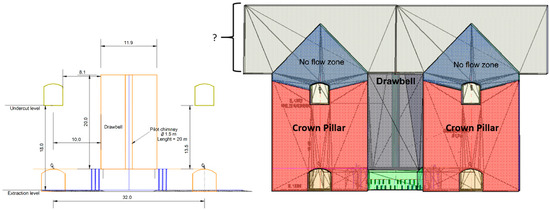
Figure 11.
Profile view of mine design of the example of application 2.
In this case, the aim is to determine what would be the undercutting height necessary to ensure successful caving. Thus, the proposed design graphs for undercutting height are useful. Here, we only need to know the dimensions of the crown pillar. The drawbell chute is 0 m given the drawbell design applied. The width of the crown pillar for this case is 20 m. Then, using the design graph for medium fragmentation, the undercutting height to be considered should be 19 m to ensure adequate caving as presented in Figure 12.
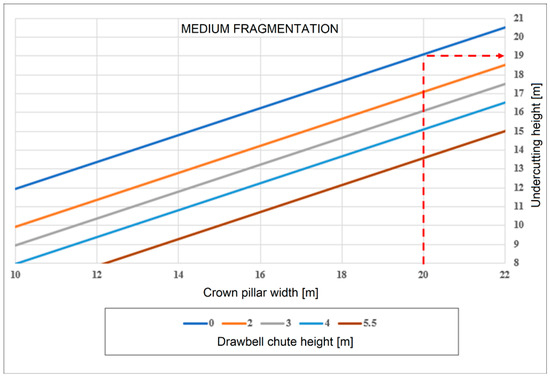
Figure 12.
Example 2 of application of the undercutting height chart—medium fragmentation.
In the two examples presented, the crown pillar and fragmentation emerge as key variables in the design, facilitating the definition of the required undercut height to initiate the caving. This study encompasses a geometric analysis, which could potentially be enhanced by including variables that influence the angle of repose (such as confinement and humidity), the impact of preconditioning, and varying extraction rates. These variables could be incorporated into future research efforts. However, the proposed methodology offers a viable technique for determining this critical parameter at the beginning of a block caving operation for preliminary engineering phases. Furthermore, by adhering to the same steps employed in this study, it may be possible to broaden its application to other variants of undercutting, given that the relevant limitations are taken into account.
5. Conclusions
Our literature review of undercut height indicates that, currently, there is no clear trend regarding criteria to determine the undercutting height for block/panel mines. Based on the variables analyzed in this study, the undercut height should be considered as part of the mining design when the extraction layouts are defined. From a geometric perspective, the undercutting height primarily depends on the height of the stagnant cone, which is formed by the angle of repose of the broken ore. This, in turn, largely relies on the dimensions of the crown pillar and the drawbell. As the crown pillar increases in size, so does the base of the cone, leading to an increase in its height. This document presents an initial approach to an accurate calculation, which should be considered during the early engineering stages of post-undercutting in cave mining. The calculation methodology outlined in this document delivers an undercutting height, providing an evaluation methodology for ongoing operations. Any height exceeding this suggests a conservative approach, potentially offering an opportunity to improve the design and align it with the parameters described here.
Author Contributions
Conceptualization, D.M. and R.C.; methodology, D.M.; validation, D.M.; formal analysis, R.C. and R.G.; investigation, D.M. and R.G.; resources, R.C.; writing—original draft preparation, D.M.; writing—review and editing, R.G.; visualization, D.M. and R.G.; supervision, R.C.; funding acquisition, R.C. All authors have read and agreed to the published version of the manuscript.
Funding
This paper/work was funded by the CONICYT/PIA Project AFB230001.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Acknowledgments
The authors thank Diane Greenstein for her support in editing.
Conflicts of Interest
Danko Morales is employed by the company Enaex. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Laubscher, D. Block Cave Manual; Julius Kruttschnitt Mineral Research Centre: Brisbane, Australia, 2000. [Google Scholar]
- Brown, E.T. Cave initation by undercutting. In Block Caving Geomechanics; Julius Kruttschnitt Mineral Research Centre: Brisbane, Australia, 2007; pp. 229–287. [Google Scholar]
- Trueman, R.; Pierce, M.; Wattimena, R. Quantifying stresses and support requirements in the undercut and production level drifts of block and panel caving mines. Int. J. Rock Mech. Min. Sci. 2002, 39, 617–632. [Google Scholar] [CrossRef]
- Fernandez, F.; Evans, P.; Gelson, R. Design and implementation of a damage assessment system at Argyle Diamond’s block cave project. In Proceedings of the Second International Symposium on Block and Sublevel Caving, Perth, Australia, 20–22 April 2010; pp. 65–81. [Google Scholar]
- Lett, J.L.; Brunton, I.; Capes, G.W.; Jager, A.; Mobilio, B.; Rachocki, J.; Sharrock, G.B.; Secheny, M. Undercutting to surface breakthrough—Cadia East panel cave (stage 1). In Proceedings of the Seventh International Conference & Exhibition on Mass Mining, Massmin 2016, Sydney, Australia, 9–11 May 2016; AusIMM: Sydney, Australia, 2016; pp. 65–82. [Google Scholar]
- Snyman, L.; Webster, S.; Samosir, J. E48 cave extension at Northparkes. In Proceedings of the Seventh International Conference & Exhibition on Mass Mining, Massmin 2016, Sydney, Australia, 9–11 May 2016; AusIMM: Sydney, Australia, 2016; pp. 111–117. [Google Scholar]
- Rojas, E.; Molina, R.; Bonani, A.; Constanzo, H. The pre-undercut caving method at the El Teniente mine, Codelco Chile. In Massmin 2000 Proceedings; The Australasian Institute of Mining and Metallurgy: Brisbane, Australia, 2000; pp. 261–266. [Google Scholar]
- Vasquez, P.; Díaz-Salas, J.; Barindelli, G. Lecciones aprendidas, colapsos MB N01S02, Chuquicamata Subterránea. In 1o Congreso Chileno Mecánica de Rocas; Universidad de Santiago de Chile: Santiago, Chile, 2023; pp. 940–947. [Google Scholar]
- Gómez, R.; Labbé, E. An option for the change to massive underground mining: The current Chilean methodology of block caving. Bol. Geol. Min. 2019, 130, 181–198. [Google Scholar] [CrossRef]
- Pardo, C.; Rojas, E. Selection of the explotation method based on the experience of hydraulic fracture techniques at the El Teniente mine. In Proceedings of the Seventh International Conference & Exhibition on Mass Mining, Massmin 2016, Sydney, Australia, 9–11 May 2016; AusIMM: Sydney, Australia, 2016; pp. 97–104. [Google Scholar]
- Navarrete, R.; Soto, C.; Henriquez, F.; Godoy, H. Hydraulic fracturing in the construction of Andes Norte project. In Caving 2022, Proceedings of the Fifth International Conference on Block and Sublevel Caving, Adelaide, Australia, 30 August–1 September 2022; Potvin, Y., Ed.; Australian Centre for Geomechanics: Adelaide, Australia, 2022; pp. 1227–1240. [Google Scholar]
- Paredes, P.; Lopa, I.; Kline, P.; Sykes, M. Undercutless caving at Newcrest: Towards the next generation of cave mining. In Proceedings of the Eighth International Conference & Exhibition on Mass Mining, Massmin 2020, Santiago, Chile, 9–11 December 2020; Castro, R., Baez, F., Suzuki, K., Eds.; ACG: Santiago, Chile, 2020; pp. 166–181. [Google Scholar] [CrossRef]
- Rivera, N.; Music, A.; Quiroz, R.; Díaz, M.; Vergara, C. Undercutting confined blasting in Esmeralda and Dacita case study at El Teniente. In UMining 2016, 1er Congreso Internacional en Minería Subterránea; Castro, R., Valencia, M.E., Eds.; Universidad Chile: Santiago, Chile, 2016; pp. 403–424. [Google Scholar]
- Butcher, R.J. Block Cave Undercutting—Aims, Strategies, Methods and Management. In Massmin 2000 Proceedings; AusIMM: Brisbane, Australia, 2000; pp. 423–428. [Google Scholar]
- Henriquez, J.P. Evaluación de la Altura de Socavación en la Productividad de la Minería de Block/Panel Caving; University of Chile: Santiago, Chile, 2018. [Google Scholar]
- Hormazabal, E.; Alvarez, R.; Russo, A.; Acevedo, D. Influence of the undercut height on the behaviour of pillars at the extraction level in block and panel caving operations. In Caving 2018; Potvin, Y., Jakubec, J., Eds.; Australian Centre for Geomechanics: Vancouber, BC, Canada, 2018; pp. 351–362. [Google Scholar]
- Galilea, B. Estimación de la Tasa de Incorporación de Área Socavada en Block Caving Mediante Técnicas de Simulación; University of Chile: Santiago, Chile, 2017. [Google Scholar]
- Fernandez, R. Impacto del Cambio de Diámetro de la Perforación de Socavación de División Andina; Codelco Chile, University of Chile: Santiago, Chile, 2020. [Google Scholar]
- Brunton, I.; Sharrock, G.; Lett, G. Full Scale Near Field Flow Behaviour at the Ridgeway Deeps Block Cave Mine. In Proceedings of the 6th International Conference & Exhibition on Mass Mining, Massmin 2012, Sudbury, ON, Canada, 10–14 June 2012; Canadian Institute of Mining, Metallurgy and Petroleum: Sudbury, MA, USA, 2012. [Google Scholar]
- Flores, G.; Karzulovic, A. Benchmarking Report; International Caving Study Stage 2 (ICS-II): Brisbane, Australia, 2002. [Google Scholar]
- Laubscher, D.H. Cave mining-the state of the art. J. S. Afr. Inst. Min. Metall. 1994, 94, 279–293. [Google Scholar]
- Laubscher, D.H. Cavability, in A Practical Manual on Block Caving; JKMRC and Itasca Consulting Group, Inc.: Brisbane, Australia, 2000; Volume 27. [Google Scholar]
- Castro, R.; Gómez, R.; Hekmat, A. Experimental quantification of hang-up for block caving applications. Int. J. Rock Mech. Min. Sci. 2016, 85, 1–9. [Google Scholar] [CrossRef]
- Castro, R.; López, S.; Gómez, R.; Ortiz, S.; Carreño, N. Experimental Study of the Influence of Drawbell Geometry on Hang-Ups in Cave Mine Applications. Rock Mech. Rock Eng. 2020, 54, 1–10. [Google Scholar] [CrossRef]
- Gómez, R.; Sanhueza, V.; Fustos, R.; Nelis, G. A new approach for hang-ups prediction in block caving mines based on drawbell geometry and vertical stress. Min. Metall. Explor. 2022, 39, 2393–2400. [Google Scholar] [CrossRef]
- Castro, R.L.; Vargas, R.; De La Huerta, F. Determination of drawpoint spacing in panel caving: A case study at the el teniente mine. J. S. Afr. Inst. Min. Metall. 2012, 112, 871–876. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).