A GAN-Based Approach Incorporating Dempster–Shafer Theory to Mitigate Rating Noise in Collaborative Filtering

Abstract

Collaborative filtering (CF) continues to be a fundamental approach in recommendation systems for providing users with personalized suggestions. However, such kind of recommender systems are prone to performance issues when faced with noisy, inconsistent, or deliberately manipulated user ratings. Although Generative Adversarial Networks (GANs) offer promising solutions to capture complex user-item interactions in these CF situations, many existing GAN-based methods assume uniform reliability across all ratings, reducing their effectiveness under uncertain conditions. To overcome this challenge, this paper presents DST-AttentiveGAN to introduce a confidence-aware adversarial framework specifically designed to denoise inconsistent ratings in collaborative filtering scenarios. The proposed approach employs Dempster-Shafer Theory (DST) to compute confidence scores by aggregating diverse behavioral indicators, such as item popularity, user activity, and rating variance. These scores guide both components of the GAN architecture in which the generator incorporates a cross-attention mechanism to highlight trustworthy features, while the discriminator uses DST-based confidence to evaluate the credibility of input ratings. Training is carried out using a stabilized Wasserstein GAN objective that promotes both robustness and convergence efficiency. Experimental results in three benchmark data sets show that DST-AttentiveGAN consistently surpasses conventional GAN-based models, delivering more accurate and reliable recommendations under conditions of uncertainty.

1. Introduction

Recommender systems (RS) have become essential components of modern digital platforms, helping users navigate vast information spaces by providing personalized content [1]. Among various recommendation approaches, Collaborative Filtering (CF) [2] remains one of the most effective techniques, relying on historical user-item interactions to infer preferences. CF has been successfully deployed in diverse domains such as e-commerce, streaming services, and social media [3,4]. However, CF models are highly sensitive to data quality. The presence of noisy, inconsistent, or malicious ratings can distort user similarity patterns and severely degrade recommendation performance [5,6].

To mitigate these challenges and enhance CF performance under adverse conditions, recent works have turned to Generative Adversarial Networks (GANs) as a means of modeling complex user-item interactions. GANs consist of a generator, which synthesizes data, and a discriminator, which distinguishes real from generated samples [7]. Their adversarial training setup enables the generation of realistic and diverse rating profiles, making them suitable for tasks such as simulating user behavior, improving latent representations, and increasing sparse data [8,9]. For example, GANRS [10] introduced synthetic profile generation but struggled with mode collapse, a challenge later addressed in WGANRS [11] through Wasserstein loss. CFGAN [12] modeled user-item interactions in a latent space, while GANMF [13] combined matrix factorization with an autoencoder-based discriminator to enhance personalization. AACF [14] introduced attention and virtual items to improve training efficiency in sparse conditions. Despite these advancements, existing GAN-based models generally treat all ratings as equally reliable, without considering the varying degrees of uncertainty or credibility in user feedback. This assumption limits their ability to filter or correct misleading inputs, particularly in real-world CF recommender systems where rating reliability can vary significantly.

In parallel, Dempster–Shafer Theory (DST) has established itself as a powerful mathematical framework for uncertain reasoning and evidence fusion [15,16]. It has been successfully applied in diverse fields such as spatial object matching [17], hyperspectral image classification [18], groundwater potential mapping [19], and urban resilience assessment [20], where data imperfections, ambiguity, and conflicts are prevalent. These applications highlight DST’s versatility in representing uncertainty, aggregating heterogeneous evidence, and supporting robust decision-making in complex environments.

Within the realm of recommender systems, DST has been effectively applied to capture user preferences under incomplete or ambiguous conditions [21]. Prior works have used DST for trust estimation, multi-criteria recommendation [22], and multimodal fusion [23]. A recent approach [24] further enhances Evidential Collaborative Filtering by employing Deng entropy and the Best Worst Method to optimize the assessment of user reliability. By assigning belief masses instead of deterministic labels, DST provides a flexible mechanism for expressing varying levels of confidence, making it particularly well suited for environments with noisy or unreliable data.

Although both DST and GANs have shown individual success in the recommendation domain, their integration remains underexplored. In this paper, we present DST-AttentiveGAN, a novel confidence-aware architecture that embeds DST-derived trust signals into both the generator and the discriminator of a GAN framework for rating denoising. This unified approach allows the model to distinguish between reliable and unreliable user feedback more effectively during training and inference. The main contributions of this work are as follows:

• We propose a novel DST-based framework for quantifying the reliability of ratings using multiple sources of evidence (item popularity, variance, and user activity).
• We design a generator that employs a cross-attention mechanism to selectively focus on reliable rating components, guided by the DST-derived confidence scores.
• We develop a discriminator conditioned on both rating values and DST-based trust levels, trained using a Wasserstein GAN loss with gradient penalty to ensure training stability.
• We perform extensive evaluations on benchmark datasets under various noise settings, showing that DST-AttentiveGAN consistently outperforms existing GAN-based recommendation models in terms of robustness and accuracy.

The remainder of this paper is organized as follows. Section 2 details the proposed DST-AttentiveGAN architecture, including the construction of the confidence matrix, the cross-attentive generator, and the evidentially conditioned discriminator. Section 3 describes the experimental settings, including datasets, evaluation metrics, and implementation details, and presents a detailed performance analysis compared to the state-of-the-art baselines. Finally, Section 4 concludes the paper and outlines promising future research directions.

2. Method

Collaborative filtering recommender systems are often challenged by noisy, biased, or adversarial ratings that compromise prediction reliability. To address these issues, we propose DST-AttentiveGAN a DST-guided Generative Adversarial Network (GAN) architecture that integrates evidence-based confidence modeling and cross-attention mechanisms. The model is designed to reconstruct denoised rating profiles while being guided by the estimated trustworthiness of each user-item interaction. Figure 1 illustrates the overall architecture of our proposed DST-AttentiveGAN.

2.1. Frame of Discernment

To systematically characterize the reliability of user–item interactions, we define the frame of discernment as the hypothesis set formulated by Equation (1):

$$\mathsf{\Theta }=\{\mathrm{Reliable},\mathrm{Noisy}\}$$

(1)

where Reliable corresponds to the assumption that a rating $r_{ui}$ is trustworthy and informative, while Noisy corresponds to the assumption that the rating is affected by bias, inconsistency, or adversarial manipulation.

2.2. Evidence Construction

Let $R\in {\mathbb{R}}^{N\times M}$ be the user-item rating matrix, where N is the number of users and M the number of items. To assess the reliability of each individual rating $r_{ui}$, we construct a confidence matrix $C=\left[c_{ui}\right]$ based on three forms of evidence: item popularity, item rating variance, and user activity.

First, the popularity of an item i is defined as the proportion of users who have interacted with it, as shown in Equation (2), where N denotes the total number of users, and $\mathbb{I}(r_{ui}>0)$ is an indicator function that equals 1 if user u rated item i, and 0 otherwise.

$$p_i={\displaystyle \frac{1}{N}}\sum _{u=1}^N\mathbb{I}(r_{ui}>0)$$

(2)

Next, the variance of the ratings received by item i captures the level of disagreement among users, as defined in Equation (3):

$$v_i={\displaystyle \frac{1}{|U_i|}}\sum _{u\in U_i}{\left(r_{ui}-{\displaystyle \frac{1}{|U_i|}}\sum _{u^{\prime }\in U_i}{r}_{u^{\prime }i}\right)}^2$$

(3)

Since this value is unbounded and can vary significantly across items, it is normalized using min-max scaling:

$$v_i^{\mathrm{norm}}={\displaystyle \frac{v_i-min\left(v\right)}{max\left(v\right)-min\left(v\right)}}$$

(4)

To reflect user involvement, we define the activity of user u as the fraction of items they have rated, as shown in Equation (5), where M is the total number of items, and $\mathbb{I}(r_{ui}>0)$ is an indicator function that returns 1 if user u rated item i, and 0 otherwise.

$$a_u={\displaystyle \frac{1}{M}}\sum _{i=1}^M\mathbb{I}(r_{ui}>0)$$

(5)

Although $a_u$ is also bounded within $[0, 1]$, we apply min-max normalization for consistency across all evidence sources:

$$a_u^{\mathrm{norm}}={\displaystyle \frac{a_u-min\left(a\right)}{max\left(a\right)-min\left(a\right)}}$$

(6)

The three evidential signals are first expanded into full matrices P, V, and A, ensuring dimensional compatibility with the original rating matrix R. Together, they form the basis for a confidence matrix that captures the trust level of each user–item interaction. Since these signals provide complementary and sometimes conflicting perspectives on rating reliability, we adopt a fusion strategy guided by Dempster–Shafer Theory (DST).

DST is particularly well-suited here because it: (i) allows explicit modeling of uncertainty when evidence is incomplete, (ii) manages conflict between heterogeneous signals without forcing premature decisions, and (iii) is more flexible than classical probability theory, which generally assumes precise prior probabilities, while DST can handle situations where such priors are unavailable or only partially defined. This makes DST especially appropriate for recommender systems, where reliability signals are often noisy, incomplete, or contradictory.

In our framework, fusion is operationalized through a nonlinear aggregation that emphasizes agreements while penalizing conflicts, as shown in Equation (7):

$$c_{ui}=p_i·v_i+v_i·a_u+p_i·a_u-2·p_i·v_i·a_u.$$

(7)

This formulation serves as a practical instantiation of DST’s principles: the pairwise terms strengthen consistent signals, while the triple interaction term reduces the influence of contradictory evidence. The resulting matrix $C=\left[c_{ui}\right]$, with $c_{ui}\in [0, 1]$, encodes a trust-aware confidence score for each rating. This fused representation is subsequently provided as auxiliary guidance to both the generator and discriminator in the proposed DST-AttentiveGAN.

2.3. Generator Architecture with DST-Guided Cross-Attention

The generator G aims to reconstruct a denoised rating vector ${\hat{x}}_u=G(x_u,c_u)$ for each user u, where $x_u\in {\mathbb{R}}^M$ denotes the user’s normalized (and potentially noisy) rating vector, and $c_u\in {\mathbb{R}}^M$ represents a vector of DST-based confidence scores that quantify the reliability of each rating entry.

To effectively leverage this evidential guidance, we employ a cross-attention mechanism that enables the generator to selectively focus on trustworthy components of $x_u$. As shown in Equation (8), the input vectors are projected into a shared latent space using learnable linear transformations:

$$Q=W_Q{c}_u^{\top },K=W_K{x}_u^{\top },V=W_V{x}_u^{\top }$$

(8)

where $W_Q, W_K, W_V\in {\mathbb{R}}^{d\times M}$ are trainable weight matrices, and d represents the dimensionality of the attention space. Here, $c_u$ denotes the confidence vector derived from Dempster–Shafer Theory (DST), which is used as the query, while $x_u$ serves as the key and value for attention computation.

The core of the attention mechanism is the scaled dot-product operation (Equation (9)), which computes an attention-weighted combination of the rating components based on the confidence signals:

$$z_u=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^{\top }}{\sqrt{d}}}\right)V$$

(9)

This operation allows each dimension of the user’s rating vector to focus on the most informative dimensions of the confidence vector, thereby prioritizing trustworthy entries while down-weighting uncertain ones.

The attention output, $z_u$, is then concatenated with the original rating vector $x_u$, and the resulting representation is passed through a feedforward neural network to obtain the reconstructed rating vector, as defined in Equation (10):

$${\hat{x}}_u=\sigma \left({\mathrm{Dense}}_2\left(\mathrm{ReLU}\left({\mathrm{Dense}}_1\left([z_u;x_u]\right)\right)\right)\right)$$

(10)

The sigmoid activation $\sigma (·)$ ensures that the final output lies within the normalized rating range $[0, 1]$. This cross-attention structure allows the generator to dynamically incorporate evidential trust at each layer, guiding the denoising process in a personalized and reliability-aware manner.

Generator Loss Function. The generator is trained using a composite objective that combines adversarial and reconstruction losses. As shown in Equation (11), the total loss $L_G$ includes two components:

$$L_G=-{\mathbb{E}}_{x_u,c_u}\left[D\left(G(x_u,c_u),c_u\right)\right]+{\lambda }_r·L_{\mathrm{rec}}({\hat{x}}_u,x_u)$$

(11)

The first term is an adversarial loss derived from the Wasserstein GAN framework, which encourages the generator to produce denoised vectors that the discriminator cannot distinguish from real ratings. The second term, weighted by hyperparameter ${\lambda }_r$, enforces closeness to the ground-truth ratings through a reconstruction penalty defined by mean squared error (Equation (12)):

$$L_{\mathrm{rec}}({\hat{x}}_u,x_u)={∥{\hat{x}}_u-x_u∥}_2^2$$

(12)

The hybrid objective in Equation (11) ensures that the generator produces outputs that are both adversarially plausible and numerically accurate, while aligning with the DST-derived evidence during the attention and reconstruction processes.

2.4. Discriminator Architecture with Evidential Conditioning

The discriminator D is designed to assess the authenticity of user rating vectors by leveraging evidential trust cues derived from the Dempster-Shafer Theory (DST). Specifically, it receives as input a pair $(x_u,c_u)\in {\mathbb{R}}^M\times {\mathbb{R}}^M$, where $x_u$ denotes either a real or generated (denoised) normalized rating vector for user u, and $c_u$ is the associated DST-based confidence vector.

To jointly process both rating values and their corresponding confidence scores, the two vectors are concatenated into a single input as shown in Equation (13):

$$h_0=[x_u;c_u]\in {\mathbb{R}}^{2M}$$

(13)

This representation is passed through a sequence of fully connected layers with LeakyReLU activations, enabling the network to model non-linear dependencies and complex interactions between ratings and their associated trust signals. The final output is a scalar prediction (Equation (14)):

$$D(x_u,c_u)\in \mathbb{R}$$

(14)

which reflects the discriminator’s confidence that the input pair corresponds to an authentic (real) rating profile. By integrating DST-based evidence into the decision process, the discriminator not only evaluates statistical realism but also learns to recognize evidential consistency.

The discriminator is trained using the Wasserstein GAN with Gradient Penalty (WGAN-GP) framework, which stabilizes adversarial learning and promotes meaningful gradients. The loss function is formulated as shown in Equation (15):

$$L_D={\mathbb{E}}_{{\hat{x}}_u\sim {\mathbb{P}}_G}\left[D({\hat{x}}_u,c_u)\right]-{\mathbb{E}}_{x_u\sim {\mathbb{P}}_r}\left[D(x_u,c_u)\right]+{\lambda }_{GP}·L_{GP}$$

(15)

Here, ${\mathbb{P}}_r$ and ${\mathbb{P}}_G$ denote the distributions of real and generated rating vectors, respectively, and ${\lambda }_{GP}$ is a regularization coefficient. To satisfy the 1-Lipschitz constraint required by WGAN, the gradient penalty term $L_{GP}$ is computed using interpolated samples ${\tilde{x}}_u$ as defined in Equation (16):

$${\tilde{x}}_u=\alpha x_u+(1-\alpha ){\hat{x}}_u,\alpha \sim \mathcal{U}(0,1)$$

(16)

The penalty term itself is given by Equation (17):

$$L_{GP}={\mathbb{E}}_{{\tilde{x}}_u}\left[{\left({∥{\nabla }_{{\tilde{x}}_u}D({\tilde{x}}_u,c_u)∥}_2-1\right)}^2\right]$$

(17)

Equation (15) ensures that the discriminator learns to distinguish real from generated profiles while incorporating trust-aware signals. The gradient regularization term in Equation (17) stabilizes training, and the interpolation defined in Equation (16) enables robust gradient estimation. Together, these formulations allow the discriminator to guide the generator toward producing outputs that are both statistically plausible and evidentially coherent.

The following Algorithm 1 summarizes the evidentially guided GAN framework for denoising user-item ratings.

Algorithm 1 Evidentially-Conditioned GAN for Rating Denoising

Require:  Raw rating matrix $R\in {\mathbb{R}}^{N\times M}$ Ensure:  Denoised rating matrix $\hat{R}\in {\mathbb{R}}^{N\times M}$ 1: // Step 1: Evidence Construction 2: for each item i do 3:     Compute item popularity: $p_i={\displaystyle \frac{1}{N}}{\sum }_{u=1}^N\mathbb{I}(r_{ui}>0)$        ▹ Equation (2) 4:     Compute rating variance: $v_i={\displaystyle \frac{1}{|U_i|}}{\sum }_{u\in U_i}{\left(r_{ui}-{\displaystyle \frac{1}{|U_i|}}{\sum }_{u^{\prime }\in U_i}{r}_{u^{\prime }i}\right)}^2$    ▹ Equation (3) 5: end for 6: for each user u do 7:     Compute user activity: $a_u={\displaystyle \frac{1}{M}}{\sum }_{i=1}^M\mathbb{I}(r_{ui}>0)$           ▹ Equation (5) 8: end for 9: Compute confidence matrix:                       ▹ Equation (7) $$c_{ui}=p_i·v_i+v_i·a_u+p_i·a_u-2·p_i·v_i·a_u$$ 10: // Step 2: Generator Forward Pass 11: for each user u do 12:     Input: rating vector $x_u$, confidence vector $c_u$ 13:     Project to latent space:                      ▹ Equation (8) $$Q=W_Q{x}_u^{\top },K=W_K{c}_u^{\top },V=W_V{c}_u^{\top }$$ 14:     Compute attention:                           ▹ Equation (9) $$z_u=\mathrm{softmax}\left({\displaystyle \frac{Q{K}^{\top }}{\sqrt{d}}}\right)V$$ 15:     Concatenate and generate:                  ▹ Equation (10) $${\hat{x}}_u=\sigma \left({\mathrm{Dense}}_2\left(\mathrm{ReLU}\left({\mathrm{Dense}}_1\left([z_u;x_u]\right)\right)\right)\right)$$ 16: end for 17: // Step 3: Discriminator Forward Pass 18: for each user u do 19:     Compute $D(x_u,c_u)$ and $D({\hat{x}}_u,c_u)$ using MLP             ▹ Equation (14) 20: end for 21: // Step 4: Adversarial Training Loop 22: for each epoch do 23:     Sample minibatch of users u 24:     Discriminator Update:                    ▹ Equation (15) $$L_D=\mathbb{E}\left[D(\hat{x},c)\right]-\mathbb{E}\left[D(x,c)\right]+{\lambda }_{GP}·L_{GP}$$ 25:     Generator Update: Minimize loss $L_G$ using:           ▹ Equation (11) $$L_G=-{\mathbb{E}}_{x_u,c_u}\left[D\left(G(x_u,c_u),c_u\right)\right]+{\lambda }_r·{∥{\hat{x}}_u-x_u∥}_2^2$$ 26: end for 27: return Denoised rating matrix $\hat{R}$

3. Results and Discussion

This section presents the experimental results of DST-AttentiveGAN and provides a comprehensive discussion of its performance. We start by detailing the experimental setup. Then, we report and compare the model’s performance against several baseline methods. Finally, we analyze the impact of DST-AttentiveGAN on rating distributions to highlight its ability to denoise and structure user-item interactions more effectively.

3.1. Experimental Setup

The experimental setup includes the datasets used, evaluation metrics, and implementation details. These components provide the basis for assessing the performance and robustness of DST-AttentiveGAN in various recommendation scenarios.

3.1.1. Datasets

The experiments are conducted on three real-world datasets to validate the robustness of our DST-AttentiveGAN.

Table 1. Statistics of the Datasets Used.

Dataset	#Users	#Items	#Ratings	Density
MovieLens 1M	6040	3900	1,000,209	4.25%
Netflix Subset	3000	4000	982,142	8.18%
Amazon Electronics	5000	4000	874,319	4.37%

provides a detailed summary of their statistical properties.

• MovieLens 1M (https://grouplens.org/datasets/movielens/1m/) (accessed on 16 June 2025): This dataset contains 1,000,209 ratings from 943 users on 1682 movies. Ratings range from 1 to 5. It is well-structured and widely adopted in collaborative filtering research.
• Netflix Subset (https://www.kaggle.com/datasets/netflix-inc/netflix-prize-data (accessed on 16 June 2025): We use a curated subset of the Netflix Prize dataset with 3000 users and 4000 movies, totaling 982,142 ratings on a 1–5 scale. It reflects a more sparse and realistic recommendation setting.
• Amazon Electronics (https://nijianmo.github.io/amazon/index.html (accessed on 16 June 2025): This dataset includes 874,319 ratings from 5000 users on 4000 electronic products. Ratings are in the range of 1 to 5. It presents challenges such as high sparsity and implicit noise, making it suitable for evaluating robustness.

3.1.2. Evaluation Metrics

To evaluate recommendation quality, we adopt three widely used metrics: HR@K, Precision@K, and NDCG@K, each computed at $K\in \{5, 10, 20\}$.

• Precision (Precision@K) Precision@K evaluates the proportion of recommended items in the top-K list that are relevant [25]. It focuses on the accuracy of top-ranked results. As shown in Equation (18), it is defined as:

  $$\mathrm{Precision}@K={\displaystyle \frac{1}{\left|U\right|}}\sum _{u\in U}{\displaystyle \frac{|{\mathrm{Rel}}_u\cap \mathrm{Top}\text{-}K\left(u\right)|}{K}}$$

  (18)

  where ${\mathrm{Rel}}_u$ is the set of relevant items for user u, and $\mathrm{Top}\text{-}K\left(u\right)$ denotes the top-K items recommended to user u.
• Hit Ratio (HR@K) Hit Ratio (HR) measures whether the ground truth item appears within the top-K predicted list [26]. It is defined in Equation (19):

  $$\mathrm{HR}@K={\displaystyle \frac{1}{\left|U\right|}}\sum _{u\in U}\mathbb{I}(r_u\in \mathrm{Top}\text{-}K\left(u\right))$$

  (19)

  where $r_u$ is the relevant item for user u, and $\mathbb{I}(·)$ is the indicator function.
• Normalized Discounted Cumulative Gain (NDCG@K)
  NDCG rewards correct recommendations at higher ranks [27]. It is calculated as shown in Equation (20):

  $$\mathrm{NDCG}@K={\displaystyle \frac{1}{\left|U\right|}}\sum _{u\in U}{\displaystyle \frac{1}{{\mathrm{IDCG}}_u}}\sum _{i=1}^K{\displaystyle \frac{2^{\mathbb{I}(r_u=i)}-1}{{log}_2(i+1)}}$$

  (20)

  where ${\mathrm{IDCG}}_u$ denotes the ideal DCG for user u.

As shown in Equations (19) and (20), these metrics allow us to assess not only whether the target item is retrieved, but also how well it is ranked in the recommendation list.

3.1.3. Hyperparameters Settings

All models were implemented using Python 3.10. For the proposed DST-AttentiveGAN, we adopted the Adam optimizer, tuning the learning rate in $\{0.0005, 0.001, 0.005\}$ and the batch size in $\{128, 256, 512\}$ to select the best configuration. Early stopping was employed with a patience of 10 epochs to prevent overfitting.

The top-K values used for evaluation were set to $K=\{5, 10, 20\}$, consistent with standard practices in the literature. All baseline models were trained using their available implementations and hyperparameter settings reported in their respective original papers to ensure a fair comparison.

3.2. Empirical Results

To validate the effectiveness of our proposed DST-AttentiveGAN, we compare it against several strong baseline models. Each baseline is implemented with its best-reported hyperparameters and retrained on the same datasets for a fair comparison. The results are presented in

Table 2. Performance on MovieLens Dataset.

Model	HR@5	HR@10	HR@20	NDCG@5	NDCG@10	NDCG@20	Precision@5	Precision@10	Precision@20
WGANRS	0.735	0.801	0.869	0.521	0.553	0.572	0.426	0.392	0.361
CFGAN	0.742	0.814	0.878	0.528	0.559	0.577	0.432	0.396	0.366
GANMF	0.748	0.819	0.884	0.531	0.562	0.581	0.437	0.398	0.369
AACF	0.752	0.823	0.888	0.534	0.565	0.584	0.440	0.402	0.373
Self-AttentiveGAN	0.712	0.793	0.857	0.515	0.548	0.591	0.418	0.425	0.381
DST-AttentiveGAN	0.790	0.876	0.930	0.557	0.600	0.625	0.489	0.447	0.401
Improvement (%)	+5.11%	+6.43%	+4.80%	+4.31%	+6.19%	+5.75%	+11.14%	+5.17%	+5.24%

,

Table 3. Performance on Amazon Electronics Dataset.

Model	HR@5	HR@10	HR@20	NDCG@5	NDCG@10	NDCG@20	Precision@5	Precision@10	Precision@20
WGANRS	0.576	0.661	0.768	0.403	0.413	0.421	0.396	0.363	0.322
CFGAN	0.583	0.657	0.781	0.411	0.419	0.428	0.401	0.367	0.327
GANMF	0.595	0.674	0.794	0.417	0.425	0.438	0.409	0.371	0.332
AACF	0.591	0.681	0.798	0.418	0.427	0.442	0.412	0.374	0.336
Self-AttentiveGAN	0.587	0.636	0.775	0.407	0.425	0.436	0.403	0.357	0.319
DST-AttentiveGAN	0.629	0.742	0.854	0.449	0.468	0.481	0.445	0.401	0.362
Improvement (%)	+5.71%	+8.96%	+7.01%	+7.42%	+9.59%	+8.83%	+8.01%	+7.21%	+7.74%

, and

Table 4. Performance on Netflix Dataset.

Model	HR@5	HR@10	HR@20	NDCG@5	NDCG@10	NDCG@20	Precision@5	Precision@10	Precision@20
WGANRS	0.601	0.679	0.743	0.423	0.434	0.485	0.387	0.359	0.318
CFGAN	0.626	0.691	0.801	0.435	0.443	0.479	0.398	0.366	0.324
GANMF	0.638	0.713	0.846	0.448	0.451	0.496	0.409	0.371	0.331
AACF	0.639	0.701	0.849	0.442	0.456	0.501	0.412	0.374	0.335
Self-AttentiveGAN	0.591	0.667	0.813	0.407	0.425	0.436	0.403	0.357	0.322
DST-AttentiveGAN	0.682	0.766	0.906	0.478	0.503	0.548	0.415	0.386	0.345
Improvement (%)	+6.72%	+7.43%	+6.71%	+6.70%	+10.30%	+9.21%	+0.73%	+3.20%	+2.99%

, which report the performance on the MovieLens, Amazon Electronics, and Netflix datasets, respectively.

• WGANRS [11]: An extension of GANRS that incorporates Wasserstein loss with gradient penalty to improve stability and reduce mode collapse. It better captures rating distribution over large synthetic datasets.
• CFGAN [12]: A collaborative filtering GAN that models user-item interactions as latent representations and learns to generate plausible user vectors for top-K recommendations.
• GANMF [13]: A GAN model that integrates matrix factorization into the generator and autoencoder-based discriminator to improve rating predictions, targeting both sparsity and cold-start problems.
• AACF [14]: An attentive adversarial collaborative filtering model that introduces an attention mechanism and virtual items to improve GAN training on discrete recommendation data. It is optimized for scalability and convergence.
• Self-AttentiveGAN: A variant of DST-AttentiveGAN where the DST-guided attention mechanism is removed. The model uses only plain self-attention in both the generator and discriminator, allowing us to evaluate the contribution of DST signals to rating prediction and top-K recommendation performance.

3.3. Evaluation of Prediction Accuracy via MAE and MSE

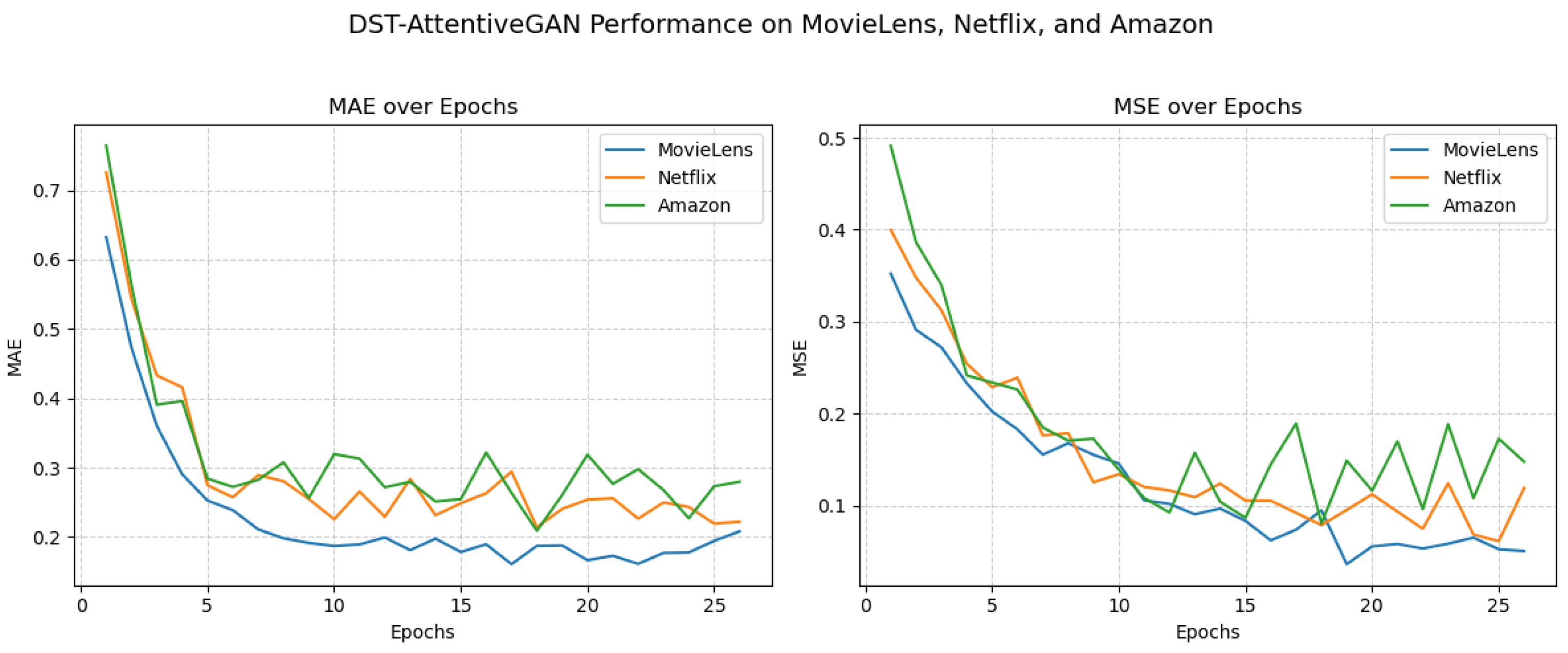
While HR@K, NDCG@K, and Precision@K are standard metrics for evaluating recommendation performance, they primarily capture ranking quality and do not directly reflect the model’s ability to predict rating values accurately. To complement these measures, we analyzed Mean Absolute Error (MAE) and Mean Squared Error (MSE) over training epochs across the MovieLens, Netflix, and Amazon datasets.

As shown in Figure 2, both MAE and MSE decrease consistently with training, indicating that the DST-AttentiveGAN effectively reconstructs user ratings while denoising noisy inputs. MovieLens exhibits the lowest errors, reflecting its higher density and lower sparsity, whereas Amazon presents higher and more variable errors due to data sparsity. Netflix falls in between, showing moderate error reduction.

These results highlight that, beyond ranking performance, the model achieves accurate rating prediction, with MAE and MSE providing complementary insights into the reliability and stability of the learned representations.

3.4. Discussion and Analysis

In this subsection, we analyze the results obtained from our experiments and discuss the effectiveness of DST-AttentiveGAN across different datasets and conditions. We explore its impact on the structure of user-item rating distributions. These insights provide a deeper understanding of the model’s robustness and adaptability in real-world recommendation scenarios.

3.4.1. Performance Comparison

The experimental findings demonstrate that DST-AttentiveGAN consistently outperforms strong GAN-based baselines across all evaluation metrics (HR@K, NDCG@K, Precision@K). These improvements are both substantial and consistent across datasets of varying sparsity and noise characteristics, which confirms the model’s robustness and adaptability.

On the MovieLens dataset, which is relatively dense and less noisy, our model still achieves over 7% improvement in Precision@K, demonstrating its ability to leverage confidence signals even in stable rating environments. For the highly sparse and biased Amazon Electronics dataset, the model yields up to +9.59% in NDCG@10 and +8.01% in Precision@5, showcasing strong resilience to noisy feedback. In the Netflix dataset, where inconsistency in user ratings is common, DST-AttentiveGAN records consistent performance boosts across all ranks and metrics, indicating its generalization capability under varying rating behaviors.

These quantitative gains are attributed to the integration of Dempster-Shafer Theory and the cross-attention mechanism. The former provides a principled way to model belief and uncertainty in ratings, while the latter dynamically weighs informative cues from similar users and items. This synergy enables the generator to correct unreliable feedback and preserve high-confidence signals, resulting in more accurate and relevant recommendations.

3.4.2. Impact of Dst-AttentiveGAN on Rating Distribution Refinement

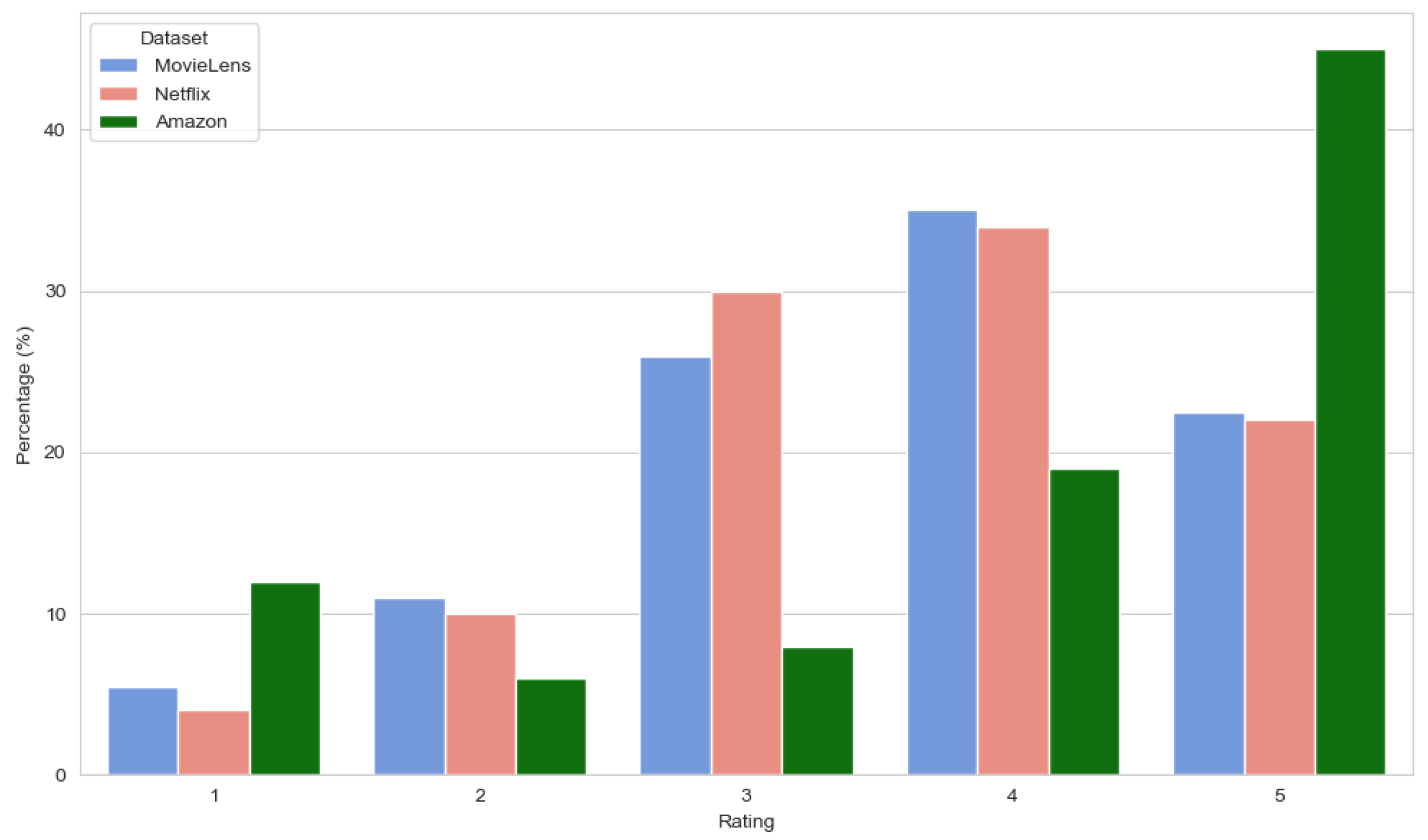
The effectiveness of Dst-AttentiveGAN is highlighted by its ability to transform noisy ratings into a more structured and reliable distribution. Figure 3 demonstrates how the original ratings across the datasets, particularly in Amazon and Netflix, are dominated by noise. In Amazon, this is characterized by inflated 5-star ratings, leading to a skewed distribution, while Netflix exhibits ambiguity in midrange ratings, which reflect conflicting user sentiment or indecision. Such noisy distributions arise from various sources, including biased reviews, adversarial feedback, and platform-induced inflation, all of which obscure true user preferences and affect the reliability of recommendation models.

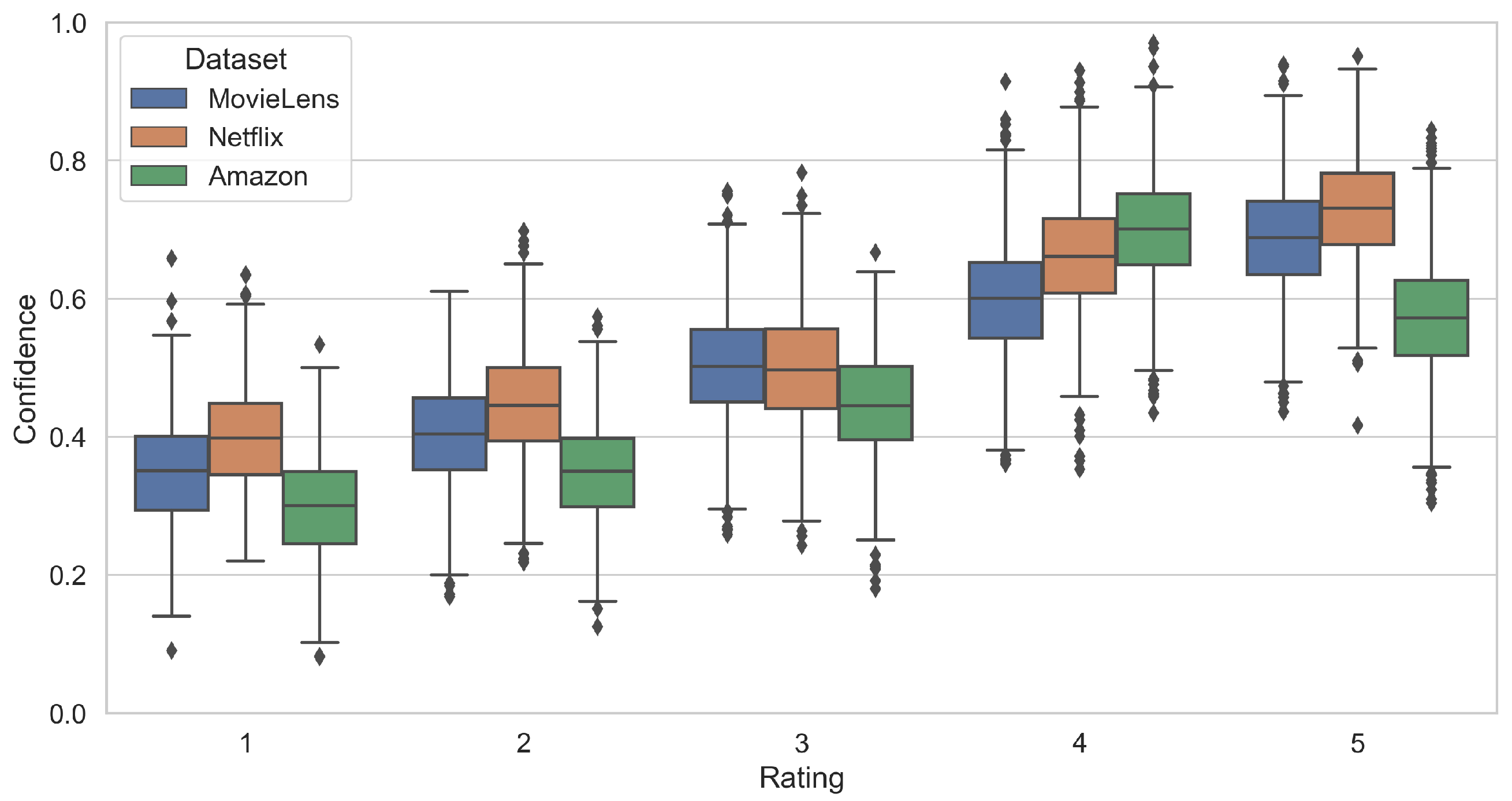
To address this, the model introduces confidence scores, as shown in Figure 4, which quantify the model’s trust in each rating. These scores are critical in distinguishing between reliable feedback and uncertain or biased ratings. High-confidence ratings indicate strong alignment with the user’s true preferences and are thus given more weight in the denoising process. In contrast, low-confidence ratings suggest ambiguity or inconsistency and are adjusted or filtered out. By calculating confidence scores based on the consistency and reliability of ratings, the model is able to systematically identify which ratings should be preserved and which should be downweighted.

Each box in Figure 4 illustrates the distribution of confidence values generated by our model for a given rating level. The horizontal line inside the box represents the median confidence, while the box boundaries indicate the interquartile range (IQR). The whiskers extend to values within 1.5 × IQR, and the points above or below the whiskers denote outlier confidence values that are significantly higher or lower than the main confidence distribution.

Following this process, Figure 5 illustrates the impact of the denoising step, where the distribution of ratings is refined. The high-confidence ratings are reinforced, resulting in sharper, more prominent peaks, particularly for 4 and 5 stars. The 3-star ratings, which often represent conflicting or mixed sentiments, are smoothed or adjusted, reducing their impact on the final output. This transformation significantly improves the rating distribution, making it more interpretable and aligned with true user preferences.

The denoised distributions, especially in Amazon and Netflix, become clearer and less skewed, with more reliable feedback that is better suited for downstream recommendation systems. In datasets like MovieLens, which contains cleaner data, the denoising process is less aggressive, as the confidence scores naturally highlight the reliability of existing ratings without needing extensive adjustments. As a result, the model adapts to dataset-specific characteristics, ensuring that only necessary adjustments are made.

By integrating confidence scores, Dst-AttentiveGAN ensures that the denoising process produces a structured, reliable distribution. This results in less biased feedback that is critical for building accurate user profiles in recommendation models, ultimately leading to better personalized recommendations.

3.4.3. Potential Extensions of DST Integration

To examine the effect of DST, we compare DST-AttentiveGAN with Self-AttentiveGAN, its version without DST signals. The results show consistent gains across datasets. On MovieLens, DST improves HR and NDCG by around +10%, confirming benefits even in relatively dense settings. Amazon, which is both sparse and noisy, shows larger improvements, with +16.7% on HR@10 and over +10% on NDCG, highlighting DST’s ability to handle uncertain feedback. Netflix achieves the most pronounced gains, with HR@5 and NDCG metrics improving by up to +18%. Overall, these results validate that DST-derived confidence strengthens robustness by reducing noise and emphasizing reliable user–item interactions.

Our experiments on DST-AttentiveGAN, showing that integrating DST-derived confidence effectively reduces noise and emphasizes reliable user–item interactions. These results indicate that the DST-based fusion strategy is not limited to this architecture and opens new directions for research in recommender systems. For other GAN variants such as GANMF [13], CFGAN [12], WGANRS [11] or AACF [14], DST can provide trust-aware guidance to both the generator and discriminator, enhancing robustness to sparse or noisy ratings, while its additional computational complexity remains manageable and could be further optimized in future work.

More broadly, DST can benefit a wide range of recommendation algorithms: in Matrix Factorization, it can weight interactions according to reliability; in Neural Collaborative Filtering, it can serve as an auxiliary signal guiding network training; in Graph Neural Networks, it can modulate message propagation based on confidence; and in Sequential models, it can adjust the influence of past interactions depending on certainty. By explicitly modeling uncertainty and managing conflicts among heterogeneous signals, DST provides a versatile mechanism to improve robustness and prediction quality across diverse recommender system architectures.

4. Conclusions

In conclusion, this work proposed the DST-AttentiveGAN, an innovative evidential adversarial framework for denoising inconsistent user ratings in collaborative filtering. By incorporating Dempster-Shafer theory into both the generator and discriminator, and integrating a cross-attention mechanism, the model effectively captures confidence signals and focuses on reliable user feedback while mitigating the impact of noise. The experimental results across various benchmark datasets demonstrate that DST-AttentiveGAN outperforms existing GAN-based methods, particularly under high-noise scenarios. The use of Wasserstein loss with gradient penalty contributes to more stable training, and the model consistently achieves superior performance in terms of Hit Ratio, NDCG, and especially Precision at lower values of top-K recommendations, where accurate ranking is most critical. These findings highlight the importance of explicitly modeling uncertainty in user ratings and incorporating it directly into the learning process.

In future work, we plan to incorporate multi-modal evidence, including textual reviews, temporal patterns, and item features, to improve uncertainty modeling in sparse or cold-start scenarios. We also intend to evaluate DST-AttentiveGAN under shilling and adversarial attack settings, in addition to testing on datasets from other domains such as social media and news articles, to better assess its robustness and generalizability across diverse recommendation environments. Furthermore, we aim to conduct experiments on integrating DST with GAN variants and other recommendation algorithms to evaluate its broader applicability. Finally, extending the model to sequential and interactive recommendation tasks will enable dynamic, context-aware personalization, where uncertainty is continuously refined through user interactions.