Battery Current Estimation and Prediction During Charging with Ant Colony Optimization Algorithm
Abstract
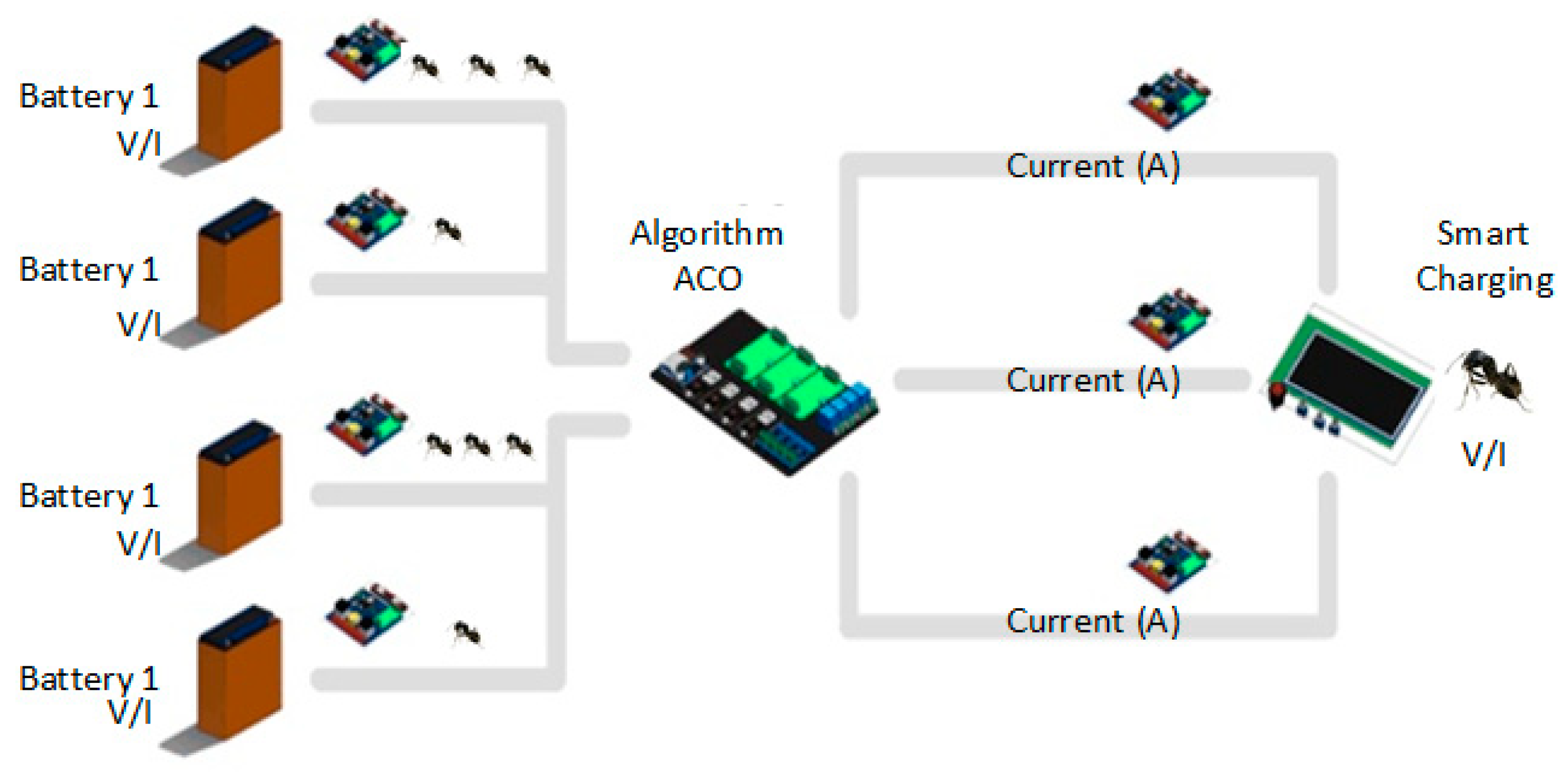
1. Introduction
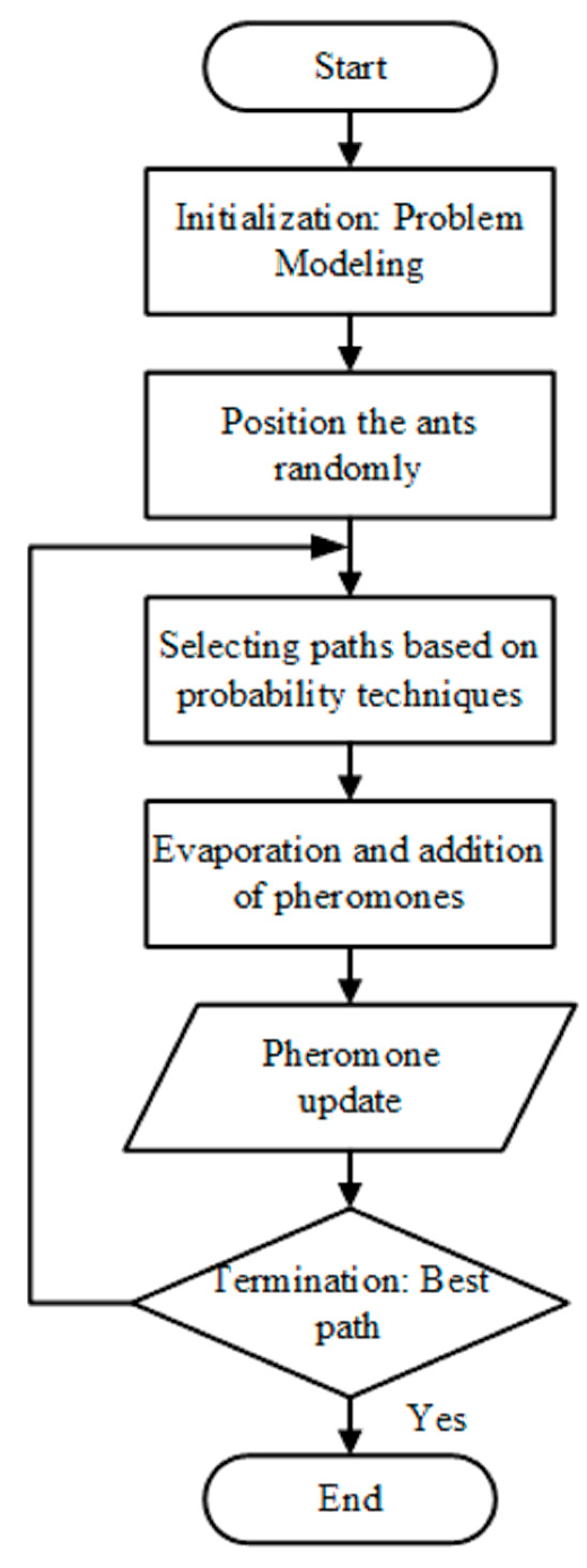
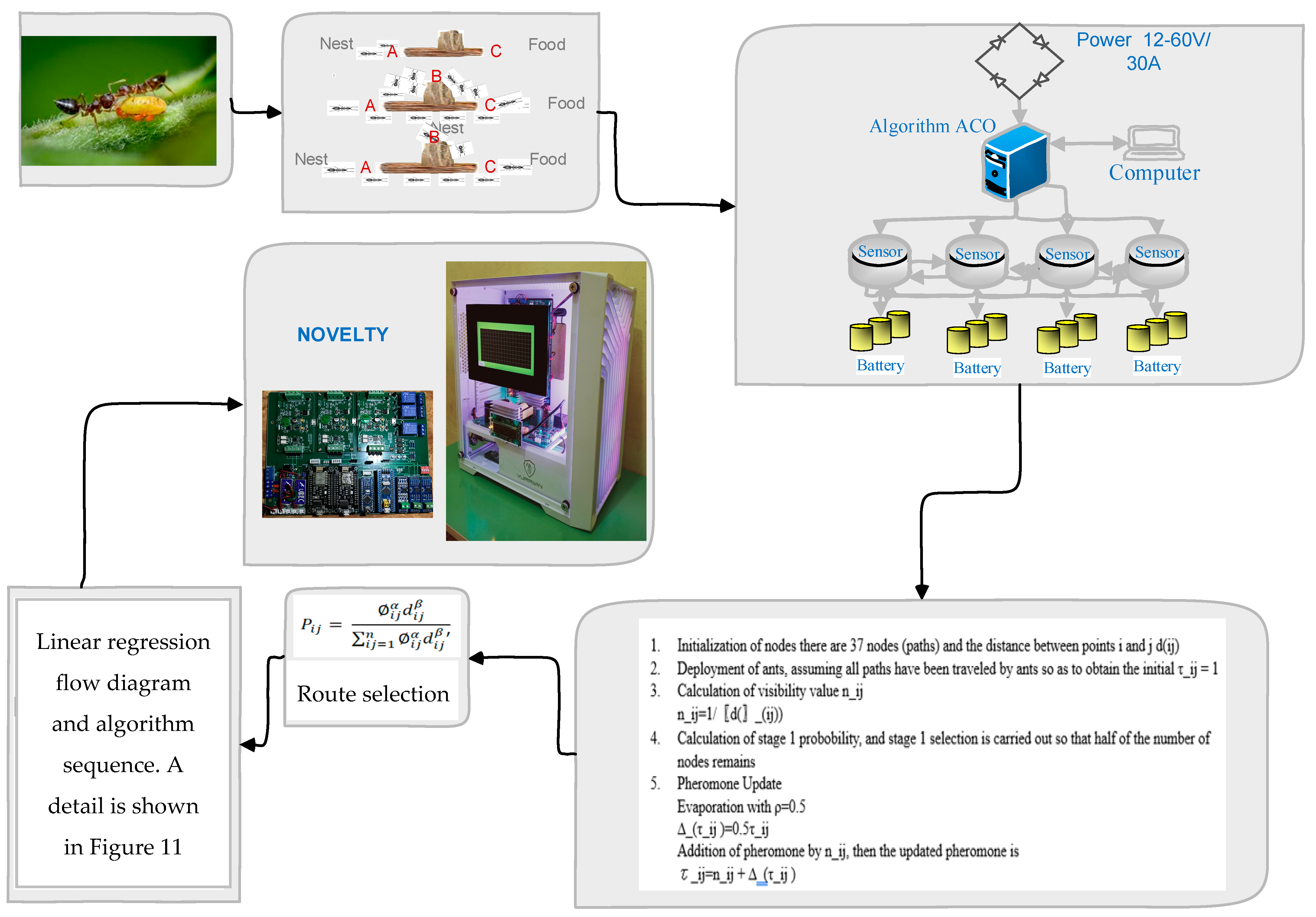
2. ACO Algorithm Stages
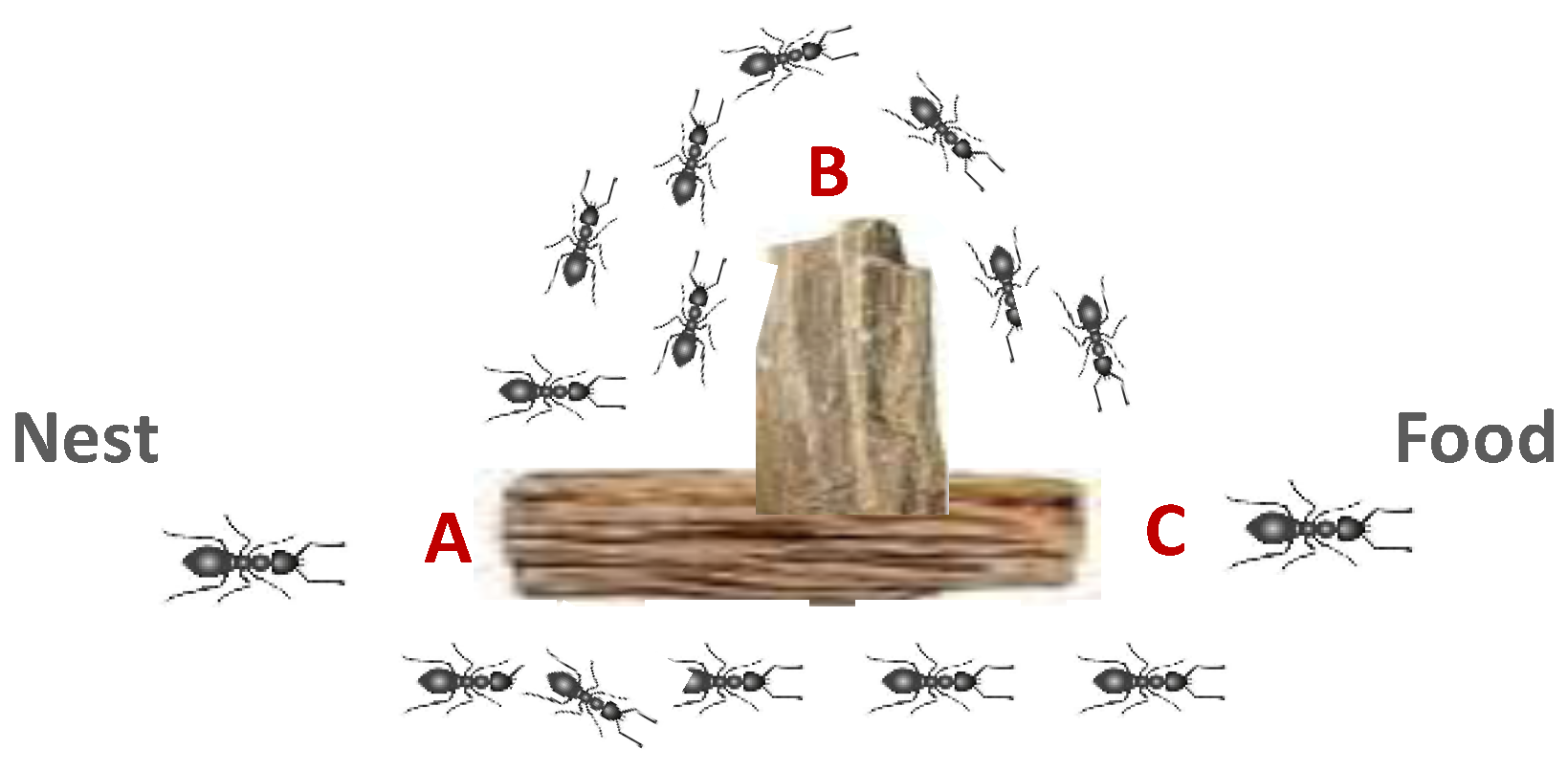
2.1. Initialization and Ant Spread
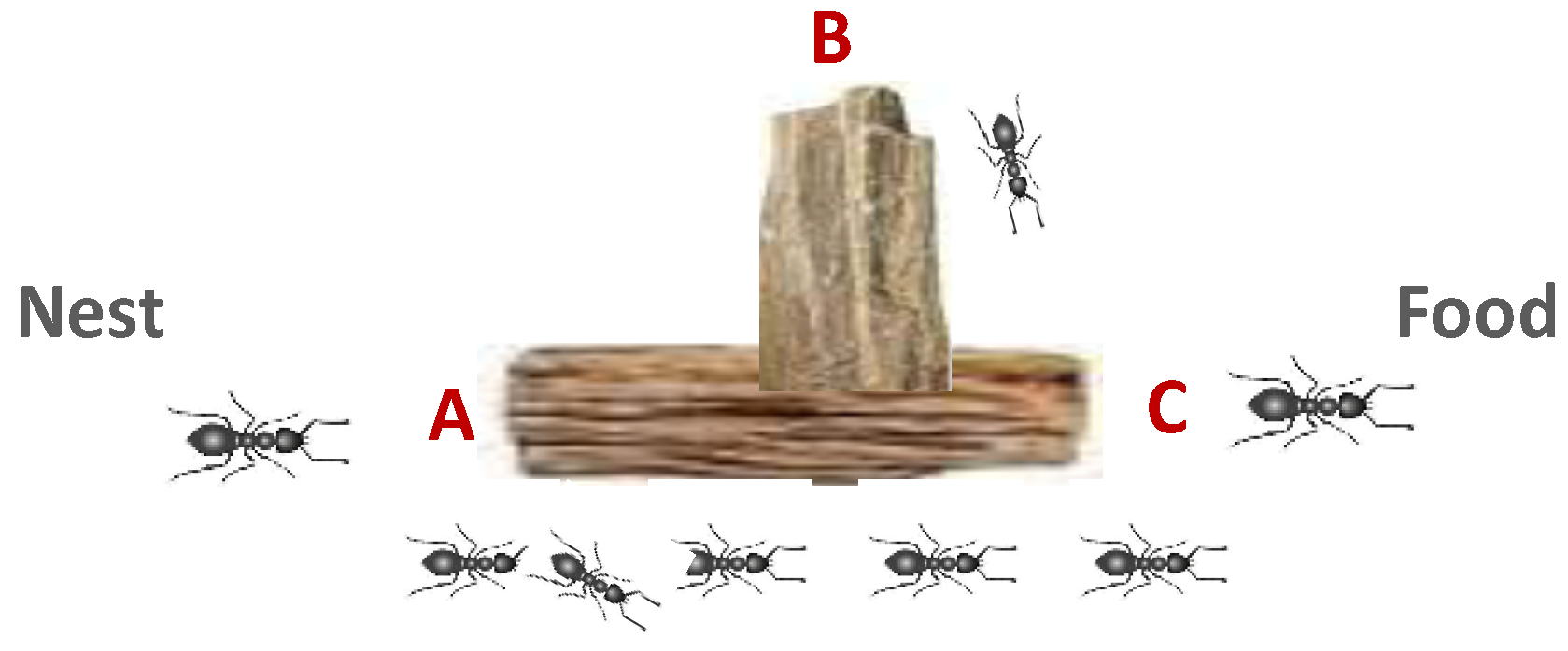
2.2. Path Selection
2.3. Pheromone Addition and Evaporation
2.4. Pheromone Update
3. Lead Acid Batteries
4. Root Mean Squared Error (RMSE)
5. Mean Absolute Error (MAE)
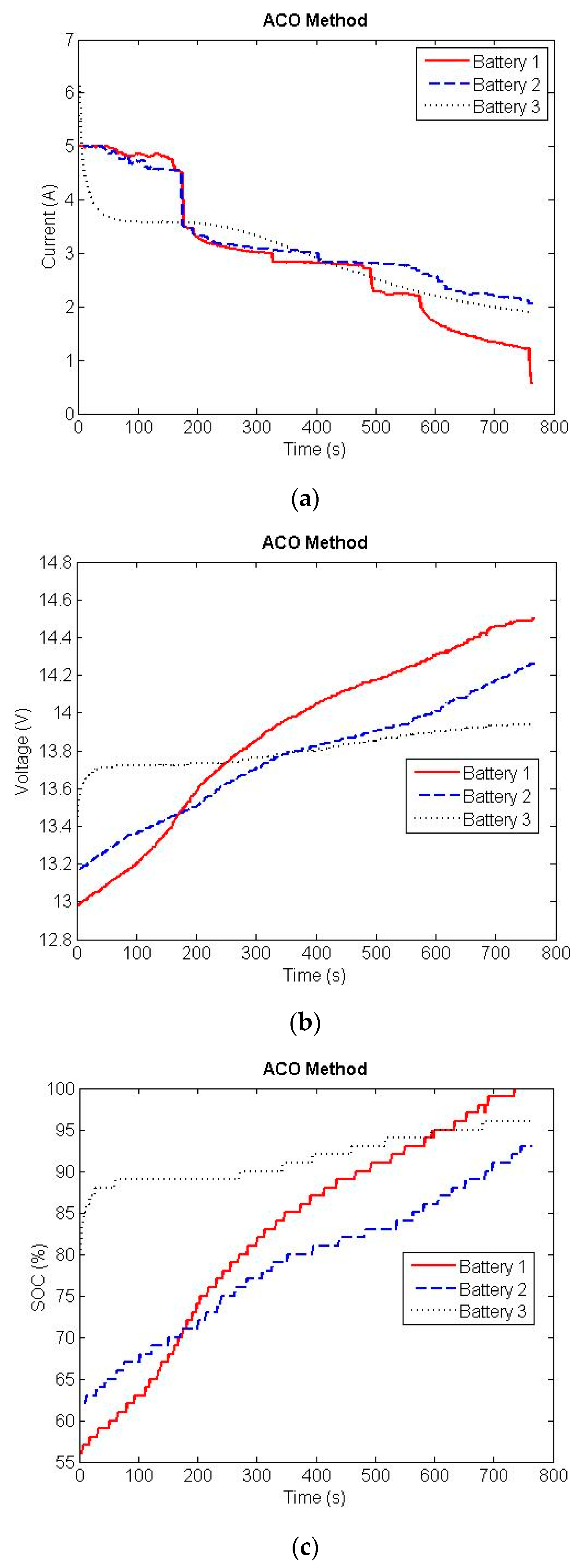
6. Results
- Influence control parameter for ;
- Influence control parameter for ;
- Pheromone vaporization parameter, .
7. Discussion
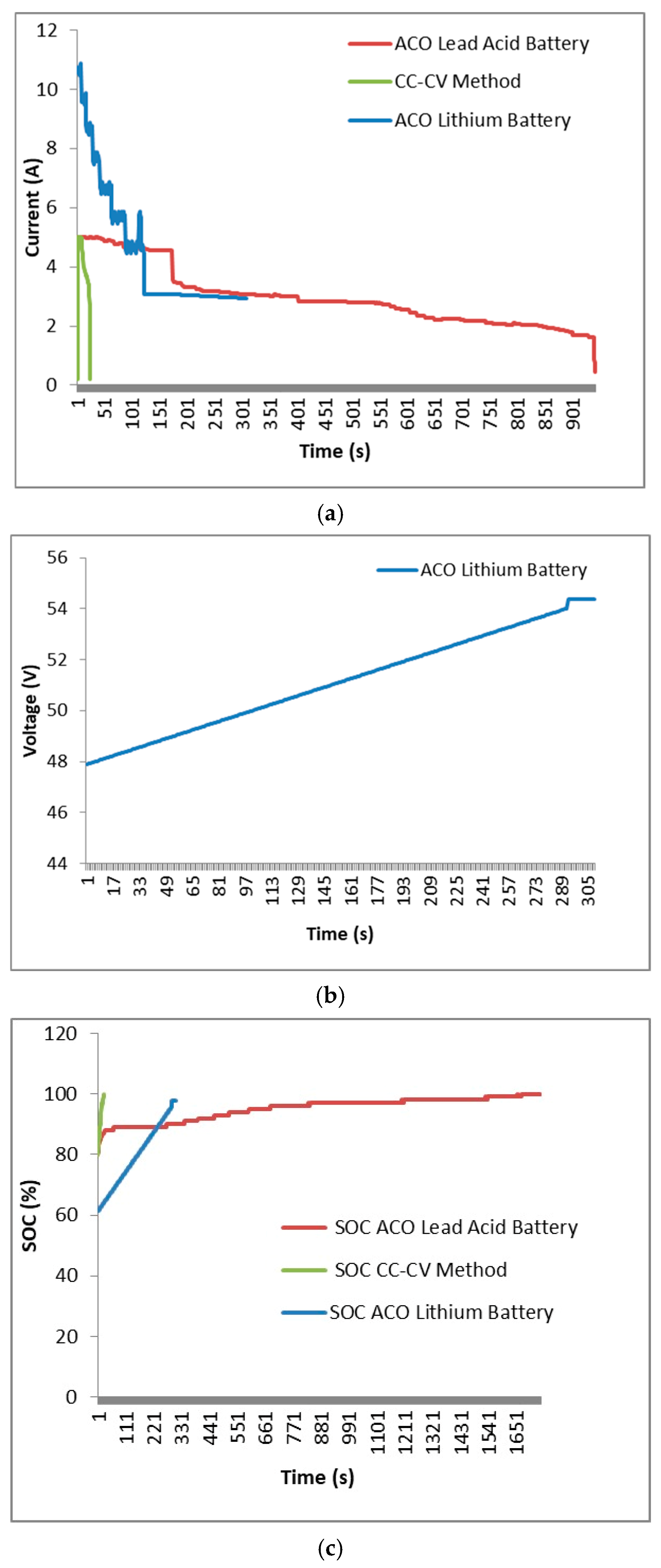
7.1. ACO Prediction
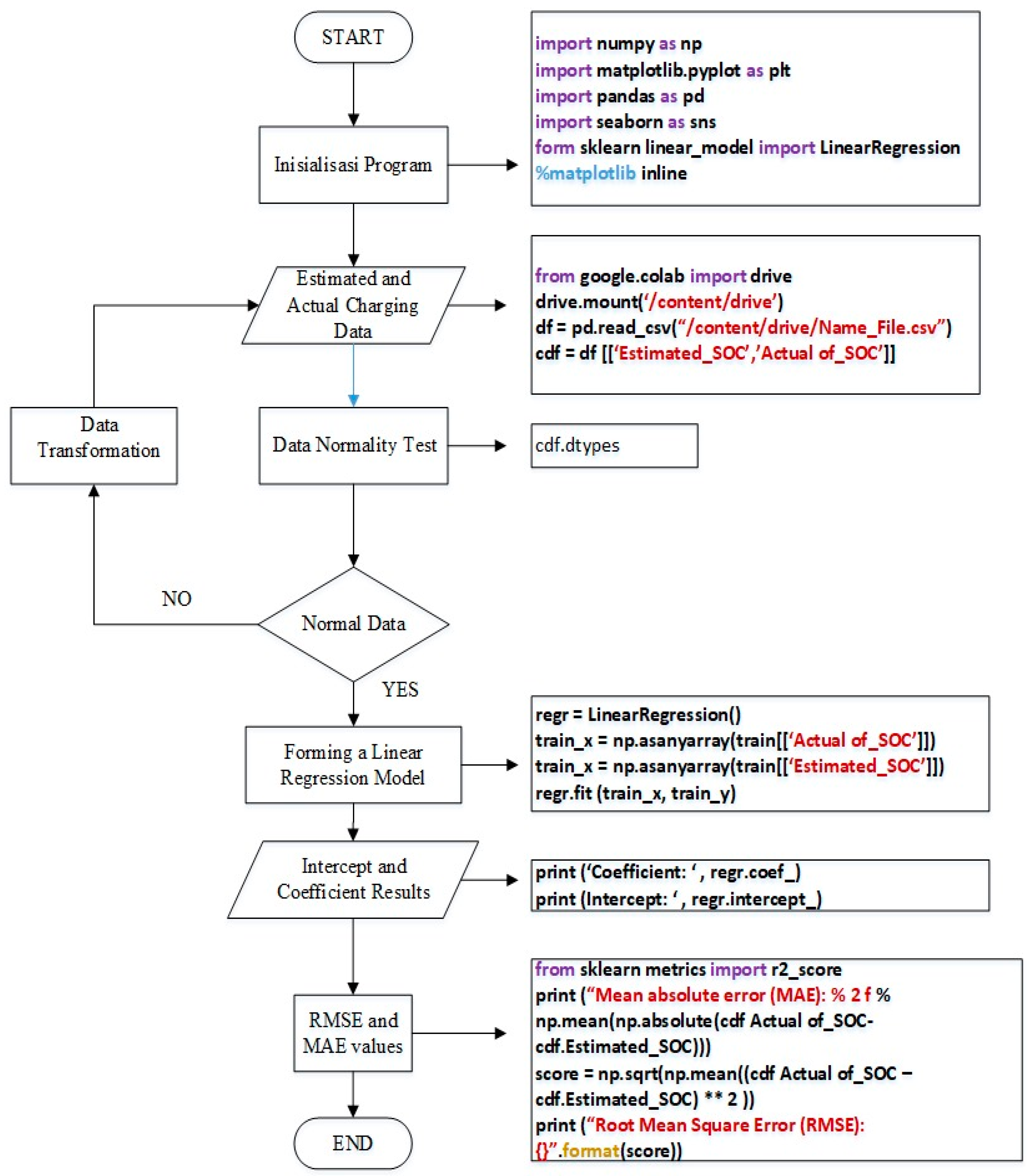
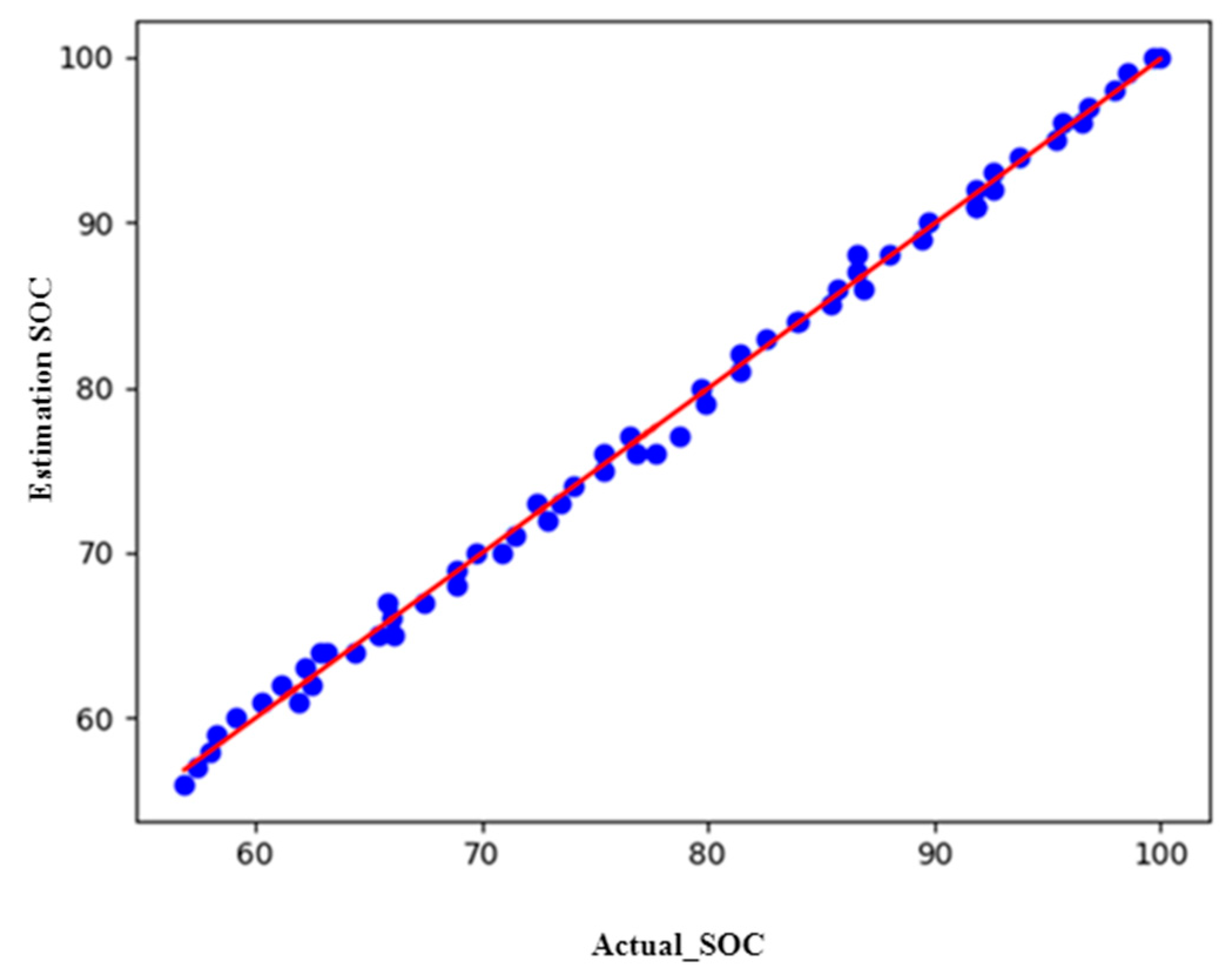
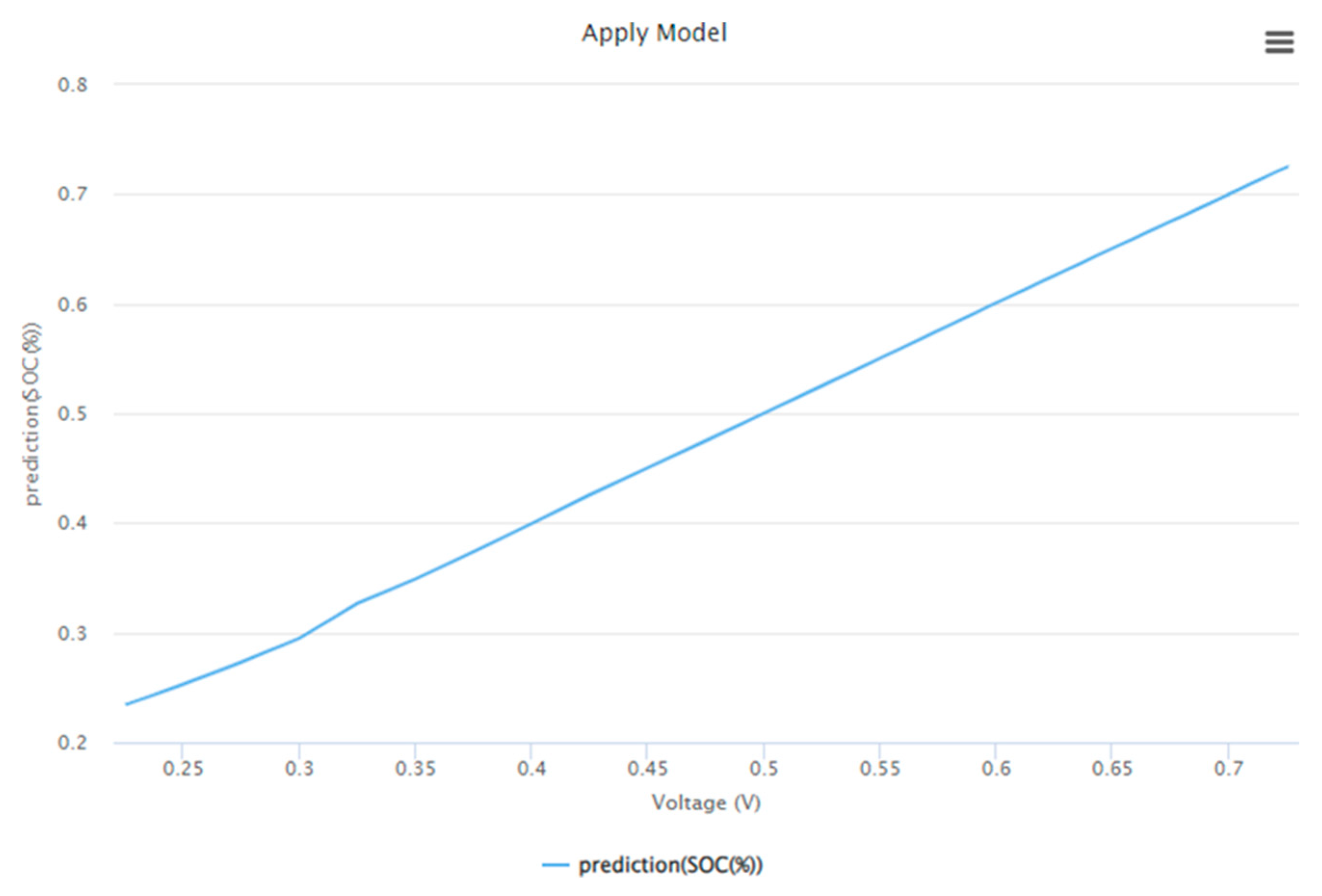
7.2. Data Processing Using Linear Regression
8. Conclusions
- The Ant Colony algorithm uses both supervised learning and unsupervised learning and produces current patterns of 10 A, 5 A, 3 A, 2 A, and 0 A as the best current path in the battery charging system to produce a fast and safe charging process for the battery.
- The SOC estimation results of lead acid batteries using the Ant Colony algorithm, based on linear regression data, produce good accuracy, with an RMSE value of 0.32238 and an MAE of 0.27002.
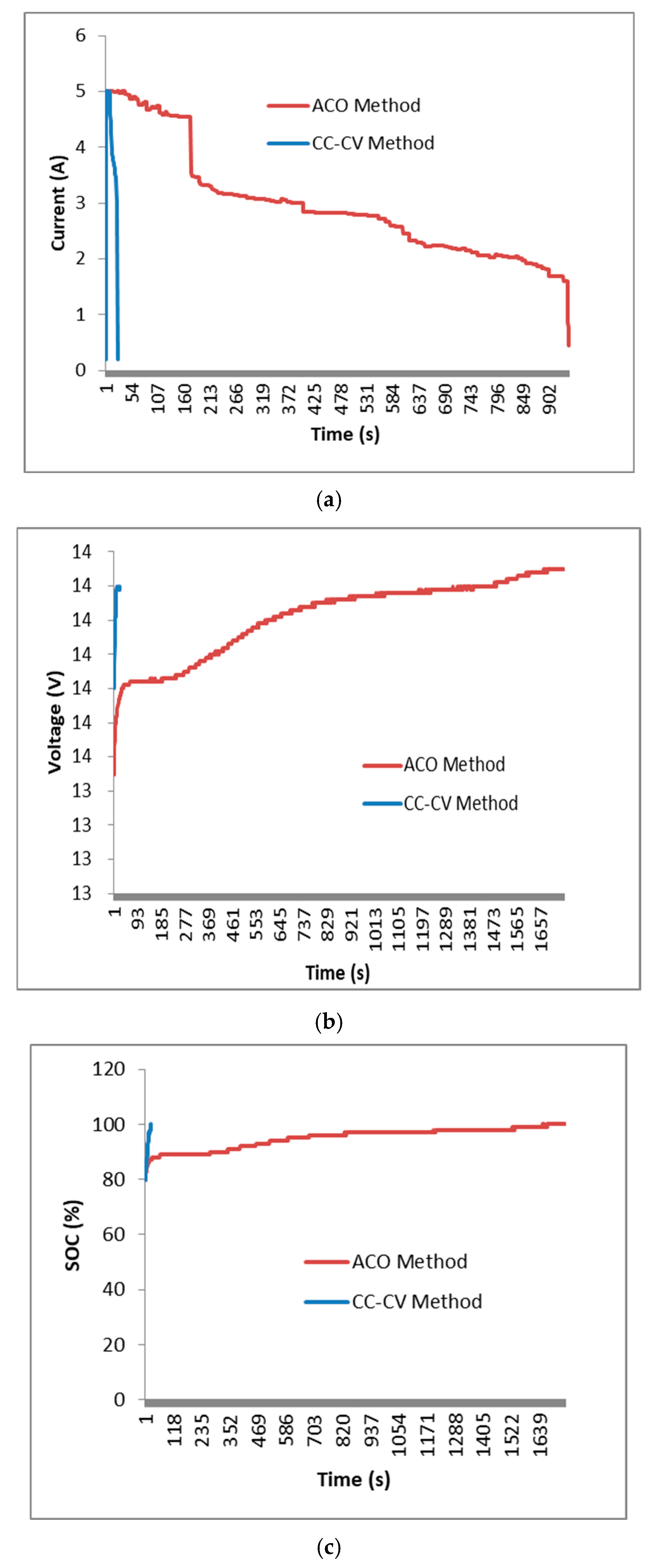
- The charging system with the Ant Colony Optimization algorithm has a charging current when charging the battery that is more stable compared to charging without the Ant Colony Optimization algorithm, which has spikes and high fluctuations. As such, it can be said that charging with the ACO algorithm is a safe way to charge the battery.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hou, H.; Du, B.; Guo, D.; Xu, H.; Fan, Y. Path to the Sustainable Development of China’s Secondary Lead Industry: An Overview of the Current Status of Waste Lead-Acid Battery Recycling. Environ. Impact Assess. Rev. 2024, 15, 107389. [Google Scholar] [CrossRef]
- Queiroz, M.B.; Duarte RC, O.; Lima, J.F.; Vilar, E.O. Comparative Evaluation of Grid Corrosion of Lead-Acid Batteries Formed by Casting and Rolling Process. J. Power Sources 2024, 596, 234113. [Google Scholar] [CrossRef]
- Khan, A.B.; Akram, A.S.; Choi, W. State of Charge Estimation of Flooded Lead Acid Battery Using Adaptive Unscented Kalman Filter. Energies 2024, 17, 1275. [Google Scholar] [CrossRef]
- Yin, L.; Liu, S.; Yin, D.; Du, K.; Yan, J.; Armwood-Gordon, C.K.; Li, L. Development of Rechargeable Cement-Based Batteries with Carbon Fiber Mesh for Energy Storage Solutions. J. Energy Storage 2024, 93, 112181. [Google Scholar] [CrossRef]
- Su, W.; Zhang, Y.; Wang, H.; Yang, M.; Niu, Z. An Ultrafast Air Self-Charging Zinc Battery. Adv. Mater. 2024, 36, 2308042. [Google Scholar] [CrossRef]
- Du, X.Y.; Song, L.N.; Liang, S.; Wang, Y.F.; Wang, Y.; Wang, H.F.; Xu, J.J. Photo-Assisted Chemical Self-Rechargeable Zinc Ion Batteries with High Charging and Discharging Efficiency. Angew. Chem. 2024, 136, e202411845. [Google Scholar] [CrossRef]
- Rani, N.N.; Drenganathan, R.K.; Praveen, G.D.; Santhoshkumar, B.; Prasad, S.G. Self Charging In E-Vehicle Using Two Batteries. In Proceedings of the 2024 International Conference on Communication, Computing and Internet of Things (IC3IoT), Chennai, India, 17–18 April 2024. [Google Scholar]
- Song, H.; Liu, C.; Amani, A.M.; Gu, M.; Jalili, M.; Meegahapola, L.; Yu, X.; Dickeson, G. Smart Optimization in Battery Energy Storage Systems: An Overview. Energy AI 2024, 17, 100378. [Google Scholar] [CrossRef]
- Nouri, A.; Lachheb, A.; El Amraoui, L. Optimizing Efficiency of Vehicle-to-Grid System with Intelligent Management and ANN-PSO Algorithm for Battery Electric Vehicles. Electr. Power Syst. Res. 2024, 226, 109936. [Google Scholar] [CrossRef]
- Rauf, M.; Kumar, L.; Zulkifli, S.A.; Jamil, A. Aspects of Artificial Intelligence in Future Electric Vehicle Technology for Sustainable Environmental Impact. Environ. Chall. 2024, 14, 100854. [Google Scholar] [CrossRef]
- Iqbal, S.; Alshammari, N.F.; Shouran, M.; Massoud, J. Smart and Sustainable Wireless Electric Vehicle Charging Strategy with Renewable Energy and Internet of Things Integration. Sustainability 2024, 16, 2487. [Google Scholar] [CrossRef]
- Qi, Z. Application of Improved Ant Colony Algorithm in Optimizing the Charging Path of Electric Vehicles. World Electr. Veh. J. 2024, 15, 230. [Google Scholar] [CrossRef]
- Li, Z.; Wei, Y.; Park, J.H. An Improved Bilevel Algorithm Based on Ant Colony Optimization and Adaptive Large Neighborhood Search for Routing and Charging Scheduling of Electric Vehicles. IEEE Trans. Transp. Electrif. 2024; early access. [Google Scholar]
- Karno, S.P.A.; Ristono, A.; Soepardi, A. Allocation Optimization of An Electrical Vehicle Charging Station Using Ant Colony Algorithm; IEOM Society International: Southfield, MI, USA, 2024. [Google Scholar] [CrossRef]
- Banerjee, A.; Pradhan, S.; Misra, B.; Chakraborty, S. A Guide to Meta-Heuristic Algorithms for Multi-objective Optimization: Concepts and Approaches. In Applied Multi-Objective Optimization; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Ourouss, K.; Naja, N.; Jamali, A. Defending Against Smart Grayhole Attack Within MANETs: A Reputation-Based Ant Colony Optimization Approach for Secure Route Discovery in DSR Protocol. Wirel. Pers. Commun. 2021, 116, 207–226. [Google Scholar] [CrossRef]
- Shahriar, S.; Al-Ali, A.R.; Osman, A.H.; Dhou, S.; Nijim, M. Prediction of EV Charging Behavior Using Machine Learning. IEEE Access 2021, 9, 111576–111586. [Google Scholar] [CrossRef]
- Mazhar, T.; Asif, R.N.; Malik, M.A.; Nadeem, M.A.; Haq, I.; Iqbal, M.; Kamran, M.; Ashraf, S. Electric Vehicle Charging System in the Smart Grid Using Different Machine Learning Methods. Sustainability 2023, 15, 2603. [Google Scholar] [CrossRef]
- Yaghoubi, E.; Yaghoubi, E.; Khamees, A.; Razmi, D.; Lu, T. A Systematic Review and Meta-Analysis of Machine Learning, Deep Learning, and Ensemble Learning Approaches in Predicting EV Charging Behavior. Eng. Appl. Artif. Intell. 2024, 135, 108789. [Google Scholar] [CrossRef]
- Bairwa, B.; Saleem, S.A.; Jampala, K. Machine Learning for Battery Charging: From Prediction to Categorization. In Proceedings of the 2024 15th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kamand, India, 24–28 June 2024. [Google Scholar]
- Shi, T.; Zhao, F.; Zhou, H.; Qi, C. Research on Intelligent Energy Management Method of Multifunctional Fusion Electric Vehicle Charging Station Based on Ma-Chine Learning. Electr. Power Syst. Res. 2024, 229, 110037. [Google Scholar] [CrossRef]
- Reddy, M.R.; Pandian, R. Edge Detection of an Image based on Ant Colony Optimization Technique. Int. J. Sci. Res. 2013, 2, 1256–1260. [Google Scholar]
- Hua, C.C.; Lin, M.Y. A Study of Charging Control of Lead-Acid Battery for Electric Vehicles. In Proceedings of the 2000 IEEE International Symposium on Industrial Electronics (Cat. No. 00TH8543), Cholula, Puebla, Mexico, 4–8 December 2000. [Google Scholar]

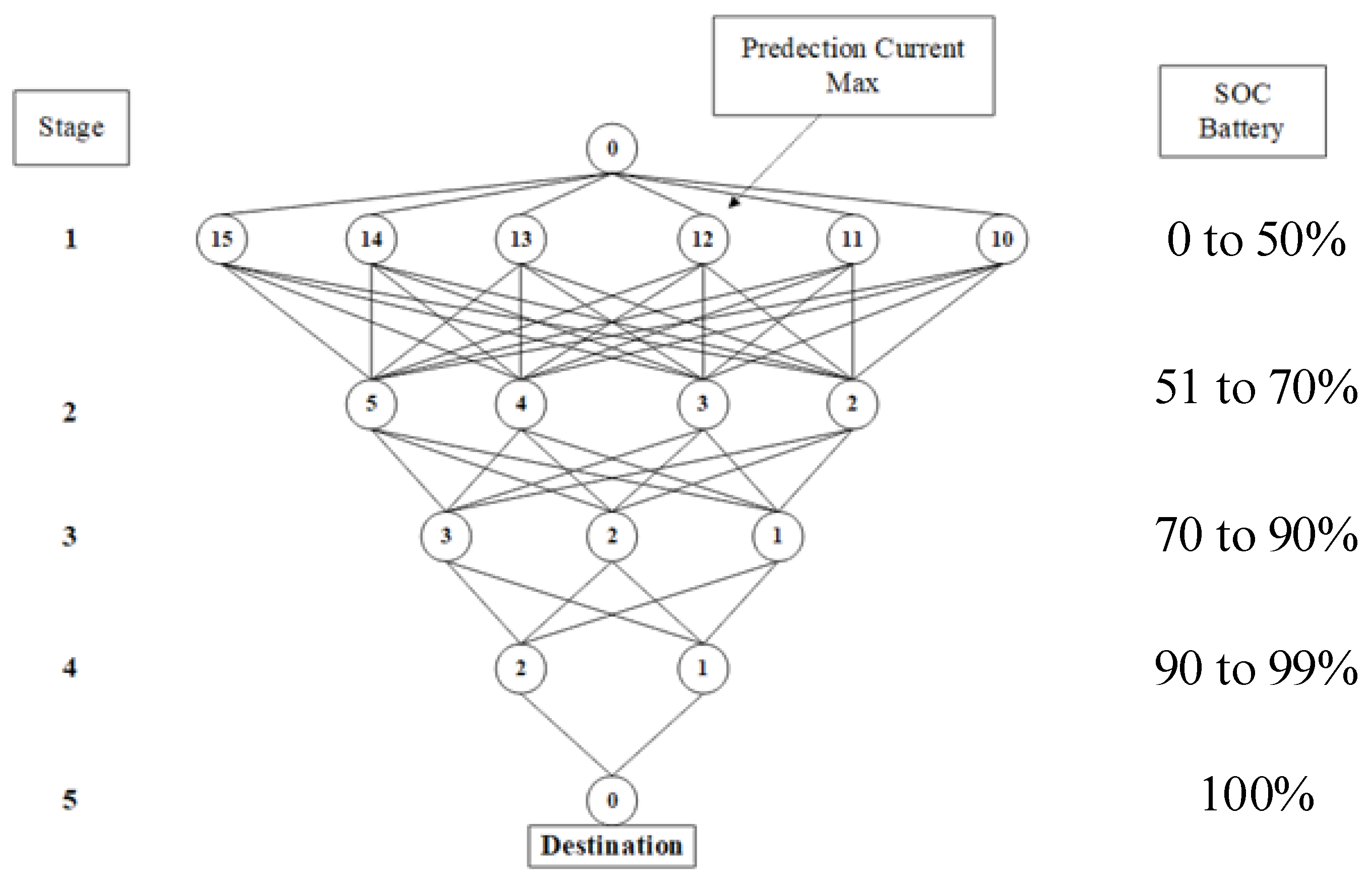
| Stage | Possible Current (A) | |||||
|---|---|---|---|---|---|---|
| 1 | 15 | 14 | 13 | 12 | 11 | 10 |
| 2 | 5 | 4 | 3 | 2 | ||
| 3 | 3 | 2 | 1 | |||
| 4 | 2 | 1 | ||||
| 5 | 0 | |||||
| Stage | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Current (A) | 10 | 5 | 3 | 2 | 0 |
| Range (A) | 9.5–10.5 | 4.5–5.5 | 2.5–3.5 | 1.5–2.5 | 0–0.5 |
| Path (Line) | Distance | Selected | ||||
|---|---|---|---|---|---|---|
| 15 A | 2 | 1 | 0.5 | 0.5 | 0.459 | Yes |
| 10 A | 3 | 1 | 0.33 | 0.33 | 0.303 | Yes |
| 5 A | 6 | 1 | 0.16 | 0.16 | 0.146 | No |
| 3 A | 10 | 1 | 0.1 | 0.1 | 0.092 | No |
| Path | Distance | Remaining Pheromone | Pheromone Added | Selected | ||||
|---|---|---|---|---|---|---|---|---|
| 15 A | 2 | 0.5 | 0.5 | 1 | 0.5 | 0.5 | 0.646 | Yes |
| 10 A | 3 | 0.5 | 0.33 | 0.83 | 0.33 | 0.274 | 0.354 | No |
| Battery Charging Information | Description |
|---|---|
| Initial battery voltage | 12.98 V |
| Full battery voltage | 14.50 V |
| Initial battery SOC | 56% |
| Full battery SOC | 100% |
| Total charging time | 12.73 min |
| Data retrieval interval | 1 s |
| No. | Voltage (V) | Estimation SoC (%) | Actual SoC (%) | Absolute Error | (Error)2 | RMSE | MAE |
|---|---|---|---|---|---|---|---|
| 1. | 12.98 | 56 | 56.57 | 0.57 | 0.32 | 0.32 | 0.27 |
| 2. | 12.99 | 56 | 56.85 | 0.85 | 0.73 | ||
| 3. | 13.00 | 57 | 57.14 | 0.14 | 0.02 | ||
| 4. | 13.01 | 57 | 57.42 | 0.42 | 0.18 | ||
| 5. | 13.02 | 58 | 57.71 | 0.28 | 0.08 | ||
| 151. | 14.49 | 100 | 99.71 | 0.28 | 0.08 | ||
| 152. | 14.50 | 100 | 100.00 | 0.00 | 0.00 | ||
| Total: | 41.04 | 15.79 | |||||
| Coefficient | Intercept | RMSE | MAE |
|---|---|---|---|
| 1.00426298 | −0.39176098 | 0.32238 | 0.27002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muslimin, S.; Prihatini, E.; Husni, N.L.; Dewi, T.; Wartam Bin Umar, M.; Bela, A.C.A.; Handayani, S.U.; Caesarendra, W. Battery Current Estimation and Prediction During Charging with Ant Colony Optimization Algorithm. Digital 2025, 5, 6. https://doi.org/10.3390/digital5010006
Muslimin S, Prihatini E, Husni NL, Dewi T, Wartam Bin Umar M, Bela ACA, Handayani SU, Caesarendra W. Battery Current Estimation and Prediction During Charging with Ant Colony Optimization Algorithm. Digital. 2025; 5(1):6. https://doi.org/10.3390/digital5010006
Chicago/Turabian StyleMuslimin, Selamat, Ekawati Prihatini, Nyayu Latifah Husni, Tresna Dewi, Mukhidin Wartam Bin Umar, Auvi Crisanta Ana Bela, Sri Utami Handayani, and Wahyu Caesarendra. 2025. "Battery Current Estimation and Prediction During Charging with Ant Colony Optimization Algorithm" Digital 5, no. 1: 6. https://doi.org/10.3390/digital5010006
APA StyleMuslimin, S., Prihatini, E., Husni, N. L., Dewi, T., Wartam Bin Umar, M., Bela, A. C. A., Handayani, S. U., & Caesarendra, W. (2025). Battery Current Estimation and Prediction During Charging with Ant Colony Optimization Algorithm. Digital, 5(1), 6. https://doi.org/10.3390/digital5010006







