Defect Isolation from Whole to Local Field Separation in Complex Interferometry Fringe Patterns through Development of Weighted Least-Squares Algorithm
Abstract
:1. Introduction
2. Experimental Methodology
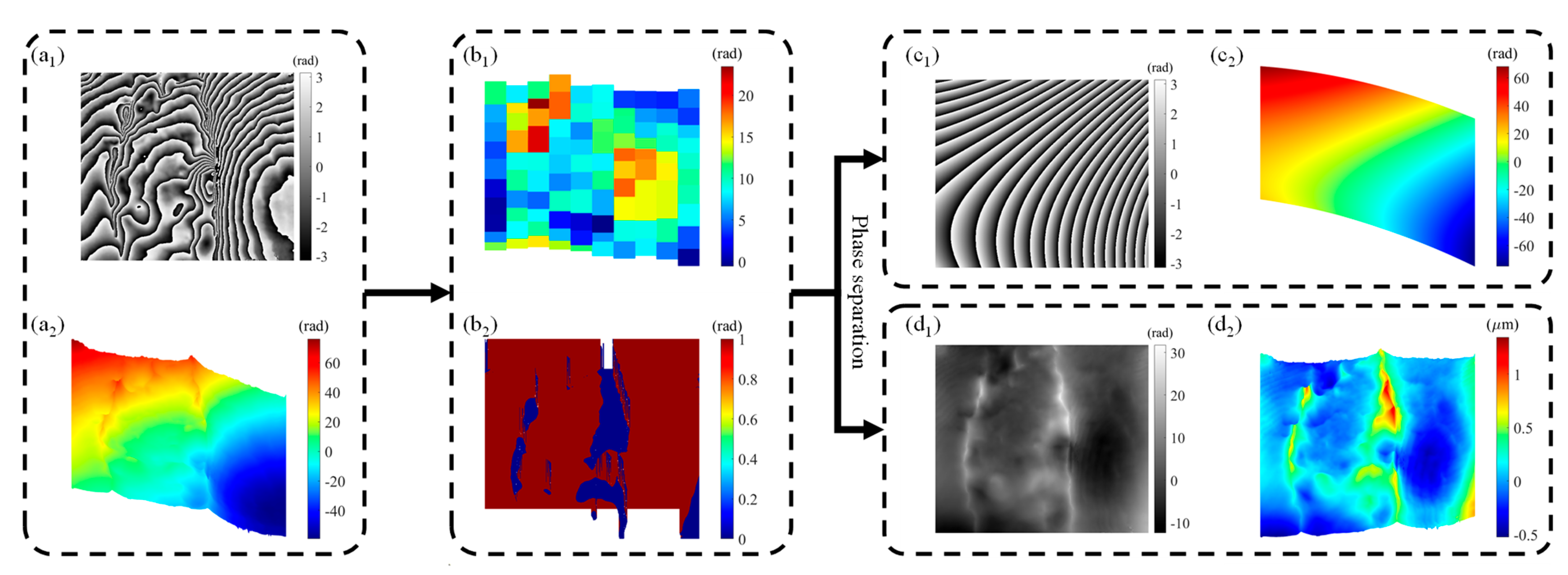
2.1. Phase Separation Method of Whole Field vs. Local Field
2.2. System View
3. Experimental Results
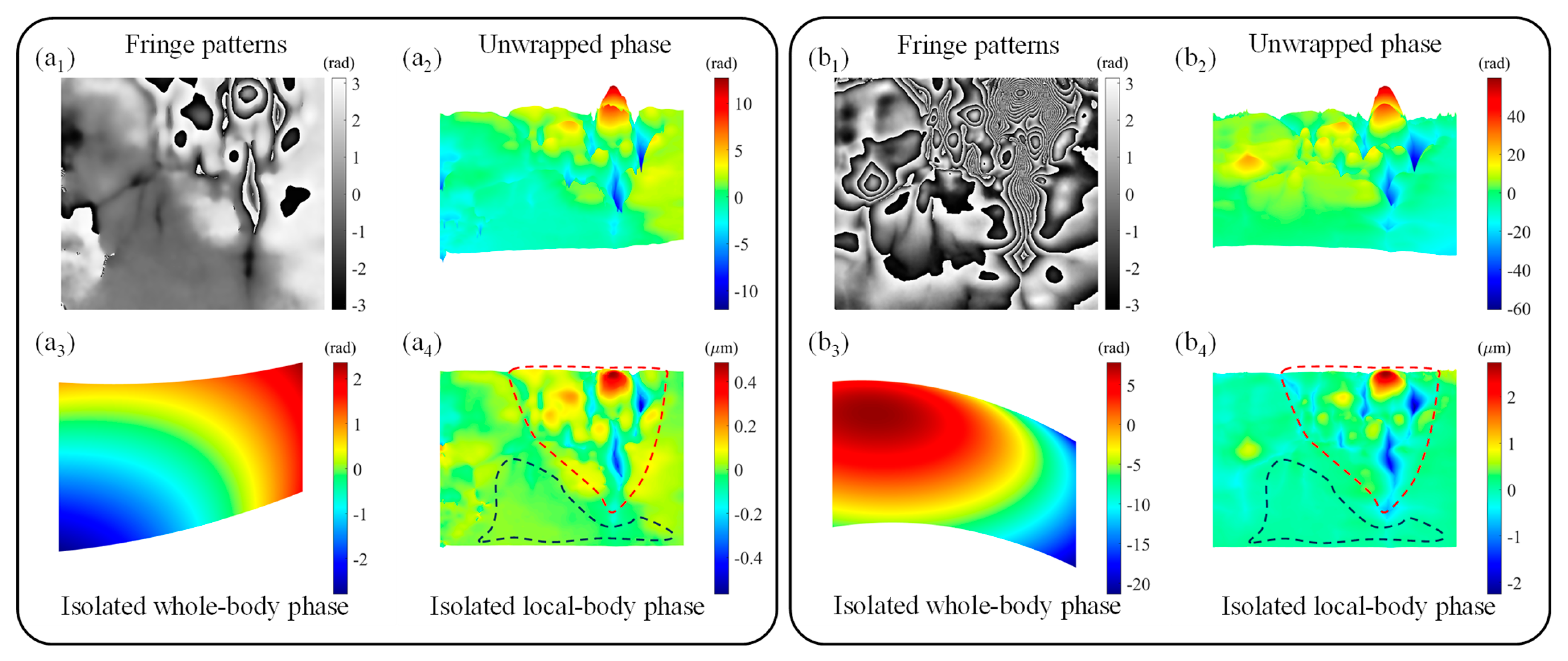
3.1. Comparison of Quantitative Methods
3.2. Contrast Treatment of Simple and Complex Fringe Patterns
3.3. Mural Cooling Process
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anaf, W.; Cabal, A.; Robbe, M.; Schalm, O. Real-Time Wood Behaviour: The Use of Strain Gauges for Preventive Conservation Applications. Sensors 2020, 20, 305. [Google Scholar] [CrossRef] [PubMed]
- Tiennot, M.; Iannuzzi, D.; Hermens, E. Evolution of the Viscoelastic Properties of Painting Stratigraphies: A Moisture Weathering and Nanoindentation Approach. Herit. Sci. 2021, 9, 77. [Google Scholar] [CrossRef]
- Gülker, G.; Hinsch, K.D.; Kraft, A. TV-Holography on a Microscopic Scale: Deformation Monitoring on Polychrome Terracotta Warriors. In Interferometry in Speckle Light; Jacquot, P., Fournier, J.-M., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 337–344. ISBN 978-3-642-63230-3. [Google Scholar]
- Buchta, D.; Heinemann, C.; Pedrini, G.; Krekel, C.; Osten, W. Combination of FEM Simulations and Shearography for Defect Detection on Artwork. Strain 2018, 54, e12269. [Google Scholar] [CrossRef]
- Zhao, Q.; Dan, X.; Sun, F.; Wang, Y.; Wu, S.; Yang, L. Digital Shearography for NDT: Phase Measurement Technique and Recent Developments. Appl. Sci. 2018, 8, 2662. [Google Scholar] [CrossRef]
- Picollo, M.; Fukunaga, K.; Labaune, J. Obtaining Noninvasive Stratigraphic Details of Panel Paintings Using Terahertz Time Domain Spectroscopy Imaging System. J. Cult. Herit. 2015, 16, 73–80. [Google Scholar] [CrossRef]
- Groves, R.M.; Pradarutti, B.; Kouloumpi, E.; Osten, W.; Notni, G. 2D and 3D Non-Destructive Evaluation of a Wooden Panel Painting Using Shearography and Terahertz Imaging. NDT E Int. 2009, 42, 543–549. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Erdmann, R.G. Automatic Thread-Level Canvas Analysis: A Machine-Learning Approach to Analyzing the Canvas of Paintings. IEEE Signal Process. Mag. 2015, 32, 38–45. [Google Scholar] [CrossRef]
- Baxter, J. Quasi-Reflectography. Nat. Photon 2012, 6, 572. [Google Scholar] [CrossRef]
- Eveno, M.; Moignard, B.; Castaing, J. Portable Apparatus for In Situ X-Ray Diffraction and Fluorescence Analyses of Artworks. Microsc. Microanal. 2011, 17, 667–673. [Google Scholar] [CrossRef]
- Daher, C.; Paris, C.; Le Hô, A.-S.; Bellot-Gurlet, L.; Échard, J.-P. A Joint Use of Raman and Infrared Spectroscopies for the Identification of Natural Organic Media Used in Ancient Varnishes: Spectroscopic Identification of Natural Organic Media Used in Ancient Varnishes. J. Raman Spectrosc. 2010, 41, 1494–1499. [Google Scholar] [CrossRef]
- Georges, M.P.; Scauflaire, V.S.; Lemaire, P.C. Compact and Portable Holographic Camera Using Photorefractive Crystals. Application in Various Metrological Problems. Appl. Phys. B 2001, 72, 761–765. [Google Scholar] [CrossRef]
- Memmolo, P.; Arena, G.; Fatigati, G.; Grilli, M.; Paturzo, M.; Pezzati, L.; Ferraro, P. Automatic Frames Extraction and Visualization From Noisy Fringe Sequences for Data Recovering in a Portable Digital Speckle Pattern Interferometer for NDI. J. Disp. Technol. 2015, 11, 417–422. [Google Scholar] [CrossRef]
- Kang, Y.-J.; Baik, S.-H.; Ryu, W.-J.; Kim, K.-S. Measurement of Shock Waves Using Phase Shifting Pulsed Holographic Interferometer. Opt. Laser Technol. 2003, 35, 323–329. [Google Scholar] [CrossRef]
- Osten, W.; Jueptner, W.P.O.; Mieth, U. Knowledge-Assisted Evaluation of Fringe Patterns for Automatic Fault Detection; Pryputniewicz, R.J., Brown, G.M., Jueptner, W.P.O., Eds.; Springer: San Diego, CA, USA, 1994; pp. 256–268. [Google Scholar]
- Ding, L.; Wan, H.; Lu, Q.; Chen, Z.; Jia, K.; Ge, J.; Yan, X.; Xu, X.; Ma, G.; Chen, X.; et al. Using Deep Learning to Identify the Depth of Metal Surface Defects with Narrowband SAW Signals. Opt. Laser Technol. 2023, 157, 108758. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, W.; Duan, L.; Zhang, H.; Zheng, H.; Xia, X.; Yu, Y.; Poon, T. Automatic Elimination of Phase Aberrations in Digital Holography Based on Gaussian 1σ- Criterion and Histogram Segmentation. Opt. Express 2023, 31, 13627. [Google Scholar] [CrossRef]
- Di, J.; Zhao, J.; Sun, W.; Jiang, H.; Yan, X. Phase Aberration Compensation of Digital Holographic Microscopy Based on Least Squares Surface Fitting. Opt. Commun. 2009, 282, 3873–3877. [Google Scholar] [CrossRef]
- Liu, S.; Xiao, W.; Pan, F. Automatic Compensation of Phase Aberrations in Digital Holographic Microscopy for Living Cells Investigation by Using Spectral Energy Analysis. Opt. Laser Technol. 2014, 57, 169–174. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Z.; Xu, Z.; Han, Y.; Liu, F. Automatic and Accurate Compensation for Phase Aberrations in Digital Holographic Microscopy Based on Iteratively Reweighted Least Squares Fitting. Opt. Laser Technol. 2023, 167, 109704. [Google Scholar] [CrossRef]
- Ren, Z.; Zhao, J.; Lam, E.Y. Automatic Compensation of Phase Aberrations in Digital Holographic Microscopy Based on Sparse Optimization. APL Photonics 2019, 4, 110808. [Google Scholar] [CrossRef]
- Tornari, V.; Tsigarida, A.; Ziampaka, V.; Kousiaki, F.; Kouloumpi, E. Interference Fringe Patterns in Documentation on Works of Art: Application on Structural Diagnosis of a Fresco Painting. Am. J. Art. Des. 2017, 2, 1–15. [Google Scholar] [CrossRef]
- Roye, W.; Crostack, H.-A. Profile- and Deformation-Measurements with High Axial Resolution Using the Acoustical Holography. Nucl. Eng. Des. 1987, 102, 313–317. [Google Scholar] [CrossRef]
- Rippa, M.; Pagliarulo, V.; Lanzillo, A.; Grilli, M.; Fatigati, G.; Rossi, P.; Cennamo, P.; Trojsi, G.; Ferraro, P.; Mormile, P. Active Thermography for Non-Invasive Inspection of an Artwork on Poplar Panel: Novel Approach Using Principal Component Thermography and Absolute Thermal Contrast. J. Nondestruct. Eval. 2021, 40, 21. [Google Scholar] [CrossRef]
- Daffara, C.; Ambrosini, D.; Pezzati, L.; Paoletti, D. Thermal Quasi-Reflectography: A New Imaging Tool in Art Conservation. Opt. Express 2012, 20, 14746. [Google Scholar] [CrossRef]
- Wang, D.; Li, N.-N.; Li, Y.-L.; Zheng, Y.-W.; Nie, Z.-Q.; Li, Z.-S.; Chu, F.; Wang, Q.-H. Large Viewing Angle Holographic 3D Display System Based on Maximum Diffraction Modulation. Light Adv. Manuf. 2023, 4, 1. [Google Scholar] [CrossRef]
- Wang, D.; Li, Z.-S.; Zheng, Y.-W.; Li, N.-N.; Li, Y.-L.; Wang, Q.-H. High-Quality Holographic 3D Display System Based on Virtual Splicing of Spatial Light Modulator. ACS Photonics 2023, 10, 2297–2307. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Zhou, W.; Yu, Y.; Tornari, V.; Artioli, G. Defect Isolation from Whole to Local Field Separation in Complex Interferometry Fringe Patterns through Development of Weighted Least-Squares Algorithm. Digital 2024, 4, 104-113. https://doi.org/10.3390/digital4010004
Chen Z, Zhou W, Yu Y, Tornari V, Artioli G. Defect Isolation from Whole to Local Field Separation in Complex Interferometry Fringe Patterns through Development of Weighted Least-Squares Algorithm. Digital. 2024; 4(1):104-113. https://doi.org/10.3390/digital4010004
Chicago/Turabian StyleChen, Zhenkai, Wenjing Zhou, Yingjie Yu, Vivi Tornari, and Gilberto Artioli. 2024. "Defect Isolation from Whole to Local Field Separation in Complex Interferometry Fringe Patterns through Development of Weighted Least-Squares Algorithm" Digital 4, no. 1: 104-113. https://doi.org/10.3390/digital4010004
APA StyleChen, Z., Zhou, W., Yu, Y., Tornari, V., & Artioli, G. (2024). Defect Isolation from Whole to Local Field Separation in Complex Interferometry Fringe Patterns through Development of Weighted Least-Squares Algorithm. Digital, 4(1), 104-113. https://doi.org/10.3390/digital4010004






