Deep Generative Modeling of Protein Conformations: A Comprehensive Review
Abstract
1. Introduction
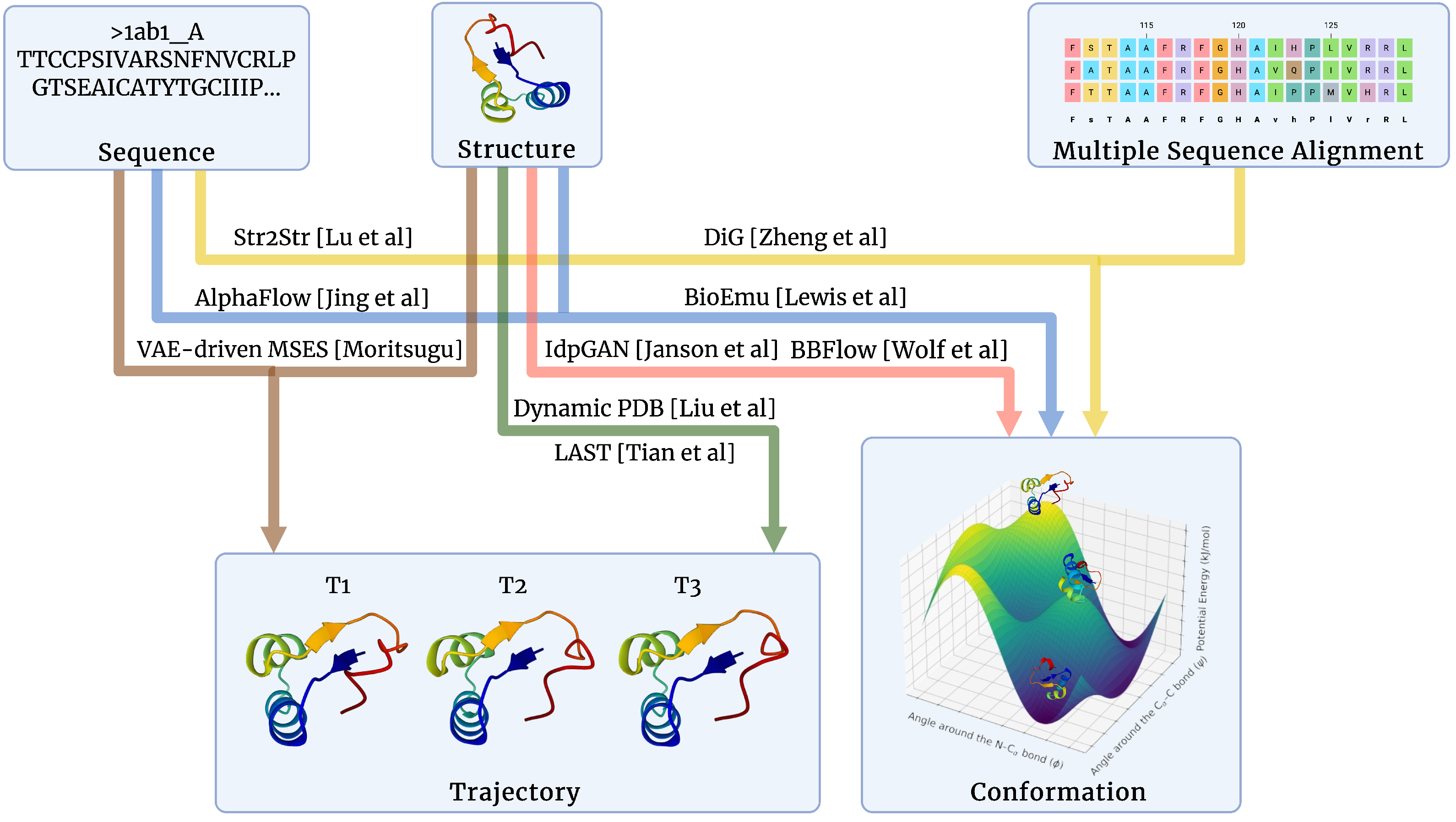
2. Problem Definition
2.1. Protein Conformation Sampling
2.2. Protein Trajectory Generation
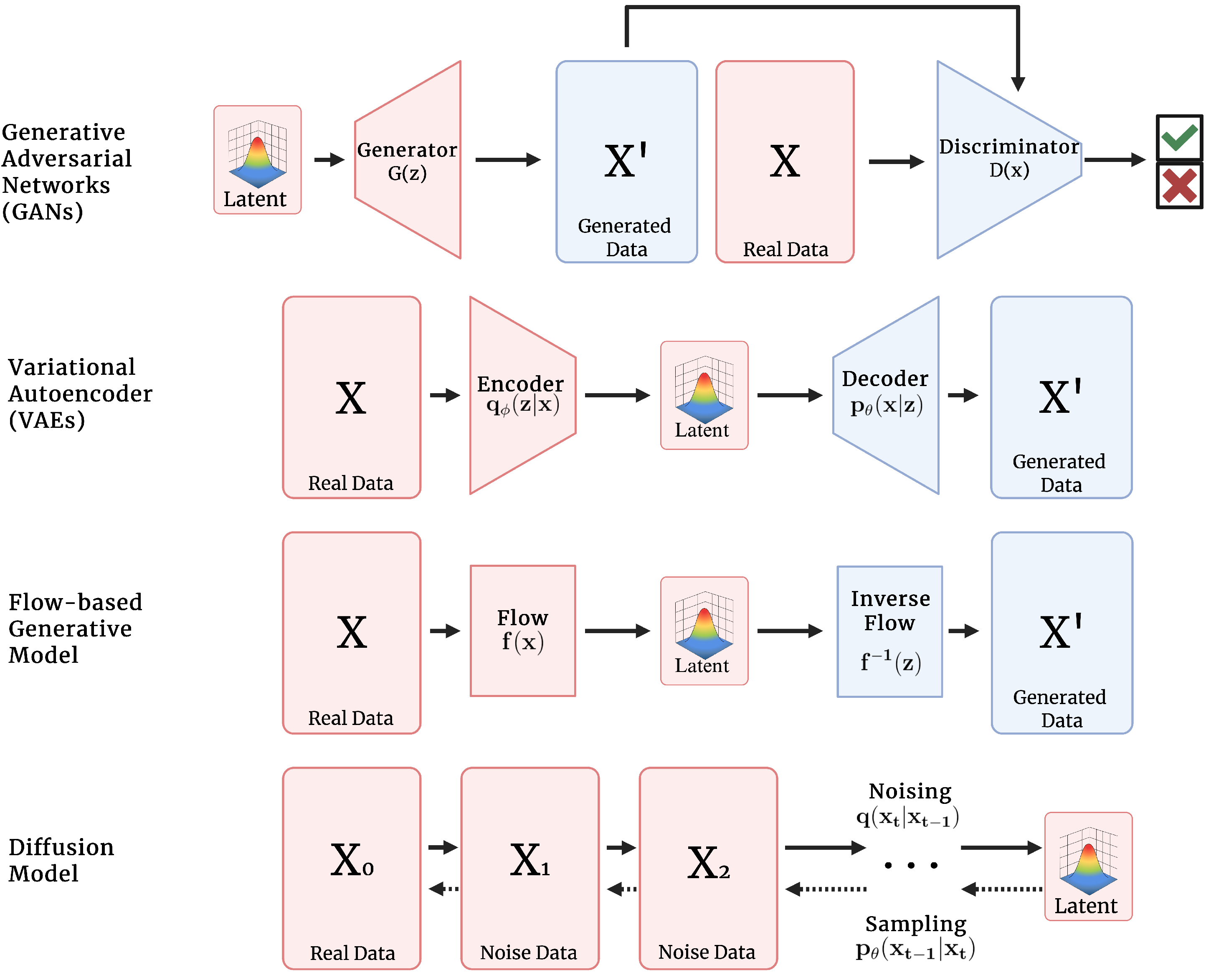
3. Basics of Deep Generative Modeling
3.1. Generative Adversarial Networks
3.2. Variational Autoencoders
3.3. Flow
3.4. Diffusion
4. Taxonomy
4.1. GAN
4.1.1. Application of Generative Adversarial Networks
4.1.2. Discussion
4.2. VAE
4.2.1. Protein Conformation Sampling
4.2.2. Protein Trajectory
4.2.3. Other Applications
4.2.4. Discussion
4.3. Flow
4.3.1. Alphaflow and Its Variants
4.3.2. Integration of Equivariance and Full Atom Modeling
4.3.3. Discussion
4.4. Diffusion
4.4.1. Perturb and Anneal Based Diffusion
4.4.2. Other Approaches
4.4.3. Modeling Instrinsically Disordered Proteins
4.4.4. Discussion
5. Dataset
5.1. Protein Data Bank
5.2. AlphaFold Protein Structure Database
5.3. Atlas of Protein Molecular Dynamics
5.4. Bovine Pancreatic Trypsin Inhibitor
5.5. MEGAScale
5.6. CATH
6. Metrics
7. Future Work
7.1. Challenges
7.1.1. Lack of Interpretability
7.1.2. Simulation of Full-Atom Protein Trajectory
7.1.3. Integration of Other Biomolecules
7.2. Opportunities (See Box 1)
7.2.1. Aligning with Physical Feedback
7.2.2. Textual Representation
7.2.3. Structural Language Models for Conformational Plasticity
7.2.4. Full-Atom End-to-End Structure Generation
7.2.5. Generative Modeling of Peptide Dynamics
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MD | Molecular Dynamics |
| MSA | Multiple Sequence Alignment |
| IDP | Intrinsically Disordered Proteins |
| PDB | Protein Data Bank |
| ADK | Adenosin Kinase |
| VAE | Variational Autoencoder |
| GAN | Generative Adversarial Network |
| MAT-R | Matching Precision |
| MAT-P | Matching Recall |
| RMSD | Root-Mean-Square Deviation |
| RMSF | Root Mean Square Fluctuation |
| Rg | Radius of Gyration |
| SASA | Solvent Accessible Surface Area |
| JS-PwD | Jensen-Shannon divergence of Pair Wise Distributions |
| JS-TIC | Jensen-Shannon divergence of Total Internal Coordinates |
| JS-Rg | Jensen-Shannon divergence of Radius of Gyration |
| TICA | Time-lagged Independent Component Analysis |
Appendix A. Metrics
Appendix A.1. Validity
Appendix A.2. Precision and Accuracy
Appendix A.3. Diversity
Appendix A.4. Distributional Similarity
Appendix A.5. Structural Dynamics and Stability
References
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Schauperl, M.; Denny, R.A. AI-based protein structure prediction in drug discovery: Impacts and challenges. J. Chem. Inf. Model. 2022, 62, 3142–3156. [Google Scholar] [CrossRef]
- Nero, T.L.; Parker, M.W.; Morton, C.J. Protein structure and computational drug discovery. Biochem. Soc. Trans. 2018, 46, 1367–1379. [Google Scholar] [CrossRef] [PubMed]
- Kiss, G.; Çelebi-Ölçüm, N.; Moretti, R.; Baker, D.; Houk, K. Computational enzyme design. Angew. Chem. Int. Ed. 2013, 52, 5700–5725. [Google Scholar] [CrossRef] [PubMed]
- Humphreys, I.R.; Pei, J.; Baek, M.; Krishnakumar, A.; Anishchenko, I.; Ovchinnikov, S.; Zhang, J.; Ness, T.J.; Banjade, S.; Bagde, S.R.; et al. Computed structures of core eukaryotic protein complexes. Science 2021, 374, eabm4805. [Google Scholar] [CrossRef] [PubMed]
- Evans, R.; O’Neill, M.; Pritzel, A.; Antropova, N.; Senior, A.; Green, T.; Žídek, A.; Bates, R.; Blackwell, S.; Yim, J.; et al. Protein complex prediction with AlphaFold-Multimer. bioRxiv 2021. bioRxiv:2021.10.04.463034. [Google Scholar] [CrossRef]
- Varadi, M.; Bertoni, D.; Magana, P.; Paramval, U.; Pidruchna, I.; Radhakrishnan, M.; Tsenkov, M.; Nair, S.; Mirdita, M.; Yeo, J.; et al. AlphaFold Protein Structure Database in 2024: Providing structure coverage for over 214 million protein sequences. Nucleic Acids Res. 2024, 52, D368–D375. [Google Scholar] [CrossRef]
- Bryant, P.; Pozzati, G.; Zhu, W.; Shenoy, A.; Kundrotas, P.; Elofsson, A. Predicting the structure of large protein complexes using AlphaFold and Monte Carlo tree search. Nat. Commun. 2022, 13, 6028. [Google Scholar] [CrossRef]
- Mazhibiyeva, A.; Pham, T.T.; Pats, K.; Lukac, M.; Molnár, F. Bridging prediction and reality: Comprehensive analysis of experimental and AlphaFold 2 full-length nuclear receptor structures. Comput. Struct. Biotechnol. J. 2025, 27, 1998–2013. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, C.; Xu, X.F.; Xu, W.; Liu, S.W. Structural and functional properties of SARS-CoV-2 spike protein: Potential antivirus drug development for COVID-19. Acta Pharmacol. Sin. 2020, 41, 1141–1149. [Google Scholar] [CrossRef]
- Park, H.Y.; Kim, S.A.; Korlach, J.; Rhoades, E.; Kwok, L.W.; Zipfel, W.R.; Waxham, M.N.; Webb, W.W.; Pollack, L. Conformational changes of calmodulin upon Ca2+ binding studied with a microfluidic mixer. Proc. Natl. Acad. Sci. USA 2008, 105, 542–547. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, H.; Soma, N.; Kretsinger, R.H. Molecular Dynamics Study of the Changes in Conformation of Calmodulin with Calcium Binding and/or Target Recognition. Sci. Rep. 2019, 9, 10688. [Google Scholar] [CrossRef]
- Noé, F.; Clementi, C. Collective variables for the study of long-time kinetics from molecular trajectories: Theory and methods. Curr. Opin. Struct. Biol. 2017, 43, 141–147. [Google Scholar] [CrossRef] [PubMed]
- Fiorin, G.; Klein, M.L.; Hénin, J. Using collective variables to drive molecular dynamics simulations. Mol. Phys. 2013, 111, 3345–3362. [Google Scholar] [CrossRef]
- Hayward, S.; Go, N. Collective variable description of native protein dynamics. Annu. Rev. Phys. Chem. 1995, 46, 223–250. [Google Scholar] [CrossRef]
- Sittel, F.; Stock, G. Perspective: Identification of collective variables and metastable states of protein dynamics. J. Chem. Phys. 2018, 149, 150901. [Google Scholar] [CrossRef]
- McCarty, J.; Parrinello, M. A variational conformational dynamics approach to the selection of collective variables in metadynamics. J. Chem. Phys. 2017, 147, 204109. [Google Scholar] [CrossRef]
- Zhu, F.; Hummer, G. Convergence and error estimation in free energy calculations using the weighted histogram analysis method. J. Comput. Chem. 2012, 33, 453–465. [Google Scholar] [CrossRef]
- Sauer, M.A.; Mondal, S.; Neff, B.; Maiti, S.; Heyden, M. Fast Sampling of Protein Conformational Dynamics. arXiv 2024, arXiv:2411.08154. [Google Scholar] [CrossRef]
- Abrams, C.F.; Vanden-Eijnden, E. Large-Scale Conformational Sampling of Proteins Using Temperature-Accelerated Molecular Dynamics. Biophys. J. 2010, 98, 26a. [Google Scholar] [CrossRef]
- Kleiman, D.E.; Nadeem, H.; Shukla, D. Adaptive Sampling Methods for Molecular Dynamics in the Era of Machine Learning. arXiv 2023, arXiv:2307.09664. [Google Scholar] [CrossRef]
- Zwier, M.C.; Chong, L.T. Reaching biological timescales with all-atom molecular dynamics simulations. Curr. Opin. Pharmacol. 2010, 10, 745–752. [Google Scholar] [CrossRef]
- Nocito, D.; Beran, G.J.O. Reduced computational cost of polarizable force fields by a modification of the always stable predictor-corrector. J. Chem. Phys. 2019, 150, 151103. [Google Scholar] [CrossRef]
- Barman, A.; Batiste, B.; Hamelberg, D. Pushing the Limits of a Molecular Mechanics Force Field To Probe Weak CH·π Interactions in Proteins. J. Chem. Theory Comput. 2015, 11, 1854–1863. [Google Scholar] [CrossRef]
- Fogel, D.; Fogel, L.; Atmar, J. Meta-evolutionary programming. In Proceedings of the [1991] Conference Record of the Twenty-Fifth Asilomar Conference on Signals, Systems & Computers, Pacific Grove, CA, USA, 4–6 November 1991; pp. 540–545. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence, 1st ed.; Complex Adaptive Systems; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Boumedine, N.; Bouroubi, S. A new hybrid genetic algorithm for protein structure prediction on the 2D triangular lattice. arXiv 2019, arXiv:1907.04190. [Google Scholar] [CrossRef]
- Geng, X.; Guan, J.; Dong, Q.; Zhou, S. An improved genetic algorithm for statistical potential function design and protein structure prediction. Int. J. Data Min. Bioinform. 2012, 6, 162. [Google Scholar] [CrossRef] [PubMed]
- Supady, A.; Blum, V.; Baldauf, C. First-principles molecular structure search with a genetic algorithm. arXiv 2015, arXiv:1505.02521. [Google Scholar] [CrossRef] [PubMed]
- Comte, P.; Vassiliev, S.; Houghten, S.; Bruce, D. Genetic algorithm with alternating selection pressure for protein side-chain packing and pK(a) prediction. Biosystems 2011, 105, 263–270. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Liu, H. Genetic algorithms for protein conformation sampling and optimization in a discrete backbone dihedral angle space. J. Comput. Chem. 2006, 27, 1593–1602. [Google Scholar] [CrossRef]
- Khimasia, M.M.; Coveney, P.V. Protein structure prediction as a hard optimization problem: The genetic algorithm approach. arXiv 1997, arXiv:PHYSICS/9708012. [Google Scholar] [CrossRef][Green Version]
- Zaman, A.B.; Inan, T.T.; De Jong, K.; Shehu, A. Adaptive Stochastic Optimization to Improve Protein Conformation Sampling. IEEE/ACM Trans. Comput. Biol. Bioinform. 2023, 20, 2759–2771. [Google Scholar] [CrossRef]
- Chen, Y.; He, J. Average convergence rate of evolutionary algorithms in continuous optimization. Inf. Sci. 2021, 562, 200–219. [Google Scholar] [CrossRef]
- Saleh, S.; Olson, B.; Shehu, A. A population-based evolutionary search approach to the multiple minima problem in de novo protein structure prediction. BMC Struct. Biol. 2013, 13, S4. [Google Scholar] [CrossRef] [PubMed]
- Abramson, J.; Adler, J.; Dunger, J.; Evans, R.; Green, T.; Pritzel, A.; Ronneberger, O.; Willmore, L.; Ballard, A.J.; Bambrick, J.; et al. Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature 2024, 630, 493–500. [Google Scholar] [CrossRef]
- Lin, Z.; Akin, H.; Rao, R.; Hie, B.; Zhu, Z.; Lu, W.; Smetanin, N.; Verkuil, R.; Kabeli, O.; Shmueli, Y.; et al. Evolutionary-scale prediction of atomic-level protein structure with a language model. Science 2023, 379, 1123–1130. [Google Scholar] [CrossRef] [PubMed]
- Sala, D.; Engelberger, F.; Mchaourab, H.; Meiler, J. Modeling conformational states of proteins with AlphaFold. Curr. Opin. Struct. Biol. 2023, 81, 102645. [Google Scholar] [CrossRef] [PubMed]
- Del Alamo, D.; Sala, D.; Mchaourab, H.S.; Meiler, J. Sampling alternative conformational states of transporters and receptors with AlphaFold2. eLife 2022, 11, e75751. [Google Scholar] [CrossRef]
- Barethiya, S.; Huang, J.; Chen, J. Predicting protein conformational ensembles using deep generative models. Biophys. J. 2024, 123, 549a. [Google Scholar] [CrossRef]
- Erdos, G.; Dosztanyi, Z. Deep learning for intrinsically disordered proteins: From improved predictions to deciphering conformational ensembles. Curr. Opin. Struct. Biol. 2024, 89, 102950. [Google Scholar] [CrossRef]
- Ovchinnikov, S.; Huang, P.S. Structure-based protein design with deep learning. Curr. Opin. Chem. Biol. 2021, 65, 136–144. [Google Scholar] [CrossRef]
- Notin, P.; Rollins, N.; Gal, Y.; Sander, C.; Marks, D. Machine learning for functional protein design. Nat. Biotechnol. 2024, 42, 216–228. [Google Scholar] [CrossRef] [PubMed]
- Karplus, M.; McCammon, J.A. Molecular dynamics simulations of biomolecules. Nat. Struct. Biol. 2002, 9, 646–652. [Google Scholar] [CrossRef]
- Dror, R.O.; Dirks, R.M.; Grossman, J.; Xu, H.; Shaw, D.E. Biomolecular Simulation: A Computational Microscope for Molecular Biology. Annu. Rev. Biophys. 2012, 41, 429–452. [Google Scholar] [CrossRef]
- Janson, G.; Valdes-Garcia, G.; Heo, L.; Feig, M. Direct generation of protein conformational ensembles via machine learning. Nat. Commun. 2023, 14, 774. [Google Scholar] [CrossRef]
- Xie, X.; Valiente, P.A.; Kim, P.M. HelixGAN a deep-learning methodology for conditional de novo design of α-helix structures. Bioinformatics 2023, 39, btad036. [Google Scholar] [CrossRef]
- Kingma, D.P.; Dhariwal, P. Glow: Generative Flow with Invertible 1x1 Convolutions. arXiv 2018, arXiv:1807.03039. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Zhu, J.J.; Zhang, N.J.; Wei, T.; Chen, H.F. Enhancing Conformational Sampling for Intrinsically Disordered and Ordered Proteins by Variational Autoencoder. Int. J. Mol. Sci. 2023, 24, 6896. [Google Scholar] [CrossRef]
- Tian, H.; Jiang, X.; Xiao, S.; La Force, H.; Larson, E.C.; Tao, P. LAST: Latent Space-Assisted Adaptive Sampling for Protein Trajectories. J. Chem. Inf. Model. 2023, 63, 67–75. [Google Scholar] [CrossRef]
- Dinh, L.; Sohl-Dickstein, J.; Bengio, S. Density estimation using Real NVP. arXiv 2017, arXiv:1605.08803. [Google Scholar] [CrossRef]
- Dinh, L.; Krueger, D.; Bengio, Y. NICE: Non-linear Independent Components Estimation. arXiv 2015, arXiv:1410.8516. [Google Scholar] [CrossRef]
- Lipman, Y.; Chen, R.T.Q.; Ben-Hamu, H.; Nickel, M.; Le, M. Flow Matching for Generative Modeling. arXiv 2023, arXiv:2210.02747. [Google Scholar] [CrossRef]
- Jin, Y.; Huang, Q.; Song, Z.; Zheng, M.; Teng, D.; Shi, Q. P2DFlow: A Protein Ensemble Generative Model with SE(3) Flow Matching. J. Chem. Theory Comput. 2025, 21, 3288–3296. [Google Scholar] [CrossRef]
- Jing, B.; Berger, B.; Jaakkola, T. AlphaFold Meets Flow Matching for Generating Protein Ensembles. arXiv 2024, arXiv:2402.04845. [Google Scholar] [CrossRef]
- Lewis, S.; Hempel, T.; Jiménez Luna, J.; Gastegger, M.; Xie, Y.; Foong, A.Y.K.; García Satorras, V.; Abdin, O.; Veeling, B.S.; Zaporozhets, I.; et al. Scalable emulation of protein equilibrium ensembles with generative deep learning. bioRxiv 2024. bioRxiv 2024.12.05.626885. [Google Scholar] [CrossRef]
- Lu, J.; Zhong, B.; Zhang, Z.; Tang, J. Str2Str: A Score-based Framework for Zero-shot Protein Conformation Sampling. arXiv 2023, arXiv:2306.03117. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Shen, Y.; Wang, Y.; Yuan, H.; Wu, Y.; Gu, Q. Protein Conformation Generation via Force-Guided SE(3) Diffusion Models. arXiv 2024, arXiv:2403.14088. [Google Scholar] [CrossRef]
- Pang, Y.T.; Yang, L.; Gumbart, J.C. From static to dynamic: Rapid mapping of protein conformational transitions using DeepPath. Biophys. J. 2024, 123, 45a. [Google Scholar] [CrossRef]
- Xian, R.; Rauscher, S. Current Topics, Methods, and Challenges in the Modelling of Intrinsically Disordered Protein Dynamics. arXiv 2022, arXiv:2211.06020. [Google Scholar] [CrossRef]
- Liu, Y.; Amzel, L.M. Conformation Clustering of Long MD Protein Dynamics with an Adversarial Autoencoder. arXiv 2018, arXiv:1805.12313. [Google Scholar] [CrossRef]
- Bouvier, B. Substituted Oligosaccharides as Protein Mimics: Deep Learning Free Energy Landscapes. J. Chem. Inf. Model. 2024, 64, 2195–2204. [Google Scholar] [CrossRef] [PubMed]
- Mescheder, L.; Geiger, A.; Nowozin, S. Which Training Methods for GANs do actually Converge? arXiv 2018, arXiv:1801.04406. [Google Scholar] [CrossRef]
- Salimans, T.; Goodfellow, I.; Zaremba, W.; Cheung, V.; Radford, A.; Chen, X. Improved Techniques for Training GANs. arXiv 2016, arXiv:1606.03498. [Google Scholar] [CrossRef]
- Durall, R.; Chatzimichailidis, A.; Labus, P.; Keuper, J. Combating Mode Collapse in GAN training: An Empirical Analysis using Hessian Eigenvalues. arXiv 2020, arXiv:2012.09673. [Google Scholar] [CrossRef]
- Mansoor, S.; Baek, M.; Park, H.; Lee, G.R.; Baker, D. Protein Ensemble Generation Through Variational Autoencoder Latent Space Sampling. J. Chem. Theory Comput. 2024, 20, 2689–2695. [Google Scholar] [CrossRef]
- Krishna, R.; Wang, J.; Ahern, W.; Sturmfels, P.; Venkatesh, P.; Kalvet, I.; Lee, G.R.; Morey-Burrows, F.S.; Anishchenko, I.; Humphreys, I.R.; et al. Generalized biomolecular modeling and design with RoseTTAFold All-Atom. Science 2024, 384, eadl2528. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Guan, X.; Zhang, X.; Luan, X.; Song, Z.; Cheng, X.; Zhang, W.; Qin, J.J. Targeting KRAS mutant cancers: From druggable therapy to drug resistance. Mol. Cancer 2022, 21, 159. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Guo, Z.; Wang, F.; Fu, L. KRAS mutation: From undruggable to druggable in cancer. Signal Transduct. Target. Ther. 2021, 6, 386. [Google Scholar] [CrossRef]
- Tian, H.; Jiang, X.; Trozzi, F.; Xiao, S.; Larson, E.C.; Tao, P. Explore Protein Conformational Space With Variational Autoencoder. Front. Mol. Biosci. 2021, 8, 781635. [Google Scholar] [CrossRef]
- Xiao, S.; Song, Z.; Tian, H.; Tao, P. Assessments of Variational Autoencoder in Protein Conformation Exploration. J. Comput. Biophys. Chem. 2023, 22, 489–501. [Google Scholar] [CrossRef]
- Ruzmetov, T.; Hung, T.I.; Jonnalagedda, S.P.; Chen, S.h.; Fasihianifard, P.; Guo, Z.; Bhanu, B.; Chang, C.e.A. Sampling Conformational Ensembles of Highly Dynamic Proteins via Generative Deep Learning. J. Chem. Inf. Model. 2025, 65, 2487–2502. [Google Scholar] [CrossRef]
- Afrasiabi, F.; Dehghanpoor, R.; Haspel, N. Using Autoencoders to Explore the Conformational Space of the Cdc42 Protein. In Computational Structural Bioinformatics; Communications in Computer and Information Science; Haspel, N., Molloy, K., Eds.; Springer Nature Switzerland: Cham, Switzerland, 2025; Volume 2396, pp. 45–57. [Google Scholar] [CrossRef]
- Degiacomi, M.T. Coupling Molecular Dynamics and Deep Learning to Mine Protein Conformational Space. Structure 2019, 27, 1034–1040.e3. [Google Scholar] [CrossRef]
- Jin, Y.; Johannissen, L.O.; Hay, S. Predicting new protein conformations from molecular dynamics simulation conformational landscapes and machine learning. Proteins: Struct. Funct. Bioinform. 2021, 89, 915–921. [Google Scholar] [CrossRef]
- Gupta, A.; Dey, S.; Zhou, H.X. Artificial Intelligence Guided Conformational Mining of Intrinsically Disordered Proteins. bioRxiv 2021. bioRxiv 2021.11.21.469457. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Shaw, D.E. How Fast-Folding Proteins Fold. Science 2011, 334, 517–520. [Google Scholar] [CrossRef]
- Laio, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef]
- Bernardi, R.C.; Melo, M.C.; Schulten, K. Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Biophys. Acta (BBA)—Subj. 2015, 1850, 872–877. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.D.; Noé, F. Markov state models of biomolecular conformational dynamics. Curr. Opin. Struct. Biol. 2014, 25, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Harada, R.; Shigeta, Y. Efficient Conformational Search Based on Structural Dissimilarity Sampling: Applications for Reproducing Structural Transitions of Proteins. J. Chem. Theory Comput. 2017, 13, 1411–1423. [Google Scholar] [CrossRef]
- Hamelberg, D.; Mongan, J.; McCammon, J.A. Accelerated molecular dynamics: A promising and efficient simulation method for biomolecules. J. Chem. Phys. 2004, 120, 11919–11929. [Google Scholar] [CrossRef] [PubMed]
- Moritsugu, K. Multiscale Enhanced Sampling Using Machine Learning. Life 2021, 11, 1076. [Google Scholar] [CrossRef] [PubMed]
- Koike, R.; Ota, M.; Kidera, A. Hierarchical Description and Extensive Classification of Protein Structural Changes by Motion Tree. J. Mol. Biol. 2014, 426, 752–762. [Google Scholar] [CrossRef]
- Kleiman, D.E.; Shukla, D. Active learning of Conformational ensemble of Proteins. J. Chem. Theory Comput. 2023, 19, 4377–4388. [Google Scholar] [CrossRef] [PubMed]
- Bozkurt Varolgüneş, Y.; Bereau, T.; Rudzinski, J.F. Interpretable embeddings from molecular simulations using Gaussian mixture variational autoencoders. Mach. Learn. Sci. Technol. 2020, 1, 015012. [Google Scholar] [CrossRef]
- Albu, A.I. Towards learning transferable embeddings for protein conformations using Variational Autoencoders. Procedia Comput. Sci. 2021, 192, 10–19. [Google Scholar] [CrossRef]
- Pandini, A.; Fornili, A.; Kleinjung, J. Structural alphabets derived from attractors in conformational space. BMC Bioinform. 2010, 11, 97. [Google Scholar] [CrossRef]
- Ward, M.D.; Zimmerman, M.I.; Meller, A.; Chung, M.; Swamidass, S.J.; Bowman, G.R. Deep learning the structural determinants of protein biochemical properties by comparing structural ensembles with DiffNets. Nat. Commun. 2021, 12, 3023. [Google Scholar] [CrossRef] [PubMed]
- Bandyopadhyay, S.; Mondal, J. A deep autoencoder framework for discovery of metastable ensembles in biomacromolecules. J. Chem. Phys. 2021, 155, 114106. [Google Scholar] [CrossRef]
- Macenski, S.; Singh, S.; Martin, F.; Gines, J. Regulated Pure Pursuit for Robot Path Tracking. arXiv 2023, arXiv:2305.20026. [Google Scholar] [CrossRef]
- Datta, D.; Lee, E.S. Exploring Thermal Transport in Electrochemical Energy Storage Systems Utilizing Two-Dimensional Materials: Prospects and Hurdles. arXiv 2023, arXiv:2310.08592. [Google Scholar] [CrossRef]
- Mahmoud, A.H.; Masters, M.; Lee, S.J.; Lill, M.A. Accurate Sampling of Macromolecular Conformations Using Adaptive Deep Learning and Coarse-Grained Representation. J. Chem. Inf. Model. 2022, 62, 1602–1617. [Google Scholar] [CrossRef]
- Burley, S.K.; Berman, H.M.; Kleywegt, G.J.; Markley, J.L.; Nakamura, H.; Velankar, S. Protein Data Bank (PDB): The single global macromolecular structure archive. In Protein Crystallography: Methods and Protocols; Humana Press: New York, NY, USA, 2017; pp. 627–641. [Google Scholar]
- Vander Meersche, Y.; Cretin, G.; Gheeraert, A.; Gelly, J.C.; Galochkina, T. ATLAS: Protein flexibility description from atomistic molecular dynamics simulations. Nucleic Acids Res. 2024, 52, D384–D392. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, M.; Wang, Y.; He, X.; Zheng, N.; Zhang, J.; Heng, P.A. Improving AlphaFlow for Efficient Protein Ensembles Generation. arXiv 2024, arXiv:2407.12053. [Google Scholar] [CrossRef]
- Wolf, N.; Seute, L.; Viliuga, V.; Wagner, S.; Stühmer, J.; Gräter, F. Learning conformational ensembles of proteins based on backbone geometry. arXiv 2024, arXiv:2503.05738. [Google Scholar] [CrossRef]
- Rives, A.; Meier, J.; Sercu, T.; Goyal, S.; Lin, Z.; Liu, J.; Guo, D.; Ott, M.; Zitnick, C.L.; Ma, J.; et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proc. Natl. Acad. Sci. USA 2021, 118, e2016239118. [Google Scholar] [CrossRef]
- Satorras, V.G.; Hoogeboom, E.; Welling, M. E(n) Equivariant Graph Neural Networks. arXiv 2021, arXiv:2102.09844. [Google Scholar] [CrossRef]
- Klein, F.; Soñora, M.; Helene Santos, L.; Nazareno Frigini, E.; Ballesteros-Casallas, A.; Rodrigo Machado, M.; Pantano, S. The SIRAH force field: A suite for simulations of complex biological systems at the coarse-grained and multiscale levels. J. Struct. Biol. 2023, 215, 107985. [Google Scholar] [CrossRef]
- He, L.; Chen, Y.; Dong, Y.; Wang, Y.; Lin, Z. Efficient equivariant network. Adv. Neural Inf. Process. Syst. 2021, 34, 5290–5302. [Google Scholar]
- Brehmer, J.; Behrends, S.; de Haan, P.; Cohen, T. Does equivariance matter at scale? arXiv 2024, arXiv:2410.23179. [Google Scholar] [CrossRef]
- Pozdnyakov, S.N.; Ceriotti, M. Smooth, exact rotational symmetrization for deep learning on point clouds. arXiv 2023, arXiv:2305.19302. [Google Scholar] [CrossRef]
- Wang, Y.; Elhag, A.A.; Jaitly, N.; Susskind, J.M.; Bautista, M.A. Swallowing the Bitter Pill: Simplified Scalable Conformer Generation. arXiv 2024, arXiv:2311.17932. [Google Scholar] [CrossRef]
- Gruver, N.; Stanton, S.; Frey, N.C.; Rudner, T.G.J.; Hotzel, I.; Lafrance-Vanasse, J.; Rajpal, A.; Cho, K.; Wilson, A.G. Protein Design with Guided Discrete Diffusion. arXiv 2023, arXiv:2305.20009. [Google Scholar] [CrossRef]
- Li, W.r.; Cadet, X.F.; Medina-Ortiz, D.; Davari, M.D.; Sowdhamini, R.; Damour, C.; Li, Y.; Miranville, A.; Cadet, F. From thermodynamics to protein design: Diffusion models for biomolecule generation towards autonomous protein engineering. arXiv 2025, arXiv:2501.02680. [Google Scholar] [CrossRef]
- Zhao, L.; He, Q.; Song, H.; Zhou, T.; Luo, A.; Wen, Z.; Wang, T.; Lin, X. Protein A-like Peptide Design Based on Diffusion and ESM2 Models. Molecules 2024, 29, 4965. [Google Scholar] [CrossRef]
- Nakata, S.; Mori, Y.; Tanaka, S. End-to-end protein–ligand complex structure generation with diffusion-based generative models. BMC Bioinform. 2023, 24, 233. [Google Scholar] [CrossRef] [PubMed]
- Cao, D.; Chen, M.; Zhang, R.; Wang, Z.; Huang, M.; Yu, J.; Jiang, X.; Fan, Z.; Zhang, W.; Zhou, H.; et al. SurfDock is a surface-informed diffusion generative model for reliable and accurate protein–ligand complex prediction. Nat. Methods 2025, 22, 310–322. [Google Scholar] [CrossRef] [PubMed]
- Yim, J.; Stärk, H.; Corso, G.; Jing, B.; Barzilay, R.; Jaakkola, T.S. Diffusion models in protein structure and docking. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2024, 14, e1711. [Google Scholar] [CrossRef]
- Wu, K.E.; Yang, K.K.; Van Den Berg, R.; Alamdari, S.; Zou, J.Y.; Lu, A.X.; Amini, A.P. Protein structure generation via folding diffusion. Nat. Commun. 2024, 15, 1059. [Google Scholar] [CrossRef]
- Anand, N.; Achim, T. Protein Structure and Sequence Generation with Equivariant Denoising Diffusion Probabilistic Models. arXiv 2022, arXiv:2205.15019. [Google Scholar] [CrossRef]
- Jing, B.; Erives, E.; Pao-Huang, P.; Corso, G.; Berger, B.; Jaakkola, T. EigenFold: Generative Protein Structure Prediction with Diffusion Models. arXiv 2023, arXiv:2304.02198. [Google Scholar] [CrossRef]
- Fan, J.; Li, Z.; Alcaide, E.; Ke, G.; Huang, H.; E, W. Accurate Conformation Sampling via Protein Structural Diffusion. J. Chem. Inf. Model. 2024, 64, 8414–8426. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Cai, Z.; Wang, Y.; Kuang, H.; Cheng, K.; Zhang, L.; Su, Q.; Tang, Y.; Cao, F.; et al. Dynamic PDB: A New Dataset and a SE(3) Model Extension by Integrating Dynamic Behaviors and Physical Properties in Protein Structures. arXiv 2024, arXiv:2408.12413. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, Z.; Lindsay, R.J.; Lin, G.; Chen, M.; Sahoo, A.; Hanson, S.M. ExEnDiff: An Experiment-guided Diffusion model for protein conformational Ensemble generation. bioRxiv 2024. bioRxiv 2024.10.04.616517. [Google Scholar] [CrossRef]
- Lu, J.; Zhang, Z.; Zhong, B.; Shi, C.; Tang, J. Fusing Neural and Physical: Augment Protein Conformation Sampling with Tractable Simulations. arXiv 2024, arXiv:2402.10433. [Google Scholar] [CrossRef]
- Zheng, S.; He, J.; Liu, C.; Shi, Y.; Lu, Z.; Feng, W.; Ju, F.; Wang, J.; Zhu, J.; Min, Y.; et al. Predicting equilibrium distributions for molecular systems with deep learning. Nat. Mach. Intell. 2024, 6, 558–567. [Google Scholar] [CrossRef]
- Huang, X.; Pearce, R.; Zhang, Y. FASPR: An open-source tool for fast and accurate protein side-chain packing. Bioinformatics 2020, 36, 3758–3765. [Google Scholar] [CrossRef]
- Argaman, N.; Makov, G. Density functional theory: An introduction. Am. J. Phys. 2000, 68, 69–79. [Google Scholar] [CrossRef]
- Tsuboyama, K.; Dauparas, J.; Chen, J.; Laine, E.; Mohseni Behbahani, Y.; Weinstein, J.J.; Mangan, N.M.; Ovchinnikov, S.; Rocklin, G.J. Mega-scale experimental analysis of protein folding stability in biology and design. Nature 2023, 620, 434–444. [Google Scholar] [CrossRef]
- Tang, Y.; Yu, M.; Bai, G.; Li, X.; Xu, Y.; Ma, B. Deep learning of protein energy landscape and conformational dynamics from experimental structures in PDB. bioRxiv 2024. bioRxiv 2024.06.27.600251. [Google Scholar] [CrossRef]
- Watson, J.L.; Juergens, D.; Bennett, N.R.; Trippe, B.L.; Yim, J.; Eisenach, H.E.; Ahern, W.; Borst, A.J.; Ragotte, R.J.; Milles, L.F.; et al. De novo design of protein structure and function with RFdiffusion. Nature 2023, 620, 1089–1100. [Google Scholar] [CrossRef]
- Maddipatla, A.; Sellam, N.B.; Bojan, M.; Vedula, S.; Schanda, P.; Marx, A.; Bronstein, A.M. Inverse problems with experiment-guided AlphaFold. arXiv 2025, arXiv:2502.09372. [Google Scholar] [CrossRef]
- Hu, Y.; Cheng, K.; He, L.; Zhang, X.; Jiang, B.; Jiang, L.; Li, C.; Wang, G.; Yang, Y.; Liu, M. NMR-Based Methods for Protein Analysis. Anal. Chem. 2021, 93, 1866–1879. [Google Scholar] [CrossRef]
- Zhu, J.; Li, Z.; Zhang, B.; Zheng, Z.; Zhong, B.; Bai, J.; Hong, X.; Wang, T.; Wei, T.; Yang, J.; et al. Precise Generation of Conformational Ensembles for Intrinsically Disordered Proteins via Fine-tuned Diffusion Models. bioRxiv 2024. bioRxiv 2024.05.05.592611. [Google Scholar] [CrossRef]
- Piovesan, D.; Monzon, A.M.; Tosatto, S.C.E. Intrinsic protein disorder and conditional folding in AlphaFoldDB. Protein Sci. 2022, 31, e4466. [Google Scholar] [CrossRef]
- Ruff, K.M.; Pappu, R.V. AlphaFold and Implications for Intrinsically Disordered Proteins. J. Mol. Biol. 2021, 433, 167208. [Google Scholar] [CrossRef] [PubMed]
- Taneja, I.; Lasker, K. Machine-learning-based methods to generate conformational ensembles of disordered proteins. Biophys. J. 2024, 123, 101–113. [Google Scholar] [CrossRef]
- Ho, J.; Jain, A.; Abbeel, P. Denoising diffusion probabilistic models. Adv. Neural Inf. Process. Syst. 2020, 33, 6840–6851. [Google Scholar]
- Janson, G.; Feig, M. Transferable deep generative modeling of intrinsically disordered protein conformations. PLoS Comput. Biol. 2024, 20, e1012144. [Google Scholar] [CrossRef]
- Hoffman, M. Straightening Out the Protein Folding Puzzle: A newpaper suggests an old model is wrong—and the subject is too hot for protein chemists to touch. Science 1991, 253, 1357–1358. [Google Scholar] [CrossRef] [PubMed]
- Sillitoe, I.; Bordin, N.; Dawson, N.; Waman, V.P.; Ashford, P.; Scholes, H.M.; Pang, C.S.M.; Woodridge, L.; Rauer, C.; Sen, N.; et al. CATH: Increased structural coverage of functional space. Nucleic Acids Res. 2021, 49, D266–D273. [Google Scholar] [CrossRef] [PubMed]
- Cheng, K.; Liu, C.; Su, Q.; Wang, J.; Zhang, L.; Tang, Y.; Yao, Y.; Zhu, S.; Qi, Y. AlphaFolding: 4D Diffusion for Dynamic Protein Structure Prediction with Reference and Motion Guidance. arXiv 2024, arXiv:2408.12419. [Google Scholar] [CrossRef]
- Wu, F.; Li, S.Z. DiffMD: A Geometric Diffusion Model for Molecular Dynamics Simulations. Proc. AAAI Conf. Artif. Intell. 2023, 37, 5321–5329. [Google Scholar] [CrossRef]
- Wang, B.; Wang, C.; Chen, J.; Liu, D.; Sun, C.; Zhang, J.; Zhang, K.; Li, H. Conditional Diffusion with Locality-Aware Modal Alignment for Generating Diverse Protein Conformational Ensembles. bioRxiv 2025. bioRxiv 2025.02.21.639488. [Google Scholar] [CrossRef]
- Xu, M.; Yu, L.; Song, Y.; Shi, C.; Ermon, S.; Tang, J. GeoDiff: A Geometric Diffusion Model for Molecular Conformation Generation. arXiv 2022, arXiv:2203.02923. [Google Scholar] [CrossRef]
- Jing, B.; Stärk, H.; Jaakkola, T.; Berger, B. Generative Modeling of Molecular Dynamics Trajectories. arXiv 2024, arXiv:2409.17808. [Google Scholar] [CrossRef]
- Lu, J.; Chen, X.; Lu, S.Z.; Lozano, A.; Chenthamarakshan, V.; Das, P.; Tang, J. Aligning Protein Conformation Ensemble Generation with Physical Feedback. arXiv 2025, arXiv:2505.24203. [Google Scholar] [CrossRef]
- Simon, E.; Zou, J. InterPLM: Discovering Interpretable Features in Protein Language Models via Sparse Autoencoders. bioRxiv 2024. bioRxiv 2024.11.14.623630. [Google Scholar] [CrossRef]
- Schwing, G.; Palese, L.L.; Fernández, A.; Schwiebert, L.; Gatti, D.L. Molecular dynamics without molecules: Searching the conformational space of proteins with generative neural networks. arXiv 2022, arXiv:2206.04683. [Google Scholar] [CrossRef]
- Lu, J.; Chen, X.; Lu, S.Z.; Shi, C.; Guo, H.; Bengio, Y.; Tang, J. Structure Language Models for Protein Conformation Generation. arXiv 2025, arXiv:2410.18403. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, L.; Liu, H. Diffusion in a quantized vector space generates non-idealized protein structures and predicts conformational distributions. bioRxiv 2023. bioRxiv 2023.11.18.567666. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
| Paper | Input | Output | Gran. | MSA | Equiv. | Metric | Dataset |
|---|---|---|---|---|---|---|---|
| Bandyopadhyay et al. [91] | Pairwise C distances | Latent space repr. | Residue-level (–) representation | No | No | VAMP-2 score, Chapman–Kolmogorov (CK) test | 200 MD traj (30–100 ns) |
| Gupta et al. [77] | Heavy-atom Cartesian coords | Reconstruct coords | Heavy-atom level | No | No | RMSD, Experimental data | Q15, A40, ChiZ (1–3.5 s) |
| Xiao et al. [72] | Normalize heavy-atom coords | Reconstruct + 3D confs | Heavy-atom level | No | No | Correlation coefficient, RMSD | Calmodulin, -lactamase, Ubiquitin MD |
| Degiacomi et al. [75] | Heavy-atom Cartesian coords | Reconstruct coords | Backbone, C atoms | No | No | RMSD | MurD open/closed MD |
| Ward et al. [90] | Heavy-atom Cartesian coords | Reconstruct coords | Heavy-atom level | No | No | RMSD, ROC–AUC, Correlation | TEM -lactamase, HIV-1 capsomer MD |
| Tian et al. [51] | Normalize heavy-atom coords | 2D latent embeddings | Heavy-atom level | No | No | RMSD, Sampling efficiency | 100–200 ps MD (NVT/NPT) |
| Jin et al. [76] | Selected atom coords (snapshots) | New conformation coords | Heavy-atom level | No | No | RMSD | L-Ala, Calmodulin (20 ns MD) |
| Mansoor et al. [67] | 2D RoseTTAFold templates | 2D → 3D structures | Backbone, C atoms | Yes | No | RMSD, CCE | K Ras (10 ns MD) |
| Ruzmetov et al. [73] | BAT vector representation | All-atom conformation | All-atom | No | Yes | RMSD, Rg | Amyloid- (1 s MD) |
| Paper | Input | Output | Gran. | MSA | Equiv. | Metric | Dataset |
|---|---|---|---|---|---|---|---|
| Mahmoud et al. [94] | Coarse-grained protein structures | Full atom protein conformations | All-atom | No | Yes | Dihedral distributions, TICA | MD of Bromodomain and Chignolin |
| Jing et al. [56] | Protein sequence | Protein backbone conformation | Backbone | Yes | No | lDDT-C | PDB [95], ATLAS [96] |
| Li et al. [97] | Protein sequence + MSA | Protein backbone conformation | All-atom | No | No | RMSD, RMSF, DCCM correlation | ATLAS [96] |
| Wolf et al. [98] | Equilibrium backbone structure | Protein backbone conformation | Backbone | No | Yes | RMSD, RMSF, PCA W2 | ATLAS [96] |
| Jin et al. [55] | Protein sequence + Approx. energy | Protein backbone conformation | Backbone | No | Yes | RMSF, RMWD, Rg, PWD | ATLAS [96] |
| Paper | Input | Output | Gran. | MSA | Equiv. | Metric | Dataset |
|---|---|---|---|---|---|---|---|
| Fan et al. [115] | Protein sequence and MSA | 3D protein conformation | All-atom | Yes | Yes | MAT-R, MAT-P, TM-score | All PDB structures before 30 April 2022 |
| Liu et al. [116] | Protein sequence | MD trajectory | All-atom | No | Yes | RMSD, RMSF, MAE | Dynamic PDB |
| Liu et al. [117] | Protein sequence and Experimental data | Protein conformational ensemble | Backbone | No | Yes | Rg, SASA | Ground truth generated via MD |
| Lu et al. [118] | Protein sequence | Protein backbone conformations | Backbone | No | Yes | JS-PwD, JS-TIC, JS-Rg | PDB |
| Wang et al. [59] | Protein sequence | Backbone conformation ensemble | Backbone | No | Yes | RMSD, RMSF, Val-C | PDB |
| Lu et al. [58] | A starting structure of a target Protein sequence | All-atom protein conformations | All-atom | No | Yes | Val-Clash, RMSD, TICA, Rg | PDB |
| Zheng et al. [119] | CG protein representation | Protein conformation | All-atom | No | Yes | RMSD, TICA | MD data and force field |
| Lewis et al. [57] | Protein Sequence | Protein backbone conformations | Backbone | Yes | Yes | RMSD, Free-energy agreement | PDB+ MD+ NMR data |
| Metric Category | Score Name | Definition and References |
|---|---|---|
| Validity | Val-Clash | Validation metric for bond lengths/angles; [118] |
| Steric-clash | Fraction of structures free from Cα clashes [58] | |
| Ramachandran Plot Score | Measures fraction of backbone angles within allowed regions [55,116] | |
| Contact-map Frequency | Frequency of residue pairs maintained within contact threshold across conformations [116] | |
| Sanity-check Pass Rate | Fraction of conformations passing comprehensive validation (steric, bonding, and dihedral angle checks) [55] | |
| Precision & Accuracy | TM-score | Template-modeling score (0–1 scale) quantifying global fold similarity and structural alignment quality [115,119] |
| RMSD | Root-mean-square deviation measuring atomic position accuracy relative to reference structures [135,136] | |
| Pearson Correlation | Correlation coefficient between predicted and reference per-residue measurements [56,137] | |
| Diversity | MAT-P/MAT-R | Matching precision/recall: average RMSD to nearest reference/generated structure [115] |
| COV-P/COV-R | Coverage precision/recall: percentage of structures covered within distance threshold [138] | |
| lDDT-Cα | Average local structural dissimilarity between pairs of sampled conformations [56] | |
| Distributional Similarity | JS Divergence (PwD, Rg, TIC) | Jensen-Shannon divergence measuring similarity between generated and MD reference distributions [97,137] |
| JS-PwD | Fidelity score derived from Jensen-Shannon divergence of pairwise distance distributions [137] | |
| Sampler Score | Composite metric combining global (JS divergence) and local (RMSF, secondary structure) similarity [117] | |
| RMWD | Root-mean Wasserstein distance across atom-wise positional probability distributions [56] | |
| Coverage/k-recall | Fraction of MD reference structures covered and average distance to k-nearest generated samples [59] | |
| Structural Dynamics | RMSF | Root-mean-square fluctuation quantifying per-residue mobility across conformational ensembles [97,98,116] |
| Radius of Gyration (Rg) | Time-dependent measure of overall protein compactness and conformational changes [116] | |
| Weak/Transient Contacts | Frequency of non-covalent contact formation relative to reference structure [55] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dao, T.M.; Rahman, T. Deep Generative Modeling of Protein Conformations: A Comprehensive Review. BioChem 2025, 5, 32. https://doi.org/10.3390/biochem5030032
Dao TM, Rahman T. Deep Generative Modeling of Protein Conformations: A Comprehensive Review. BioChem. 2025; 5(3):32. https://doi.org/10.3390/biochem5030032
Chicago/Turabian StyleDao, Tuan Minh, and Taseef Rahman. 2025. "Deep Generative Modeling of Protein Conformations: A Comprehensive Review" BioChem 5, no. 3: 32. https://doi.org/10.3390/biochem5030032
APA StyleDao, T. M., & Rahman, T. (2025). Deep Generative Modeling of Protein Conformations: A Comprehensive Review. BioChem, 5(3), 32. https://doi.org/10.3390/biochem5030032






