Benchmarking the Base Randomization Algorithm as a Possible Tool for the Initial Step of Generating a Virtual RNA Aptamers Library
Abstract
1. Introduction
2. Theory and Methodology
2.1. Base Randomization Algorithm
2.2. Generation of Aptamers Sequences
| Algorithm 1: Base Randomization Algorithm (BRA) |
| Input: - length: the length of the aptamers to generate (either a specific length or “randomize”) - aptamers numbers: the number of aptamers to generate Output: - A list of unique aptamers based on the aptamer number input Steps: 1. seed (0) 2. Initialize an empty set() aptamers to avoid the repeats in list 3. If length is “randomize”, then: a. While the size of aptamers is less than aptamers numbers: i. Generate a random length number between 16 and 60 (inclusive) ii. Generate a random aptamer as an item using characters ‘ACUG’ iii. If the aptamer sequence is not in aptamers, then add it to aptamers 4. If length is a specific value, then: a. Generate a random aptamer of the specified length using characters ‘ACUG’ b. While the size of aptamers is less than aptamers numbers: i. Generate a random aptamer of the specified length using characters ‘ACUG’ ii. If the aptamer is not in aptamers, add it to aptamers 5. Convert the set aptamers to a list and return the list |
2.3. Secondary and Tertiary Structure Prediction
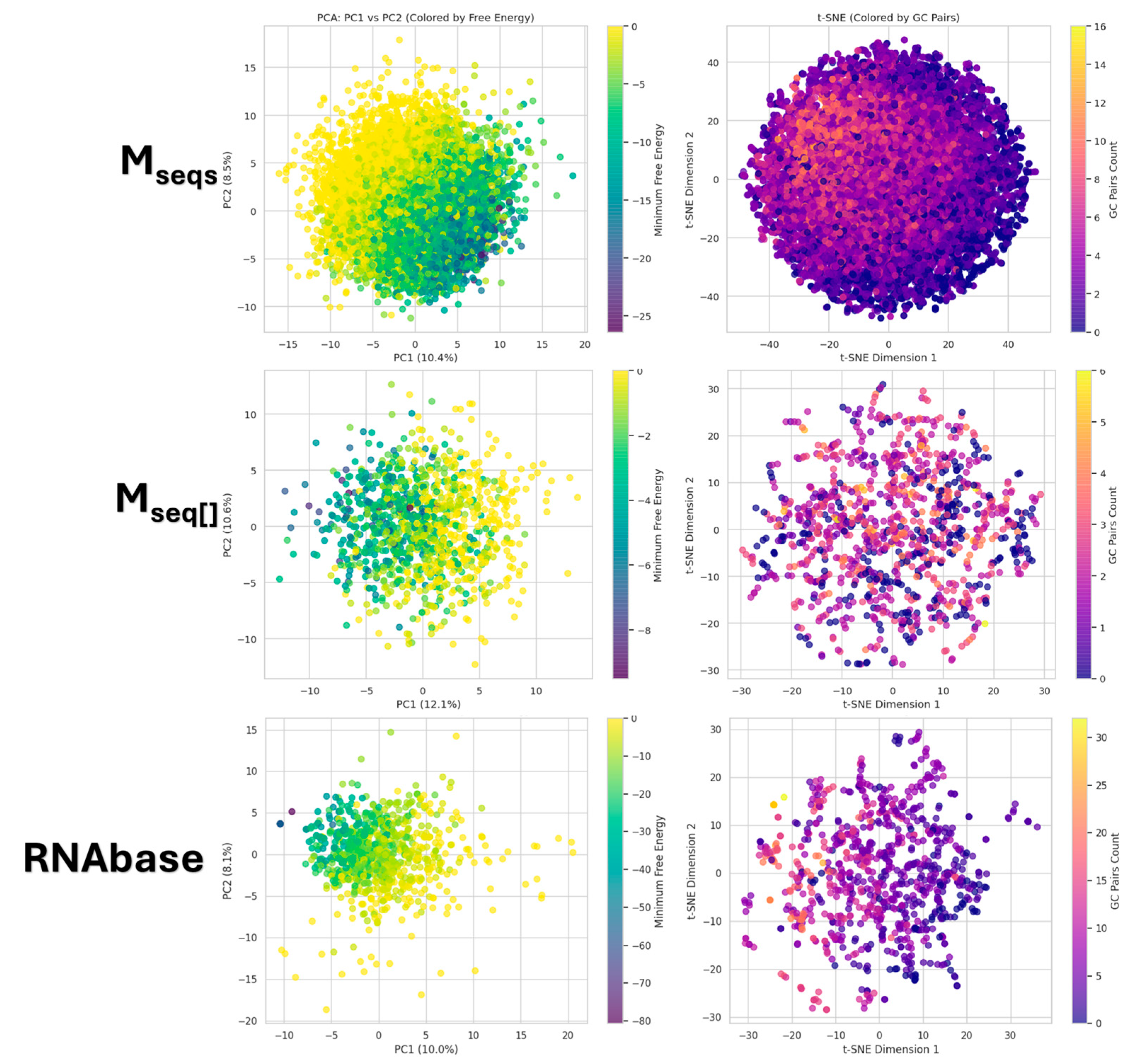
3. Results and Discussion
3.1. Us, Gs, Cs and Us Composition Analysis
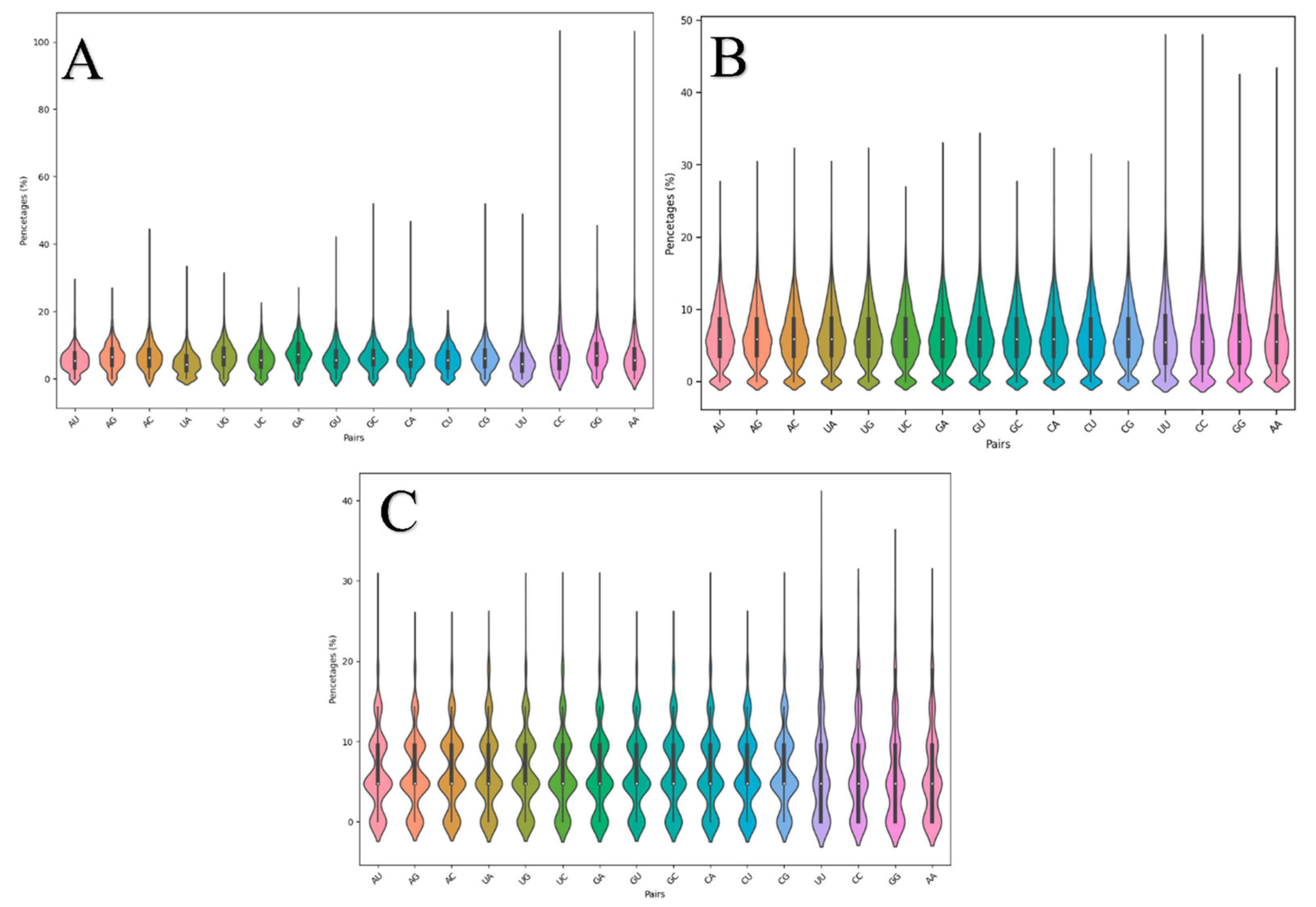
3.2. Adjacent Base Composition
3.3. Folding, Secondary Structure, and 3D Predictions
3.4. PCA and t-SNE Nucleic and Chemical Space
4. Remarks and Propositions
- Statement, Equation (11)
- 2.
- Statement Equation (13)
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Minchin, S.; Lodge, J. Understanding biochemistry: Structure and function of nucleic acids. Essays Biochem. 2019, 63, 433–456. [Google Scholar] [CrossRef]
- Lakhin, A.V.; Tarantul, V.Z.; Gening, L.V. Aptamers: Problems, solutions and prospects. Acta Naturae 2013, 5, 34–43. [Google Scholar] [CrossRef] [PubMed]
- Kolpashchikov, D.; Gerasimova, Y. Nucleic Acid Detection—Methods and Protocols; Springer Nature: London, UK, 2013; Volume 1039, ISBN 978-1-62703-534-7. [Google Scholar]
- Yu, A.C.H.; Vatcher, G.; Yue, X.; Dong, Y.; Li, M.H.; Tam, P.H.K.; Tsang, P.Y.L.; Wong, A.K.Y.; Hui, M.H.K.; Yang, B.; et al. Nucleic acid-based diagnostics for infectious diseases in public health affairs. Front. Med. China 2012, 6, 173–186. [Google Scholar] [CrossRef] [PubMed]
- Gubu, A.; Zhang, X.; Lu, A.; Zhang, B.; Ma, Y.; Zhang, G. Nucleic acid amphiphiles: Synthesis, properties and applications. Mol. Ther. Nucleic Acids 2023, 33, 144–163. [Google Scholar] [CrossRef]
- Barr, G.C.; Butler, J.A. Biosynthesis of Nucleic Acids in Bacillus Megaterium. 2. the Formation. Biochem. J. 1963, 88, 252–259. [Google Scholar] [CrossRef]
- Kong, H.Y.; Byun, J. Nucleic acid aptamers: New methods for selection, stabilization, and application in biomedical science. Biomol. Ther. 2013, 21, 423–434. [Google Scholar] [CrossRef]
- Savla, R.; Taratula, O.; Garbuzenko, O.; Minko, T. Tumor targeted quantum dot-mucin 1 aptamer-doxorubicin conjugate for imaging and treatment of cancer. J. Control. Release 2011, 153, 16–22. [Google Scholar] [CrossRef]
- Lauhon, C.T.; Szostak, J.W. RNA Aptamers that Bind Flavin and Nicotinamide Redox Cofactors. J. Am. Chem. Soc. 1995, 117, 1246–1257. [Google Scholar] [CrossRef]
- Bruno, J.G.; Carrillo, M.P.; Phillips, T.; Vail, N.K.; Hanson, D. Competitive FRET-aptamer-based detection of methylphosphonic acid, a common nerve agent metabolite. J. Fluoresc. 2008, 18, 867–876. [Google Scholar] [CrossRef]
- Tang, Z.; Parekh, P.; Turner, P.; Moyer, R.W.; Tan, W. Generating aptamers for recognition of virus-infected cells. Clin. Chem. 2009, 55, 813–822. [Google Scholar] [CrossRef]
- Chen, T.; Hongdilokkul, N.; Liu, Z.; Thirunavukarasu, D.; Romesberg, F.E. The expanding world of DNA and RNA. Curr. Opin. Chem. Biol. 2016, 34, 80–87. [Google Scholar] [CrossRef]
- BasePair Biotechnologies. “DNA Aptamers or RNA Aptamers?—Base Pair Biotechnologies,” DNA Aptamers or RNA Aptamers? 2018. Available online: https://www.basepairbio.com/dna-aptamers-rna-aptamers/ (accessed on 5 August 2023).
- Takei, Y.; Kadomatsu, K.; Itoh, H.; Sato, W.; Nakazawa, K.; Kubota, S.; Muramatsu, T. 5′-,3′-inverted thymidine-modified antisense oligodeoxynucleotide targeting midkine: Its design and application for cancer therapy. J. Biol. Chem. 2002, 277, 23800–23806. [Google Scholar] [CrossRef]
- White, R.R.; Sullenger, B.A.; Rusconi, C.P. Developing aptamers into therapeutics. J. Clin. Investig. 2000, 106, 929–934. [Google Scholar] [CrossRef]
- Famulok, M.; Klug, S.J. All you wanted to know about SELEX. Mol. Biol. Rep. 1994, 20, 97–107. [Google Scholar] [CrossRef]
- White, R.; Rusconi, C.; Scardino, E.; Wolberg, A.; Lawson, J.; Hoffman, M.; Sullenger, B. Generation of species cross-reactive aptamers using “toggle” SELEX. Mol. Ther. 2001, 4, 567–573. [Google Scholar] [CrossRef]
- Hybarger, G.; Bynum, J.; Williams, R.F.; Valdes, J.J.; Chambers, J.P. A microfluidic SELEX prototype. Anal. Bioanal. Chem. 2006, 384, 191–198. [Google Scholar] [CrossRef]
- Lauridsen, L.H.; Shamaileh, H.A.; Edwards, S.L.; Taran, E.; Veedu, R.N. Rapid one-step selection method for generating nucleic acid aptamers: Development of a DNA Aptamer against α-bungarotoxin. PLoS ONE 2012, 7, e41702. [Google Scholar] [CrossRef]
- Nitsche, A.; Kurth, A.; Dunkhorst, A.; Pänke, O.; Sielaff, H.; Junge, W.; Muth, D.; Scheller, F.; Stöcklein, W.; Dahmen, C.; et al. One-step selection of Vaccinia virus-binding DNA aptamers by MonoLEX. BMC Biotechnol. 2007, 7, 48. [Google Scholar] [CrossRef]
- Hamula, C.L.A.; Le, X.C.; Li, X.F. DNA aptamers binding to multiple prevalent M-types of streptococcus pyogenes. Anal. Chem. 2011, 83, 3640–3647. [Google Scholar] [CrossRef]
- Vieira, R. Designing In-Silico Aptamers for Potential Use in Marine Bioremediation. Master’s Thesis, Universidade do Porto, Porto, Portugal. Available online: https://github.com/rpgv/AptaCom (accessed on 29 July 2025).
- Zhou, Q.; Xia, X.; Luo, Z.; Liang, H.; Shakhnovich, E. Searching the Sequence Space for Potent Aptamers Using SELEX in Silico. J. Chem. Theory Comput. 2015, 11, 5939–5946. [Google Scholar] [CrossRef]
- James, F. A review of pseudorandom number generators. Comput. Phys. Commun. 1990, 60, 329–344. [Google Scholar] [CrossRef]
- Kietzmann, P.; Schmidt, T.C.; Wählisch, M. A guideline on pseudorandom number generation (PRNG) in the IoT. ACM Comput. Surv. (CSUR) 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Mascagni, M.; Srinivasan, A. Algorithm 806: SPRNG: A scalable library for pseudorandom number generation. ACM Trans. Math. Softw. (TOMS) 2000, 26, 436–461. [Google Scholar] [CrossRef]
- Tian, X.; Benkrid, K. Mersenne twister random number generation on FPGA, CPU and GPU. In Proceedings of the 2009 NASA/ESA Conference on Adaptive Hardware and Systems, San Francisco, CA, USA, 29 July–1 August 2009; IEEE: Piscataway, NY, USA; pp. 460–464. [Google Scholar]
- Murthy, V.L.; Rose, G.D. RNABase: An annotated database of RNA structures. Nucleic Acids Res. 2003, 31, 502–504. [Google Scholar] [CrossRef]
- Lorenz, R.; Bernhart, S.H.; Höner zu Siederdissen, C.; Tafer, H.; Flamm, C.; Stadler, P.F.; Hofacker, I.L. ViennaRNA Package 2.0. Algorithms Mol. Biol. 2011, 6, 26. [Google Scholar] [CrossRef]
- Zuker, M. Mfold web server for nucleic acid folding and hybridization prediction. Nucleic Acids Res. 2003, 31, 3406–3415. [Google Scholar] [CrossRef]
- Mokgopa, K.P.; Lobb, K.A.; Tshiwawa, T. T_SELEX program: Theoretical SELEX tool for Rational Design and Selection of RNA Aptamers Targeting Macromolecules. 2024. [Google Scholar] [CrossRef]
- McCaskill, J.S. The equilibrium partition function and base pair binding probabilities for RNA secondary structure. Biopolym. Orig. Res. Biomol. 1990, 29, 1105–1119. [Google Scholar] [CrossRef]
- Biesiada, M.; Purzycka, K.J.; Szachniuk, M.; Blazewicz, J.; Adamiak, R.W. Automated RNA 3D structure prediction with RNAComposer. In RNA Structure Determination: Methods and Protocols; Humana Press: New York, NY, USA, 2016; pp. 199–215. [Google Scholar]
- Cruz-Toledo, J.; McKeague, M.; Zhang, X.; Giamberardino, A.; McConnell, E.; Francis, T.; DeRosa, M.C.; Dumontier, M. Aptamer base: A collaborative knowledge base to describe aptamers and SELEX experiments. Database 2012, 2012, bas006. [Google Scholar] [CrossRef]
- Fay, M.M.; Lyons, S.M.; Ivanov, P. RNA G-Quadruplexes in Biology: Principles and Molecular Mechanisms. J. Mol. Biol. 2017, 429, 2127–2147. [Google Scholar] [CrossRef]
- Zuker, M.; Stiegler, P. Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res. 1981, 9, 133–148. [Google Scholar] [CrossRef]
- Zuker, M.; Stiegler, P. Information This paper presents a new computer method for folding an RNA molecule Nucleic Acids Research. Nucleic Acids Res. 1980, 9, 133–148. [Google Scholar]
- Trotta, E. On the normalization of the minimum free energy of RNAs by sequence length. PLoS ONE 2014, 9, e113380. [Google Scholar] [CrossRef]
- Chang, K.Y.; Varani, G.; Bhattacharya, S.; Choi, H.; McClain, W.H. Correlation of deformability at a tRNA recognition site and aminoacylation specificity. Proc. Natl. Acad. Sci. USA 1999, 96, 11764–11769. [Google Scholar] [CrossRef]
- Varani, G.; Mcclain, W.H. The G-U wobble base pair diverse biological systems. EMBO Rep. 2000, 1, 18–23. [Google Scholar] [CrossRef]
- Petersheim, M.; Turner, D.H. Base-Stacking and Base-Pairing Contributions to Helix Stability: Thermodynamics of Double-Helix Formation with CCGG, CCGGp, CCGGAp, ACCGGp, CCGGUp, and ACCGGUp. Biochemistry 1983, 22, 256–263. [Google Scholar] [CrossRef]
- Yakovchuk, P.; Protozanova, E.; Frank-Kamenetskii, M.D. Base-stacking and base-pairing contributions into thermal stability of the DNA double helix. Nucleic Acids Res. 2006, 34, 564–574. [Google Scholar] [CrossRef]
- Gruber, A.R.; Lorenz, R.; Bernhart, S.H.; Neuböck, R.; Hofacker, I.L. The Vienna RNA websuite. Nucleic Acids Res. 2008, 36, 70–74. [Google Scholar] [CrossRef]
- Zuker, M.; Mathews, D.H.; Turner, D.H. Algorithms and thermodynamics for RNA secondary structure prediction: A practical guide. In RNA Biochemistry and Biotechnology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999; pp. 11–43. [Google Scholar]
- Morgan, S.R.; Higgs, P.G. Evidence for kinetic effects in the folding of large RNA molecules. J. Chem. Phys. 1996, 105, 7152–7157. [Google Scholar] [CrossRef]
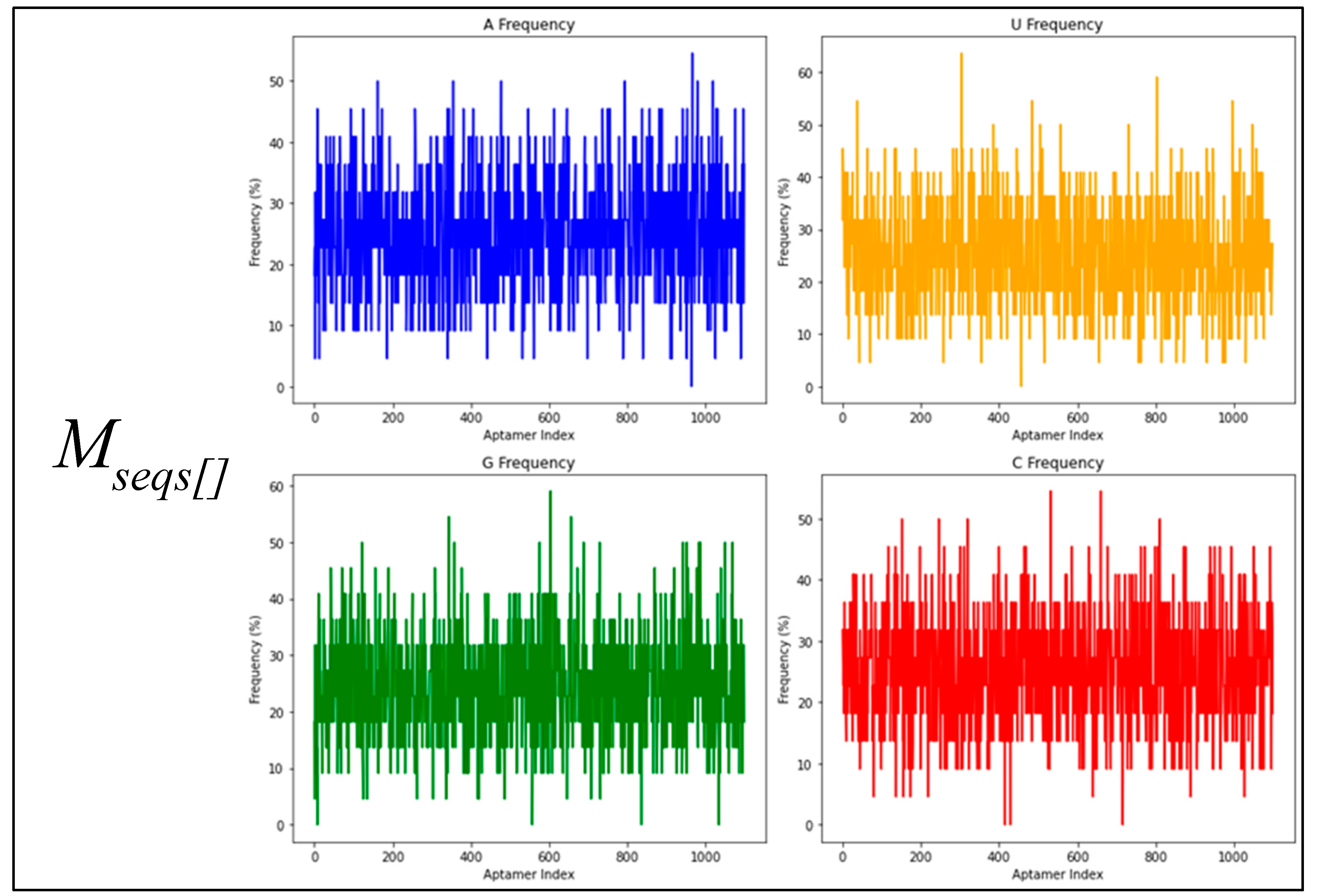
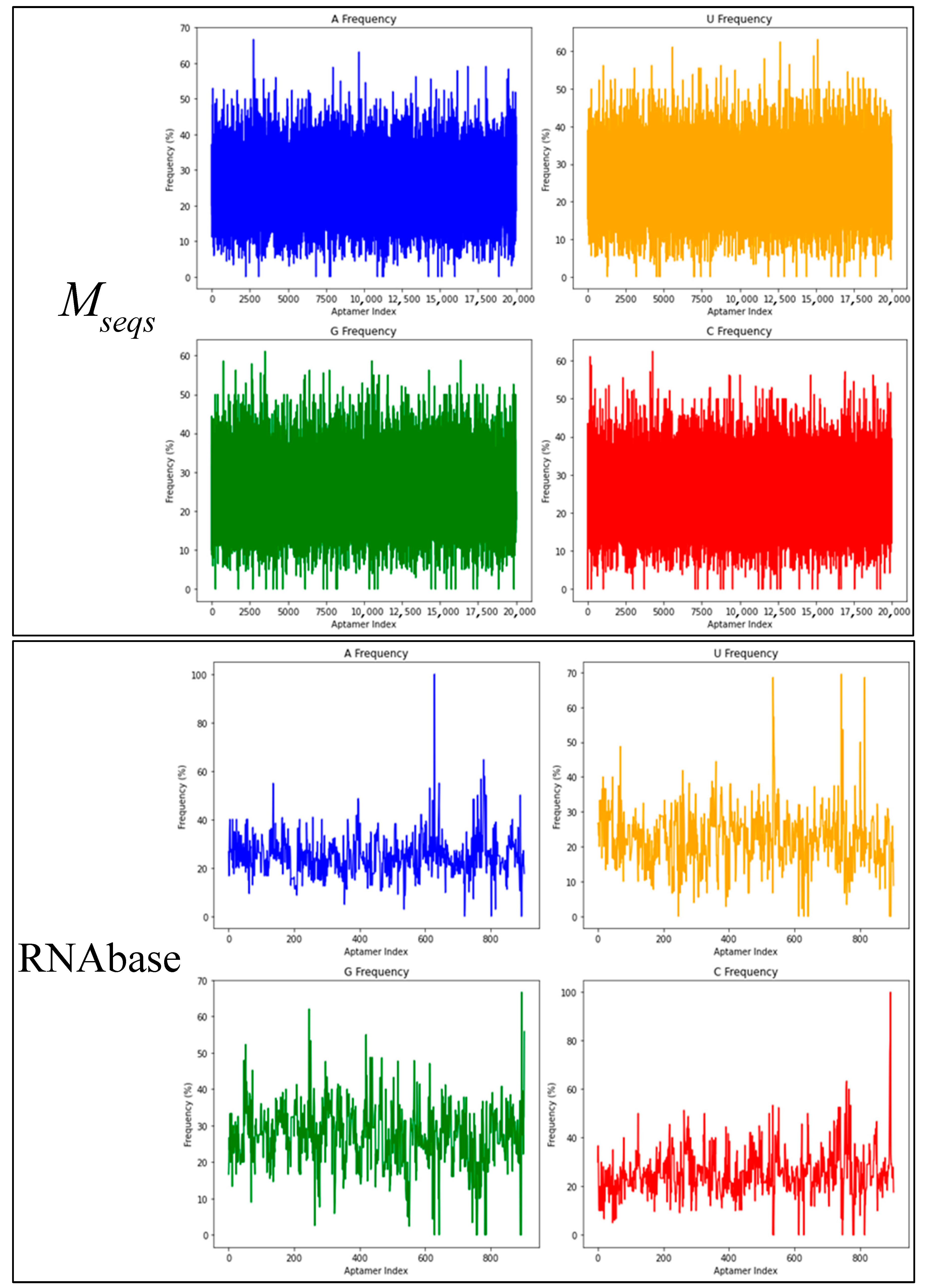
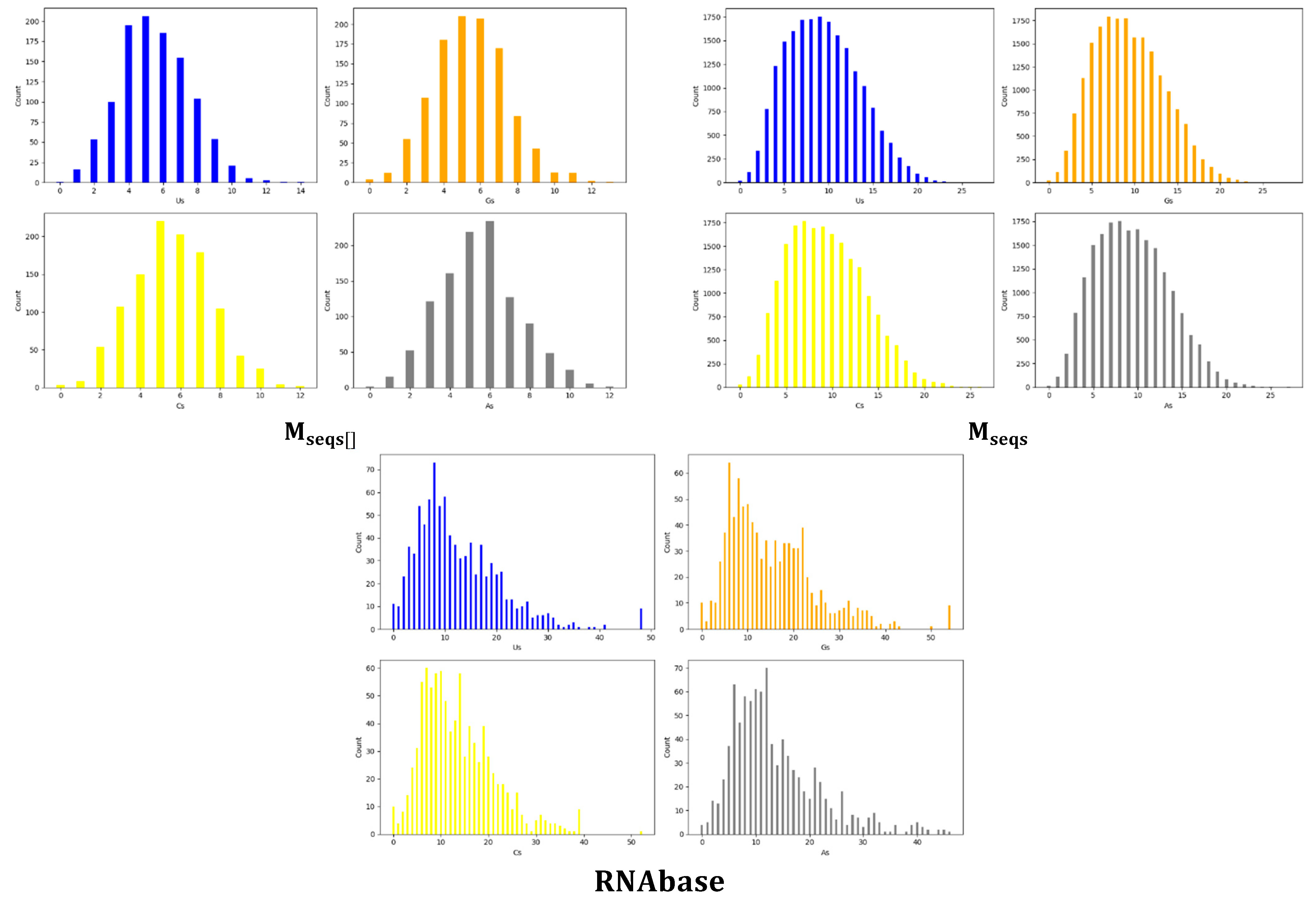
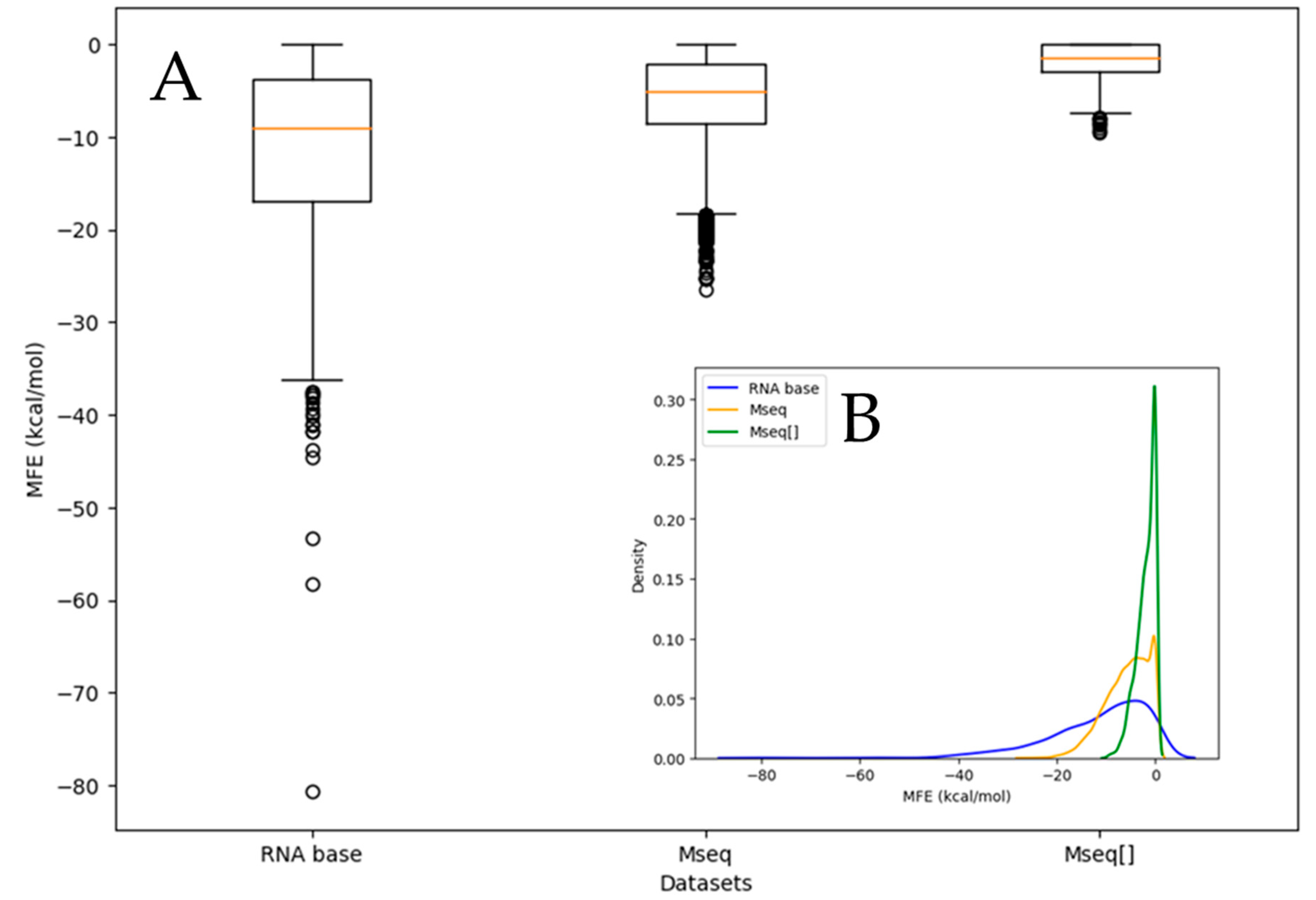
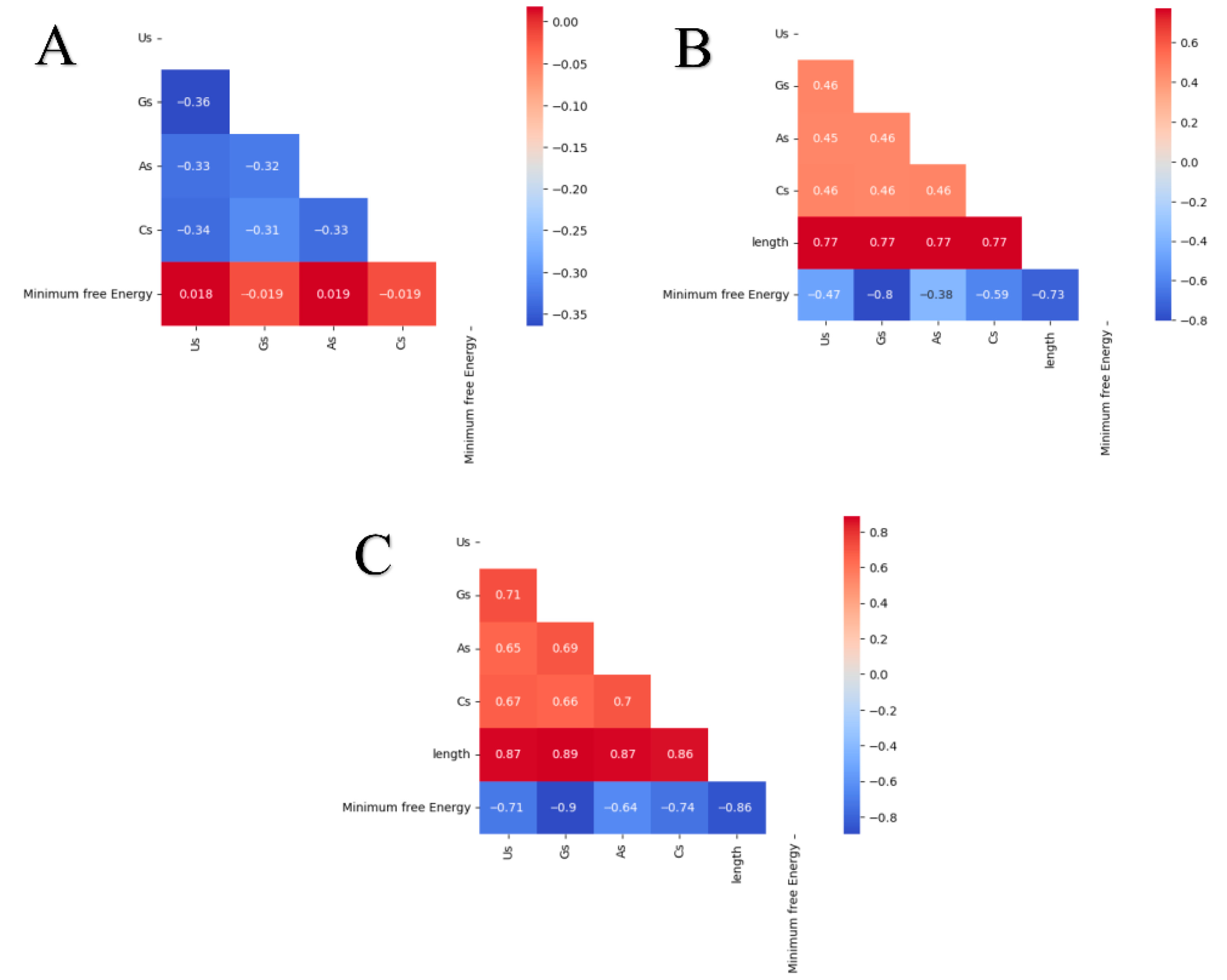
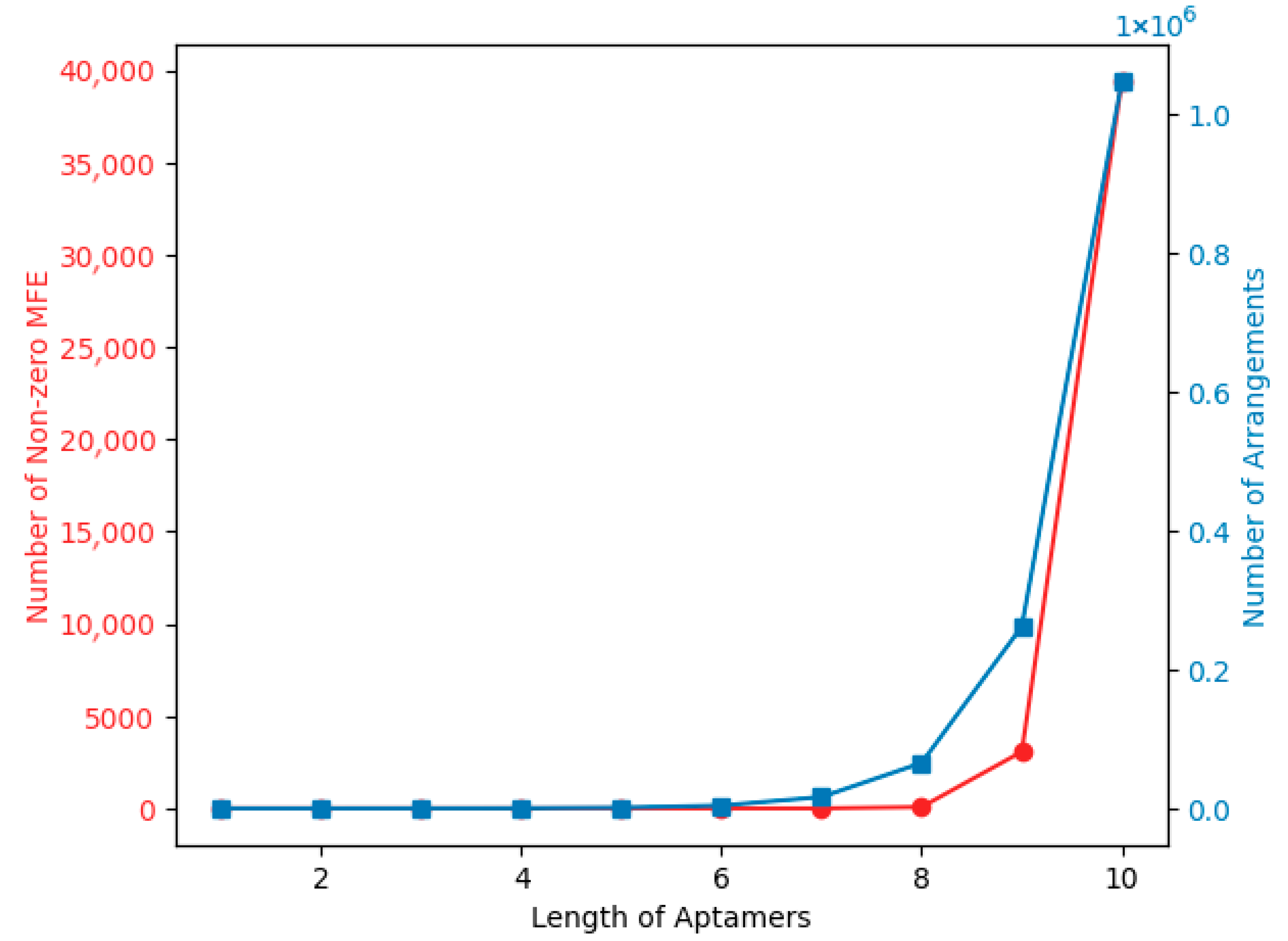
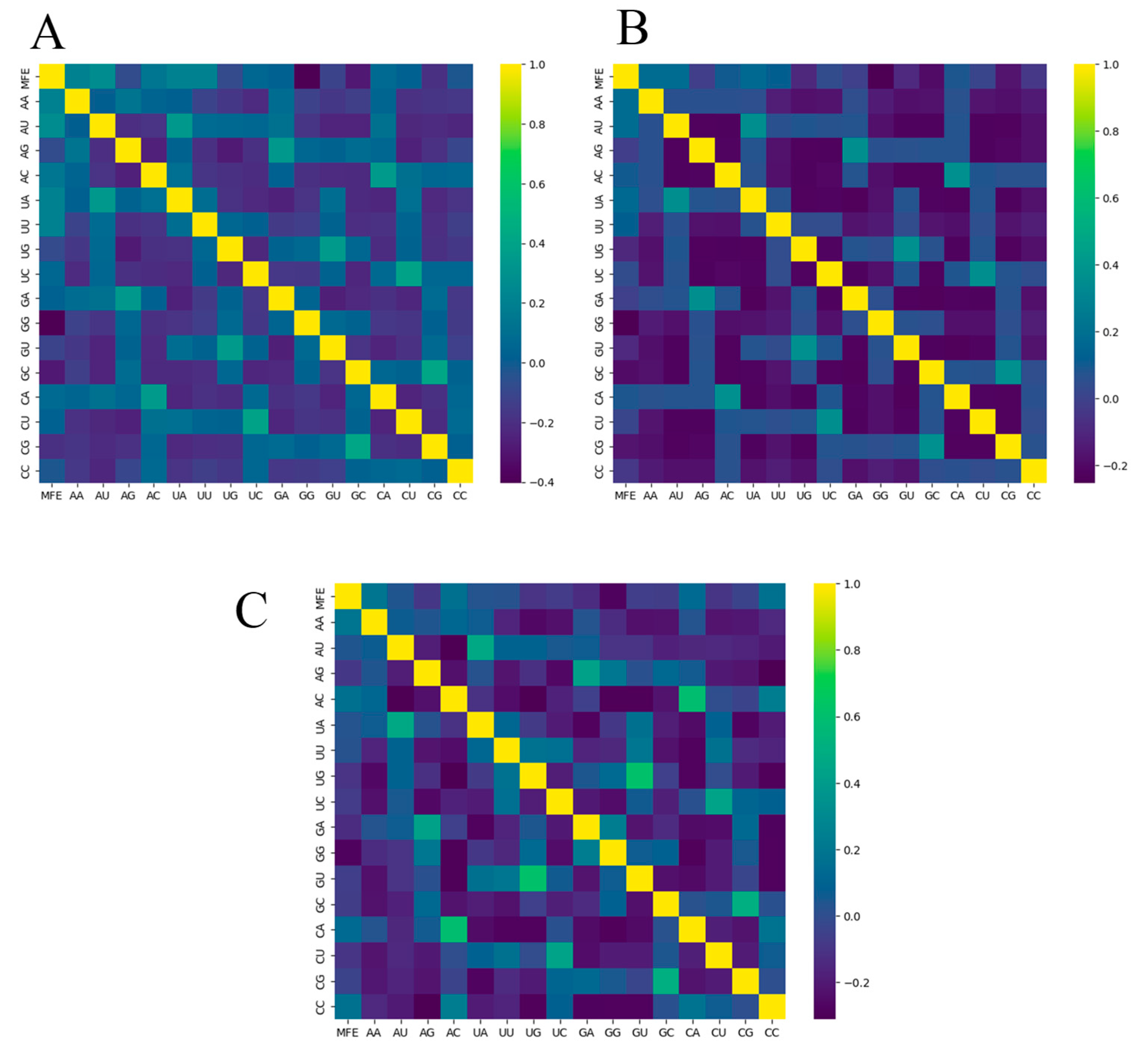
| Dataset | Base | Count | Sum | Average | Variance |
|---|---|---|---|---|---|
| U | 20,000 | 186,997 | 9.3498 | 17.0529 | |
| G | 20,000 | 187,102 | 9.3551 | 17.0290 | |
| A | 20,000 | 187,605 | 9.3802 | 17.1471 | |
| C | 20,000 | 187,053 | 9.3526 | 17.3570 | |
| U | 1100 | 6073 | 5.5209 | 4.2371 | |
| G | 1100 | 6003 | 5.4573 | 4.0173 | |
| A | 1100 | 5994 | 5.4491 | 3.9728 | |
| C | 1100 | 6130 | 5.5727 | 3.9119 | |
| RNAbase | U | 904 | 11,292 | 12.4912 | 67.5304 |
| G | 904 | 13,669 | 15.1206 | 90.6200 | |
| A | 904 | 12,327 | 13.6361 | 67.9062 | |
| C | 904 | 12,317 | 13.6250 | 59.3465 |
| Dataset | Source of Variation | SS | df | MS | F | p-Value | F Crit | Significance (α = 0.05) |
|---|---|---|---|---|---|---|---|---|
| Between Groups | 11.180 | 3 | 3.933 | 0.229 | 0.876 | 2.605 | No | |
| Within Groups | 1.37 × 106 | 79,996 | 17.146 | |||||
| Total | 1.37 × 106 | 79,999 | ||||||
| Between Groups | 11.158 | 3 | 3.719 | 0.922 | 0.429 | 2.607 | No | |
| Within Groups | 17,736.842 | 4396 | 4.035 | |||||
| Total | 17,748.000 | 4399 | ||||||
| RNAbase | Between Groups | 3152.917 | 3 | 1050.972 | 14.730 | 0.000 | 2.607 | Yes |
| Within Groups | 257,718.926 | 3612 | 71.351 | |||||
| Total | 260,871.843 | 3615 |
| Dataset | Base | Shapiro–Wilk (Stat, p-Value) | Anderson–Darling (Stat) |
|---|---|---|---|
| U | 0.9745, 0.0000 | 11.6846 | |
| G | 0.9752, 0.0000 | 11.6548 | |
| A | 0.9739, 0.0000 | 12.4270 | |
| C | 0.9765, 0.0000 | 11.6131 | |
| U | 0.9811, 0.0000 | 109.7242 | |
| G | 0.9807, 0.0000 | 116.2862 | |
| A | 0.9808, 0.0000 | 110.7593 | |
| C | 0.9803, 0.0000 | 116.5028 | |
| RNAbase | U | 0.9079, 0.0000 | 17.4529 |
| G | 0.9171, 0.0000 | 16.7724 | |
| A | 0.9076, 0.0000 | 22.9033 | |
| C | 0.9407, 0.0000 | 13.0821 |
| Base | Comparison | D-Statistic | p-Value |
|---|---|---|---|
| U | vs. | 0.4727 | ~0.0 |
| vs. RNAbase | 0.2215 | ~0.0 | |
| vs. RNAbase | 0.5433 | ~0.0 | |
| G | vs. | 0.4925 | ~0.0 |
| vs. RNAbase | 0.3423 | ~0.0 | |
| vs. RNAbase | 0.6456 | ~0.0 | |
| A | vs. | 0.4819 | ~0.0 |
| vs. RNAbase | 0.2404 | ~0.0 | |
| vs. RNAbase | 0.6352 | ~0.0 | |
| C | vs. | 0.4786 | ~0.0 |
| vs. RNAbase | 0.2752 | ~0.0 | |
| vs. RNAbase | 0.6471 | ~0.0 |
| Aptamer ID | Sequence (5′ to 3′) and Pseudoknots | MFE 2d Structure | Tertiary Structure/3D Structure |
|---|---|---|---|
| RNAbase | |||
| RNAse69 | AUUUCUCUGAGAUGUUCGCAAGCGGGCC AGUCCCCUGAGCCGAUAUUUCAUACCAC AAGAAAUGUGGCGCUCCGCGGUUGGUGA GCAUGCUCGGUCCGUCCGAGAAGCCUUA AAACUGCGACGACACAUUCACCUUGAAC CAAGGGUUCAAGGGUUACAGCCUGCGGC GGCAUCUCGGAGAUUCC ...((((((((((((.(((..((((((.........(((((.(((((((.........))))))). ).))))(((((((..((((....(((((.....)))))....)))).)))))))............(( (((((((...)))))))))......)))))).))))))))))))))).... | 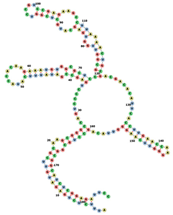 | 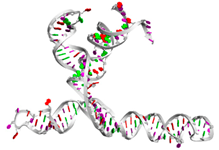 |
| RNAse192 | GGGAGAAUUCCGACCAGAAGCUUGUGAG ACCAGCCGAGUGGUGUCUGGCUAUUCAC UGGAGCGUGGGUGGAACCCCUGCGCACU CGUUUGGCUGUCCGGGCCUUCGGGCCGG GAUUAUCUCUUUGGGUUUUGUGAUUUGG UCAUAUGUGCGUCUACAUGGAUCCUCA ((((.(((((((.((.((((((((.((.(((((.((((((.(((..((((((((((......))) )))))...))..))))))))).)))).).)))))).)))).)).))))))).))))........... (((...((((.((((((....)))))))))).))) | 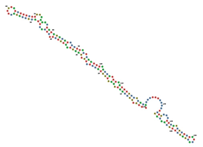 | 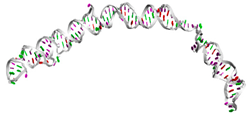 |
| aptamerd5165 | CAAGCACACCACGAUGCCCCA CGCAUCGUGGUGUGGCACAUC CAGCGUGAGCGA ....(((((((((((((.....)))))))))))))((.(((.....))).)).. | 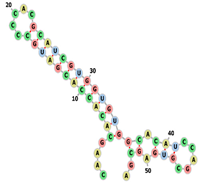 | 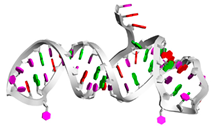 |
| aptamerd18670 | UGCCAUUGCUGCCUGUGCUGU GUUGGUUGGAGCGCAGCUAGC AAUGGAGCG ..(((((((((.(((((((.((.....)).))))))).))))))))).... | 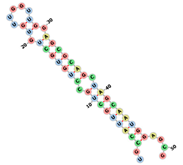 |  |
| Aptamer1084 | CGUUGGCUUAGUCACUAAGCCA ...((((((((...)))))))) | 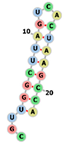 | 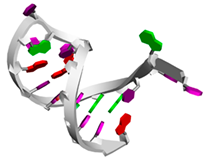 |
| Aptamer960 | GGCCCGGACUAGUCAUUCGGGC .(((((((.......))))))) | 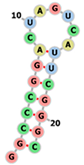 | 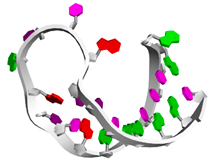 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mokgopa, K.P.; Oloniiju, S.D.; Lobb, K.A.; Tshiwawa, T. Benchmarking the Base Randomization Algorithm as a Possible Tool for the Initial Step of Generating a Virtual RNA Aptamers Library. BioTech 2025, 14, 72. https://doi.org/10.3390/biotech14030072
Mokgopa KP, Oloniiju SD, Lobb KA, Tshiwawa T. Benchmarking the Base Randomization Algorithm as a Possible Tool for the Initial Step of Generating a Virtual RNA Aptamers Library. BioTech. 2025; 14(3):72. https://doi.org/10.3390/biotech14030072
Chicago/Turabian StyleMokgopa, Kabelo P., Shina D. Oloniiju, Kevin A. Lobb, and Tendamudzimu Tshiwawa. 2025. "Benchmarking the Base Randomization Algorithm as a Possible Tool for the Initial Step of Generating a Virtual RNA Aptamers Library" BioTech 14, no. 3: 72. https://doi.org/10.3390/biotech14030072
APA StyleMokgopa, K. P., Oloniiju, S. D., Lobb, K. A., & Tshiwawa, T. (2025). Benchmarking the Base Randomization Algorithm as a Possible Tool for the Initial Step of Generating a Virtual RNA Aptamers Library. BioTech, 14(3), 72. https://doi.org/10.3390/biotech14030072






