Effect of Tacticity on London Dispersive Surface Energy, Polar Free Energy and Lewis Acid-Base Surface Energies of Poly Methyl Methacrylate by Inverse Gas Chromatography

Abstract

This research was devoted to study the effect of the tacticity on the surface physicochemical properties of PMMA. (1) Background: The determination of the surface free energy of polymers is generally carried out by inverse gas chromatography (IGC) at infinite dilution. The dispersive, polar and surface acid-base properties of PMMA at different tacticities were obtained via IGC technique with the help of the net retention time and volume of adsorbed. (2) Methods: The London dispersion equation was used to quantify the polar free energy of adsorption, while the London dispersive surface energy ${\gamma }_s^d\left(T\right)$ of PMMAs was determined using the thermal model. (3) Results: The results showed non-linear variations of ${\gamma }_s^d\left(T\right)$ of atactic, isotactic, and syndiotactic PMMAs with three maxima characterizing the three transition temperatures of PMMAs. The obtained values of the enthalpic and entropic Lewis’s acid-base parameters showed that the basicity of the atactic PMMA was about four times larger than its acidity. (4) Conclusions: A large difference in the behavior of the various PMMAs was proven in the different values of the polar acid and base surface energies of the three PMMAs with an important effect of the tacticity of PMMA on its acid-base surface energies.

1. Introduction

The tacticity of polymers plays an important role in many industrial processes. Indeed, polymer crystallinity and many macroscopic properties such as the density, glass and melting temperatures, clarity, and stiffness of a polymer depend on it. Furthermore, the determination of polymer tacticity is of crucial interest in the knowledge of polymerization mechanisms [1]. The stereochemistry in polymers has been used to influence and control their physical and mechanical properties, as well as begin to control their function. Several studies were devoted to the effect of stereochemistry on mechanical properties, biodegradation, conductivity, and applications of stereodefined polymers for enantioseparation and as supports for catalysts in asymmetric transformations [2].

A tactic polymer is defined as a regular polymer, the molecules of which can be described in terms of only one species of configurational repeating unit in a single sequential arrangement [3]. Tacticity then refers to the relative spatial arrangement of substituents along a polymer chain. At that time, three main types of tacticities were distinguished: isotactic, syndiotactic, and atactic [1].

It is well known that the atactic polymers have their pendant groups organized randomly around the principal linear chain of the polymers. They lead to the formation of amorphous and soft materials. Whereas, the syndiotactic polymers are characterized by their pendant groups organized in alternating ways around the principal chain by forming crystal structures. The tacticity of polymers affects the physical and chemical properties of polymeric materials [4,5,6,7,8,9,10,11,12]. The isotactic polymers are characterized by pendant groups spatially located on the same side of the principal chain. The crystallinity of polymers strongly depends on their tacticity. In general, syndiotactic polymers form the most rigid, crystalline structures, while isotactic polymers exhibit a semi-crystalline structure and an amorphous form for atactic polymers. This affects the thermo-mechanic properties of polymers. For example, the highest melting points are obtained with the syndiotactic polymers.

Izzo et al. [4] investigated the effect of polymer tacticity on physico-chemical and biological properties relevant to the use of polymer therapeutics using poly (methacrylic acid) (PMA) as a model polymer. They studied the physicochemical behavior of an aqueous solution of atactic and syndiotactic PMAs obtained from the hydrolysis of PMMAs.

Grigoriadi et al. [5] studied the effect of tacticity on the ageing kinetics of glassy amorphous polymers at high and low ageing temperatures for atactic, isotactic, and syndiotactic polystyrene using flash-DSC in their glassy state.

The spatial configuration of polymers can be modified by the various parameters of their physicochemical properties. Chat et al. [6] used dielectric spectroscopy (DS) to study the effect of tacticity on the glass-transition dynamics of confined polymer films [7].

Several studies were interested in the determination of the tacticity effect on the properties of polymers [11,12,13,14]. The polymer tacticity gives information on the arrangement of atoms and/or groups of atoms on the polymer backbone [6]. For poly(methyl methacrylate) (PMMA) and poly(ethyl methacrylates) (PEMA), it has been observed that different spatial configurations of the polymers are characterized by the various relaxation times and the glass transition temperatures [12,13,14].

Tretinnikov [15] used the contact angle measurements of water on stereoregular poly(methyl methacrylate)s. He proved that the selectivity at the surface of functional groups increased rapidly with syndiotacticity. However, the isotactic films showed no effect of the polarity of the contacting medium on the surface chemical composition or the wettability of the films.

The tacticity effect on the surface activity of stereoregular PMMAs was interpreted in terms of the surface conformational structure of these materials. Sharma et al. [16] observed significant differences in the sensitivity of PMMA depending on its tacticity. They showed that the isotactic polymer was more sensitive than either the syndiotactic or atactic polymers. They also observed that the tacticity of PMMA affected the contact angle measurements and, therefore, the surface energy and adhesion work [16].

Jha et al. [17] using molecular dynamics (MD) simulations, calculated the surface tension of melt PMMA as a function of tacticity. They found that isotactic PMMA, in comparison to syndiotactic and atactic PMMA, shows a larger surface concentration of polar ester-methyl and carbonyl groups on the surface versus nonpolar α-methyl groups. They highlighted a certain effect of the tacticity on the surface composition and surface tension, which are controlled by both polarity and steric constraints.

The effect of tacticity and temperature on the surface structure of PMMA at the polymer-vacuum interface was studied by Jha et al. [18] by considering the surface normal and the surface number densities of the α-methyl, ester-methyl, carbonyl, and backbone methylene groups. They proved that the orientation of ester-methyl, α-methyl, and carbonyl groups was independent of the tacticity. However, the lowest value of the surface number density ratios of ester-methyl to α-methyl groups was obtained for syndiotactic PMMA but the highest for isotactic PMMA [18].

The effects of tacticity and molecular weight (MW) of isotactic polypropylene (i-PP) on crystallization kinetics and crystal morphology were studied by Rungswang et al. [19]. An important influence of the tacticity of i-PP on the nucleation rate was highlighted, but a slight effect was shown on the crystallization and normalized spherulite-growth rates. The stereochemistry in polymers has also been used to influence and control their physical and mechanical, thermal, and conductive properties, as well as begin to control their performance and function [20].

The physical properties of polymers, like solubility, mechanical properties, and thermal stability, etc. can be affected by the stereoregularity of polymers. Biswas et al. [21] investigated the effect of some physical properties of high molecular weight linear poly(N-isopropylacrylamide)s (PNIPAM) having different isotacticities (m, meso dyad = 47, 62, 68, 81, and 88%). The effect of tacticity on the transition temperatures was studied by several scientists [21,22,23,24,25].

Nevertheless, we did not find any study in the literature concerning the influence of tacticity on the surface properties of polymers, such as their London dispersive energy, Lewis’s acid-base parameters and acid and base polar surface energies. This paper is interested in filling this gap in this research area by studying the effect of the tacticity of poly(methyl methacrylate) on the dispersive component of the surface energy of polymer, the polar and dispersive free energies, as well as the various surface variables relative to Lewis’s acid-base surface properties.

The technique used in this study is inverse gas chromatography at infinite dilution, which proved to be a very interesting technique capable of examiningthe surface properties of solid substrates and quantifying the various surface parameters of interaction between polymers and the adsorbed organic solvents by varying the temperature [22,23,26,27,28,29,30,31,32].

Different chromatographic methods and molecular models were used in the literature to characterize the physicochemical properties of solid surfaces [26,27,28,29,30,31,32]. We applied the new method recently developed that utilized the thermal model [30,31,32] to determine the London dispersive energy and used the London dispersion equation [30,31,32,33] based on the deformation polarizability ${\alpha }_{0X}$ of the probe and the ionization energies of the solid ${\epsilon }_S$ and the solvent ${\epsilon }_X$ with a new chromatographic thermodynamic parameter ${\mathcal{P}}_{SX}$. By using the thermal model, we compared between the dispersive surface energy of atactic, isotactic, and syndiotactic PMMA, and by applying the parameter ${\mathcal{P}}_{SX}$, we determined the polar and dispersive free interaction energy of organic solvents adsorbed on the polymer surfaces, as well as Lewis’s acid-base surface energy and parameters as a function of temperature.

2. Methods and Materials

Inverse gas chromatography (IGC) at infinite dilution [26,27,28,29,30,31,32] was used to characterize the surface physicochemical properties of PMMA at different tacticities. The IGC technique allowed obtaining the experimental values of the net retention time $t_n$ and volume $V_n$ of polar and non-polar adsorbed solvents on the different PMMAs as a function of temperature. The free energy of adsorption $∆G_a^0(T)$ of adsorbed molecules on PMMA surfaces was therefore obtained from Equation (1):

$$∆G_a^0=-RT ln\frac{V_n\left(T\right)}{V_0\left(T\right)}$$

(1)

where T is the absolute temperature of the chromatographic column containing the solid material, R the perfect gas constant, and $V_0\left(T\right)$ a constant volume depending on the temperature and reference characteristics referred to the two-dimensional state of the adsorbed film.

In the case of polar molecules adsorbed on solid surfaces, two contributions of the free energy of adsorption $∆G_a^0(T)$ were distinguished: the London dispersion component $∆G_a^d$ and the polar or specific component $∆G_a^p$ (Equation (2))

$$∆G_a^0=∆G_a^d+∆G_a^p$$

(2)

By using our new method recently developed [30,31,32] that consisted of the separation of the London dispersive and polar components of the free surface, it was possible to obtain the London dispersion energy $∆G_a^d\left(T\right)$:

$$∆G_a^d\left(T\right)=-\frac{{\alpha }_{0S} }{ H^6}\left[\frac{3\mathcal{N}}{{2\left(4\pi {\epsilon }_0\right)}^2}\left(\frac{{\epsilon }_S {\epsilon }_X}{\left({\epsilon }_S+{\epsilon }_X\right)}{\alpha }_{0X}\right)\right]$$

(3)

where and $\mathcal{N}$ is the Avogadro’s number, ${\epsilon }_0$ the permittivity of vacuum, S denoting the solid particle and X the solvent molecule separated by a distance $H$, and ${\epsilon }_S$ and ${\epsilon }_X$ are the respective ionization energies of the solid and the solvent ${\epsilon }_X$.

The new method proposed to use the new parameter of interaction ${\mathcal{P}}_{SX}$ given by

$${\mathcal{P}}_{SX}=\frac{{\epsilon }_S {\epsilon }_X}{\left({\epsilon }_S+{\epsilon }_X\right)}{\alpha }_{0X}$$

(4)

In the case of n-alkanes $\left(C_n\right)$ adsorbed on PMMA, one obtained:

$$RTlnVn\left(C_n\right)=A\left[\frac{3\mathcal{N}}{{2\left(4\pi {\epsilon }_0\right)}^2}{\mathcal{P}}_{SX}\left(C_n\right)\right]-B$$

(5)

where $A$ and B are given by:

$$\left\{\begin{array}{c}A=\frac{{\alpha }_{0S} }{ H^6} \\ B=ln{V}_0\left(T\right)\end{array}\right.$$

(6)

The polar free energy $\left(-∆G_a^p\left(T\right)\right)$ of polar organic solvents adsorbed on PMMA was obtained from the experimental straight-line of n-alkanes (Equation (7)) representing the variations of $RTlnVn\left(C_n\right)$ against $\frac{3\mathcal{N}}{{2\left(4\pi {\epsilon }_0\right)}^2}{\mathcal{P}}_{SX}\left(C_n\right)$ for different temperatures:

$$-∆G_a^p(T)=RTlnVn\left(X\right)-A\left[\frac{3\mathcal{N}}{{2\left(4\pi {\epsilon }_0\right)}^2}{\mathcal{P}}_{S-X}\right]+B$$

(7)

The use of Equations (8) and (9) led to the determination of the polar enthalpy $-∆H_a^p\left(T\right)$ and entropy $-∆S_a^p\left(T\right)$ of organic solvents adsorbed on PMMA:

$$∆H_a^p(T)=\frac{\partial \left(\frac{∆G_a^p\left(T\right)}{T}\right)}{\partial \left(\frac{1}{T}\right)}$$

(8)

$$∆S_a^p(T)=-\left(\frac{\partial \left(∆G_a^p\left(T\right)\right)}{\partial T}\right)$$

(9)

The Lewis’s enthalpic acid base constants $K_A\left(T\right)$ and $K_D\left(T\right)$, and entropic acid base parameters ${\omega }_A\left(T\right)$ and ${\omega }_D\left(T\right)$ were obtained from the expressions of of $-∆H_a^p\left(T\right)$ and $-∆S_a^p\left(T\right)$:

$$-∆H^p\left(T\right)= {DN\times K}_A\left(T\right)+AN\times K_D\left(T\right)$$

(10)

$$-∆S^p\left(T\right)= {DN\times \omega }_A\left(T\right)+AN\times {\omega }_D\left(T\right)$$

(11)

where AN and DN are respectively the Gutmann electron donor and acceptor numbers of the polar solvents [34]. The used values were those corrected by Riddle and Fowkes [35].

-

Two kinds of probe molecules were used:

-

Non-polar molecules such as the n-alkanes (${\mathit{C}}_{\mathit{n}}$) such as n-pentane (${\mathit{C}}_5$), n-hexane (${\mathit{C}}_6$), n-heptane (${\mathit{C}}_7$), n-octane (${\mathit{C}}_8$), and n-nonane (${\mathit{C}}_9$)

-

Polar molecules, divided into three groups:

➢

Lewis’s acid solvents such as dichloromethane, chloroform, and carbon tetrachloride

➢

Basic solvent such as ethyl acetate, diethyl ether, tetrahydrofuran (THF)

➢

Amphoteric molecule such as toluene

The isotactic (i), syndiotactic (s) and atactic (a) PMMAs used in this paper have the following respective molecular mass Mn = 102 kg/mol, 100 kg/mol and 100 kg/mol. They were the same as the polymers previously characterized in other studies by using other classic chromatographic methods and models [22,23].

The previous experimental values of $\mathit{R}\mathit{T}\mathit{l}\mathit{n}\mathit{V}\mathit{n}$ of the various n-alkanes and polar molecules adsorbed on i-PMM, s-PMMA, and a-PMMA, obtained from chromatographic measurements, were used to investigate the tacticity effect on the surface physicochemical properties of the different PMMA surfaces.

The organic solvents of highly pure-grade (i.e., 99%) were purchased from Sigma-Aldrich (Beirut, Lebanon). The various non-polar molecules used in this study were n-alkanes (pentane, hexane, heptane, octane, and nonane); acidic (Tetrachloromethane, chloroform, and dichloromethane); amphoteric (ether and toluene); and basic solvents (ethyl acetate and tetrahydrofuran (THF)). The measurements were carried out with a DELSI GC 121 FB Chromatograph equipped with a flame ionization detector of high sensitivity. A mass of 1 g of polymer particles was packed into a stainless-steel column of length 30 cm and a 2 mm internal diameter. Helium was used as a carrier gas with a flow rate equal to 25 mL/min. The retention times of the different injected organic solvents, measured at infinite dilution, led to interactions between the organic molecules and the polymer, supposing that there is no interaction between the probe molecules themselves. The column temperatures varied from 30 to 200 °C. Average retention times and volumes were determined by repeating three times each solvent injection with a standard deviation less than 1% in all chromatographic measurements.

3. Experimental Results

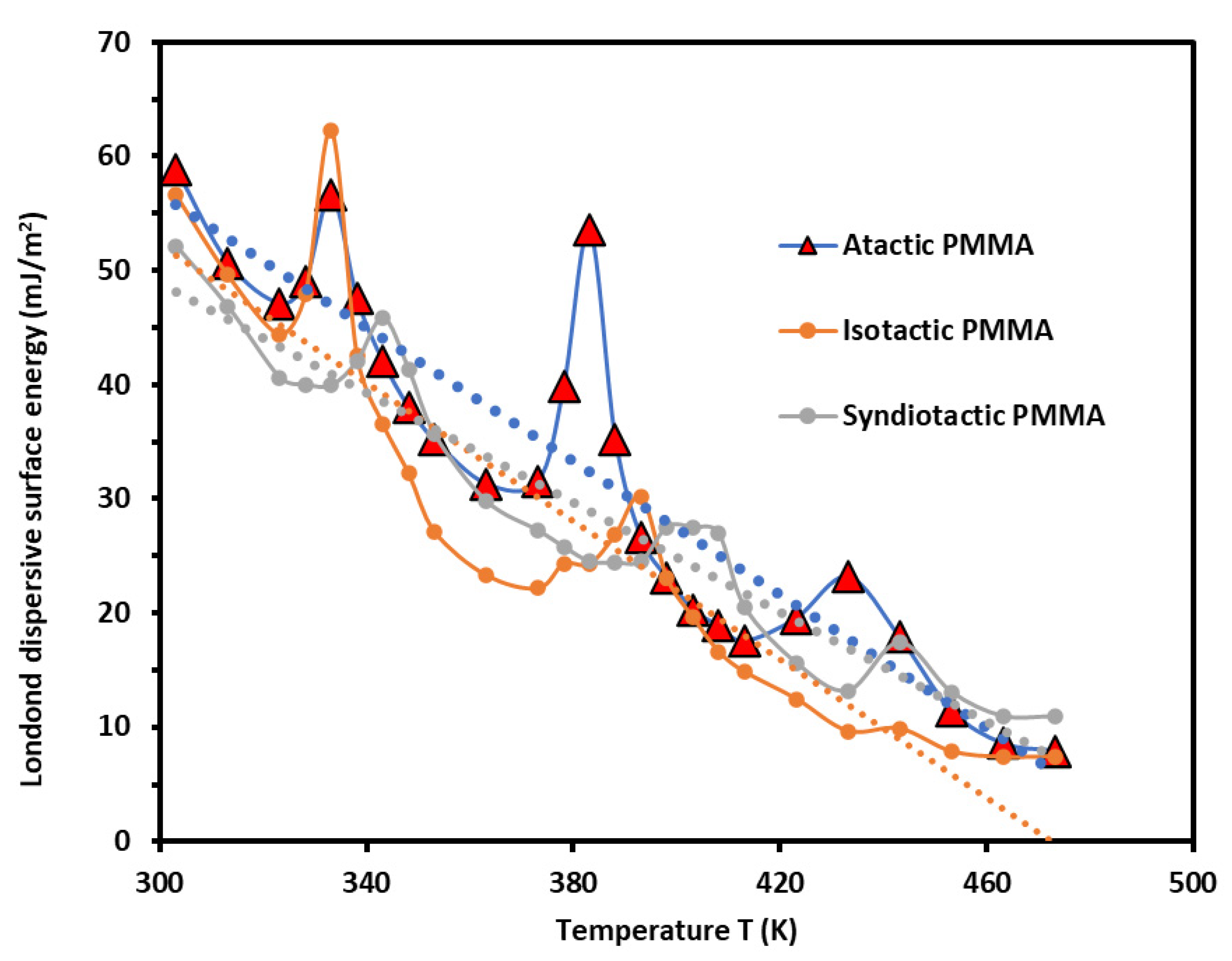
3.1. London Dispersive Component of Surface Energy of PMMA Polymers

In previous papers [30,31,32], a new methodology for determining the accurate value of the London dispersive surface energy ${\gamma }_s^d$ of materials was proposed. It is based on the thermal effect on the surface areas of organic molecules that is necessary to be known as a function of temperature to obtain accurate values of ${\gamma }_s^d\left(T\right)$ of solid surfaces.

In this section, the same procedure previously developed [22,23,30,31,32] was used to determine the ${\gamma }_s^d\left(T\right)$ of the different PMMAs. The determination of the net retention volumes of the various organic molecules adsorbed on i-PMMA, s-PMMA, and a-PMMA allowed for the $RTlnVn$ of such molecules. The obtained results of $RTlnVn$ are given in Table S1 (Supplementary Materials).

The Hamieh thermal model [30,31,32] was applied to determine ${\gamma }_s^d\left(T\right)$ for the various PMMA surfaces. Figure 1 shows the variations of ${\gamma }_s^d\left(T\right)$ of PMMA at different tacticities as a function of the temperature.

The curves in Figure 1 showed a non-linear evolution of ${\gamma }_s^d\left(T\right)$, contrary to other cases relative to oxides and other solid materials [30,31,32] where the linearity of ${\gamma }_s^d\left(T\right)$ was clearly observed. The precious information collected from Figure 1 showed not only the large variations of ${\gamma }_s^d\left(T\right)$ versus the temperature with a permanent change of the slope $\frac{d{\gamma }_s^d\left(T\right)}{dT}$, but also highlighted an important difference in the behavior of PMMA strongly depending on the tacticity of the polymer. Indeed, larger values of ${\gamma }_s^d\left(T\right)$ of atactic PMMA were globally observed, respectively, followed by those of syndiotactic and isotactic. However, an inversion of this tendency between isotactic and syndiotactic PMMAs was found for temperatures lower than 60 °C.

The curves of ${\gamma }_s^d\left(T\right)$ for each of the three examined PMMAs clearly showed three maxima varying from one polymer to another. This interesting observation has to be correlated to the transition phenomena resulting from the influence of the increasing temperature. Indeed, it was shown in previous works [22,23] that the PMMA presents three transition temperatures;

-

The beta-relaxation $T_{\beta }=60 °\mathrm{C}$;

-

The glass transition $T_g=110 °\mathrm{C}$;

-

The liquid–liquid transitions $T_{liq-liq}=160 °\mathrm{C}$.

The above results were perfectly confirmed by the curves of ${\gamma }_s^d\left(T\right)$ of atactic PMMA in Figure 1 and showed the same values obtained in other works. The presence of the maxima in Figure 1 led to the following

Table 1. Values of beta-relaxation, glass transition and liquid-liquid transition temperatures of a-PMMA, i-PMMA and s-PMMA.

Transition Temperature	${\mathit{T}}_{\mathit{\beta }}$	${\mathit{T}}_{\mathit{g}}$	${\mathit{T}}_{\mathit{l}\mathit{i}\mathit{q}-\mathit{l}\mathit{i}\mathit{q}}$
Atactic PMMA	60 °C	110 °C	160 °C
Isotactic PMMA	60 °C	120 °C	170 °C
Syndiotactic PMMA	70 °C	130° C	170 °C

.

Table 1 showed that a shift of 10 °C was observed in the values of $T_g$ and $T_{liq-liq}$ when passing from atactic-PMMA to isotactic, and this shift increased by an additional 10 °C in the case of syndiotactic PMMA. This shift in the transition temperatures is certainly due to the geometric configuration and position of the methacrylate group relative to the principal chain of PMMA, showing that the tacticity of the polymer strongly affects the transition temperatures [22,23].

The variations of ${\gamma }_s^d\left(T\right)$ of each PMMA are composed of four parts of parabolic arcs represented by parabolic equations as shown in

Table 2. Equations of ${\gamma }_s^d\left(T\right)$ of different PMMAs with the corresponding linear regression coefficients in the case of parabolic interpolation.

Atactic PMMA
Equation of ${\gamma }_s^d\left(T\right)$	R2	Temperature interval
${\gamma }_s^d\left(T\right)=0.0451T^2+28.851T+4657.9$	0.935	303.15–333.15 K
${\gamma }_s^d\left(T\right)=0.0282T^2-20.47T+3745.4$	0.9722	333.15–378.15 K
${\gamma }_s^d\left(T\right)=0.0408T^2-33.635T+6940.9$	0.9477	378.15–423.15 K
${\gamma }_s^d\left(T\right)=0.0091T^2-8.647T+2061.4$	0.9902	423.15–473.15 K
Isotactic PMMA
Equation of ${\gamma }_s^d\left(T\right)$	R2	Temperature interval
${\gamma }_s^d\left(T\right)=0.0299T^2-19.277T+3152$	0.9398	303.15–333.15 K
${\gamma }_s^d\left(T\right)=0.0342T^2-25.053T+4607.6$	0.9557	333.15–393.15 K
${\gamma }_s^d\left(T\right)=0.0077T^2-6.795T+1501.7$	0.9925	393.15–443.15 K
${\gamma }_s^d\left(T\right)=0.0051T^2-4.787T+1121.9$	0.9896	443.15–473.15 K
Syndiotactic PMMA
Equation of ${\gamma }_s^d\left(T\right)$	R2	Temperature interval
${\gamma }_s^d\left(T\right)=0.0051T^2-4.790T+1121.9$	0.9485	303.15–343.15 K
${\gamma }_s^d\left(T\right)=0.0115T^2-8.900T+1740.8$	0.9900	343.15–403.15 K
${\gamma }_s^d\left(T\right)=0.0099T^2-8.798T+1967.3$	0.9569	403.15–443.15 K
${\gamma }_s^d\left(T\right)=0.0108T^2-10.079T+2370$	1.000	443.15–473.15 K

and having the following general form:

$${\gamma }_s^d\left(T\right)=a{T}^2+bT+c$$

Table 2 showed the large difference between the ${\gamma }_s^d\left(T\right)$ of the different PMMAs with various tacticities, with a sensitive variation as a function of the temperature. The parabolic interpolation was obtained for the various cases with good linear regression coefficients. The variations of ${\gamma }_s^d\left(T\right)$ are due to the magnitude of the second-order transition temperatures and also to the tacticity of PMMA, as shown in Figure 1.

The linear interpolation shown in

Table 3. Equations of ${\gamma }_s^d\left(T\right)$ of different PMMAs with the corresponding linear regression coefficients with a linear approximation.

	$\mathbf{Equation} \mathbf{of} {\mathit{\gamma }}_{\mathit{s}}^{\mathit{d}}\left(\mathit{T}\right)$	R2	Temperature Interval
Atactic PMMA	${\gamma }_s^d\left(T\right)=-0.292T+144.37$	0.8368	303.15–473.15 K
Isotactic PMMA	${\gamma }_s^d\left(T\right)=-0.303T+143.16$	0.8491	303.15–473.15 K
Syndiotactic PMMA	${\gamma }_s^d\left(T\right)=-0.240T+120.8$	0.8368	303.15–473.15 K

was obtained with a moderate value of the linear regression. This bad correlation is due to the non-linearity of the London dispersive energy as a function of the temperature for the different PMMAs.

However, Table 3 allowed to obtain some useful information on the surface entropy $S_s=-\frac{{d\gamma }_s^d}{dT}$, the London dispersive energy ${\gamma }_s^d(0 \mathrm{K})$ at 0 K and the intrinsic temperature $T_{int.}$ of PMMA surfaces. These values were given in

Table 4. Values of the surface entropy $S_s=-\frac{{d\gamma }_s^d}{dT}$, the London dispersive energy ${\gamma }_s^d(0 \mathrm{K})$ at 0 K and the intrinsic temperature $T_{int.}$ of a-PMMA i-PMMA and s-PMMA.

	${\mathit{S}}_{\mathit{s}}=-{\mathit{d}\mathit{\gamma }}_{\mathit{s}}^{\mathit{d}}/\mathit{d}\mathit{T}(\mathbf{m}\mathbf{J}\times {\mathbf{m}}^{-2}\times {\mathbf{K}}^{-1})$	${\mathit{\gamma }}_{\mathit{s}}^{\mathit{d}}\left(0 \mathbf{K}\right)(\mathbf{m}\mathbf{J}\times {\mathbf{m}}^{-2})$	${\mathit{T}}_{\mathit{i}\mathit{n}\mathit{t}.}\left(\mathbf{K}\right)$
Atactic PMMA	$0.292$	144.37	494.1
Isotactic PMMA	$0.303$	143.16	472.6
Syndiotactic PMMA	$0.240$	120.8	503.8

.

The values of the surface characteristics of the different PMMAs showed an important difference in the behavior of PMMA following its tacticity. It seems that the obtained values of the intrinsic temperatures $T_{int.}$ correspond to the degradation temperatures of PMMAs and can be considered as a specific identity of the polymer. The non-linear variations of ${\gamma }_s^d\left(T\right)$ of different polymers represented by parabolic functions in the different temperature intervals can be considered an original result of this work that also showed important differences in the behavior of the London dispersive energies and an effect of the tacticity of the polymer on ${\gamma }_s^d\left(T\right)$. This result is in good agreement with that obtained by Sharma et al. [16], who proved the effect of polymer tacticity on the contact angle measurements and the surface energy.

3.2. Polar Free Surface Energy of Atactic, Isotactic, and Syndiotactic PMMAs

The chromatographic measurements obtained from the IGC technique led to variations in the $RTlnVn$ of the non-polar and polar solvents adsorbed on the various PMMAs. The results are given in Table S1.

Using the values of the deformation polarizability ${\mathsf{\alpha }}_{0\mathrm{X}}$ and the ionization energies of the various n-alkanes and polar molecules adsorbed on the different PMMA surfaces obtained from the Handbook of Physics and Chemistry [36], it was possible to study the variations of $RTlnVn$ as a function of the chromatographic parameter $\frac{3\mathcal{N}}{{2\left(4\pi {\epsilon }_0\right)}^2}{\mathcal{P}}_{S-X}$ of the different solvents, and therefore to deduce the values of the free polar surface energy ($-∆G_a^p\left(T\right)$) of polar solvents adsorbed on three studied PMMAs. The obtained results are given in Table S2.

The comparison between the polar interaction free energy of the different PMMAs shown in Table S2 for the different polar organic molecules globally highlighted higher values of ($-∆G_a^p\left(T\right)$) in the case of atactic PMMA, followed by syndiotactic PMMA and isotactic PMMA. A higher basic interaction was observed in all PMMAs, showing their higher basicity with an important amphoteric character (Table S2).

The effect of tacticity on the adsorption of polar solvents on PMMA is shown in Figure 2. The curves of the adsorbed polar molecules plotted in Figure 2 also showed a specific signature at the various transition temperatures previously highlighted by the variations of the London dispersive surface energy. The shift in the transition temperatures was also observed in Figure 2 for the different PMMAs. The results presented in Figure 2 show an important variation in the behavior of the different polymers. The atactic PMMA exhibited the highest values with the various solvents, followed by syndiotactic and isotactic PMMAs.

The variations of ($-∆G_a^p\left(T\right)$) of adsorbed solvents on PMMAs led to the determination of their polar enthalpy ($-∆H_a^p\left(T\right)$) and entropy ($-∆S_a^p\left(T\right)$) as a function of the temperature. The obtained values of ($-∆H_a^p\left(T\right)$) and ($-∆S_a^p\left(T\right)$) of the adsorbed solvents on the various PMMAs are given in Tables S3 and S4, and their variations are plotted in Figure 3.

It was observed that the different curves in Figure 3 clearly reflected the various behaviors of the PMMAs based on their tacticities. Three minima of each curve were observed for all PMMAs. These minimal elucidated the presence of the three transition temperatures for the different polymers with a shift of these temperatures for the isotactic and syndiotactic PMMAs.

The positive values of ($-∆H_a^p\left(T\right))$ evocated an adsorption rather than desorption process, while the negative ones signify a desorption reaction. This led to the conclusion that the interaction between the polar solvents and PMMAs is repulsive and that the transition phases are characterized by smaller polar interactions. The comparison between the polar entropy change ($-∆S_a^p\left(T)\right)$ of the solvents adsorbed on the various polymers in general showed an ordered and organized surface of polymers remaining constant for temperatures lower than the beta-relaxation temperature $(T<T_{\beta }=60 °\mathrm{C})$, whereas the disorder dramatically increased around $T_{\beta }$, then decreased after this transition temperature, and stabilized between the temperature interval $T_{\beta }<T<T_g$.

This process continued by repeating the same evolution with a maximum disorder of the surface groups of the different PMMAs around each transition temperature. These observations were more accentuated with the atactic PMMA, and the more ordered case was obtained with the syndiotactic PMMA, justifying its higher crystallinity relative to other PMMAs.

Figure 3 shows the non-linearity variations of ($-∆H_a^p\left(T\right)$) and ($-∆S_a^p\left(T\right)$) against the temperature and this will strongly affect the Lewis acid-base properties which was detailed in the next section.

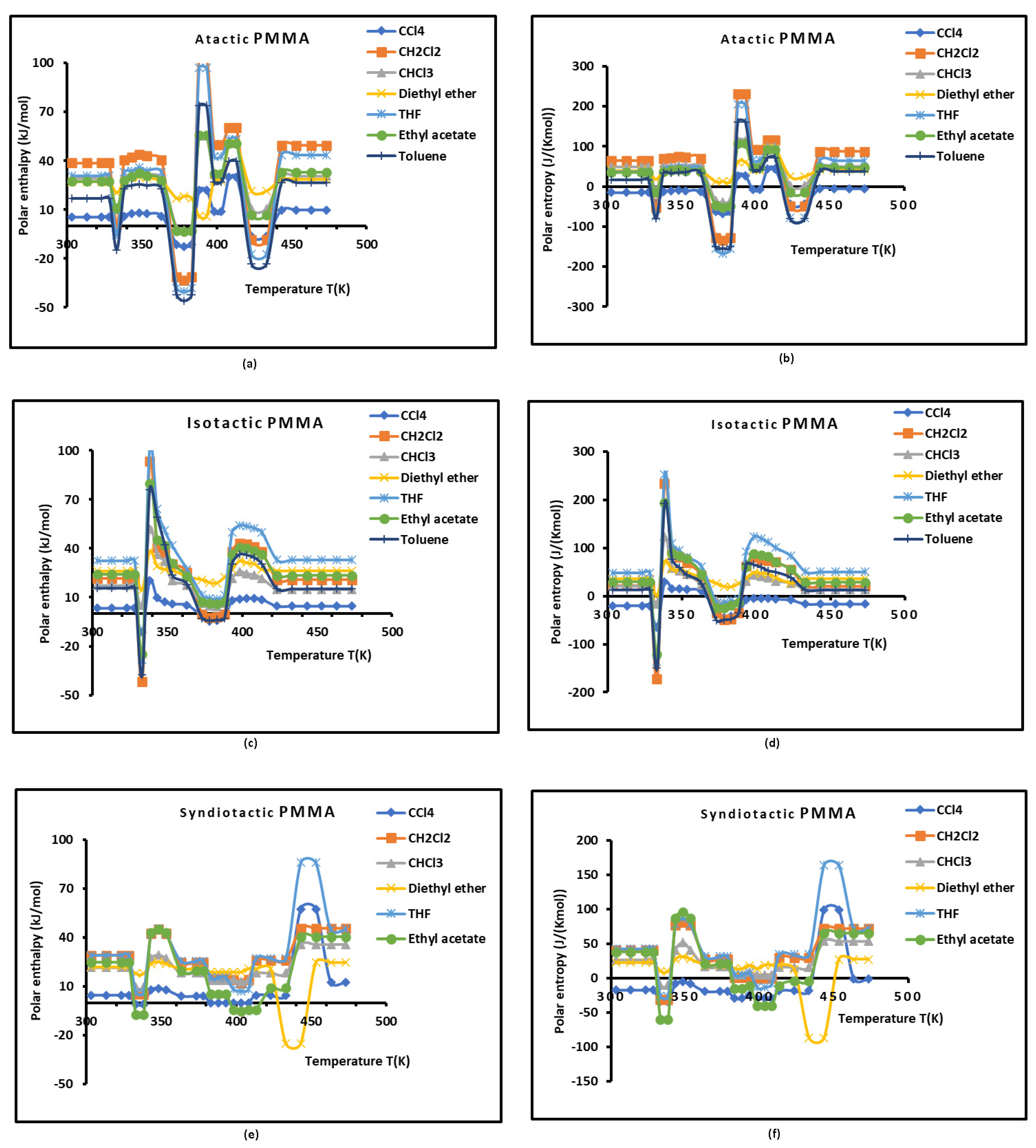
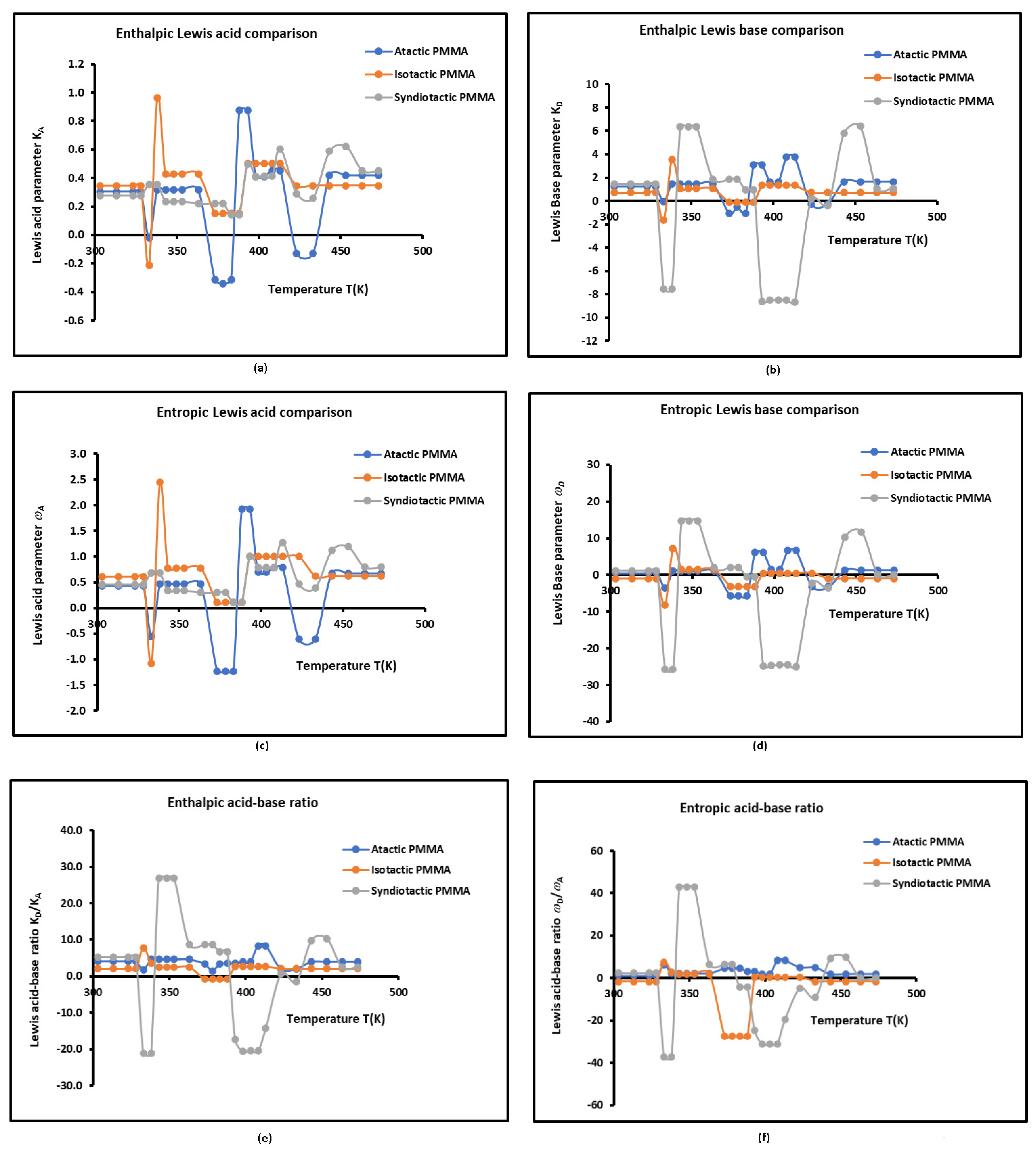
3.3. Lewis’s Acid-Base Properties

The results in Tables S3 and S4 and Figure 3 with the thermodynamic relations 10 and 11 led to the determination of the enthalpic acid base parameters $K_A$ and $K_D$and the entropic acid base parameters ${\omega }_A$ and ${\omega }_D$ of atactic, isotactic, and syndiotactic PMMAs versus the temperature. The non-linearity of ($-∆H_a^p\left(T\right)$) and ($-∆S_a^p\left(T\right)$) of adsorbed solvents necessarily implied the strong variations of the acid-base parameters of PMMAs as a function of temperature. The values of the different enthalpic and entropic acid-base parameters of PMMAs at different tacticities were presented in Table S5 as a function of temperature and led to the corresponding curves in Figure 4. The information collected from Table S5 and Figure 4 is very numerous and precious.

-

The three examined polymers are more basic than acidic in Lewis terms. The basicity of the tactic PMMA is about four times greater than its acidity outside the neighborhood of the transition temperatures of the polymer (Table S5 and Figure 4). Whereas, isotactic PMMA is about 2 to 2.5 times more basic than acid, while syndiotactic PMMA exhibits the highest basicity by showing a surface 5 to 8 times more basic than acid, of course outside the neighborhood of the transition temperatures of the polymer (Table S5 and Figure 4).

-

The Lewis acid $K_A$ parameter of atactic PMMA is comparable to that of isotactic PMMA with a slightly higher value in the isotactic PMMA but greater than that of syndiotactic PMMA. However, the basicity of the latter polymer is higher than that of atactic and isotactic PMMAs. In fact, the alternate acrylate groups present in syndiotactic PMMA principal chain confer the highest basicity of this polymer, whereas the methyl groups in isotactic and atactic PMMAs give the highest Lewis acidity.

-

The Lewis amphoteric character given by the values of $(K_D+K_A)$ and ${(\omega }_D+{\omega }_A)$ which are shown in Table S5 and Figure 4, led to the conclusion that the highest amphoteric surface is obtained with the syndiotactic PMMA followed by the atactic PMMA and isotactic PMMA, certainly due to the highest activity of the surface groups of syndiotactic PMMA.

-

Once again, the curves plotted in Figure 4 showed the three transition temperatures and sudden changes around each transition temperature with a drop in the values of the different acid-base parameters at these transition temperatures of the three polymers. The different parameters rapidly increase after reaching the different minima to be stabilized on positive parameter stages between two transition temperatures of PMMA.

-

The changes in the values of the different acid-base parameters in atactic PMMA are higher than those that happened in isotactic and syndiotactic PMMAs. This is due to the random distribution of the acrylate groups in the PMMA principal chain.

-

An important effect of the temperature on the Lewis acid-base properties of the various PMMAs was highlighted (Table S5 and Figure 4).

-

Results proved an important effect of the tacticity polymer on the Lewis acid-base parameters and the polar surface interactions between the polymers and the organic solvents.

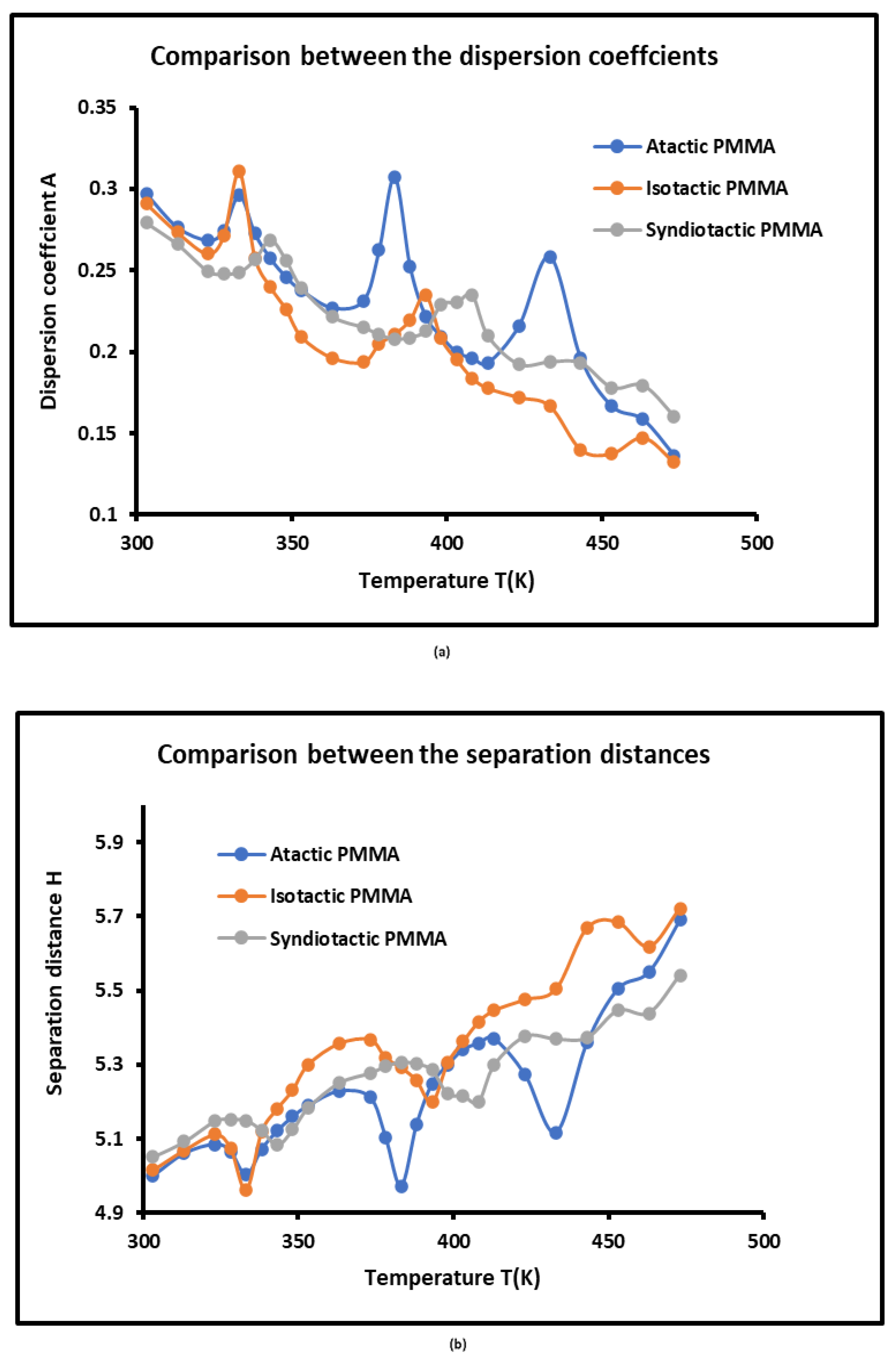
3.4. London Dispersive Free Energies of PMMAs and Dispersion Factor

The values of the dispersion factor $A$ and the London dispersive free energies $∆G_a^d\left(T\right)$ of organic solvents adsorbed on the various PMMAS at different temperatures were obtained from Equations (3) and (5). The obtained results of $∆G_a^d\left(T\right)$ were reported in Table S6 and Figure 5.

The values in Table S6 show that the dispersive interaction energy of atactic PMMA is stronger than that of isotactic and syndiotactic PMMAs. The curves in Figure 5 highlighted the presence of the three transition temperatures of PMMAs, confirming those previously obtained.

The values of the dispersion factor $A$ and the separation distance $H$ of the various PMMA polymers deduced from Equation (5) are given in Table S7. The curves of $A$ and $H$ also showed the presence of the three transition temperatures of the various PMMAs (Figure 6), with a shift in their values from tactic PMMA to another. Even if one observed slight variations of the parameters $A$ and $H$ against the temperature, the transition phenomena were clearly elucidated.

It was shown in Figure 6b that the average separation distance $H$ between the solvents adsorbed on PMMA surfaces increased when the temperature increased, justifying the effect of the thermal agitation on the separation distance. A larger separation distance was observed with the isotactic PMMA, with respect to the two other PMMAs, certainly due to the lower attractive free interaction energy. This new result also showed the tacticity effect on the separation distance between the polymer and the adsorbed organic molecules.

3.5. Lewis Acid-Base Surface Energies of PMMAs and Polar Component of the Surface Energy of Polar Molecules

The Lewis acid ${\gamma }_s^{+}$ and base ${\gamma }_s^{-}$ surface energies of atactic, isotactic, and syndiotactic PMMA were determined using the following Van Oss’s relation [37]:

$$-∆G_a^p\left(X-Polar\right)=2\mathcal{N}{a}_X\left(\sqrt{{\gamma }_{lX}^{-}{\gamma }_s^{+}}+\sqrt{{\gamma }_{lX}^{+}{\gamma }_s^{-}}\right)$$

(12)

where ${\gamma }_{lX}^{+}$ and ${\gamma }_{lX}^{-}$ are the respective acid and base surface energies of the polar molecule $X$ adsorbed on polymer surface with $a_X$ the surface area of the adsorbed solvent.

Knowing that the experimental values of Lewis acid-base energies of ethyl acetate (EA) and dichloromethane (CH₂Cl₂) are given by ${\gamma }_{EA}^{+}=0,{\gamma }_{EA}^{-}=19.2 \mathrm{m}\mathrm{J}/{\mathrm{m}}^2$ and ${\gamma }_{CH2Cl2}^{+}=5.2 \mathrm{m}\mathrm{J}/{\mathrm{m}}^2,{\gamma }_{CH2Cl2}^{-}=0$, respectively, we were able to determine the values of ${\gamma }_s^{+}$ and ${\gamma }_s^{-}$ of PMMAs using Equations (13):

$$\left\{\begin{array}{c}\begin{array}{c}{\gamma }_s^{+}=\frac{{\left[∆G_a^{sp}\left(T\right)\left(EA\right)\right]}^2}{{4\mathcal{N}}^2{\left[a\left(EA\right)\right]}^2{\gamma }_{EA}^{-}} \end{array} \\ {\gamma }_s^{-}=\frac{{\left[∆G_a^{sp}\left(T\right)\left(CH2Cl2\right)\right]}^2}{{4\mathcal{N}}^2{\left[a\left(CH2Cl2\right)\right]}^2{\gamma }_{CH2Cl2}^{+}} \end{array}\right.$$

(13)

The polar acid-base surface energy ${\gamma }_s^{AB}$ of PMMAs was then determined from Equation (14):

$${\gamma }_s^{AB}=2\sqrt{{\gamma }_s^{+}{\gamma }_s^{-}}$$

(14)

The determination of ${\gamma }_s^{AB}$ of PMMAs with the values of the London dispersive surface energy previously discussed in this paper, led to the determination of the Lifshitz—Van der Waals (LW) surface energy ${\gamma }_s^{LW}$ (or total surface energy of the polymer) by using Equation (14):

$${\gamma }_s^{LW}={{\gamma }_s^d+\gamma }_s^{AB}$$

(15)

The values of the different polar acid and base surface energies ${\gamma }_s^{+}$, ${\gamma }_s^{-}$, and ${\gamma }_s^{AB}$ (mJ/m²) of atactic, isotactic, and syndiotactic PMMAs as a function of the temperature were given in

Table 5. Values of the polar acid and base surface energies ${\gamma }_s^{+}$, ${\gamma }_s^{-}$, and ${\gamma }_s^{AB}$ (mJ/m²) of atactic, isotactic, and syndiotactic PMMAs as a function of the temperature.

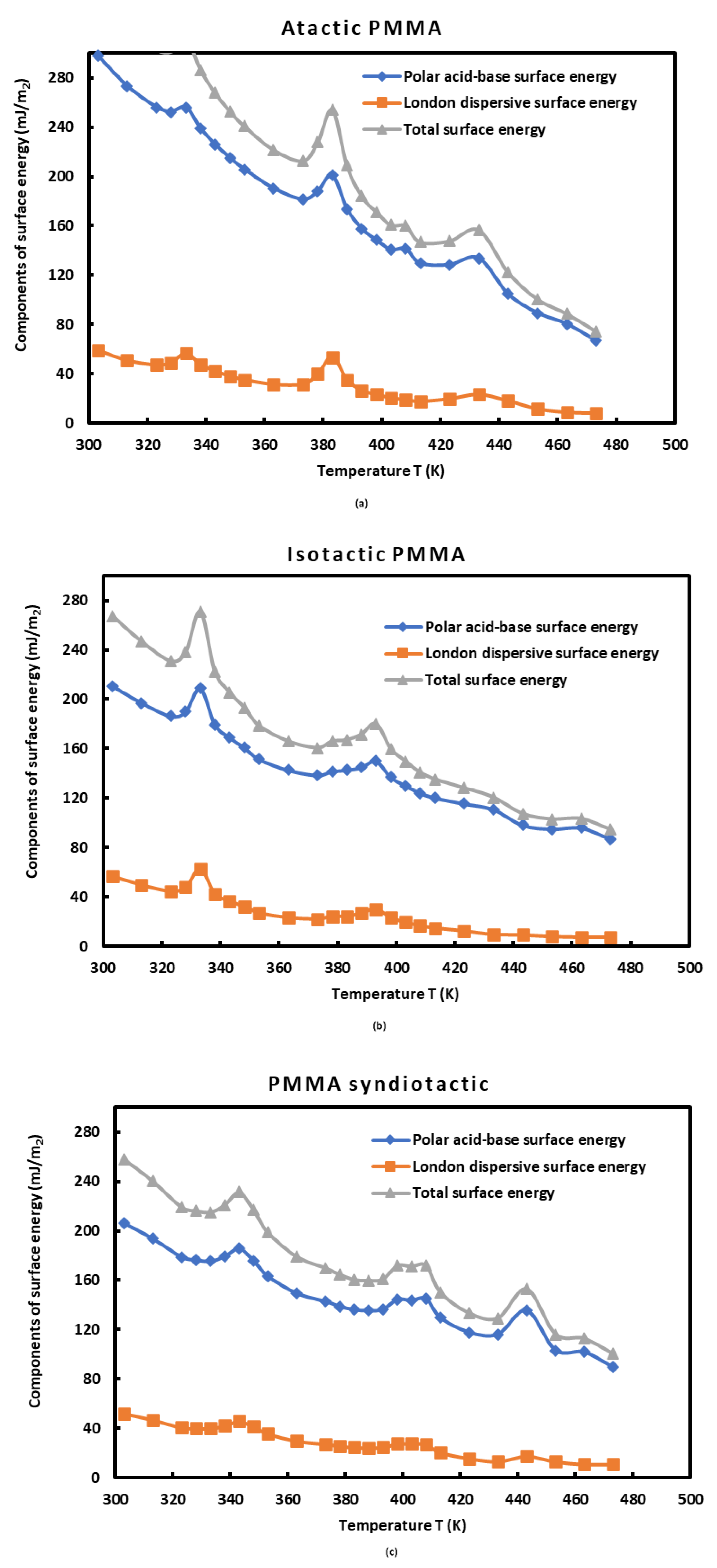
	Atactic PMMA			Isotactic PMMA			Syndiotactic PMMA
T(K)	${\mathit{\gamma }}_{\mathit{s}}^{-}$	${\mathit{\gamma }}_{\mathit{s}}^{+}$	${\mathit{\gamma }}_{\mathit{s}}^{\mathit{A}\mathit{B}}$	${\mathit{\gamma }}_{\mathit{s}}^{-}$	${\mathit{\gamma }}_{\mathit{s}}^{+}$	${\mathit{\gamma }}_{\mathit{s}}^{\mathit{A}\mathit{B}}$	${\mathit{\gamma }}_{\mathit{s}}^{-}$	${\mathit{\gamma }}_{\mathit{s}}^{+}$	${\mathit{\gamma }}_{\mathit{s}}^{\mathit{A}\mathit{B}}$
303.15	203.75	108.73	297.68	123.27	90.13	210.82	151.82	69.97	206.14
313.15	183.42	101.70	273.16	115.44	84.06	197.02	143.04	65.44	193.50
323.15	169.77	96.59	256.11	109.56	79.16	186.25	133.06	59.99	178.69
328.15	167.38	95.20	252.46	112.78	80.16	190.16	130.89	59.37	176.30
333.15	171.41	95.61	256.03	125.91	86.53	208.76	129.50	59.34	175.32
338.15	156.91	90.97	238.96	106.91	75.36	179.52	130.68	61.25	178.94
343.15	146.17	87.28	225.89	100.41	71.04	168.91	133.41	64.53	185.56
348.15	137.38	84.13	215.02	95.56	67.65	160.81	127.25	60.68	175.74
353.15	130.01	81.38	205.72	89.82	63.79	151.39	119.60	55.66	163.18
363.15	118.03	76.64	190.22	84.91	59.76	142.47	110.49	50.45	149.32
373.15	111.70	73.58	181.32	83.16	57.51	138.31	105.40	48.28	142.68
378.15	118.18	74.88	188.14	85.83	58.30	141.48	102.57	46.95	138.79
383.15	129.80	77.62	200.74	87.09	58.32	142.53	100.32	46.05	135.93
388.15	107.09	70.48	173.76	89.07	58.72	144.64	99.29	46.10	135.31
393.15	94.01	65.98	157.52	93.16	60.20	149.77	99.14	46.82	136.26
398.15	87.01	63.28	148.40	84.75	55.19	136.79	102.80	50.62	144.27
403.15	81.01	60.87	140.44	80.55	52.40	129.94	101.53	50.77	143.59
408.15	80.65	61.82	141.22	77.02	49.97	124.08	101.82	51.59	144.95
413.15	73.10	57.31	129.46	74.87	48.29	120.25	92.89	45.13	129.50
423.15	73.07	56.31	128.29	72.51	45.96	115.46	85.25	40.62	117.70
433.15	78.33	57.00	133.64	70.27	43.74	110.89	83.23	40.53	116.15
443.15	56.38	48.50	104.59	62.22	38.64	98.07	94.44	48.59	135.48
453.15	45.40	43.84	89.22	60.93	37.02	94.99	73.62	36.11	103.13
463.15	39.51	40.86	80.36	62.44	36.80	95.87	71.77	36.02	101.68
473.15	30.81	36.16	66.75	56.99	33.15	86.93	63.57	31.50	89.50

.

The atactic PMMA exhibited the highest polar basic surface energy ${\gamma }_s^{-}$, whereas the syndiotactic PMMA presented the highest polar acid surface energy. However, the atactic PMMA had the highest polar acid-base surface energy ${\gamma }_s^{AB}$ due to its highest amphoteric character.

The values in Table 5 led to drawing the curves of Figure 7, giving the polar acid-base surface energy ${\gamma }_s^{AB}$ (mJ/m²), the London dispersive surface energy ${\gamma }_s^d$ (mJ/m²), and the Lifshitz—Van der Waals surface energy ${\gamma }_s^{LW}$ (mJ/m²) of atactic, isotactic, and syndiotactic PMMAs as a function of temperature. It was interesting to notice that the different curves in Figure 7 had the same shape as the previous curves obtained in the study of the various surface thermodynamic parameters, again highlighting the three transition temperatures of the PMMAs.

These results led to the determination of the polar free energy ${\gamma }_l^{\mathrm{p}}$ of polar molecules adsorbed on the various PMMAs with the help of the polar components of the surface energy of PMMA ${\gamma }_s^{\mathrm{p}}$ using relation 16 and the previous results.

$$\left\{\begin{array}{c}-∆G_a^p\left(X\right)=2N{a}_X \sqrt{{\gamma }_s^{\mathrm{p}}{\gamma }_l^{\mathrm{p}}}\\ or {\gamma }_l^{\mathrm{p}}=\frac{{\left(-∆G_a^p\left(X\right)\right)}^2}{4{\mathcal{N}}^2{a_X}^2{\gamma }_s^{\mathrm{p}}} \end{array}\right.$$

(16)

Table S8 reports the values ${\gamma }_l^{\mathrm{p}}\left(T\right)$ of the polar solvents adsorbed on the atactic, isotactic, and syndiotactic PMMAs. The results in Table S8 showed that the highest values of ${\gamma }_l^{\mathrm{p}}\left(T\right)$ were obtained with dichloromethane for the three PMMAs, due to their strong Lewis basicity. However, it was noticed that the different values of ${\gamma }_l^{\mathrm{p}}\left(T\right)$, even if they decrease when the temperature increases, are very small relative to their dispersive components.

The results of the polar acid-base surface energies obtained with the different PMMAs showing a larger deviation in the polar behavior of atactic, isotactic, and syndiotactic PMMAs are in excellent agreement with those obtained by Tretinnikov [15], Sharma et al. [16], and Jha et al. [17,18], who highlighted a certain effect of the tacticity on the polarity and orientation of the a-methyl, ester-methyl, and carbonyl groups of PMMA. This certainly causes an important difference in the Lewis acid-base parameters and polar surface energies of polymers.

4. Conclusions

Inverse gas chromatography at infinite dilution allowed us to study the effect of tacticity on the surface properties of the atactic, isotactic, and syndiotactic PMMAs. The effect of tacticity on London dispersive surface energy, polar free energy, and Lewis’s acid-base surface energies of PMMA was highlighted. The London dispersion interaction energy was applied to separate the polar and dispersive energies of the different n-alkanes and polar solvents adsorbed on the different polymer surfaces. Non-linear variations of ${\gamma }_s^d\left(T\right)$ of the different PMMAs were shown with three maxima highlighting the three transition temperatures of PMMA, the beta-relaxation $T_{\beta }$, glass transition $T_g$, and the liquid-liquid transition $T_{liq-liq}$, with a shift of 10 °C in the values of $T_g$ and $T_{liq-liq}$ when passing from atactic-PMMA to isotactic and an additional shift of 10 °C in the case of syndiotactic PMMA. The curves of ${\gamma }_s^d\left(T\right)$ were assimilated into four parts of perfect parabolic equations, with an important difference in the values of ${\gamma }_s^d\left(T\right)$ between atactic, isotactic, and syndiotactic. The polar interaction free energy $∆G_a^p\left(T\right)$ of polar solvents adsorbed on PMMAs was calculated as a function of temperature. A non-linearity of the different acid-base parameters was observed on all polymer surfaces, proving the highest effect of temperature and tacticity on these parameters and confirming other results obtained in the literature [15,16,17,18]. Our results showed that the basicity of the tactic PMMA is about four times greater than its acidity outside the neighborhood of the transition temperatures of the polymer. Whereas, isotactic PMMA is about 2 to 2.5 times more basic than acid, while syndiotactic PMMA exhibits the highest basicity by showing a surface 5 to 8 times more basic than acid. The Lewis acid $K_A$ parameter of atactic PMMA had a value comparable to that of the isotactic PMMA but greater than that of syndiotactic PMMA. However, the basicity of the latter polymer was higher than that of atactic and isotactic PMMAs.

An important effect of tacticity was proven on the average separation distance between the organic molecules and the polymers, which depends on the temperature. The separation distance was the lowest with atactic PMMA and the highest with syndiotactic PMMA, revealing a maximum of repulsion between the polymer and the solvent in the case of syndiotactic PMMA. This led to larger differences in the values of polar acid-base surface energy ${\gamma }_s^{AB}$, the London dispersive surface energy ${\gamma }_s^d$, and the Lifshitz—Van der Waals surface energy ${\gamma }_s^{LW}$ (mJ/m²) of atactic, isotactic, and syndiotactic PMMAs as a function of temperature.