Molecular Dynamics Calculations for the Temperature Response of Poly(alkylated tri(ethylene oxide)isocyanate) Aqueous Solution
Abstract
:1. Introduction
2. Methodology
2.1. Simulation Details
2.2. Analysis
3. Results and Discussion
3.1. Rigidity of the Main Chain
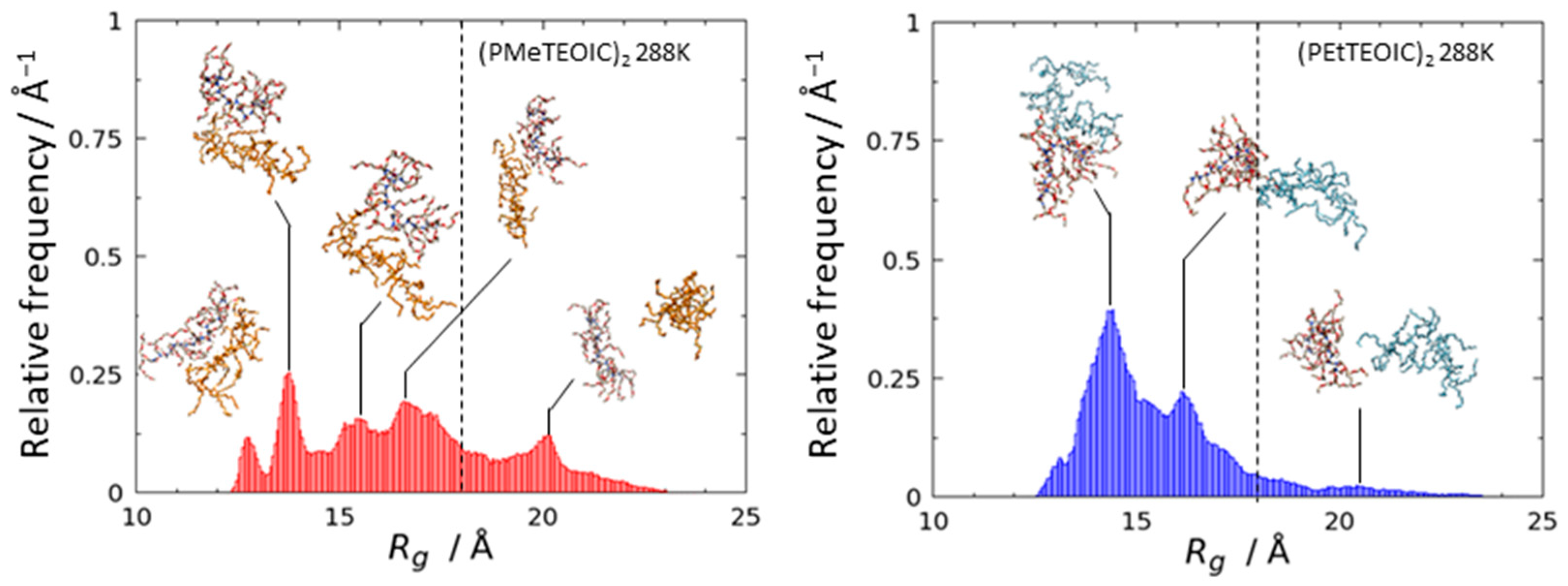
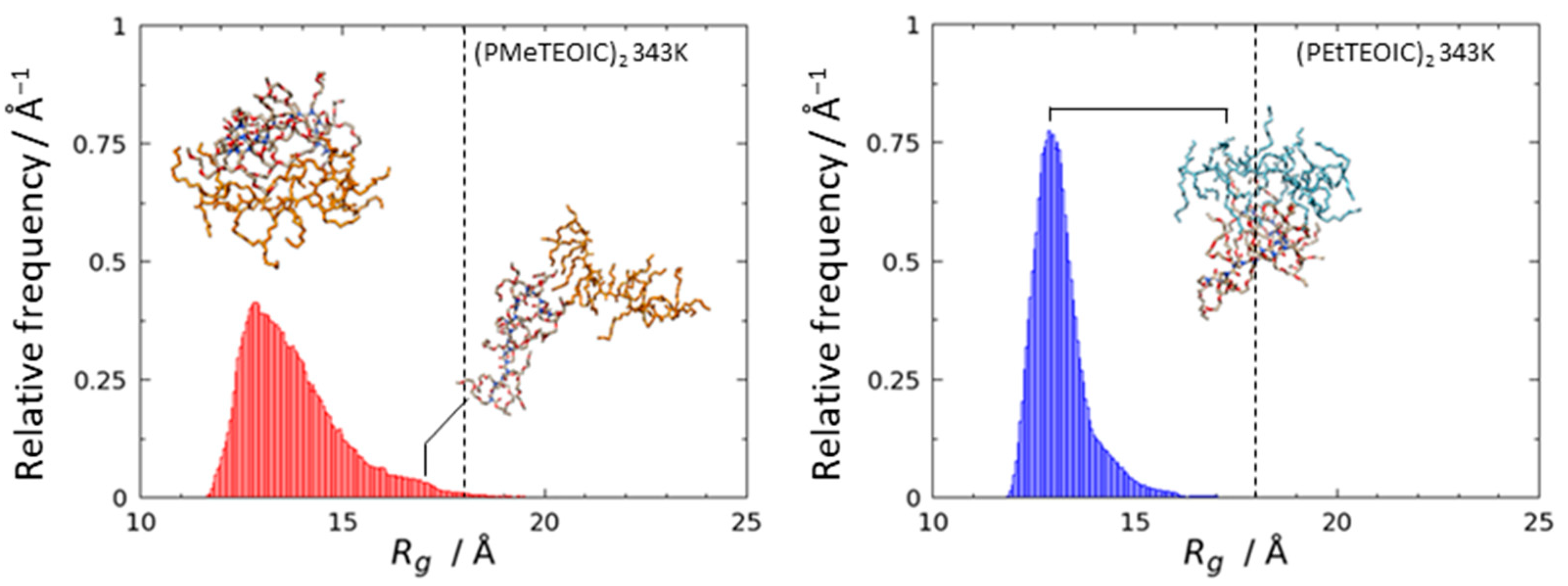
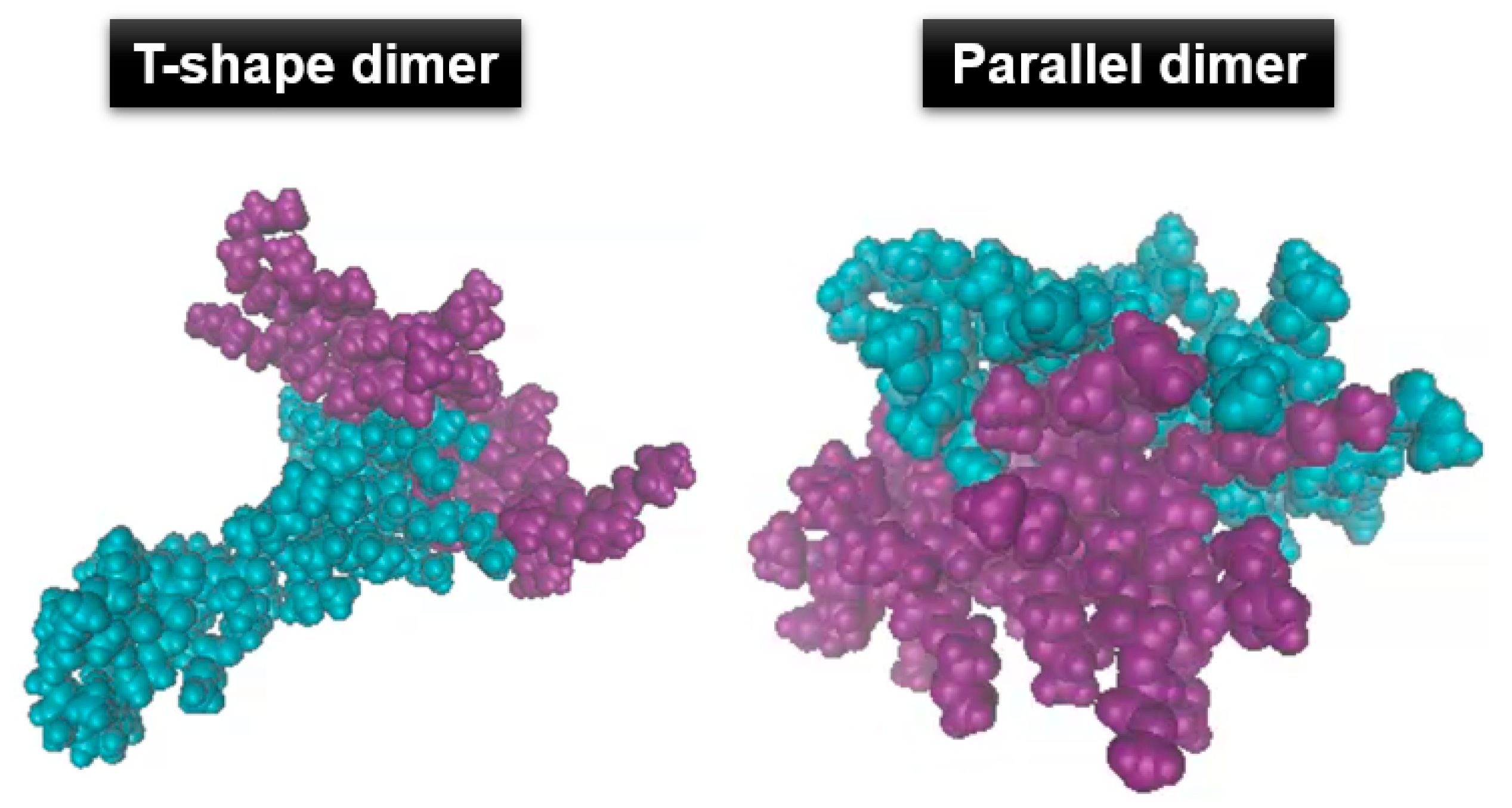
3.2. Agglomeration of (PRTEOIC)2
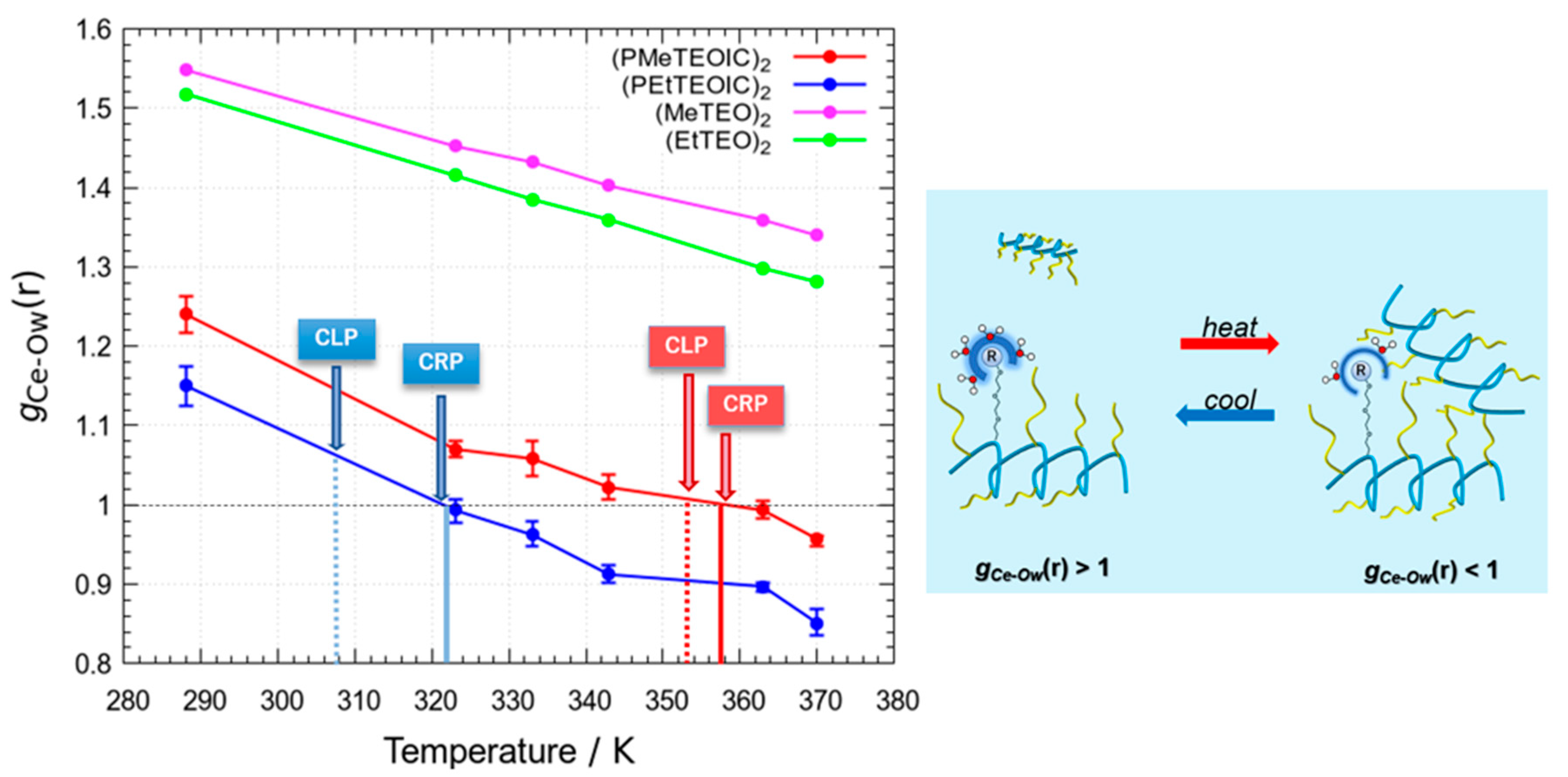
3.3. Radial Distribution Functions of Water Molecules around the PRTEOIC Dimer
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crespy, D.; Rossi, R.M. Temperature-Responsive Polymers with LCST in the Physiological Range and Their Applications in Textiles. Polym. Int. 2007, 56, 1461–1468. [Google Scholar] [CrossRef]
- Baba, S.; Enomoto, Y.; Duan, Q.; Kiba, T.; Kakuchi, T.; Sato, S.-I. Temperature-Sensitive Association Properties of End-Functionalized Poly(N-Isopropylacrylamide) in Dilute Aqueous Solutions. Mol. Cryst. Liq. Cryst. 2009, 505, 247–256. [Google Scholar] [CrossRef]
- Duan, Q.; Narumi, A.; Miura, Y.; Shen, X.; Sato, S.-I.; Satoh, T.; Kakuchi, T. Thermoresponsive Property Controlled by End-Functionalization of Poly(N-Isopropylacrylamide) with Phenyl, Biphenyl, and Triphenyl Groups. Polym. J. 2006, 38, 306–310. [Google Scholar] [CrossRef]
- Chiessi, E.; Paradossi, G. Influence of Tacticity on Hydrophobicity of Poly(N-Isopropylacrylamide): A Single Chain Molecular Dynamics Simulation Study. J. Phys. Chem. B 2016, 120, 3765–3776. [Google Scholar] [CrossRef] [PubMed]
- Winnik, F.M. Fluorescence Studies of Aqueous Solutions of Poly(N-Isopropylacrylamide) below and above Their LCST. Macromolecules 1990, 23, 233–242. [Google Scholar] [CrossRef]
- Farinha, J.P.S.; Piçarra, S.; Miesel, K.; Martinho, J.M.G. Fluorescence Study of the Coil-Globule Transition of a PEO Chain in Toluene. J. Phys. Chem. B 2001, 105, 10536–10545. [Google Scholar] [CrossRef]
- Susana Piçarra, P.R.; Afonso, C.A.M.; Martinho, J.M.G.; Farinha, J.P.S. Coil-Globule Transition of Poly(Dimethylacrylamide): Fluorescence and Light Scattering Study. Macromolecules 2003, 36, 8119–8129. [Google Scholar] [CrossRef]
- Kubota, K.; Fujishige, S.; Ando, I. Single-Chain Transition of Poly(N-Isopropylacrylamide) in Water. J. Phys. Chem. 1990, 94, 5154–5158. [Google Scholar] [CrossRef]
- Wang, X.; Wu, C. Light-Scattering Study of Coil-to-Globule Transition of a Poly(N-Isopropylacrylamide) Chain in Deuterated Water. Macromolecules 1999, 32, 4299–4301. [Google Scholar] [CrossRef]
- Lessard, D.G.; Ousalem, M.; Zhu, X.X.; Eisenberg, A.; Carreau, P.J. Study of the Phase Transition of Poly(N,N-Diethylacrylamide) in Water by Rheology and Dynamic Light Scattering. J. Polym. Sci. Part B Polym. Phys. 2003, 41, 1627–1637. [Google Scholar] [CrossRef]
- Yanase, K.; Buchner, R.; Sato, T. Microglobule Formation and a Microscopic Order Parameter Monitoring the Phase Transition of Aqueous Poly(N-Isopropylacrylamide) Solution. Phys. Rev. Mater. 2018, 2, 85601. [Google Scholar] [CrossRef]
- Lerch, A.; Käfer, F.; Prévost, S.; Agarwal, S.; Karg, M. Structural Insights into Polymethacrylamide-Based LCST Polymers in Solution: A Small-Angle Neutron Scattering Study. Macromolecules 2021, 54, 7632–7641. [Google Scholar] [CrossRef]
- Deshmukh, S.A.; Sankaranarayanan, S.K.R.S.; Suthar, K.; Mancini, D.C. Role of Solvation Dynamics and Local Ordering of Water in Inducing Conformational Transitions in Poly(N-Isopropylacrylamide) Oligomers through the LCST. J. Phys. Chem. B 2012, 116, 2651–2663. [Google Scholar] [CrossRef] [PubMed]
- Tavagnacco, L.; Zaccarelli, E.; Chiessi, E. On the Molecular Origin of the Cooperative Coil-to-Globule Transition of Poly(N-Isopropylacrylamide) in Water. Phys. Chem. Chem. Phys 2018, 20, 9997–10010. [Google Scholar] [CrossRef]
- Futscher, M.H.; Philipp, M.; Müller-Buschbaum, P.; Schulte, A. The Role of Backbone Hydration of Poly(N-Isopropyl Acrylamide) Across the Volume Phase Transition Compared to Its Monomer. Sci. Rep. 2017, 7, 17012. [Google Scholar] [CrossRef]
- Tonelli, A.E. Conformational Characteristics of the Poly(n-Alkyl Isocyanates). Macromolecules 1974, 7, 628–631. [Google Scholar] [CrossRef]
- Cook, R. Flexibility in Rigid Rod Poly(n-Alkyl Isocyanates). Macromolecules 1987, 20, 1961–1964. [Google Scholar] [CrossRef]
- Young, J.A.; Cook, R.C. Helix Reversal Motion in Polyisocyanates. Macromolecules 2001, 34, 3646–3653. [Google Scholar] [CrossRef]
- Mayer, S.; Zentel, R. Chiral Polyisocyanates, a Special Class of Helical Polymers. Prog. Polym. Sci. 2001, 26, 1973–2013. [Google Scholar] [CrossRef]
- Ute, K.; Fukunishi, Y.; Jha, S.K.; Cheon, K.-S.; Muñ Oz, B.; Hatada, K.; Green, M.M. Dynamic NMR Determination of the Barrier for Interconversion of the Left-and Right-Handed Helical Conformations in a Polyisocyanate. Macromolecules 1999, 32, 1304–1307. [Google Scholar] [CrossRef]
- Green, M.M.; Peterson, N.C.; Sato, T.; Teramoto, A.; Cook, R.; Shneior, L. A Helical Polymer with a Cooperative Response to Chiral Information. Science 1995, 268, 1860–1866. [Google Scholar] [CrossRef]
- Green, M.M.; Gross, R.A.; Crosby, C., III; Schilling, F.C. Macromolecular Stereochemistry: The Effect of Pendant Group Structure on the Axial Dimension of Polyisocyanates. Macromolecules 1987, 20, 992–999. [Google Scholar] [CrossRef]
- Berger, M.N.; Tidswell, B.M. Dilute Solution Viscosity and Conformation of Poly-n-Hexyl Isocyanate. J. Polym. Sci. Polym. Symp. 1973, 42, 1063–1075. [Google Scholar] [CrossRef]
- Murakami, H.; Norisuye, T.; Fujita, H. Dimensional and Hydrodynamic Properties of Poly(Hexyl Isocyanate) in Hexane. Macromolecules 1980, 13, 345–352. [Google Scholar] [CrossRef]
- Conio, G.; Bianchi, E.; Ciferri, A.; Krigbaum, W.R. Mesophase Formation by Semirigid Polymers: Poly(n-Hexyl Isocyanate) in Dichloromethane and Toluene. Macromolecules 1984, 17, 856–861. [Google Scholar] [CrossRef]
- Cook, R.; Johnson, R.D.; Wade, C.G.; O’Leary, D.J.; Munoz, B.; Green, M.M. Solvent Dependence of the Chain Dimensions of Poly(n-Hexyl Isocyanate). Macromolecules 1990, 23, 3454–3458. [Google Scholar] [CrossRef]
- Pica, A.; Graziano, G. On the Effect of Sodium Salts on the Coil-to-Globule Transition of Poly(N-Isopropylacrylamide). Phys. Chem. Chem. Phys. 2015, 17, 27750–27757. [Google Scholar] [CrossRef]
- Pica, A.; Graziano, G. Effect of Sodium Thiocyanate and Sodium Perchlorate on Poly(: N -Isopropylacrylamide) Collapse. Phys. Chem. Chem. Phys. 2019, 22, 189–195. [Google Scholar] [CrossRef]
- Case, D.A.; Babin, V.; Berryman, J.T.; Betz, R.M.; Cai, Q.; Cerutti, D.S.; Cheatham, T.E., III; Darden, T.A.; Duke, R.E.; Gohlke, H.; et al. Amber14 2014, AMBER 14; University of California: San Francisco, CA, USA, 2014. [Google Scholar]
- Sakai, N.; Jin, M.; Sato, S.I.; Satoh, T.; Kakuchi, T. Synthesis of Water-Soluble Polyisocyanates with the Oligo(Ethylene Glycol) Side-Chain as New Thermoresponsive Polymers. Polym. Chem. 2014, 5, 1057–1062. [Google Scholar] [CrossRef]
- Jakalian, A.; Bruce, L.; Bush, D.B.; Jack, C.I.B. Fast, Efficient Generation of High-Quality Atomic Charges. AM1-BCC Model: I. Method. Comput. Chem. 2000, 21, 132–146. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic Atom Type and Bond Type Perception in Molecular Mechanical Calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and Testing of a General AMBER Force Field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An N⋅Log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089. [Google Scholar] [CrossRef]
- Dalgakiran, E.; Tatlipinar, H. The Role of Hydrophobic Hydration in the LCST Behaviour of POEGMA300by All-Atom Molecular Dynamics Simulations. Phys. Chem. Chem. Phys. 2018, 20, 15389–15399. [Google Scholar] [CrossRef]
- Dalgakiran, E.; Tatlipinar, H. Atomistic Insights on the LCST Behavior of PMEO2MA in Water by Molecular Dynamics Simulations. J. Polym. Sci. Part B Polym. Phys. 2018, 56, 429–441. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision, C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Miyazaki, M.; Fujii, M. Real Time Observation of the Excimer Formation Dynamics of a Gas Phase Benzene Dimer by Picosecond Pump-Probe Spectroscopy. Phys. Chem. Chem. Phys. 2015, 17, 25989–25997. [Google Scholar] [CrossRef]
- Matsuyama, A.; Tanaka, F. Theory of Solvation-Induced Reentrant Phase Separation in Polymer Solutions. Phys. Rev. Lett. 1990, 65, 341–344. [Google Scholar] [CrossRef]
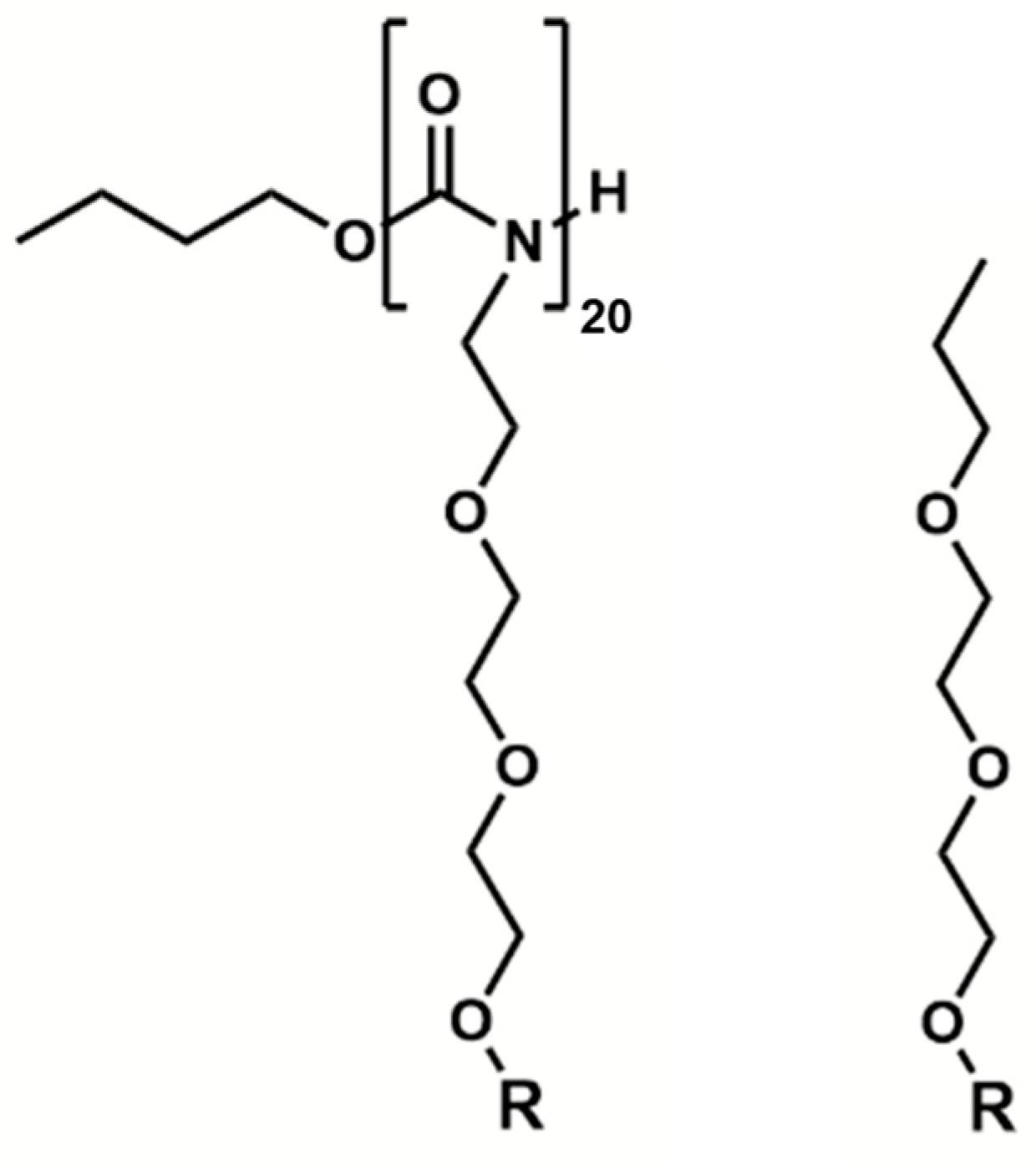



| Polymer Chains | |Eelec/EvdW| | 1 | 2 | |||||
|---|---|---|---|---|---|---|---|---|
| 283 K | 323 K | 333 K | 343 K | 363 K | 370 K | |||
| (PMeTEOIC)2 | 3.45 ± 0.27 | 3.17 ± 0.28 | 3.31 ± 0.29 | 3.24 ± 0.31 | 3.23 ± 0.28 | 3.15 ± 0.03 | 3.26 | 0.10 |
| (PEtTEOIC)2 | 2.99 ± 0.22 | 3.15 ± 0.23 | 3.06 ± 0.25 | 2.91 ± 0.28 | 3.16 ± 0.35 | 2.99 ± 0.01 | 3.04 | 0.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mizutani, S.; Kita, S.; Sakai, N.; Yamamoto, T.; Koleżyński, A.; Kakuchi, T.; Sato, S.-i. Molecular Dynamics Calculations for the Temperature Response of Poly(alkylated tri(ethylene oxide)isocyanate) Aqueous Solution. Macromol 2023, 3, 653-664. https://doi.org/10.3390/macromol3030036
Mizutani S, Kita S, Sakai N, Yamamoto T, Koleżyński A, Kakuchi T, Sato S-i. Molecular Dynamics Calculations for the Temperature Response of Poly(alkylated tri(ethylene oxide)isocyanate) Aqueous Solution. Macromol. 2023; 3(3):653-664. https://doi.org/10.3390/macromol3030036
Chicago/Turabian StyleMizutani, Shunsuke, Shunya Kita, Naoya Sakai, Takuya Yamamoto, Andrej Koleżyński, Toyoji Kakuchi, and Shin-ichiro Sato. 2023. "Molecular Dynamics Calculations for the Temperature Response of Poly(alkylated tri(ethylene oxide)isocyanate) Aqueous Solution" Macromol 3, no. 3: 653-664. https://doi.org/10.3390/macromol3030036
APA StyleMizutani, S., Kita, S., Sakai, N., Yamamoto, T., Koleżyński, A., Kakuchi, T., & Sato, S.-i. (2023). Molecular Dynamics Calculations for the Temperature Response of Poly(alkylated tri(ethylene oxide)isocyanate) Aqueous Solution. Macromol, 3(3), 653-664. https://doi.org/10.3390/macromol3030036








