Development and Characterization of Novel Anisotropic Skin Graft Simulants
Abstract
1. Introduction
2. Materials and Methods
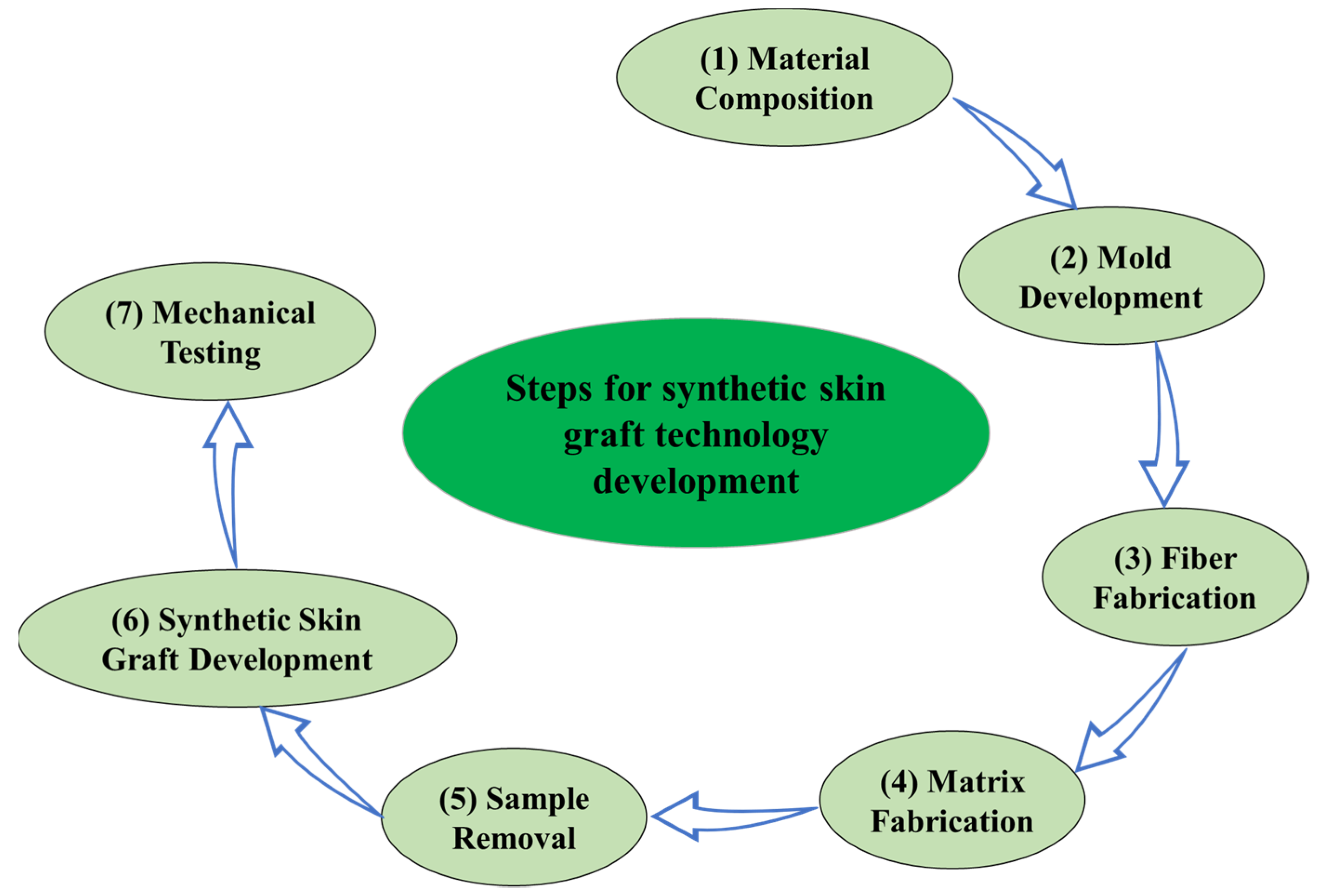
- Material composition: A suitable material composition was selected for the matrix and fibers to develop the anisotropic synthetic skin.
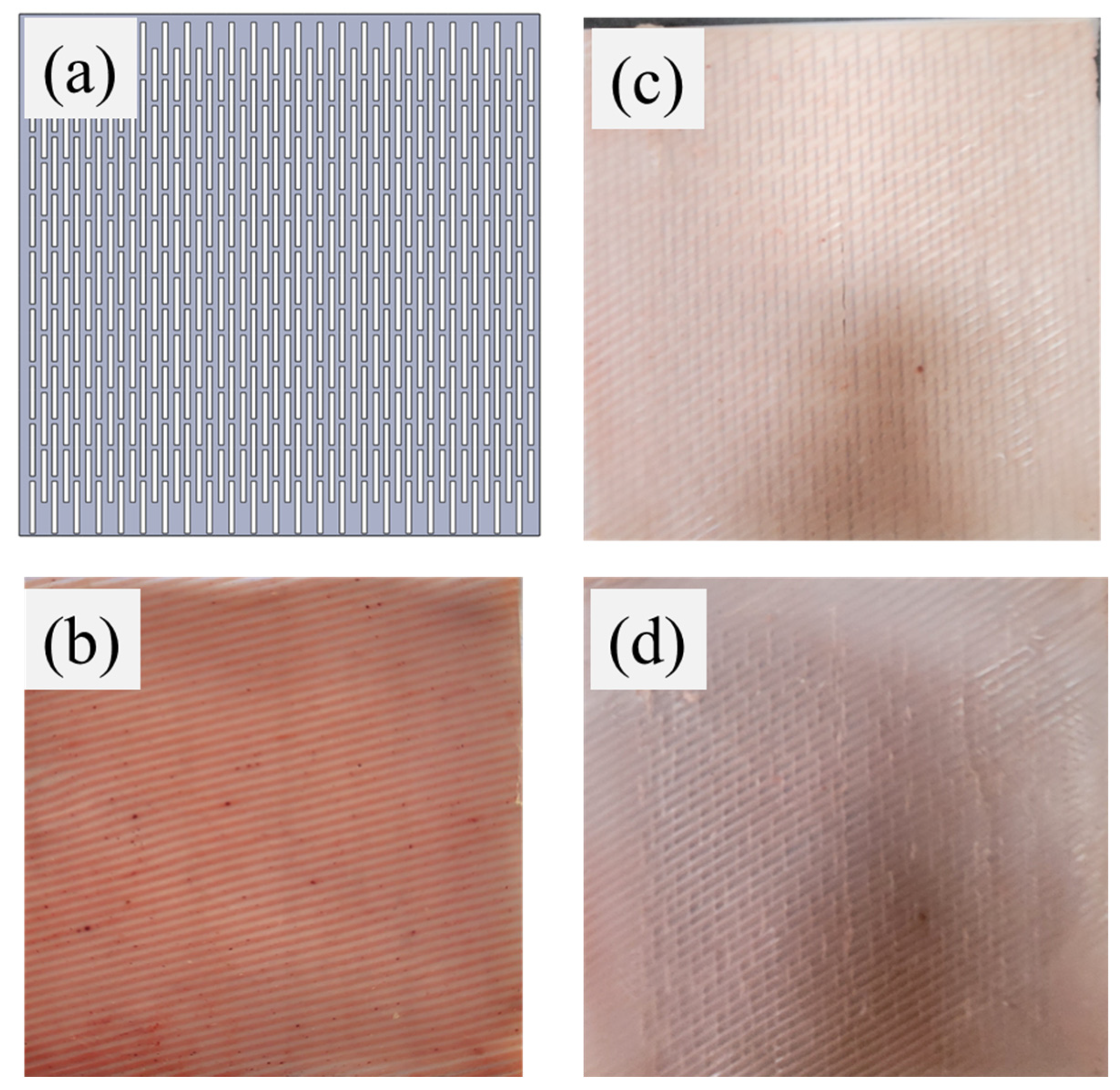
- Mold development: Different molds were designed for different fiber orientations and for hosting the material compositions for the fiber and matrix. The designs were printed using a high-definition 3D printer.
- Fiber fabrication: The material for the fibers was first poured into the channels in the mold, and then left to set for 30 min.
- Matrix fabrication: The material for the matrix was poured on top of the partially set fibers and filled the entire mold after 30 min, and was left to set for 8 h.
- Sample removal: After 8 h, the fibers and matrix were integrated, and the synthetic skin sample could be removed from the mold.
- Synthetic skin graft development: Stencils or dies with a slit cut pattern as per the meshing ratios (e.g., 1:3) were 3D printed and a cutting knife could be used to cut the slits, or they could be cut directly using a 3D cutter.
2.1. Design and Development of One-Layer Synthetic Skin
2.2. Development of Two-Layer Synthetic Skin
2.3. Development of Anisotropic Synthetic Skin Grafts
2.4. Material Characterization
3. Results
3.1. Biaxial Expansion of Anisotropic Synthetic Skin Grafts
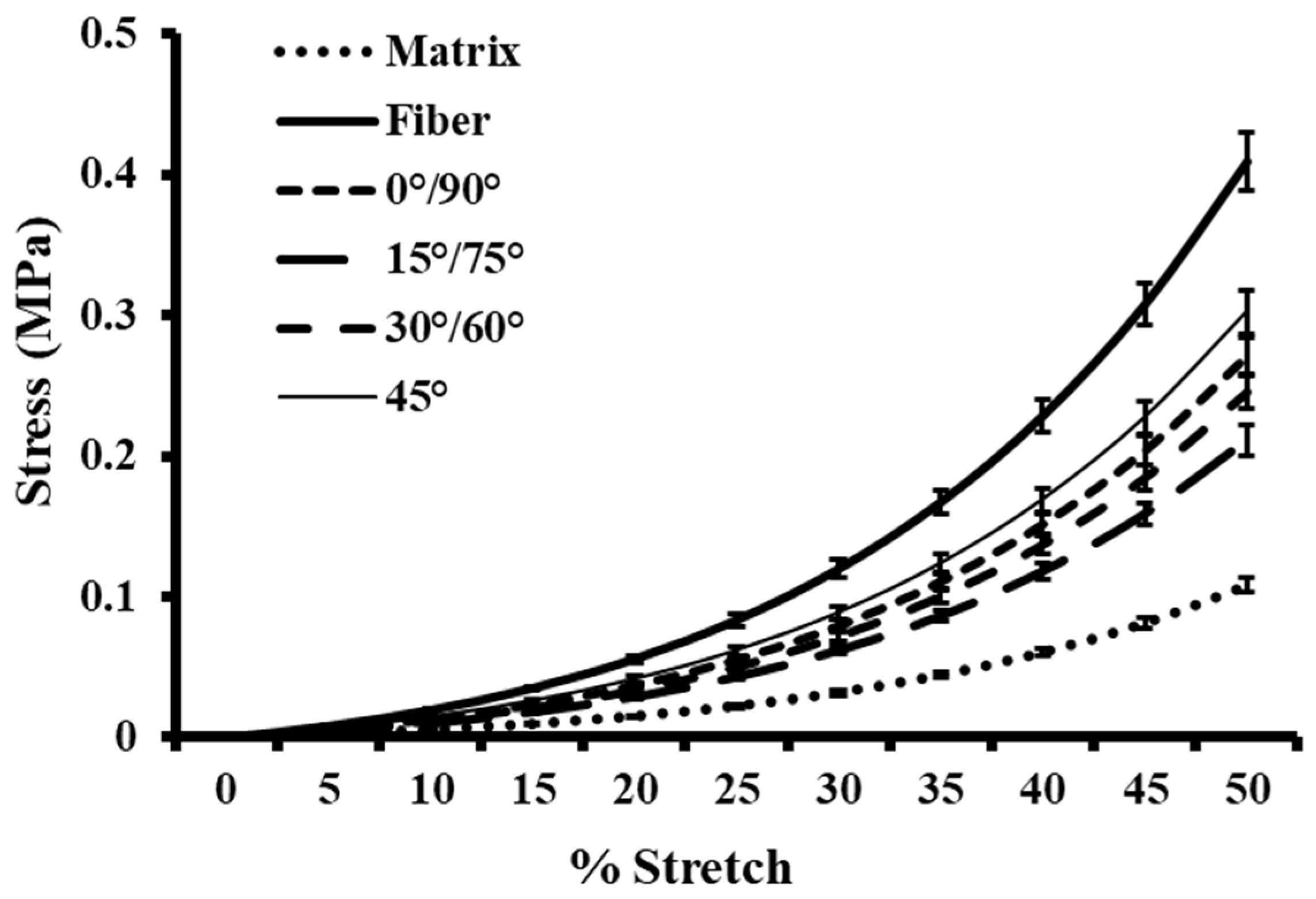
3.2. Biomechanical Behavior of Anisotropic One-Layer Synthetic Skin Grafts
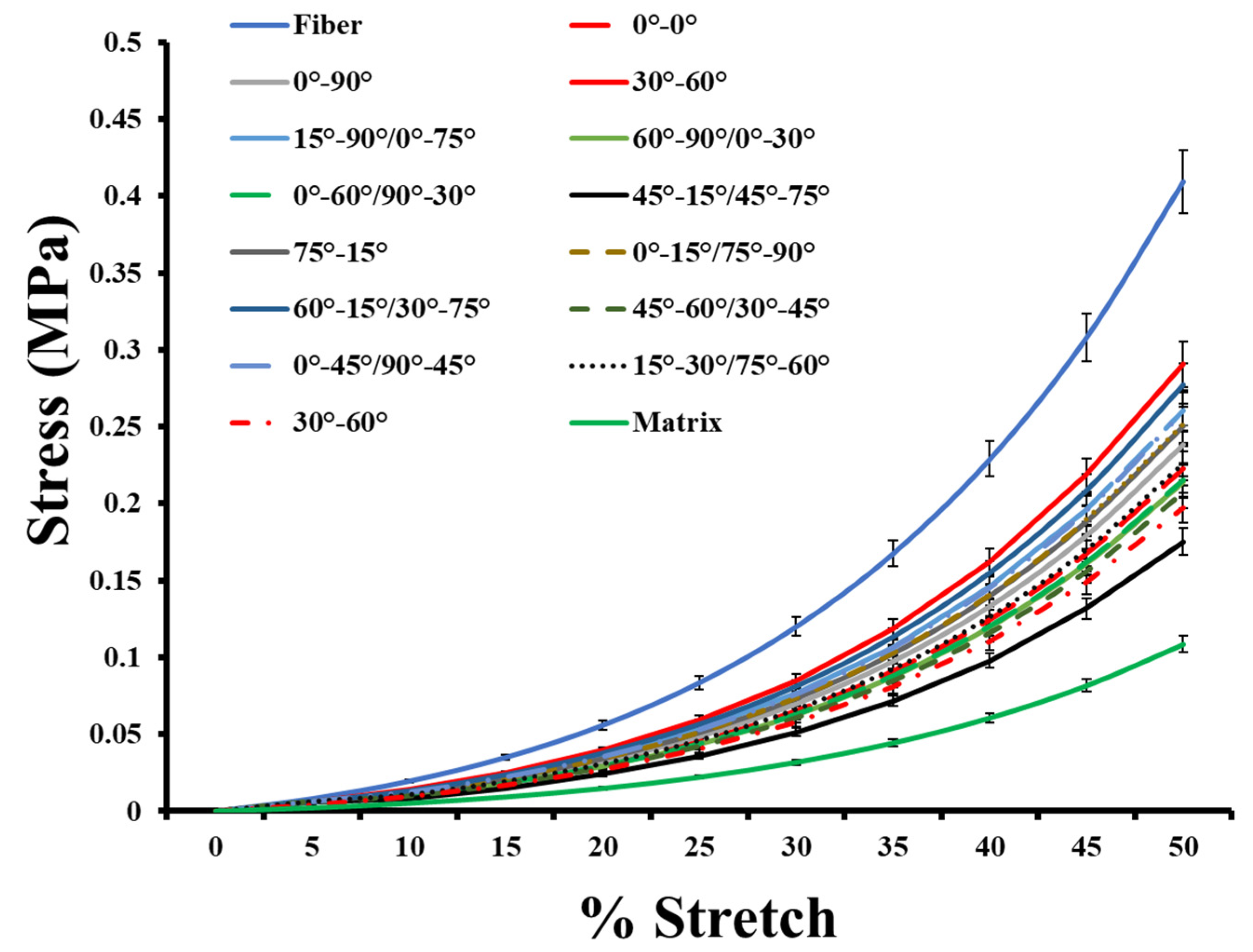
3.3. Biomechanical Behavior of Anisotropic Two-Layer Synthetic Skin Grafts
3.4. Hyperelastic Modelling of Anisotropic Synthetic Skin Grafts
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Capek, L.; Flynn, C.; Molitor, M.; Chong, S.; Henys, P. Graft orientation influences meshing ratio. Burns 2018, 44, 1439–1445. [Google Scholar] [CrossRef]
- Gupta, V.; Chanda, A. Biomechanics of skin grafts: Effect of pattern size, spacing and orientation. Eng. Res. Express 2022, 4, 015006. [Google Scholar] [CrossRef]
- Johnson, T.M.; Ratner, D.; Nelson, B.R. Soft tissue reconstruction with skin grafting. J. Am. Acad. Dermatol. 1992, 27, 151–165. [Google Scholar] [CrossRef]
- Marín-Martínez, F.M.; Martínez-Valls, P.L.G.; Dekalo, S.; Weiss, J.; Haran, O. Aesthetic and Functional Results after Single- and Two-Stage Resection and Reconstruction of Penile Paraffinomas—Experience from Two Tertiary Centers and a Surgical Management Algorithm. Urology 2023, 171, 227–235. [Google Scholar] [CrossRef]
- Kohlhauser, M.; Luze, H.; Nischwitz, S.P.; Kamolz, L.P. Historical evolution of skin grafting—A journey through time. Medicina 2021, 57, 348. [Google Scholar] [CrossRef]
- Khan, Z.; Utheim, T.P.; Byholt, M.; Fiabema, T.; Sylvester-Jensen, H.C.; Tønseth, K.A. Hudtransplantasjon. Tidsskr. Nor. Laegeforening 2022, 142, 671. [Google Scholar] [CrossRef]
- Singh, G.; Gupta, V.; Chanda, A. Mechanical Characterization of Rotating Triangle Shaped Auxetic Skin Graft Simulants. Facta Univ. Ser. Mech. Eng. 2022, 1–16. [Google Scholar] [CrossRef]
- Gupta, S.; Gupta, V.; Chanda, A. Biomechanical modeling of novel high expansion auxetic skin grafts. Int. J. Numer. Method. Biomed. Eng. 2022, 38, e3586. [Google Scholar] [CrossRef] [PubMed]
- Persinal-Medina, M.; Llames, S.; Chacón, M.; Vázquez, N.; Pevida, M.; Alcalde, I.; Alonso-Alonso, S.; Martínez-López, L.M.; Merayo-Lloves, J.; Meana, A. Polymerizable Skin Hydrogel for Full Thickness Wound Healing. Int. J. Mol. Sci. 2022, 23, 4837. [Google Scholar] [CrossRef] [PubMed]
- Jeschke, M.G.; Van Baar, M.E.; Choudhry, M.A.; Chung, K.K.; Gibran, N.S.; Logsetty, S. Burn injury. Nat. Rev. Dis. Prim. 2020, 6, 11. [Google Scholar] [CrossRef] [PubMed]
- Shukla, S.; Behera, B.K. Auxetic fibrous materials and structures in medical engineering–A review. Bioeng. Transl. Med. 2022, 7, 1–12. [Google Scholar] [CrossRef]
- Liu, T.; Qiu, C.; Lu, H.; Li, H.; Zhu, S.; Ma, L. A novel recombinant human collagen hydrogel as minced split-thickness skin graft overlay to promote full-thickness skin defect reconstruction. Burns 2023, 49, 169–181. [Google Scholar] [CrossRef]
- Ozhathil, D.K.; Tay, M.W.; Wolf, S.E.; Branski, L.K. A narrative review of the history of skin grafting in burn care. Medicina 2021, 57, 380. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, J.; Wang, B.; Wang, Y.; Kang, C.; Zhang, Q. Total Auricular Reconstruction Using a Single Extended Postauricular Flap without Skin Grafting in Two Stages: Experiences of 106 Cases. Aesthetic Plast. Surg. 2020, 44, 365–372. [Google Scholar] [CrossRef]
- Schlottmann, F.; Bucan, V.; Vogt, P.M.; Krezdorn, N. A short history of skin grafting in burns: From the gold standard of autologous skin grafting to the possibilities of allogeneic skin grafting with immunomodulatory approaches. Medicina 2021, 57, 225. [Google Scholar] [CrossRef]
- Łabuś, W.; Kitala, D.; Klama-Baryła, A.; Szapski, M.; Smętek, W.; Kraut, M.; Poloczek, R.; Glik, J.; Pielesz, A.; Binias, D.; et al. A new approach to the production of a biovital skin graft based on human acellular dermal matrix produced in-house, in vitro revitalized internally by human fibroblasts and keratinocytes on the surface. J. Biomed. Mater. Res. Part B Appl. Biomater. 2019, 108, 1281–1294. [Google Scholar] [CrossRef] [PubMed]
- Larson, K.W.; Austin, C.L.; Thompson, S.J. Treatment of a full-thickness burn injury with novosorb biodegradable temporizing matrix and recell autologous skin cell suspension: A case series. J. Burn Care Res. 2020, 41, 215–219. [Google Scholar] [CrossRef] [PubMed]
- Yoon, J.; Yoon, D.; Lee, H.; Lee, J.; Jo, S.; Kym, D.; Yim, H.; Hur, J.; Chun, W.; Kim, G.; et al. Wound healing ability of acellular fish skin and bovine collagen grafts for split-thickness donor sites in burn patients: Characterization of acellular grafts and clinical application. Int. J. Biol. Macromol. 2022, 205, 452–461. [Google Scholar] [CrossRef]
- Rijpma, D.; Claes, K.; Hoeksema, H.; de Decker, I.; Verbelen, J.; Monstrey, S.; Pijpe, A.; van Zuijlen, P.; Vries, A.M.-D. The Meek micrograft technique for burns; review on its outcomes: Searching for the superior skin grafting technique. Burns 2022, 48, 1287–1300. [Google Scholar] [CrossRef]
- Lari, A.R.; Gang, R.K. Expansion technique for skin grafts (Meek technique) in the treatment of severely burned patients. Burns 2001, 27, 61–66. [Google Scholar] [CrossRef]
- Kreis, R.; Mackie, D.; Vloemans, A.; Hermans, R.; Hoekstra, M. Widely expanded postage stamp skin grafts using a modified Meek technique in combination with an allograft overlay. Burns 1993, 19, 142–145. [Google Scholar] [CrossRef]
- Vandeput, J.; Nelissen, M.; Tanner, J.C.; Boswick, J. A review of skin meshers. Burns 1995, 21, 364–370. [Google Scholar] [CrossRef]
- Karaçal, N.; Ambarcioǧlu, Ö.; Topal, U.; Gülçelik, N.; Kutlu, N. Skin graft mesher: An easy method of cartilage graft dicing. Plast. Reconstr. Surg. 2004, 114, 826–828. [Google Scholar] [CrossRef]
- Noureldin, M.A.; Said, T.A.; Makeen, K.; Kadry, H.M. Comparative study between skin micrografting (Meek technique) and meshed skin grafts in paediatric burns. Burns 2022, 48, 1632–1644. [Google Scholar] [CrossRef]
- Kan, T.; Takahagi, S.; Kawai, M.; Ashizawa, S.; Matsubara, D.; Mizuno, H.; Tanaka, A.; Hide, M. Calculation of practical skin donor area for meshed skin grafting in real-world surgery. Dermatol. Ther. 2020, 33, e14393. [Google Scholar] [CrossRef]
- Hohmann, E. Editorial Commentary: Long Head Biceps Tendon Can Be Used Like a Split Skin Graft: Mesh It and Augment Rotator Cuff Repairs. Arthrosc. J. Arthrosc. Relat. Surg. 2022, 38, 49–50. [Google Scholar] [CrossRef]
- Singh, M.; Nuutila, K.; Collins, K.C.; Huang, A. Evolution of skin grafting for treatment of burns: Reverdin pinch grafting to Tanner mesh grafting and beyond. Burns 2017, 43, 1149–1154. [Google Scholar] [CrossRef]
- Guo, Y.; Song, Y.; Xiong, S.; Wang, T.; Liu, W.; Yu, Z.; Ma, X. Mechanical Stretch Induced Skin Regeneration: Molecular and Cellular Mechanism in Skin Soft Tissue Expansion. Int. J. Mol. Sci. 2022, 23, 9622. [Google Scholar] [CrossRef] [PubMed]
- Uhljar, L.; Ambrus, R. Electrospinning of Potential Medical Devices (Wound Dressings, Tissue Engineering Scaffolds, Face Masks) and Their Regulatory Approach. Pharmaceutics 2023, 15, 417. [Google Scholar] [CrossRef]
- Byun, S.; Kim, S.; Lee, H.; Lim, H.; Kim, J.; Lee, U.; Lee, J.; Park, S.; Kim, S.; Song, J.-D.; et al. Soft tissue expander for vertically atrophied alveolar ridges: Prospective, multicenter, randomized controlled trial. Clin. Oral Implant. Res. 2020, 31, 585–594. [Google Scholar] [CrossRef]
- Gawande, D.D.; Singh, A.; Ukey, V.T.; Madan, R.S.; Manjula, V.; Shrivastava, S. Tissue expansion in oral and maxillofacial surgery. Int. J. Heal. Sci. 2022, 14, 3329–3339. [Google Scholar] [CrossRef]
- Stepniewski, A.; Lehmann, W.; Schilderoth, M.; Behringer, D.; Emmerich, N.; Daugardt, J.; von der Brelie, C.; Kauffmann, P.; Felmerer, G. The Efficacy of Local Flaps in the Treatment of Traumatic Scalp Defects. J. Neurol. Surg. Part A: Central Eur. Neurosurg. 2021, 83, 330–337. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.P.; Kwon, J.G. Flaps in Plastic Surgery. Textb. Plast. Reconstr. Surg. 2022, 103–123. [Google Scholar] [CrossRef]
- Taghizadeh, R.; Gilbert, P.M. Comparison of commonly used mesher types in burns surgery revisited. Burns 2008, 34, 109–110. [Google Scholar] [CrossRef] [PubMed]
- Pripotnev, S.; Papp, A. Split thickness skin graft meshing ratio indications and common practices. Burns 2017, 43, 1775–1781. [Google Scholar] [CrossRef]
- Lyons, J.L.; Kagan, R.J. The True Meshing Ratio of Skin Graft Meshers. J. Burn. Care Res. 2014, 35, 257–260. [Google Scholar] [CrossRef]
- Henderson, J.; Arya, R.; Gillespie, P. Skin graft meshing, over-meshing and cross-meshing. Int. J. Surg. 2012, 10, 547–550. [Google Scholar] [CrossRef]
- Makode, S.; Singh, G.; Chanda, A. Development of novel anisotropic skin simulants. Phys. Scr. 2021, 96, 125019. [Google Scholar] [CrossRef]
- Sharma, S.; Batra, S. Recent advances of chitosan composites in artificial skin: The next era for potential biomedical application. Mater. Biomed. Eng. Nanobiomaterials Tissue Eng. 2019, 97–119. [Google Scholar] [CrossRef]
- Snyder, D.E.; Sapper, E.D. See Me, Feel Me, Touch Me, Heal Me: A Contextual Overview of Conductive Polymer Composites as Synthetic Human Skin. J. Compos. Sci. 2022, 6, 141. [Google Scholar] [CrossRef]
- Rajab, T.K.; O’malley, T.J.; Tchantchaleishvili, V. Decellularized scaffolds for tissue engineering: Current status and future perspective. Artif. Organs 2020, 44, 1031–1043. [Google Scholar] [CrossRef] [PubMed]
- Charbe, N.B.; Tambuwala, M.; Palakurthi, S.S.; Warokar, A.; Hromić-Jahjefendić, A.; Bakshi, H.; Zacconi, F.; Mishra, V.; Khadse, S.; Aljabali, A.A.; et al. Biomedical applications of three-dimensional bioprinted craniofacial tissue engineering. Bioeng. Transl. Med. 2022, 8, e10333. [Google Scholar] [CrossRef]
- Joseph, J.; Deshmukh, K.; Tung, T.T.; Chidambaram, K.; Pasha, S.K.K. 3D Printing Technology of Polymer Composites and Hydrogels for Artificial Skin Tissue Implementations. In Lecture Notes in Bioengineering; Springer: Berlin/Heidelberg, Germany, 2019; pp. 205–233. [Google Scholar]
- Veerabagu, U.; Palza, H.; Quero, F. Review: Auxetic Polymer-Based Mechanical Metamaterials for Biomedical Applications. ACS Biomater. Sci. Eng. 2022, 8, 2798–2824. [Google Scholar] [CrossRef] [PubMed]
- Benítez, J.M.; Montáns, F.J. The mechanical behavior of skin: Structures and models for the finite element analysis. Comput. Struct. 2017, 190, 75–107. [Google Scholar] [CrossRef]
- Chanda, A. Biomechanical Modeling of Human Skin Tissue Surrogates. Biomimetics 2018, 3, 18. [Google Scholar] [CrossRef]
- Annaidh, A.N.; Bruyère-Garnier, K.; Destrade, M.; Gilchrist, M.D.; Otténio, M. Characterization of the anisotropic mechanical properties of excised human skin. J. Mech. Behav. Biomed. Mater. 2012, 5, 139–148. [Google Scholar] [CrossRef]
- Chanda, A.; Chatterjee, S.; Gupta, V. Soft composite based hyperelastic model for anisotropic tissue characterization. J. Compos. Mater. 2020, 54, 4525–4534. [Google Scholar] [CrossRef]
- Saager, R.B.; Kondru, C.; Au, K.; Sry, K.; Ayers, F.; Durkin, A.J. Multilayer silicone phantoms for the evaluation of quantitative optical techniques in skin imaging. In Proceedings of the Design and Performance Validation of Phantoms Used in Conjunction with Optical Measurement of Tissue II, San Francisco, CA, USA, 24 February 2010; p. 756706. [Google Scholar] [CrossRef]
- Qi, H.J.; Joyce, K.; Boyce, M.C. Durometer Hardness and the Stress-Strain Behavior of Elastomeric Materials. Rubber Chem. Technol. 2003, 76, 419–435. [Google Scholar] [CrossRef]
- Pissarenko, A.; Meyers, M.A. The materials science of skin: Analysis, characterization, and modeling. Prog. Mater. Sci. 2020, 110, 100634. [Google Scholar] [CrossRef]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. Comparison of recent fiber orientation models in injection molding simulation of fiber-reinforced composites. J. Thermoplast. Compos. Mater. 2020, 33, 35–52. [Google Scholar] [CrossRef]
- Rosin, N.L.; Agabalyan, N.; Olsen, K.; Martufi, G.; Gabriel, V.; Biernaskie, J.; Di Martino, E.S. Collagen structural alterations contribute to stiffening of tissue after split-thickness skin grafting. Wound Repair Regen. 2016, 24, 263–274. [Google Scholar] [CrossRef]
- Yang, Y.; Song, X.; Li, X.; Chen, Z.; Zhou, C.; Zhou, Q.; Chen, Y. Recent Progress in Biomimetic Additive Manufacturing Technology: From Materials to Functional Structures. Adv. Mater. 2018, 30, e1706539. [Google Scholar] [CrossRef] [PubMed]
- Singh, G.; Gupta, V.; Chanda, A. Artificial skin with varying biomechanical properties. Mater. Today Proc. 2022, 62, 3162–3166. [Google Scholar] [CrossRef]
- Gajewski, M.; Szczerba, R.; Jemioło, S. Modelling of elastomeric bearings with application of Yeoh hyperelastic material model. in Procedia Eng. 2015, 111, 220–227. [Google Scholar] [CrossRef]
- Wissler, M.; Mazza, E. Modeling and simulation of dielectric elastomer actuators. Smart Mater. Struct. 2005, 14, 1396. [Google Scholar] [CrossRef]
- Mohammadi, A.K.; Barforooshi, S.D. Nonlinear Forced Vibration Analysis of Dielectric-Elastomer Based Micro-Beam with Considering Yeoh Hyper-Elastic Model. Lat. Am. J. Solids Struct. 2017, 14, 643–656. [Google Scholar] [CrossRef]
- Barforooshi, S.D.; Mohammadi, A.K. Study Neo-Hookean and Yeoh Hyper-Elastic Models in Dielectric Elastomer-Based Micro-Beam Resonators. Lat. Am. J. Solids Struct. 2016, 13, 1823–1837. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Ghayesh, M.H.; Chin, R.; Amabili, M. Hyperelastic structures: A review on the mechanics and biomechanics. Int. J. Non. Linear. Mech. 2023, 148, 104275. [Google Scholar] [CrossRef]
- Wex, C.; Arndt, S.; Stoll, A.; Bruns, C.; Kupriyanova, Y. Isotropic incompressible hyperelastic models for modelling the mechanical behaviour of biological tissues: A review. Biomed. Eng./Biomed. Tech. 2015, 60, 577–592. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Ghayesh, M.H.; Chin, R.; Amabili, M. A review on the nonlinear dynamics of hyperelastic structures. Nonlinear Dyn. 2022, 110, 963–994. [Google Scholar] [CrossRef]
- Chagnon, G.; Rebouah, M.; Favier, D. Hyperelastic Energy Densities for Soft Biological Tissues: A Review. J. Elast. 2014, 120, 129–160. [Google Scholar] [CrossRef]
- Gallagher, J.; Ní Anniadh, A.; Bruyere, K.; Otténio, M.; Xie, H.; Gilchrist, M.D. Dynamic tensile properties of human skin. In Proceedings of the 2012 IRCOBI Conference Proceedings—International Research Council on the Biomechanics of Injury, Dublin, Ireland, 2–14 September 2012; pp. 494–502. [Google Scholar]
- Chanda, A.; Graeter, R. Human Skin-Like Composite Materials for Blast Induced Injury Mitigation. J. Compos. Sci. 2018, 2, 44. [Google Scholar] [CrossRef]
- Gupta, V.; Singh, G.; Chanda, A. Development and testing of skin grafts models with varying slit orientations. Mater. Today Proc. 2022, 62, 3462–3467. [Google Scholar] [CrossRef]
- Chavan, V.; Chittoria, R.; Elankumar, S.; Reddy, K.S.; Aggarwal, A.; Gupta, S.; Reddy, C.L.; Mohan, P.L.B. Pixel Grafting: A Novel Skin Graft Expansion Technique. J. Cutan. Aesthet. Surg. 2021, 14, 229. [Google Scholar] [CrossRef] [PubMed]
- Koetsier, K.S.; Wong, J.N.; Muffley, L.A.; Carrougher, G.J.; Pham, T.N.; Gibran, N.S. Prospective observational study comparing burn surgeons’ estimations of wound healing after skin grafting to photo-assisted methods. Burns 2019, 45, 1562–1570. [Google Scholar] [CrossRef] [PubMed]




| Anisotropic Skin Graft | Unit Cell Void Area (mm2) | Average Meshing Ratio |
|---|---|---|
| At 0% stretch | 5 | 1 |
| At 10% stretch | 8.33 ± 10% | 1.33 |
| At 20% stretch | 10.86 ± 10% | 1.71 |
| At 30% stretch | 16.6 ± 10% | 2.14 |
| At 40% stretch | 26.69 ± 10% | 2.61 |
| At 50% stretch | 33.51 ± 10% | 3.13 |
| Anisotropic Skin Graft Model | Neo-Hookean Curve Fit Coefficient | R2 |
|---|---|---|
| c1 | ||
| 0° | 0.0814 | 0.9972 |
| 15° | 0.0702 | 0.9246 |
| 30° | 0.0794 | 0.9968 |
| 45° | 0.0949 | 0.9981 |
| 0°–0° | 0.0784 | 0.9645 |
| 0°–90° | 0.0785 | 0.9950 |
| 30°–60° | 0.1037 | 0.9771 |
| 15°–90°/0°–75° | 0.0862 | 0.9957 |
| 60°–90°/0°–30° | 0.0751 | 0.8986 |
| 0°–60°/90°–30° | 0.0741 | 0.9841 |
| 45°–15°/45°–75° | 0.0630 | 0.9901 |
| 75°–15° | 0.0992 | 0.8862 |
| 0°–15°/75°–90° | 0.0872 | 0.9893 |
| 60°–15°/30°–75° | 0.1049 | 0.9379 |
| 45°–60°/30°–45° | 0.0717 | 0.9877 |
| 0°–45°/90°–45° | 0.0919 | 0.9014 |
| 15°–30°/75°–60° | 0.0829 | 0.9618 |
| Anisotropic Skin Graft Model | Mooney–Rivlin Curve Fit Coefficients | R2 | |
|---|---|---|---|
| c1 | c2 | ||
| 0° | 0.0814 | 0.0001 | 0.9972 |
| 15° | 0.0001 | 0.0975 | 0.9528 |
| 30° | 0.0794 | 0.0001 | 0.9968 |
| 45° | 0.0949 | 0.0001 | 0.9981 |
| 0°–0° | 0.0000 | 0.1091 | 0.9898 |
| 0°–90° | 0.0785 | 0.0001 | 0.9950 |
| 30°–60° | 0.0096 | 0.1307 | 0.9924 |
| 15°–90°/0°–75° | 0.0718 | 0.0201 | 0.9967 |
| 60°–90°/0°–30° | 0.0001 | 0.1048 | 0.9404 |
| 0°–60°/90°–30° | 0.0001 | 0.1028 | 0.9971 |
| 45°–15°/45°–75° | 0.063 | 0.0001 | 0.9901 |
| 75°–15° | 0.0001 | 0.1390 | 0.9445 |
| 0°–15°/75°–90° | 0.0095 | 0.1078 | 0.9983 |
| 60°–15°/30°–75° | 0.0001 | 0.1465 | 0.9773 |
| 45°–60°/30°–45° | 0.0355 | 0.0503 | 0.9928 |
| 0°–45°/90°–45° | 0.0001 | 0.1277 | 0.9180 |
| 15°–30°/75°–60° | 0.0001 | 0.1154 | 0.9898 |
| Anisotropic Skin Graft Model | Yeoh Curve Fit Coefficients | R2 | ||
|---|---|---|---|---|
| c1 | c2 | c3 | ||
| 0° | 0.0730 | 0.0105 | 0.0001 | 0.9986 |
| 15° | 0.0702 | 0.0001 | 0.0001 | 0.9246 |
| 30° | 0.0793 | 0.0001 | 0.0001 | 0.9968 |
| 45° | 0.0914 | 0.0044 | 0.0001 | 0.9975 |
| 0°–0° | 0.0784 | 0.0001 | 0.0001 | 0.9645 |
| 0°–90° | 0.0785 | 0.0001 | 0.0001 | 0.9950 |
| 30°–60° | 0.1037 | 0.0001 | 0.0001 | 0.9771 |
| 15°–90°/0°–75° | 0.0862 | 0.0001 | 0.0001 | 0.9957 |
| 60°–90°/0°–30° | 0.0751 | 0.0001 | 0.0001 | 0.8986 |
| 0°–60°/90°–30° | 0.0741 | 0.0001 | 0.0001 | 0.9841 |
| 45°–15°/45°–75° | 0.0518 | 0.0140 | 0.0001 | 0.9926 |
| 75°–15° | 0.0992 | 0.0001 | 0.0001 | 0.8862 |
| 0°–15°/75°–90° | 0.0872 | 0.0001 | 0.0001 | 0.9893 |
| 60°–15°/30°–75° | 0.1049 | 0.0001 | 0.0001 | 0.9379 |
| 45°–60°/30°–45° | 0.0717 | 0.0001 | 0.0001 | 0.9877 |
| 0°–45°/90°–45° | 0.0919 | 0.0001 | 0.0001 | 0.9014 |
| 15°–30°/75°–60° | 0.0829 | 0.0001 | 0.0001 | 0.9618 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, V.; Singla, R.; Chanda, A. Development and Characterization of Novel Anisotropic Skin Graft Simulants. Dermato 2023, 3, 114-130. https://doi.org/10.3390/dermato3020010
Gupta V, Singla R, Chanda A. Development and Characterization of Novel Anisotropic Skin Graft Simulants. Dermato. 2023; 3(2):114-130. https://doi.org/10.3390/dermato3020010
Chicago/Turabian StyleGupta, Vivek, Rohan Singla, and Arnab Chanda. 2023. "Development and Characterization of Novel Anisotropic Skin Graft Simulants" Dermato 3, no. 2: 114-130. https://doi.org/10.3390/dermato3020010
APA StyleGupta, V., Singla, R., & Chanda, A. (2023). Development and Characterization of Novel Anisotropic Skin Graft Simulants. Dermato, 3(2), 114-130. https://doi.org/10.3390/dermato3020010







