Optimal Forecast Combination for Japanese Tourism Demand
Abstract
1. Introduction
2. Literature Review
2.1. Forecasting Combination in Tourism Demand Forecasting
“An approach that generates a set of forecasts for the same demand variable by using different methods, and then combines these forecasts into one final, summarised forecast.”
2.2. Decomposition Models in Tourism Demand Forecasting
3. Methodology and Material
3.1. EEMD
- Generate a new time series, by adding the original time series to a normally distributed white noise time series, :
- For the time series generated in (1), obtain the values of maximum and minimum.
- Employ an interpolation method and join the maximums to obtain the upper envelop and join all the minimum to generate the lower envelope.
- Compute the average of the upper and lower envelopes
- Obtain the mean deleted data, by subtracting the average computed in (2) from (1), the original time-series with added noise.
- If the IMF conditions are satisfied for , then repeat step one to step four until to achieve a monotonic function for the remainder. This procedure decomposes the original series into a remainder and a set of n independent IMFs, as shown below.
- Simulate a random time series of noise, and repeat step 2 to step 6, k-times.
- Finally, compute the means of the (k-times repeated) decomposed IMFs obtained in the previous steps.
- (1)
- Throughout the entire time scale, the difference between the number of maxima, minima, and zero crossings of the IMF should not be greater than 1.
- (2)
- At any given time, the mean value of the upper envelope and the lower envelope must be zero.
3.2. Support Vector Machine (SVM)
3.3. Neural Networks (NN)
- The inputs into hidden layer neuron j are combined, using a weighted linear combination, to obtain the input signal j:where is the threshold for the jth node and indicates the weight for jth neuron.
- Compute the output value from the hidden neuron node j, using a non-linear activation function:
- To start with, the weights, , take random values, and are then updated until minimizing a cost function such as Mean Square Errors (MSE), using the observed data.
3.4. Selection of Parameters
4. Forecast Evaluation
Forecasting Results
5. Discussions and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Ali, M., Prasad, R., Xiang, Y., & Yaseen, Z. M. (2020). Complete ensemble empirical mode decomposition hybridized with random forest and kernel ridge regression model for monthly rainfall forecasts. Journal of Hydrology, 584, 124–647. [Google Scholar] [CrossRef]
- Andonian, A., Kuwabara, T., Yamakawa, N., & Ishida, R. (2016). The future of Japan’s tourism: Path for sustainable growth towards 2020. McKinsey Japan and Travel, Transport and Logistics Practice. Retrieved February, 10, 2018. [Google Scholar]
- Atiya, A. F. (2020). Why does forecast combination work so well? International Journal of Forecasting, 36(1), 197–200. [Google Scholar] [CrossRef]
- Bekiroglu, K., Gulay, E., & Duru, O. (2022). A multi-method forecasting algorithm: Linear unbiased estimation of combine forecast. Knowledge-Based Systems, 239, 107990. [Google Scholar] [CrossRef]
- Bosupeng, M. (2019). Forecasting tourism demand: The Hamilton filter. Annals of Tourism Research, 79(C), 102823. [Google Scholar] [CrossRef]
- Chen, C. F., Lai, M. C., & Yeh, C. C. (2012). Forecasting tourism demand based on empirical mode decomposition and neural network. Knowledge-Based Systems, 26, 281–287. [Google Scholar] [CrossRef]
- Chen, W., Sun, J., Gao, S., Cheng, J. J., Wang, J., & Todo, Y. (2017). Using a single dendritic neuron to forecast tourist arrivals to Japan. IEICE Transactions on Information and Systems, 100(1), 190–202. [Google Scholar] [CrossRef]
- Fang, Y., Guan, B., Wu, S., & Heravi, S. (2020). Optimal forecast combination based on ensemble empirical mode decomposition for agricultural commodity futures prices. Journal of Forecasting, 39(6), 877–886. [Google Scholar] [CrossRef]
- Fritz, R. G., Brandon, C., & Xander, J. (1984). Combining time-series and econometric forecast of tourism activity. Annals of Tourism Research, 11(2), 219–229. [Google Scholar] [CrossRef]
- Gunter, U., Önder, I., & Smeral, E. (2020). Are combined tourism forecasts better at minimizing forecasting errors? Forecasting, 2(3), 211–229. [Google Scholar] [CrossRef]
- Harvey, D., Leybourne, S., & Newbold, P. (1997). Testing the equality of prediction mean squared errors. International Journal of Forecasting, 13(2), 281–291. [Google Scholar] [CrossRef]
- Hassani, H., Heravi, S., & Zhigljavsky, A. (2009). Forecasting European industrial production with singular spectrum analysis. International Journal of Forecasting, 25(1), 103–118. [Google Scholar] [CrossRef]
- Hassani, H., Webster, A., Silva, E. S., & Heravi, S. (2015). Forecasting US tourist arrivals using optimal singular spectrum analysis. Tourism Management, 46, 322–335. [Google Scholar] [CrossRef]
- Heravi, S., Osborn, D. R., & Birchenhall, C. R. (2004). Linear versus neural network forecasts for European industrial production series. International Journal of Forecasting, 20(3), 435–446. [Google Scholar] [CrossRef]
- Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H., Zheng, Q., Yen, N. C., Tung, C. C., & Liu, H. H. (1998). The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 454(1971), 903–995. [Google Scholar] [CrossRef]
- Jiao, E. X., & Chen, J. L. (2019). Tourism forecasting: A review of methodological developments over the last decade. Tourism Economics, 25(3), 469–492. [Google Scholar] [CrossRef]
- Kourentzes, N., Saayman, A., Jean-Pierre, P., Provenzano, D., Sahli, M., Seetaram, N., & Volo, S. (2021). Visitor arrivals forecasts amid COVID-19: A perspective from the Africa team. Annals of Tourism Research, 88, 103197. [Google Scholar] [CrossRef] [PubMed]
- Kummong, R., & Supratid, S. (2016). Thailand tourism forecasting based on a hybrid of discrete wavelet decomposition and NARX neural network. Industrial Management & Data Systems, 116(6), 1242–1258. [Google Scholar]
- Lai, M. C., Yeh, C. C., & Shieh, L. F. (2013). A hybrid model by empirical mode decomposition and support vector regression for tourist arrivals forecasting. Journal of Testing and Evaluation, 41(3), 351–358. [Google Scholar] [CrossRef]
- Law, R. (2001). The impact of the Asian financial crisis on Japanese demand for travel to Hong Kong: A study of various forecasting techniques. Journal of Travel & Tourism Marketing, 10(2–3), 47–65. [Google Scholar]
- Li, G., Wu, D. C., Zhou, M., & Liu, A. (2019). The combination of interval forecasts in tourism. Annals of Tourism Research, 75, 363–378. [Google Scholar] [CrossRef]
- Li, X., & Law, R. (2020). Forecasting tourism demand with decomposed search cycles. Journal of Travel Research, 59(1), 52–68. [Google Scholar] [CrossRef]
- Liu, A., Vici, L., Ramos, V., Giannoni, S., & Blake, A. (2021). Visitor arrivals forecasts amid COVID-19: A perspective from the Europe team. Annals of Tourism Research, 88, 103182. [Google Scholar] [CrossRef]
- Pai, P. F., Hong, W. C., Chang, P. T., & Chen, C. T. (2006). The application of support vector machines to forecast tourist arrivals in Barbados: An empirical study. International Journal of Management, 23(2), 375–385. [Google Scholar]
- Park, S., Lee, J., & Song, W. (2017). Short-term forecasting of Japanese tourist inflow to South Korea using Google trends data. Journal of Travel & Tourism Marketing, 34(3), 357–368. [Google Scholar]
- Polunin, I. (1989). Japanese travel boom. Tourism Management, 10(1), 4–8. [Google Scholar] [CrossRef]
- Russell, L. (2017). Assessing Japan’s inbound tourism: A SWOT analysis. Hannami Theory Social Science, 53(1), 21–50. [Google Scholar]
- Silva, E. S., Ghodsi, Z., Ghodsi, M., Heravi, S., & Hassani, H. (2017). Cross country relations in European tourist arrivals. Annals of Tourism Research, 63, 151–168. [Google Scholar] [CrossRef]
- Silva, E. S., Hassani, H., Heravi, S., & Huang, X. (2019). Forecasting tourism demand with denoised neural networks. Annals of Tourism Research, 74, 134–154. [Google Scholar] [CrossRef]
- Song, H., Qiu, R. T., & Park, J. (2019). A review of research on tourism demand forecasting: Launching the Annals of Tourism Research Curated Collection on tourism demand forecasting. Annals of Tourism Research, 75, 338–362. [Google Scholar] [CrossRef]
- Song, H., Witt, S. F., & Li, G. (2003). Modelling and forecasting the demand for Thai tourism. Tourism Economics, 9(4), 363–387. [Google Scholar] [CrossRef]
- Soshiroda, A. (2005). Inbound tourism policies in Japan from 1859 to 2003. Annals of Tourism Research, 32(4), 1100–1120. [Google Scholar] [CrossRef]
- Sun, Y., Zhang, J., Li, X., & Wang, S. (2021). Forecasting tourism demand with a new time-varying forecast averaging approach. Journal of Travel Research, 62(2), 305–323. [Google Scholar] [CrossRef]
- Tang, L. H., Bai, Y. L., Yang, J., & Lu, Y. N. (2020). A hybrid prediction method based on empirical mode decomposition and multiple model fusion for chaotic time series. Chaos, Solitons & Fractals, 141, 110366. [Google Scholar]
- Turner, L. W., Kulendran, N., & Fernando, H. (1997). Univariate modelling using periodic and non-periodic analysis: Inbound tourism to Japan, Australia and New Zealand compared. Tourism Economics, 3(1), 39–56. [Google Scholar] [CrossRef]
- UNWTO. (2019). International tourism highlights: 2019 edition. Available online: https://www.e-unwto.org/doi/pdf/10.18111/9789284421152 (accessed on 10 May 2024).
- UNWTO. (2024). International tourist arrivals hit 96% of pre-pandemic levels through July 2024. Available online: https://www.unwto.org/news/international-tourist-arrivals-hit-96-of-pre-pandemic-levels-through-july-2024 (accessed on 10 May 2024).
- Vapnik, V. (1998). Statistical learning theory new york. Wiley. [Google Scholar]
- Wong, K. K., Song, H., Witt, S. F., & Wu, D. C. (2007). Tourism forecasting: To combine or not to combine? Tourism Management, 28(4), 1068–1078. [Google Scholar] [CrossRef]
- Wu, J., Cheng, X., & Liao, S. S. (2020). Tourism forecast combination using the stochastic frontier analysis technique. Tourism Economics, 26(7), 1086–1107. [Google Scholar] [CrossRef]
- Wu, Z., & Huang, N. E. (2009). Ensemble empirical mode decomposition: A noise-assisted data analysis method. Advances in Adaptive Data Analysis, 1(01), 1–41. [Google Scholar] [CrossRef]
- Xie, G., Qian, Y., & Wang, S. (2020). A decomposition-ensemble approach for tourism forecasting. Annals of Tourism Research, 81, 102891. [Google Scholar] [CrossRef]
- Xu, X., Law, R., Chen, W., & Tang, L. (2016). Forecasting tourism demand by extracting fuzzy Takagi-Sugeno rules from trained SVMs. CAAI Transactions on Intelligence Technology, 1(1), 30–42. [Google Scholar] [CrossRef]
- Yagasaki, N. (2021). Impact of COVID-19 on the Japanese travel market and the travel market of overseas visitors to Japan, and subsequent recovery. IATTS Research, 45, 451–458. [Google Scholar] [CrossRef]
- Yahya, N. A., Samsudin, R., & Shabri, A. (2017). Tourism forecasting using hybrid modified empirical mode decomposition and neural network. International Journal of Advances in Soft Computing and Its Applications, 9(1), 14–31. [Google Scholar]
- Yeh, J. R., Shieh, J. S., & Huang, N. E. (2010a). Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Advances in Adaptive Data Analysis, 2(02), 135–156. [Google Scholar] [CrossRef]
- Yeh, J. R., Sun, W. Z., Shieh, J. S., & Huang, N. E. (2010b). Investigating fractal property and respiratory modulation of human heartbeat time series using empirical mode decomposition. Medical Engineering & Physics, 32(5), 490–496. [Google Scholar]
- Zhang, G., Wu, J., Pan, B., Li, J., Ma, M., Zhang, M., & Wang, J. (2017). Improving daily occupancy forecasting accuracy for hotels based on EEMD-ARIMA model. Tourism Economics, 23(7), 1496–1514. [Google Scholar] [CrossRef]
- Zhang, Y., Li, G., Muskat, B., & Law, R. (2021). Tourism demand forecasting: A decomposed deep learning approach. Journal of Travel Research, 60(5), 981–997. [Google Scholar] [CrossRef]
- Zhang, Z., & Hong, W. C. (2019). Electric load forecasting by complete ensemble empirical mode decomposition adaptive noise and support vector regression with quantum-based dragonfly algorithm. Nonlinear Dynamics, 98(2), 1107–1136. [Google Scholar] [CrossRef]
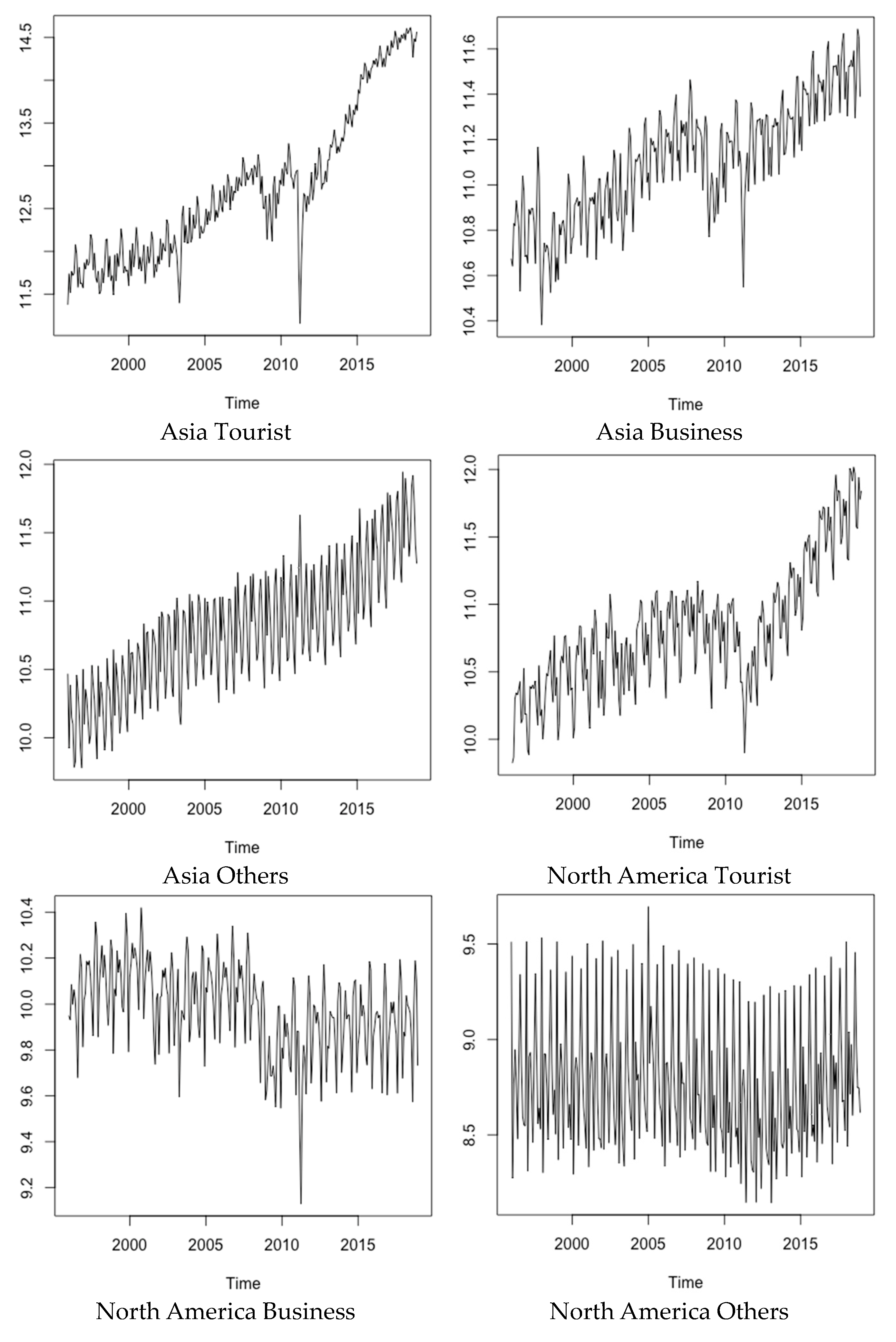
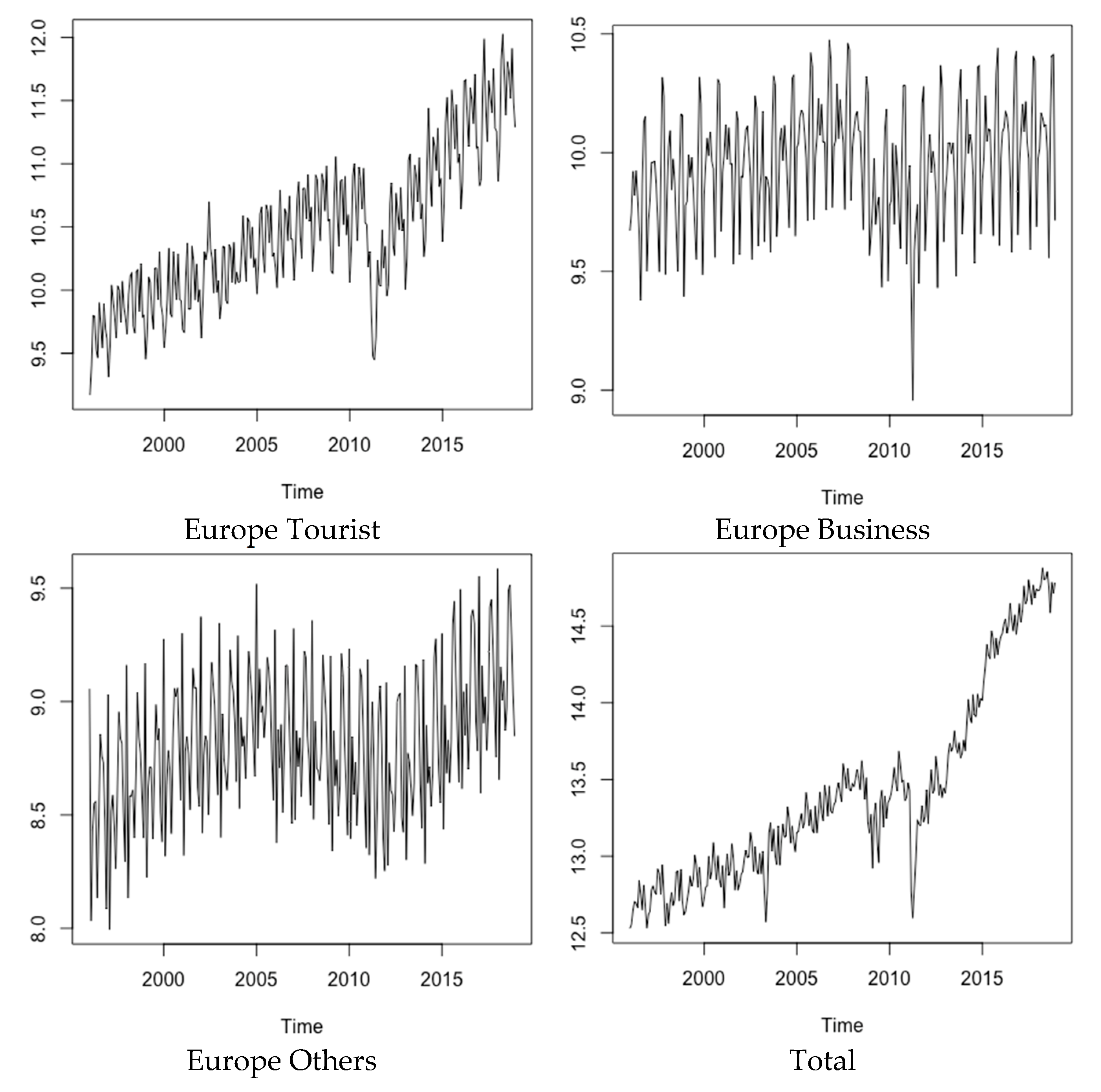
| Category | Mean | SD | Seasonal R2 |
|---|---|---|---|
| Asia Tourist | 1.178 | 23.2 | 0.479 |
| Asia Business | 0.311 | 15.7 | 0.732 |
| Asia Others | 0.559 | 35.4 | 0.924 |
| North America Tourist | 0.575 | 26.5 | 0.855 |
| North America Business | −0.027 | 19.9 | 0.811 |
| North America Others | 0.0003 | 54.1 | 0.960 |
| Europe Tourist | 0.641 | 33.0 | 0.811 |
| Europe Business | 0.115 | 30.3 | 0.896 |
| Europe Others | 0.200 | 42.9 | 0.946 |
| Total | 0.835 | 13.8 | 0.577 |
| Region | Models | 1 | 3 | 6 | 12 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tourist | Business | Others | Tourist | Business | Others | Tourist | Business | Others | Tourist | Business | Others | ||
| Asia | EEMD | 0.039 | 0.008 | 0.008 | 0.041 | 0.007 | 0.008 | 0.044 | 0.010 | 0.011 | 0.049 | 0.01 | 0.011 |
| SVM | 0.014 | 0.018 ** | 0.052 ** | 0.017 | 0.028 ** | 0.068 ** | 0.026 | 0.028 ** | 0.073 * | 0.057 | 0.034 | 0.074 | |
| NN | 0.022 | 0.018 ** | 0.050 ** | 0.215 ** | 0.035 ** | 0.071 ** | 0.179 * | 0.036 * | 0.101 * | 0.179 | 0.034 | 0.336 | |
| ARIMA | 0.013 | 0.160 ** | 0.033 ** | 0.013 | 0.016 ** | 0.033 ** | 0.013 | 0.016 ** | 0.033 ** | 0.017 | 0.017 * | 0.033 * | |
| Europe | EEMD | 0.020 | 0.010 | 0.027 | 0.020 | 0.011 | 0.028 | 0.020 | 0.014 | 0.030 | 0.021 | 0.010 | 0.032 |
| SVM | 0.072 ** | 0.012 * | 0.028 ** | 0.094 ** | 0.014 | 0.029 | 0.115 * | 0.027 | 0.032 | 0.134 | 0.021 | 0.030 | |
| NN | 0.043 ** | 0.016 ** | 0.030 ** | 0.084 ** | 0.054 | 0.038 * | 0.086 * | 0.077 | 0.091 | 0.109 | 0.030 | 0.045 | |
| ARIMA | 0.049 ** | 0.031 ** | 0.049 * | 0.053 ** | 0.050 ** | 0.054 ** | 0.058 ** | 0.046 ** | 0.051 * | 0.044 | 0.038 * | 0.052 ** | |
| North America | EEMD | 0.012 | 0.007 | 0.019 | 0.014 | 0.007 | 0.032 | 0.015 | 0.008 | 0.035 | 0.019 | 0.007 | 0.039 |
| SVM | 0.044 ** | 0.011 ** | 0.011 | 0.0686 ** | 0.014 ** | 0.010 * | 0.102 * | 0.015 * | 0.011 | 0.074 | 0.019 * | 0.012 | |
| NN | 0.034 ** | 0.018 ** | 0.022 | 0.112 ** | 0.023 ** | 0.037 | 0.037 * | 0.019 ** | 0.052 | 0.101 | 0.021 * | 0.044 | |
| ARIMA | 0.026 ** | 0.020 ** | 0.036 ** | 0.029 ** | 0.020 ** | 0.040 | 0.029 ** | 0.020 ** | 0.041 | 0.030 | 0.020 * | 0.041 | |
| Total | EEMD | 0.008 | 0.008 | 0.009 | 0.014 | ||||||||
| SVM | 0.023 ** | 0.060 ** | 0.075 * | 0.096 | |||||||||
| NN | 0.027 ** | 0.131 ** | 0.211 * | 0.131 | |||||||||
| ARIMA | 0.010 ** | 0.010 ** | 0.010 | 0.013 | |||||||||
| 1 | 3 | 6 | 12 | Overall | ||
| EEMD/SVM | RRMSE | 0.794 | 0.723 | 0.695 | 0.664 | 0.72 |
| Score | 8 | 8 | 8 | 8 | 32/40 | |
| EEMD/NN | RRMSE | 0.714 | 0.471 | 0.463 | 0.500 | 0.54 |
| Score | 9 | 10 | 10 | 10 | 39/40 | |
| EEMD/ARIMA | RRMSE | 0.746 | 0.793 | 0.847 | 0.872 | 0.81 |
| Score | 9 | 9 | 9 | 8 | 35/40 | |
| Overall | RRMSE | 0.75 | 0.66 | 0.67 | 0.67 | 0.69 |
| Score | 26/30 | 27/30 | 27/30 | 26/30 | 106/120 |
| 1 | 3 | 6 | 12 | |
| EEMD | −0.0312 | −0.3457 | −0.464 | −0.7981 |
| SVM | 1.5236 | 2.1589 | 3.1556 | 3.16722 |
| NN | 0.9648 | 4.9988 | 5.0601 | 3.4588 |
| ARIMA | 0.1535 | 0.0366 | −0.0915 | −0.3533 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Silva, E.S.; Guan, B.; Hassani, H.; Heravi, S. Optimal Forecast Combination for Japanese Tourism Demand. Tour. Hosp. 2025, 6, 79. https://doi.org/10.3390/tourhosp6020079
Fang Y, Silva ES, Guan B, Hassani H, Heravi S. Optimal Forecast Combination for Japanese Tourism Demand. Tourism and Hospitality. 2025; 6(2):79. https://doi.org/10.3390/tourhosp6020079
Chicago/Turabian StyleFang, Yongmei, Emmanuel Sirimal Silva, Bo Guan, Hossein Hassani, and Saeed Heravi. 2025. "Optimal Forecast Combination for Japanese Tourism Demand" Tourism and Hospitality 6, no. 2: 79. https://doi.org/10.3390/tourhosp6020079
APA StyleFang, Y., Silva, E. S., Guan, B., Hassani, H., & Heravi, S. (2025). Optimal Forecast Combination for Japanese Tourism Demand. Tourism and Hospitality, 6(2), 79. https://doi.org/10.3390/tourhosp6020079







