The Decomposition of Hotel Productivity Change in Taiwan from Overall and Disaggregate Perspectives
Abstract
:1. Introduction
2. Literature Review
3. Previous Study Analysis
4. Empirical Methodology
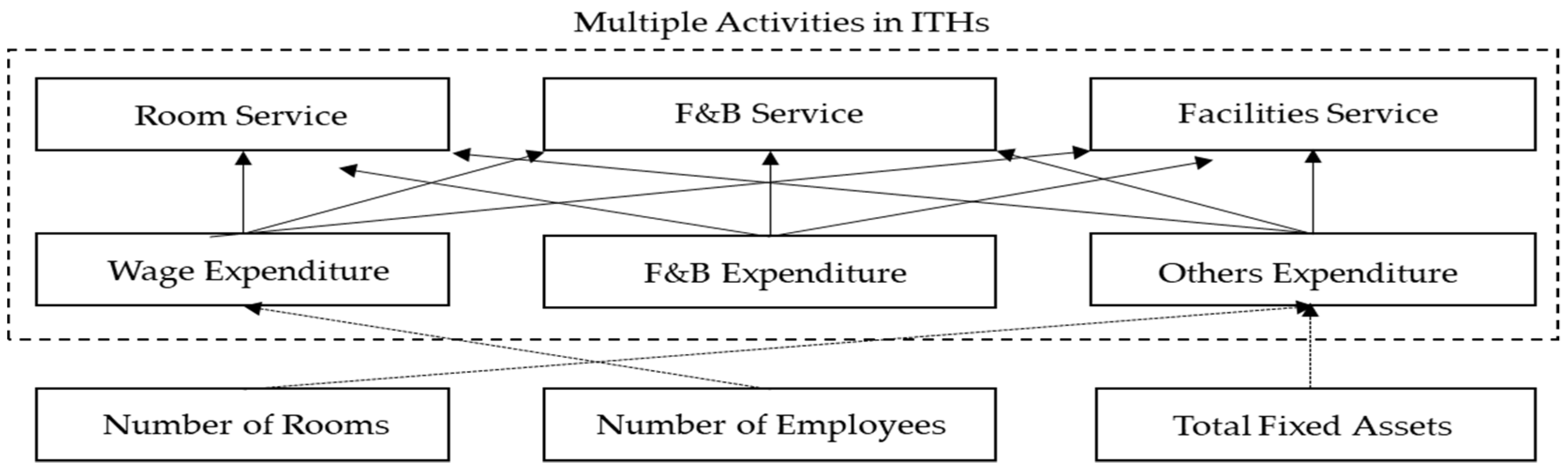
4.1. Overall and Disaggregate Hotel Luenberger Productivity Indices
4.2. Model Specification and Evaluation
5. Empirical Results
5.1. Data Descriptions and Sources
5.2. Overall Hotel Productivity Change Index and Its Components
5.3. Disaggregate Hotel Luenberger Productivity Change Indices
6. Summary and Discussions
- Hotel productivity change in Taiwan slightly reaches a growth of 0.5894% during the sample periods. No matter what kind of operation-type, hotels show a positive growth trend, but the independent-operated hotels are averagely higher than chain-operated hotels.
- As for the changes in Taiwan’s hotel productivity change in different regions, the southern and eastern regions showed growth, while the northern and central regions showed a decline trend.
- The main source of growth in Taiwan’s hotel productivity is from technological progress rather than efficiency improvement, implying that the innovation effect dominates the catch-up effect, especially for independent-operated ITHs.
- Hotel productivity change based on the disaggregate perspective can provide more detailed information for the individual output’s productivity change. Productivity growth from hotel facilities’ service is more beneficial to the overall hotel’s performance, especially in Taiwan’s ITHs.
- Although accommodation service is still the main service for all hotels, independent operators need to pay more attention to the productivity growth from hotel facilities’ services.
7. Conclusions and Implications
- This disaggregate hotel productivity index easily evaluates total factor productivity growth and decomposes overall productivity growth into the productivity change in each output.
- The overall hotel productivity growth is measured by the arithmetic mean of each output’s productivity change, implying it is the main force behind the hotel’s total factor productivity growth.
- The framework of this study can directly explore productivity changes by using financial data such as revenues and expenditure when more detailed hotel operational data are not available.
- Hotel managers should analyze the main source of hotel productivity growth for how to allocate their resources more efficiently and what is the best strategy in their hotel’s operations for improving productivity from the main output factor.
- Understanding the source of productivity growth is not only limited to the hotel industry. Similarly, the tourism and catering industry also need to pay more attention to the relationship between overall and disaggregate productivity growth.
- The results of overall and disaggregate productivity change are not only applicable to interpreting the Taiwan case but can also be extended to investigating other country’s cases.
- Since hotel performance has gradually been discussed through a dynamic framework in recent years, it is still less accurate to grasp the dynamic correlation of resource usage between the input and output factors across time periods in a hotel’s operation process. Thus, how to describe the dynamic framework of a hotel’s business performance still needs to be developed.
- The framework of this study does not take into account the sources or types of a hotel’s residents, especially in the face of the increasing number of visitor arrivals year after year for Taiwan. Due to the characteristics of different sources or types of a hotel’s residents, the performance of each hotel may seem to be different. Therefore, if this characteristic can be included in the analysis framework, then it will be more in line with practical needs.
- If detailed data are available, then examining the productivity change in general tourist hotels and comparing this to international tourist hotels can provide more insightful implications for the hotel industry within a country, especially for Taiwan’s case.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Article | Method | Aim | Variables | Findings | Contribution | Conclusion |
|---|---|---|---|---|---|---|
| Tsaur (2001) | DEA | To assess hotel performance and efficiency using DEA | Input variables: labor, capital, operating costs; Output variables: revenue, room nights sold | Demonstrated how DEA offers detailed insights into hotel performance | Contributed to the application of DEA in hotel industry efficiency analysis | The study concludes that DEA is a powerful tool for evaluating hotel performance and can reveal inefficiencies that other methods may overlook. |
| Barros (2004) | SFA | To evaluate hotel efficiency and competitiveness across different regions | Input variables: labor, capital; Output variables: revenue, occupancy rate | Evaluated hotel efficiency and competitiveness | Contributed to the understanding of hotel performance in different regions | The study concludes that efficiency improvements are crucial for enhancing competitiveness but also emphasizes the need for region-specific strategies. |
| Barros and Mascarenhas (2005) | DEA | To evaluate hotel efficiency across different types of hotels | Input variables: capital, labor; Output variables: revenue, room occupancy, guest satisfaction | Applied DEA to evaluate hotel efficiency across different types of hotels | Provided evidence that different hotel types exhibit varying levels of efficiency | The study concludes that hotel efficiency is heavily influenced by hotel type, and thus, benchmarking needs to consider these differences to be meaningful. |
| Barros and Dieke (2008) | DEA | To assess hotel efficiency across various regions in Brazil | Input variables: rooms, labor, capital; Output variables: revenue, room occupancy | Applied DEA to evaluate hotel efficiency across different regions | Highlighted regional variations in hotel performance | The study concludes that there are significant regional differences in hotel efficiency, and a tailored approach is necessary to address these variations. |
| Cordero and Tzeremes (2017) | MPI | To analyze hotel productivity change over time using the Malmquist productivity index | Input variables: labor, capital, operating costs; Output variables: revenue, room occupancy | Analyzed hotel productivity change over time using MPI | Used MPI to evaluate hotel efficiency and productivity trends | The study concludes that while the MPI is useful for assessing overall productivity changes, it fails to account for the contribution of individual factors to productivity growth. |
| Wheeler and Zang (2018) | LPI | To evaluate hotel productivity changes using the Luenberger productivity index | Input variables: labor, capital, operating costs; Output variables: revenue, guest satisfaction | Evaluated productivity changes in hotels using LPI | Advanced the understanding of hotel productivity dynamics using LPI | The study concludes that LPI provides a more accurate and detailed measure of productivity change compared to traditional methods like MPI. |
| Tzeremes (2019) | LPI | To assess hotel productivity dynamics using LPI | Input variables: labor, capital, operating expenses; Output variables: revenue, room occupancy, guest satisfaction | Assessed hotel productivity dynamics using LPI | Contributed to the evaluation of productivity changes using a more flexible index | The study concludes that LPI captures productivity changes more effectively, offering better insights into individual factor contributions compared to traditional methods. |
| Higuerey et al. (2020) | DEA | To measure the efficiency of the hotel industry in Ecuador | Input: labor, capital, and resources; Output: hotel revenue, occupancy rates | The study found inefficiencies in resource utilization among hotels in Ecuador, with small hotels showing lower efficiency compared to larger ones. | Provides a comprehensive evaluation of hotel efficiency in Ecuador and suggests ways to optimize resource use for improved hotel performance. | The study concludes that improving operational efficiency, resource management, and adopting best practices are key for enhancing hotel performance in Ecuador. |
| Yin et al. (2020) | DEA | To analyze hotel performance from an internal cooperation perspective using a two-stage DEA model | Input: labor, capital, operational costs; Output: revenue, guest satisfaction | Internal cooperation within departments was found to significantly impact hotel performance. Hotels that promoted internal coordination showed better performance. | Introduces a new perspective on hotel performance by emphasizing internal cooperation, offering insights into how internal management can influence overall performance. | The conclusion highlights the importance of internal cooperation among departments for improving hotel performance. The study recommends strategies to enhance collaboration. |
| El Alaoui et al. (2023) | DEA | To analyze productivity, efficiency, and sustainability in the Tunisian hotel industry using a two-stage DEA approach | Input: resources (labor, capital); Output: revenue, productivity; Intermediate: service quality | Tunisian hotels showed mixed results, with larger hotels generally being more efficient. Smaller hotels, however, demonstrated better sustainability practices. | The study introduces a two-stage model to assess efficiency, sustainability, and productivity, particularly in developing economies like Tunisia. | The study concludes that sustainability practices should be integrated into productivity and efficiency evaluations for a more comprehensive performance measurement. |
| Zhu et al. (2023) | DEA | To measure the performance of Taiwan hotels using a hierarchical network DEA model that incorporates shared inputs | Input: labor, capital, resources (shared across departments); Output: revenue, occupancy rates, guest satisfaction | The study found that hotels using shared inputs across departments improved their efficiency and overall performance, especially in larger hotels. | Introduces the concept of shared inputs into the performance measurement model, providing a more accurate assessment of hotel operations. | The conclusion emphasizes that shared inputs contribute to better hotel performance, and suggests that hotels focus on optimizing shared resources to enhance efficiency. |
| Choi and Kim (2024) | DEA | To measure hotel service productivity | Input Variables: Labor, capital, operating costs, facilities. Output Variables: Revenue, room occupancy, guest satisfaction. Intermediate Variables: Service quality (measured through guest reviews and service metrics). | The two-stage network DEA model effectively highlights the importance of service quality as an intermediary variable in hotel service productivity analysis. | Provided empirical evidence on how hotels in different categories (based on star ratings) manage service quality and productivity. | The study concludes that a two-stage network DEA model incorporating service quality as an intermediary variable is more effective in measuring hotel service productivity. |
| Vidali et al. (2024) | Systematic literature review | To review the parametric and non-parametric methods for measuring efficiency in the hotel industry | N/A (Literature review) | The review highlights the strengths and weaknesses of both parametric and non-parametric methods (like SFA and DEA) in measuring hotel efficiency. | The paper systematically reviews and compares different efficiency measurement methods in the hotel industry, providing a clear overview of the existing research. | The conclusion discusses the need for a more integrated approach that combines parametric and non-parametric methods for a more accurate efficiency measurement. |
| No. | Name | Region | Operation Type |
|---|---|---|---|
| 1 | Regent Taipei Hotel | North | Chain |
| 2 | Sheraton Grand Taipei Hotel | North | Chain |
| 3 | Grand Hyatt Taipei | North | Chain |
| 4 | Shangri-La’s Far Eastern Plaza Hotel, Taipei | North | Chain |
| 5 | Ambassador Hotel Taipei | North | Chain |
| 6 | The Howard Plaza Hotel Taipei | North | Chain |
| 7 | The Grand Hotel | North | Chain |
| 8 | The Westin Taipei | North | Chain |
| 9 | The Sherwood Taipei | North | Chain |
| 10 | Caesar Park Hotel Taipei | North | Chain |
| 11 | San Want Hotel Taipei | North | Independent |
| 12 | Brother Hotel | North | Independent |
| 13 | The Landis Taipei | North | Chain |
| 14 | Imperial Hotel Taipei | North | Independent |
| 15 | Gloria Prince Hotel Taipei | North | Chain |
| 16 | Santos Hotel | North | Independent |
| 17 | United Hotel | North | Independent |
| 18 | Hotel Riverview Taipei | North | Independent |
| 19 | Emperor Hotel | North | Independent |
| 20 | Landis Resort Yangmingshan | North | Chain |
| 21 | Hotel Royal-Nikko Taipei | North | Chain |
| 22 | Golden China Hotel | North | Independent |
| 23 | Miramar Garden Taipei | North | Independent |
| 24 | Pleasant Hotels International | North | Independent |
| 25 | Ambassador Hotel Hsinchu | North | Chain |
| 26 | Hotel Royal Hsinchu | North | Chain |
| 27 | Evergreen Laurel Hotel (Taichung) | Central | Chain |
| 28 | Hotel International | Central | Independent |
| 29 | Plaza International Hotel | Central | Independent |
| 30 | The Howard Prince Hotel Taichung | Central | Chain |
| 31 | The Splendor Hotel Taichung | Central | Chain |
| 32 | The Lalu Sun Moon Lake | Central | Independent |
| 33 | Nice Prince Hotel | South | Chain |
| 34 | Hibiscus Resorts Hotel | South | Independent |
| 35 | Tayih Landis Hotel Tainan | South | Chain |
| 36 | Evergreen Plaza Hotel (Tainan) | South | Chain |
| 37 | Hotel Tainan | South | Independent |
| 38 | Grand Hi Lai Hotel | South | Independent |
| 39 | Ambassador Hotel Kaohsiung | South | Chain |
| 40 | Han Hsien International Hotel | South | Independent |
| 41 | The Howard Plaza Hotel Kaohsiung | South | Chain |
| 42 | Holiday Garden Hotel | South | Independent |
| 43 | The Grand Hotel Kaohsiung | South | Chain |
| 44 | Hotel Kingdom | South | Independent |
| 45 | The Lees Hotel | South | Independent |
| 46 | 85 Sky Tower Hotel | South | Chain |
| 47 | Caesar Park Hotel Kenting | South | Chain |
| 48 | Howard Beach Resort Kenting | South | Chain |
| 49 | Hotel Royal Chiao Hsi | East | Chain |
| 50 | Parkview Hotels Hualien | East | Independent |
| 51 | Marshal Hotel | East | Independent |
| 52 | Chateau de Chine Hotel Hualien | East | Chain |
| 53 | Silks Place Taroko Hotel | East | Chain |
| 54 | Hualien Farglory Hotel | East | Independent |
| 55 | Hotel Royal Chihpen | East | Chain |
| 56 | Formosan Naruwan Hotel Taitung | East | Independent |
| 1 | In fact, this model’s DDF is similar to the Russell-based directional distance function (RDDF, hereafter) approach. Moreover, P. C. Chen et al. (2015) prove that the RDDF model presents some well-behaved properties and has a higher discriminating power than the Farrell efficiency measure. |
| 2 | Tourism statistics website: https://reurl.cc/VYad2n (accessed on 30 March 2024). |
References
- Anderson, R. I., Fish, M., Xia, Y., & Michello, F. (1999). Measuring efficiency in the hotel industry: A stochastic frontier approach. International Journal of Hospitality Management, 18, 45–57. [Google Scholar]
- Anderson, R. I., Fok, R., & Scott, J. (2000). Hotel industry efficiency: An advanced linear programming examination. American Business Review, 18, 40–48. [Google Scholar]
- Arbelo, A., Pérez-Gómez, P., & Arbelo-Pérez, M. (2017). Cost efficiency and its determinants in the hotel industry. Tourism Economics, 23, 1056–1068. [Google Scholar]
- Assaf, A. (2012). Benchmarking the Asia Pacific tourism industry: A Bayesian combination of DEA and stochastic frontier. Tourism Management, 33, 1122–1127. [Google Scholar]
- Assaf, A., & Barros, C. P. (2013). A global benchmarking of the hotel industry. Tourism Economics, 19, 811–821. [Google Scholar]
- Assaf, A., Barros, C. P., & Josiassen, A. (2012). Hotel efficiency: A bootstrapped metafrontier approach. International Journal of Hospitality Management, 31, 621–629. [Google Scholar]
- Assaf, A., & Tsionas, M. (2018). Measuring hotel performance: Toward more rigorous evidence in both scope and methods. Tourism Management, 69, 69–87. [Google Scholar] [CrossRef]
- Barros, C. P. (2004). A stochastic cost frontier in the Portuguese hotel industry. Tourism Economics, 10, 177–192. [Google Scholar]
- Barros, C. P. (2005a). Evaluating the efficiency of a small hotel chain with a Malmquist productivity index. International Journal of Tourism Research, 7, 173–184. [Google Scholar]
- Barros, C. P. (2005b). Measuring efficiency in the hotel sector. Annals of Tourism Research, 32, 456–477. [Google Scholar]
- Barros, C. P. (2006). Analyzing the rate of technical change in the Portuguese hotel industry. Tourism Economics, 12, 325–346. [Google Scholar] [CrossRef]
- Barros, C. P., & Alves, F. P. (2004). Productivity in the tourism industry. International Advances in Economic Research, 10, 215–225. [Google Scholar] [CrossRef]
- Barros, C. P., & Dieke, P. U. C. (2008). Technical efficiency of African hotels. International Journal of Hospitality Management, 27, 438–447. [Google Scholar] [CrossRef]
- Barros, C. P., & Mascarenhas, M. J. (2005). Technical and allocative efficiency in a chain of small hotels. International Journal of Hospitality Management, 24, 415–436. [Google Scholar]
- Boussemart, J. P., Briec, W., Kerstens, K., & Poutineau, J. C. (2003). Luenberger and Malmquist productivity indices: Theoretical comparisons and empirical illustration. Bulletin of Economic Research, 55, 391–405. [Google Scholar]
- Caves, D. W., Christensen, L. R., & Diewert, W. E. (1982). The economic theory of index numbers and the measurement of input, output, and productivity. Econometrica, 50, 1393–1414. [Google Scholar]
- Chambers, R. G., Chung, Y. H., & Färe, R. (1996). Benefit and distance function. Journal of Economic Theory, 70, 407–419. [Google Scholar] [CrossRef]
- Chang, T. P., Hu, J. L., Chou, R. Y., & Sun, L. (2012). The sources of bank productivity growth in China during 2002–2009: A disaggregation view. Journal of Banking and Finance, 36, 1997–2006. [Google Scholar]
- Chen, C. (2007). Applying the stochastic frontier approach to measure hotel managerial efficiency in Taiwan. Tourism Management, 28, 696–702. [Google Scholar] [CrossRef]
- Chen, C. P., Hu, J. L., & Yang, C. H. (2011). An international comparison for R&D efficiency of multiple innovative outputs: The role of the national innovative system. Innovation: Management, Policy, and Practice, 13, 341–360. [Google Scholar]
- Chen, C. P., Hu, J. L., & Yang, C. H. (2013). Produce patents or journal articles? A cross-country comparison of R&D productivity change. Scientometrics, 94, 833–849. [Google Scholar]
- Chen, P. C., Yu, M. M., Chang, C. C., Hsu, S. H., & Managi, S. (2015). The enhanced Russell-based directional distance measure with undesirable outputs: Numerical example considering CO2 emissions. Omega, 53, 30–40. [Google Scholar] [CrossRef]
- Chiang, W., Tsai, M., & Wang, L. S. (2004). A DEA evaluation of Taipei hotels. Annals of Tourism Research, 31, 712–715. [Google Scholar] [CrossRef]
- Chiu, Y. H., & Wu, M. F. (2010). Performance evaluation of international tourist hotels in Taiwan—Application of context-dependent DEA. INFOR: Information Systems and Operational Research, 48, 155–170. [Google Scholar]
- Choi, K., & Kim, J. (2024). Measuring hotel service productivity using two-stage network DEA. Sustainability, 16, 8995. [Google Scholar] [CrossRef]
- Coelli, T., Rao, D. S. P., O’Donnell, C. J., & Battese, G. E. (2005). An introduction to efficiency and productivity analysis (2nd ed.). Spinger. [Google Scholar]
- Cordero, J., & Tzeremes, N. (2017). Evaluating hotel productivity growth in Balearic and Canary islands. Tourism Economics, 23, 1146–1154. [Google Scholar] [CrossRef]
- El Alaoui, M. H., Ibrahim, M. D., Daneshvar, S., Alola, U. V., & Alola, A. A. (2023). A two-stage data envelopment analysis approach to productivity, efficiency and their sustainability in the hotel industry of Tunisia. Quality & Quantity, 57, 955–972. [Google Scholar]
- Higuerey, A., Viñan-Merecí, C., Malo-Montoya, Z., & Martínez-Fernández, V. A. (2020). Data envelopment analysis (DEA) for measuring the efficiency of the hotel industry in Ecuador. Sustainability, 12, 1590. [Google Scholar] [CrossRef]
- Hu, J. L., Chiu, C. N., Shieh, H. S., & Huang, C. H. (2010). A stochastic cost efficiency analysis of international tourist hotels in Taiwan. International Journal of Hospitality Management, 29, 99–107. [Google Scholar] [CrossRef]
- Hu, J. L., Shieh, H. S., Huang, C. H., & Chiu, C. N. (2009). Cost efficiency of international tourist hotels in Taiwan: A data envelopment analysis application. Asia Pacific Journal of Tourism Research, 14, 371–384. [Google Scholar] [CrossRef]
- Hwang, S. N., & Chang, T. Y. (2003). Use data envelopment analysis to measure hotel managerial efficiency change in Taiwan. Tourism Management, 24, 357–369. [Google Scholar]
- Kim, S. (2011). Factor determinants of total factor productivity growth in the Malaysian hotel industry: A stochastic frontier approach. Cornell Hospitality Quarterly, 52, 35–47. [Google Scholar]
- Lin, Y. H. (2011). Estimating cost efficiency and the technology gap ratio using the metafrontier approach for Taiwanese international tourist hotels. Cornell Hospitality Quarterly, 52, 341–353. [Google Scholar]
- Lovell, C. A. K., & Schmidt, P. (1993). Production frontiers and productive efficiency: Techniques and applications. Oxford University Press. [Google Scholar]
- Luo, H., Yang, Y., & Law, R. (2014). How to achieve a high efficiency level of the hotel industry? International Journal of Contemporary Hospitality Management, 26, 1140–1161. [Google Scholar] [CrossRef]
- Managi, S. (2003). Luenberger and Malmquist productivity indices in Japan, 1955–1995. Applied Economics Letters, 10, 581–584. [Google Scholar]
- Manasakis, C., Apostolakis, A., & Datseris, G. (2013). Using data envelopment analysis to measure hotel efficiency in Crete. International Journal of Contemporary Hospitality Management, 25, 510–535. [Google Scholar]
- Morey, R. C., & Dittman, D. A. (1995). Evaluating a hotel GM’s performance: A case study in benchmarking. Cornell Hotel Restaurant and Administration Quarterly, 36, 30–35. [Google Scholar]
- Phillips, P. A. (1999). Performance measurement systems and hotels: A new conceptual framework. International Journal of Hospitality Management, 18, 171–182. [Google Scholar]
- Ramanathan, R., Ramanathan, U., & Zhang, Y. (2016). Linking operations, marketing and environmental capabilities and diversification to hotel performance: A data envelopment analysis approach. International Journal of Production Economics, 176, 111–122. [Google Scholar]
- Salman Saleh, A., Assaf, A. G., & Son Nghiem, H. (2012). Efficiency of the Malaysian hotel industry: A distance function approach. Tourism Analysis, 17, 721–732. [Google Scholar]
- Shieh, H. S. (2012). Does cost efficiency lead to better financial performance? A study on Taiwan international tourist hotels. The Journal of Hospitality Financial Management, 20, 17–30. [Google Scholar]
- Tan, Y., & Despotis, D. (2021). Investigation of efficiency in the UK hotel industry: A network data envelopment analysis approach. International Journal of Contemporary Hospitality Management, 33, 1080–1104. [Google Scholar]
- Tourism Administration. (2016). Tourism statistics annual report 2016. Tourism Administration, Ministry of Transportation and Communications. [Google Scholar]
- Tsaur, S. H. (2001). The operating efficiency of international tourist hotels in Taiwan. Asia Pacific Journal of Tourism Research, 6, 73–81. [Google Scholar]
- Tzeremes, N. (2019). Hotel productivity: A robust Luenberger productivity indicator. Tourism Economics, 25, 987–996. [Google Scholar]
- Vidali, M. E., Menegaki, A. N., & Ahmad, N. (2024). Parametric and nonparametric measurement of efficiency in hotel industry: A systematic literature review. Journal of Economic Surveys. [Google Scholar] [CrossRef]
- Wang, F. C., Hung, W. T., & Shang, J. K. (2006a). Measuring pure managerial efficiency of international tourist hotels in Taiwan. Service Industries Journal, 26, 59–71. [Google Scholar]
- Wang, F. C., Shang, J. K., & Hung, W. T. (2006b). Productivity and service quality changes of international tourist hotels in Taiwan. Annals of Tourism Research, 33, 571–574. [Google Scholar]
- Wheeler, B., & Zang, L. (2018). Profit Luenberger and Malmquist-Luenberger indexes for multi-activity decision-making units: The case of the star-rated hotel industry in China. Tourism Management, 69, 1–11. [Google Scholar]
- Yin, P., Chu, J., Wu, J., Ding, J., Yang, M., & Wang, Y. (2020). A DEA-based two-stage network approach for hotel performance analysis: An internal cooperation perspective. Omega, 93, 102035. [Google Scholar] [CrossRef]
- Yu, M. M., & Chen, L. H. (2016). Productivity growth of Taiwanese international tourist hotels in a metafrontier framework. Cornell Hospitality Quarterly, 57, 38–50. [Google Scholar]
- Yu, M. M., & Lee, C. Y. (2009). Efficiency and effectiveness of service business: Evidence from international tourist hotels in Taiwan. Tourism Management, 30, 571–580. [Google Scholar] [CrossRef]
- Zhu, W., Lin, H., Yu, Y., & Ghiyasi, M. (2023). Performance measurement of Taiwan hotels with a hierarchical network DEA with shared inputs. International Journal of Applied Decision Sciences, 16, 474–507. [Google Scholar] [CrossRef]
| Name | Mean | SD | Min | Max | |
|---|---|---|---|---|---|
| Input variable | |||||
| x1 | Wage expenditure | 190.04 | 165.42 | 7.97 | 803.21 |
| x2 | Food and beverage expenditure | 113.72 | 123.71 | 3.43 | 1241.82 |
| x3 | Other expenditure | 271.08 | 295.54 | 20.39 | 2732.90 |
| Output variable | |||||
| y1 | Room revenue | 259.37 | 223.00 | 25.75 | 1312.17 |
| y2 | Food and beverage revenue | 284.11 | 291.83 | 7.63 | 1630.80 |
| y3 | Other facilities revenue | 107.30 | 418.61 | 0.09 | 9207.28 |
| Variable | Correlation Matrix | |||||
|---|---|---|---|---|---|---|
| Input Variable | ||||||
| x1 | 1.0000 | |||||
| x2 | 0.6963 * | 1.0000 | ||||
| x3 | 0.7224 * | 0.5996 * | 1.0000 | |||
| Output Variable | ||||||
| y1 | 0.8644 * | 0.6237 * | 0.8012 * | 1.0000 | ||
| y2 | 0.9294 * | 0.7790 * | 0.7699 * | 0.8522 * | 1.0000 | |
| y3 | 0.2606 * | 0.2430 * | 0.2110 * | 0.2178 * | 0.2724 * | 1.0000 |
| Year | 2005/2006 | 2006/2007 | 2007/2008 | 2008/2009 | 2009/2010 | 2010/2011 | 2011/2012 | 2012/2013 | 2013/2014 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| Chain | −0.1499 | 0.1487 | −0.1201 | −0.2446 | −0.2678 | 12.5354 | −7.0353 | 0.0896 | −0.0109 | 0.5495 |
| Independent | 0.1387 | 0.2129 | −1.6791 | 0.8385 | −0.7081 | 27.9883 | −22.7384 | −1.1707 | 2.9716 | 0.6504 |
| North | 0.2510 | 0.1070 | −0.3513 | 0.1989 | −0.2171 | 16.0584 | −18.6604 | 0.1266 | 0.4104 | −0.2307 |
| Central | −0.2958 | 0.1332 | 0.1100 | −0.8013 | 0.4984 | 5.7685 | −5.4718 | −0.1681 | −0.1609 | −0.0431 |
| South | −0.2969 | 0.2497 | −1.9046 | 0.6068 | −0.6227 | 19.4152 | −2.3579 | −1.8038 | 3.0350 | 1.8134 |
| East | −0.2968 | 0.2694 | −0.2594 | 0.0074 | −1.5080 | 34.8967 | −22.9647 | 0.4836 | 0.8421 | 1.2745 |
| ALL | −0.0333 | 0.1736 | −0.7325 | 0.1809 | −0.4407 | 18.6061 | −13.2043 | −0.4055 | 1.1607 | 0.5894 |
| Year | 05/06 | 06/07 | 07/08 | 08/09 | 09/10 | 10/11 | 11/12 | 12/13 | 13/14 | Average | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| HEC | Chain | −0.3126 | 0.1605 | 0.0598 | −0.1264 | −0.0200 | −18.2405 | 18.4187 | 0.0889 | −1.4513 | −0.1581 |
| Independent | −0.3993 | −0.0782 | −0.9261 | 1.2281 | −0.6488 | −32.2670 | 31.3995 | −0.8440 | −1.6210 | −0.4619 | |
| North | −0.0821 | −0.0255 | −0.1727 | 0.3807 | −0.0733 | −8.1190 | 7.1203 | −0.0021 | −1.6722 | −0.2940 | |
| Central | −0.5252 | 0.0283 | 0.3423 | −0.8894 | 0.7272 | −15.4994 | 15.6772 | −0.2162 | −1.9436 | −0.2554 | |
| South | −0.5875 | 0.1708 | −1.1773 | 1.1748 | −0.6280 | −48.7666 | 49.2542 | −1.0851 | −1.2576 | −0.3225 | |
| East | −0.6637 | 0.1952 | 0.3664 | −0.0795 | −0.9203 | −30.7121 | 31.2207 | 0.3963 | −1.2179 | −0.1572 | |
| ALL | −0.3476 | 0.0676 | −0.3275 | 0.4057 | −0.2670 | −23.7509 | 23.5182 | −0.2776 | −1.5179 | −0.2774 | |
| HTC | Chain | 0.1627 | −0.0112 | −0.1799 | −0.1182 | −0.2478 | 30.7759 | −25.4540 | 0.0006 | 1.4403 | 0.7076 |
| Independent | 0.5380 | 0.2911 | −0.7530 | −0.3896 | −0.0592 | 60.2553 | −54.1379 | −0.3266 | 4.5925 | 1.1123 | |
| North | 0.3331 | 0.1326 | −0.1786 | −0.1818 | −0.1438 | 24.1774 | −25.7807 | 0.1287 | 2.0827 | 0.0633 | |
| Central | 0.2294 | 0.1049 | −0.2323 | 0.0881 | −0.2288 | 21.2679 | −21.1490 | 0.0480 | 1.7827 | 0.2123 | |
| South | 0.2906 | 0.0790 | −0.7273 | −0.5680 | 0.0053 | 68.1818 | −51.6121 | −0.7186 | 4.2926 | 2.1359 | |
| East | 0.3669 | 0.0742 | −0.6258 | 0.0869 | −0.5877 | 65.6088 | −54.1854 | 0.0873 | 2.0600 | 1.4317 | |
| ALL | 0.3142 | 0.1059 | −0.4050 | −0.2248 | −0.1736 | 42.3571 | −36.7226 | −0.1279 | 2.6787 | 0.8668 |
| Year | 2005/2006 | 2006/2007 | 2007/2008 | 2008/2009 | 2009/2010 | 2010/2011 | 2011/2012 | 2012/2013 | 2013/2014 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| Chain | −0.0567 | −0.0246 | 0.5855 | −0.9575 | 0.1919 | −0.0695 | 0.2706 | 0.0007 | −0.0360 | −0.0106 |
| Independent | −0.0245 | −0.0394 | 0.4400 | −0.4456 | 0.0934 | −0.0027 | 0.1528 | −0.0186 | −0.0775 | 0.0087 |
| North | −0.0264 | −0.0091 | 0.2730 | −0.6356 | 0.1371 | −0.2087 | 0.2474 | 0.0294 | −0.0619 | −0.0283 |
| Central | −0.0226 | −0.3086 | 1.4001 | −1.6242 | 0.2932 | −0.1136 | 0.1714 | −0.0101 | −0.0601 | −0.0305 |
| South | −0.0709 | −0.0206 | 0.6893 | −0.8867 | 0.1466 | 0.2224 | 0.2254 | −0.0723 | 0.0003 | 0.0259 |
| East | −0.0689 | 0.0936 | 0.3823 | −0.2375 | 0.1139 | 0.0158 | 0.1870 | 0.0086 | −0.1201 | 0.0416 |
| ALL | −0.0436 | −0.0303 | 0.5283 | −0.7564 | 0.1531 | −0.0432 | 0.2243 | −0.0068 | −0.0522 | −0.0030 |
| Year | 2005/2006 | 2006/2007 | 2007/2008 | 2008/2009 | 2009/2010 | 2010/2011 | 2011/2012 | 2012/2013 | 2013/2014 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| Chain | 0.0135 | 0.0716 | −0.1277 | 0.1605 | −0.0020 | −0.0443 | −0.2243 | 0.1566 | 0.0753 | 0.0088 |
| Independent | 0.1231 | 0.0428 | −0.1529 | 0.1344 | −0.0014 | −0.0340 | −0.0049 | −0.1250 | −0.4576 | −0.0528 |
| North | 0.1143 | 0.0655 | −0.1439 | 0.1336 | 0.0006 | −0.0750 | 0.0299 | −0.0724 | 0.0807 | 0.0148 |
| Central | 0.0005 | −0.0422 | −0.1419 | 0.1740 | −0.0507 | −0.0897 | 0.0555 | −0.0294 | 0.0240 | −0.0111 |
| South | −0.0191 | 0.1330 | −0.1662 | 0.2107 | 0.0090 | 0.0048 | −0.5494 | 0.3610 | 0.1154 | 0.0110 |
| East | 0.0582 | −0.0149 | −0.0566 | 0.0655 | 0.0056 | 0.0196 | −0.0066 | −0.1431 | −1.4495 | −0.1691 |
| ALL | 0.0577 | 0.0603 | −0.1375 | 0.1502 | −0.0017 | −0.0402 | −0.1381 | 0.0459 | −0.1340 | −0.0153 |
| Year | 2005/2006 | 2006/2007 | 2007/2008 | 2008/2009 | 2009/2010 | 2010/2011 | 2011/2012 | 2012/2013 | 2013/2014 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| Chain | −0.4066 | 0.3991 | −0.8180 | −1.2383 | −0.9931 | 37.8696 | −21.1523 | 0.0063 | −0.0722 | 1.5105 |
| Independent | 0.3175 | 0.6352 | −5.3244 | 4.2060 | −2.2127 | 84.2629 | −68.3425 | −3.5315 | 9.4498 | 2.1623 |
| North | 0.6650 | 0.2647 | −1.1830 | 0.6377 | −0.7859 | 48.5536 | −56.2584 | 0.3167 | 1.2125 | −0.7308 |
| Central | −0.8654 | 0.7505 | −0.9281 | −3.3282 | 1.2528 | 17.5830 | −16.6424 | −0.4790 | −0.4466 | −0.3448 |
| South | −0.8007 | 0.6368 | −6.2370 | 3.8558 | −2.0236 | 58.4071 | −6.7214 | −5.9482 | 8.9893 | 5.5731 |
| East | −0.8798 | 0.7296 | −1.1039 | −0.9842 | −4.6436 | 104.8681 | −69.0745 | 1.5414 | 4.0959 | 3.8388 |
| ALL | −0.1141 | 0.4909 | −2.5883 | 0.9005 | −1.4722 | 56.0955 | −39.6912 | −1.3835 | 3.6685 | 1.7673 |
| Hotel No. | HLPI | Rank | RHLPI | Rank | FHLPI | Rank | OHLPI | Rank |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.1401 | 19 | −0.0617 | 45 | 0.0064 | 24 | 0.4039 | 16 |
| 2 | 0.1445 | 18 | −0.0760 | 49 | −0.0294 | 47 | 0.3164 | 18 |
| 3 | 0.2900 | 13 | −0.0306 | 38 | −0.0190 | 42 | 0.8266 | 13 |
| 4 | −0.1146 | 35 | −0.0941 | 51 | 0.0017 | 27 | −0.3887 | 34 |
| 5 | −0.0439 | 26 | −0.0436 | 40 | −0.0182 | 40 | −0.2612 | 29 |
| 6 | −0.0802 | 31 | 0.0364 | 14 | 0.0160 | 19 | −0.3648 | 32 |
| 7 | −0.1287 | 38 | −0.0413 | 39 | 0.0118 | 22 | −0.5055 | 41 |
| 8 | −0.4236 | 47 | 0.1100 | 5 | −0.0108 | 36 | −1.4750 | 48 |
| 9 | −0.0633 | 27 | −0.0142 | 33 | 0.0155 | 20 | −0.2559 | 28 |
| 10 | −0.1739 | 42 | −0.0581 | 44 | −0.0199 | 43 | −0.4196 | 35 |
| 11 | 0.2800 | 14 | −0.0960 | 52 | 0.0860 | 8 | 0.3877 | 17 |
| 12 | 0.0219 | 23 | −0.0291 | 36 | −0.0766 | 54 | −0.0415 | 24 |
| 13 | −0.2384 | 44 | −0.0125 | 32 | 0.1038 | 4 | −1.0277 | 46 |
| 14 | 0.1482 | 17 | 0.0140 | 21 | 0.0729 | 10 | 0.0537 | 22 |
| 15 | 1.2332 | 9 | 0.0039 | 25 | 0.0385 | 11 | 3.6967 | 8 |
| 16 | −0.1404 | 41 | 0.0531 | 8 | 0.0324 | 12 | −0.4991 | 40 |
| 17 | −0.1213 | 37 | −0.0093 | 31 | 0.0223 | 17 | −0.3869 | 33 |
| 18 | 2.3517 | 5 | 0.0314 | 17 | −0.0122 | 37 | 7.0912 | 5 |
| 19 | −5.0371 | 56 | −0.0006 | 26 | 0.0883 | 7 | −12.1215 | 56 |
| 20 | 0.0183 | 24 | −0.1074 | 53 | −0.0053 | 30 | 0.1541 | 20 |
| 21 | −0.0782 | 30 | −0.0248 | 35 | −0.0006 | 28 | −0.3517 | 31 |
| 22 | −0.0651 | 28 | 0.0122 | 22 | −0.0226 | 44 | 0.1119 | 21 |
| 23 | 0.0062 | 25 | −0.0672 | 47 | −0.0091 | 34 | −0.4329 | 38 |
| 24 | −2.1291 | 54 | 0.0259 | 18 | 0.0912 | 6 | −8.3534 | 54 |
| 25 | −0.1125 | 34 | −0.2468 | 56 | −0.0050 | 29 | −0.0901 | 26 |
| 26 | −1.7205 | 52 | −0.0209 | 34 | 0.0049 | 25 | −5.2665 | 53 |
| 27 | 0.0436 | 21 | −0.0047 | 27 | 0.0306 | 14 | −0.0663 | 25 |
| 28 | −0.0845 | 32 | −0.1386 | 55 | −0.0096 | 35 | −0.6784 | 43 |
| 29 | −0.1188 | 36 | 0.0323 | 16 | −0.1095 | 55 | −0.7137 | 44 |
| 30 | −0.5603 | 49 | −0.0477 | 41 | 0.0031 | 26 | −2.0303 | 50 |
| 31 | 0.5945 | 12 | −0.0814 | 50 | −0.0122 | 38 | 1.8429 | 11 |
| 32 | −0.1331 | 40 | 0.0571 | 7 | 0.0311 | 13 | −0.4230 | 37 |
| 33 | 1.3280 | 8 | 0.3092 | 1 | 0.1701 | 1 | 3.3069 | 9 |
| 34 | −0.2994 | 45 | 0.1435 | 4 | 0.0927 | 5 | −0.1729 | 27 |
| 35 | −0.0888 | 33 | −0.0639 | 46 | −0.0185 | 41 | −0.4658 | 39 |
| 36 | 1.7858 | 6 | 0.2515 | 2 | −0.0748 | 53 | 4.6726 | 6 |
| 37 | 1.5502 | 7 | 0.0359 | 15 | −0.0587 | 52 | 4.2134 | 7 |
| 38 | 0.0254 | 22 | −0.0499 | 42 | 0.0749 | 9 | −0.0343 | 23 |
| 39 | −0.4242 | 48 | 0.0412 | 12 | 0.0130 | 21 | −1.8291 | 49 |
| 40 | 2.6671 | 4 | −0.0718 | 48 | −0.0562 | 51 | 7.7602 | 4 |
| 41 | −0.1320 | 39 | −0.0564 | 43 | −0.0077 | 33 | −0.5811 | 42 |
| 42 | −1.8540 | 53 | −0.0064 | 29 | −0.0234 | 45 | −5.2036 | 52 |
| 43 | 0.7048 | 10 | −0.1307 | 54 | −0.0390 | 49 | 2.4663 | 10 |
| 44 | 21.0092 | 1 | 0.0517 | 9 | 0.1328 | 2 | 66.6774 | 1 |
| 45 | 2.7590 | 3 | 0.0435 | 11 | −0.0402 | 50 | 7.8919 | 3 |
| 46 | 0.6920 | 11 | 0.0063 | 24 | 0.0188 | 18 | 1.7987 | 12 |
| 47 | −0.3320 | 46 | −0.0086 | 30 | −0.0069 | 32 | −0.4217 | 36 |
| 48 | 0.2635 | 15 | 0.0116 | 23 | 0.0226 | 16 | 0.8100 | 15 |
| 49 | −0.0676 | 29 | −0.0048 | 28 | 0.0084 | 23 | −0.2816 | 30 |
| 50 | −3.0419 | 55 | 0.1045 | 6 | −0.0321 | 48 | −9.3453 | 55 |
| 51 | −0.7922 | 51 | −0.0304 | 37 | −1.4335 | 56 | −1.0314 | 47 |
| 52 | 14.7399 | 2 | 0.0399 | 13 | −0.0285 | 46 | 43.3732 | 2 |
| 53 | −0.7039 | 50 | 0.0462 | 10 | 0.0304 | 15 | −2.0955 | 51 |
| 54 | −0.2380 | 43 | 0.0201 | 19 | −0.0171 | 39 | −0.8487 | 45 |
| 55 | 0.0849 | 20 | 0.0160 | 20 | 0.1209 | 3 | 0.1858 | 19 |
| 56 | 0.2399 | 16 | 0.1488 | 3 | −0.0067 | 31 | 0.8201 | 14 |
| Average | 0.5997 | −0.0015 | −0.0154 | 1.7928 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, M.-C.; Chen, C.-P.; Chou, K.-W. The Decomposition of Hotel Productivity Change in Taiwan from Overall and Disaggregate Perspectives. Tour. Hosp. 2025, 6, 61. https://doi.org/10.3390/tourhosp6020061
Chang M-C, Chen C-P, Chou K-W. The Decomposition of Hotel Productivity Change in Taiwan from Overall and Disaggregate Perspectives. Tourism and Hospitality. 2025; 6(2):61. https://doi.org/10.3390/tourhosp6020061
Chicago/Turabian StyleChang, Ming-Chung, Chiang-Ping Chen, and Kuo-Wei Chou. 2025. "The Decomposition of Hotel Productivity Change in Taiwan from Overall and Disaggregate Perspectives" Tourism and Hospitality 6, no. 2: 61. https://doi.org/10.3390/tourhosp6020061
APA StyleChang, M.-C., Chen, C.-P., & Chou, K.-W. (2025). The Decomposition of Hotel Productivity Change in Taiwan from Overall and Disaggregate Perspectives. Tourism and Hospitality, 6(2), 61. https://doi.org/10.3390/tourhosp6020061






