Abstract
In this work, we analyze non-Darcy two-component single-phase isothermal flow in naturally fractured tight gas reservoirs. The model is applied in a scenario of enhanced gas recovery (EGR) with the possibility of carbon dioxide storage. The properties of the gases are obtained via the Peng–Robinson equation of state. The finite volume method is used to solve the governing partial differential equations. This process leads to two subsystems of algebraic equations, which, after linearization and use of an operator splitting method, are solved by the conjugate gradient (CG) and biconjugate gradient stabilized (BiCGSTAB) methods for determining the pressure and fraction molar, respectively. We include inertial effects using the Barree and Conway model and gas slippage via a more recent model than Klinkenberg’s, and we use a simplified model for the effects of effective stress. We also utilize a mesh refinement technique to represent the discrete fractures. Finally, several simulations show the influence of inertial, slippage and stress effects on production in fractured tight gas reservoirs.
1. Introduction
Fluid flow in porous media is present in several areas of scientific and technological knowledge [1]. In this context, due to technological advances, the so-called unconventional reservoirs have aroused great interest in the oil industry. However, even with the most recent advances in technology, the economically viable production of these reservoirs still presents challenges when aiming to increase gas recovery rates [2]. On the other hand, they present great potential regarding the geological storage of carbon dioxide. Therefore, the numerical simulation of flow in these reservoirs is a topic of great importance for the energy sector on a global scale.
Tight and shale gas reservoirs are examples of unconventional reservoirs. The first is characterized by having low permeability (0.1 millidarcy or less), while the second is characterized by having very low permeability. Unlike conventional reservoirs, commercial exploration of gas from these reservoirs is more difficult.
Usually, to extract gas from shale and tight reservoirs a process called hydraulic fracturing (fracking) is used. It involves the injection of a mixture of water, sand, and chemicals into the porous rock to create fractures, which allow gas to flow more easily. This extraction method differs from traditional natural gas production methods where it is not necessary to fracture the reservoir, which is not effective for shale and tight-type gas reservoirs [3].
1.1. Brief Review: Shale and Tight Gas Reservoirs
In recent years, investigations about low- and very-low-permeability reservoirs containing natural gas have intensified. Among the topics explored, it is possible to highlight the following: flow mechanisms in shale gas reservoirs [4,5], correlations for absolute permeability as a function of pressure [6,7,8], fractured horizontal wells in shale gas reservoirs [9], with respect to naturally fractured reservoirs [10], two-phase flow including gas slippage and production through fractured horizontal wells [11,12,13], and the effects of heterogeneity and non-Darcy flow in tight gas reservoirs [14].
Guria [15] addressed the effects of non-ideal gas behavior and slippage when measuring permeability in porous media. The author used cubic equations of state such as van der Waals, Soave–Redlich–Kwong, and Peng–Robinson to model the non-ideal behavior of gases, including or not including hydrocarbons. He also proposed a comprehensive mathematical model for evaluating the apparent permeability depending on pressure and temperature for real gas flows in porous media.
Rubin et al. [16] performed experiments on shales of the Marcellus formation. They showed that the effects of gas slippage and matrix compaction are significant when evaluating gas production due to the substantial depletion of reservoir pressure, especially at the end of the production period. However, their impact on gas recovery and hydraulic fracturing design has not yet been understood and systematically investigated. According to the authors, the results showed that ignoring both effects when simulating flow in the reservoir leads to an incorrect estimate of gas production.
In the work of Ding et al. [17], experiments to understand the nonlinear behavior of flow in tight gas reservoirs were carried out, including the effects of slippage and inertial/turbulent effects. The authors also attested that experimental methods applicable to conventional reservoirs lead to significant errors when applied to these unconventional reservoirs.
Friedel and Voigt [18] applied numerical reservoir simulations to study the inertial effects in a fractured reservoir. They ran simulations considering a fully implicit formulation and investigated synthetic cases for gas production. The results indicated that non-Darcy flow influenced productivity, even for relatively low gas production rates. The authors also mentioned that they evaluated a scenario in which they verified a reduction of between 21% and 40% in gas production.
In 2012, Clarkson et al. [19] discussed the rapid evolution of the technology used to evaluate the properties of unconventional gas reservoirs and hydraulic fracturing. The authors proposed a model for optimizing the development of unconventional gas reservoir fields, raising critical issues related to the analysis of reservoir samples, production data analysis, and transient flow responses. The authors aimed, for example, to review existing methods for reservoir evaluation and to introduce new methods for evaluating heterogeneities, focusing on tight and shale reservoirs and discussing the influence of non-Darcy inertial effects.
On the other hand, Ye et al. [20] considered non-Darcy inertial effects using Forchheimer’s model and unconventional coalbed methane reservoirs. According to experimental results, the so-called non-Darcy flow factor, , associated with the inertial effects can be expressed as a power law depending on absolute permeability. The authors point out that for certain conventional gas reservoirs, can be considered constant, but this may not be suitable for coalbed methane, which has an important change in permeability. They also report that when the paper was published, few studies considered as a function of coal permeability in reservoir simulations. The results of the simulations showed that considering a constant factor can underestimate or overestimate the gas production rate for coalbed methane wells.
Other authors have also pointed to the possibility of errors in calculating the productivity of gas wells if the inertial effects are not considered, including cases with and without fractures and the use of horizontal wells. Wang et al. [21] dealt with this issue by introducing the concept of the apparent equivalent radius of the well to include the non-Darcy inertial flow in a fracture. First, the authors presented an iterative process to calculate the productivity of vertical fractured gas wells using the proposed concept, followed by an analysis of the productivity of horizontal multi-fractured gas-producing wells. The results showed that non-Darcy inertial effects can significantly decrease production even in low-permeability reservoirs (less than 1 mD) and reduce the potential interference between hydraulic fractures.
According to Farahani et al. [22], two main effects for accurately modeling the productivity of gas reservoirs are slippage and inertial flow in porous media. These effects lead to an apparent permeability for the gas phase, which is different from the absolute permeability measured when we have a single liquid phase flow. Therefore, we must consider these elements when performing pressure tests to characterize gas reservoirs. The authors studied gas flow conditions in laboratory measurements using Iranian Kangan and Dalan carbonates, developing a correlation to estimate the inertia factor of the samples. In addition, they introduced an equation to estimate the maximum allowable pressure variation per length to keep the laminar flow regime (Darcy flow) in the samples.
Furthermore, Fu et al. [12] proposed a new productivity model for multi-fractured horizontal wells and considered the beta inertial factor to incorporate the effects of high velocity. Besides that, the authors considered the consequences of stress reduction (negative on effective permeability) and slip (positive on absolute permeability). The authors analyzed tight gas reservoirs, including the impacts of the presence of the water phase in the porous medium.
Assessing the economic viability of unconventional gas reservoirs has been challenging due to the inherent difficulties in accurately quantifying absolute permeabilities on the micro/nano-Darcy scale [23]. These greatly influence the behavior of gas mass transport in porous media with low permeability. However, correctly measuring the permeability of this type of porous media is difficult. Gas flow differs from liquid flow, for example, due to its high compressibility, the effect of slippage, and, sometimes, adsorption [24].
The work of Luo et al. [25] aimed to analyze temperature variation and quantitatively diagnose water production in multi-fractured horizontal wells for two-phase flows in tight gas reservoirs. The work led to a model for determining temperature considering effects such as Joule–Thomson and thermal expansion. They simulated synthetic cases to illustrate temperature behavior. The sensitivity analysis indicated that the gas phase slippage was responsible for reducing the well temperature. They also concluded that it was significantly impacted depending on the reservoir permeability values and the length of the fractures. Subsequently, they applied the proposed model to a field case, and the comparison showed good agreement between the results.
Liu et al. [26] experimentally evaluated the effect of the pore–throat structure on the behavior of gas–water flow in a low permeability sandstone reservoir bearing natural gas. More specifically, they carried out mercury injection tests under controlled pressure to measure capillary pressure and identify the characteristics of a pore–throat structure and its connectivity and distribution of pore diameters. Subsequently, the characteristics of the flow, including the saturation variation of the mobile fluid, the relative permeability, and the degree of water blockage, were quantified using displacement experiments and the nuclear magnetic resonance technique. The pore–throat structure, especially its connectivity, was estimated to be the dominant factor in the distribution of mobile fluid saturation and the infiltration characteristics of the two phases in a tight gas sandstone reservoir. This study allowed us to understand how the structure of the pore throat influences the behavior of gas–water flow in a low-permeability gas reservoir, emphasizing the importance of identifying and classifying flow patterns.
The ultra-deep Kelasu field tight gas reservoir in the Tarim basin (China) contains fractures at various scales within the matrix, including faults. The reservoir flow was modeled by Sun et al. [27] via numerical simulations of pressure tests in vertical wells by considering the porous matrix, fractures, and faults and combining the random generation of natural fracture networks with the use of discrete unstructured fractures. The numerical methodology used the mixed finite element method, and the authors obtained typical curves using different random fracture networks. Based on the observed results, they classified the distribution of the fracture network of fractured low-permeability sandstone reservoirs. Furthermore, they also discussed the influence of the random generation of fracture networks on well tests.
1.2. Carbon Sequestration
To address the impacts of greenhouse gas emissions into the atmosphere, one of the strategies to mitigate the problem of carbon dioxide release is its capture and sequestration in underground rock formations, which can have other purposes besides storage [28]. One example would be the enhanced gas recovery of low-permeability reservoirs, as the controlled injection of CO2 into these formations may improve the ultimate recovery factor and can also be used to store carbon dioxide [29].
According to Liu et al. [30], CO2 storage to enhance natural gas recovery (CO2 storage with enhanced gas recovery (CSEGR)) is a promising option. It can reduce the concentration of carbon dioxide in the environment by sequestering it in gas reservoirs and can simultaneously increase the production of natural gas, which can be used, for example, in sustainable hydrogen production through methane reforming [31].
Therefore, tight gas and shale gas reservoirs have become increasingly important regarding unconventional reserves. Among other applications, we can cite carbon dioxide injection into the reservoir, aiming for carbon sequestration and natural gas recovery [32]. For example, due to the competitive adsorption between carbon dioxide and methane, the capture and carbon storage in tight and shale gas reservoirs also constitutes an opportunity to improve methane recovery. Furthermore, CO2 injection is already also used as a miscible technique of enhanced oil recovery.
Aminu and Manovic [33] emphasized that it is feasible to achieve a reduction in greenhouse gas emissions through carbon capture and storage. The authors cited the Bunter sandstone formation in the North Sea as an example of a rock capable of storing large quantities of carbon dioxide. Its properties make it possible to store CO2 on an industrial scale. However, due to the impurities contained in the captured gas, the amount required for storage may be higher. They also analyzed the influence of impurities (NO2, SO2 and H2S) mixed with carbon dioxide on reservoir production.
Due to heterogeneities, Wang et al. [34] highlighted that it is common to find natural or induced fractures in reservoirs. Therefore, the issue of long-term storage of CO2 requires a detailed evaluation of their existence and structure. Among the risks incurred, they emphasized the possibility of leakage of stored gas. Near fractured regions, there is also the possibility of significant pressure gradients because fractures can act as obstacles to flow. However, the authors understand that the role of fractures in storage processes is not yet fully understood. They performed numerical simulations of CO2 flow in reservoirs containing simple and complex discrete fractures. As a consequence, they concluded that, depending on the storage mechanism, fractures will provide different effects.
From what has been seen so far, we can conclude that large-scale storage can contribute positively to reducing climate effects. As discussed in Parvin et al. [35], storage in aquifers appears as another alternative. However, the authors showed that more research is necessary to understand the importance of high-rate injection on the properties of the aquifer regions close to the injection wells. For example, a loss of injectivity can occur when salt precipitation occurs due to brine evaporation when CO2 is injected.
2. Non-Darcy Flow
Depending on the properties of the porous media and flow rates, the Reynolds number can be high. In these cases, there is no longer a linear relationship between the flow rate and the pressure gradient [36] due to inertial effects. In petroleum engineering, the inertial effects are essentially related to flow rate values. According to Amao [37], different behavior from that predicted by Darcy’s law due to inertial effects appears mainly in the following cases: near the wellbore, for hydraulically fractured wells, for gas reservoirs, for condensate reservoirs, for high flow potential wells, for naturally fractured reservoirs, and for gravel packs. Therefore, in these cases, it is recommended that specific flow models be used that take into account inertial effects.
Barree and Conway [38] proposed a model that introduces the notion of apparent permeability as a way of including inertial effects [39,40]:
where is the apparent velocity, is the fluid viscosity, p is the pressure, is the density, g is the magnitude of the acceleration due to gravity, z is the depth, and the apparent permeability tensor is given by
and is a minimum permeability value at high flow rates, is the permeability tensor, F and E are dimensionless constants, and is the inverse of the characteristic length. It is an advantageous alternative to the Forchheimer model [36].
Usually, we take and introduce [38] to obtain the form used here:
where
is the Reynolds number, and is the identity tensor.
As already mentioned, this model has some advantages, such as providing a limit value for the apparent permeability at high flows [39]. Furthermore, it allows a better representation of transitions between flow regimes in the porous medium, according to Lai et al. [39].
In this work, we also consider a simplified model to account for the effects of effective stress on permeability variation [41]:
where is the permeability modulus, and and are the initial pressure and absolute permeability tensor, respectively.
Furthermore, we know that slippage effects can be introduced in terms of the Knudsen number [42,43]. Therefore, the combined effects of gas slippage and effective stress on permeability variation are determined by
where is the Knudsen number of the mixture, and according to Wang et al. [44], for two-component flow,
where is the hydraulic radius, and for each component, and are the mean free path of gas molecules [45], and (CO2) and (CH4) represent the molar fractions.
3. Two-Component Single-Phase Flow Model
In this article, we are interested in simulating the enhanced gas recovery process when injecting carbon dioxide into a naturally fractured tight gas reservoir (in general, with matrix permeability less than 0.1 mD and porosity less than 10%) containing methane. When developing our numerical code, we considered the following hypotheses: compressible fluids, fractured media using discrete fracture networks (DFNs) [46], Newtonian fluids, no adsorption effects, no chemical reactions, low-compressibility rock [40], and three-dimensional one-phase isothermal flow.
The governing equations for two-component single-phase flow can be obtained from the continuity equation [47] and modified Darcy’s law (1) [39,40]. Therefore, after combining these two equations, we obtain [48,49]
where represents the porosity, q is a source term, and is the molar density, which is given by the real gas law:
where R is the universal gas constant, T is the temperature, and Z is the compressibility factor.
On the other hand, by writing the conservation equation in terms of molar fractions, the governing equation is given by [48,49]
where , is the molar fraction, is a source term, is the number of components, and is the effective dispersion tensor, which can be introduced as [49,50]:
where is the tortuosity, is the molecular diffusion coefficient, and are the transversal and longitudinal hydrodynamic dispersion tensor coefficients, and is given by Equation (1). In the simulations, we considered that [50]
where and are known parameters, and represents a characteristic length.
The dependent variables, the pressure and mole fraction of one of the two components, are obtained by solving the partial differential Equations (8) and (10) numerically.
The Peng–Robinson cubic equation of state is employed to calculate the compressibility factor Z [49,50]. For this purpose, we start from its original form:
where v is the gas molar volume, and the parameters of each component are given by
where is the acentric factor of a component, and and are the critical pressure and temperature, respectively.
For a mixture of components [51],
where is a binary interaction parameter, which is considered to be null in our simulations.
Thus, as the values of the universal gas constant (R), pressure (p) and temperature (T) of the system are known, the compressibility factor (Z) from the Peng–Robinson Equation (14) can be rewritten as
where
and a and b are calculated using Equations (18) and (19).
Finally, the molar density value can be calculated using Equation (9), and the viscosity can be calculated using the correlation proposed by Lohrenz et al. [52].
4. Finite Volume Formulation
We used the finite volume method (FVM) [53] for the numerical solution of the governing equations. As usual in the case of this method, a finite number of control volumes are superimposed on the domain, and the governing equations are discretized by integrating them in time (from to ) and space over a finite volume [53].
To obtain the discrete equations, time-implicit formulations are adopted. Approximations such as three-point centered differences for the spatial derivatives, with the exception of advective terms (approximated through a first-order upwind type scheme) were chosen [49].
Furthermore, we employ a structured three-dimensional mesh when partitioning the domain, and the planar fractures are discretized and inserted into it.
Figure 1 presents a three-dimensional structured mesh, where the nodes are located at the centers of finite volumes, and we highlight the one belonging to the central finite volume as well as those of its six neighbors.
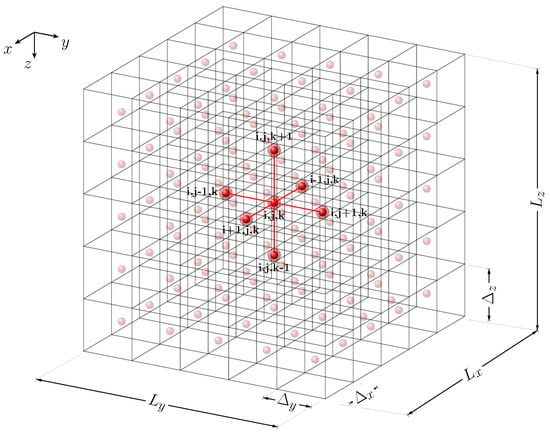
Figure 1.
Three−dimensional mesh.
The integer subscripts i, j and k indicate the nodes positioned at the center of the finite volumes (or cells) along the x-, y- and z-axis, respectively. On the other hand, in a similar way, the cell faces are indicated by the subscripts , and .
The steps related to the integration of the governing equations will be omitted since the usual procedures inherent to the method were employed. More details can be found in Versteeg and Malalasekera [53]. Therefore, considering that the apparent permeability () and effective dispersion () tensors are diagonal [47], the discrete final form of Equation (8) is [48,49]
where must be calculated numerically, knowing that
where Equation (23) was obtained from a conservative expansion [54], the last partial derivative is calculated from Equation (20), and we consider constant rock compressibility.
On the other hand, to determine the molar fraction, Equation (10) is used to find
where . Here, , , and , where , and are the grid sizes in the x-, y- and z-directions, respectively.
In these equations, the transmissibilities are defined as
and .
We also introduce the discrete dispersion coefficients as
for the three spatial directions, respectively.
In terms of boundary conditions, the reservoir is sealed (zero flow across its boundaries) and gas is injected at a prescribed flow rate () in the lower left corner and produced in the upper right corner at the same flow rate ().
The reference pressure () and reference temperature () values are provided at the initial time, and the reservoir contains only methane gas at the beginning of the simulations.
When simulating discrete fractures, depending on their dimensions and properties, we must avoid the appearance of discontinuities through the use of mesh refinement, introducing a transition region in their neighborhood [40,55]. For this purpose, the spatial dimensions of the cells neighboring the fractures will vary according to a logarithmic function, and they will increase in size according to the distance from the fractures [49].
Because the discretized governing equations are nonlinear, it is not possible to employ algebraic methods formulated specifically for solving systems of linear algebraic equations. First, it is necessary to linearize these equations. As a result, there will be a coupled system of equations for determining the pressure and mole fraction. Aiming to decouple them [49], we employ an operator-splitting method [56].
Once the system of equations is decoupled, two well-known and efficient methods are applied to obtain the numerical solutions. As the coefficient matrix is symmetric in the case of the algebraic system for which the dependent variable is pressure, the conjugate gradient method (CG) is adopted [57]. For the mole fractions, we chose the biconjugate gradient stabilized method (BiCGSTAB) [57].
Concluding this section, we must highlight that the numerical results obtained with this simulator were previously validated for the case of flow in a square domain containing two orthogonal fractures that intersect each other in the region to the right of the reservoir, forming an inverted “L”. In this test case, we considered the tracer transport in single-phase flow of an incompressible fluid in a two-dimensional domain in the presence of these two fractures. The results were compared with those obtained by the discrete fracture matrix (DFM) methods module of the MATLAB Reservoir Simulation Toolbox (MRST) [58]. Additional information about the geometry, dimensions and fracture position, besides the physical properties, can be found in Debossam et al. [49].
5. Material and Methods
The main objective of this work is to evaluate the influence of inertial, gas slippage and effective stress effects on production in naturally fractured tight gas reservoirs. In enhanced gas recovery techniques, a fluid can be injected into the reservoir to produce a greater amount of gas. As the environmental issue is currently of great importance, we analyzed the injection of carbon dioxide (CO2) into a reservoir containing methane (CH4). Therefore, in addition to increasing the volume of gas produced, the reservoir is used to store this fluid.
As we are considering two-component single-phase flow in a naturally fractured reservoir, it is necessary to use a model to represent the fracture network within the porous medium. Among the different options for structured meshes, we chose the pattern known as sugar cube [59]. It is based on Barenblatt et al. [60]’s double porosity model, which solves the pressure for a system of fractures with high permeability, a porous matrix with low permeability and flow from the porous matrix to the fractures.
As previously stated, fractures are represented using the discrete fracture networks (DFNs) [46] technique. In this model, fractures are inserted into the computational mesh and are represented by a set of finite volumes. The differences between the fractures and the porous matrix are their dimensions and their different physical properties, porosity and absolute permeability. Furthermore, due to the discrepancy between the thickness of the fracture and the dimensions of the finite volumes, mesh refinement is introduced in the regions around the fractures [40].
Table 1 shows the dimensions of the reservoir and other properties and parameters common to all simulations. It is important to point out that the subscript r refers to the porous matrix, while f refers to the fractures.

Table 1.
Common data for all simulations.
In Table 2, the physical properties of the injected and in situ fluids—carbon dioxide and methane, respectively—are presented.

Table 2.
Thermophysical properties of components.
Finally, the length of the fractures () and their thickness (w), permeability () and porosity () can be found in Table 3. In the sugar cube configuration, the fractures are positioned in the vertical and horizontal directions, are equidistant and orthogonal to each other, and have the same length and thickness. There are nine fractures in each -plane that are parallel and equidistant from each other and are along the longitudinal and transversal directions.

Table 3.
Fracture properties.
From the results of previous simulations for mesh refinement evaluation [49], numerical convergence is achieved and numerical diffusion is minimized to acceptable levels when a mesh containing 320 × 320 × 3 finite volumes is employed. Therefore, all simulations are performed considering this mesh.
6. Numerical Results
In this work, we simulated a closed reservoir with the specified flow rate conditions for the injection and production fluids. Therefore, production curves will not be presented, but rather, we present the advance front of CO2 inside the reservoir in pre-established plans. As a result of the flow rate being constant, the inertial effects, gas slippage and effective stress will be noted in the variation of the molar fraction field inside the reservoir. Subsequently, in future work, we intend to introduce a well–reservoir coupling model [61] and work with the prescribed pressure condition in the producer well.
As previously stated, our interest is the evaluation of the influence of inertial effects, gas slippage and effective stress on the displacement of the advance front of the gas injected into the reservoir. These objectives are achieved by monitoring the variation of the molar fraction of CO2 inside the reservoir. Comparisons are made based on the results obtained with Darcy’s law.
For all simulations, the maximum production time was 6000 days, and we presented the molar fraction values in the -plane for a value of z corresponding to half of and for four different time instants.
Therefore, we begin with the advance of carbon dioxide in the case of flow governed by classical Darcy’s law; see Figure 2. These are the reference results against which the impacts caused by including the effects will be compared.
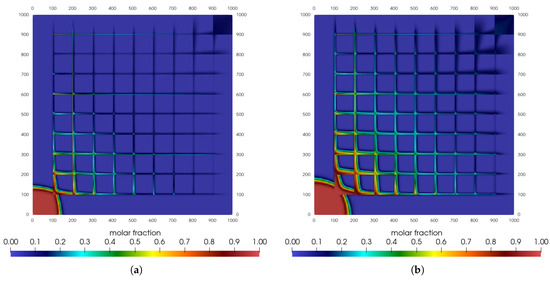
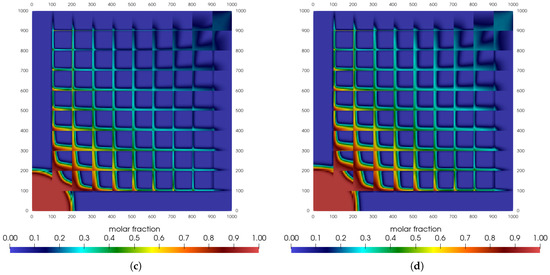
Figure 2.
Carbon dioxide mole fraction for sugar cube configuration: classical Darcy’s law. (a) t = 1500 days. (b) t = 3000 days. (c) t = 4500 days. (d) t = 6000 days.
Observing the distribution of the molar fraction, it can be seen that when the maximum time is reached, a portion of the CO2, due to the presence of fractures, has already reached the production region, with the value of this portion being approximately equal to 0.2.
In the injection region, we find that the first square region delimited by the crossing of the fractures has not yet been filled with the injected gas, and the maximum molar fraction value is higher than 0.8.
Next, we evaluate the case of Darcy’s law modified to account for inertial effects. With the introduction of apparent permeability in the model proposed by [38], its values are limited between (for a Reynolds number approaching zero) and at the limit of tending to infinity, with less than one. Note that in regions where the flow has a higher Reynolds number, the apparent permeability values are lower than those obtained by Darcy’s law.
This trend is seen in the fields presented in Figure 3. As the apparent permeability is lower in fractures, the gas that advances closer to the injection point will take longer to reach the production region. We also verify that the mole fraction is less than 0.2, which is different from the previous case. So it is possible to conclude that inertial effects are slowing down the displacement of the injected gas.
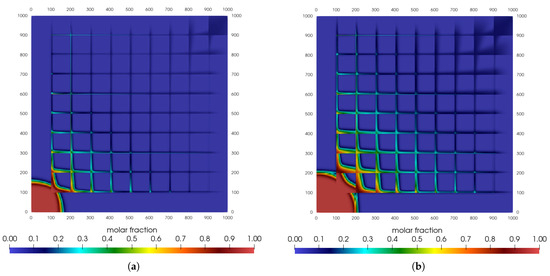
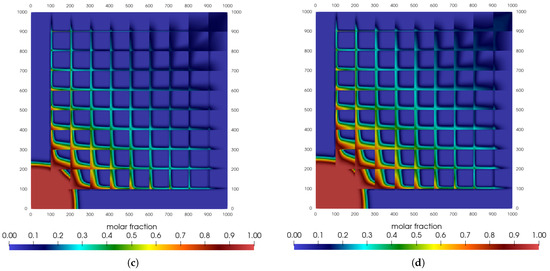
Figure 3.
Carbon dioxide mole fraction for sugar cube configuration: inertial effects. (a) t = 1500 days. (b) t = 3000 days. (c) t = 4500 days. (d) t = 6000 days.
Next, the effects arising from the stress field are evaluated. We know that permeability can change depending on pressure. Its change will increase exponentially and will be higher when the reservoir pressure is higher than the initial one.
In regions of the reservoir that have not yet been perturbed by gas injection, the permeability will tend to be equal to that of Darcy’s law. On the other hand, where the pressure is higher than the initial pressure, permeability will also be higher. However, this effect is not taken into account in fractures.
Note that for the evaluated parameters, there were only little variations concerning the distribution of CO2 when we compare the values to those of the first example (Figure 4). We can distinguish smaller filling of the region delimited by the fractures in the lower left corner and a smaller molar fraction of the injected gas than in the case where the permeability is constant (at the upper right corner).
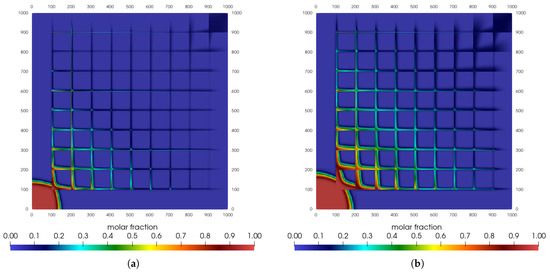
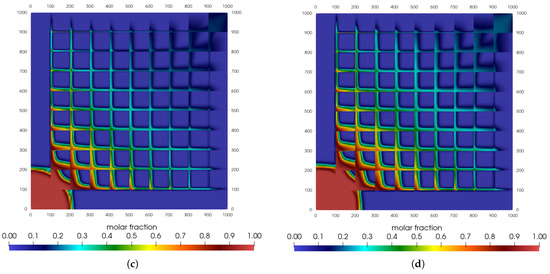
Figure 4.
Carbon dioxide mole fraction for sugar cube configuration: effective stress. (a) t = 1500 days. (b) t = 3000 days. (c) t = 4500 days. (d) t = 6000 days.
The last effect incorporated was the gas slippage. In this model, if the Knudsen number of the mixture of the components tends to zero, the permeability is the same as the initial permeability. On the other hand, when it tends to infinity, its value becomes five times greater than the initial one.
Nevertheless, the slip regime is characterized by . Thus, the highest variation will appear for an apparent permeability equal to 1.4.
Unfortunately, depending on the parameters and properties chosen, the variation range of the mixture’s Knudsen number does not lead to changes that are different from using Darcy’s classical law; see Figure 5.
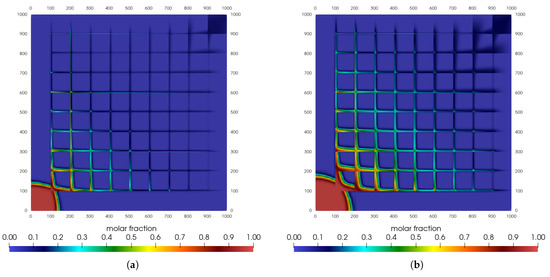
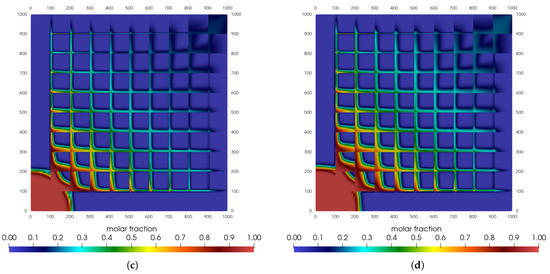
Figure 5.
Carbon dioxide mole fraction for sugar cube configuration: gas slippage. (a) t = 1500 days. (b) t = 3000 days. (c) t = 4500 days. (d) t = 6000 days.
It is not possible to clearly notice the differences in the mole fraction values when we compare these two cases. The case considered here does not allow the appearance of the effects of gas slippage since the reservoir does not have extremely low permeability. Therefore, it was not possible to capture these effects.
Finally, we present the results of the simulations encompassing all the effects added to our model. Although separately they may have a greater or smaller influence on the flow of injected carbon dioxide, their combination will lead to a different methane gas production scenario in the long-term behavior.
From the results presented above, inertial effects were the most important, followed by those arising from effective stress. On the other hand, gas slippage did not affect the results. Figure 6 highlights the changes in the mole fraction field due to the combination of the effects discussed in this paper.
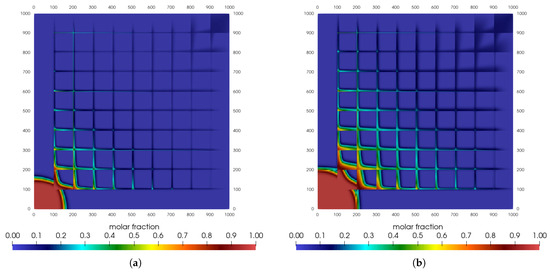
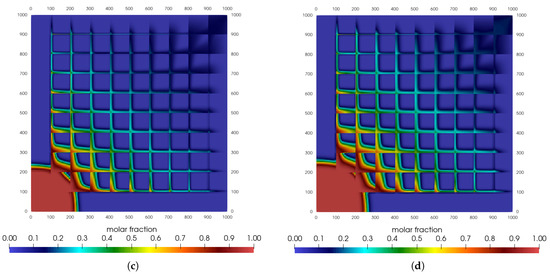
Figure 6.
Carbon dioxide mole fraction for sugar cube configuration: all effects combined. (a) t = 1500 days. (b) t = 3000 days. (c) t = 4500 days. (d) t = 6000 days.
We found that the first region between the fractures in the injection region (bottom left corner) is practically filled with CO2, which is different from when these effects are not included. In the methane production region, as the volume of produced and injected fluids are the same, CO2 may arrive earlier in the production zone, and injected CO2 is produced together with CH4.
Therefore, it is possible to say that gas production will not be the same when the combined effects are not considered, and gas production should be higher than in field operations.
7. Conclusions
We addressed the numerical simulation of single-phase two-component gas flow in a naturally fractured tight reservoir with low permeability and porosity.
The main objective was the evaluation of the effects on the production of using classical Darcy’s law in flow simulation, especially in the presence of fractures. It is well known that fractures are responsible for the introduction of preferential paths for flow and for higher Reynolds numbers than those of regions without fractures.
Therefore, inertial, effective stress and gas slippage effects are incorporated in the mathematical model. In the first case, the apparent permeability varies as a function of the Reynolds number and has an upper limit value. Considering the effects of effective stress, permeability grows exponentially depending on the difference between the current and initial pressure in the reservoir. Finally, the correction due to gas slippage depends on the value of the flow’s Knudsen number and has an upper limit.
A reference case to represent a naturally fractured tight gas reservoir (sugar cube configuration) was adopted, allowing us run simulations in a domain with no-flow boundaries and prescribed injection (CO2) and production (CH4) flow rates.
Compared to the case of classical Darcy’s law, we verified that the distribution of the molar fraction of carbon dioxide presented a different pattern when all effects were considered simultaneously. This fact indicates that production is affected and that future predictions based on simulations made without taking their influence into account may be incorrect.
From the specific case analyzed, it was found that the inertial and effective stress effects were dominant, with the first being the most important. On the other hand, we did not observe changes due to gas slippage.
Finally, for future work, it is important to quantitatively evaluate the importance of these effects in addition to including the gas adsorption and a well–reservoir coupling technique.
Author Contributions
Conceptualization, G.d.S., H.P.A.S. and A.P.P.; methodology, G.d.S., H.P.A.S. and A.P.P.; software, J.G.S.D., M.M.d.F. and G.d.S.; validation, J.G.S.D., G.d.S., H.P.A.S. and A.P.P.; formal analysis, J.G.S.D., M.M.d.F., G.d.S., H.P.A.S. and A.P.P.; investigation, J.G.S.D., M.M.d.F., G.d.S., H.P.A.S. and A.P.P.; writing—original draft preparation, H.P.A.S.; writing—review and editing, M.M.d.F., G.d.S., H.P.A.S. and A.P.P.; visualization, M.M.d.F., G.d.S. and H.P.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Carlos Chagas Filho Foundation for Research Support of the State of Rio de Janeiro (FAPERJ) grant numbers E-26/010.001790/2019, E-26/010.002226/2019, E-26/211.776/2021, and E-26/210.476/2024.
Data Availability Statement
Data will be available on request.
Acknowledgments
The authors gratefully thank Rio de Janeiro State University, Coordination for the Improvement of Higher Education Personnel (CAPES)—Finance Code 001, the National Council for Science, and the Carlos Chagas Filho Foundation for Research Support of the State of Rio de Janeiro (FAPERJ) for their support.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EGR | Enhanced Gas Recovery |
| CG | Conjugate Gradient Method |
| CSEGR | CO2 Storage with Enhanced Gas Recovery |
| BiCGSTAB | Biconjugate Gradient Stabilized Method |
| DFN | Discrete Fracture Networks |
| FVM | Finite Volume Method |
References
- Bear, J. Modeling Phenomena of Flow and Transport in Porous Media; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Halsey, T.C. Computational sciences in the upstream oil and gas industry. Philos. Trans. R. Soc. 2016, 374, 1–12. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Boudet, H.; Clarke, C.; Bugden, D.; Maibach, E.; Roser-Renouf, C.; Leiserowitz, A. Fracking controversy and communication: Using national survey data to understand public perceptions of hydraulic fracturing. Energy Policy 2014, 65, 57–67. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Shan, B. Mathematical model of fractured horizontal well in shale gas reservoir with rectangular stimulated reservoir volume. J. Nat. Gas Sci. Eng. 2018, 59, 67–79. [Google Scholar] [CrossRef]
- Sheng, G.; Javadpour, F.; Su, Y. Effect of microscale compressibility on apparent porosity and permeability in shale gas reservoirs. Int. J. Heat Mass Transf. 2018, 120, 56–65. [Google Scholar] [CrossRef]
- Shi, J.; Li, X.; Li, Q.; Wang, F.; Sepehrnoori, K. Gas permeability model considering rock deformation and slippage in low permeability water-bearing gas reservoirs. J. Pet. Sci. Eng. 2014, 120, 61–72. [Google Scholar] [CrossRef]
- Moghaddam, R.N.; Jamiolahmady, M. Fluid transport in shale gas reservoirs: Simultaneous effects of stress and slippage on matrix permeability. Int. J. Coal Geol. 2016, 163, 87–99. [Google Scholar] [CrossRef]
- Afagwu, C.; Abubakar, I.; Kalam, S.; Al-Afnan, S.F.; Awotunde, A.A. Pressure-transient analysis in shale gas reservoirs: A review. J. Nat. Gas Sci. Eng. 2020, 78, 103319. [Google Scholar] [CrossRef]
- Miao, Y.; Li, X.; Zhou, Y.; Lee, J.; Sun, Z.; Chang, Y.; Wang, S.; Hou, C. A new rate-transient analysis model for shale gas reservoirs coupled the effect of slip flow and surface diffusion. Int. J. Heat Mass Transf. 2018, 124, 1–10. [Google Scholar] [CrossRef]
- Li, B.; Zhou, F.; Fan, W.; Ren, D.; Li, H.; Li, M. Experimental investigation and theoretical modeling of stress-dependent permeability in naturally fractured tight gas reservoir. J. Pet. Sci. Eng. 2020, 188, 106949. [Google Scholar] [CrossRef]
- Wang, L.; Wang, S.; Zhang, R.; Wang, C.; Xiong, Y.; Zheng, X.; Li, S.; Jin, K.; Rui, Z. Review of multi-scale and multi-physical simulation technologies for shale and tight gas reservoirs. J. Nat. Gas Sci. Eng. 2017, 37, 560–578. [Google Scholar] [CrossRef]
- Fu, J.; Su, Y.; Li, L.; Wang, W.; Wang, C.; Li, D. Productivity model with mechanisms of multiple seepage in tight gas reservoir. J. Pet. Sci. Eng. 2022, 209, 109825. [Google Scholar] [CrossRef]
- Zhang, Y.; Jin, Y.; Yang, D. Semi-analytical modeling of transient pressure behaviour for a multifractured horizontal well in a gas reservoir with a complex fracture network by considering effects of slippage, stress-sensitivity, and gas adsorption/desorption. J. Pet. Sci. Eng. 2022, 214, 110504. [Google Scholar] [CrossRef]
- Song, H.; Cao, Y.; Yu, M.; Wang, Y.; Killough, J.E.; Leung, J. Impact of permeability heterogeneity on production characteristics in water-bearing tight gas reservoirs with threshold pressure gradient. J. Nat. Gas Sci. Eng. 2015, 22, 172–181. [Google Scholar] [CrossRef]
- Guria, C. Pressure- and temperature-dependent Klinkenberg slippage effect in porous media to non-ideal gases. Geoenergy Sci. Eng. 2023, 224, 211629. [Google Scholar] [CrossRef]
- Rubin, C.; Zamirian, M.; Takbiri-Borujeni, A.; Gu, M. Investigation of gas slippage effect and matrix compaction effect on shale gas production evaluation and hydraulic fracturing design based on experiment and reservoir simulation. Fuel 2019, 241, 12–24. [Google Scholar] [CrossRef]
- Ding, J.; Yang, S.; Nie, X.; Wang, Z. Dynamic threshold pressure gradient in tight gas reservoir. J. Nat. Gas Sci. Eng. 2014, 20, 155–160. [Google Scholar] [CrossRef]
- Friedel, T.; Voigt, H.D. Investigation of non-Darcy flow in tight-gas reservoirs with fractured wells. J. Pet. Sci. Eng. 2006, 54, 112–128. [Google Scholar] [CrossRef]
- Clarkson, C.; Jensen, J.; Chipperfield, S. Unconventional gas reservoir evaluation: What do we have to consider? J. Nat. Gas Sci. Eng. 2012, 8, 9–33. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, D.; Wang, J. Evaluation of the non-Darcy effect in coalbed methane production. Fuel 2014, 121, 1–10. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.P.; Li, H.; Wei, Q.; Bai, R.T. A new method to calculate the productivity of fractured horizontal gas wells considering non-Darcy flow in the fractures. J. Nat. Gas Sci. Eng. 2015, 26, 981–991. [Google Scholar] [CrossRef]
- Farahani, M.; Saki, M.; Ghafouri, A.; Khaz’ali, A.R. Laboratory measurements of slippage and inertial factors in carbonate porous media: A case study. J. Pet. Sci. Eng. 2018, 162, 666–673. [Google Scholar] [CrossRef]
- Feng, R.; Chen, S.; Bryant, S.; Liu, J. Stress-dependent permeability measurement techniques for unconventional gas reservoirs: Review, evaluation, and application. Fuel 2019, 256, 115987. [Google Scholar] [CrossRef]
- Wang, J.; Yu, L.; Yuan, Q. Experimental study on permeability in tight porous media considering gas adsorption and slippage effect. Fuel 2019, 253, 561–570. [Google Scholar] [CrossRef]
- Luo, H.; Li, H.; Zhou, X.; Li, Y.; Li, Y.; Zhu, X. Modeling temperature behavior of multistage fractured horizontal well with two-phase flow in low-permeability gas reservoirs. J. Pet. Sci. Eng. 2019, 173, 1187–1209. [Google Scholar] [CrossRef]
- Liu, G.; Xie, S.; Tian, W.; Wang, J.; Li, S.; Wang, Y.; Yang, D. Effect of pore-throat structure on gas-water seepage behaviour in a tight sandstone gas reservoir. Fuel 2022, 310, 121901. [Google Scholar] [CrossRef]
- Sun, H.; Ouyang, W.; Zhu, S.; Wan, Y.; Tang, Y.; Cao, W. A new numerical well test method of multi-scale discrete fractured tight sandstone gas reservoirs and its application in the Kelasu Gas Field of the Tarim Basin. Nat. Gas Ind. B 2023, 10, 103–113. [Google Scholar] [CrossRef]
- Tapia, J.F.D.; Lee, J.Y.; Ooi, R.E.; Foo, D.C.; Tan, R.R. A review of optimization and decision-making models for the planning of CO2 capture, utilization and storage (CCUS) systems. Sustain. Prod. Consum. 2018, 13, 1–15. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, Z.; Wang, B.; Liao, X.; Li, D.; Zhou, B. A Multi-medium and Multi-mechanism model for CO2 injection and storage in fractured shale gas reservoirs. Fuel 2023, 345, 128167. [Google Scholar] [CrossRef]
- Liu, S.Y.; Ren, B.; Li, H.Y.; Yang, Y.Z.; Wang, Z.Q.; Wang, B.; Xu, J.; Agarwal, R. CO2 storage with enhanced gas recovery (CSEGR): A review of experimental and numerical studies. Pet. Sci. 2022, 19, 594–607. [Google Scholar] [CrossRef]
- Haq, B.; Salahu Muhammed, N.; Liu, J.; Tong Chua, H. Enhanced natural gas production using CO2 injection: Application to sustainable hydrogen production. Fuel 2023, 347, 128474. [Google Scholar] [CrossRef]
- Tang, C.; Zhou, W.; Chen, Z.; Wei, J. Numerical simulation of CO2 sequestration in shale gas reservoirs at reservoir scale coupled with enhanced gas recovery. Energy 2023, 277, 127657. [Google Scholar] [CrossRef]
- Aminu, M.D.; Manovic, V. A modelling study to evaluate the effect of impure CO2 on reservoir performance in a sandstone saline aquifer. Heliyon 2020, 6, E04597. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Vuik, C.; Hajibeygi, H. CO2 Storage in deep saline aquifers: Impacts of fractures on hydrodynamic trapping. Int. J. Greenh. Gas Control. 2022, 113, 103552. [Google Scholar] [CrossRef]
- Parvin, S.; Masoudi, M.; Sundal, A.; Miri, R. Continuum scale modelling of salt precipitation in the context of CO2 storage in saline aquifers with MRST compositional. Int. J. Greenh. Gas Control. 2020, 99, 103075. [Google Scholar] [CrossRef]
- Zeng, F.; Zhao, G. Semianalytical Model for Reservoirs with Forchheimer’s Non-Darcy Flow. Soc. Pet. Eng. Reserv. Eval. Eng. 2008, 11, 280–291. [Google Scholar] [CrossRef]
- Amao, A.M. Mathematical Model for Darcy-Forchheimer Flow with Applications to Well Performance Analysis. Master’s Thesis, Texas Tech University, Lubbock, TX, USA, 2007. [Google Scholar]
- Barree, R.D.; Conway, M.W. Beyond Beta Factors: A Complete Model for Darcy, Forchheimer, and Trans-Forchheimer Flow in Porous Media. In Proceedings of the Society of Petroleum Engineers Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004. [Google Scholar] [CrossRef]
- Lai, B.; Miskimins, J.L.; Wu, Y.S. Non-Darcy Porous Media Flow According to the Barree and Conway’s Model: Laboratory and Numerical Modeling Studies. In Proceedings of the Society of Petroleum Engineers Rocky Mountain Petroleum Technology Conference, Denver, CO, USA, 14–16 April 2009. [Google Scholar] [CrossRef]
- Souza, G.; Amaral Souto, H.P. A comparative study of non-Darcy flows in naturally fractured gas reservoirs. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1701–1715. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, D. Modeling two-phase flow behaviour in a shale gas reservoir with complex fracture networks and flow dynamics. Gas Sci. Eng. 2023, 119, 205112. [Google Scholar] [CrossRef]
- Civan, F.; Rai, C.S.; Sondergeld, C.H. Shale-Gas Permeability and Diffusivity Inferred by Improved Formulation of Relevant Retention and Transport Mechanisms. Transp. Porous Media 2011, 86, 925–944. [Google Scholar] [CrossRef]
- Florence, F.A.; Rushing, J.A.; Newsham, K.E.; Blasingame, T.A. Improved Permeability Prediction Relations for Low-Permeability Sands. In Proceedings of the SPE Rocky Mountain Petroleum Technology Conference/Low Permeability Reservoirs Symposium 2007, Denver, CO, USA, 16–18 April 2007. [Google Scholar] [CrossRef]
- Wang, S.; Lukyanov, A.A.; Wu, Y.S. Second-order gas slippage model for the Klinkenberg effect of multicomponent gas at finite Knudsen numbers up to 1. Fuel 2019, 235, 1275–1286. [Google Scholar] [CrossRef]
- de Queiroz, R.Z.H.G.; do Rosário, R.C.D.; de Souza, G.; Amaral Souto, H.P. On the numerical simulation of wellbore pressure in gas reservoirs incorporating the phenomena of slippage, formation damage and wellbore storage. Int. J. Adv. Eng. Res. Sci. 2020, 7, 224–239. [Google Scholar] [CrossRef]
- Secchi, S.; Schrefler, B.A. A method for 3-D hydraulic fracturing simulation. Int. J. Fract. 2012, 178, 245–258. [Google Scholar] [CrossRef]
- Chen, Z. Reservoir Simulation—Mathematical Techniques in Oil Recovery; Society of Industrial and Applied Mathematics: Philadelphia, PA, USA, 2007. [Google Scholar]
- Debossam, J.G.S.; dos Santos Heringer, F.D.; de Souza, G.; Amaral Souto, H.P. Numerical simulation of single-phase two-components flow in naturally fractured oil reservoirs. Coupled Syst. Mech. 2019, 8, 129–146. [Google Scholar] [CrossRef]
- Debossam, J.G.S.; de Souza, G.; Amaral Souto, H.P.; Pires, A.P. Numerical simulation of single-phase two-component non-Darcy flow in naturally fractured reservoirs for enhanced gas recovery and carbon dioxide storage. Braz. J. Chem. Eng. 2023, 41, 197–219. [Google Scholar] [CrossRef]
- Böttcher, N.; Singh, A.K.; Kolditz, O.; Liedl, R. Non-isothermal, compressible gas flow for the simulation of an enhanced gas recovery application. J. Comput. Appl. Math. 2012, 236, 4933–4943. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Lohrenz, J.; Bray, B.G.; Clark, C.R. Calculating viscosities of reservoir fluids from their compositions. J. Pet. Technol. 1964, 16, 1171–1176. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics: The Finite Volume Method; Pearson: London, UK, 2007. [Google Scholar]
- Ertekin, T.; Abou-Kassem, J.; King, G. Basic Applied Reservoir Simulation; Society of Petroleum Engineers: Richardson, TX, USA, 2001. [Google Scholar]
- Biryukov, D.; Kuchuk, F.J. Transient Pressure Behavior of Reservoirs with Discrete Conductive Faults and Fractures. Transp. Porous Media 2012, 95, 239–268. [Google Scholar] [CrossRef]
- Vennemo, S. Multiscale Simulation of Thermal Flow in Porous Media. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2016. [Google Scholar]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society of Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
- Sandve, T.; Berre, I.; Nordbotten, J. An efficient multi-point flux approximation method for Discrete Fracture—Matrix simulations. J. Comput. Phys. 2012, 231, 3784–3800. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The behavior of naturally fractured reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Barenblatt, G.; Zheltov, I.; Kochina, I. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks [strata]. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- do Rosário, R.C.D.; de Souza, G.; Amaral Souto, H.P. A comparative study of some well-reservoir coupling models in the numerical simulation of oil reservoirs. Int. J. Adv. Eng. Res. Sci. 2020, 7, 126–148. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).