An Investigation into the Volumetric Flow Rate Requirement of Hydrogen Transportation in Existing Natural Gas Pipelines and Its Safety Implications
Abstract
:1. Introduction
2. Theory
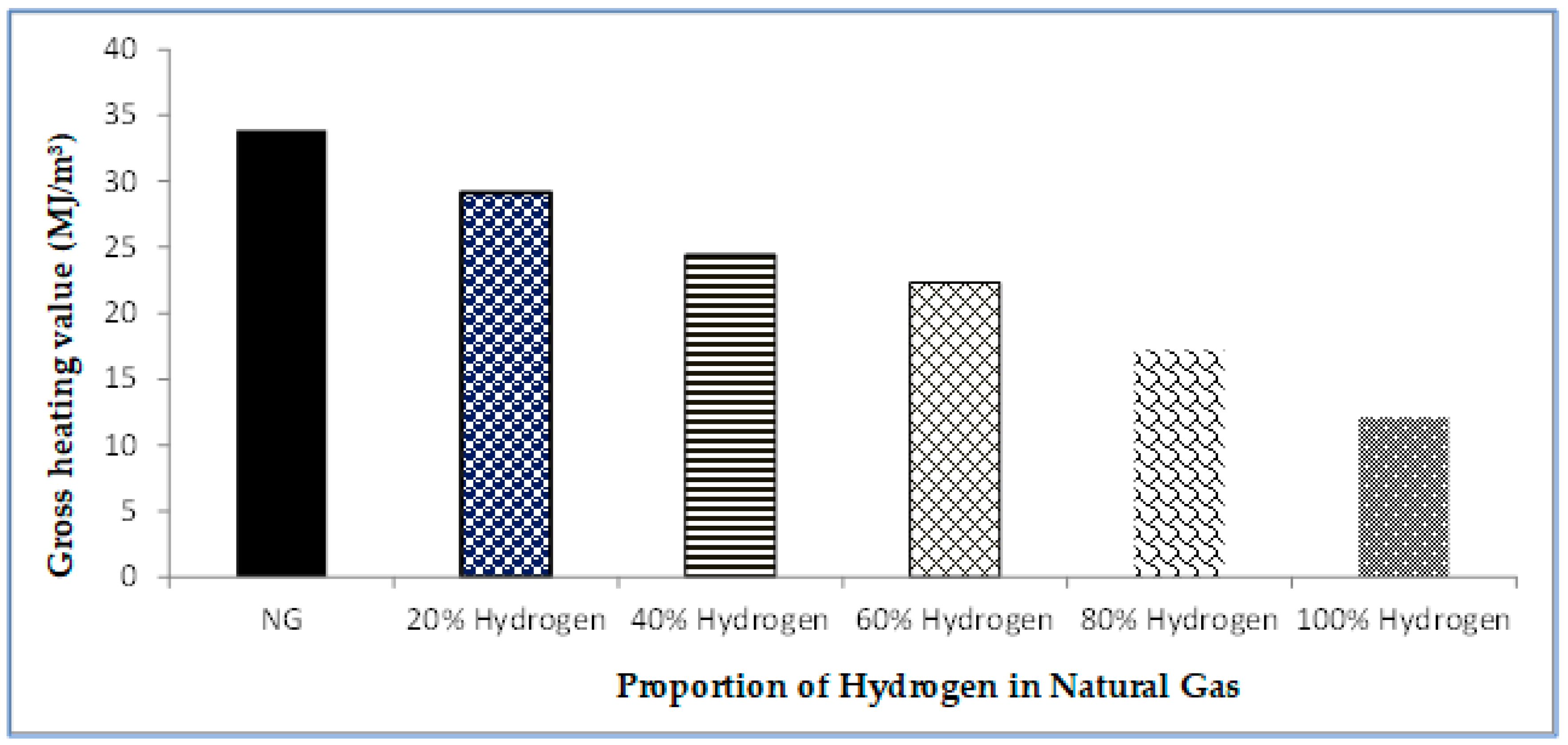
2.1. Energy Contents of Natural Gas and Hydrogen Blends
2.2. Pipeline Transportation of Gases
2.3. Hydrogen Pipelines: A Case for Adopting Existing Natural Gas Pipelines
2.4. Flow Parameters in Hydrogen Pipelines
2.4.1. Hydrogen Blending Effect on Flow Parameters during Hydrogen Transportation in Existing Pipelines
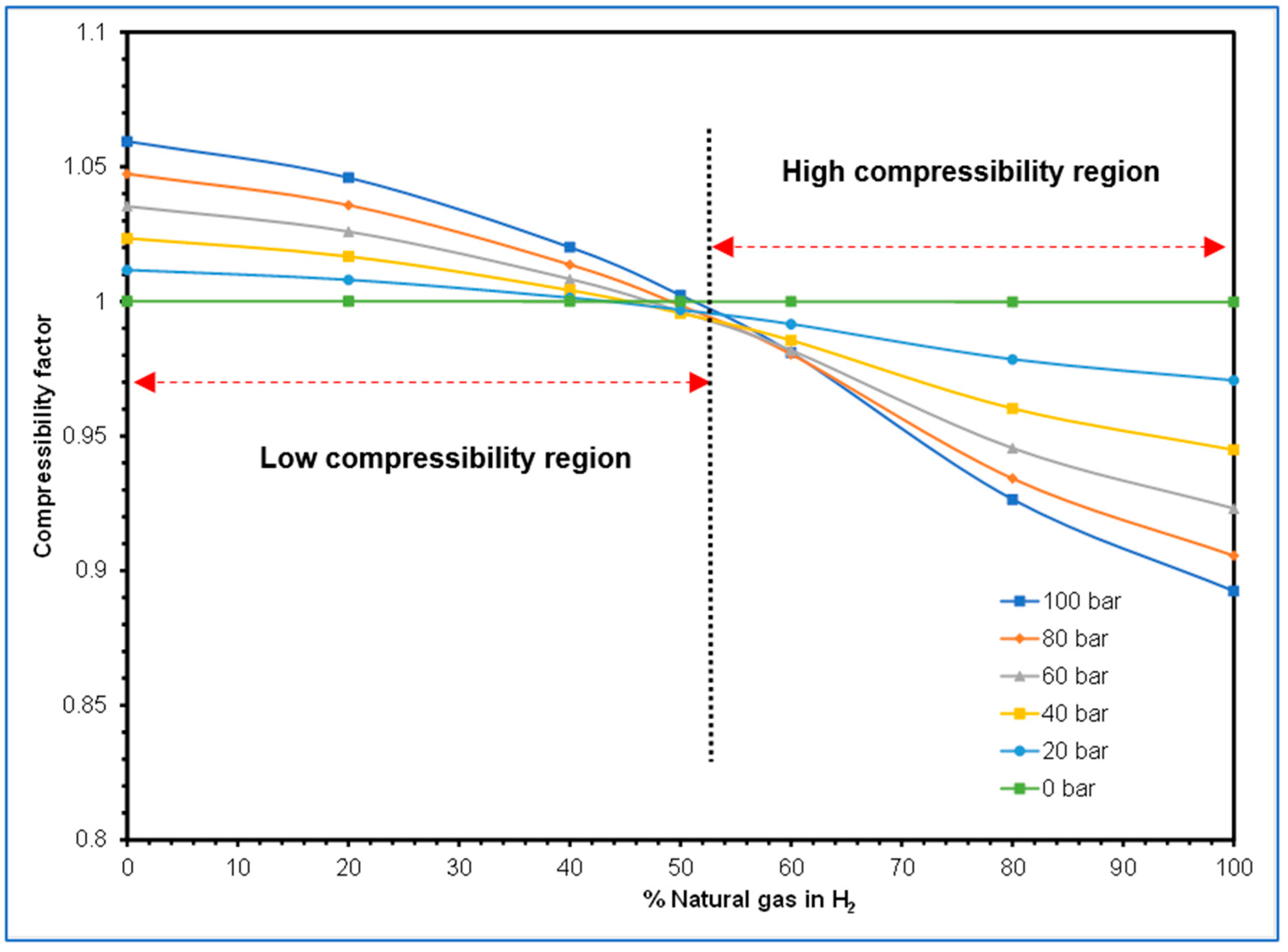
2.4.2. Gas Compressibility and Compressibility Factor Effects on Hydrogen Transport in Existing Gas Pipelines
2.4.3. Embrittlement Concerns and How They Can Be Avoided in Hydrogen Pipelines
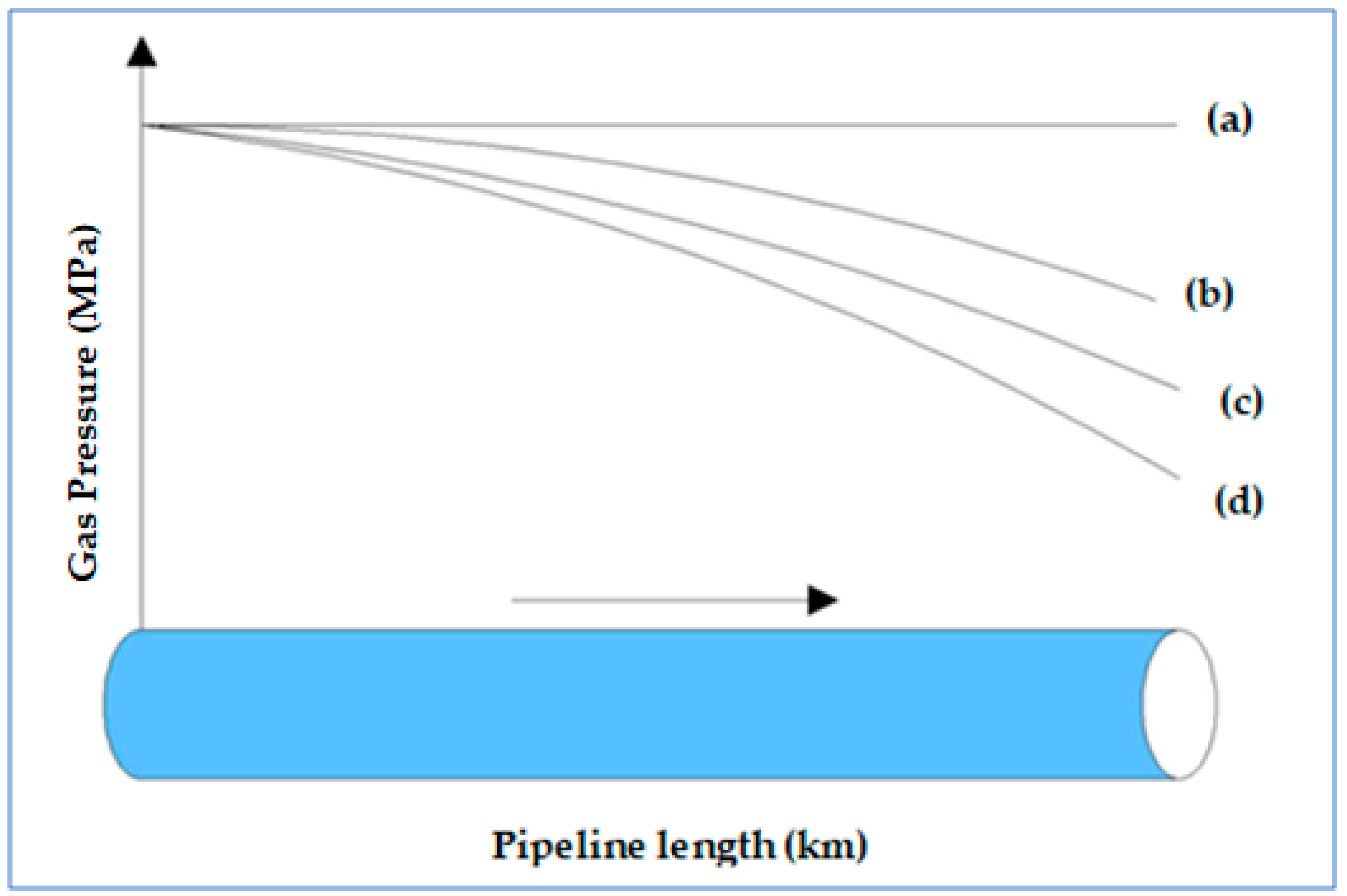
2.4.4. Hydrogen Blending Effect on Pressure Behaviour in Gas Pipeline Transport of Hydrogen
2.4.5. Hydrogen Blending Effect on Velocity during Hydrogen Transportation in Existing Gas Pipelines
2.4.6. The Concept of Erosional Velocity Limit
2.5. Gas Network Modelling
2.5.1. Capturing Individual Particle Interaction in Modelling of Gas and Hydrogen Blend Flow
2.5.2. Pressure Gradient and Pressure Losses Modelling
3. Study Methodology
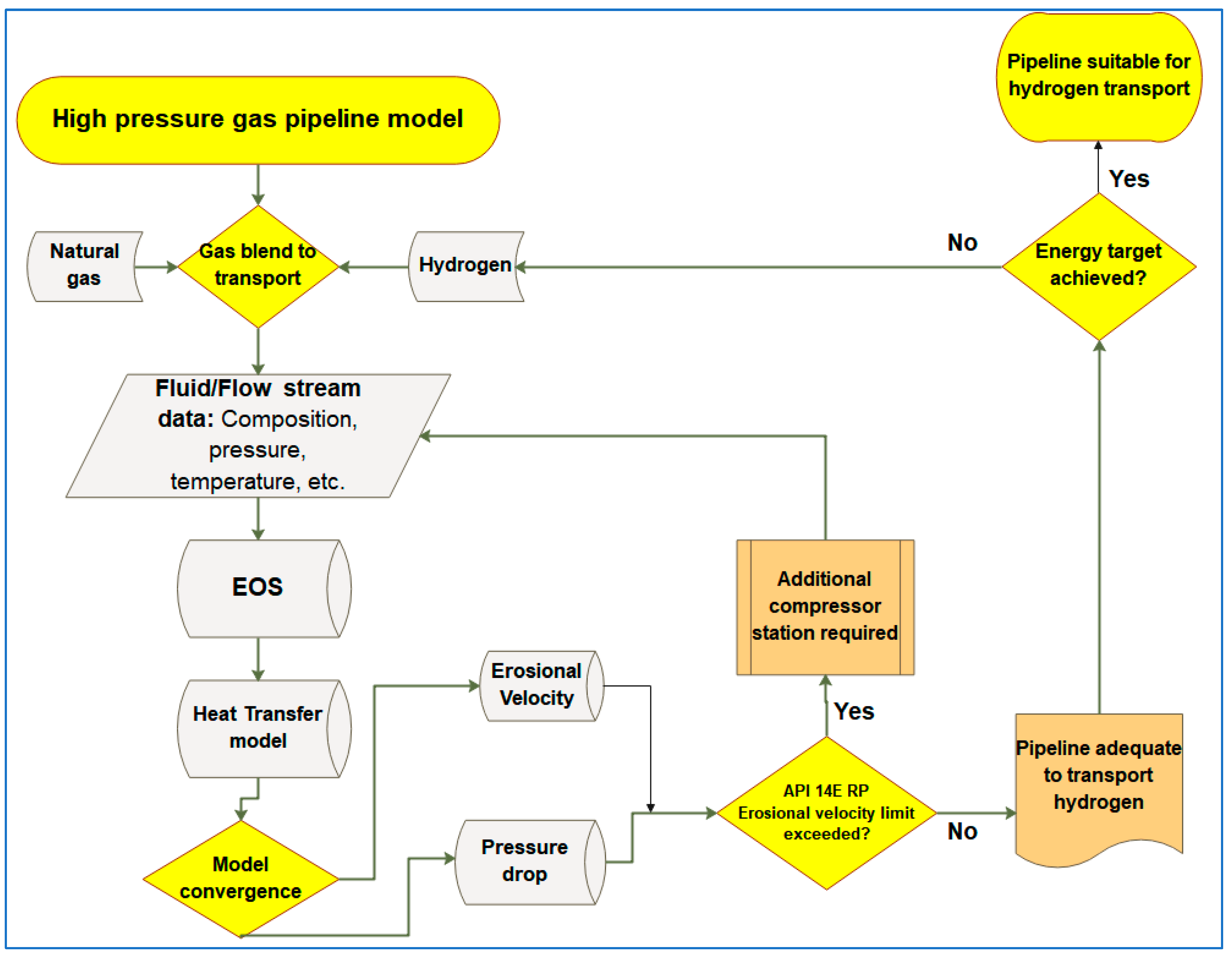
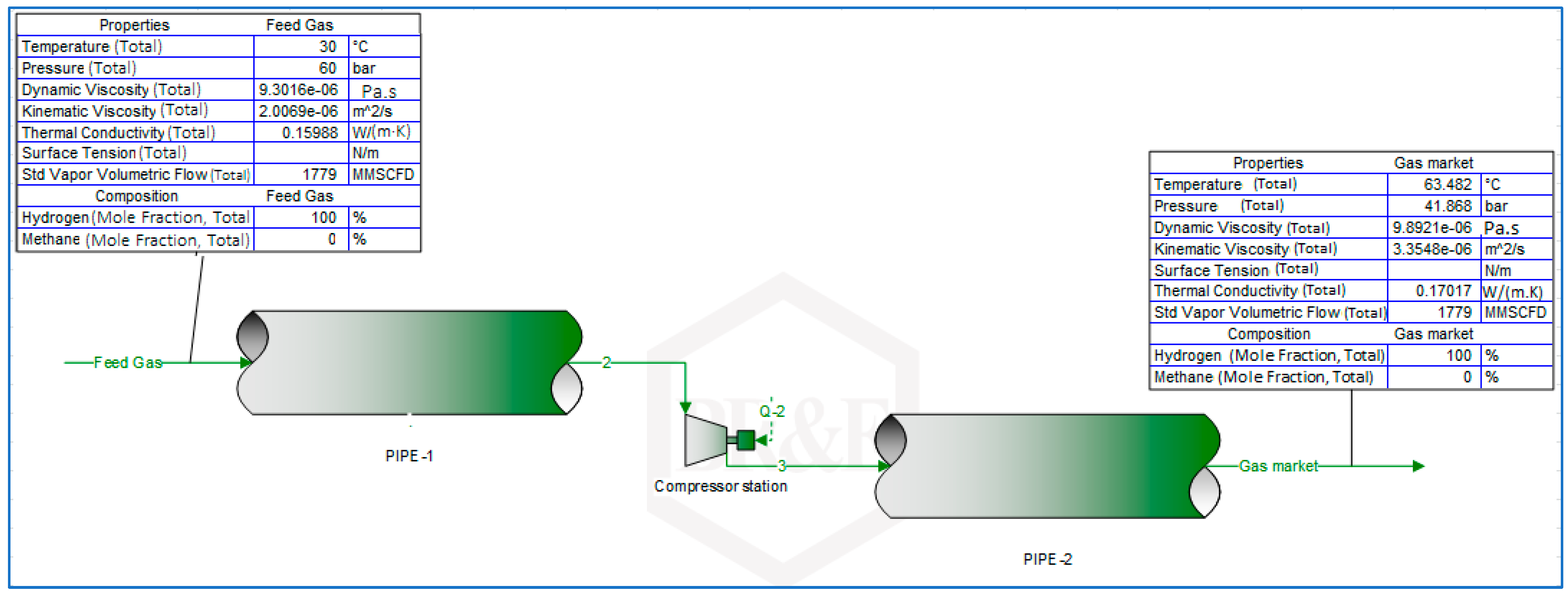
3.1. Simulation Workflow for the Transportation of Hydrogen and Natural Gas Blends in Existing Gas Pipelines
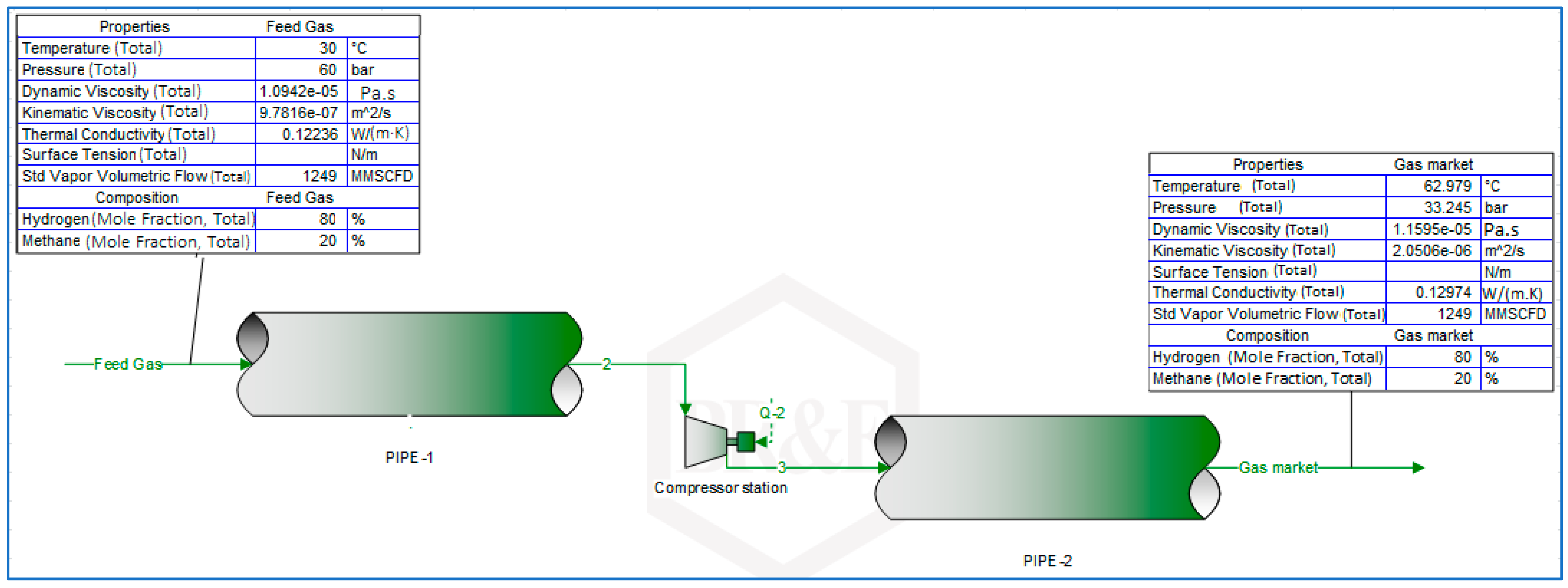
3.2. Determination of Volumetric Flowrate Requirements for Constant Energy Delivery by Hydrogen and Natural Gas Blends through Natural Gas Pipelines (Free-Flow Modelling)
3.3. Investigating Safety Concerns of Hydrogen Transportation in Gas Pipelines
3.3.1. Investigating Hydrogen Blending Effects on Compressibility Factor in HP Pipelines
3.3.2. Investigating Hydrogen Blending Effect on Flow Velocity in HP Gas Pipelines
3.4. Keeping Pipeline Velocity Profiles within Recommended Limits with the Use of Compressor Stations
4. Results Presentation and Analysis
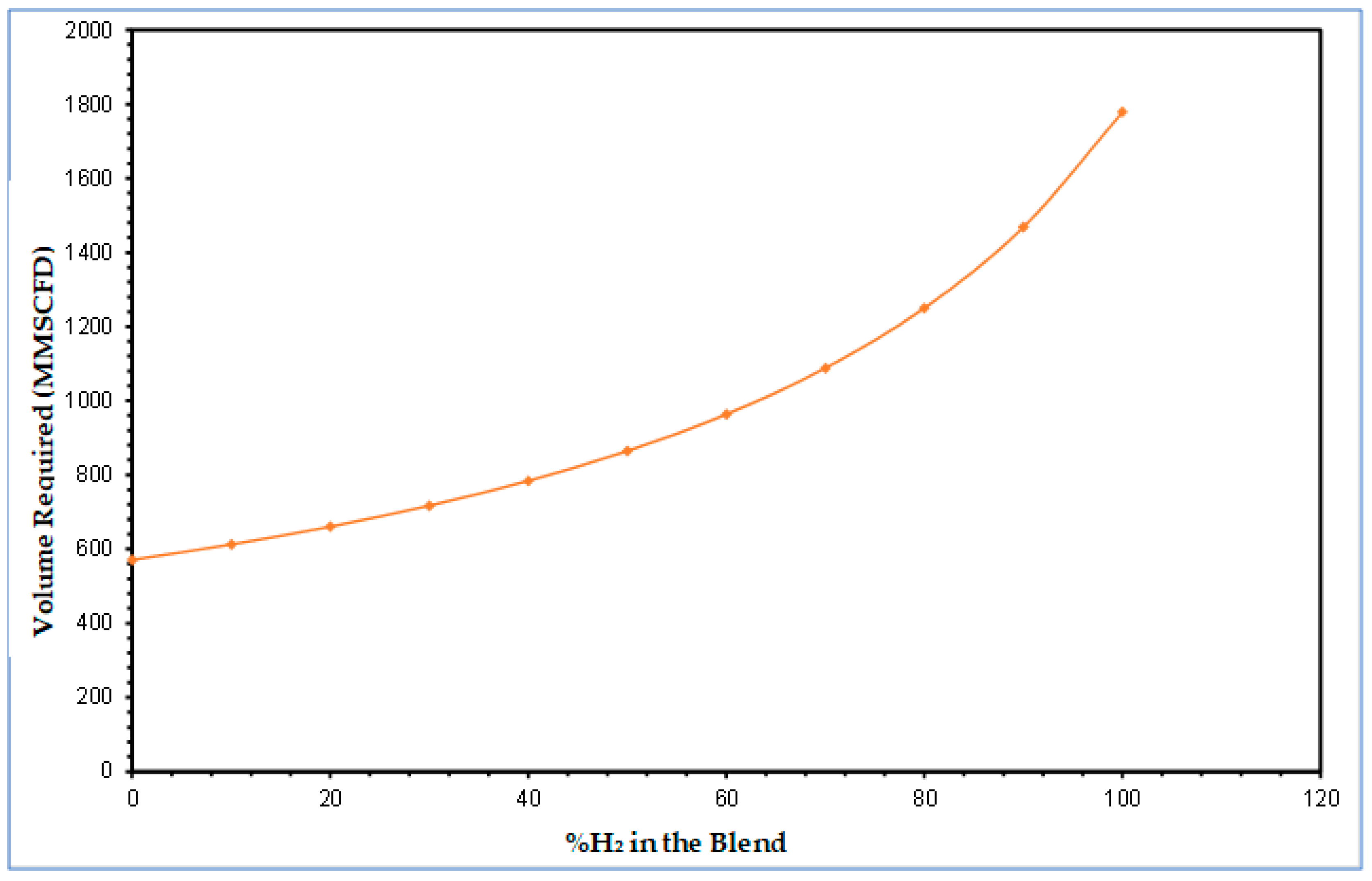
4.1. Constant Energy Delivery Volumetry Requirements of Transitioning from Natural Gas to Hydrogen
4.2. Investigating Safety Concerns in Transporting Hydrogen with Natural Gas Pipelines
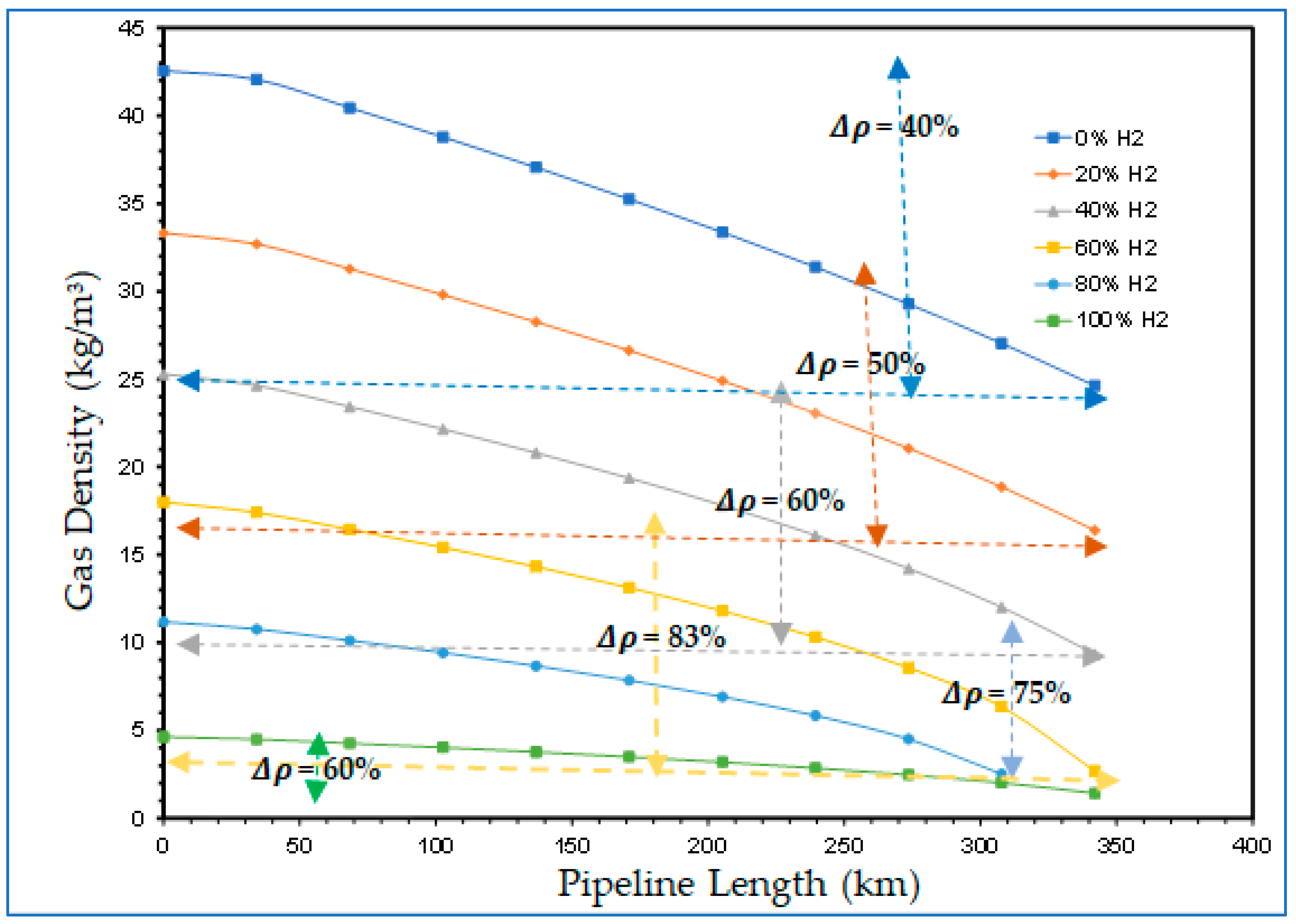
4.2.1. Hydrogen Blending Effect on Compressibility Factor along the High-Pressure Pipeline
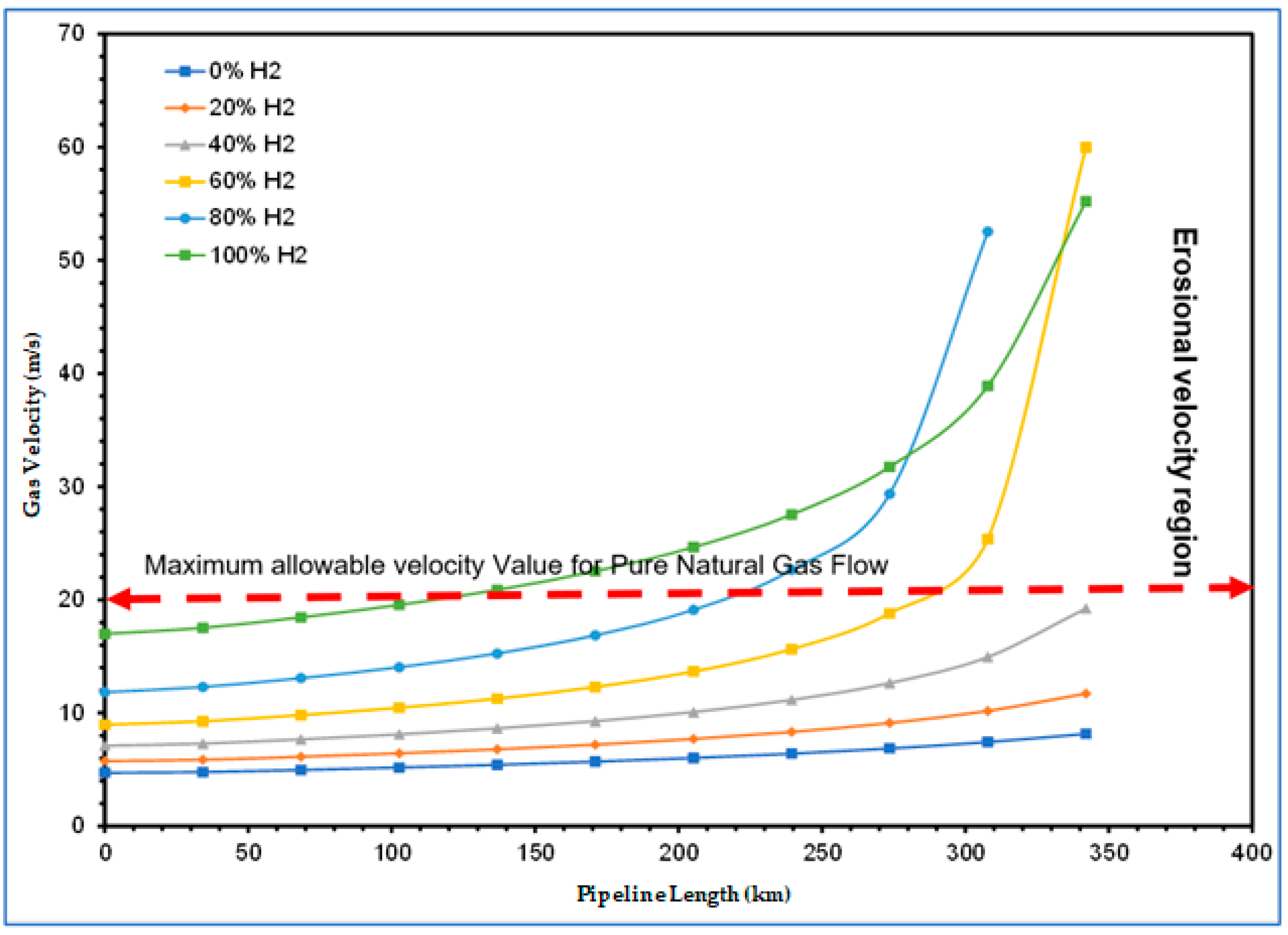
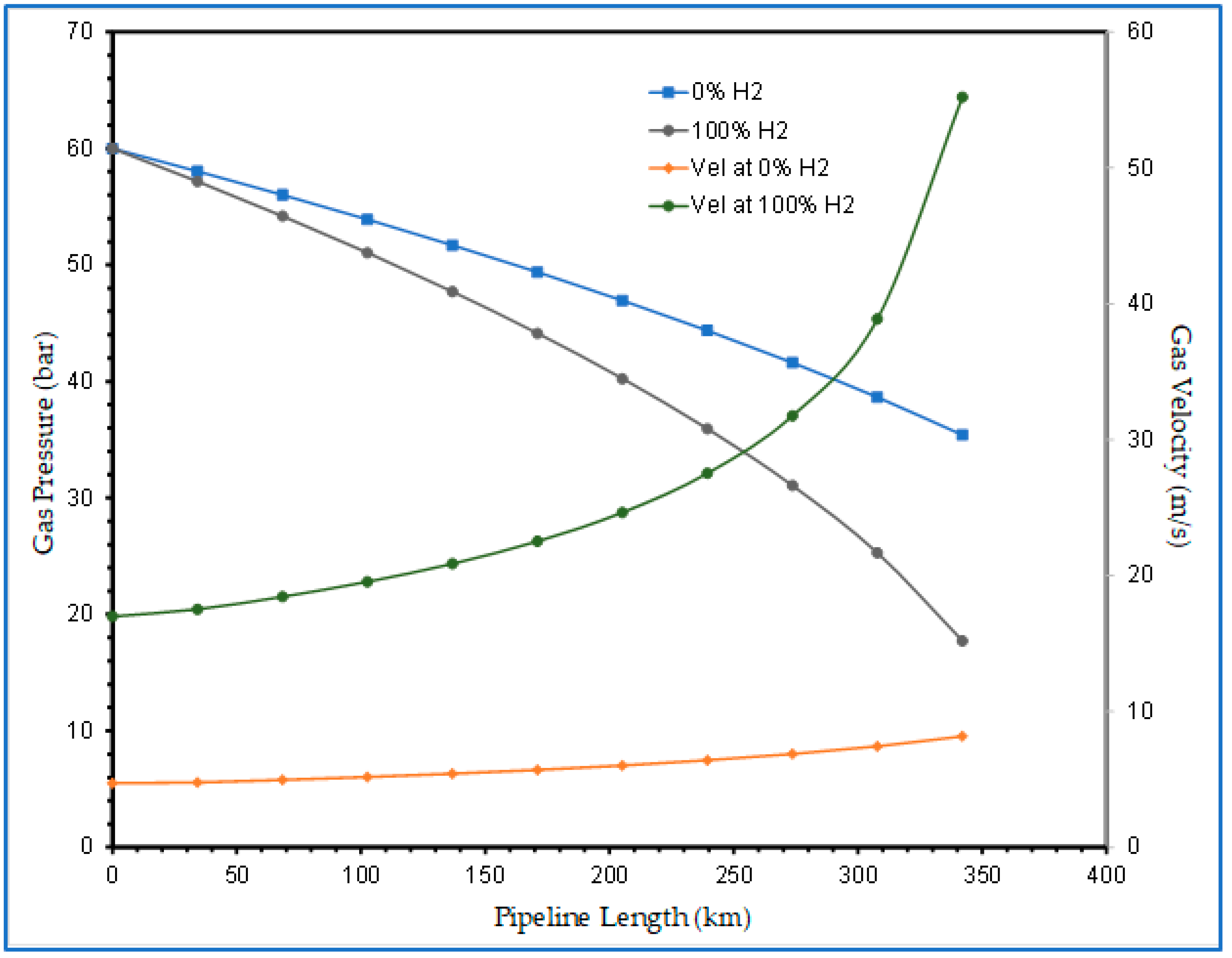
4.2.2. Hydrogen Blending Effect on Flow Velocity along High-pressure Gas Pipelines
4.3. Velocity Profiles Behaviour with Compressor Stations in Existing Gas Pipeline Networks for Flow of Hydrogen and Hydrogen and Natural Gas Blends
4.4. Downstream Pressure versus Velocity Trade-Off
5. Discussion
6. Conclusions
- This study explored the adoption of the existing natural gas pipelines for hydrogen delivery. A single pipeline flow was modelled to estimate the required volume of hydrogen needed to deliver the same amount of energy for a given volume of natural gas. Preliminary results from the study confirmed that a given volume of pure hydrogen gas would need to be tripled to deliver the same amount of energy as the same volume of natural gas, indicating the accuracy and validity of the model predictions.
- The second stage of the study also confirmed that an existing gas pipeline can accommodate hydrogen and natural gas blends with up to 40% hydrogen without the need for additional changes or investment in the pipeline infrastructure to mitigate internal erosion because the velocity profile was within the acceptable limits prescribed by API RP 14E. However, as the proportion of hydrogen in the blends was increased up to and beyond 60%, excessive pressure losses became eminent. This was characterised by the rising velocity, which eventually exceeded the erosional velocity limits before the gas reached the discharge point. This is a cause for concern because the pipeline could fail earlier than it is designed to last. To remedy this, technical solutions of using compressor stations or pipeline looping are recommended.
- A third objective of the study that investigated the effect of hydrogen blending on the behaviour of the compressibility factor also revealed that the compressibility factor could possess a wide range of values as the proportions of hydrogen and natural gas in the blends change. Consequently, disparate flow behaviours and resultant varying flow challenges would be faced when transporting hydrogen blends within existing pipelines.
- In a nutshell, this study has shown that increasing the capacity of a hydrogen pipeline by up to three-folds of a given capacity of an existing natural gas pipeline will result in the delivery of the same amount of energy but present peculiar flow behaviours and challenges that are different from those observed in conventional natural gas pipelines. This work, therefore, provides insights into the volumetric and safety considerations of designing hydrogen transportation through pipelines by blending with natural gas as the global community considers the replacement of natural gas with hydrogen in the energy transition and decarbonisation campaigns.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Staffel, I.; Scamman, D.; Abdad, A.V.; Balcombe, P.; Dodds, P.E.; Ekins, P.; Shahd, N.; Ward, R.K. The role of hydrogen and fuel cells in the global energy system. Energy Environ. Sci. 2019, 12, 463. [Google Scholar] [CrossRef] [Green Version]
- Bossel, U. Does a Hydrogen Economy Make Sense? Proc. IEEE 2006, 94, 1826–1836. [Google Scholar] [CrossRef]
- Jones, D.R.; Al-Masry, W.A.; Dunnill, C.W. Hydrogen-enriched natural gas as a domestic fuel: An analysis based on flash-back and blow-off limits for domestic natural gas appliances within the UK. Sustain. Energy Fuels 2018, 2, 710–723. [Google Scholar] [CrossRef] [Green Version]
- Witkowski, A.; Rusin, A.; Majkut, M.; Stolecka, K. Comprehensive analysis of hydrogen compression and pipeline transportation from thermodynamics and safety aspects. Energy 2017, 141, 2508–2518. [Google Scholar] [CrossRef]
- Bainier, F.; Kurz, R.; Bass, P. Managing the pressure to increase the H2 capacity through a natural gas transmission network. Proc. ASME Turbo Expo 2020, 9, 1–9. [Google Scholar]
- André, J.; Auray, S.; De Wolf, D.; Memmah, M.M.; Simonnet, A. Time development of new hydrogen transmission pipeline networks for France. Int. J. Hydrogen Energy 2014, 39, 10323–10337. [Google Scholar] [CrossRef] [Green Version]
- Guandalini, G.; Colbertaldo, P.; Campanari, S. Dynamic modeling of natural gas quality within transport pipelines in presence of hydrogen injections. Appl. Energy 2017, 185, 1712–1723. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, X.; Liu, J.; Fan, L. Experimental study of a single-cylinder engine fueled with natural gas-hydrogen mixtures. Int. J. Hydrogen Energy 2010, 35, 2909–2914. [Google Scholar] [CrossRef]
- Di Lullo, G.; Oni, A.O.; Kumar, A. Blending blue hydrogen with natural gas for direct consumption: Examining the effect of hydrogen concentration on transportation and well-to-combustion greenhouse gas emissions. Int. J. Hydrogen Energy 2021, 46, 19202–19216. [Google Scholar] [CrossRef]
- Çeper, B.A. Use of Hydrogen-Methane Blends in Internal Combustion Engines. In Hydrogen Energy—Challenges and Perspectives; IntechOpen: London, UK, 2012; pp. 175–200. [Google Scholar]
- Economides, M.J.; Hill, A.D.; Ehlig-Economides, C. Petroleum Production Systems; Prentice Hall Petroleum Engineering Series; Sun, B., Trentacoste, C., Intindola, K., Eds.; Pearson: London, UK, 1994; ISBN 0-13-658683-X. [Google Scholar]
- Ahmed, T. Reservoir Engineering Handbook, 2nd ed.; Gulf Professional Publishing: Houston, TX, USA, 2001; ISBN 0884157709. [Google Scholar]
- Folga, S.M. Natural Gas Pipeline Technology Overview; Argonne National Laboratory: Argonne, IL, USA, 2007. [Google Scholar]
- Gerboni, R. Introduction to hydrogen transportation. In Compendium of Hydrogen Energy; Elsevier: Amsterdam, The Netherlands, 2016; pp. 283–298. [Google Scholar]
- Seymour, E.H.; Murray, L.; Fernandes, R. Key Challenges to the introduction of hydrogen-European stakeholder views. Int. J. Hydrogen Energy 2008, 33, 3015–3020. [Google Scholar] [CrossRef]
- Gillette, J.; Kolpa, R. Overview of Interstate Hydrogen Pipeline Systems; Argonne National Laboratory: Argonne, IL, USA, 2007; p. 52. [Google Scholar]
- Hydrogen Pipeline Length by Country|Statista. 2016. Available online: https://www.statista.com/statistics/1147797/hydrogen-pipeline-length-by-country/ (accessed on 17 August 2021).
- Department of Energy US. Enabling A Low-Carbon Economy; Department of Energy US: Washington, DC, USA, 2020; p. 24. Available online: https://www.energy.gov/sites/prod/files/2020/07/f76/USDOE_FE_Hydrogen_Strategy_July2020.pdf (accessed on 15 September 2021).
- IRENA Hydrogen: A Renewable Energy Perspective; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2019; ISBN 9789292601515.
- Field, R.A.; Derwent, R.G. Global warming consequences of replacing natural gas with hydrogen in the domestic energy sectors of future low-carbon economies in the United Kingdom and the United States of America. Int. J. Hydrogen Energy 2021, 46, 30190–30203. [Google Scholar] [CrossRef]
- Petak, K.; Vidas, H.; Manik, J.; Palagummi, S.; Ciatto, A.; Griffith, A. Infrastructure Investment an Engine for Economic Growth; American Petroleum Institute (API): Washington, DC, USA, 2017. [Google Scholar]
- Parker, N. Using Natural Gas Transmission Pipeline Costs to Estimate Hydrogen Pipeline Costs; Institute of Transportation Studies, University of California: Davis, CA, USA, 2015; p. 27. [Google Scholar]
- Witkowski, A.; Rusin, A.; Majkut, M.; Stolecka, K. Analysis of compression and transport of the methane/hydrogen mixture in existing natural gas pipelines. Int. J. Press. Vessel. Pip. 2018, 166, 24–34. [Google Scholar] [CrossRef]
- Oney, F.; Veziro~lut, T.N.; Dulger, Z. Evaluation of pipeline transportation of hydrogen and natural gas mixtures. Int. J. Hydrogen Energy 1994, 19, 813–822. [Google Scholar] [CrossRef]
- Quintino, F.M.; Nascimento, N.; Fernandes, E.C. Aspects of Hydrogen and Biomethane Introduction in Natural Gas Infrastructure and Equipment. Hydrogen 2021, 2, 301–318. [Google Scholar] [CrossRef]
- Chen, T.P. Hydrogen Delivery Infrastructure Options Analysis; DOE Award Number: DE-FG36-05GO15032; Nexant, Inc.: San Francisco, CA, USA, 2008. [Google Scholar]
- Melaina, M.W.; Antonia, O.; Penev, M. Blending Hydrogen into Natural Gas Pipeline Networks: A Review of Key Issues; Technical Report NREL/TP-5600-51995; National Renewable Energy Laboratory: Golden, CO, USA, 2013; Volume 303, pp. 275–3000. Available online: http://www.osti.gov/servlets/purl/1068610/ (accessed on 6 September 2021).
- Ahmed, T. Reservoir Engineering Handbook, 4th ed.; Gulf Professional Publishing: Oxford, UK, 2010; Volume 27. [Google Scholar]
- Nasir, G.G. Gas Flow and Network Analysis. In Gas Flow in Circular Pipes; Department of Gas Engineering and Management, University of Salford, Manchester: Manchester, UK, 2002; Volume 1, pp. 1–6. [Google Scholar]
- Li, J.; Su, Y.; Yu, B.; Wang, P.; Sun, D. Influences of Hydrogen Blending on the Joule-Thomson Coefficient of Natural Gas. ACS Omega 2021, 6, 16722–16735. [Google Scholar] [CrossRef]
- Simpson, D.A. Practical Onshore Gas Field Engineering; Gulf Professional Publishing: Oxford, UK, 2017; ISBN 9780128130223. [Google Scholar]
- Guo, B.; Ghalambor, A. Properties of Natural Gas. In Natural Gas Engineering Handbook; Elsevier: Amsterdam, The Netherlands, 2005; Volume 97, pp. 13–33. [Google Scholar]
- Mouser, G.F.; Govier, J.P. Compressibility Effects on Transient Gas Pipe Flow. Soc. Pet. Eng. J. 1972, 12, 315–320. [Google Scholar] [CrossRef]
- Farzaneh-Gord, M.; Rahbari, H.R.; Mohseni-Gharesafa, B.; Toikka, A.; Zvereva, I. Accurate determination of natural gas compressibility factor by measuring temperature, pressure and Joule-Thomson coefficient: Artificial neural network approach. J. Pet. Sci. Eng. 2021, 202, 108427. [Google Scholar] [CrossRef]
- Khosravi, A.; Machado, L.; Nunes, R.O. Estimation of density and compressibility factor of natural gas using artificial intelligence approach. J. Pet. Sci. Eng. 2018, 168, 201–216. [Google Scholar] [CrossRef]
- Liu, H.; Wu, Y.; Guo, P.; Liu, Z.; Wang, Z.; Chen, S.; Wang, B.; Huang, Z. Compressibility factor measurement and simulation of five high-temperature ultra-high-pressure dry and wet gases. Fluid Phase Equilib. 2019, 500, 112256. [Google Scholar] [CrossRef]
- USDrive. Hydrogen Delivery Technical Team Roadmap. 2013. Available online: www.uscar.org (accessed on 18 August 2021).
- Nykyforchyn, H.; Tsyrulnyk, O.; Zvirko, O. Laboratory method for simulating hydrogen assisted degradation of gas pipeline steels. Procedia Struct. Integr. 2019, 17, 568–575. [Google Scholar] [CrossRef]
- Dwivedi, S.K.; Vishwakarma, M. Hydrogen embrittlement in different materials: A review. Int. J. Hydrogen Energy 2018, 43, 21603–21616. [Google Scholar] [CrossRef]
- Wasim, M.; Djukic, M.B.; Ngo, T.D. Influence of hydrogen-enhanced plasticity and decohesion mechanisms of hydrogen embrittlement on the fracture resistance of steel. Eng. Fail. Anal. 2021, 123, 105312. [Google Scholar] [CrossRef]
- Ogden, J.M. Prospects for building a hydrogen energy infrastructure. Annu. Rev. Energy Environ. 1999, 24, 227–279. [Google Scholar] [CrossRef]
- Abd, A.A.; Naji, S.Z.; Thian, T.C.; Othman, M.R. Evaluation of hydrogen concentration effect on the natural gas properties and flow performance. Int. J. Hydrogen Energy 2021, 46, 974–983. [Google Scholar] [CrossRef]
- American Petroleum Institute. Recommended Practice for Design and Installation of Offshore Production Platform Piping Systems, 5th ed.; American Petroleum Institute: Washington, DC, USA, 2012; pp. 23–26. [Google Scholar]
- Nasr, G.G.; Connor, N.E. Natural Gas Engineering and Safety Challenges: Downstream Process, Analysis, Utilization and Safety; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 9783319089485. [Google Scholar]
- Andrade-Mahecha, J.F.; Massy-Sanchez, G.I. Simulation of the operation of a natural gas transport system based on a criterion of minimum operating cost. DYNA 2019, 86, 308–316. [Google Scholar] [CrossRef] [Green Version]
- Osiadacz, A.J.; Isoli, N. Multi-Objective Optimization of Gas Pipeline Networks. Energies 2020, 13, 5141. [Google Scholar] [CrossRef]
- Munoz, J.; Jimenez-Redondo, N.; Perez-Ruiz, J.; Barquin, J. Natural gas network modeling for power systems reliability studies. In Proceedings of the 2003 IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003; Volume 4, pp. 20–27. [Google Scholar]
- Tabkhi, F. Optimization of Gas Transmission Networks; National Polytechnique Institute of Toulouse: Toulouse, France, 2007. [Google Scholar]
- Dorin, B.C.; Leonida, D.T. On Modelling and Simulating Natural Gas Transmission Systems (Part 1). J. Control Eng. Appl. Inform. 2008, 10, 27–36. Available online: https://www.researchgate.net/publication/228661898%0AOn (accessed on 8 September 2021).
- Woldeyohannes, A.D.; Majid, M.A.A. Simulation model for natural gas transmission pipeline network system. Simul. Model. Pract. Theory 2011, 19, 196–212. [Google Scholar] [CrossRef]
- Stoecker, W.F. Design of Thermal System; McGraw-Hill Book Company: New York, NY, USA, 1989; ISBN 0070616205. [Google Scholar]
- Abbaspour, M.; Chapman, K.S.; Glasgow, L.A. Transient modeling of non-isothermal, dispersed two-phase flow in natural gas pipelines. Appl. Math. Model. 2010, 34, 495–507. [Google Scholar] [CrossRef]
- Kessal, M. Simplified numerical simulation of transients in gas networks. Chem. Eng. Res. Des. 2000, 78, 925–931. [Google Scholar] [CrossRef] [Green Version]
- Badr, E.; Almotairi, S.; Ghamry, A. El A comparative study among new hybrid root finding algorithms and traditional methods. Mathematics 2021, 9, 1306. [Google Scholar] [CrossRef]
- Ehiwario, J.C.; Aghamie, S.O. Comparative Study of Bisection, Newton-Raphson and Secant Methods of Root-Finding Problems. IOSR J. Eng. 2014, 4, 1–7. [Google Scholar]
- Recommended Practice for Design and Installation of Offshore Production Platform Piping Systems; API-RP-14E; American Petroleum Institute Production: Washington, DC, USA, 1991; p. 11.
- Herrán-González, A.; De La Cruz, J.M.; De Andrés-Toro, B.; Risco-Martín, J.L. Modeling and simulation of a gas distribution pipeline network. Appl. Math. Model. 2009, 33, 1584–1600. [Google Scholar] [CrossRef]
- Alliander, W. Gas Distribution Network Modelling and Optimization—New Methods for Smarter Observation and Operation of Large Scale Gas Networks; Delft University of Technology (TUDelft): Delft, The Netherlands, 2016. [Google Scholar]
- Ashour, I.; Al-Rawahi, N.; Fatemi, A.; Vakili-Nezh, G. Applications of Equations of State in the Oil and Gas Industry. In Thermodynamics—Kinetics of Dynamic Systems; IntechOpen: London, UK, 2011. [Google Scholar] [CrossRef] [Green Version]
- Esmaeilzadeh, F.; Roshanfekr, M. A new cubic equation of state for reservoir fluids. Fluid Phase Equilib. 2006, 239, 83–90. [Google Scholar] [CrossRef]
- Bonyadi, M.; Rahimpour, M.R.; Esmaeilzadeh, F. A new fast technique for calculation of gas condensate well productivity by using pseudopressure method. J. Nat. Gas Sci. Eng. 2012, 4, 35–43. [Google Scholar] [CrossRef]
- Beggs, H.D.; Brill, J.R. A Study of Two-Phase Flow in Inclined Pipes. J. Pet. Technol. 1973, 25, 607–617. [Google Scholar] [CrossRef]
- Ahmed, M.M.; Ayoub, M.A. A Comprehensive Study on the Current Pressure Drop Calculation in Multiphase Vertical Wells; Current Trends and Future Prospective. J. Appl. Sci. 2014, 14, 3162–3171. [Google Scholar] [CrossRef] [Green Version]
- Colebrook, C.F.; White, C.M. The Reduction of Carrying Capacity of Pipes with Age. J. Inst. Civ. Eng. 1937, 7, 99–118. [Google Scholar] [CrossRef]
- Abohamzeh, E.; Salehi, F.; Sheikholeslami, M.; Abbassi, R.; Khan, F. Review of hydrogen safety during storage, transmission, and applications processes. J. Loss Prev. Process Ind. 2021, 72, 104569. [Google Scholar] [CrossRef]
- Sani, F.M.; Nesic, S. Review of the API RP 14E Erosional Velocity Equation: Origin, Applications, Mis-uses and Limitations. In Proceedings of the NACE International Corrosion Conference and Expo 2019, Nashville, TN, USA, 24–28 March 2019; Volume 148, pp. 148–162. [Google Scholar]
- Yang, Z.; Fahmi, A.; Drescher, M.; Teberikler, L.; Merat, C.; Langsholt, M.; Liu, L. Improved understanding of flow assurance for CO2 transport and injection. In Proceedings of the 15th Greenhouse Gas Control Technologies Conference, Online, 15–18 March 2021; pp. 1–2. [Google Scholar]



| Property | Methane | Hydrogen |
|---|---|---|
| Molecular weight (g/mol) | ||
| Density (kg/m3) | ||
| Specific gravity | ||
| Dynamic viscosity (Pa·s) | ||
| Kinematic viscosity (m2/s) | ||
| Gross heating value (MJ/m3) | ||
| Thermal conductivity(W/(m·K)) |
| Component | Mole Fraction (%) |
|---|---|
| Methane | 93.76 |
| Ethane | 3.14 |
| Propane | 0.62 |
| Butane | 0.2 |
| Pentane | 0.07 |
| Nitrogen | 2.03 |
| Carbon Dioxide | 0.18 |
| Input Variable | Value | Unit |
|---|---|---|
| Pipe length | 342 | km |
| Nominal pipe size, NPS | 36 | inch |
| Pipe wall thickness | 0.25 | inch |
| Maximum allowable operating pressure, MAOP (inlet) | 70 | bar (g) |
| Outlet pressure | 17.34 | bar (g) |
| Gas specific heat ratio | 1.4 | NA |
| Standard temperature | 15.5 | °C |
| Atmospheric pressure | 1.01325 | bar |
| Number of length of pipe increment | 200 | NA |
| The material of pipe construction | Carbon steel | NA |
| Inclination angle | 0 | degrees |
| Inlet pressure | 60 | bar (g) |
| 100 | 125 | 150 | 175 | 200 | 225 | 250 | |
| (m/s) | 18.149 | 22.687 | 27.224 | 31.761 | 36.299 | 40.836 | 45.374 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, A.J.; Hassani, H.; Burby, M.; John, I.J. An Investigation into the Volumetric Flow Rate Requirement of Hydrogen Transportation in Existing Natural Gas Pipelines and Its Safety Implications. Gases 2021, 1, 156-179. https://doi.org/10.3390/gases1040013
Abbas AJ, Hassani H, Burby M, John IJ. An Investigation into the Volumetric Flow Rate Requirement of Hydrogen Transportation in Existing Natural Gas Pipelines and Its Safety Implications. Gases. 2021; 1(4):156-179. https://doi.org/10.3390/gases1040013
Chicago/Turabian StyleAbbas, Abubakar Jibrin, Hossein Hassani, Martin Burby, and Idoko Job John. 2021. "An Investigation into the Volumetric Flow Rate Requirement of Hydrogen Transportation in Existing Natural Gas Pipelines and Its Safety Implications" Gases 1, no. 4: 156-179. https://doi.org/10.3390/gases1040013
APA StyleAbbas, A. J., Hassani, H., Burby, M., & John, I. J. (2021). An Investigation into the Volumetric Flow Rate Requirement of Hydrogen Transportation in Existing Natural Gas Pipelines and Its Safety Implications. Gases, 1(4), 156-179. https://doi.org/10.3390/gases1040013







