Modulational Instability of Ion-Acoustic Waves and Associated Envelope Solitons in a Multi-Component Plasma
Abstract
:1. Introduction
2. Governing Equations
3. Derivation of the NLSE
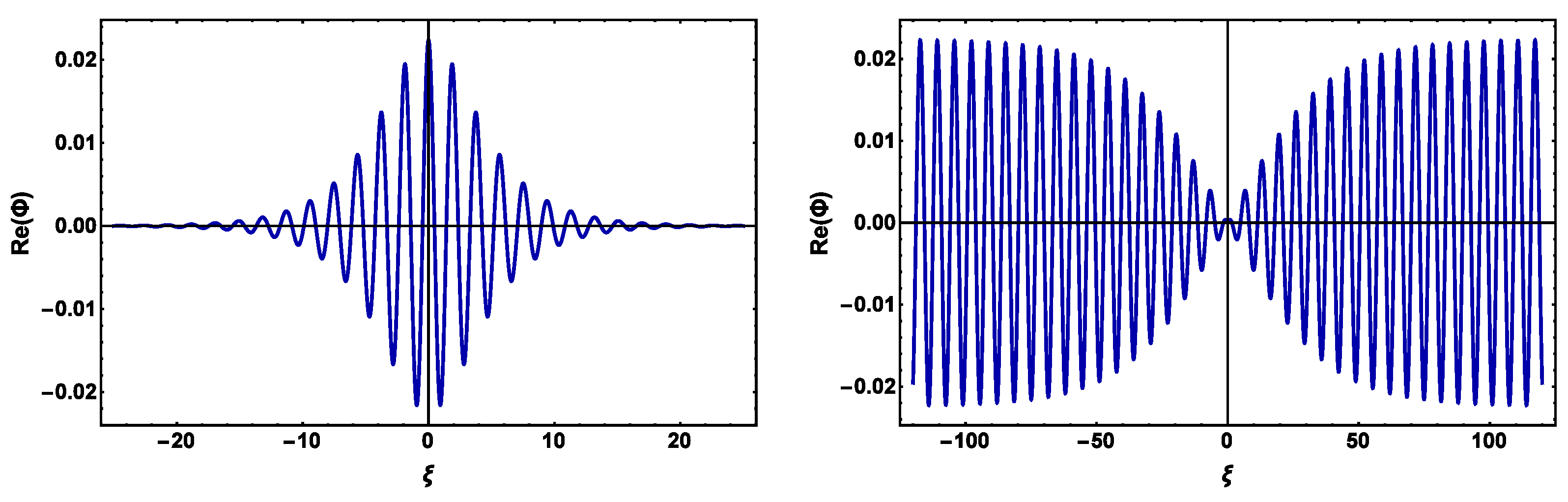
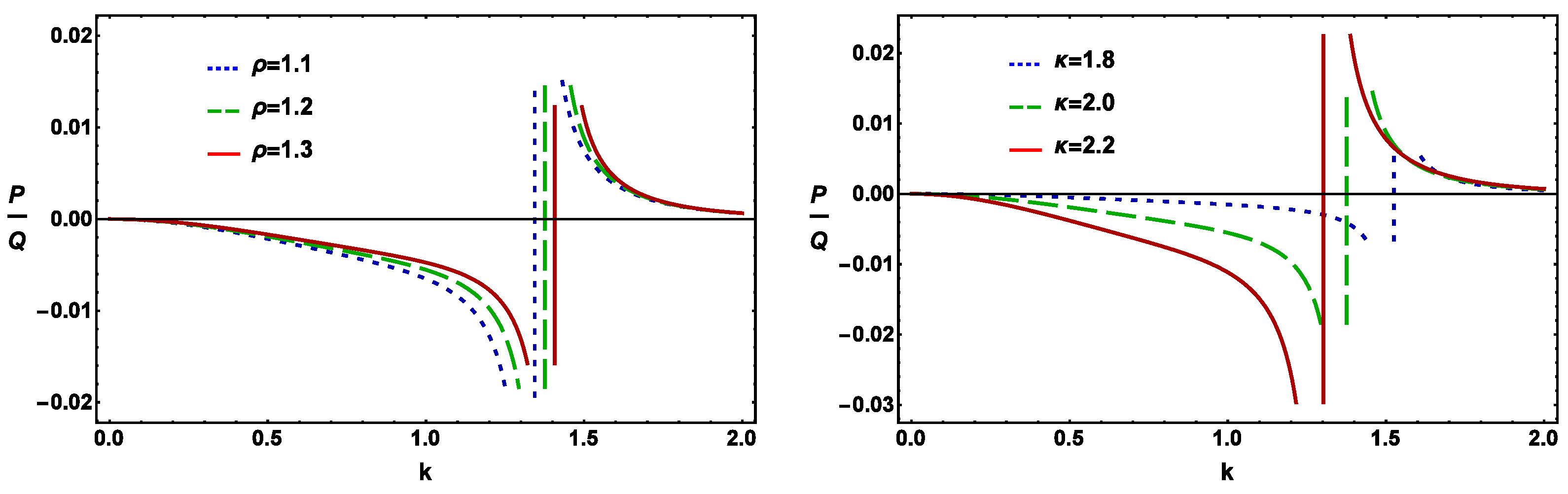
4. Modulational Instability and Envelope Solitons
5. Numerical Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ergun, R.E.; Carlson, C.W.; McFadden, J.P.; Mozer, F.S.; Delory, G.T.; Peria, W.; Chaston, C.C.; Temerin, M.; Elphic, R.; Strangeway, R.; et al. FAST satellite wave observations in the AKR source region. Geophy. Res. Lett. 1998, 25, 2061. [Google Scholar] [CrossRef]
- Temerin, M.; Cerny, K.; Lotko, W.; Mozer, F.S. Observations of double layers and solitary waves in the auroral plasma. Phys. Rev. Lett. 1982, 48, 1175. [Google Scholar] [CrossRef]
- Shahmansouri, M.; Alinejad, H. Electrostatic wave structures in a magnetized superthermal plasma with two-temperature electrons. Phys. Plasmas 2013, 20, 082130. [Google Scholar] [CrossRef]
- Rehman, M.A.; Mishra, M.K. Ion-acoustic Gardner solitons in electron-positron-ion plasma with two-electron temperature distributions. Phys. Plasmas 2016, 23, 012302. [Google Scholar] [CrossRef]
- Kourakis, I.; Shukla, P.K. Ion-acoustic waves in a two-electron-temperature plasma: Oblique modulation and envelope excitations. J. Phys. A Math. Gen. 2003, 36, 11901. [Google Scholar] [CrossRef] [Green Version]
- Alinejad, H.; Mahdavi, M.; Shahmansouri, M. Modulational instability of ion-acoustic waves in a plasma with two-temperature kappa-distributed electrons. Astrophys. Space Sci. 2014, 352, 0571. [Google Scholar] [CrossRef]
- Ali, R.; Saha, A.; Chatterjee, P. Dynamics of the positron acoustic waves in electron-positron-ion magnetoplasmas. Indian J. Phys. 2017, 91, 689. [Google Scholar] [CrossRef]
- Panwar, A.; Ryu, C.M.; Bains, A.S. Oblique ion-acoustic cnoidal waves in two temperature superthermal electrons magnetized plasma. Phys. Plasmas 2014, 21, 0122105. [Google Scholar] [CrossRef] [Green Version]
- Shalini; Saini, N.S.; Misra, A.P. Modulation of ion-acoustic waves in a nonextensive plasma with two-temperature electrons. Phys. Plasmas 2015, 22, 092124. [Google Scholar] [CrossRef] [Green Version]
- Baluku, T.K.; Hellberg, M.A. Ion acoustic solitons in a plasma with two-temperature kappa-distributed electrons. Phys. Plasmas 2012, 19, 012106. [Google Scholar] [CrossRef]
- Baluku, T.K.; Hellberg, M.A.; Mace, R.L. Electron acoustic waves in double–kappa plasmas: Application to Saturn’s magnetosphere. J. Geophys. Res. 2011, 116, A04227. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.F. Introduction to Plasma Physics and Controlled Fusion, 3rd ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Chowdhury, N.A.; Mannan, A.; Hasan, M.M.; Mamun, A.A. Heavy ion-acoustic rogue waves in electron-positron multi-ion plasmas. Chaos 2017, 27, 093105. [Google Scholar] [CrossRef]
- Chowdhury, N.A.; Hasan, M.M.; Mannan, A.; Mamun, A.A. Nucleus-acoustic envelope solitons and their modulational instability in a degenerate quantum plasma system. Vacuum 2018, 147, 31. [Google Scholar] [CrossRef] [Green Version]
- Jahan, S.; Haque, M.N.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Ion-acoustic rogue waves in double pair plasma having non-extensive particles. Universe 2021, 7, 63. [Google Scholar] [CrossRef]
- Paul, S.N.; Chowdhury, A.R.; Paul, I. Modulation instability of bright envelope soliton and rogue waves in ultra-relativistic degenerate dense electron-ion-positron plasma. Plasma Phys. Rep. 2019, 45, 1011. [Google Scholar] [CrossRef]
- Sittler, E.C.; Ogilvie, K.W.; Scudder, J.D. Survey of low-energy plasma electrons in Saturn’s magnetosphere: Voyagers 1 and 2. J. Geophys. Res. 1983, 88, 8847. [Google Scholar] [CrossRef] [Green Version]
- Young, D.T.; Berthelier, J.-J.; Blanc, M.; Burch, J.L.; Bolton, S.; Coates, A.J.; Crary, F.J.; Goldstein, R.; Grande, M.; Hill, T.W.; et al. Composition and dynamics of plasma in Saturn’s magnetosphere. Science 2005, 307, 1262. [Google Scholar] [CrossRef] [Green Version]
- Pottelette, R.; Ergun, R.E.; Treumann, R.A.; Treumann, R.A.; Berthomier, T.M.; Carlson, C.W.; McFadden, J.P.; Roth, I. Modulated electron-acoustic waves in auroral density cavities: FAST observations. Geophys. Res. Lett. 1999, 26, 2629. [Google Scholar] [CrossRef]
- Vasyliunas, V.M. A survey of low-energy electrons in the evening sector of the magnetosphere with OGO 1 and OGO 3. J. Geophys. Res. 1968, 73, 2839. [Google Scholar] [CrossRef]
- Ahmed, N.; Mannan, A.; Chowdhury, N.A.; Mamun, A.A. Electrostatic rogue waves in double pair plasmas. Chaos 2018, 28, 123107. [Google Scholar] [CrossRef] [Green Version]
- Noman, A.A.; Islam, M.K.; Hassan, M.; Banik, S.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Dust-ion-acoustic rogue waves in a dusty plasma having super-thermal electrons. Gases 2021, 1, 106–116. [Google Scholar] [CrossRef]
- Heera, N.M.; Akter, J.; Tamanna, N.K.; Chowdhury, N.A.; Rajib, T.I.; Sultana, S.; Mamun, A.A. Ion-acoustic shock waves in a magnetized plasma featuring super-thermal distribution. AIP Adv. 2021, 11, 055117. [Google Scholar] [CrossRef]
- Kourakis, I.; Shukla, P.K. Exact theory for localized envelope modulated electrostatic wavepackets in space and dusty plasmas. Nonlinear Proc. Geophys. 2005, 12, 407. [Google Scholar] [CrossRef]
- Sultana, S.; Kourakis, I. Electrostatic solitary waves in the presence of excess superthermal electrons: Modulational instability and envelope soliton modes. Plasma Phys. Control. Fusion 2011, 53, 045003. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.H.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Dust-acoustic rogue waves in an electron-positron-ion-dust plasma medium. Galaxies 2021, 9, 31. [Google Scholar] [CrossRef]
- Sikta, J.N.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Electrostatic dust-acoustic rogue waves in an electron depleted dusty plasma. Plasma 2021, 4, 230–238. [Google Scholar] [CrossRef]
- Schippers, P.; Blanc, M.; Andre, N.; Dandouras, I.; Lewis, G.R.; Gilbert, L.K.; Persoon, A.M.; Krupp, N.; Gurnett, D.A.; Coates, A.J.; et al. Multi-instrument analysis of electron populations in Saturn’s magnetosphere. J. Geophys. Res. 2008, 113, A07208. [Google Scholar] [CrossRef]
- Gaffey, J.D.; LaQuey, R.E. Upper hybrid resonance in the magnetosphere. J. Geophys. Res. 1976, 81, 595. [Google Scholar] [CrossRef]
- Bostrom, R.; Gustafsson, G.; Holback, B.; Holmgren, G.; Koskinen, H.; Kintner, P. Characteristics of solitary waves and weak double layers in the magnetospheric plasma. Phys. Rev. Lett. 1988, 61, 82. [Google Scholar] [CrossRef]
- Nishida, Y.; Nagasawa, T. Excitation of ion-acoustic rarefactive solitons in a two-electron temperature plasma. Phys. Fluids 1986, 29, 345. [Google Scholar] [CrossRef]
- Kenser, J. Axisymmetric, wall-stabilized tandem mirrors. Nucl. Fusion 1985, 25, 275. [Google Scholar]
- Sheridan, T.E.; Goeckner, M.J.; Goree, J. Observation of two-temperature electrons in a sputtering magnetron plasma. J. Vac. Sci. Tech. A 1991, 9, 688. [Google Scholar] [CrossRef]
- Baboolal, S.; Bharuthram, R.; Hellberg, M.A. Arbitrary-amplitude theory of ion-acoustic solitons in warm multi-fluid plasmas. J. Plasma Phys. 1989, 41, 341. [Google Scholar] [CrossRef]
- Krall, N.A.; Trivelpiece, A.W. Principles of Plasma Physics; McGraw-Hill: New York, NY, USA, 1973. [Google Scholar]

| R () | (eV) | (eV) | (cm−3) | (cm−3) |
|---|---|---|---|---|
| 5.40 | 1.8 | 300 | 10.5 | 0.02 |
| 6.30 | 2.0 | 400 | 10.5 | 0.01 |
| 9.80 | 8.0 | 1100 | 2.5 | 0.07 |
| 12.0 | 6.0 | 1200 | 1.0 | 0.11 |
| 13.1 | 10.2 | 1000 | 0.21 | 0.18 |
| 14.0 | 30 | 900 | 0.15 | 0.10 |
| 15.2 | 70 | 900 | 0.25 | 0.10 |
| 17.8 | 28 | 1000 | 0.15 | 0.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Banik, S.; Heera, N.M.; Yeashna, T.; Hassan, M.R.; Shikha, R.K.; Chowdhury, N.A.; Mannan, A.; Mamun, A.A. Modulational Instability of Ion-Acoustic Waves and Associated Envelope Solitons in a Multi-Component Plasma. Gases 2021, 1, 148-155. https://doi.org/10.3390/gases1030012
Banik S, Heera NM, Yeashna T, Hassan MR, Shikha RK, Chowdhury NA, Mannan A, Mamun AA. Modulational Instability of Ion-Acoustic Waves and Associated Envelope Solitons in a Multi-Component Plasma. Gases. 2021; 1(3):148-155. https://doi.org/10.3390/gases1030012
Chicago/Turabian StyleBanik, Subrata, Nadiya Mehzabeen Heera, Tasfia Yeashna, Md. Rakib Hassan, Rubaiya Khondoker Shikha, Nure Alam Chowdhury, Abdul Mannan, and A A Mamun. 2021. "Modulational Instability of Ion-Acoustic Waves and Associated Envelope Solitons in a Multi-Component Plasma" Gases 1, no. 3: 148-155. https://doi.org/10.3390/gases1030012
APA StyleBanik, S., Heera, N. M., Yeashna, T., Hassan, M. R., Shikha, R. K., Chowdhury, N. A., Mannan, A., & Mamun, A. A. (2021). Modulational Instability of Ion-Acoustic Waves and Associated Envelope Solitons in a Multi-Component Plasma. Gases, 1(3), 148-155. https://doi.org/10.3390/gases1030012







