Next Article in Journal
An Interesting Case of Allergic Bronchopulmonary Aspergillosis Resulting in Type II Respiratory Failure
Previous Article in Journal
The Journal of Respiration—A Look to the Future
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
JoR
Volume 2
Issue 4
10.3390/jor2040015
jor-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Pulmonary Oxygen Exchange in a Rhythmically Expanding–Contracting Alveolus–Capillary Model

by
Xiuhua April Si
1 and
Jinxiang Xi
2,*
1
Department of Aerospace, Industrial, and Mechanical Engineering, California Baptist University, Riverside, CA 92504, USA
2
Department of Biomedical Engineering, University of Massachusetts, Lowell, MA 01854, USA
*
Author to whom correspondence should be addressed.
J. Respir. 2022, 2(4), 159-173; https://doi.org/10.3390/jor2040015
Submission received: 10 October 2022 / Revised: 31 October 2022 / Accepted: 3 November 2022 / Published: 8 November 2022
Browse Figures
Versions Notes

Abstract

:
Pulmonary gas exchanges are vital to human health, and disruptions to this process have been associated with many respiratory diseases. Previous gas exchange studies have predominately relied on whole-body testing and theoretical analysis with 1D or static models. However, pulmonary gas exchanges are inherently a dynamic process in 3D spaces with instantaneous interactions between air, blood, and tissue. This study aimed to develop a computational model for oxygen exchange that considered all factors mentioned above. Therefore, an integrated alveolus–membrane–capillary geometry was developed with prescribed rhythmic expansion/contraction. Airflow ventilation, blood perfusion, and oxygen diffusion were simulated using COMSOL. The temporal and spatial distribution of blood flow and oxygen within the capillaries were simulated under varying breathing depths and cardiac outputs. The results showed highly nonuniform blood flow distributions in the capillary network, while the rhythmic oscillation further increased this nonuniformity, leading to stagnant blood flow in the distal vessels. A static alveolus–capillary geometry underestimated perfusion by 11% for normal respirations, and the deviation grew with breathing depth. The rhythmic motion caused a phase lag in the blood flow. The blood PO2 reached equilibrium with the alveolar air after traveling 1/5–1/3 of the capillary network. The time to reach this equilibrium was significantly influenced by the air–blood barrier diffusivity, while it was only slightly affected by the perfusion rate. The computational platform in this study could be instrumental in obtaining refined knowledge of pulmonary O2 exchanges.

1. Introduction

Normal oxygen exchanges in the lungs are critical to human health. Interruptions to pulmonary gas exchanges have been frequently observed in patients with respiratory distress, leading to ventilator usage and high rates of mortalities. The oxygen (O2) is inhaled into the pulmonary alveoli, enters the blood to bind with the hemoglobin in red blood cells, and is then transported to body tissues, where metabolism occurs. Within alveoli, O2 moves across thin respiratory membranes, which consist of alveolar squamous cells, capillary endothelial cells, and basement membranes [1]. Oxygen exchange occurs mainly through diffusion driven by the gradient of concentration or partial pressure (PO2) [2]. Ambient air is a gas mixture, with each gas contributing independently to the total pressure. Note that only a fraction of air in the alveoli can be refreshed with each breath. This makes the air composition in the alveoli significantly different from that of inhaled air. Typically, the partial pressure in the alveolar was 569 mmHg for N2, 100–104 mmHg for O2, 50 mmHg for CO2, and 47 mmHg for water vapor (i.e., Henry’s Law). By comparison, blood enters the lung capillaries with a partial pressure of 40 mmHg for O2 and 46 mmHg for CO2 [3].
The oxygen exchange between air and blood takes place across the alveoli–capillary interface. Because the blood volume in pulmonary capillaries at any moment is much lower than the alveolar air volume (i.e., 100 mL blood vs. 3500 mL air), the gas exchange essentially brings the blood oxygen level to the same level as the alveolar air. It is important that the composition of the alveolar air is monitored and adjusted to maintain amenable values [4]. For instance, if the O2 level drops, deeper breathing will be taken automatically to bring PO2 back to normal, or vice versa. Factors affecting O2 exchange include partial pressure gradient, membrane thickness, and air–blood contact area. Respiratory diseases such as pulmonary edema or pneumonia thicken the alveolar membrane and hinder diffusion. Likewise, emphysema reduces the alveolar surface, decreases oxygen exchange, and leads to lower blood oxygen levels [5].
Previous pulmonary gas exchange studies predominately relied on whole-body lung diffusion capacity testing or theoretical analysis with 1D or static models [6,7,8,9]. However, the gas exchange between the alveoli and microvascular is inherently a dynamic process, which is featured by rhythmic motions of the geometry and instantaneous interactions between airflow ventilation, gas diffusion, and blood perfusion. The ventilation–perfusion ratio (V/Q ratio) that we often referred to was based on constant values of air and blood flows in/out of the alveoli and capillaries. However, both the airflow ventilation and capillary perfusion are highly variant in time and space, leading to a time-varying V/Q ratio, which can also significantly vary at different locations of the capillary network. A prominent example of the significance of transient O2 exchange is the Nobel Prize in Physiology or Medicine 2019, awarded jointly to Kaelin, Ratcliffe, and Semenza “for their discoveries of how cells sense and adapt to oxygen availability” [10]. Moreover, the accumulated blood flow rate can also be influenced by the capillary’s oscillating motion, leading to a modified V/Q ratio and subsequent oxygen availability [11].
The objective of this study was to numerically simulate the oxygen exchange in a dynamic alveolus–capillary model. Specific aims include:
(1)
Develop a computational platform for O2 exchange in an expanding/contracting geometry that consists of an alveolus, a capillary network, and a membrane between them;
(2)
Determine the diffusivity of the air–blood interface (membrane) in comparison to empirical O2 exchange data;
(3)
Quantify the effects of capillary pressure drop and breathing depth on the temporal blood flow rate;
(4)
Study the membrane diffusivity and perfusion rate on the temporal–spatial distribution of O2 in the capillary network.

2. Materials and Methods

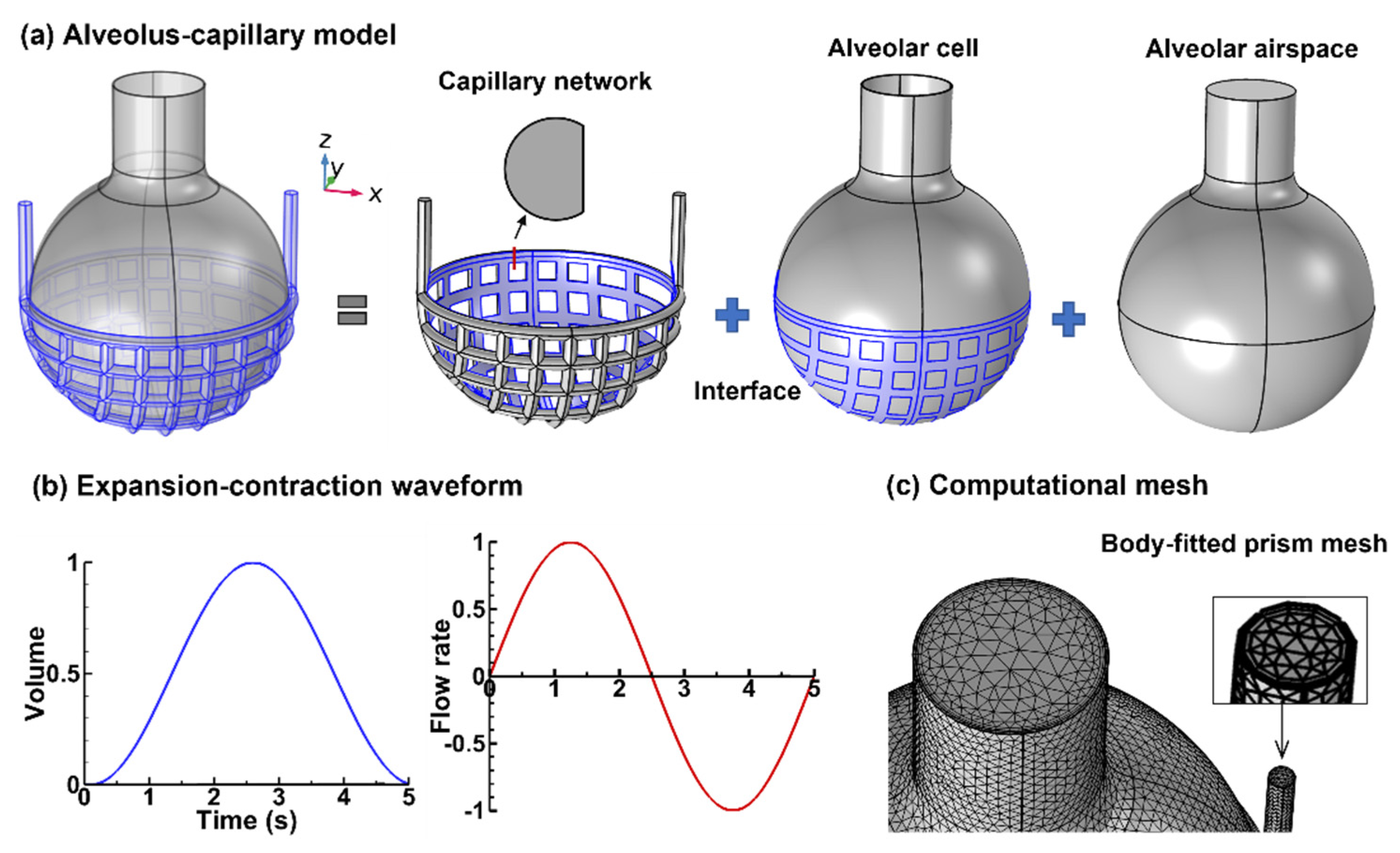
2.1. Alveolus–Capillary Model

A computer model was developed that consisted of one alveolus, a capillary network wrapping the alveolus, and the alveolar membrane between them, as illustrated in Figure 1a. The diameter of the alveolar duct was 70 µm [12,13], and the diameter of the alveolus (i.e., sphere) was 200 µm [14,15,16]. Under normal breathing conditions, the breathing depth, or tidal volume expansion ratio (η = ΔV/V), was 23% [15,17,18], which was equivalent to a radius expansion ratio of 7.15% (i.e., ( 1 + 0.23 3 ) − 1). The capillary had one inlet and outlet, with a network of interconnected vessels between them (Figure 1a). The network consisted of four tori (circular vessels) along the vertical direction, seven half-tori in the x-direction, and one torus in the y-direction. The last torus aligned with the inlet and outlet and was considered the major vessel of the capillary network. Each capillary vessel had a C-ring chape with a hydraulic diameter of 8 µm (Figure 1a, second panel).

2.2. Numerical Methods

COMSOL Multiphysics was used to develop the alveolus–membrane–capillary model geometry. Three materials (i.e., air, tissue, and blood) were applied to the above three domains, respectively (Figure 1a). The oxygen diffusivity in the air and blood was 0.242 × 10−4 m2/s and 2.18 × 10−9 m2/s, respectively [19,20]. No measured oxygen diffusivity through the alveolar membrane (Dm) has been found in the literature [21,22,23]. Note that the traditional O2 diffusion capacity (mL/min) was measured in the whole-body capacity, which cannot be applied to the alveolus–capillary model without introducing additional uncertainties [24,25,26]. In order to fill this gap, an inverse approach was used to identify the Dm value that gave an O2-equilibrium time of 0.25 s (i.e., the time that the blood O2 level reached the alveolar level), which was a well-accepted value for a normal lung under resting conditions [27,28]. Note that the lack of O2 diffusivity through the alveolus–capillary barrier is mainly due to the complex underlying mechanisms. First, O2 dissolves in and diffuses through the surfactant film, the alveolar epithelium, the interstitium, and the capillary endothelium; it then diffuses through the plasma, enters the erythrocyte, combines with hemoglobin, and is transported out of the capillary [29].
Figure 1c shows the computational mesh of the three-compartment models generated in COMSOL. The physics-controlled mesh was used for the alveolus and capillary with normal internal element size and fine prism element in the near-wall region, which were essential to capture near-wall transitions [30,31]. The extra fine mesh was implemented in the membrane (Figure 1c). The simulations were conducted in an AMD Ryzen 3960X 24-Core workstation with 3.79 GHz processors and 256 RAM.
A moving mesh was implemented to the three domains with a prescribed mesh displacement, which first expanded, then contracted, following a sinusoidal waveform (Figure 1b). The period of the waveform was 5 s, and the oscillation amplitude was determined by the breathing depths, as described in 2.1. Four breathing depths were investigated, 11.5%, 23%, 34.5%, and 46%, which gave the radius expansion ratios of 3.70%, 7.15%, 10.38%, and 13.44%, respectively.
Laminar flow was used to simulate airflow ventilation in and out of the expanding–contracting alveolus. An open boundary condition (BC) was specified at the alveolar inlet. The blood flow was also simulated as laminar, considering the mean velocity of approximately 1 mm/s [32,33]. Varying pressure drops (50–300 Pa) were prescribed at the capillary inlet and outlet. The mass transfer was simulated using the diluted species transport model. The oxygen partial pressure (PO2) was 159 mmHg (8.557 mol/m3) at the alveolar inlet (flux BC) and 40 mmHg (2.153 mol/m3) at the capillary inlet. The initial PO2 in the alveolus was 100 mmHg (5.382 mol/m3). The inhaled oxygen was transported to the alveolar wall through both convection and diffusion, where it continued to diffuse through the membrane and enter the capillary vessels. The blood flow conveyed the O2 towards the capillary outlet and further distributed it to different regions of the body.

3. Results

3.1. Flow Fields

3.1.1. Airflow

Airflow in the alveolus and blood flow in the capillary vessels are shown in Figure 2 at varying instants within one expansion and contraction cycle. The tidal expansion ratio was 23% (i.e., amplitude = 7.15% R0), and the capillary pressure was 100 Pa [15,34]. The airflow streamlines appeared regular in distribution, which did not change much during the entire expansion phase. A similar streamline pattern was also observed during exhalation, only with the flow direction being reversed (lower panel, Figure 2). The mid-plane contour shows the velocity magnitude variations during one respiration cycle. The peak airflow velocity was found at 1.25 s during inhalation and 3.75 s during exhalation.

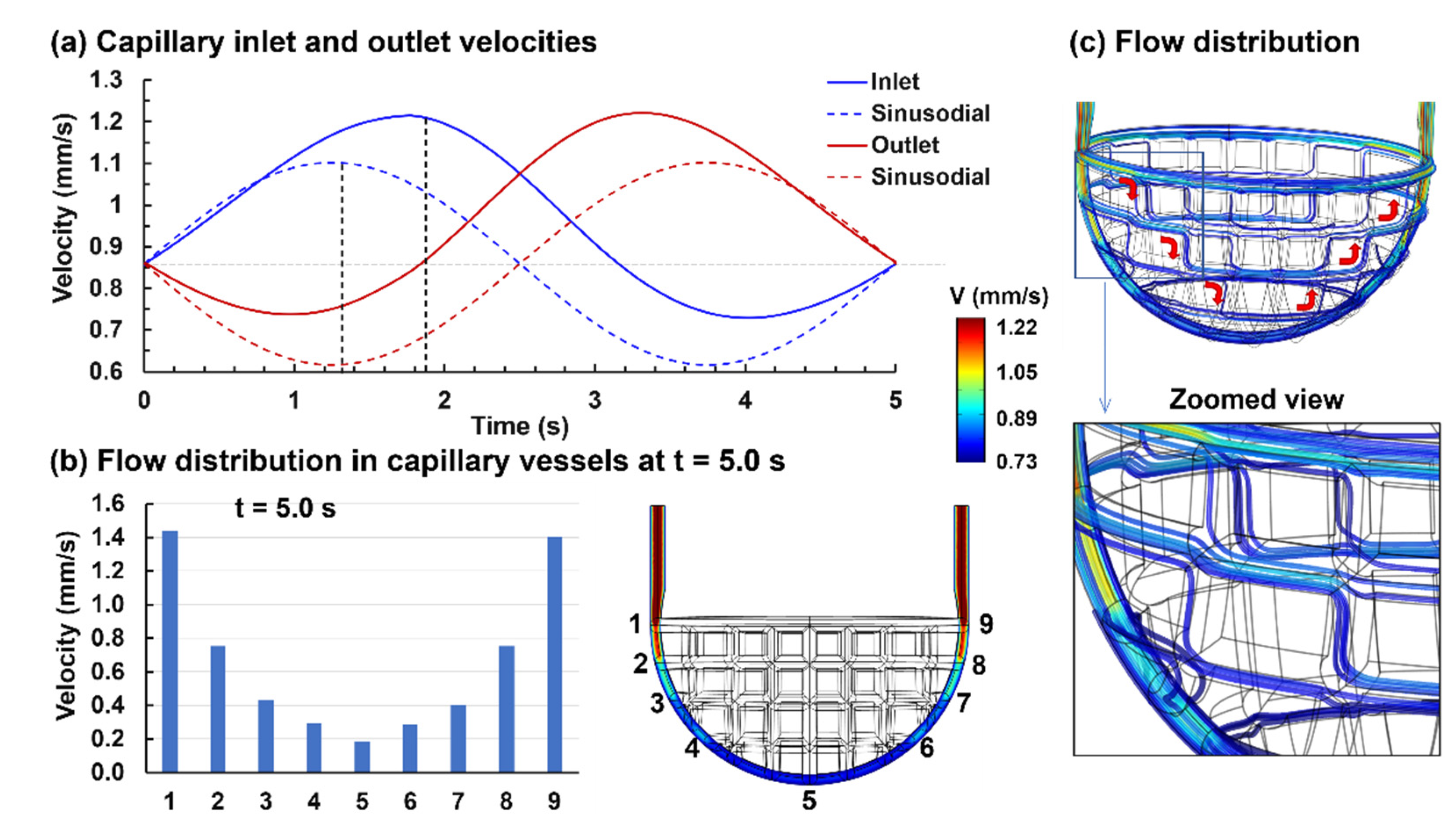
3.1.2. Capillary Blood Flow

One salient feature of the capillary flow was the oscillations of the capillary volumetric flow rate due to the rhythmic motion (Figure 2). During expansion, the increased volume of the capillary network drew more blood into the vessels from both openings (inlet and outlet, upper panel, Figure 2). The storage of blood in the stretched capillary network slowed down the blood flow within it. At the center of the capillary network, the compliance-incurred speed decrease could become so significant that the blood flow becomes stagnant. This was especially obvious at t2 = 1.25 s when the expansion speed was the highest. After t2 = 1.25 s, the expansion slowed down, and the stagnant capillaries were gradually recruited. At the end of the expansion (t4 = 2.5 s), all capillaries were recruited and perfused, even though their flow rates could be highly heterogeneous.
The blood flows were further examined in Figure 3 by comparing the perfusion distributions among capillaries within one breathing cycle. The white color in the capillaries means stagnant flow. Again, highly heterogeneous perfusions were observed throughout the entire respiration cycle, and locally stagnant flows occurred most of the time except at the beginning/end of expansion/contraction (t = 2.5, 5.0 s, Figure 3). The two most perfused regions were either close to the inlet or outlet. However, these two regions were not symmetric, with the inlet-proximity region more perfused during expansion and the outlet-proximity region more perfused during contraction (Figure 3). Note that only the perfused capillaries could transport the ventilated O2 out of the pulmonary region; without an efflux, a stagnant capillary could only absorb a limited amount of O2 (i.e., till equilibrium). On the other hand, constant O2 absorption occurred into an efflux. The absorption rate would increase with the efflux rate (perfusion limited). If the efflux was significantly large to carry away all available O2, the absorption rate could change to ventilation limited.
Quantitation of perfusion distributions among capillaries within one breathing cycle is presented in Figure 4. In comparison to a perfectly sinusoidal waveform with no phase shift (dashed line), the inlet flow (blue color) had an apparent phase lag, while the outlet flow (red color) had a phase forward shift of approximately 0.55 s (Figure 4a). The velocity at 2.5 s (peak expansion) was higher than that at t = 0.0 s and 5.0 s (minimal volume) because the expansion drew in more blood flow through the capillary inlet. Figure 4b shows the blood flow speeds along the major capillary at nine points at t = 5.0 s. It was clear that the closer to the inlet or outlet, the higher the flow speeds. The perfusion distribution was approximately symmetric right vs. left; however, subtle differences were still discernable. For instance, using the grid line as a reference, it was observed that the flow speeds at points 1 and 3 were slightly higher than that at the corresponding points 9 and 7 (Figure 4b). Such differences were presumably attributed to the inherent compliance elicited from the expanding–contracting model geometry.
Figure 4c shows the flow distribution within the capillary network. By starting from the inlet, there was a cascade of bifurcations of the flow from the upper vessels to the lower vessels, as illustrated by the red clockwise curved arrows. The flows diverted from the upper vessels subsequently merged (but did not mix) with the flow in the lower vessel, which further bifurcated into two streams (zoomed view, Figure 4c). After the half capillary network, a reverse pattern existed for the flows towards the outlet, where a cascade of the flow-merging process occurred from the bottom to the top (counter-clockwise curved arrows, Figure 4c).

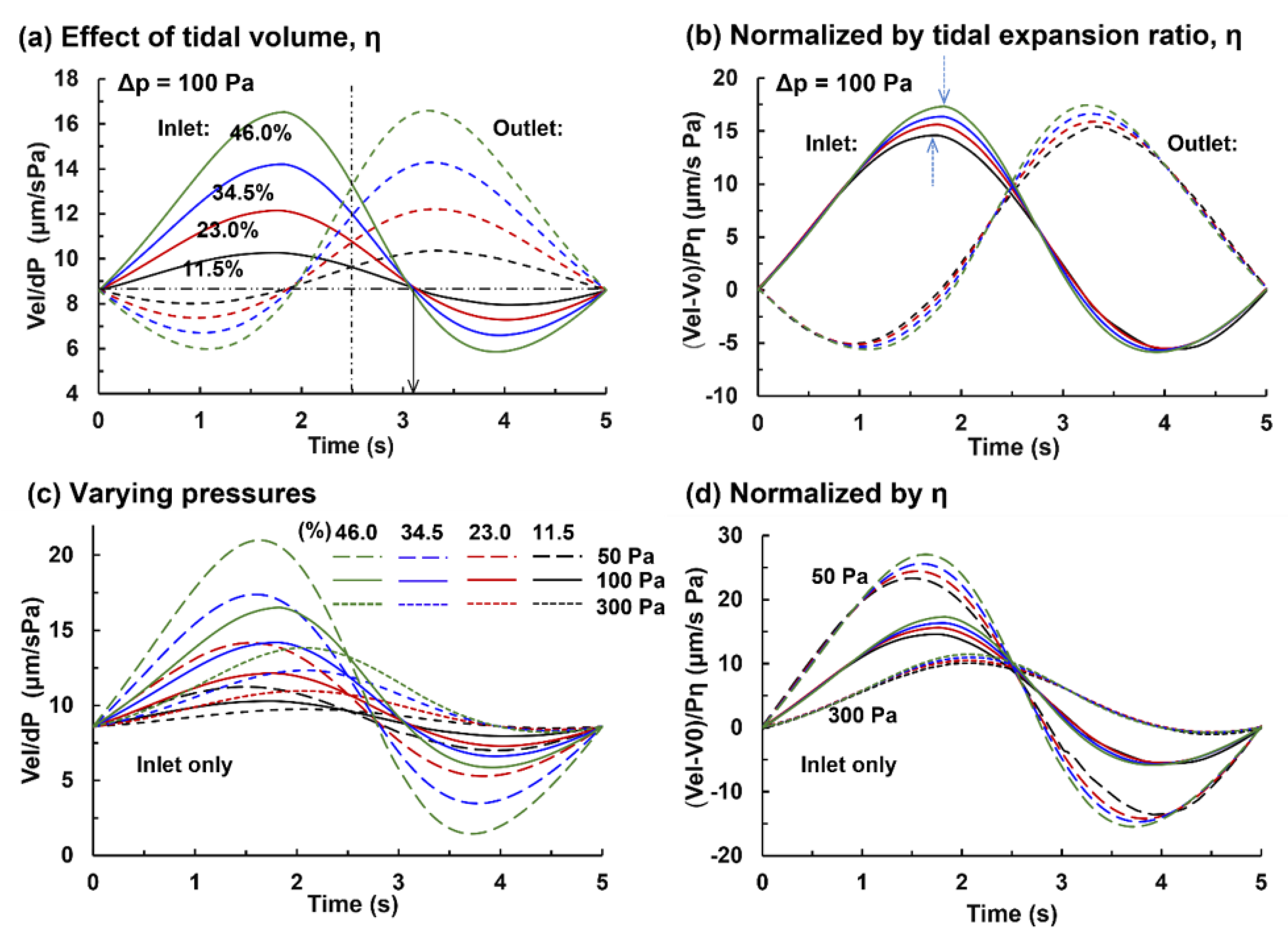
3.2. Capillary Flow under Varying Pressures and Tidal Volumes

3.2.1. Capillary Blood Flow Rate

The effects of the capillary pressure drop on the blood flow rate are presented in Figure 5. Overall, the capillary blood flow rate is proportional to the pressure drop (Figure 5a). However, the phase shift increases with increasing pressure drop, which can be seen more clearly when replotted in Figure 5b by subtracting the instantaneous velocities from their averages. Here the solid lines represent the inlet velocities, and the dashed lines represent the outlet velocities. Note the approximate symmetry of the flow responses between the right and left vs. the apparent asymmetry between the upper and lower relative to the average (Figure 5b). The latter is because of the net positive flow within the capillary despite the flow velocity oscillations. The difference in the phase shift is caused by the interaction of the flow inertia and compliance, where a longer delay reaching the peak is observed for a larger pressure drop (Figure 5b). Figure 5c shows the normalized blood velocities by dividing the pressure drop. Therefore, the velocities under varying pressures successfully collapsed at the start/end of expansion/contraction (i.e., 0.0, 2.5, and 5.0 s). By contrast, the oscillating amplitudes of the normalized velocities were nonlinear, with a descending order from lower pressures to higher pressures (i.e., from 50 to 300 Pa, Figure 5c).
The effects of the tidal volume (i.e., expansion ratio, η = ΔV/V) on the capillary flows are shown in Figure 6. For a given pressure drop of 100 Pa (Figure 6a), the capillary flow speed remained approximately unchanged at 0, 2.5, and 5.0 s (the end of expansion or contraction). However, the flow oscillation increased with the tidal expansion ratio. Interestingly, all flow profiles under varying tidal volumes met at the same point, i.e., 3.1 s (Figure 6a). The data in Figure 6a were replotted in Figure 6b in terms of the flow fluctuations divided by the tidal expansion ratio η. Normalizing the flows using η nicely collapsed four profiles, and all profiles crossed one point at 2.5 s. Slight differences still existed at the flow peaks (Figure 6b). The larger the tidal volume, the higher the normalized peak and the more phase shift (arrows in Figure 6b).
The combined influences from the tidal volume and pressure on capillary flows are shown in Figure 6c. Results under two more pressure drops (50 and 300 Pa) were added to Figure 6c, with long-dashed lines for 50 Pa and dotted lines for 300 Pa (Figure 6c). The flow fluctuations were sensitive to both the pressures and tidal volumes considered in this study, as flow profiles under categories covered the entire velocity range (Figure 6c). As in Figure 6d, normalizing the flow fluctuations by η regressed well into three groups. Moreover, the higher the pressure, the less scattered the η-normalized flow fluctuations.

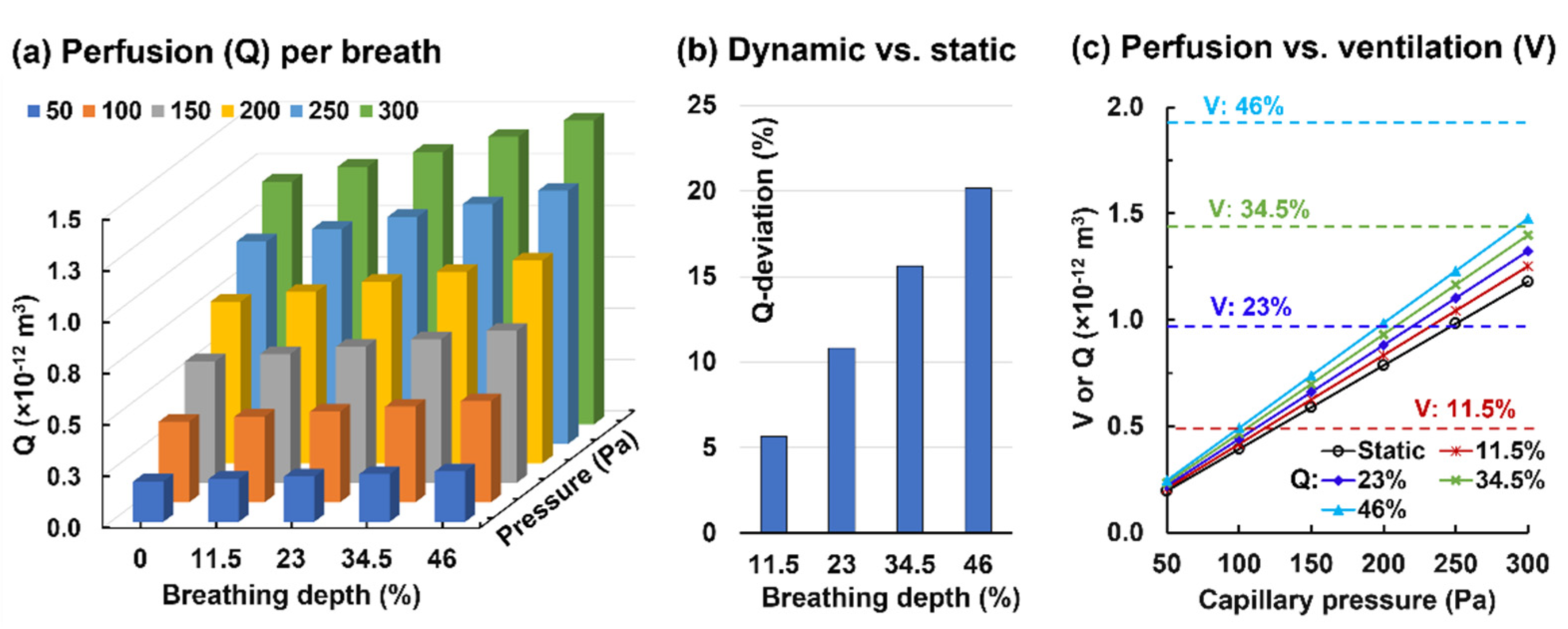
3.2.2. Alveolar Perfusion and Ventilation

The perfusion volume to the alveolus per breath was calculated by integrating the capillary blood flow rate over one respiration cycle (5 s). Figure 7a shows the calculated alveolar perfusion at varying capillary pressures and breathing depths. The breathing depth of 0% represents a static alveolus–capillary geometry. As alluded to in Figure 5 and Figure 6, the rhythmic oscillation increased the alveolar perfusion more than a static geometry, and the increasing magnitude was sensitive to the breathing depth (Figure 7a). Relative to the static case, the increase was 5.7%, 10.8%, 15.6%, and 20.2% for the breathing depth of 11.5%, 23%, 34.5%, and 46%, respectively (Figure 7b). A similar observation of increased pulmonary perfusion with inspiration was also reported by Hayano et al. [35]. The perfusion per breath was also compared to the alveolar ventilation (V), which was calculated as the product of the alveolus volume and breathing depth, as shown in Figure 7c. It was observed that at η = 11.5%, the ventilation and perfusion matched at 115 Pa (dashed and solid red lines), while at η = 23%, the ventilation–perfusion match was found at 220 Pa (dashed and solid blue lines). Note that the prefusion Q varied with the capillary pressure (x-axis), while the ventilation V was independent of the capillary pressure (Figure 7c). The larger the capillary pressure drop between the vessel inlet and outlet, the higher the perfusion, and the more airflow ventilation was needed to achieve the V-Q matching.

3.3. Oxygen Exchange and Transport

3.3.1. Control Case (η = 0.23 and Dm = 2.0 × 10−10 m2/s)

Figure 8 shows the oxygen (O2) exchange in the alveolus–capillary model geometry, which involved both convection (alveolar airflow ventilation and blood-flow perfusion) and diffusion (within the alveolar airspace and blood, as well as across the alveolar membrane). In this example (control case), the tidal expansion ratio η was 0.23, and the diffusivity in the air, blood, and membrane were 2.42 × 10−5 m2/s, 2.18 × 10−9 m2/s, and 2.00 × 10−10 m2/s, respectively. The initial O2 partial pressure (PO2) was 159 mmHg at the alveolar inlet, 100 mmHg inside the alveolus, and 40 mmHg at the capillary vessel inlet. Figure 8a shows the O2 temporal variation with a tidal volume of 235 and capillary pressure of 100 Pa at seven points (upper: 3, lower: 4). As expected, the O2 partial pressure at the capillary vessel inlet remained at 40 mmHg throughout the cycle (upper panel, Figure 8a). At the capillary outlet, the PO2 increased with time and reached equilibrium around 0.25 s. Meanwhile, the PO2 inside the alveolus decreased slightly from 100 mmHg to 97 mmHg during 0–0.14 s due to the O2 transport from the alveolus to blood and recovered back to 98.2 mmHg hereafter.
Figure 8b displays the streamlines for PO2 at varying instants between 0 and 0.25 s. Similar to the velocity streamlines, the PO2 streamlines represent the instantaneous direction of the mass flux. The capillary O2 was at 40 mmHg at t = 0.00 s (blue color, Figure 8b) and increased quickly with alveolar expansion. Note the drastic color change from blue to red during the first 0.10 s. After 0.10 s, the capillary O2 increased at an ever-decreasing speed and reached full equilibrium around 0.25 s. The PO2 streamlines appeared uniform during 0–0.10 s but became apparently skewed to the vessel inlet after that. This was reasonable considering the more intensified mass transfer near the inlet than in other regions. The lower panel of Figure 8a shows the O2 partial pressure at P4–P1 with descending magnitudes, denoting an increasing O2 diffusion from air to blood. The location of the sampling points P1–P4 is illustrated in Figure 8b with t = 0.1 s.

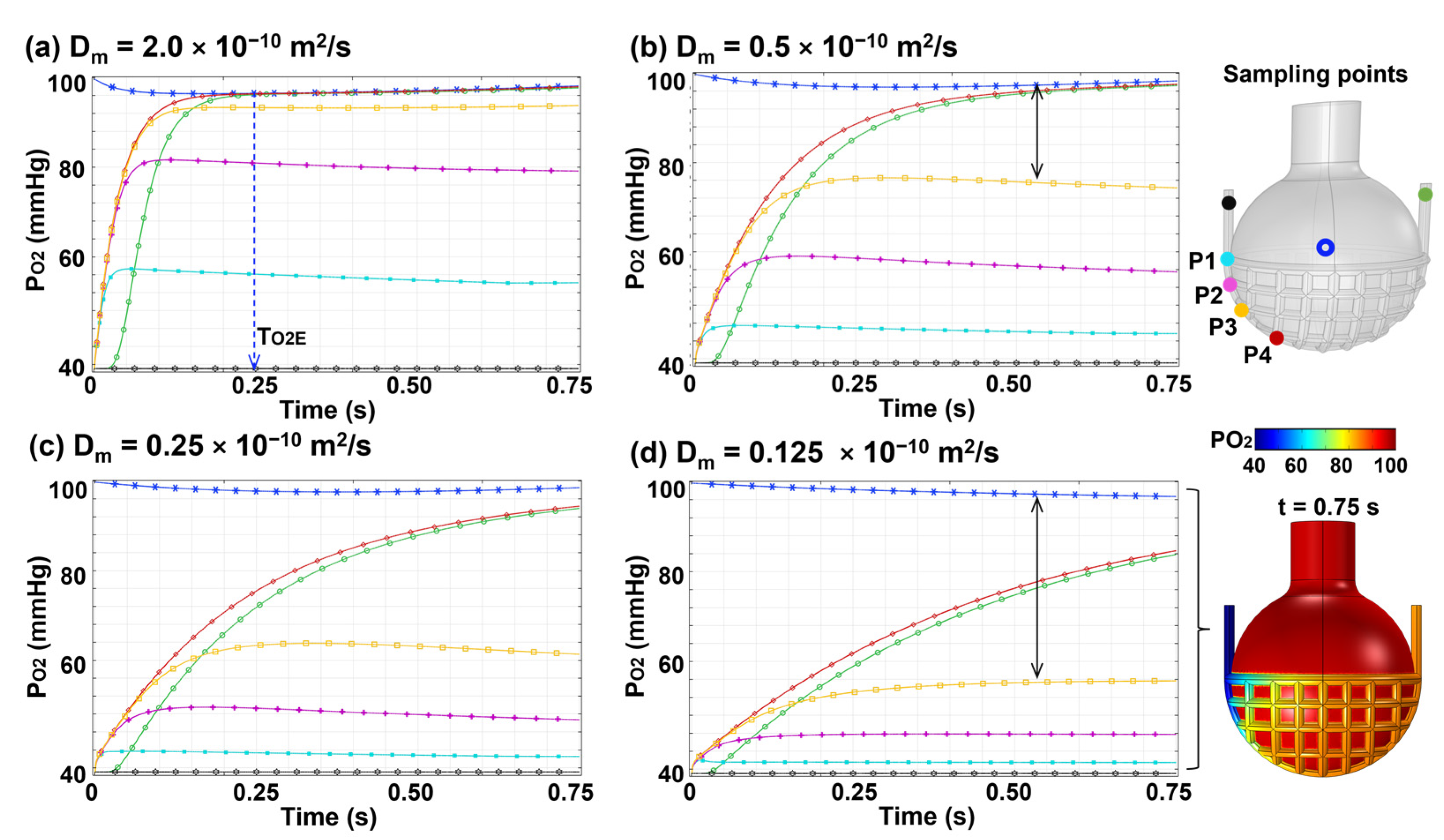
3.3.2. Effects of Membrane Diffusivity (Dm)

Effects of the membrane diffusivity (Dm) on the oxygen exchange and transport in the alveolus–capillary model are shown in Figure 9. In the diffusivities considered herein (i.e., 2.0 × 10−10 − 0.125 × 10−10 m2/s), decreasing Dm notably prolonged the time that the oxygen reached an equilibrium between the alveolus and capillary vessels (i.e., the O2-equilibrium time, or tO2E, Figure 9a). In comparison to 0.25 s under 2.0 × 10−10 m2/s, the O2-equilibrium time was around 0.75 s at 0.5 × 10−10 m2/s (Figure 9a vs. Figure 9b), would be even longer at 0.25 × 10−10 and 0.125 × 10−10 m2/s (Figure 9c,d). The PO2 at the capillary vessels close to the inlet also decreased with decreasing membrane diffusivities. This resulted in a larger PO2 gradient between the alveolus and vessel that would partially compensate for the reduced O2 exchange from a lower Dm; however, the net O2 flux could still be lower than the capacity that the blood flow perfused, leading to a diffusion-limited O2 exchange (Figure 9c,d). Note that the difference between the red and green lines was due to the time difference in the blood flow from P4 to the vessel outlet.

3.3.3. Effects of Perfusion Rate

Figure 10 shows the effects of the perfusion rate on temporal–spatial oxygen exchange by varying the capillary pressure ∆P (50–200 Pa) with membrane diffusivity Dm being 2.0 × 10−10 m2/s. Relative to the control case (∆P = 100 Pa), decreasing the perfusion rate increased the time difference between the red and green lines (∆t) and increased the PO2 in the vessels close to the inlet (i.e., P1–4, Figure 10a vs. Figure 10b). Conversely, this time difference ∆t was very small at a high perfusion rate (e.g., ∆P = 200 Pa, Figure 10d), reflective of the faster perfusion through the capillary network. The PO2 in the inlet-proximity vessels was also much lower under ∆P = 200 Pa, leading to a larger air–blood gradient in PO2 and a higher oxygen flux from the alveolus to capillary vessels, which was further transported out of the capillary by the blood flow. Note that 1 Pa = 0.0075 mmHg.
The tO2E (time for O2 to reach equilibrium with the alveolar level) at P4 (red line) appeared to be insensitive to the perfusion rate, which was around 0.2 s for the four perfusion rates considered (Figure 10a–d). This suggested that for a Dm of 2.0 × 10−10 m2/s, the O2 exchange was still perfusion limited for the four perfusion rates, as illustrated by the limited membrane area for mass diffusion (cyan dashed rectangle) at 0.2 s. By contrast, a large portion of the membrane still existed to be recruited for extra O2 demand (Figure 10b).

4. Discussion

In this study, high sensitivity was observed in the temporal/spatial O2 distribution to the alveolus–capillary membrane diffusivity Dm. Surprisingly, direct measurements of Dm through the membrane have not yet been found; even though the O2 diffusing capacity has been measured in the whole-body capacity (e.g., in mL/min) [36], it cannot be applied in the microscale model in this study. This lack of O2 air–blood diffusivity can be partially from the alveolus’ tiny dimension that defies current quantification techniques and partially from the limited knowledge regarding the O2 diffusion pathway that includes not only the alveolar wall but also the red blood cell wall and hemoglobin binding [37,38]. The latter is also demonstrated by the 2019 Nobel Prize in Physiology or Medicine, which recognizes the discoveries related to cells’ response to oxygen availability [39]. In order to find an appropriate O2 diffusivity to start with, preliminary simulations have been conducted. We started with a water-equivalent diffusivity (2.18 × 10−9 m2/s) for the air–blood barrier but obtained an alveolar-capillary O2 equilibrium time of 20 ms, which was too short in comparison to 0.25 s. After a series of trial-and-error, an O2 diffusivity of 2.0 × 10−10 m2/s was selected, which gave the alveolar–capillary equilibrium time at 0.25 s under resting conditions (Figure 8). Note that this Dm value was merely a result from the attempt of filling the data-missing gap; future in vivo or in vitro measurements are needed to verify/improve the data accuracy.
The results in Figure 9 can have implications in patients with impaired diffusions of the lungs, such as alveolar fibrosis (thickening of the alveolar wall). Other conditions that decrease the diffusing capacity include interstitial edema, sarcoidosis, scleroderma, and pneumonia [40,41,42,43]. In these patients, the capillary PO2 may not be able to reach the alveolar PO2 within the breathing cycle, and the oxygen flux from the air to blood is limited by the membrane diffusivity (i.e., diffusion-limited). As a result, an insufficient amount of oxygen can reach the cells and satisfy the demand for cell metabolism [44,45]. By contrast, the results in Figure 8 and Figure 10 represent healthy conditions. With a normal membrane diffusivity, the capillary PO2 reaches the alveolar PO2 when the blood is about one-fifth to one-third of the way through the capillary network (Figure 8 and Figure 10). Within this region, diffusion drives the oxygen transfer occurred because of the PO2 gradient, even though this gradient decreases progressively from the capillary inlet to the equilibrium point. Beyond that region, the oxygen transfer becomes perfusion limited. In circumstances when a larger cardiac output is needed, the diffusion region becomes larger (i.e., microvacuolar recruitment) to meet the increased demand, as illustrated by the gradually increasing PO2 gradient at the four sampling points (P1–P4) in Figure 10a–d.
The computational model can serve as a platform to study gas exchange under healthy and abnormal breathing conditions. Ideally, the oxygen via ventilation (V) is just sufficient to fully saturate the blood perfusion (Q), as indicated by the cross points in Figure 7c. These two variables, V and Q, act as the major determinants of blood oxygen level [46,47]. In this regard, Figure 8 can be used as a guideline to understand the V-Q match or determine the V needed for a given physical activity (i.e., ~Q). For a typical adult, one-liter blood can hold approximately 200 mL of oxygen, while one-liter air contains around 210 mL of oxygen [48]. Thus, the ideal ventilation/perfusion ratio (V/Q) is around 0.95. On the other hand, a V/Q mismatch can elicit Type 1 respiratory failure [49,50]. A shunt has a zero V/Q, which has perfusion but no ventilation, while a dead space has an infinite V/Q, with ventilation but no perfusion [51]. Exercise leads to a higher demand for oxygen, which regulates the ventilation and perfusion rates, and eventually reaches a new equilibrium [52], a similar transition process as shown in Figure 10a–d.
Surprisingly long computational times were required to simulate O2 exchange in the computational model developed in this study, even though simplified alveolar and capillary morphologies were used. With a normal mesh for fluid physics in the alveolus and capillary and a refined mesh in the membrane (Figure 1b), the computational time for O2 exchange during 0–0.75 s was 39–64 COMSOL hours using an AMD Ryzen 3960X 24-Core workstation with 3.79 GHz processors and 256 RAM. The lower the membrane diffusivity, the longer the computation time was required. Several reasons may be responsible for this high demand: a large mesh for the multi-compartment system, multi-physics, multi-phases, multi-scale, and fluid-structure interactions. The speeds for the wall motion, airflow ventilation, and blood perfusion were in the range of 0.1–1 mm/s, and the diffusion speeds through the membrane were even lower. It was also observed that COMSOL automatically refined the time step to improve convergence. Time step sizes of 1 × 10−6 s were often used during simulations, even though a step size of 0.01 s was specified. In addition, this COMSOL-based model was highly CPU demanding; running two test cases would take nearly 100% CPU. In this regard, simulating O2 exchange in more complex alveoli–capillary geometries can still be prohibitive.
Limitations of this numerical investigation included the lack of comparable measurements, idealized alveolus–capillary model geometry, simplified motion waveforms, constant capillary pressures, and oxygen only. Due to the submicron dimensions of both the alveoli and capillaries, direct in vivo measurements of the gas exchange parameters and associated physical properties were rare (if not existent at all). This lack of data is not surprising considering that the alveolar diameter is 0.2–0.4 mm and the capillary vessel is 8 µm or so, which falls below the resolutions of current characterization or visualization techniques [5,53,54]. The acinar region has complex morphologies with multiple alveoli ventilated via the alveolar duct or pores of Kohn [55]. Even more complicated is the pulmonary microvasculature that wraps the alveolar sac and has sophisticated architectures [56]. Adopting a simplified model as in this study circumvented the prohibitive computational resource that was otherwise required to resolve the above complexities while could still provide insights into the O2 behaviors in this dynamic, multi-phase (gas, liquid, solid), and multi-physics (convection and diffusion) system. No pathological conditions were considered in this study, such as shunt, partial obstruction, membrane abnormality, etc. [57,58,59]. This study did not consider CO2 removal. As a result, the interactions between O2 and CO2 in the blood, i.e., the Bohr and Haldane effects, were also excluded, which might limit full equilibration between air and blood in certain scenarios [60]. By considering the dead spaces in the respiratory tract, the assumption of the alveolar inlet PO2 equivalent to the ambient condition should also be improved in future studies.

5. Conclusions

No previous studies have been reported that considered the dynamic interactions among pulmonary ventilation, membrane diffusion, and capillary perfusion in moving, three-dimensional alveoli–capillary geometry. This study aimed to fill this gap and develop a numerical platform that could evaluate all aforementioned factors, albeit with simplified geometries, kinematics, and physical properties. Temporal–spatial distributions of the blood flow and O2 were simulated under varying ventilation and perfusion conditions. Specific findings include:
(1)
Blood perfusion was nonuniform among the capillary vessels, and the geometry oscillation further increased the nonuniformity;
(2)
A static alveolus–capillary model underestimated the blood flow rate by 11% under resting conditions and increased linearly with the breathing depth for a given capillary pressure;
(3)
The blood flow had a phase lag (~0.55 s) than the alveolar motion under resting conditions; the phase lag increased with increasing cardiac output;
(4)
The blood oxygen level reached the alveolar level around 1/5–1/3 of the capillary; oxygen exchange was diffusion driven within this region and was perfusion limited beyond this region;
(5)
The time to reach the air–blood equilibrium in PO2 was sensitive to the membrane diffusivity and was relatively insensitive to the blood flow rate;
(6)
Without measured alveolus–capillary barrier diffusivity for oxygen in the literature, a value of 2.0 × 10−10 m2/s was proposed for normal conditions based on the match to empirical data.

Author Contributions

Conceptualization, X.A.S. and J.X.; methodology, X.A.S. and J.X.; software, X.A.S. and J.X.; validation, X.A.S. and J.X.; formal analysis, X.A.S. and J.X.; investigation, X.A.S. and J.X.; resources, X.A.S. and J.X.; data curation, X.A.S. and J.X.; writing—original draft preparation, J.X.; writing—review and editing, X.A.S.; All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data in this study are available from the corresponding author.

Acknowledgments

Amr Seifelnasr at UMass Lowell Biomedical Engineering was gratefully acknowledged for technical support and for reviewing this manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Nova, Z.; Skovierova, H.; Calkovska, A. Alveolar-capillary membrane-related pulmonary cells as a target in endotoxin-induced acute lung injury. Int. J. Mol. Sci. 2019, 20, 831. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Lavin, K.M.; Straub, A.M.; Uhranowsky, K.A.; Smoliga, J.M.; Zavorsky, G.S. Alveolar-membrane diffusing capacity limits performance in Boston marathon qualifiers. PLoS ONE 2012, 7, e44513. [Google Scholar] [CrossRef] [Green Version]
  3. Klabukov, I.D.; Krasilnikova, O.A.; Baranovskii, D.S. Quantitative human physiology: An introduction guide for advanced tissue engineering. Biotechnol. J. 2022, 17, 2100481. [Google Scholar] [CrossRef] [PubMed]
  4. Wilson, H.K. Breath analysis. Physiological basis and sampling techniques. Scand. J. Work Environ. Health 1986, 12, 174–192. [Google Scholar] [CrossRef] [PubMed]
  5. Xi, J.; Talaat, M. Nanoparticle deposition in rhythmically moving acinar models with interalveolar septal apertures. Nanomaterials 2019, 9, 1126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  6. Al-Ashkar, F.; Mehra, R.; Mazzone, P.J. Interpreting pulmonary function tests: Recognize the pattern, and the diagnosis will follow. Cleve. Clin. J. Med. 2003, 70, 866–881. [Google Scholar] [CrossRef] [Green Version]
  7. Frija-Masson, J.; Bancal, C.; Plantier, L.; Benzaquen, H.; Mangin, L.; Penaud, D.; Arnoult, F.; Flamant, M.; d’Ortho, M.P. Alteration of diffusion capacity after SARS-CoV-2 infection: A pathophysiological approach. Front. Physiol. 2021, 12, 624062. [Google Scholar] [CrossRef]
  8. Si, X.; Xi, J.S.; Talaat, M.; Donepudi, R.; Su, W.-C.; Xi, J. Evaluation of impulse oscillometry in respiratory airway casts with varying obstruction phenotypes, locations, and complexities. J. Respir. 2022, 2, 44–58. [Google Scholar] [CrossRef]
  9. Yuan, J.; Chiofolo, C.M.; Czerwin, B.J.; Karamolegkos, N.; Chbat, N.W. Alveolar tissue fiber and surfactant effects on lung mechanics-model development and validation on ARDS and IPF patients. IEEE Open J. Eng. Med. Biol. 2021, 2, 44–54. [Google Scholar] [CrossRef]
  10. Ledford, H.; Callaway, E. Biologists who decoded how cells sense oxygen win medicine Nobel. Nature 2019, 574, 161–162. [Google Scholar] [CrossRef]
  11. Forouzan, O.; Yang, X.; Sosa, J.M.; Burns, J.M.; Shevkoplyas, S.S. Spontaneous oscillations of capillary blood flow in artificial microvascular networks. Microvasc. Res. 2012, 84, 123–132. [Google Scholar] [CrossRef] [PubMed]
  12. Darquenne, C.; Harrington, L.; Prisk, G.K. Alveolar duct expansion greatly enhances aerosol deposition: A three-dimensional computational fluid dynamics study. Philos. Trans. A Math. Phys. Eng. Sci. 2009, 367, 2333–2346. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Hajari, A.J.; Yablonskiy, D.A.; Quirk, J.D.; Sukstanskii, A.L.; Pierce, R.A.; Deslée, G.; Conradi, M.S.; Woods, J.C. Imaging alveolar-duct geometry during expiration via ³He lung morphometry. J. Appl. Physiol. 2011, 110, 1448–1454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Xi, J.; Talaat, M.; Si, X.A.; Han, P.; Dong, H.; Zheng, S. Alveolar size effects on nanoparticle deposition in rhythmically expanding-contracting terminal alveolar models. Comput. Biol. Med. 2020, 121, 103791. [Google Scholar] [CrossRef]
  15. Talaat, K.; Xi, J. Computational modeling of aerosol transport, dispersion, and deposition in rhythmically expanding and contracting terminal alveoli. J. Aerosol Sci. 2017, 112, 19–33. [Google Scholar] [CrossRef]
  16. Talaat, M.; Si, X.; Tanbour, H.; Xi, J. Numerical studies of nanoparticle transport and deposition in terminal alveolar models with varying complexities. Med One 2019, 4, e190018. [Google Scholar]
  17. Si, X.; Talaat, M.; Xi, J. SARS COV-2 virus-laden droplets coughed from deep lungs: Numerical quantification in a single-path whole respiratory tract geometry. Phy. Fluids 2021, 33, 023306. [Google Scholar]
  18. Talaat, M.; Si, X.A.; Xi, J. Lower inspiratory breathing depth enhances pulmonary delivery efficiency of proair sprays. Pharmaceuticals 2022, 15, 706. [Google Scholar] [CrossRef]
  19. Pittman, R.N. Regulation of Tissue Oxygenation. In San Rafael (CA): Regulation of Tissue Oxygenation; Morgan & Claypool Publishers: Kentfield, CA, USA, 2011. [Google Scholar]
  20. Dunn, J.-O.; Mythen, M.; Grocott, M. Physiology of oxygen transport. BJA Educ. 2016, 16, 341–348. [Google Scholar] [CrossRef] [Green Version]
  21. Zanen, P.; van der Lee, I.; van der Mark, T.; van den Bosch, J.M.M. Reference values for alveolar membrane diffusion capacity and pulmonary capillary blood volume. Eur. Respir. J. 2001, 18, 764–769. [Google Scholar] [CrossRef] [Green Version]
  22. Wilson, R.H.; Evans, R.L.; Johnson, R.S.; Dempsey, M.E. An estimation of the effective alveolar respiratory surface and other pulmonary properties in normal persons. Am. Rev. Tuberc. 1954, 70, 296–303. [Google Scholar] [PubMed]
  23. Huang, C.; Chambers, D.; Matthews, G. Alveolar diffusion. In Basic Physiology for Anaesthetists; Huang, C., Chambers, D., Matthews, G., Eds.; Cambridge University Press: Cambridge, UK, 2015; pp. 40–44. [Google Scholar]
  24. Beretta, E.; Grasso, G.S.; Forcaia, G.; Sancini, G.; Miserocchi, G. Differences in alveolo-capillary equilibration in healthy subjects on facing O2 demand. Sci. Rep. 2019, 9, 16693. [Google Scholar] [CrossRef] [PubMed]
  25. Park, J.O.; Choi, I.S.; Park, K.O. Normal predicted values of single-breath diffusing capacity of the lung in healthy nonsmoking adults. Korean J. Intern Med. 1986, 1, 178–184. [Google Scholar] [CrossRef] [PubMed]
  26. Munkholm, M.; Marott, J.L.; Bjerre-Kristensen, L.; Madsen, F.; Pedersen, O.F.; Lange, P.; Nordestgaard, B.G.; Mortensen, J. Reference equations for pulmonary diffusing capacity of carbon monoxide and nitric oxide in adult Caucasians. Eur. Respir. J. 2018, 52, 1500677. [Google Scholar] [CrossRef] [Green Version]
  27. Rummer, J.L.; Brauner, C.J. Root effect haemoglobins in fish may greatly enhance general oxygen delivery relative to other vertebrates. PLoS ONE 2015, 10, e0139477. [Google Scholar] [CrossRef] [Green Version]
  28. MacDougall, J.D.; McCabe, M. Diffusion coefficient of oxygen through tissues. Nature 1967, 215, 1173–1174. [Google Scholar] [CrossRef]
  29. Zimmerman, R.A.; Tsai, A.G.; Intaglietta, M.; Tartakovsky, D.M. A mechanistic analysis of possible blood transfusion failure to increase circulatory oxygen delivery in anemic patients. Ann. Biomed. Eng. 2019, 47, 1094–1105. [Google Scholar] [CrossRef]
  30. Xi, J.; Kim, J.; Si, X.A.; Corley, R.A.; Zhou, Y. Modeling of inertial deposition in scaled models of rat and human nasal airways: Towards in vitro regional dosimetry in small animals. J. Aerosol Sci. 2016, 99, 78–93. [Google Scholar] [CrossRef]
  31. Xi, J.; Si, X.; Kim, J.; Zhang, Y.; Jacob, R.E.; Kabilan, S.; Corley, R.A. Anatomical details of the rabbit nasal passages and their implications in breathing, air conditioning, and olfaction. Anat. Rec. 2016, 299, 853–868. [Google Scholar] [CrossRef] [Green Version]
  32. Horimoto, M.; Koyama, T.; Mishina, H.; Asakura, T.; Murao, M. Blood flow velocity in pulmonary microvessels of bullfrog. Respir. Physiol. 1979, 37, 45–59. [Google Scholar] [CrossRef]
  33. Razavi, M.S.; Shirani, E.; Kassab, G.S. Scaling laws of flow rate, vessel blood volume, lengths, and transit times with number of capillaries. Front. Physiol. 2018, 9, 581. [Google Scholar] [CrossRef] [PubMed]
  34. Czerwin, B.; Patel, S.; Chiofolo, C.; Yuan, J.; Chbat, N. Modeling the steady-state effects of mean arterial pressure on the kidneys. IEEE Open J. Eng. Med. Biol. 2020, 2, 1–10. [Google Scholar] [CrossRef] [PubMed]
  35. Hayano, J.; Yasuma, F.; Okada, A.; Mukai, S.; Fujinami, T. Respiratory sinus arrhythmia. A phenomenon improving pulmonary gas exchange and circulatory efficiency. Circulation 1996, 94, 842–847. [Google Scholar] [CrossRef]
  36. Hyde, R.W.; Forster, R.E.; Power, G.G.; Nairn, J.; Rynes, R. Measurement of O2 diffusing capacity of the lungs with a stable O2 isotope. J. Clin. Investig. 1966, 45, 1178–1193. [Google Scholar] [CrossRef] [PubMed]
  37. Richardson, S.L.; Swietach, P. Red blood cell thickness is evolutionarily constrained by slow, hemoglobin-restricted diffusion in cytoplasm. Sci. Rep. 2016, 6, 36018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  38. Butler, J.P.; Tsuda, A. Transport of gases between the environment and alveoli--theoretical foundations. Compr. Physiol. 2011, 1, 1301–1316. [Google Scholar]
  39. Zhang, Q.; Yan, Q.; Yang, H.; Wei, W. Oxygen sensing and adaptability won the 2019 Nobel Prize in Physiology or medicine. Genes Dis. 2019, 6, 328–332. [Google Scholar] [CrossRef]
  40. Yu, M.; Sandhu, V.K.; Lezcano, S.D.; Maken, K.; Kirk, S.; Torralba, K.D. Sarcoidosis and systemic sclerosis: Strange bedfellows. Case Rep. Rheumatol. 2017, 2017, 7851652. [Google Scholar] [CrossRef] [Green Version]
  41. Cottin, V.; Hirani, N.A.; Hotchkin, D.L.; Nambiar, A.M.; Ogura, T.; Otaola, M.; Skowasch, D.; Park, J.S.; Poonyagariyagorn, H.K.; Wuyts, W.; et al. Presentation, diagnosis and clinical course of the spectrum of progressive-fibrosing interstitial lung diseases. Eur. Respir. Rev. 2018, 27, 180076. [Google Scholar] [CrossRef] [Green Version]
  42. Solomon, J.J.; Olson, A.L.; Fischer, A.; Bull, T.; Brown, K.; Raghu, G. Scleroderma lung disease. Eur. Respir. Rev. 2013, 22, 6–19. [Google Scholar] [CrossRef]
  43. Eklund, A.; Broman, L.; Broman, M.; Holmgren, A. V/Q and alveolar gas exchange in pulmonary sarcoidosis. Eur. Respir. J. 1989, 2, 135–144. [Google Scholar] [PubMed]
  44. Cottin, V.; Brown, K.K. Interstitial lung disease associated with systemic sclerosis (SSc-ILD). Respir. Res. 2019, 20, 13. [Google Scholar] [CrossRef] [PubMed]
  45. Xi, J.; Si, X.; Dong, H.; Zhong, H. Effects of glottis motion on airflow and energy expenditure in a human upper airway model. Eur. J. Mech. B 2018, 72, 23–37. [Google Scholar] [CrossRef]
  46. Chan, E.D.; Chan, M.M.; Chan, M.M. Pulse oximetry: Understanding its basic principles facilitates appreciation of its limitations. Respir. Med. 2013, 107, 789–799. [Google Scholar] [CrossRef] [Green Version]
  47. Petersson, J.; Glenny, R.W. Gas exchange and ventilation–perfusion relationships in the lung. Eur. Respir. J. 2014, 44, 1023–1041. [Google Scholar] [CrossRef] [Green Version]
  48. O’Driscoll, B.R.; Howard, L.S.; Davison, A.G. BTS guideline for emergency oxygen use in adult patients. Thorax 2008, 63, vi1–vi68. [Google Scholar] [CrossRef] [Green Version]
  49. Neder, J.A.; Kirby, M.; Santyr, G.; Pourafkari, M.; Smyth, R.; Phillips, D.B.; Crinion, S.; de-Torres, J.P.; O’Donnell, D.E. V/Q mismatch: A novel target for COPD treatment. Chest 2022, in press.
  50. Rodriguez-Roisin, R. Pulmonary gas exchange in acute respiratory failure. Eur. J. Anaesthesiol. 1994, 11, 5–13. [Google Scholar]
  51. Karbing, D.S.; Panigada, M.; Bottino, N.; Spinelli, E.; Protti, A.; Rees, S.E.; Gattinoni, L. Changes in shunt, ventilation/perfusion mismatch, and lung aeration with PEEP in patients with ARDS: A prospective single-arm interventional study. Crit. Care 2020, 24, 111. [Google Scholar] [CrossRef] [Green Version]
  52. Schaffartzik, W.; Poole, D.C.; Derion, T.; Tsukimoto, K.; Hogan, M.C.; Arcos, J.P.; Bebout, D.E.; Wagner, P.D. VA/Q distribution during heavy exercise and recovery in humans: Implications for pulmonary edema. J. Appl. Physiol. 1992, 72, 1657–1667. [Google Scholar] [CrossRef]
  53. Conhaim, R.L.; Rodenkirch, L.A. Functional diameters of alveolar microvessels at high lung volume in zone II. J. Appl. Physiol. 1998, 85, 47–52. [Google Scholar] [CrossRef] [PubMed]
  54. Xi, J.; Talaat, K.; Si, X. Deposition of bolus and continuously inhaled aerosols in rhythmically moving terminal alveoli. J. Comput. Multiphase Flow 2018, 10, 178–193. [Google Scholar] [CrossRef]
  55. Xi, J.; Talaat, M.; Tanbour, H.; Talaat, K. Airflow and particle deposition in acinar models with interalveolar septal walls and different alveolar numbers. Comput. Math. Methods Med. 2018, 2018, 3649391. [Google Scholar] [CrossRef]
  56. De Paepe, M.E.; Mao, Q.; Powell, J.; Rubin, S.E.; DeKoninck, P.; Appel, N.; Dixon, M.; Gundogan, F. Growth of pulmonary microvasculature in ventilated preterm infants. Am. J. Respir. Crit. Care. Med. 2006, 173, 204–211. [Google Scholar] [CrossRef] [Green Version]
  57. Guazzi, M. Alveolar-capillary membrane dysfunction in heart failure: Evidence of a pathophysiologic role. Chest 2003, 124, 1090–1102. [Google Scholar] [CrossRef]
  58. Puri, S.; Baker, B.L.; Dutka, D.P.; Oakley, C.M.; Hughes, J.M.B.; Cleland, J.G.F. Reduced alveolar-capillary membrane diffusing capacity in chronic heart failure. Circulation 1995, 91, 2769–2774. [Google Scholar] [CrossRef]
  59. Ahlfeld, S.K.; Conway, S.J. Assessment of inhibited alveolar-capillary membrane structural development and function in bronchopulmonary dysplasia. Birth. Defects. Res. A Clin. Mol. Teratol. 2014, 100, 168–179. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  60. Malte, H.; Lykkeboe, G. The Bohr/Haldane effect: A model-based uncovering of the full extent of its impact on O2 delivery to and CO2 removal from tissues. J. Appl. Physiol. 2018, 125, 916–922. [Google Scholar] [CrossRef]
Jor 02 00015 g001 550
Figure 1. Computational model: (a) alveolus–capillary model geometry consisting of a capillary vessel network, alveolar cells (membrane), and alveolar airspace, (b) model expansion–contraction waveforms, with the oscillation amplitude depending on the tidal volume, and (c) computational mesh with fine prism mesh in the near-wall region.
Figure 1. Computational model: (a) alveolus–capillary model geometry consisting of a capillary vessel network, alveolar cells (membrane), and alveolar airspace, (b) model expansion–contraction waveforms, with the oscillation amplitude depending on the tidal volume, and (c) computational mesh with fine prism mesh in the near-wall region.
Jor 02 00015 g001
Jor 02 00015 g002 550
Figure 2. Streamlines and velocity contours at varying instants during alveolar expansion (upper panel) and contraction (lower panel).
Figure 2. Streamlines and velocity contours at varying instants during alveolar expansion (upper panel) and contraction (lower panel).
Jor 02 00015 g002
Jor 02 00015 g003 550
Figure 3. Streamlines of the blood flow within the capillary vessels at varying instants during alveolar expansion (upper panel) and contraction (lower panel).
Figure 3. Streamlines of the blood flow within the capillary vessels at varying instants during alveolar expansion (upper panel) and contraction (lower panel).
Jor 02 00015 g003
Jor 02 00015 g004 550
Figure 4. Perfusion distributions among capillaries within one breathing cycle: (a) phase shifts of the blood flow vs. a sinusoidal waveform at the inlet and outlet, (b) flow distribution in capillary vessels at the end of contraction (t = 5.0 s), and (c) flow distribution within the capillary network.
Figure 4. Perfusion distributions among capillaries within one breathing cycle: (a) phase shifts of the blood flow vs. a sinusoidal waveform at the inlet and outlet, (b) flow distribution in capillary vessels at the end of contraction (t = 5.0 s), and (c) flow distribution within the capillary network.
Jor 02 00015 g004
Jor 02 00015 g005 550
Figure 5. Effect of the capillary pressure drop: (a) instantaneous capillary flow velocities within one respiration cycle at varying pressure drops, (b) replot the instantaneous velocities minus the average, and (c) normalized the instantaneous flow velocities by the pressure drop.
Figure 5. Effect of the capillary pressure drop: (a) instantaneous capillary flow velocities within one respiration cycle at varying pressure drops, (b) replot the instantaneous velocities minus the average, and (c) normalized the instantaneous flow velocities by the pressure drop.
Jor 02 00015 g005
Jor 02 00015 g006 550
Figure 6. Effect of tidal volume (i.e., expansion ratio, η = ΔV/V): (a) instantaneous flow speeds normalized by pressure at different tidal volumes, and (b) instantaneous flow oscillations normalized by pressure and expansion ratio, (c) normalized capillary flow speed (by pressure) vs. time, and (d) normalized capillary flow speed (by pressure and tidal expansion ratio η) vs. time.
Figure 6. Effect of tidal volume (i.e., expansion ratio, η = ΔV/V): (a) instantaneous flow speeds normalized by pressure at different tidal volumes, and (b) instantaneous flow oscillations normalized by pressure and expansion ratio, (c) normalized capillary flow speed (by pressure) vs. time, and (d) normalized capillary flow speed (by pressure and tidal expansion ratio η) vs. time.
Jor 02 00015 g006
Jor 02 00015 g007 550
Figure 7. Alveolar perfusion: (a) the alveolar perfusion (×10−12 m3) integrated over one breathing cycle at varying capillary pressures and breathing depths, (b) the perfusion rate deviation from the static case vs. breathing depth, and (c) perfusion (Q) vs. ventilation (V).
Figure 7. Alveolar perfusion: (a) the alveolar perfusion (×10−12 m3) integrated over one breathing cycle at varying capillary pressures and breathing depths, (b) the perfusion rate deviation from the static case vs. breathing depth, and (c) perfusion (Q) vs. ventilation (V).
Jor 02 00015 g007
Jor 02 00015 g008 550
Figure 8. Oxygen exchange in the alveolus–capillary model: (a) temporal variation in oxygen partial pressure (PO2) at various locations: the alveolar center, capillary vessel inlet, vessel outlet (upper panel), and four points (P1–P4) within the vessel network (lower panel); (b) streamlines for PO2 (the instantaneous direction of PO2) at varying instants.
Figure 8. Oxygen exchange in the alveolus–capillary model: (a) temporal variation in oxygen partial pressure (PO2) at various locations: the alveolar center, capillary vessel inlet, vessel outlet (upper panel), and four points (P1–P4) within the vessel network (lower panel); (b) streamlines for PO2 (the instantaneous direction of PO2) at varying instants.
Jor 02 00015 g008
Jor 02 00015 g009 550
Figure 9. Effects of the membrane diffusivity (Dm) on the temporal and spatial distribution of PO2: (a) Dm = 2.0 × 10−10 m2/s, (b) Dm = 0.5 × 10−10 m2/s, (c) Dm = 0.25 × 10−10 m2/s, and (d) Dm = 0.125 × 10−10 m2/s.
Figure 9. Effects of the membrane diffusivity (Dm) on the temporal and spatial distribution of PO2: (a) Dm = 2.0 × 10−10 m2/s, (b) Dm = 0.5 × 10−10 m2/s, (c) Dm = 0.25 × 10−10 m2/s, and (d) Dm = 0.125 × 10−10 m2/s.
Jor 02 00015 g009
Jor 02 00015 g010 550
Figure 10. Effects of the perfusion rate on temporal–spatial oxygen exchange by varying the capillary pressure ∆P: (a) 50 Pa, (b) 100 Pa, (c) 150 Pa, and (d) 200 Pa. Dm = 2.0 × 10−10 m2/s.
Figure 10. Effects of the perfusion rate on temporal–spatial oxygen exchange by varying the capillary pressure ∆P: (a) 50 Pa, (b) 100 Pa, (c) 150 Pa, and (d) 200 Pa. Dm = 2.0 × 10−10 m2/s.
Jor 02 00015 g010
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Si, X.A.; Xi, J. Pulmonary Oxygen Exchange in a Rhythmically Expanding–Contracting Alveolus–Capillary Model. J. Respir. 2022, 2, 159-173. https://doi.org/10.3390/jor2040015

AMA Style

Si XA, Xi J. Pulmonary Oxygen Exchange in a Rhythmically Expanding–Contracting Alveolus–Capillary Model. Journal of Respiration. 2022; 2(4):159-173. https://doi.org/10.3390/jor2040015

Chicago/Turabian Style

Si, Xiuhua April, and Jinxiang Xi. 2022. "Pulmonary Oxygen Exchange in a Rhythmically Expanding–Contracting Alveolus–Capillary Model" Journal of Respiration 2, no. 4: 159-173. https://doi.org/10.3390/jor2040015

APA Style

Si, X. A., & Xi, J. (2022). Pulmonary Oxygen Exchange in a Rhythmically Expanding–Contracting Alveolus–Capillary Model. Journal of Respiration, 2(4), 159-173. https://doi.org/10.3390/jor2040015

Article Metrics

Back to TopTop