Models to Estimate the Bark Volume for Larix sp. in Poland ^†

Abstract

Bark constitutes one of the main residues and by-products of the timber harvest. Therefore, in order to conduct effective forest management, it is essential to estimate the possible amount of that product, which can be obtained during the harvest process. Our objective was to develop a model to estimate bark volume and bark volume fraction (i.e., its share in the total volume of a tree). For the study, we choose larch (Larix sp.) which is a rare but valuable forest raw material in Poland. The research material was collected in northern (2 sites), central (1 site), and southern (2 sites) in Poland. In total, we obtained data from nearly 600 trees growing on oligo-, meso-, and eutrophic sites. We used the tree’s breast height diameter, height, and total volume as independent variables. Both analyzed bark parameters varied significantly with regard to location, site type, and age class. Bark volume is strongly and significantly dependent on the tree’s breast height diameter, height, and total volume. For bark volume fraction, this correlation is significant but very weak. The best results of bark volume estimation are achieved for the model with total tree volume as an independent variable. Because of the strong effect of location on bark volume estimates, it is recommended to elaborate locally-based models for this parameter determination.

1. Introduction

As timber sale is the primary source of income in the forestry, it is crucial to estimate timber volume and its value with the highest achievable accuracy. In Central Europe, it is a common practice to sell the timber with the bark, however the customer pays for the volume estimated under the bark. The conversion of over-bark measurements to under-bark records is made using various methods of bark thickness or bark volume determination [1,2]. Therefore, in addition to the improvement of the measurement methods and equipment, efforts are undertaken to develop better and better models that allow to determine bark features precisely [3].

Recent shift of the bark reception from a harvest by-product or residue towards the perspective and commercially important fuel or biomaterial and source of tannins caused the increase interest in bark volume estimates development [4,5,6]. Moreover, assessment of bark volume is also important for quantifying carbon stocks [7].

Our objectives included: (i) analysis of the variability of bark volume and bark volume fraction for Larix sp. in Poland as well as (ii) development of models to estimate the investigated parameters with regard to the basic dendrometric attributes.

2. Material and Methods

Data that served for bark volume (bV) and bark volume fraction (%bV) modeling was collected in 5 locations in various parts of Poland: Dobrzany and Kolbudy—northern part, Rogów—central Poland, Pińczów and Prudnik—southern, upland, and mountain part of the country. Altogether, we measured 599 trees on 62 study plots that differed in growth conditions (oligo-, meso-, and eutrophic sites) and age (19–127 years).

For each tree, we obtained its breast height diameter (d), height (h), and total volume (V, determined with section-wise method). Using bark gauge, we determined the bark thickness that allowed to convert the over-bark volume to under-bark volume. The difference of these two constituted bark volume. Bark volume fraction was calculated as a ratio of bark volume and total over-bark volume of a tree.

The distribution of bV and %bV differed significantly from the normal one (Shapiro–Wilk test, p < 0.001), and we used the Kruskal–Wallis test to assess the impact of location (5 variants), site type (3 variants of growth conditions), and age class (we distinguished 4 ones: <40, 40–60, 60–80, >80 years-old) on the analyzed bark attributes. Pearson correlation was applied to evaluate the relationship between bV or %bV and d, h, or V, as well as between one another.

Following previous studies [5,6], we used breast height diameter, height, and total tree volume as an independent variables in models to estimate bark volume and bark volume fraction. We chose the following equations for the model elaboration:

ŷ = a + b∙x,

(1)

ŷ = a∙x^b + c,

(2)

ŷ = a∙(exp^x∙b) + c,

(3)

ŷ = a∙x/(b + x),

(4)

ŷ = a/(1 + b∙exp^-c∙x),

(5)

ŷ = a∙exp^(b∙exp^ c∙x),

(6)

where ŷ—estimated bark parameter, x—independent variable (d—breast height diameter, h—height, V—total tree volume), a, b, c—model parameters.

Based on bark volume distribution, we split our data into calibration and validation sets in proportion ²/₃ to ¹/₃. Obtained sets did not differ significantly in terms of tree’s age, breast height diameter, height, total tree volume, bark volume, and bark volume fraction (Mann–Whitney test; p > 0.4). Best model selection was based on Akaike Information Criterion (AIC) and R² goodness-of-fit measures. We chose two best performing ones (#1 and #4) and verified them based on the data from validation set using R² and root mean square error (RMSE) of the residuals as an evaluation measures. Finally, we tested obtained residuals for the impact of location, site type, and age class (Kruskal–Wallis test).

All statistical analyses were performed with PAST4.03 software [8].

3. Results and Discussion

3.1. Variability of Bark Volume and Bark Volume Fraction

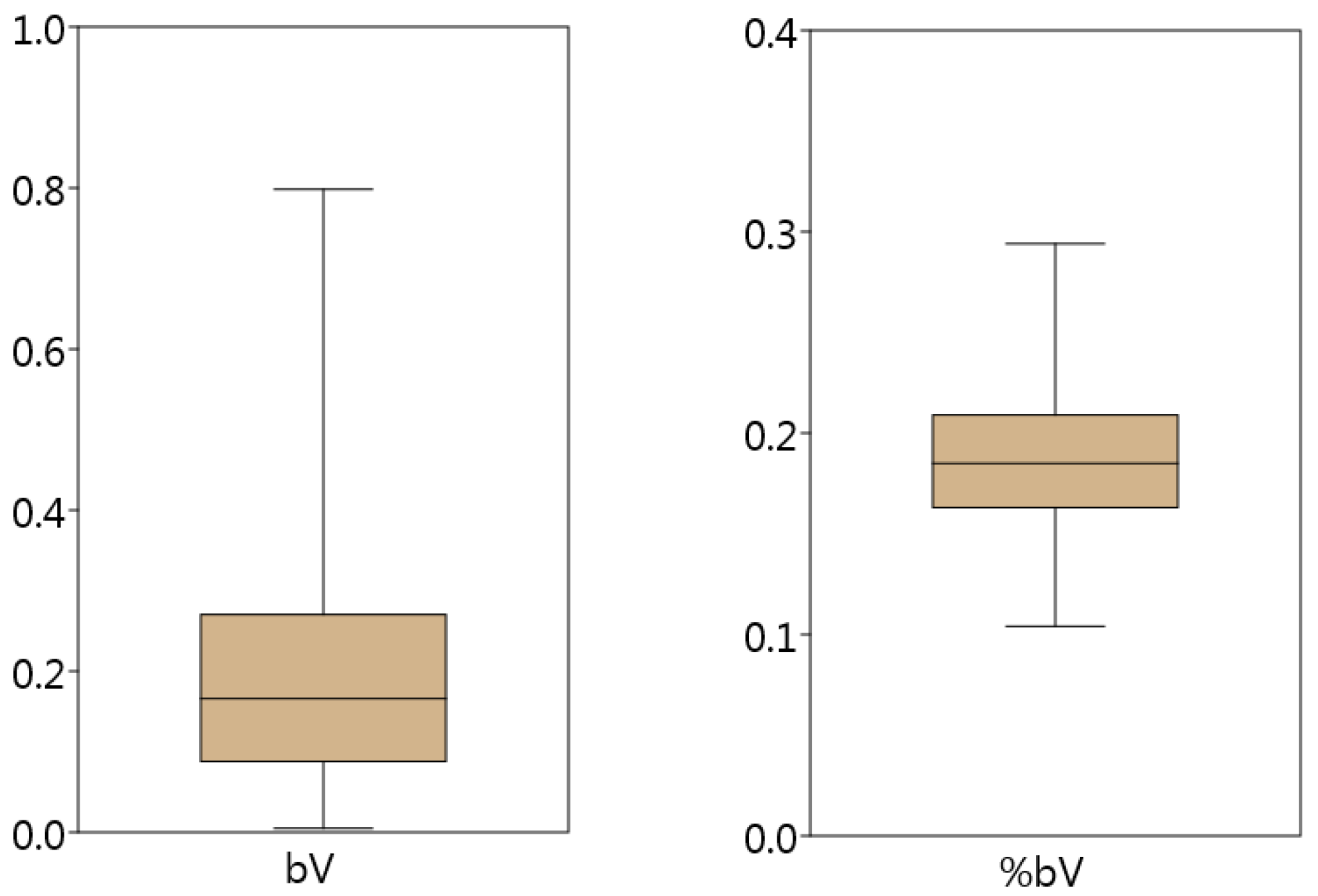
Bark volume of the analyzed larches ranged from 0.0048 to 0.7984 m³, with mean value amounting to 0.1985 ± 0.006 m³. Its distribution is characterized by strong positive asymmetry as skewness equals to 1.29 (Figure 1). Coefficient of variation for that attribute was high end reached 75.5%. In turn, bark volume fraction was not so diversified as its coefficient of variation amounted to 17.7%. Observed values varied from 0.104 to 0.294, with mean amounting to 0.188 ± 0.001. They were rather symmetrically distributed, for skewness reached 0.39 (Figure 1). These values are a little bit lower than those reported for larch in Europe [6].

Both bark volume and bark volume fraction varied significantly with regard to the analyzed location, site type, and age class (p < 0.001). The highest bV was observed for Rogów and Kolbudy (0.2891 ± 0.019 m³ and 0.2662 ± 0.016 m³, respectively), while the lowest for Dobrzany (0.1528 ± 0.011 m³). The more fertile site, the more bark larches have–bV for eutrophic sites equaled to 0.2238 ± 0.008 m³, while for oligotrophic–0.1364 ± 0.012 m³. Additionally, older have more bark than younger ones (0.3119 ± 0.015 m³ (V age class) vs. 0.083 ± 0.006 m³ (II age class)). For %bV, the highest values were noted in Rogów (0.236 ± 0.026), while the lowest in Kolbudy (0.168 ± 0.02). The least fertile site is characterized with higher values than the other sites (0.200 ± 0.003 vs. 0.182 ± 0.003 and 0.188 ± 0.002). In turn, the oldest trees had lower %bV than the other age classes (0.176 ± 0.003), while the highest values were noted for IV age class (0.192 ± 0.003). Observed relationships confirm previous findings about dependence of bark parameters on various factors [5,6,9].

3.2. Relationships between Bark Parameters and Dendrometric Attributes

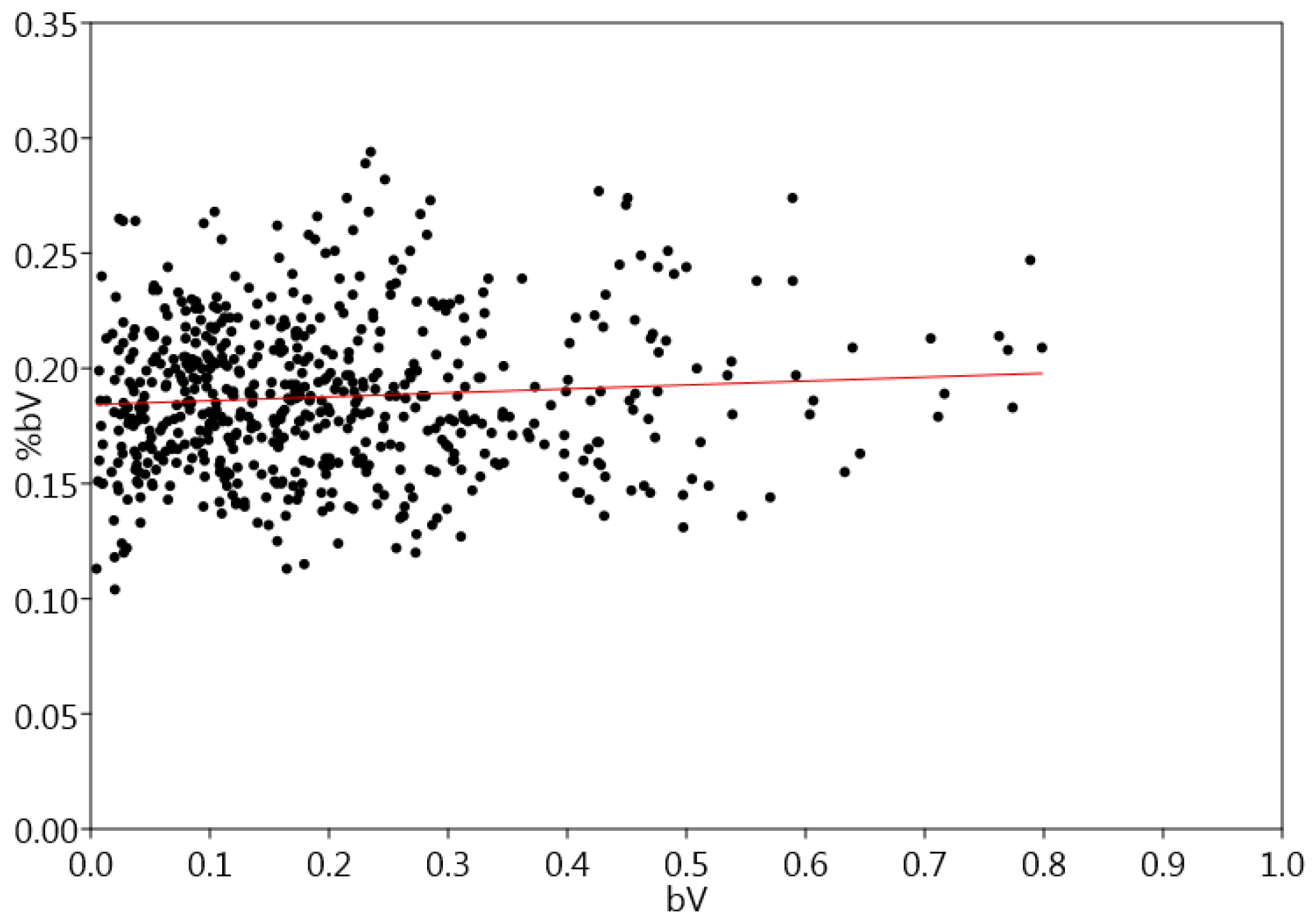
Bark volume was significantly and strongly correlated with d (r = 0.939, p < 0.001), h (r = 0.781, p < 0.001) and V (r = 0.956, p < 0.001). In turn, for bark volume fraction, we observed weak but significant negative relationship with d (r = −0.106, p < 0.001), h (r = −0.121, p =0.003), and V (r = −0.164, p < 0.001). The analyzed features were insignificantly correlated one to the other (r = 0.077, p = 0.060) (Figure 2). Similar relationships are reported for many other species in Latvia [5] or Mexico [6].

3.3. Models for Bark Parameters Estimation

For both investigated bark parameters, the lowest AIC values in the case of each independent variable (d, h, and V) were found for linear (Equation (1)) and Michaelis–Menten (Equation (4)) models. Both these equations showed similar performance for bV as well as for %bV. For bark volume, the lowest R² and RMSE values characterized models using height as the independent value, while the highest ones were observed for equations based on total tree volume (

Table 1. Goodness-of-fit measures for the best models for estimation of the bark volume (bV) or bark volume fraction (%bV) based on tree’s breast height diameter (d), height (h), or total volume (V).

			bV			%bV
Equation		d	h	V	d	h	V
#1	R2	0.880	0.631	0.912	0.008	0.007	0.022
	RMSE	0.0515	0.0905	0.0442	0.0328	0.0328	0.0326
#4	R2	0.878	0.669	0.915	0.000	0.001	0.001
	RMSE	0.0521	0.0870	0.0435	0.0329	0.0329	0.0329

). Such relationship only partially confirms previous findings as height turns to perform weaker as a bark volume descriptor than reported by other authors [5,6].

The goodness-of fit measures obtained for the validation dataset proved the good performance of the best models chosen based on AIC for bark volume prediction in the case of d and V as independent variables (

Table 2. Goodness-of-fit measures for the validation of the chosen models for estimation of the bark volume (bV) based on the tree’s breast height diameter (d), height (h), or total volume (V) and characteristics of the residue distribution (p(norm)—assessment of the distribution normality with Shapiro–Wilk test, M–mean value, p(M = 0)–Wilcoxon test p-value).

Equation		d	h	V
(1)	R2	0.886	0.567	0.916
	RMSE	0.0511	0.0996	0.0440
	p(norm)	<0.001	<0.001	<0.001
	M	−0.001	0.008	0.004
	p(M = 0)	0.341	<0.001	0.042
(4)	R2	0.900	0.605	0.915
	RMSE	0.0478	0.0951	0.0441
	p(norm)	<0.001	<0.001	<0.001
	M	0.006	0.001	0.002
	p(M = 0)	0.001	0.041	0.070

). For height, R² and RMSE values were lower than ones calculated with the calibration dataset. Residues of the validated models were not normally-distributed and their means differed significantly from 0, indicating systematic bias (Table 2). As models developed for %bV showed poor relationship of this feature with d, h, and V, no validation was performed in that case.

We found significant effect of location on the residuals of the chosen best models for estimation of bark volume (

Table 3. Effect (p-value in Kruskal–Wallis test) of location, site type, and age class on residuals of the chosen models for estimation of the bark volume based on tree’s breast height diameter (d), height (h), or total volume (V).

Equation		Location	Site Type	Age Class
(1)	d	<0.001	0.613	0.236
	h	0.007	0.918	0.004
	V	<0.001	0.024	0.137
(4)	d	<0.001	0.363	<0.001
	h	0.005	0.649	0.768
	V	<0.001	0.046	0.232

), which indicates the necessity of elaboration of locally-based formulae. Site type influenced significantly the residuals of the models based on V as the independent variable, while age class affected the results of models based on the tree’s height.

4. Conclusions

Both analyzed bark parameters varied significantly with regard to location, site type, and age class. Bark volume is strongly and significantly dependent on the tree’s breast height diameter, height, and total volume. For bark volume fraction, this correlation is significant but very weak. The best results of bark volume estimation are achieved for the model with total tree volume as an independent variable. For the weak relationship with dendrometric parameters, modeling of bark volume fraction seems to be pointless and a constant ratio should be applied. Because of the strong effect of location, it is recommended to elaborate locally-based models for bark volume estimation.