Analysis of Dynamic Forest Structures Based on Hierarchical Features Extracted from Multi-Station LiDAR Scanning †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site and Data Collection
2.2. Data Method
2.2.1. Extract Tree Height and Diameters at Various Heights
2.2.2. Obtain the Volume of Each Tree
2.2.3. Analysis of Point Cloud Hierarchical Characteristics
2.3. Modeling and Verification
3. Results and Analysis
3.1. Verification of the Extraction with Stem Analysis
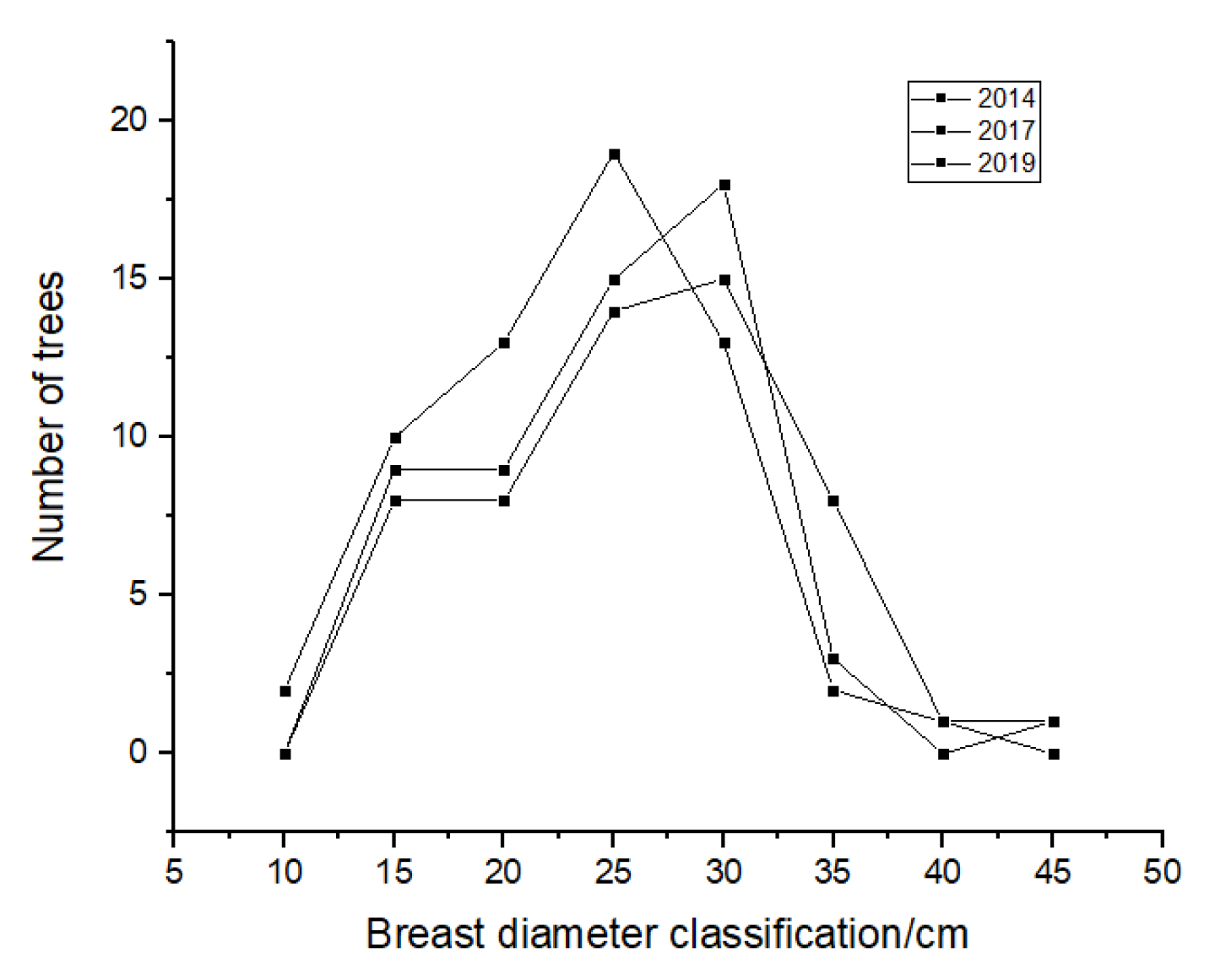
3.2. Features Extracted from the Point Cloud Data in Three Periods
3.3. Tree Volume Modeling Results
3.4. Dynamic Analysis of the Tree Structure from Features
3.4.1. Individual Tree Changes and the Growth Rate
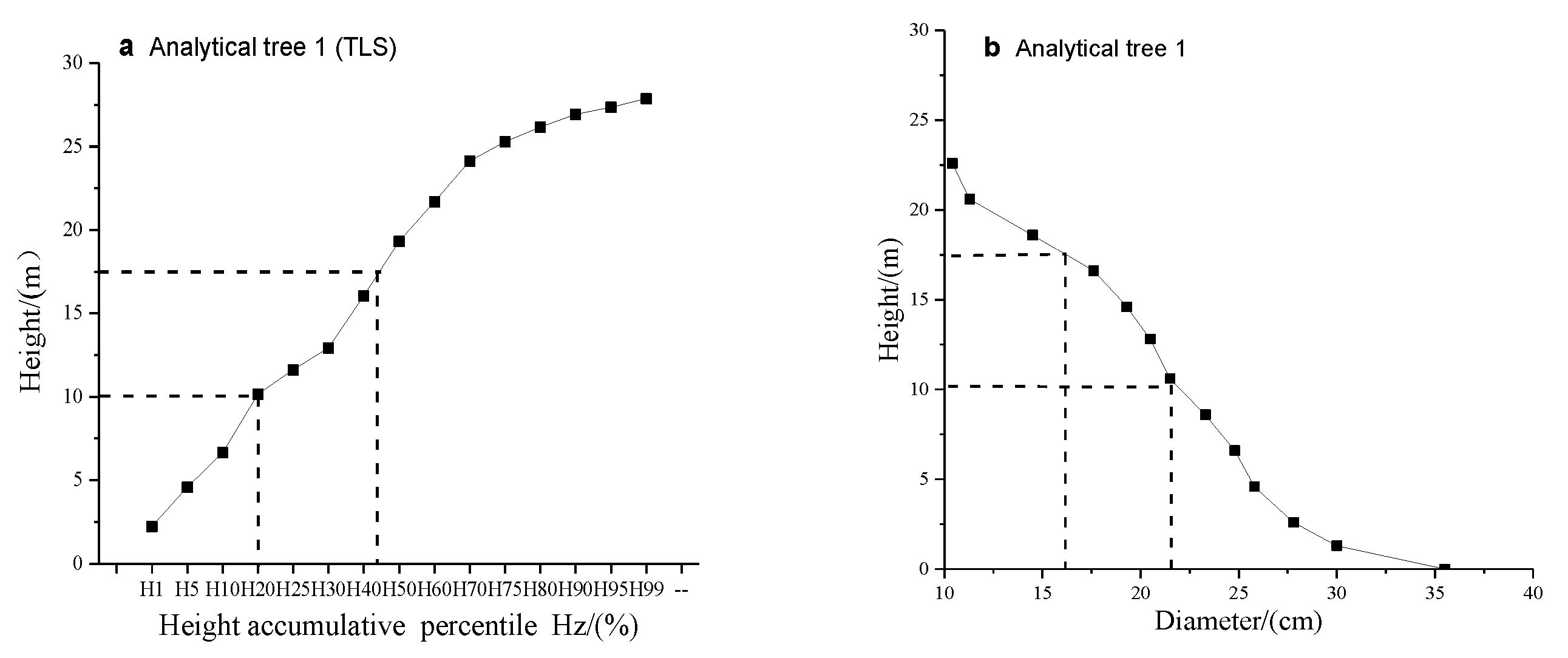
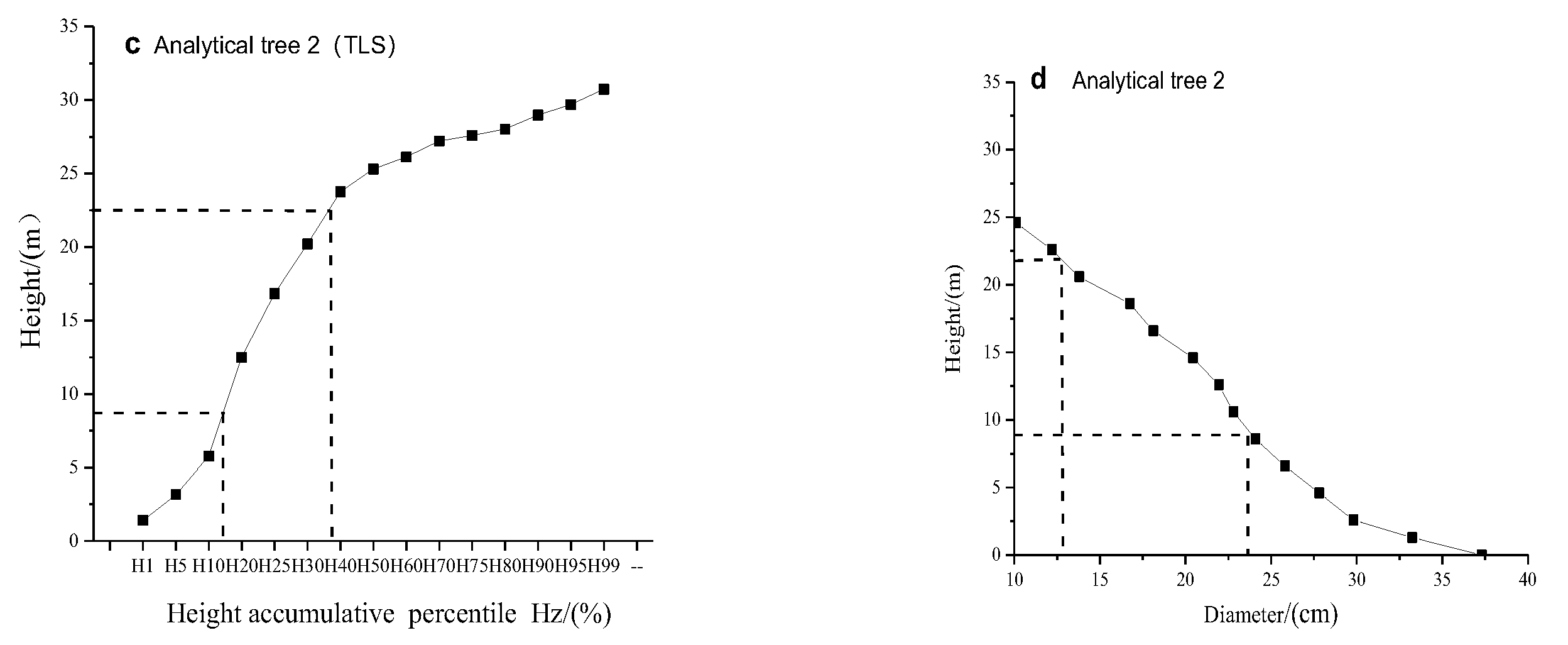
3.4.2. Height Cumulative Percentage Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hilker, T.; Wulder, M.A.; Coops, N.C. Update of forest inventory data with Lidar and high spatial resolution satellite imagery. Can. J. Remote Sens. 2014, 34, 5–12. [Google Scholar] [CrossRef]
- Simonse, M.; Aschoff, T.; Spiecker, H.; Michael, T. Automatic determination of forest inventory parameters using terrestrial laser scanning. In Proceedings of the Scandlaser Scientific Workshop on Airborne Laser Scanning of Forests; Sveriges Lantbruksuniversitet: Umeå, Sweden; 2003. (In Germany)
- Pfeifer, N. Automatic reconstruction of single trees from terrestrial laser scanner data. Int. Arch. Photogramm. Rem. Sens. 2004, 35, 114–119. [Google Scholar]
- Liang, X.L.; Kankare, V.; Hyyppä, J.; Wang, Y.S.; Kukko, A.; Haggrén, H.; Yu, X.W.; Kaartinen, H.; Jaakkola, A.; Guan, F.Y.; et al. Vastaranta, M. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Erikson, M.; Karin, V. Finding tree-stems in laser range images of young mixed stands to perform selective cleaning. In Proceedings of the Scandlaser Scientific Workshop on Airborne Laser Scanning of Forest; Sveriges Lantbruksuniversitet: Umeå, Sweden, 2003; pp. 244–250. (In Germany). [Google Scholar]
- Thies, M.; Spiecker, H. Evaluation and future Prospects of terrestrial laser scanning for standardized forest inventories. In Proceedings of the ISPRS working group VIII/2 Laser-Scanners for Forest and Landscape Assessment, Freiburg, Germany, 3–6 October 2004. (In Germany). [Google Scholar]
- Sun, Y.; Liang, X.L.; Liang, Z.Y.; Welham, C.; Li, W.Z. Deriving merchantable volume in poplar through a localized tapering function from non-destructive terrestrial laser scanning. Forests 2016, 7, 87–97. [Google Scholar] [CrossRef]
- Seidel, D.; Ehbrecht, M.; Puettmann, K. Assessing different components of three-dimensional forest structure with single-scan terrestrial laser scanning: A case study. For. Ecol. Manag. 2016, 381, 196–208. [Google Scholar] [CrossRef]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Grilli, E.; Menna, F.; Remondino, F. A review of point clouds segmentation and classification algorithms. In Proceedings of the ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Nafplio, Greece, 1–3 March 2017; pp. 339–344. [Google Scholar]
- Meng, X.Y. Forest Measuration; China Forestry Publishing House: Beijing, China, 2006. [Google Scholar]
- Li, Y.M.; Guo, Q.H.; Su, Y.J.; Tao, S.L.; Zhao, K.G.; Xu, G.C. Retrieving the gap fraction, element clumping index, and leaf area index of individual trees using single-scan data from a terrestrial laser scanner. ISPRS J. Photogramm. Remote Sens. 2017, 130, 308–316. [Google Scholar] [CrossRef]
- Srinivasans, S.; Popescu, S.C.; Eriksson, M.; Sheridan, R.D.; Ku, N.W. Multi-temporal terrestrial laser scanning for modeling tree biomass change. For. Ecol. Manag. 2014, 318, 304–317. [Google Scholar] [CrossRef]
- Maguya, A.; Tegel, K.; Junttila, V.; Tuomo, K.; Markus, K.; Janice, B.; Vesa, L.; Blanca, S. Moving voxel method for estimating canopy base height from airborne laser scanner data. Remote Sens. 2015, 7, 8950–8972. [Google Scholar] [CrossRef]
| Range | Mean Value | Standard Deviation | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Period | 2014 | 2018 | 2019 | 2014 | 2018 | 2019 | 2014 | 2018 | 2019 |
| DBH (cm) | 14.21–42.58 | 15.21–45.04 | 15.83–45.61 | 25.96 | 27.52 | 27.87 | 5.95 | 6.49 | 7.66 |
| Tree Height (m) | 17.11–32.40 | 17.53–34.32 | 17.67–35.00 | 28.3 | 29.73 | 30.12 | 3.52 | 3.93 | 4.08 |
| Volume (m3) | 0.13–1.75 | 0.14–1.96 | 0.15–1.98 | 0.69 | 0.77 | 0.8 | 0.36 | 0.4 | 0.44 |
| H75 | 11.98–29.72 | 12.59–30.79 | 9.22–22.02 | 24.51 | 23.49 | 15.29 | 11.45 | 12.1 | 3.02 |
| H55 | 18.96–26.84 | 7.75–27.99 | 7.22–17.07 | 20.51 | 18.53 | 10.47 | 7.76 | 7.51 | 5.32 |
| H25 | 14.18–20.13 | 4.98–19.57 | 2.92–8.96 | 11.443 | 9.41 | 5.55 | 3.56 | 2.93 | 10.08 |
| Hmean | 1.84–26.64 | 4.09–28.70 | 2.71–26.33 | 15.65 | 16.61 | 10.93 | 8.88 | 9.24 | 12.73 |
| Serial No. | Time | Parameter and Coefficient | R2 | F Value | RMSE/(m3) |
|---|---|---|---|---|---|
| 1 | 2014 | v = 0.106(DBH)2.035(H)1.352 | 0.974 | 122.419 | 0.059 |
| 2018 | v = 0.247(DBH)2.018(H)1.075 | 0.974 | 140.053 | 0.066 | |
| 2019 | v = 0.734(DBH)2.002(H)0.734 | 0.919 | 288.254 | 0.039 | |
| 2 | 2014 | v = −0.795 + 0.021(H25) + 4.847(DBH) | 0.951 | 570.604 | 0.083 |
| 2018 | v = −0.928 + 5.655(H25) + 0.016(DBH) | 0.957 | 661.538 | 0.086 | |
| 2019 | v = 0.062 + 0.092(H25) + 0.732(DBH) | 0.901 | 233.182 | 0.14 | |
| 3 | 2014 | v = −0.617 + 0.073(H50) − 0.002(H80) | 0.707 | 69.961 | 0.199 |
| 2018 | v = −0.699 + 0.051(H50) + 0.025(H80) | 0.712 | 72.799 | 0.219 | |
| 2019 | v = 0.494 + 0.011(H75) + 0.008(H85) | 0.632 | 28.642 | 0.274 | |
| 4 | 2014 | v = −0.747 + 0.128(H75) − 0.062(H80) | 0.612 | 45.69 | 0.229 |
| 2018 | v = −0.872 + 0.618(H75) + 0.009(H80) | 0.642 | 52.983 | 0.244 | |
| 2019 | v = −1.147 − 0.034(H50) + 0.156(H80) | 0.638 | 29.393 | 0.272 |
| Diameter Grade/(cm) | 2014 | 2018 | 2019 | Model 2 | TLS Measurement | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Number of Diameter Grade | Model 2 Prediction/(m3) | Number of Diameter Grade | Model 2 Prediction/(m3) | Number of Diameter Grade | Model 2 Prediction/(m3) | Volume Change 2019–2018/(m3) | Model 2 Prediction/(m3) | Volume Change 2019–2018/(m3) | Model 2 Prediction/(m3) | |
| 10 | 2 | 0.32 | 0 | 0 | 0 | 0 | −0.32 | 0 | −0.29 | 0 |
| 15 | 10 | 2.76 | 9 | 2.06 | 8 | 1.92 | −0.70 | −0.11 | −0.44 | −0.12 |
| 20 | 13 | 7.36 | 9 | 5.81 | 8 | 5.35 | −1.55 | −0.46 | −2.41 | −0.78 |
| 25 | 19 | 15.28 | 15 | 13.59 | 14 | 12.78 | −1.69 | −0.81 | −2.03 | −0.49 |
| 30 | 13 | 15.34 | 18 | 21.47 | 15 | 22.67 | 6.13 | 1.2 | 6.97 | 1.53 |
| 35 | 2 | 3.61 | 3 | 6.34 | 8 | 8.11 | 2.73 | 1.77 | 2.88 | 1.3 |
| 40 | 1 | 1.14 | 0 | 0 | 1 | 1.6 | −1.14 | 1.6 | −1.75 | 1.65 |
| 45 | 0 | 0 | 1 | 1.4 | 1 | 1.73 | 1.4 | 0.33 | 1.96 | 0.31 |
| Growth Rate in Four Years | Average Growth Rate | |||||
|---|---|---|---|---|---|---|
| 2014–2018 | 2018–2019 | 2014–2019 | 2014–2018 | 2018–2019 | 2014–2019 | |
| DBH/(cm) | 1.57 | 0.34 | 1.91 | 0.39 | 0.34 | 0.38 |
| Tree height/(m) | 1.43 | 0.39 | 1.82 | 0.36 | 0.39 | 0.36 |
| Volume/(m3) | 0.08 | 0.03 | 0.11 | 0.02 | 0.03 | 0.02 |
| 2014 | 2017 | 2019 | |
|---|---|---|---|
| −6.67 | −4.03 | −5.76 | |
| −10.65 | −2.75 | −2.70 | |
| 25.70 | 11.93 | 11.83 | |
| −16.51 | −7.71 | −2.12 | |
| −6.05 | −5.76 | −2.26 | |
| −3.74 | −4.42 | −0.75 | |
| −3.00 | −3.90 | −1.23 | |
| −2.04 | −1.04 | 0.64 | |
| −3.52 | −5.28 | −10.01 | |
| −0.12 | −0.36 | 1.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Gong, Y.; Sun, Y.; Jiang, J.; Zhang, Y.; Wen, X. Analysis of Dynamic Forest Structures Based on Hierarchical Features Extracted from Multi-Station LiDAR Scanning. Environ. Sci. Proc. 2021, 3, 21. https://doi.org/10.3390/IECF2020-07871
Lin X, Gong Y, Sun Y, Jiang J, Zhang Y, Wen X. Analysis of Dynamic Forest Structures Based on Hierarchical Features Extracted from Multi-Station LiDAR Scanning. Environmental Sciences Proceedings. 2021; 3(1):21. https://doi.org/10.3390/IECF2020-07871
Chicago/Turabian StyleLin, Xiuyun, Yulin Gong, Yuan Sun, Jiawen Jiang, Yanli Zhang, and Xiaorong Wen. 2021. "Analysis of Dynamic Forest Structures Based on Hierarchical Features Extracted from Multi-Station LiDAR Scanning" Environmental Sciences Proceedings 3, no. 1: 21. https://doi.org/10.3390/IECF2020-07871
APA StyleLin, X., Gong, Y., Sun, Y., Jiang, J., Zhang, Y., & Wen, X. (2021). Analysis of Dynamic Forest Structures Based on Hierarchical Features Extracted from Multi-Station LiDAR Scanning. Environmental Sciences Proceedings, 3(1), 21. https://doi.org/10.3390/IECF2020-07871






