Forest Management Criteria for Manilkara huberi (Ducke) A. Chev. (Sapotaceae) in Upland Forests of Central Amazon Based on Dendrochronological Study ^†

Abstract

This work used the Growth-Oriented Logging model to determine species-specific forest management criteria according to the growth model. The objective of this work was to define specific forest management criteria for the species Manilkara huberi (Ducke) A. Chev., using a Dendrochronology study by high frequency densitometry. The study was carried out in a forest management area, in Central Amazonia. The studied species forms annual growth rings depending on the seasonal rainfall. The annual growth rings were defined by high frequency densitometry, measuring the density variations in the wood, from the marrow to the bark. With the time series of the annual growth ring thickness obtained, it was possible to determine the forest management criteria for the studied species. The minimum logging diameter (MLD) obtained was approximately 63.4 cm, and its cutting cycles were estimated at 47 years, with an age of 297 ± 13.8 years. The estimated volume, equivalent to MLD, is 6.97 m³. With the study of Dendrochronology, it was possible to define the criteria for the specific forest management of the studied species, making it possible to apply this technique to tropical species with the same characteristics.

1. Introduction

The increase in human population in developing countries, global climate change, and the conservation of tropical forests has become one of the most important ecological challenges of our time.

The researches related to the sustainable forest management of natural forests, particularly tropical forests, have been seeking to make available more appropriate techniques and protocols that satisfy the demands coming from producers and society, indicating that the treatments, for the management of tropical species, should be directed by species, environment or region, according to the rhythm of growth and recovery potential for new cutting cycles. The information needed to evaluate the rate of growth is currently from monitoring of permanent plots, a method that demands long term and many resources to present its results [1].

The Brazilian legislation establishes technical parameters to be adopted in the elaboration, presentation, technical evaluation, and execution of a Sustainable Forest Management Plan with timber purposes, to native forests and their forms of succession in the Amazon biome.

According to this legislation is established the minimum logging diameter (MLD), which is 50 cm for all species, for which there is not yet a specific MLD. The determination of a MLD for a species must obey to a substantiated technical study [2].

Several studies have presented results that demonstrate the relationship of seasonal variation in rainfall with the growth rate of trees of tropical forest species [3,4,5,6,7,8]. Studies for analysis of growth rings in tropical regions have existed for more than one hundred years, and many species of trees in these regions have been proven to have annual growth rings [9,10]. The growth rhythm is usually induced by short periods of drought or prolonged periods of flooding, being the influence of the factor related to the photo-period questionable [9]. In addition, many dendrochronological studies indicate the influence of sea surface temperature anomalies (TSM) on tree growth, such as El Niño Oscillation South (ENOS) which is the largest inter-annual variation of the planet’s climate [3,10,11,12,13,14,15,16,17,18,19,20].

In this sense, the analysis of is an important tool, because through dendrochronology techniques, such as high frequency densitometry, it is possible to obtain long-term time series where studies can analyze the growth in diameter and volume, of each tree species specifically, this being one of the most important aspects for the ecologically sustainable management of tropical forests, serving as a basis for determining the criteria for species-specific forest management.

The GOL (Growth-Oriented Logging) model presents a concept for the sustainable management of timber resources in tropical forests, initially proposed for the floodplain forests of the Amazon, which is based on the determination of minimum logging diameter (MLD) specific to each species, as well as the respective cutting cycles, this model can be translated as a growth-oriented management system. Based on the wood stocks and growth rates throughout life, the GOL concept was created to improve forest management in the Central Amazon floodplain [21]. The minimum logging diameter of lowland timber species can be varied from 47 to 70 cm and cutting cycles have been estimated at a range of 3 to 32 years. This proposed model represents an advance for tropical forestry because today the forest management models used in the Amazon treat all species equally, although the tropical species present different characteristics, not taking into account the differences in growth rates among timber species and apply only a diameter cutting limit and a cutting cycle to harvest tree species. This practice causes great damage since it is not efficient in the harvesting of species with different growth rates.

The Manilkara huberi (Ducke) A. species. Chev. (SAPOTACEAE) is typical of dryland rainforest, open or dense ombrophilous. It occurs in the Amazon Region, Guyana, Venezuela, Colombia, and Peru. In the Brazilian Amazon it occurs frequently in Acre, Amazonas, Pará, Roraima, Rondônia, northern Mato Grosso and northeastern Maranhão [22],[23].

Manilkara huberi (Ducke) A. Chev. shows growth layers, which are demarcated by three growth markers: by radial fiber flattening, by an axial parenchyma line with radially flattened cells, constituting the marginal parenchyma, and by the presence of small diameter vessels tangenting the growth layer [24].

Specifically in this study, with the time series of the annual growth rings thickness obtained by high frequency densitometry, it was possible to determine the MLD and logging cycle for Manilkara huberi (Ducke) A. Chev., thus being able to propose a more adequate management for this species.

2. Materials and Methods

2.1. Study Area

The study was developed in a Sustainable Forest Management area, in Central Amazonia, Brazil, delimited by coordinates 02°30′ S 59°00′ W and 03°00′ S and 58°30′ W.

2.2. Vegetation

The forest characterized in the study area can be classified as lowland tropical forest of the low plateau sub-region of the Amazon Basin, where such vegetation typology is characterized by a warm climate with high precipitation. The vegetation cover is formed by several strata, composed of herbaceous or woody plants, sub bushes, shrubs and at last arboreal individuals. These forests present some characteristic emerging species, such as Dinizia excelsa (angelim pedra) and Manilkara huberi (maçaranduba), reaching large diameters, between 1.5 and 2.0 m, and can reach heights above 60 m [25].

2.3. Sample Preparation and Measurement

In tropical tree species the intra-annual variations in density are used to identify limits of annual growth rings of tree species, where these limits are hardly visible to the naked eye [26,27].

The high frequency densitometry method was developed by the Institut für Waldwachstum—IWW (Institute for Forest Growth), Freiburg University, Germany, and is based on the dielectric properties of different wood tissues [19]. Some density measurements were made in subtropical species, to detect the limits of annual growth rings and to establish the profiles of the intra-annual variation of wood density [28].

Dendrochronology techniques were used to perform cross dating; the annual growth ring series of the different trees combined with a time series correlated to a master chronology [18]. The statistics for the annual growth rings, which describe the similarity of the individual curves to each other, were performed with TSAP (Time Series Analysis and Presentation, Rinntech, Heidelberg, Germany) [29].

The wood samples of Manilkara huberi (Ducke) A. Chev. were obtained from discs of the trunk, taken from the base of the logs, located above the influence zone of the tree base. A total of16 samples were collected. Then the discs were cut with a circular saw, receiving notches with a length of about one third of the radius, with the objective of minimizing radial cracks. After this, the samples were dried outdoors for about 4 (four) weeks in a well-ventilated environment. After this initial drying, drumsticks were removed from the discs, with dimensions from 10 to 12 cm wide, and 5 to 8 cm thick, preserving the pith, center of the disc, and the length that was equivalent to the sample radius. Before processing, the samples were mounted on glass plates using double-sided high grip tape. The glass plates were vacuum fixed, and the surface preparation was done with a milling machine equipped with an ultra-accurate diamond cutter [30].

The samples were measured by high frequency densitometry; an important tool of dendrochronology that identifies with significant precision the density variation between the initial and late wood, even if this variation is very subtle, as is the case in some tropical species [19].

The diameter growth of Manilkara huberi (Ducke) A. Chev. was measured through the increment rates measured in the wood samples, from the marrow to the bark, by high frequency densitometry, and were accumulated to form individual growth curves related to the diameter at breast height (DBH) measured [30]. The cumulative mean growth curve was described by the relation between tree age and diameter relative to that age [13,31,32]. The ages of the trees were determined by counting the annual growth rings and were related to the corresponding DBH from several individuals of a species, and the age-diameter ratio was adjusted by a sigmoidal function, with the diameter as an independent variable [21]:

$$DBH=\frac{a}{1+{\left(\frac{b}{age}\right)}^c}$$

The volume was obtained using the model proposed by Chave et al. (2005), for humid tropical forest:

$$V=0.0509\ast D^{2}H$$

• V: Volume
• D: Diameter
• H: Height.

The height used was estimated using the hypersometric equation, proposed by Schöngart (unpublished data):

$$H=a\ast \left(1-e^{-b\left(DBH\right)}\right)$$

$$H=46.87\ast \left(1-e^{-0.0216\left(DBH\right)}\right)$$

The cumulative volume growth (CGW_v) of a tree species was calculated for each age. Based on the accumulated volume growth in “t” years of life of the tree, it is possible to calculate the current annual volume increment (CAI_v), and the mean annual volume increment (MAI_v), for each age “t”. The data were obtained for each tree age through the following equations [21]:

$$CA{I}_V=CG{W}_V{}_{\left(t+1\right)}-CG{W}_V{}_{\left(t\right)}$$

$$MA{I}_V=\frac{CG{W}_V{}_{\left(t\right)}}{t}$$

The period between the maximum current annual increment and the maximum average annual increment point is defined as the preferential period for harvesting. The diameter at the age of the maximum annual increment is defined as the MLD, which originates from the age x diameter ratio specific to the species. The cutting cycle is estimated by the average time of passage through classes of 10 cm in diameter, until reaching the defined MLD. This period represents the average time, from which an individual must grow from one diameter class to the next class [21].

$$Cutting cycle=\frac{Ag{e}_{\left(\mathrm{MLD}\right)}}{\left(MLD\ast 0.1\right)}$$

3. Results and Discussion

The sampled trees presented 41.0 and 67.4 cm, for the smallest and largest diameters, respectively. The age of the investigated trees varied from 174 years for the youngest to 325 years for the oldest. The thickness of the annual growth rings varied from 1.02 to 3.72 mm and the average annual growth was 1.07 mm, as can be seen in

Table 1. Average, maximum, and minimum thickness data, in mm, with the respective age, diameter at breast height (DBH) (cm), and Height (m) for each sampled tree of the tree species Manilkara huberi (Ducke) A. Chev.

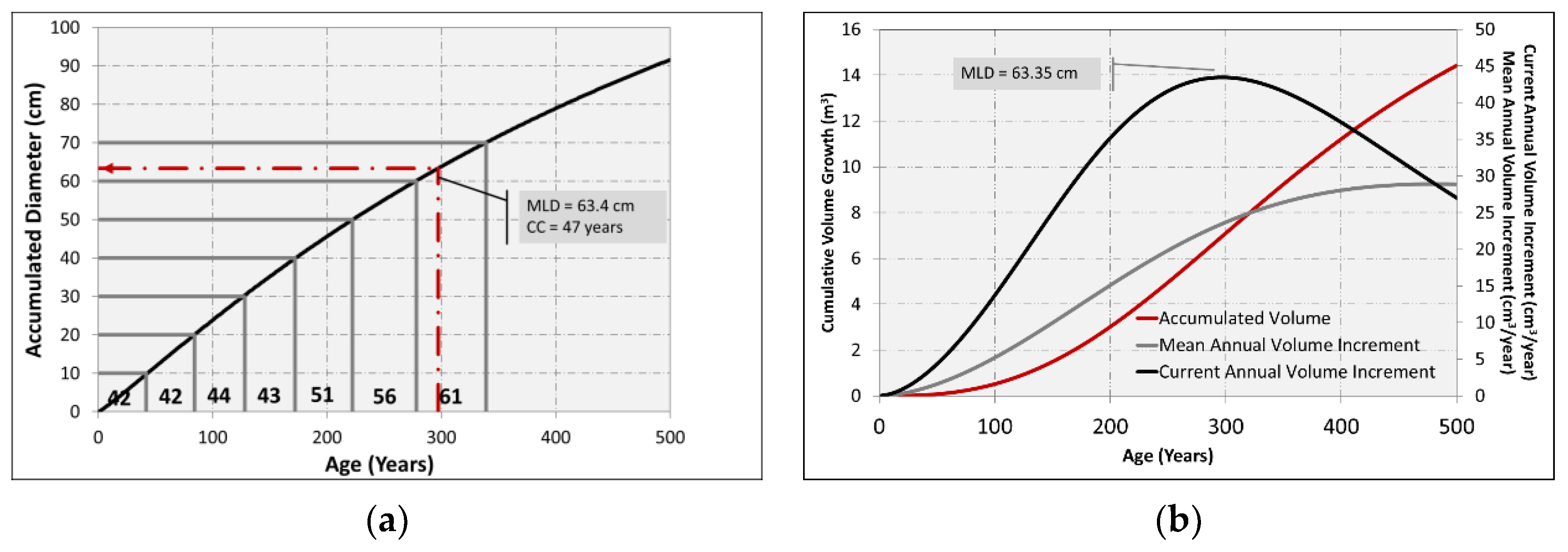
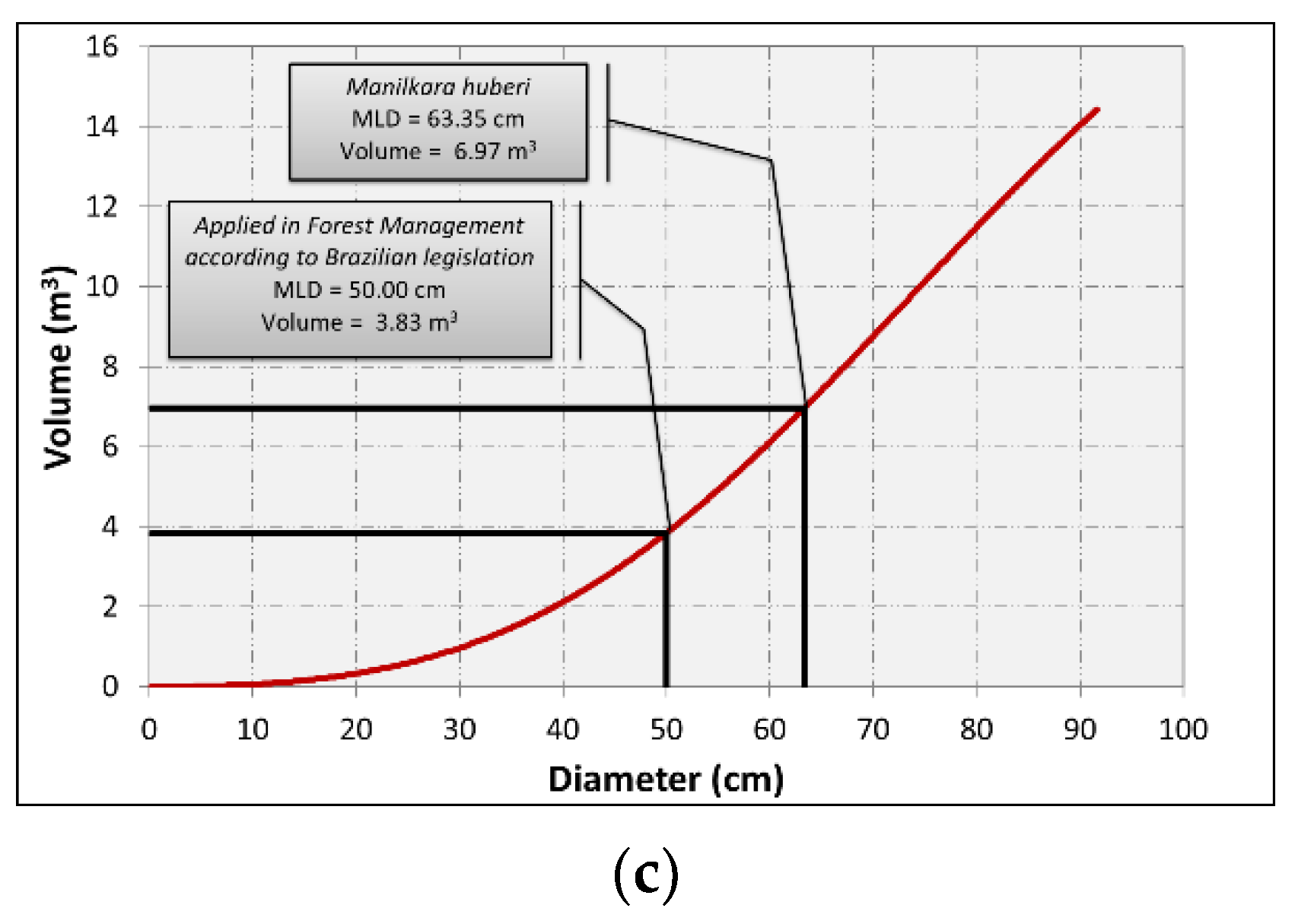
Order	Age (years)	Average Thickness (mm)	Maximum Thickness (mm)	Minimum Thickness (mm)	DBH (cm)	Height (m)
1	174	1.19	2.84	0.51	43.3	28.50
2	184	1.03	3.37	0.42	41.0	27.50
3	186	1.12	2.31	0.45	44.7	29.00
4	192	1.06	2.73	0.48	43.8	28.70
5	197	1.11	2.81	0.48	44.3	28.80
6	204	1.02	2.48	0.45	47.2	30.00
7	215	1.09	3.21	0.23	50.5	31.00
8	221	1.08	2.95	0.08	50.4	31.00
9	233	1.14	3.57	0.45	54.3	32.00
10	239	1.06	2.81	0.48	51.4	31.00
11	241	1.03	2.73	0.28	51.0	31.00
12	245	1.09	2.90	0.03	53.8	31.00
13	252	1.04	2.42	0.34	53.3	32.00
14	287	1.09	3.16	0.48	64.2	35.00
15	289	1.02	2.55	0.45	61.0	34.00
16	325	1.03	3.72	0.17	67.4	35.00

.

The equation adjusted for age and diameter relation, was adjusted for a nonlinear model and presented a correlation coefficient of 0.98. The proposed model was the sigmoidal, as seen in Figure 1a.

$$D=\frac{212.26}{1+{\left(\frac{640.11}{age}\right)}^{1.11}}$$

The model—adjusted to express the relation age and volume—is a non-linear model with a correlation coefficient of 0.98, as seen in Figure 1b.

$$V=\frac{22016.07}{1+{\left(\frac{394.52}{age}\right)}^{2.71}}$$

Applying the method for the model GOL [21], the MLD obtained was approximately 63.35 cm, and its cutting cycle was estimated at 47 years. This was the average time estimated for passage through classes of 10 cm in diameter, until reaching the MLD. This can be observed in Figure 2a,b. The estimated volume, equivalent to the minimum cutting diameter is 6.97 m³, as seen in Figure 2c.

Tropical forest management, in general, requires data for species-specific growth rates, tree ages, and regeneration processes to enable sustainable forest management [32,33]. The differences in the increment rates in diameter and volume and, consequently, cutting cycles between the commercial tree species and forest ecosystems clearly show that polycyclic systems—operating with only one cutting limit for diameter and cutting cycle for harvesting several wood species—may be compromising their efficiencies. In this sense, the GOL model represents an important advance towards reaching higher levels of sustainability in terms of forest management plans. Furthermore, this can be applied in tropical regions, particularly in the Amazon, due to the high biological diversity and complexity of relationships that are established in the ecosystem characteristics of these regions.

By analyzing the data for Manilkara huberi (Ducke) A. Chev., referring to the MLD and cutting cycle, it was verified that the applied diameter—uniformly, for all species—as well as the cutting cycle, practically standardized between 25 and 30 years. These are incompatible in the case of this species, making this form of management inefficient.

The polycyclic silvicultural systems, applied to tropical forests, can be evolved using the GOL model as they will apply appropriate management strategies for each species. Thus, this will ensure sustainability. The application of the high frequency densitometry methodology is, therefore, particularly important, since it can facilitate obtaining the necessary data for application of the GOL model. It almost impossible—without this method—to acquire sufficient long-term information to evaluate the MLD and the ideal cutting cycle for each species.

Growth models applied to floodplain species showed a significant relationship between tree age and diameter, and between DAP and tree height; requiring a period of 15 to 67 years for low density species to exceed 50 cm MLD, and between 106 and 151 years for high density species to reach this level [21].

In the case of Manilkara huberi (Ducke) A. Chev., the age at which this species exceeded the MLD of 50 cm was 223 years. At this diameter, the estimated volume was 3.83 m³, but the MLD—indicated by the GOL model—was 63.35 cm with an estimated volume of 6.97 m³. The species was estimated to have reached this diameter by the age of 297 years. By these management criteria for this species, the individual with the diameter of 50 cm would be preserved for the next harvest, where it would reach a volume of almost double that presented with this size.

For most floodplain species, the MLD—defined by the growth models—exceeded 50 cm, varying between 47 and 70 cm. The cutting cycles derived from the growth models were 3.3–13.9 years for low density species, and 21.5–32.1 years for high density species. The cutting cycle for Manilkara huberi (Ducke) A. Chev., obtained in this work was 47 years, which is compatible with its species characteristics, presenting high density (

Table 2. Comparison of forest management criteria generated through growth models for Manilkara huberi (Ducke) A species. Chev., in an upland forest, and low- and high-density tree species in the central Amazon floodplain, adapted from Schöngart (2008).

	Species	Wood Density (g/cm3)	MLD (cm)	Age at MLD (years)	Cutting Cycle (years)
Low-density	Ficus insipida Willd.	0.35	55	17.0 ± 3.6	3.3 (2.4–3.7)
	Pseudobombax munguba (Mart.) Dugand	0.23	47	39.5 ± 2.4	8.2 (7.9–8.9)
	Ilex inundata Poepp. ex Reissek	0.38	59	61.0 ± 9.7	10.5 (8.7–12.0)
	Macrolobium acaciifolium (Benth.) Benth.	0.43	62	67.0 ± 5.6	10.5 (9.9–11.7)
	Albizia subdimidiata (Splitg.) Barneby & J.W. Grimes	0.57	49	53.5 ± 7.1	10.5 (9.5–12.4)
	Luehea cymulosa Spruce ex Benth.	0.39	61	68.5 ± 11.7	11.0 (9.3–13.1)
	Sloanea terniflor (DC.) Standl.	0.57	58	82.0 ± 9.1	13.9 (12.6–15.7)
High-density	Pouteria elegans (A. DC.) Baehni	0.65	54	120.0 ± 21.8	21.5 (18.2–26.3)
	Chrysophyllum argenteum Jacq.	0.73	58	144.0 ± 22.4	24.1 (21.0–28.7)
	Eschweilera albiflora (DC.) Miers	0.83	53	164.5 ± 44.6	30.9 (22.6–39.5)
	Tabebuia barbata (E. Mey.) Sandwith	0.87	54	168.5 ± 19.8	30.6 (27.5–34.9)
	Piranhea trifoliata Baill.	0.94	70	227 ± 23.5	32.1 (29.1–35.8)
	Manilkara huberi (Ducke) A. Chev.	0.83	63	297.0 ± 13.8	46.8 (44.7–49.1)

).

It is important to note, that although the MLD was much higher than that commonly applied in current forest management plans, the estimated volume for the respective MLD of the species Manilkara huberi (Ducke) A. Chev. is almost double that estimated for the diameter of 50 cm.

The period between the maximum current annual increment and the maximum average annual increment point is the preferred period for harvest. The diameter at the age of maximum current annual increment, is defined as the minimum logging diameter, which originates from the relationship between the age and specific diameter of the species. Therefore, the harvests before the point of the maximum current annual increment configure an inefficient use of the growth potential of an arboreal species because the trees of this species for a MLD of 50 cm, have not yet reached their ideal growth phase.

4. Conclusions

Using the high-frequency densitometry method, it was possible to obtain dendrometric data for the Manilkara huberi (Ducke) A. Chev. species, permitting the establishment of a growth model through the GOL method. This allowed for the determination of the minimum logging diameter and cutting cycle specific to this species, while also showing that this method can be applied not only to floodplain forest species, but also to other tropical, upland species that have the same characteristics of this species.

In this sense, this model represents an important advance in relation to the sustainability of forest management plans, applied in tropical regions, particularly in the Amazon, due to its high biological diversity and complexity of the relationships established in the characteristic ecosystems of this region.

The management criteria found for the species Manilkara huberi (Ducke) A. Chev., specifically the minimum cutting diameter and cutting cycle, are above that established by Brazilian legislation, which guides the practice of forest management in the Amazon. This demonstrates that the polycyclic systems established in the region with a generic cutting diameter and a single cutting cycle for all species, do not guarantee the maintenance of wood stocks in the forest. This is because they do not consider the real potential for the growth of the species. Therefore, the foundations on which the current forest management sustainability practices are applied, are fragile.

Dendrochronology has proved to be an especially useful tool in the application of arboreal growth models and it can contribute to the development of forest management strategies that support the greater sustainability of natural resources.

However, more in-depth studies should be carried out for other tree species in the Amazon region, using the technique of dendrochronology by high frequency densitometry, to enable a broader knowledge about the dynamics, management and consequently the sustainable use of the forest.