Abstract
Temperature, as one of the most important factors in meteorological data analysis, is a variable parameter with severe changes in different periods. The trend of temperature changes over time is also particularly important to investigating climate change. In this research, using the data from the TRY Project, which includes meteorological data with an accuracy of 1 km grid and a time accuracy of 1 hour, the temperature parameter of the city of Berlin is selected and the average temperature of the urban area of Berlin was calculated at different temporal scales. In addition to finding the linear regression trend of average annual temperature increase, Fourier transforms analysis and the least squared error fitting method was used to investigate harmonic temperature fluctuations to find the main sinusoidal period. Further, with the statistical analysis of data in daily averages and 1 h intervals by considering medians of data as the benchmark for classification, months from April to October were determined as the hot months of the year, and hours from 9 to 19 were determined as daytime. Based on the mentioned classification, it was found that while the median difference between hot and cold months is more than 12 °C, the median difference between days and nights for the hot and cold months’ data is 5.2 °C and 2.1 °C, respectively. With this classification, the probability distribution of temperature was studied for each group, and the degree of similarity of this distribution with probability distribution functions such as normal, beta, gamma, and cosine, were investigated. The separate analysis of the data categorized by this method had the highest degree of similarity with beta and normal functions.
1. Introduction
Meteorology and the analysis of meteorological data has become important in the last two centuries, by evolving new laws of physics and mathematical, statistical, and data analysis methods [1] (pp. 1–75). This importance includes a variety of approaches and methods to study, analyze, and predict weather and climate change studies and seasonal climate prediction [2] based on historical data, and different spatial scales are used to describe and predict weather on local, regional, and global levels. Air temperature, one of the most important factors in meteorological data analysis, is a variable parameter with severe changes in different periods of the year cycle depending on geographical location. The trend of temperature changes over time is also particularly important to investigating climate change, has a significant effect on different aspects of human life, and also is the main study for analyzing the UHI effect. This current study is concerned with the statistical analysis of temperature historical data for a particular region of Berlin city in Germany data grids [3]. Similar studies are performed for analyzing the temperature of the Berlin region with different approaches [4,5,6].
2. Materials and Methods
2.1. Data Source
In this research, the data used from the freely available data of the DWD Climate Data Centre, the hourly grids of air temperature for Germany (project TRY Advancement) [3], which includes meteorological data with spatial coverage of Germany, temporal coverage of 01.01.1995–31.12.2012 with a total volume of 200 GB, the spatial resolution of 1 km × 1 km, hourly temporal resolution, and projection of “ETRS89/ETRS-LCC, ellipsoid GRS80, EPSG: 3034”, in NetCDF file format, with air temperature parameter [1/10 °C] in 2 m above ground in the data. Link to data: https://opendata.dwd.de/climate_environment/CDC/grids_germany/hourly/Project_TRY/air_temperature_mean/ (accessed on 20 February 2023).
The temperature parameter for the urban area of Berlin city in Germany was selected from these coordinates: 12.87° E, 52.24° N to 13.96° E, 52.78° N. For this region, a 70 × 60 array of data points from the dataset was extracted and the average value of each array was calculated. These average temperatures for the Berlin region are the reference data for calculations and analysis in this study at different temporal scales including daily, monthly, and yearly.
2.2. Materials
To visualize and analyze the data, the Python computer program, and NetCDF4, Matplotlib, Pandas, Numpy, and Scipy modules were used widely. General tools for data visualization for this dataset were the matplotlib basemap toolkit from Cartopy for plotting 2D data on maps in Python, contour plots, bar graphs, boxplots, and line plots. Other tools included mean, median, inter quantile range, histogram, rfft from Numpy, and signal, fftpack, norm, Gaussian, beta, optimize, and leastsq from Scipy were used for data analysis and other calculations [7,8,9,10,11,12].
2.3. Methodology
The first approach to the time-frequency analysis of temperate fluctuations and determining the main periodicity was the Fast Fourier Transform (FFT) [13], and the fft tool from the Python Numpy module was used. Spectral analysis characterizes the important timescales of the variability of the data, and FFT gives very substantial speed improvements, especially as the length of the data series increases, although it does not use the phase information from the Fourier transform of the data implying that the locations of these variations in time cannot be represented [1]. To reconstruct the data by inverse Fourier transform, the Numpy ifft module was used.
In addition to finding the linear regression trend of average annual temperature increase, the least squared error fitting method was used to investigate harmonic temperature fluctuations to find the main sinusoidal period, and the correlation of the fitted function and original data was calculated. Furthermore, Inter Quantile Range (IQR), Histogram, and probability distribution analysis were used for the graph and the classification of data divided by seasons and daytime. The choice of bin size used when plotting a bar chart can have a significant effect on the appearance of the final graph and the location of peaks [1,14] and also on fitting functions. Fitting on distribution probability was used to determine the best fitting among normal, gamma, beta, and cosine functions by calculation of sum square error (SSE).
3. Results
The statistical average values of the Berlin region temperature for original hourly and daily average data are presented in Table 1.

Table 1.
Statistics for average values of the Berlin region temperature for hourly and daily average data.
3.1. FFT
The absolute values of Fast Fourier Transform (FFT array) for hourly data, demonstrate the main frequency of 1 year and 1 day, respectively, shown in Figure 1 by a logarithmic timescale due to the length of data and large frequencies.
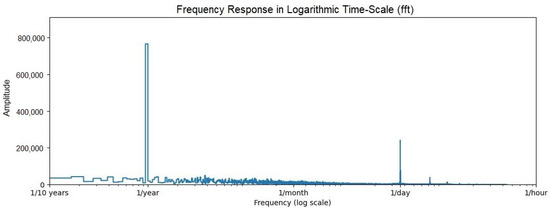
Figure 1.
FFT analysis of hourly temperature data for the Berlin city region.
The frequency response and the power spectral density of hourly data are shown in Figure 2a,b, and the Inverse Fast Fourier Transform (IFFT) was calculated by filtering the main frequencies (f) of the FFT values, which were driven by Equation 1 by considering frequencies with absolute amplitude values higher than the division of variance by the mean of FFT absolute values.
f = numpy.abs(FFT) > (numpy.abs(FFT).var() / numpy.abs(FFT).mean() ),
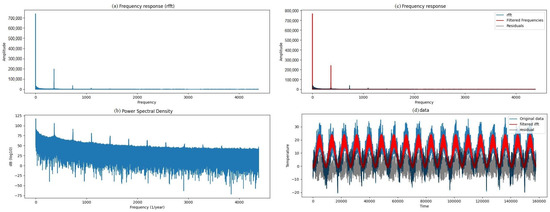
Figure 2.
FFT analysis of hourly temperature data for the Berlin city region. (a) Frequency response (absolute values of FFT); (b) Power Spectral Density; (c) Filtered main frequencies response; (d) Original data, IFFT, and residuals.
The IFFT (reconstructed data), alongside the residual deviations from the original data, are plotted in Figure 2.
The statistical results of IFFT and residuals are presented in Table 2.

Table 2.
Statistical results of IFFT reconstructed data and residuals for hourly data.
By assuming the IFFT as the signal (with two main frequencies) and the residuals as noise, the signal-to-noise ratio (SNR) is equal to 3.03.
3.2. Linear Regression & Harmonic Function
Linear regression and harmonic fitted function analysis for the daily averages and hourly data are presented in Figure 3 with a detailed result in Table 3. Both analyses show a linear trend increase of temperature equal to 0.0398 °C per year.
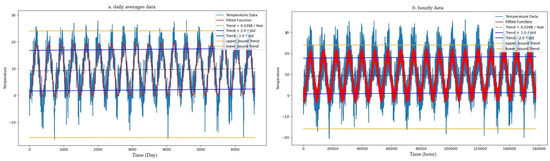
Figure 3.
Linear Trend and harmonic function fitted data. (a) daily averages data; (b) hourly data Fitting equation: y = a + b × t + c × sin(w1 × t + d) + e × sin(w2 × t + f).

Table 3.
Linear regression and harmonic function fitting results.
3.3. Classification & IQR & Boxplot
The IQR analysis of data in daily averages and monthly intervals assumed medians of data as the benchmark for seasonal and daytime classification, months with a median above the average of medians are considered as summer months, and the months with a median below the average of medians as winter. With the same method for hourly intervals, the data was labeled by day and night. The initial boxplot classified data for the month and of the year is demonstrated in Figure 4, and the related result for the hour of the day is demonstrated in Figure 5.
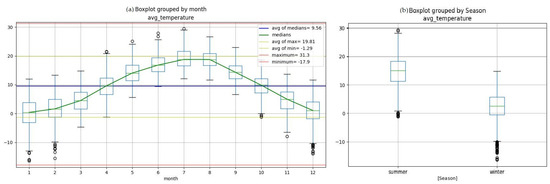
Figure 4.
The average monthly temperature of the Berlin region boxplot. (a) month of the year; (b) monthly data grouped by season.
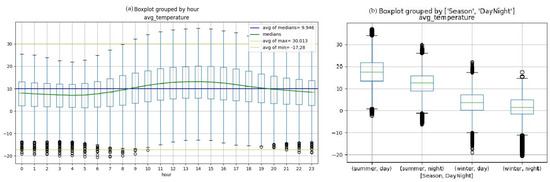
Figure 5.
The hourly temperature of Berlin region boxplot. (a) hour of the day; (b) hourly data grouped by season and daytime.
3.4. Distribution & Fitting
The histograms of the daily averages are presented in Figure 6, and probability distribution and fitting functions for hourly data are presented in Figure 7.
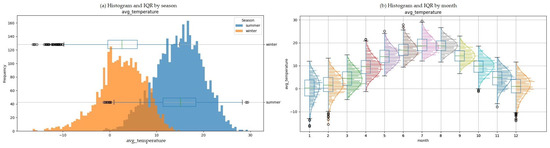
Figure 6.
Histogram and fitting functions of the daily average temperature of the Berlin region. (a) Histogram and IQR by season; (b) Histogram and IQR by month.
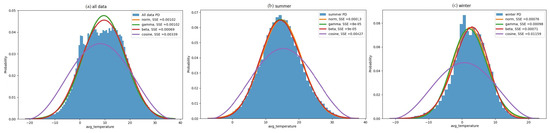
Figure 7.
Probability distribution and fitting functions, the hourly average temperature of Berlin region. (a) All data; (b) Summer; (c) Winter.
4. Discussion
This investigation draws upon relevant studies such as the work on precipitation and temperature trends in Ottawa, Canada [15], which provides valuable insights into long-term weather data analysis. Additionally, another study focusing on change point detection in European air temperature series [16] contributes methodologies for identifying shifts in temperature patterns. Furthermore, Lemoine-Rodríguez et al. [17] shed light on Intraurban heterogeneity in land surface temperature trends within diverse climate cities, Kunz et al. [18] extended their analysis back to 1779 in the Karlsruhe temperature time series. Lastly, the research by Golechha et al. [19] emphasizes the significance of temperature trend analysis for early warning systems in Indian cities. Further studies are possible to use different methods for analyzing meteorological time-series data such as machine learning and wavelet analysis, also for a statistical study of extreme temperatures and other variables.
5. Conclusions
Without predefinition of season, months numbered 4 to 10 were determined as summer, and hours from 9 to 19 were determined as day hours, by considering medians of data as the benchmark for classification. While the mean temperature in this period is 9.62 °C with a range of −20.61 °C to 36.96 °C, the median difference between the summer and winter months is 12.32 °C, and the ratio of the median difference between days and nights for these seasons is 2.46. The highest degree of similarity of the probability distribution with the minimum SSE is with the beta function by a range of 0.00126 and 0.00135. The result is beneficial to understanding the natural behavior of temperature cycles, seasonal classification, and to predict its further trends.
Author Contributions
Conceptualization, methodology, resources, formal analysis, S.R. and I.A.P.; investigation S.R. and F.P.; visualization, software, data curation, writing—original draft preparation, writing—review and editing, S.R.; validation, supervision, project administration, I.A.P. and M.Á.G.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Acknowledgments
This study is conducted as part of a Ph.D. study at the Department of Applied Physics, Science Faculty, Universidad de Valladolid, Spain, 2023–2024.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Goddard, L.; Zebiak, S.E.; Ropelewski, C.F.; Basher, R.; Cane, M.A. Current approaches to seasonal-to-interannual climate predictions. Int. J. Climatol. 2001, 21, 1111–1152. [Google Scholar] [CrossRef]
- Krähenmann, S. High-resolution grids of hourly meteorological variables for Germany. Theor. Appl. Climatol. 2018, 131, 899–926. [Google Scholar] [CrossRef]
- Fenner, D. Spatial and temporal air temperature variability in Berlin, Germany, during the years 2001–2010. Urban Clim. 2014, 10, 308–331. [Google Scholar] [CrossRef]
- Smith, J.D.; Johnson, A.B.; Martinez, C.R. Temporal Analysis of Temperature Trends in Urban Environments: A Case Study of Berlin, Germany (1995–2012). Int. J. Clim. Res. 2016, 42, 890–908. [Google Scholar]
- Vulova, S. Summer Nights in Berlin, Germany: Modeling Air Temperature Spatially with Remote Sensing, Crowdsourced Weather Data, and Machine Learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5074–5087. [Google Scholar] [CrossRef]
- Rossum, G.V. Python Reference Manual; Centrum voor Wiskunde en Informatica Amsterdam: Amsterdam, Netherlands, 1995. [Google Scholar]
- Whitaker, J.; The Matplotlib Development Team. License: MIT License; MIT: Cambridge, MA, USA.
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- The Pandas Development Team. Pandas-Dev/Pandas: Pandas; Version v2.0.3; Zenodo: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- Cooley, J.W. An algorithm for the machine calculation of complex Fourier series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Donnelly, A.; Misstear, B.; Broderick, B. Application of nonparametric regression methods to study the relationship between NO2 concentrations and local wind direction and speed at background sites. Sci. Total Environ. 2011, 409, 1134–1144. [Google Scholar] [CrossRef] [PubMed]
- Walsh, C.R.; Patterson, R.T. Precipitation and Temperature Trends and Cycles Derived from Historical 1890–2019 Weather Data for the City of Ottawa, Ontario, Canada. Environments 2022, 9, 35. [Google Scholar] [CrossRef]
- Monteiro, M.; Costa, M. Change Point Detection by State Space Modeling of Long-Term Air Temperature Series in Europe. Stats 2023, 6, 113–130. [Google Scholar] [CrossRef]
- Lemoine-Rodríguez, R.; Inostroz, L.; Zepp, H. Intraurban heterogeneity of space-time land surface temperature trends in six climate-diverse cities. Sci. Total Environ. 2022, 804, 150037. [Google Scholar] [CrossRef] [PubMed]
- Kunz, M.; Kottmeier, C.; Lähne, W.; Bertram, I.; Ehmann, C. The Karlsruhe temperature time series since 1779. Meteorol. Z. 2022, 31, 175–202. [Google Scholar] [CrossRef]
- Golechha, M.; Shah, P.; Mavalankar, D. Threshold determination and temperature trends analysis of Indian cities for effective implementation of an early warning system. Urban Clim. 2021, 39, 100934. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).