Abstract
The sensitivity of the ICON model is gauged towards the establishment of ICON-LEPS in place of the currently operational COSMO-LEPS. A broad list of the model’s parameters were tested over a domain covering the wider area of Greece and Italy in the year 2020. ICON model runs were performed on a 6.5 km horizontal grid and were enforced by the ECMWF operational forecast in 3 h intervals. The model’s sensitivities were applied to several surface meteorological fields via their areal averages in the last (132nd) lead time hour of the model runs, when they were expected to be at their climax. It was found that there was a considerable impact regarding the minimum and maximum values for many of the examined parameters in reference to their default values, providing a valuable insight into the understanding of the ICON model in reference to previous works regarding the COSMO model. In addition, due to the extensive forecast period, a seasonal dependence with respect to the considered meteorological fields was displayed. These features are expected to be of major importance in deciding the most important parameters for the application of perturbation techniques in the ensemble process and methodology.
1. Introduction
The performance of local Numerical Weather Prediction (NWP) models depends on several factors, many of them standard, like the applied numerical schemes, the considered domain, the choice of the grid mesh size and the integration time step. However, NWP model performance might also be considerably influenced by the many internal tunable parameters. A lot of them are interrelated, while their number increases as the model development progresses, especially towards the proper inclusion of complicated physical atmospheric processes. A rather crucial step towards tackling these features is to estimate the model sensitivity of these parameters [1,2,3,4,5]. In the present work, this estimation is performed for ICON, a state-of-the-art NWP model [6,7], for a large number of 24 parameters under the motivation to consider the most sensitive ones in various model performance optimization techniques [8,9].
This was the first attempt towards the development of a methodology regarding the realization of the important tasks of the COSMO Priority Project PROPHECY (PRObabilistic Prediction at High-resolution with EnhanCed perturbation strategY) [10] and is focused on January and July. These are expected to be the most diverse months from the seasonal perspective and in terms of the differences in parameter sensitivities. Another similar work regarding broader seasonal dependence and following the same methodology is also available [11].
2. Data and Methodology
The 24 considered parameters of the ICON model were examined for a domain covering the wider area of Greece and Italy (Figure 1). The list of parameters is presented in Table 1. They have been selected, ranked and updated by ICON experts [12] according to their estimated significance and in close reference to the COSMO model [1]. The parameters under evaluation cover almost all aspects regarding the tuning of a numerical weather prediction model, i.e., turbulence, convection, terra, subscale orography, grid-scale microphysics and cloud cover.
Figure 1.
Integration domain of the ICON Model, as in [11].

Table 1.
List of the 24 parameters (p01–p24) of the tested sensitivities based on their encoded names, interpretation and relevance (first column) as well as their test range (second column). The default values are denoted in bold characters, as is their recommended relevance, [H] and [M] standing for high and medium, respectively. It should be noted that for p01 and p02, the minimum and default values coincide, as in [11].
In order to display a typical seasonal performance of the model, 62 cases were investigated covering two month-long periods of January and July 2020. Forty-seven model runs were performed for each case, one referring to the default, and forty-six corresponding to the minimum and maximum parameter values (for two parameters the minimum values coincide with the default ones). The ICON model used was installed by the Israeli Meteorological Service (IMS) at the preceding high-performance computing facility (HPCF) of the European Center for Medium Range Forecasts (ECMWF) [13] and was enforced by the Integrated Forecasting System (IFS) operational forecast in 3 h intervals for 132 h.
Consequently, a total of approximately 3000 runs of 132 hr range forecasts were completed covering an equivalent period of 65 years of a single model run on a 6.5 km horizontal grid. The extensive forecast range addresses the purpose of this effort to be used within the framework of replacing the currently operational COSMO-LEPS (Local Ensemble Prediction System) with its successor ICON-LEPS [9,14].
3. Results
The considered meteorological fields are the maximum and minimum 2m temperatures (T2m_min, T2m_max) in the last 24 forecast hours as well as the dew point emperature (Td2m), total cloud cover (CLCT) and accumulated precipitation (TOTPREC) in the last (132nd) lead time hour of the model runs. The sensitivities are presented in Figure 2 via the differences in field area averages between the model runs associated with the minimum and maximum parameter values and the runs with default parameter values at the abovementioned times. Over these time slots, these differences are expected to be at their peak as they fall at the end of the forecast period. These sensitivities are displayed for the months of January and July of 2020 (blue and red colors, respectively) to highlight any clear seasonal dependencies.
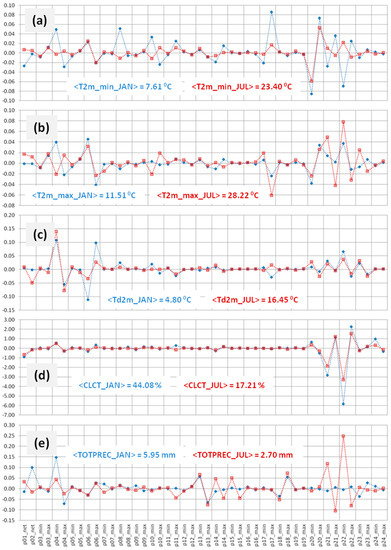
Figure 2.
Parameter differences in area-averaged sensitivity for the corresponding default values for the (a) minimum 2m temperature (T2m_min), (b) maximum 2m temperature (T2m_max), (c) dew point 2m temperature (Td2m), (d) total cloud cover (CLCT) and (e) accumulated precipitation (TOTPREC) for the 132nd hour of the model run (T2m_mim/max refer to the last 24 h of the run) for JANuary (blue) and JULy (red). The corresponding default average values are also displayed. The correspondence to the parameters of the horizontal axis is given in Table 1.
From Figure 2, it can be concluded that there is a noticeable as well as variable sensitivity regarding the parameters for both periods. However, although the sensitivities have different values, they follow relatively similar patterns. This is an important feature because in this way, it is quite straightforward to decide heuristically which are the most sensitive parameters regarding the meteorological fields under consideration. These parameters are summarized in Table 2.

Table 2.
List of area-averaged meteorological fields during the 132nd lead time and the corresponding parameters that display great sensitivity, as can be inferred from Figure 2. The most sensitive parameter for each field is emphasized with bold-faced characters.
4. Discussion
Winter versus summer seasonal behavior is noticeable for the January and July area averages with respect to the default parameter values displayed in Figure 2. As is expected, the temperature values for January are lower than these for July while the values for total cloudiness and precipitation are reversed and higher for the winter month.
From Table 2, it is possible to deduce the parameters that practically display any significant sensitivity, of which there are around sixteen out of the considered twenty-four. Although these parameters demand further investigation regarding the model response upon their change, it is important to note that the most sensitive parameters of the considered meteorological fields form a small subset of four, i.e., those of stability correction of turbulent length scale factor (p04), length scale factor for vertical diffusion of turbulent kinetic energy (p06), common scaling for minimum vertical diffusion for heat-moisture and momentum (p20), and liquid cloud diagnostic asymmetry factor (p22).
This parameter set may be extended consistently by including additional parameters of significant sensitivity from Table 2 and by assessing their magnitude from Figure 2 in a straightforward fashion. This aim is strengthened by the fact that these additional parameters might be common to most or even all considered meteorological fields. For example, box width for liquid cloud diagnostic (p21) can be added as it displays strong sensitivity to all the meteorological fields examined.
5. Conclusions
In this work, an effort towards a systematic ranking of model sensitivities was addressed. Although the ICON model was used as a prototype, the methodology can be applied and modified to any NWP model.
Such a procedure may play an important role in deciding which parameters to consider in model performance optimization techniques in support of the criteria that are generally based on the experience of model experts and/or extensive testing.
Author Contributions
Conceptualization and methodology, E.A.; software, A.S., P.K. and Y.L.; validation, E.A., A.S. and Y.L.; formal analysis, E.A.; investigation, I.C.; data curation, E.A. and A.S.; writing—original draft preparation, E.A.; writing—review and editing. All Authors; project administration, C.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The model output was stored at the ECMWF’s File Storage system (ECFS) in the domain of HNMS. Due to its exceptional data volume, some arrangements regarding data availability with E.A. might be necessary in connection with the standard policies of the ECMWF and HNMS.
Acknowledgments
The Hellenic National Meteorological Service (HNMS) is gratefully thanked for providing the computational resources necessary at the supercomputing System at the European Center of Medium Range Forecast (ECMWF).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Avgoustoglou, E.; Voudouri, A.; Carmona, I.; Bucchignani, E.; Levi, Y.; Bettems, J.-M. A Methodology towards the Hierarchy of COSMO Parameter Calibration Tests via the Domain Sensitivity over the Mediterranean Area. COSMO Tech. Rep. 2020. Available online: https://www.cosmo-model.org/content/model/cosmo/techReports/docs/techReport42.pdf (accessed on 15 May 2023).
- Baki, H.; Chinta, S.; Balaji, D.; Srinivasan, B. Determining the sensitive parameters of the Weather Research and Forecasting (WRF) model for the simulation of tropical cyclones in the Bay of Bengal using global sensitivity analysis and machine learning. Geosci. Model Dev. 2022, 15, 2133–2155. [Google Scholar] [CrossRef]
- Campos, T.B.; Sapucci, L.F.; Lima, W.; Silva Ferreira, D. Sensitivity of Numerical Weather Prediction to the Choice of Variable for Atmospheric Moisture Analysis into the Brazilian Global Model Data Assimilation System. Atmosphere 2018, 9, 123. [Google Scholar] [CrossRef]
- Kim, S.-M.; Kim, H.M. Effect of observation error variance adjustment on numerical weather prediction using forecast sensitivity to error covariance parameters. Tellus A 2018, 70, 1492839. [Google Scholar] [CrossRef]
- Merja, H.; Tölle, M.H.; Churiulin, E. Sensitivity of Convection-Permitting Regional Climate Simulations to Changes in Land Cover Input Data: Role of Land Surface Characteristics for Temperature and Climate Extremes. Front. Earth Sci. Sec. Atmos. Sci. 2021, 9, 722244. [Google Scholar] [CrossRef]
- Zängl, G.; Reinert, D.; Rípodas, P.; Baldauf, M. The ICON (ICOsahedral Non-hydrostatic) modelling framework of DWD and MPI-M: Description of the non-hydrostatic dynamical core. Q. J. R. Meteorol. Soc. 2015, 141, 563–579. [Google Scholar] [CrossRef]
- Prill, F.; Reinert, D.; Rieger, D.; Zängl, G. ICON Tutorial. Working with the ICON Model. Available online: https://www.dwd.de/DE/leistungen/nwv_icon_tutorial/pdf_einzelbaende/icon_tutorial2020.pdf?__blob=publicationFile&v=4 (accessed on 15 May 2023).
- Avgoustoglou, E.; Carmona, I.; Voudouri, A.; Levi, Y.; Will, A.; Bettems, J.M. Calibration of COSMO model in the Central-Eastern Mediterranean area adjusted over the domains of Greece and Israel. Atmos. Res. 2022, 279, 106362. [Google Scholar] [CrossRef]
- Tomasso, D.; Marsigli, C.; Montani, A.; Nerozzi, F.; Paccagnella, T. Calibration of Limited-Area Ensemble Precipitation Forecasts for Hydrological Predictions. Mon. Weather Rev. 2014, 142, 2176–2197. [Google Scholar] [CrossRef]
- COSMO Priority Project PROPHECY. Available online: http://www.cosmo-model.org/content/tasks/priorityProjects/prophecy/pp-prophecy.pdf (accessed on 15 May 2023).
- Avgoustoglou, E.; Shtivelman, A.; Khain, P.; Marsigli, C.; Levi, Y.; Cerenzia, I. On the Seasonal Sensitivity of ICON Model, COSMO Newsletter, 2023, 19–28. Available online: https://www.cosmo-model.org/content/model/documentation/newsLetters/newsLetter22/newsLetterNo22.pdf (accessed on 15 May 2023).
- Schlemmer, L.; Zängl, G.; Helmert, J.; Köhler, M.; Mironov, D.; Raschendorfer, M.; Reinert, D.; Rieger, D.; Schäfer, S.; Seifert, A. ICON Model Parameters Suitable for Model Tuning. Deutscher Wetterdienst (DWD), Offenbach. 2020. Available online: http://cosmomodel.org/content/support/icon/tuning/icon-tuning.pdf (accessed on 15 May 2023).
- Hawkins, M.; Isabella Weger, I. Supercomputing at ECMWF. ECMWF Newsletter. 2015, pp. 32–38. Available online: https://www.ecmwf.int/sites/default/files/elibrary/2015/17329-supercomputing-ecmwf.pdf (accessed on 15 May 2023).
- COSMO Limited-Area Ensemble Prediction System. Available online: https://www.cosmo-model.org/content/tasks/operational/cosmo/leps/default.htm (accessed on 15 May 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).